Rapid Exploration of Configuration Space with Diffusion Map-directed-Molecular Dynamics

Abstract

The gap between the timescale of interesting behavior in macromolecular systems and that which our computational resources can afford oftentimes limits Molecular Dynamics (MD) from understanding experimental results and predicting what is inaccessible in experiments. In this paper, we introduce a new sampling scheme, named Diffusion Map-directed-MD (DM-d-MD), to rapidly explore molecular configuration space. The method uses diffusion map to guide MD on the fly. DM-d-MD can be combined with other methods to reconstruct the equilibrium free energy, and here we used umbrella sampling as an example. We present results from two systems: alanine dipeptide and alanine-12. In both systems we gain tremendous speedup with respect to standard MD both in exploring the configuration space and reconstructing the equilibrium distribution. In particular, we obtain 3 orders of magnitude of speedup over standard MD in the exploration of the configurational space of alanine-12 at 300K with DM-d-MD. The method is reaction coordinate free and minimally dependent on a priori knowledge of the system. We expect wide applications of DM-d-MD to other macromolecular systems in which equilibrium sampling is not affordable by standard MD.

1 Introduction

Molecular Dynamics (MD) simulation serves as both a supplement to experiments and a predictive tool by revealing details inaccessible or invisible to current state-of-the-art experimental techniques. However, in most cases the relevant dynamics in complex biomolecular systems correspond to timescales longer than what can be sampled by using MD with standard computational resources, thus limiting our ability to characterize biologically important processes and to map out a system’s underlying free energy landscape. In particular, processes associated with rare events (such as the crossing of free energy barriers) may require an average simulation time much longer than what is affordable.

In the last two decades, a number of methods have been developed to enhance the sampling of rare events.¹ One class of such techniques biases the dynamics according to one or a few collective variables and then unbiases the results to obtain the equilibrium distribution as a function of the collective variables used. Such methods include umbrella sampling,² adiabatic free energy dynamics,³ temperature-accelerated MD,⁴ blue moon sampling,⁵ and metadynamics.⁶ However, oftentimes the definition of collective variables in complex macromolecular systems is per se a non trivial problem.⁷ The results obtained with these techniques depend on the collective variables used as input and the resulting free energy is as meaningful as the collective variable chosen.

Another class of methods are based on the sampling of transition paths between predefined states of the system. They require either the direct or indirect information on the system’s collective variables to define the states and/or initiate the sampling. For example the definition of reactant and product is needed for transition path sampling,⁸ an initial reactive trajectory for both transition path sampling and the string method,⁹ and interfaces between states for both transition interface sampling¹⁰ and forward flux sampling.¹¹

Other methods such as Markov state models¹² and directional milestoning¹³ necessitate an initial set of configurations spanning the important regions of configuration space. These can be obtained from either a high temperature simulation, or a biased simulation using collective variables, which again correlates the resulting free energy profile with the collective variables chosen in the simulation.

In this work we present a different approach for the sampling of rare events: Diffusion Map-directed MD (DM-d-MD). This method builds on our previously developed dimensionality reduction technique, Locally Scaled Diffusion Map (LSDMap),¹⁴ which extracts a set of global collective variables that characterizes the slowest motions of a macromolecular system. The LSDMap has been applied to a number of molecular systems,^7,14,15 as has the pre-existing Diffusion Map approach.^16–19 The global collective variables from LSDMap, the diffusion coordinates (DC), capture the slowest collective motions of the system. In contrast, the DM-d-MD algorithm uses local DCs, which correspond to the slowest local collective motions, to direct the MD. By periodically calculating DCs on the fly and restarting the dynamics from the boundary along the 1^stDC, the system is more likely to visit new regions of the configuration space instead of being trapped in local minimum. Therefore the method effectively speeds up the sampling of rare events. In this respect, DM-d-MD is similar in spirit to the free energy-guided sampling recently proposed by Zhou and Caflish;²⁰ the main difference in our method is the use of diffusion coordinates to guide the sampling.

As only local collective coordinates are needed and these can be computed on the fly, DM-d-MD does not rely on any global reaction coordinate as input. DM-d-MD can be used in both all-atom and coarse-grain MD simulations, and interfaced with any MD software or force field. As shown below, the method introduces a tremendous speedup (up to three orders of magnitude) in exploring the configuration space. Because of the bias introduced in the sampling, the direct output of DM-d-MD is not Boltzmann distributed. However, there are many techniques that allow the recovery of the Boltzmann distribution from non-equilibrium data covering the configuration space. For instance, DM-d-MD results could be used as input to methods such as transition path sampling, Markov state models, and directional milestoning. Here we reconstruct the equilibrium distribution by means of umbrella sampling performed directly in configuration space. This approach mantains the entire sampling procedure completely reaction-coordinate free. Although the umbrella sampling requires additional computation, the overall efficiency of the algorithm (including both the exploration and reconstruction phases) remain quite significant with respect to standard MD (below, we refer to “MD” as standard MD). The algorithms are described in the following section, and the applications to two test systems, alanine dipeptide and alanine-12, are presented in Section 3.

2 Methods

Simulations of alanine dipeptide were performed using GROMACS-4.5.4²¹ and the Amber03 forcefield, in vacuum.²² Stochastic dynamics were performed with time step of 1fs and an inverse friction constant of 2ps. Simulations of alanine-12 were performed using GROMACS-4.5.4 and the Amber96 forcefield²³ in vacuum, using stochastic dynamics with time step of 2fs and inverse friction constant of 2ps.

2.1 Diffusion Map and LSDMap

We recently developed LSDMap ¹⁴ as a method to extract the important global collective coordinates correlating with the slowest motions of macromolecular systems. LSDMap is based on the definition of the following kernel, which is related to the “ease” with which the system converts from configuration x_i to x_j:

$$K_{ij}=exp\left(-\frac{{\Vert {\mathit{x}}_i-{\mathit{x}}_j\Vert }^2}{2{\epsilon }_i{\epsilon }_j}\right),$$ (1)

where ||x_i − x_j|| is the root mean square deviation (RMSD) between the two configurations x_i and x_j, and ε_i is the “local scale” for x_i. The local scale corresponds to the radius in configuration space around x_i within which the underlying manifold can be approximated by a hyperplane tangent to the manifold, i.e. it is approximately linear. The eigenfunctions of a normalized version of the kernel serve as the diffusion coordinates (DCs). We refer the interested readers to papers by Coifman and Lafon^24,25 for the original mathematical details on diffusion map and our recent paper¹⁴ about the motivation and construction of a locally scaled version of diffusion map.

2.2 DM-d-MD

DM-d-MD is based on the idea that the 1^stDC characterizes the slowest motion of the system, and the fact that the rough free energy landscape associated to macromolecular systems often traps the dynamics in local minima. By periodically restarting the dynamics from the boundary along the 1^stDC (that is, the “frontier” of the explored region of the conformation space), the system is more likely to explore new regions rather than remain in the local minimum. In practice, we use the following iterative procedure:

1. Run a short MD simulation from the “frontier” configuration (or initial configuration for the first iteration).

2. Calculate the 1^stDC associated to the space explored during the short MD simulation.

3. Select the configuration with the largest value of the 1^stDC as the new frontier and restart a new short MD simulation.

Several remarks on the procedures are discussed below. In step 1 above, the time length of the MD simulation must be short enough to direct the dynamics as often as possible and make the procedure efficient, but also long enough to explore sufficiently the region of the landscape associated with a local minimum. That is, we want to direct the dynamics as often as possible but not so often that there is inadequate time for the system to relax inside small local minima. The minimum timescale satisfying this requirement can be chosen by considering the eigenvalues of the FP operator as a function of time (Figures S1 and S4): we expect the spectrum to change rapidly on very short timescale, and to become constant in time at the onset of a metastability, when a local minimum is sampled. Such spectra are shown in Figures S1 and S4 for alanine dipeptide and alanine-12, respectively.

More than one trajectory could be run in parallel starting from a frontier point in step 1 of the procedure, with the results combined as input to step 2. However, for the two systems considered here, we find that running one trajectory per iteration provides the maximum efficiency.

In step 2, we use a constant value for the local scales {ε_i} around all the sampled configurations x_i, to calculate the DCs (see Eq. 1). The reason for this choice is twofold: first, the number of points in the trajectory is not large enough to estimate a position-dependent local scale reliably (see¹⁴ for details); second, we do not expect the short trajectory to sample a large conformation change, that is, we can assume that the small region of the configuration space sampled by the short trajectory has uniform geometric properties and a constant local scale is appropriate. We observe that the boundary configuration along the 1^stDC–the new frontier point–is robust against different choices for the constant local scale.

In order to underline the importance of the guidance of the 1^stDC in the procedure, we have also combined the DM-d-MD framework with alternative approaches where frontier points are selected according to the largest value of different reaction coordinates. In particular, we have modified step 3 to use the first coordinate obtained by multidimensional scaling,²⁶ a random selection between the first two DCs, or the first nine DCs. As detailed in the Supporting Information, the original DM-d-MD scheme significantly outperforms schemes with alternative reaction coordinates in the extent of coverage of configuration space within the same computational time.

2.3 Umbrella sampling and reweighting

Umbrella sampling² is typically used to enhance the sampling along predetermined collective variables. Here we use a variant of the method that does not employ any such collective variables. We first collect all the frontier points visited during the DM-d-MD exploration, as described above (10,000 points for alanine dipeptide and 3.5 million points for alanine-12). The number of points that emerge from the DM-d-MD sampling for alanine-12 is more dense than needed for an adequate covering of the explored configuration space. Therefore we perform the following RMSD-clustering scheme to sub-sample the data. We randomly select a configuration from the data set as the first cluster center and assign all of the other points with an RMSD to that center less than a given cutoff to this first cluster. We repeat this procedure with the remaining points until every point has been assigned to a cluster.

The RMSD cut-offs for the clustering are chosen to be 1.9 Å for alanine-12 at 300K and 2.25 Å for alanine-12 at 400K. The values of these cut-offs are selected to yield a manageable number of clusters (namely, 10,530 at 300K and 13,161 at 400K). The clustering is not necessary for the alanine dipeptide system as the number of frontier points is already amenable to umbrella sampling. MD simulations are then initiated from each of the cluster center configurations, with an added harmonic bias of the form

$$V(s)=\frac{1}{2}{ks}^2,$$ (2)

where the spring constant k = 5000 kJ/mol/nm², and s is the RMSD to the starting configuration. The length of the simulation was selected to be 100ps for both systems, with data recorded every 1ps. The simulation output data is unbiased by means of the weighted histogram analysis method (WHAM, see reference²⁷ for details). In brief, the optimal estimate of the unbiased density ρ₀(x) at point x in configuration space can be obtained from the biased densities ${\rho }_i^{(b)}(\mathbf{x})$ observed during all the short trajectories {i} as

$${\rho }_0(\mathbf{x})=\frac{{\sum }_{i=1}^T{n}_i{\rho }_i^{(b)}(\mathbf{x})}{{\sum }_{j=1}^T{n}_j{e}^{-\beta (V_j(\mathbf{x})-f_j)}},$$ (3)

where V_i(x) is the biasing potential used in the i-th trajectory, which has n_i configurations, and T is the total number of trajectories. The biased distribution ${\rho }_i^{(b)}(x)$ observed in the i-th trajectory can be formally expressed as

$${\rho }_i^{(b)}(\mathbf{x})=\frac{1}{n_i}\sum _{k=1}^{n_i}\delta (\mathbf{x}-{\mathbf{x}}_{i,k}),$$ (4)

where x_i,k is the k-th configuration sampled in the i-th trajectory. The free energy of the k-th trajectory f_k can be obtained self-consistently from

$$\begin{array}{l}{e}^{-\beta f_k}=\int d\mathbf{x}{\rho }_0(\mathbf{x})e^{-\beta V_k(\mathbf{x})}\\ =\sum _{i=1}^T\sum _{l=1}^{n_i}\frac{e^{-\beta V_k({\mathbf{x}}_{i,l})}}{{\sum }_{j=1}^T{n}_j{e}^{-\beta (V_j({\mathbf{x}}_{i,l})-f_j)}}.\end{array}$$ (5)

That is, an initial set of free energies { $f_i^{(0)}$} (i.e. all zeros) is defined, new free energies can be estimated from the r.h.s. of Eq. 5 and the procedure is iterated until convergence. Finally the re-weighting factor w_i(x) for each configuration x in the umbrella sampling data set can be estimated as

$$w_i(\mathbf{x})=\frac{1}{{\sum }_{j=1}^T{n}_j{e}^{-\beta (V_j(x)-f_j)}}.$$ (6)

3 Results & Discussion

3.1 Alanine dipeptide

Alanine dipeptide is a standard test case for sampling methods as it is a small and well-studied system, and its dynamics contains processes at very different timescales. In particular, with the force field used here, two main processes are observed: the faster transition between the C₅ and C₇ minima, and the slower (by about three orders of magnitude) transition to the α_L minimum. The locations of these minima are shown in Figure 1. Since the C₅ ⇔ C₇ transition is rapid, here we focus the application of DM-d-MD to explore the transition to the α_L state. The C₅ and C₇ minima can be considered as an effective single minimum in comparison to the much higher barrier between these states and the α_L minimum.

Figure 1.

Top: Typical short trajectory of alanine dipeptide plotted as a function of the two dihedral angles and the first two DCs (inset). The configurations are colored according to the time they are visited. The initial point of the simulation is denoted by a red circle. The frontier point is denoted by a red cross. Bottom: Free energy of alanine dipeptide as a function of the dihedral angle ψ. Equilibrium MD results are shown in red; umbrella sampling with reweighting in blue; and umbrella sampling without reweighting in black.

The first step in applying DM-d-MD is the determination of an appropriate time length for the short MD simulations. As discussed above, the short trajectories should be longer than the local relaxation time (so that the dynamics cover a local minimum), but as short as possible to guide the dynamics efficiently. Ideally the diffusion map is calculated after the short trajectory has explored a local minimum, but has not been localized in the same region of the configuration space for too long.

To determine this optimal timescale, we first examine the evolution of a short swarm of trajectories initiated from a test configuration. One hundred short MD trajectories are simulated for alanine dipeptide and a diffusion map calculation is performed at regular time intervals on the set of 100 configurations at each time frame. The resulting diffusion map eigenvalues approximate those of the Fokker-Plank operator.²⁵ Each such eigenvalue corresponds to a collective motion of the system at that time frame, is related to the timescale of the collective motion, and is ordered slowest to fastest. By examining the eigenspectrum as a function of time, an example of which is shown in Figure S1, we can determine an approximate timescale where the first eigenvalue becomes constant, that is, a metastable timescale is reached. For this system, the first eigenvalue reaches a plateau at about 1ps. We expect the eigenspectrum to start changing again on much longer timescales, when different minima are explored. We use a conservative estimate of 10ps as the time length of the short MD simulations. Also, on this timescale, the local diffusion map calculation is computationally cheaper than the short MD simulation, and does not add a significant overhead to the overall DM-d-MD exploration.

At each iteration of the DM-d-MD procedure a 10-ps all-atom MD trajectory is run and a diffusion map calculation is performed on the configurations visited during this short trajectory. A typical trajectory is shown in the top panel of Figure 1. For this particular trajectory, the barrier between the C₅ and C₇ minima is crossed for the first time after 3ps, and both of these minima have been visited within 10ps. This is consistent with the results in Figure S1.

We define the “frontier” point of the region explored during the short simulation as the configuration with the largest 1^stDC, and we restart a new simulation from there. In Figure 1, the frontier point (denoted by a red cross) after the first iteration is located at the boundary of the C₇ minimum. By restarting the MD from this point (with velocities chosen from a Maxwell-Boltzmann distribution) the chances of escaping the C₅ – C₇ minimum and exploring the unknown configuration space are increased over standard MD. Indeed, after only five iterations of DM-d-MD, the α_L minimum is populated (Figure S2). This corresponds to 50ps in MD time (10ps for each iteration), a time dramatically shorter than the ~150ns required for a standard MD simulation to visit the α_L minimum. This three orders of magnitude improvement is an upper limit of the speedup for our algorithm for this particular system, because it does not include the time required for the diffusion map and the post-processing umbrella sampling to reconstruct the equilibrium distribution, which are discussed below.

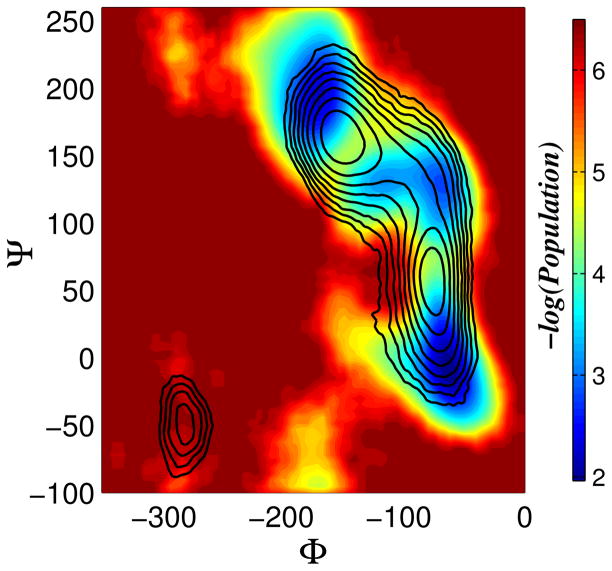
Figure 2 illustrates the distribution of frontier points collected during 10,000 DM-d-MD iterations and shows that most of the frontier points are located on the top of barriers, as expected. Trajectories initiated from frontier configurations have a greater chance of escaping a local minimum.

Figure 2.

The negative logarithm of the population of the frontier points collected during 10000 iterations of DM-d-MD on alanine dipeptide. The underlying black contours indicate the free energy obtained from an equilibrium MD simulation. As expected, the population of the frontier points is largest near transition regions.

The bias in the sampling introduced by DM-d-MD strongly perturbs the Boltzmann statistics that would be obtained by running MD over a long timescale. As stated above, to reconstruct such an equilibrium sampling, we perform umbrella sampling around the frontier points collected during the DM-d-MD iterations. No reaction coordinates are used in the umbrella sampling. The short trajectories are confined to explore the vicinity of a frontier point by means of a harmonic bias potential depending on the root mean square deviation (RMSD) to the chosen frontier configuration. The resulting umbrella sampling data are then reweighted by an extension of WHAM,²⁷ briefly discussed in the Materials and Methods section. Figure 1 shows the free energy after reweighting as a function of ψ. The reconstructed free energy profile is in perfect agreement with the control one obtained from equilibrium MD simulation almost everywhere. A slight disagreement is observed only on top of the barrier between the α_L and C₅ – C₇ minima. In this region, the sampling of regular MD is very poor, while the intensive sampling of DM-d-MD might actually yield a better estimate of the free energy.

The umbrella sampling and reconstruction phase is more computationally demanding than the DM-d-MD exploration phase itself, and limits the efficiency of the overall DM-d-MD plus reweighting method for alanine dipeptide to one order of magnitude over MD. However, as it is clear in the alanine-12 example discussed below, the cost of umbrella sampling does not increase with the height of the barrier, and the gain in efficiency with DM-d-MD becomes much more substantial for systems with higher barriers.

3.2 Alanine-12

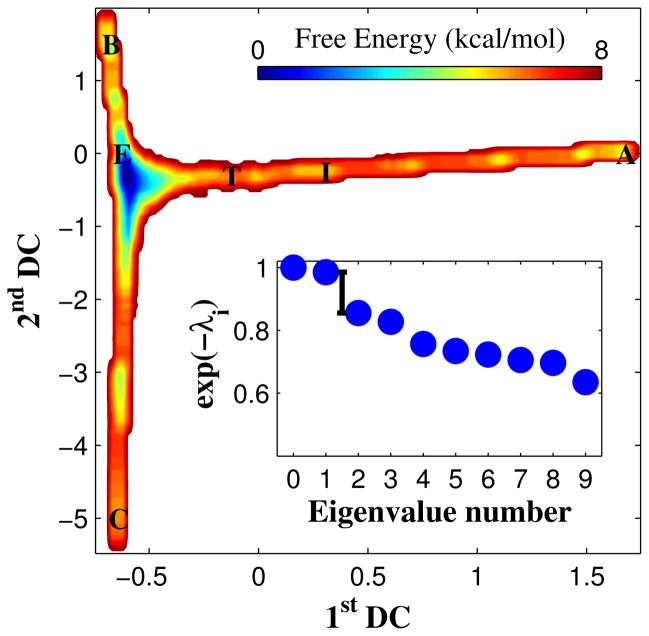
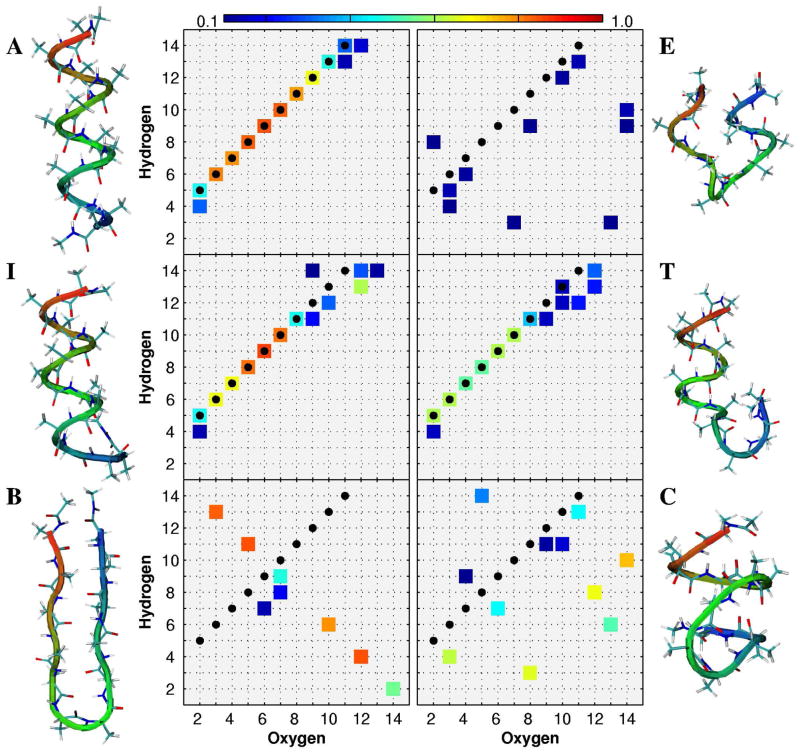
In order to test the approach on a more challenging system, we have applied DM-d-MD to sample the configuration space of alanine-12, which has a much more complex free energy landscape than alanine dipeptide. Starting from a helical configuration, the unfolding events for this system are too rare to be adequately sampled by MD at 300K with our computational resources. We have observed one single unfolding event in two full CPU days of 100 MD trajectories in parallel. To have control data with which to compare the DM-d-MD exploration, we performed 40 MD simulations, each 4 μs in length, at 400K and used LSDMap¹⁴ to analyze the data. A spectral gap between the first and second eigenvalues of LSDMap is shown in the inset of Figure 3, indicating that the system’s dynamics is dominated by one slow motion. Figure 3 also shows the free energy as a function of the first two DCs. The helical folded state (labeled as state A in the figure) is clearly separated from the unfolded state, E, and misfolded states, B and C, by the 1^stDC; this 1^stDC corresponds to the folding/unfolding of the peptide. Typical configurations in state I along the pathway between the folded and unfolded states indicate that the helical turn at the N-terminus breaks first during the unfolding. The 2^ndDC separates the misfolded states B and C from each other, and from the unfolded state E. State B corresponds to a hairpin structure whereas state C corresponds to a curved hairpin structure. The probabilities to form different hydrogen bonds in these various states are shown in Figure 4. The configurations in state A form all ten hydrogen bonds in the helical native state, while the configurations in state E do not have significant probability to form any particular set of hydrogen bonds. The free energy and these states are also mapped onto the subspace defined by the RMSD to the native (helical) state and radius of gyration (Rg) in Figure S3, as a comparison. We use both the 400K LSDMap space and the RMSD-Rg space to illustrate all the results discussed below.

Figure 3.

Free energy as a function of the first two DCs and LSDMap eigenspectrum (inset) of alanine-12 at 400K. Relevant states are labeled, representative configurations for these states are shown in Figure 4.

Figure 4.

Probability of formation for different sets of hydrogen bonds in the states labeled in Figure 3. The black dots represent the hydrogen bonds formed in the folded (helical) state, as a reference. Representative configurations for each state are shown next to the corresponding hydrogen bond map.

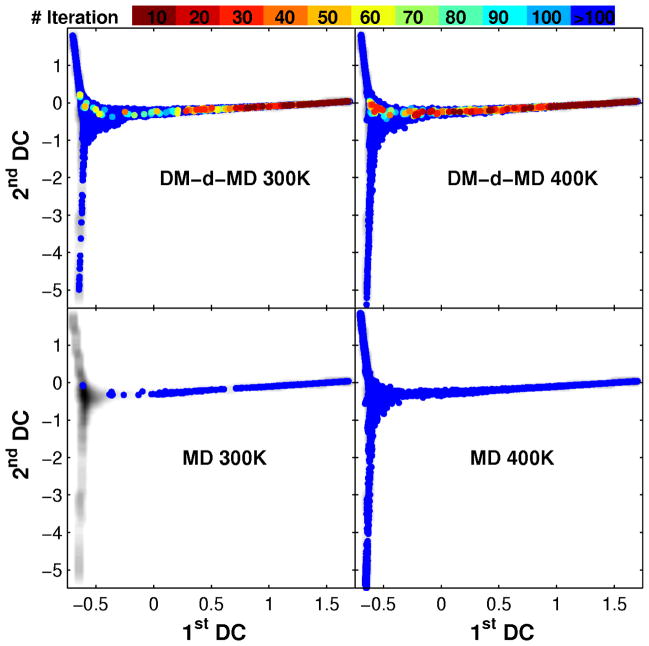
We have applied DM-d-MD to sample the configuration space of alanine-12 at both 300K and 400K. We used 10ps as the timescale for the short MD simulation, as determined by considering the eigenspectrum of the FP operator as a function of time (Figure S4), which has been discussed above. As a comparison, we also perform MD at these two temperatures. Both DM-d-MD and MD were run for two days, with 100 independent simulations, using one CPU per replica. We show the sampling plot mapped on the 400K LSDMap space in Figure 5 and on the RMSD-Rg space in Figure S5. About 20 iterations of DM-d-MD (200ps of effective MD time) are required to unfold alanine-12 at 400K, and about 50 iterations (500ps of MD) at 300K. In contrast, several tens of nanoseconds of MD are needed to unfold at 400K. As stated above, only one unfolding event was observed during the 100 independent replica simulations of 500ns each at 300K. These results provide an estimate of speedup with respect to MD of about 2 orders of magnitude at 400K and 3 orders of magnitude at 300K. A more accurate calculation of the speedup of the exploration phase of DM-d-MD taking into account the computational time spent by the diffusion map (computationally cheaper than the MD itself), is detailed in Figure S6.

Figure 5.

DM-d-MD sampling of alanine-12 configuration space projected onto the LSDMap space of the system at 400K. Top: DM-d-MD results; bottom: Classical MD results; left: 300K; right: 400K. The DM-d-MD iteration number of each point is given by the color. The grey shades underlying each of the four panels correspond to the free energy obtained from equilibrium MD simulation at 400K.

In order to reconstruct the system’s equilibrium distribution, umbrella sampling trajectories were performed. The 3.5 million frontier points accumulated during the DM-d-MD exploration of alanine-12 are clustered according to their RMSDs between each other, yielding about 10,000 clusters. Short trajectories are started from the centers of each of these clusters, and reweighted by means of the extension of WHAM²⁷ discussed in the Method section.

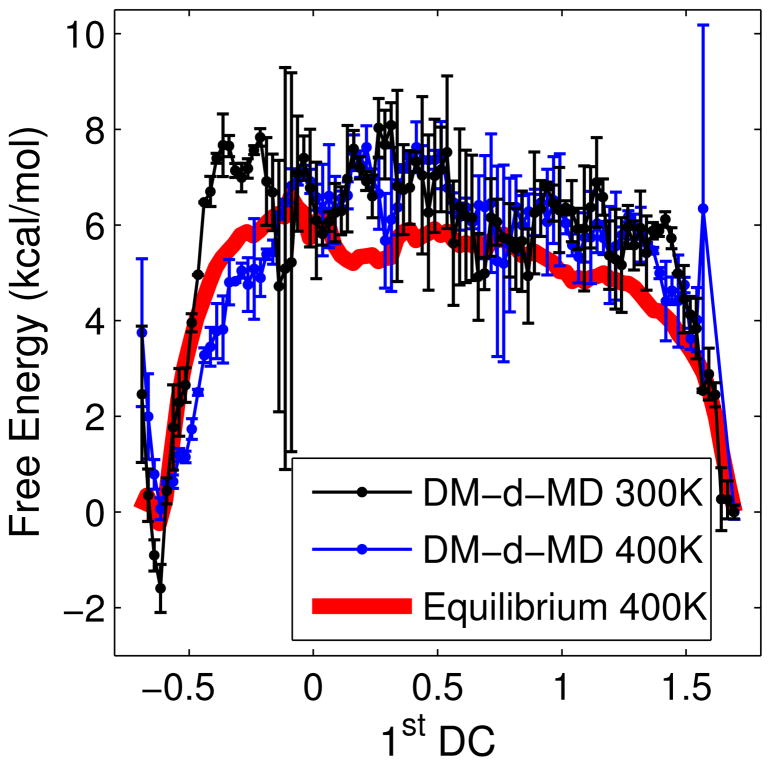
The free energy obtained after reweighting at 400K is shown in Figure 6 as a function of the 1^stDC and in Figure S7 as a function of the RMSD to the native state. It is in good agreement with the free energy obtained from equilibrium MD at 400K. The free energy obtained by performing umbrella sampling and reweighting of the DM-d-MD simulations at 300K is also shown in the same figures.

Figure 6.

Free energy of alanine-12 as a function of the 1^stDC. The result from equilibrium MD at 400K is shown in red as a reference; the result from DM-d-DM after umbrella sampling with reweighting at 400K in blue, and at 300K in black.

Including the time required to recover the equilibrium distribution by means of umbrella sampling and reweighting, the computational speed-up with respect to equilibrium sampling by MD is still significant (at least 2 orders of magnitude at 300K). As already noted in the analysis of alanine dipeptide above, most of the simulation time in our approach is spent in the umbrella sampling of the explored space, which is independent of the height of the free energy barrier, while the DM-d-MD exploration by itself is relatively cheap. This suggests that the method could be particularly useful in the characterization of systems with high free energy barriers.

4 Conclusion

We have introduced a new sampling scheme, DM-d-MD, that allows us to rapidly explore the configuration space of macromolecular systems. The method uses diffusion map to guide MD on the fly. We presented the results obtained from the application of DM-d-MD to two systems: alanine dipeptide and alanine-12. In both systems a dramatic speedup is obtained on exploring the configuration space. Even considering the time needed to reconstruct the equilibrium distribution from DM-d-MD, the computational gain with respect to standard MD is quite significant. With the DM-d-MD method, we obtained the equilibrium sampling of alanine-12 at 300K in three days with our computational resources, a feat which might take a year with MD on the same computer system.

The DM-d-MD method uses only local information to guide the dynamics and it is therefore reaction-coordinate free. After the umbrella sampling, the resulting distribution is unbiased, and can be analyzed by any global reaction coordinates (i.e. LSDMap coordinates or other physically relevant collective variables). The DM-d-MD method is minimally dependent on a priori knowledge of the system, as the only information required to begin the DM-d-MD exploration is a single initial configuration of the system.

The coverage of configuration space provided by DM-d-MD can in principle be combined with several different methods to reconstruct the equilibrium distribution. Here we used umbrella sampling and WHAM reweighting. We find the resulting free energy profiles are in good agreement with the equilibrium data available. The combination of DM-d-MD with other enhanced sampling methods could provide even more efficient procedures and more accurate results.

The framework of DM-d-MD is designed to achieve equilibrium sampling of macromolecular systems containing slow motions and/or rare events, as for instance the crossing of a high free energy barrier, which cannot be afforded by traditional MD simulation with the current computational resources. We expect wide applicability of DM-d-MD in larger systems, to the extent to allow a comparison with the experimental results, and to make predictions not yet accessible to experiment.