How Kinetics within the Unfolded State Affects Protein Folding: an Analysis Based on Markov State Models and an Ultra-Long MD Trajectory

Abstract

Understanding how kinetics in the unfolded state affects protein folding is a fundamentally important yet less well-understood issue. Here we employ three different models to analyze the unfolded landscape and folding kinetics of the miniprotein Trp-cage. The first is a 208 μs explicit solvent molecular dynamics (MD) simulation from D. E. Shaw Research containing tens of folding events. The second is a Markov state model (MSM-MD) constructed from the same ultra-long MD simulation; MSM-MD can be used to generate thousands of folding events. The third is a Markov state model built from temperature replica exchange MD simulations in implicit solvent (MSM-REMD). All the models exhibit multiple folding pathways, and there is a good correspondence between the folding pathways from direct MD and those computed from the MSMs. The unfolded populations interconvert rapidly between extended and collapsed conformations on time scales ≤ 40 ns, compared with the folding time of ≈ 5 μs. The folding rates are independent of where the folding is initiated from within the unfolded ensemble. About 90 % of the unfolded states are sampled within the first 40 μs of the ultra-long MD trajectory, which on average explores ~27 % of the unfolded state ensemble between consecutive folding events. We clustered the folding pathways according to structural similarity into “tubes”, and kinetically partitioned the unfolded state into populations that fold along different tubes. From our analysis of the simulations and a simple kinetic model, we find that when the mixing within the unfolded state is comparable to or faster than folding, the folding waiting times for all the folding tubes are similar and the folding kinetics is essentially single exponential despite the presence of heterogeneous folding paths with non-uniform barriers. When the mixing is much slower than folding, different unfolded populations fold independently leading to non-exponential kinetics. A kinetic partition of the Trp-cage unfolded state is constructed which reveals that different unfolded populations have almost the same probability to fold along any of the multiple folding paths. We are investigating whether the results for the kinetics in the unfolded state of the twenty-residue Trp-cage is representative of larger single domain proteins.

Introduction

Although much progress has been made on the protein folding problem, unresolved questions still exist concerning some of the fundamental aspects of how proteins fold^1–15. For example, how does the energy landscape of the unfolded state affect folding^3,5,16,17? Does residual structure within the unfolded ensemble influence folding rates? Why do some proteins which theory and simulation suggest have multiple folding pathways exhibit two-state, single exponential kinetics? Molecular dynamics simulations (MD) in atomic detail provide the spatial and temporal resolution required to investigate the mechanisms of protein folding in aqueous solutions. However, the time scale covered by MD is usually too short for direct unbiased folding simulations. In recent years, the D. E. Shaw lab has developed a special-purpose computer that greatly accelerates MD simulations of biomolecules, and the gap between direct simulation and biological time scales is now beginning to be closed^18–21. Using their ANTON technology on twelve structurally diverse fast-folding proteins, Shaw and coworkers were able to fold eleven of them to experimental structures and observe numerous reversible folding transitions in simulations ranging from microseconds to milliseconds ²⁰.

Other methods which do not require special purpose hardware are being developed to overcome the time scale limitation of direct MD and more efficiently sample the rare events associated with biomolecular transitions ^22–26. In this area, Markov state models (MSM) constructed from atomistic simulations have been particularly successful in sampling the rare events associated with protein folding and protein conformational transitions ^27–38. In this approach, the protein conformational space is discretized into a network of coarse grained substates. Transitions on the network are modeled by a master equation; the kinetics on the network is Markovian. The network approach provides an efficient way to extract mechanistic insights from a large amount of MD trajectory data without losing the accuracy of the underlying atomistic simulations. The folding pathways and their fluxes can be obtained by applying transition path theory (TPT) on the network ^30,31,39, yielding a statistical description of how a protein acquires the specific native conformation starting from an extremely large number of possibilities. Noe et al. studied the folding of PinWW domain by constructing a Markov state network model from many relatively short MD simulations.³¹ They found many non-overlapping pathways passing through intermediate regions to reach the native state. Based on their Markov state modeling of small single domain proteins, Pande and coworkers proposed that protein native states act as kinetic hubs connected to unfolded structures by stochastic jumps through metastable states ^34,36. In this kinetic hub model, the unfolded state ensemble is divided into collections of states that fold along different folding paths; to get from states which fold along one path to those which fold along another involves transiting through the folded state ³⁴.

To overcome the sampling limitations of constant temperature MD in constructing a network model, over the past several years our group has developed an approach that takes advantage of replica exchange molecular dynamics (REMD) in accelerating barrier crossing, and extracts kinetic information from REMD by assuming that a network of transitions can be reconstructed by applying structural similarity criteria together with reweighting techniques ^28,40,41. By exploiting transition path theory together with stochastic simulations, the kinetic network can be interrogated and information concerning the temperature dependent folding pathways can be obtained. Application of this approach to the miniprotein Trp-cage indicated that below the folding temperature, the folding flux is dominated by a small number of localized pathways ⁴⁰. Above the folding temperature, the folding pathway ensemble becomes much more diverse.

The effect of the unfolded state heterogeneity on folding was the focus of an insightful study by Ellison and Cavagnero¹⁶. One important finding from their simple kinetic model is that for proteins with heterogeneous folding pathways, deviations from single exponential are observed only when unfolded conformations exchange at rates slower than folding. This result may provide a simple explanation for the apparent two-state, single exponential kinetics shown by some proteins, even though these proteins may fold through multiple diverse pathways.

In the present study, we employ stochastic simulations, transition path theory and Markov state models constructed from atomistic simulations to investigate how the kinetics within the unfolded state ensemble affects folding. The Trp-cage miniprotein (Fig. 1) has served as a model system for studying folding in numerous experimental ^42–45 and theoretical studies ^46–52. Here we investigate the kinetics in the unfolded state and its effects on folding using the following models: (1) a 208 μs explicit solvent MD simulation from the Shaw lab²⁰ that contains several folding events; (2) a Markov state model constructed from the same ultra-long MD trajectory (MSM-MD); and (3) a kinetic network model built from REMD simulations using an implicit solvent effective potential over a wide temperature range (MSM-REMD). Direct comparison between the ultra-long MD and MSM-MD trajectories serves to test the validity of the Markov model. Pande and coworkers have reported the first such comparison using two 100 μs folding trajectories of FIP35 WW domain ⁵³. They found that the MSM has a hub-like topology and the analysis yielded more insights into the diversity of folding pathways and dynamics between two alternative native structures. Here our emphasis is on sampling within the unfolded state and its effects on folding pathways. Because stochastic simulations on a discretized network are extremely efficient, we use it in the present study to extensively explore the kinetics within the unfolded ensemble. We have developed techniques to map the reactive stochastic trajectories onto the folding pathways computed using TPT ⁴⁰. By combining stochastic simulations with TPT pathway analysis we can evaluate the folding rate along each pathway and the probability of folding along any pathway from any place within the unfolded state ensemble. By analyzing the Trp-cage kinetics in the light of a simple kinetic model calculation we determine a general relationship between the folding kinetics and the rate of mixing in the unfolded states. We discuss our network model analysis in relation to the study of Ellison and Cavagnero ¹⁶ and other folding models ^5,34,54. The main result of the present study is that proteins with heterogeneous pathways will fold with single exponential kinetics, as long as the rate of mixing within the unfolded state is comparable to or faster than folding. While the mixing within the unfolded state modulates the apparent waiting times for folding along individual paths, the overall folding rate depends only on the total folding flux and the equilibrium unfolded state population.

Figure 1.

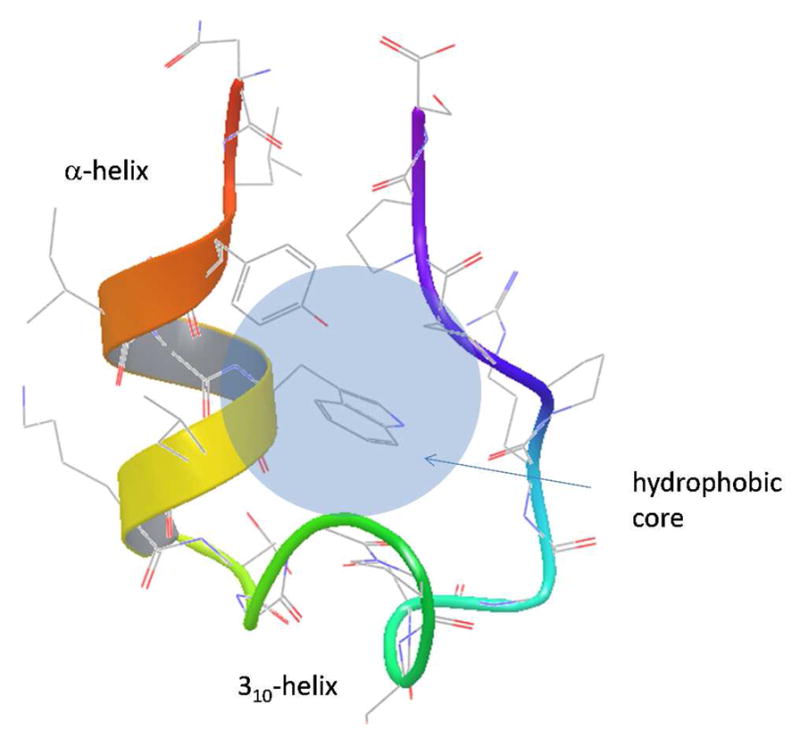
NMR structure of Trp-cage miniprotein.

Methods

Analysis of the Ultra Long MD Trajectory

A MD simulation of Trp-cage was performed by Shaw and coworkers on the Anton computer for 208 μs using a modified charmm22 all-atom force field in the TIP3P explicit solvent ²⁰. The MD trajectory contains ~10⁶ snapshots saved every 200 ps. During the course of the simulation the Trp-cage fluctuates between the low and high rmsd regions, via transiently occupied intermediate region (Fig. S1a). The distribution of rmsd is bimodal, containing a sharp peak at rmsd = 1.3 Å, which is separated from a broad peak at rmsd = 6 Å by a weakly populated intermediate region (Fig. S1b). Based on the rmsd distribution, we define three macrostates as follows: folded (rmsd ≤ 2.2 Å), intermediate (2.2 Å < rmsd ≤ 5 Å), and unfolded states (rmsd > 5 Å); the populations carried by these macrostates are: 17.5 % folded, 15.1 % intermediate, and 67.4 % unfolded. Note that the definition of the three macrostates is somewhat different from that used in the study by Shaw et al.²⁰, where the folded and unfolded states are defined based on the fraction of native contacts, Q. As a result, there are some quantitative differences between the kinetic properties calculated in this work and those found by Shaw and coworkers. In particular, using the RMSD-based cutoff scheme, the trajectory contains a number of rapid folding transitions that are not considered as folding events in the study of Shaw and coworkers which used Q-based definition of the macrostates. This does not affect the interpretation of the main results except for the reported value of the folding transit time as discussed in the following section.

Construction of MSM-MD

We constructed a Markov state model based on the 208 μs MD simulation to analyze the Trp-cage folding kinetics. The MSM-MD consists of a collection of conformational microstates and the transition probability matrix describing the memoryless jumps among these microstates. A set of 25000 microstates is generated by geometrically clustering the ~10⁶ MD snapshots according to their mutual rmsd using the k-means clustering method. The average rmsd between a structure and its cluster center is 2.45 Å. The transition matrix T_ij(τ) is estimated by projecting the MD trajectory onto the network nodes and counting the number of transitions from node i to node j within lag time τ, i.e. ${\text{T}}_{\text{ij}}(\tau )\equiv \text{P}(\text{j},\tau \mid \text{i},\text{0})={\text{C}}_{\text{i}\to \text{j}}(\tau )/\sum _{\text{k}}{\text{C}}_{\text{i}\to \text{k}}(\tau )$. To choose a lag time for which the transitions on the network are Markovian, we used a criteria based on the mean first passage time (MFPT) of folding: when the transitions are Markovian, the folding MFPT computed using T_ij(τ) should not depend on the choice of lag time τ: see Fig. S2a. Here folding MFPT is obtained from the inverse of the folding rate ${\text{k}}_{\text{f}}=\frac{\text{J}}{\sum _{\text{i}}{\text{P}}_{\text{eq}}(\text{i})[1-{\text{P}}_{\text{fold}}(\text{i})]}$³¹, where P_fold(i) is the commitor probability of folding; J is the folding flux computed using TPT³¹, $\text{J}=\frac{\sum _{\text{i}\in \text{U},\text{j}\notin \text{U}}{\text{T}}_{\text{ij}}(\tau ){\text{P}}_{\text{eq}}(\text{i}){\text{P}}_{\text{fold}}(\text{j})}{\tau }$. The calculated folding MFPT at different lag times are shown in Fig. S2a. At τ ≥ 5 ns, the folding time for the 25000-node MSM begins to level off to a plateau value close to the MFPT observed in the ultra-long MD simulation, suggesting that the model behaves Markovian for lag times t ≥ 5 ns. We also tested a coarser model with 6000 states: although the MFPT shows similar curvature, the plateau value of MFPT is considerably smaller than the folding time observed from the MD trajectory.

To further verify the Markovian property of the network, we used another criteria based on the implied timescales t_i, calculated from the eigenvalues λ_i(τ) of T’(τ), t_i = − τ / ln[λ_i(τ)].²⁷ Here T′(τ) is identical to the transition matrix T(τ) except that all the rates leaving the folded state are set to zero, which corresponds to the absorbing boundary condition for folding. The use of T’(t) allows its slowest eigenvalue to reproduce the MFPT of folding computed from TPT. As seen from Fig. S2b, at τ ≈ 5ns, the implied timescales begin to level off. The implied timescale computed for the slowest decaying eigenmode of the T’(τ) at τ = 5ns is 5.5 μs, which is in excellent agreement with the MFPT obtained using the flux from TPT calculation.

The choice of lag time τ not only determines the Markovian behavior of the MSM, but also strongly affects the kinetic resolution of the network model. At small lag time, T_ij(τ) is equivalent to the rate matrix in continuous-time Markov model via ${\text{k}}_{\text{ij}}=\underset{\tau \to \text{0}}{lim}\frac{{\text{T}}_{\text{ij}}(\tau )}{\tau }$, which gives the highest possible kinetic resolution on the network. At large τ, many of the unfolded states are connected to the folded state in one jump. At τ = 1 ns, 5 ns and 20 ns, the one-jump folding pathways were found to account for 2.7 %, 10 % and 28 % of the total folding flux, respectively. In contrast, in the 208 μs MD simulation, one-jump folding event was observed only once out of the 31 folding transitions, which corresponds to 3.2 % folding flux. Therefore, our results show that, while the lag time needs to be long enough to satisfy Markov property for memoryless transition, τ should also be small enough to allow sufficient kinetic resolution for studying folding mechanism. Likewise, the radius of the clustered nodes need to be large enough to have adequate statistics; but too much coarse graining could lead to non-Markovian behavior by grouping structures separated by significant barriers. The MSM-MD used in the present study is based on 25000-state clustering and a lag time of 5 ns, which we found give a good tradeoff between satisfying Markov property and providing adequate kinetic resolution and statistics.

Construction of MSM-REMD from Replica Exchange Simulation

We also constructed a kinetic network model for Trp-cage (MSM-REMD) by clustering the 150,000 snapshots, obtained from REMD simulations at temperatures from 363 K to 566 K, into a set of 20,000 conformational microstates. The details about the REMD simulations are described in the reference 34 ⁴⁰. The clustering is performed based on the Cα-RMSD between pair of the snapshots, using a cutoff radius of 1.1 Å. All the neighboring conformations found within the cutoff RMSD from a selected central node are merged to create a composite node. The resulting clustered nodes generally consist of contributions from many REMD snapshots observed at several temperatures.

The rates for the memoryless transitions on the network were parameterized using a scheme involving many short MD simulations. The rate constant k_ij for the transition from state j to state i is

$${\text{k}}_{\text{ij}}={\text{C}}_{\text{ij}}{\left(\frac{{\text{P}}_{\text{i},\text{eq}}}{{\text{P}}_{\text{j},\text{eq}}}\right)}^{\frac{1}{2}}$$ (1)

Here the prefactor C_ij = C_ji, which satisfies the detailed balance k_ijP_j,eq = k_jiP_i,eq. By definition, the rate k_ij can be expressed in erms of the branching probability P_j→i and the mean lifetime at node j, <T_j>:

$${\text{k}}_{\text{ij}}=\frac{{\text{P}}_{\text{j}\to \text{i}}}{{<\text{T}}_{\text{j}}>}$$ (2)

Eq. 2 suggests a way to parameterize k_ij based on the lifetime observed from many short MD trajectories. The branching probability P_j→i can be approximately expressed in terms of the RMSD distance between node i and j, Δr_ij. From running many short MD trajectories, we found that the average probabilities of jumping to a neighboring node at Δr can be fitted with

$${\text{P}}_{\text{j}\to \text{i}}(\mathrm{\Delta }{\text{r}}_{\text{ij}})\propto \frac{\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}}{{<\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}>}_{\text{j}}}$$ (3)

(Fig. S3). Additionally, P_j→i decreases approximately with the number of neighbors of node j, i.e. ${\text{P}}_{\text{j}\to \text{i}}(\mathrm{\Delta }{\text{r}}_{\text{ij}})\propto \frac{1}{{\text{N}}_{\text{j}}^{\text{nb}}}$. From Eq. 2 and Eq. 3, the rate constant k_ij is expressed as

$${\text{k}}_{\text{ij}}\approx \frac{\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}}{{<\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}>}_{\text{j}}{\text{N}}_{\text{j}}^{\text{nb}}{\text{T}}_{\text{j},\text{MD}}}{\left(\frac{{\text{P}}_{\text{i},\text{eq}}}{{\text{P}}_{\text{j},\text{eq}}}\right)}^{\frac{1}{2}}$$ (4)

Here the prefactor is identified with C_ij in Eq. 1, i.e. ${\text{C}}_{\text{ij}}\approx \frac{\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}}{{<\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}>}_{\text{j}}{\text{N}}_{\text{j}}^{\text{nb}}{\text{T}}_{\text{j},\text{MD}}}$. Since C_ij = C_ji (needed for maintain detailed balance), we symmetrize C_ij and write ${\text{C}}_{\text{ij}}\approx \frac{1}{2}(\frac{\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}}{{<\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}>}_{\text{j}}{\text{N}}_{\text{j}}^{\text{nb}}{\text{T}}_{\text{j},\text{MD}}}+\frac{\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}}{{<\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}>}_{\text{i}}{\text{N}}_{\text{i}}^{\text{nb}}{\text{T}}_{\text{i},\text{MD}}})$. Taken these considerations together, we obtain

$${\text{k}}_{\text{ij}}\approx \frac{1}{2}\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}(\frac{1}{{<\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}>}_{\text{j}}{\text{N}}_{\text{j}}^{\text{nb}}{\text{T}}_{\text{j},\text{MD}}}+\frac{1}{{<\mathrm{\Delta }{\text{r}}_{\text{ij}}^{-6}>}_{\text{i}}{\text{N}}_{\text{i}}^{\text{nb}}{\text{T}}_{\text{i},\text{MD}}}){\left(\frac{{\text{P}}_{\text{i},\text{eq}}}{{\text{P}}_{\text{j},\text{eq}}}\right)}^{\frac{1}{2}}$$ (5)

To test how well the rates parameterized using Eq. 5 describe the kinetics, we compare the distributions of state lifetimes obtained from many short MD simulations and those from stochastic simulations on the MSM-REMD. The results show that the two distributions of the state lifetimes agree well with each other (Fig. S4).

The procedures of the decomposition of the folding flux into folding pathways, the clustering of folding pathways into folding tubes, and the mapping of stochastic simulation trajectories onto folding tubes were described in a previous paper⁴¹.

Results

Below we first present the results of sampling the Trp-cage unfolded state by MD and the MSM built from MD (MSM-MD), including the time scales of structural reorganization in the unfolded state, the kinetic partitioning of the unfolded state into populations that fold along different paths and the folding rates associated with different folding paths. We then analyze the distribution of the folding passage times, transit times, and the nature of the heterogeneity in the folding pathways. Finally, we discuss the results for the MSM constructed from REMD sampling (MSM-REMD) to investigate how the folding kinetics is influenced as a function of temperature and for comparison with the ultra-long MD trajectory from the Shaw group.

Sampling of the Unfolded States by MD and MSM-MD

We first examine to what extent the sampling of the unfolded states has converged in the 208 μs MD trajectory, by estimating the fraction of the unfolded conformational space sampled by the trajectory as a function of simulation time. To this end we cluster the trajectory; the clustering scheme we employed is described in the Methods. We calculated the fraction of the unfolded state clusters visited by the trajectory as a function of simulation time and found that about 90 % of the unfolded states are sampled within the first 40 μs, which is one-fifth of the total simulation time (Fig. S5, Supporting Information). The trajectory spends the remaining 80 % of the simulation time mostly revisiting the structures seen earlier. This result is reasonably robust with respect to the variation in the granularity of the clustering (see Fig. S5). It is therefore an indication that the ultra-long MD simulation exhibits good convergence in the sampling of the unfolded state ensemble.⁵⁵

We characterized the structural reorganization in the unfolded state to address (1) how heterogeneous are the structures explored between two adjacent unfolding/folding events? (2) What is the time scale for chain extension and collapse for unfolded Trp-cage before it folds? We choose the radius of gyration (R_g) as the order parameter to characterize the structural reorganization in the unfolded region. Fig. 2 shows the distribution of R_g and its fluctuations in the MD trajectory. The folded structure has an R_g of ~7 Å; for the unfolded state R_g spans broadly the range from 6.5 Å to 15 Å, which correspond respectively to compact unfolded conformations and fully extended chains, two examples of which are shown in Fig. S6. As seen from Fig. 2b, the MD trajectory visits both extended conformations (R_g ≥ 14 Å) and compact unfolded structures (R_g ≤ 8 Å) many times before it folds. We computed the distribution Γ(τ) of relaxation times τ for the radius of gyration in the unfolded state (see Fig. S7) and found a dominant relaxation mode at τ = 6 ns along with a much weaker mode centered at τ = 38 ns. The relaxation times for the fluctuation between the extended and collapsed forms of Trp-cage are much shorter than the average residence time of (~5 μs) in the unfolded state between adjacent folding events. We also examined the time scale of collective motions in the unfolded state by computing the autocorrelation functions for the principal components. The relaxation time along the slowest principal component is found to be ≤ 40 ns, i.e. similar to the time scale of fluctuations in R_g (Fig. S8).

Figure 2.

(a) The distribution of radius of gyration from the 208 μs MD trajectory ²⁰. The R_g corresponding to the native structure is indicated by the red arrow. (b) A 50 μs portion of the time series of R_g obtained from the MD trajectory and from the stochastic simulation trajectory on the MSM-MD. The letter U indicates a time span in the unfolded state.

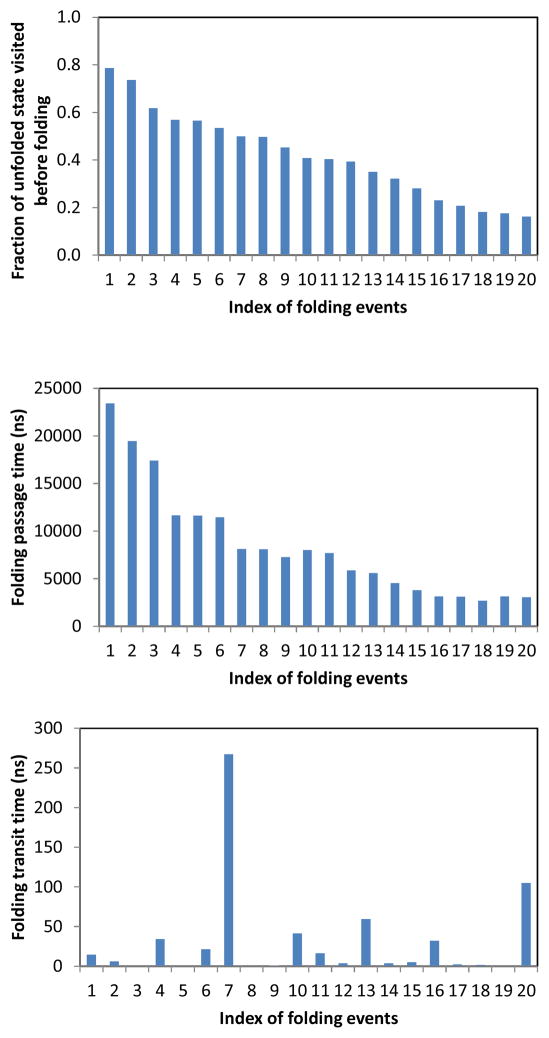
In order to gain further insight into the kinetic properties of the unfolded state ensemble, we analyze the fraction of the total conformational space of the unfolded ensemble visited by the MD trajectory, between two adjacent unfolding/folding transitions. We compute this quantity by analyzing unfolded intervals between each consecutive unfolding/folding event. Here, an unfolded interval starts from the time when the trajectory enters the unfolded region and ends when the trajectory enters the folded state. Fig. 3 shows the fraction of unfolded conformations visited during each of the unfolded intervals before the trajectory folds. In 45 % of the folding events, the trajectory visits > 30 % of the unfolded states before it folds. On average, a trajectory typically explores about 27 % of the unfolded conformational space between consecutive unfolding/folding events. Fig. 3 also shows that the fraction of unfolded states visited is strongly correlated with the folding passage time. This correlation is an indication of substantial mixing within the unfolded state ensemble, as discussed below.

Figure 3.

For each unfolding/folding transition observed in the ultra-long MD trajectory, from top to bottom: the fraction of unfolded state space sampled before folding ordered from largest to smallest; the corresponding passage time for folding; the folding transit time. The x-axis is the index of each folding transition, in descending order of fraction of visited unfolded states.

Using the ultra-long MD trajectory we constructed a 25,000-state kinetic network model (MSM-MD): see Methods. We performed a kinetic Monte Carlo (KMC) simulation for 64 milliseconds, which contains ~10,000 folding and unfolding events. The radius of gyration time series are nearly indistinguishable from those observed in the direct molecular dynamics simulation MD (Fig. 2b; see also Table 1).

Table 1.

Time scales of Trp-Cage folding and unfolded state kinetics from the ultra-long MD and MSM-MD model.

	Mean folding time	Conformational relaxation time in the unfolded states3	Time to sample 90% of the unfolded states	Transit time of folding
MD (208 μs)1	5.5 μs	Mode 1: 6 ns; Mode 2: ~ 38 ns	~ 40 μs	23.6 ns
MSM-MD2	5.3 μs	Mode 1: 7 ns; Mode 2: ~ 30 ns	~ 44 μs	30 ns

¹The MD trajectory contains 31 folding events.

²The Markov state model contains 25000 microstates. The time scales are obtained by running kinetic Monte-Carlo simulation which generated 10000 folding events.

³Estimated from the time correlation functions of R_g.

We computed the folding pathways and their fluxes using transition path theory (TPT) ^31,39 to analyze the MSM-MD network model; ~5000 pathways were generated. To obtain mechanistic insights, the pathways were clustered into a much smaller number of folding tubes (~100), each containing between 10–100 structurally similar pathways. The grouping of folding pathways into tubes is based on structural similarity between the structures along two pathways ^40,41; the average RMSD distance between two pathways in different tubes is at least 4 Å.

Kinetic Partition of the Unfolded State by Folding Tubes

We now discuss the results on the kinetic partitioning of the unfolded state by folding tubes and the characterization of the unfolded populations and folding rates associated with different folding tubes. By projecting the stochastic MSM-MD trajectories onto the different folding tubes, we determined three important kinetic quantities associated with each folding tube: J(α), the flux through tube α; k(α), the folding rate corresponding to the tube; and P(α), the fraction of the unfolded population that folds through tube α. The flux J(α) is defined by the number of folding events through tube α per unit time. The tube rate constant k(α) is obtained from the inverse of the mean first passage time for the folding events through tube α. The population P(α) of the unfolded state which fold through tube α is calculated using $\text{P}(\mathrm{\alpha })=\sum _{\text{i}\in \text{U}}\text{t}(\text{i}\mid \mathrm{\alpha })/{\text{T}}_{\text{total}}$, where t(i|α) is the residence time that trajectories which fold through tube α spend on unfolded node i, and T_total is the total simulation time. The set {P(α)} corresponds to a kinetic partition of the unfolded state ensemble into populations which fold along each tube; the partition has the property that $\sum _{\mathrm{\alpha }}\text{P}(\mathrm{\alpha })={\text{P}}_{\text{Unfold}}^{\text{total}}$. Additionally, for the hub folding model, as different unfolded populations folding independently along different paths, $\sum _{\text{i}}\text{P}(\text{i}\mid \mathrm{\alpha })\text{P}(\text{i}\mid \mathrm{\beta })$ is expected to be small, although this is not observed for the kinetic network model of Trp-cage folding constructed from the ultra-long MD trajectory (see below).

The values for P(α), J(α) and k(α) calculated for the top 16 folding tubes are shown in Fig. 4. Although the fluxes vary by more than three fold along the different folding tubes, they all have very similar folding rates i.e. k(α) ≈ constant. Consequently, the tube fluxes are proportional to the corresponding populations, i.e. P(α) ∝ J(α). We discuss how these results are a direct consequence of the significant mixing within the unfolded state before folding.

Figure 4.

The tube fluxes J(α), tube population P(α) and tube folding rates k(α) for the top 16 folding tubes obtained using MSM-MD.

We have also computed the overlap between the distributions of the unfolded state populations which fold along different tubes. This is another indication of the extent of mixing within the unfolded state between folding events. We define the conditional probability $\text{P}(\text{i}\mid \mathrm{\alpha })=\frac{\text{t}(\text{i}\mid \mathrm{\alpha })}{\sum _{\text{i}\in \text{U}}\text{t(i}\mid \mathrm{\alpha }\text{)}}$. It corresponds to the fraction of the time the system spends on unfolded node i given that it folds along tube α. It is obtained by normalizing t(i|α) with the total time trajectories which fold through tube α spend in the entire unfolded region. The distribution P(i|α) over all the unfolded nodes describes the extent to which the unfolded states are explored before folding through tube α. In the case of extensive mixing between unfolded state populations, P(i|α) should be only weakly dependent on i. In contrast, for a kinetic hublike scenario, in which the exchanges between unfolded states are severely limited, each folding tube’s P(i|α) distribution is confined to a local area of the unfolded ensemble.

To examine the extent to which the P(i|α) distributions overlap, we define a quantitative measure of the overlap between the two normalized distributions P(i|α) and P(i|β) in discretized space $\mathrm{\Omega }(\mathrm{\alpha },\mathrm{\beta })=\frac{\sum _{\text{i}\in \text{U}}\text{P(i}\mid \mathrm{\alpha }\text{)}\times \text{P(i}\mid \mathrm{\beta }\text{)}]}{\sqrt{\sum _{\text{i}\in \text{U}}\text{P}{(\text{i}\mid \mathrm{\alpha })}^2}\sqrt{\sum _{\text{i}\in \text{U}}\text{P}{(\text{i}\mid \mathrm{\beta })}^2}}$. For the case of rapid mixing, Ω(α,β) will be ≈ 1. In the opposite regime, if the two folding tubes α and β are connected with very different regions of the unfolded ensemble, then Ω(α,β) will be ≈ 0. We found that all the matrix elements of Ω(α,β) for the top 16 folding tubes are greater than 0.95, which implies extensive mixing prior to folding.

Another unresolved question in protein folding concerns the role of residual structures in the unfolded states in modulating folding kinetics ¹⁴. For example, UV-Raman measurements found significant α-helical content of Trp-cage under denaturing condition ⁴³. It has been speculated that residual secondary structure may help accelerate Trp-cage folding. To probe the role of preexisting residual structure in folding, we performed a large number of stochastic simulations initiated from unfolded conformations with and without the residual secondary structure. In the MD trajectory, about 7 % of the unfolded conformations contain an intact N-terminal α-helix (residues 2-9). This value is consistent with the UV-resonance Raman study ⁴³. We initiated 8000 folding simulations from (1) unfolded conformations with intact N-terminal α-helix and (2) unfolded states with a disordered N-terminal segment. The folding starting from the conformations with α-helix is only slightly faster than that starting from those conformations without the secondary structure.

We also examine in a similar fashion the influence of nonnative compactness in the unfolded region. Folding simulations starting from collapsed unfolded conformations (Rg < 7.0 Å) and from extended conformations (Rg > 15 Å) result in virtually identical MFPT. Therefore, neither the preexisting N-terminal α-helix nor nonnative compactness was found to significantly influence the Trp-cage folding rate.

Comparison of the Folding Kinetics and Pathways from MD and MSM-MD

There are 31 folding events in the 208 μs MD trajectory. The distribution of the first passage times of the folding events can be approximately fit to a single exponential (Fig. S9). The mean first passage time (MFPT) of the 31 folding transitions is found to be ≈ 5.5 μs, in good agreement with the experimental folding time of 4 μs at room temperature ⁵⁶. Another quantity describing the folding kinetics is the transit time, which is the time for a folding trajectory to traverse the intermediate region. The average transit time of all the folding transitions is 23.6 ns; the range is between 1.8 ns and 267 ns. The observation that the average transit time is ~ 200 times smaller than the mean folding passage time of ~ 5 μs indicates that the Trp-cage folding is highly cooperative.

Examination of the folding transitions sampled by the ultra-long MD trajectory revealed heterogeneous structural pathways leading to the folded state. Here we discuss two representative paths (Fig. 5). In pathway A, the polypeptide chain first undergoes a hydrophobic collapse, forming a compact molten globule containing multiple non-native H-bonds; later on, the non-native interactions are loosened, which is followed by the formation of the N-terminal α-helix and native hydrophobic core. In pathway B, the folding starts from more extended conformation with pre-formed α-helix in the unfolded state; the hydrophobic core and the 3₁₀-helix then form in concert to complete the folding process. The two pathways have very different transit times: in pathway A, the trajectory has to loosen the non-native contacts and gradually replace them with native hydrophobic core; these localized structural rearrangements take place in a relatively long transit time of 44 ns. By contrast, the folding along pathway B is much simpler because the starting unfolded structure contains fewer non-native interactions; the associated transit time in this pathway is only 3 ns. We also found that the pathway B is a more dominant pathway, i.e. there are more folding transitions in which the α-helix forms before the hydrophobic collapse.

Figure 5.

Two representative folding transitions extracted from the 208 μs MD trajectory.

By carrying out stochastic simulations on the kinetic network generated from the MD simulation, a large number of folding transitions are obtained. The folding passage time distribution exhibits single exponential decay (Fig. S10), with a folding time close to the average of the 31 transitions observed in the ultra-long MD simulation.

We have compared the folding tubes constructed using transition path theory applied to the MSM-MD kinetic network with the folding transitions observed in the MD trajectory. Using a rmsd = 3.0 Å as the cutoff distance between a TPT folding pathway and an MD folding pathway, we found that 29 out of 31 MD folding transitions can be assigned to TPT folding tubes. Fig. 6 shows the fluxes of the top 12 TPT folding tubes compared with the number of the MD folding transitions assigned to each folding tube. There is a general correspondence between the folding transitions observed in the ultra-long MD simulation and the flux through folding tubes generated from the kinetic network (Fig. 6). The MSM folding tube with the largest flux is also the one that contains the largest number of MD folding transitions among all the folding tubes. The folding mechanism in this tube is the same as in the MD pathway B discussed above, which features an early formation of the α-helix (Fig. 5). The analysis of the TPT folding tubes shows that about 45 % of the flux is carried by pathways in which the α-helix forms early. In the remaining pathways the hydrophobic compaction either occurs early or forms in concert with the α-helix.

Figure 6.

The blue histogram shows the distribution of fluxes along the top 12 folding tubes generated from the MSM-MD kinetic network using TPT. The red histogram represents the fluxes of MD folding transitions projected onto the folding tubes.

It should be noted that in general, MSM predicts more folding pathways than that contained in the raw MD trajectory. For example, two such pathways that are predicted by MSM-MD but not observed in the original MD data are shown in Fig. S11. The reason for the richer folding pathways in MSM can be qualitatively understood by considering the schematic transition diagram shown in Fig. S12, where a MD trajectory contains transitions U1→I→U2 and separately N→I→N. There is no direct folding transition in this MD transition diagram. The corresponding MSM, however, would predict folding pathways U1→I→N and U2→I→N.

MSM Constructed from REMD Simulations

The MSM-MD model we have analyzed in the previous sections was based on MD simulations performed well above the Trp-cage folding temperature with just 17 % native population ²⁰. What is the kinetic picture of Trp-cage folding below the folding temperature? To address the temperature dependence of folding kinetics, here we study a Markov network model of Trp-cage built from temperature replica exchange (REMD) simulations with implicit solvation over a wide temperature range.^40,41 We call this Markov network model MSM-REMD.

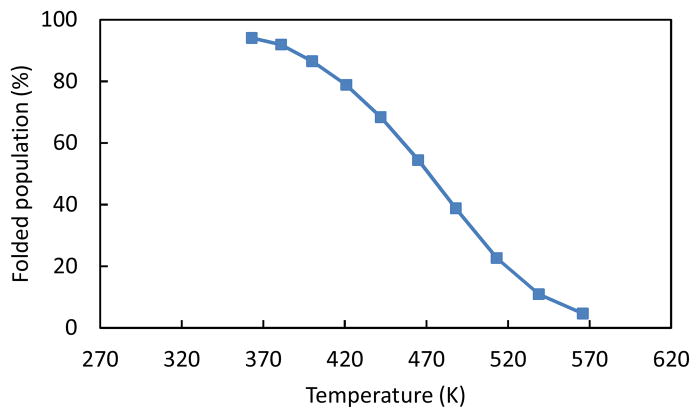
Using the REMD data obtained over a wide temperature range we determined the Trp-cage melting behavior (Fig. 7); the folding temperature T_f was found to be ≈ 468 K. The high melting temperature compared to the experimental T_f is typical of the results found with implicit solvent models and is partially attributable to the overly attractive intramolecular interactions in the OPLS-AA force field with AGBNP implicit solvent model ⁵⁷ used in the REMD simulations.

Figure 7.

The melting curve of Trp-cage obtained from REMD simulation.

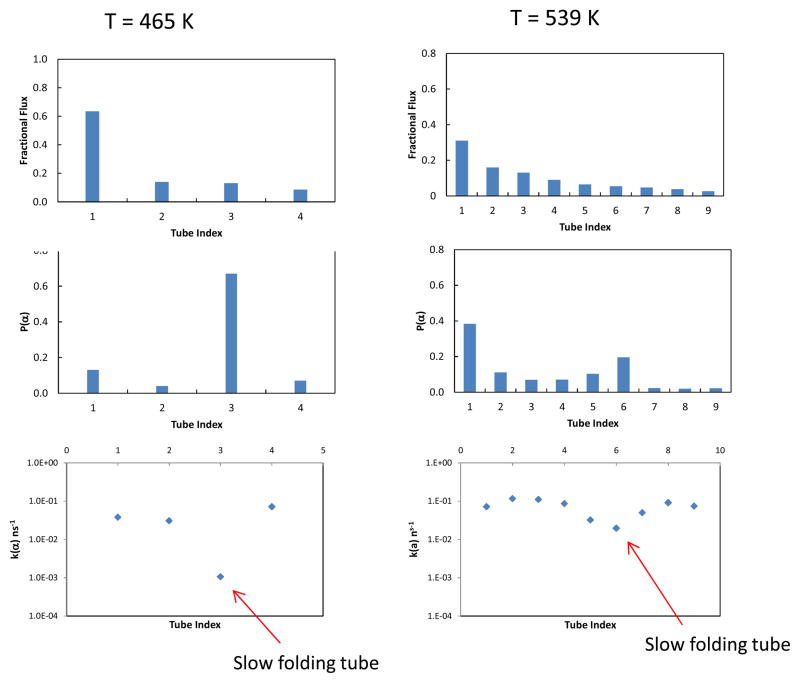
To investigate Trp-cage kinetics below and above the folding temperature, we performed TPT pathway calculations and stochastic simulations using the MSM-REMD model at T = 465 K and 539 K, at which 54 % and 11 % of the populations are folded, respectively. We found that both the rate of mixing within the unfolded state and the diversity of the folding pathways vary strongly with temperature. The folding pathway ensemble becomes more diverse at the higher temperature. At T = 465 K, the top folding tube carries 61 % of the total flux and the top three folding tubes account for ≥ 90 % of the total flux. In contrast at T = 539 K, the top folding tube carries just 30 % of the flux and it takes nine folding tubes to accumulate 90 % of the total flux (Fig. 8, top row). Below the folding temperature we observe very slow folding through one of the folding tubes (Fig. 8). The folding through this tube is ~ 60 times slower than the fastest folding tube.

Figure 8.

Results of J(α), P(α) and k(α) calculated using the MSM-REMD model at T = 465 K and T = 539 K.

Next, we examine the temperature dependence for the mixing within the unfolded states by computing the conditional probabilities P(i|α) for the different folding tubes α, and the overlaps of P(i|α) with P(i|β) among the folding tubes at both T = 465 K and T = 539 K. Table 2 shows the overlap factor Ω(α,β) between different pairs of unfolded population distributions P(i|α) and P(i|β) associated with the top folding tubes. At T = 465 K, overlaps between the P(i|α) of the slow folding tube (No. 3) and that of the rest of the tubes are zero, indicating that the unfolded populations associated with the slow tube and those with the other tubes fold independently. At the high temperature T = 539 K, the overlaps between the P(α) of slow tube (No. 6) and those of the other tubes increased significantly (Table 2). This trend reflects more extensive mixing within the unfolded ensemble above the folding temperature. How does this enhanced mixing in the unfolded state affect the folding kinetics at higher temperature? For this, we compare the tube populations P(α), fluxes J(α) and folding rates k(α) for the different folding tubes at the two temperatures (Fig. 8). It can be seen that the difference in the folding rates between the slowest and fastest folding tubes decreases significantly as the temperature is increased (Fig. 8, bottom row). At the lower temperature T = 465 K the ratio of the slowest folding rate to the fastest folding rate is k_slow/k_fast ≈ 0.015. At the higher temperature T = 539 K this ratio becomes k_slow/k_fast ≈ 0.2.

Table 2.

MSM-REMD results: The overlap factor matrix Ω(α,β) involving the top folding tubes that account for ≥ 95 % of the total folding flux. The slow folding tubes are indicated by red.

(a) T = 465 K
Folding tube	1	2	3	4
1	1.00	0.24	0.00	0.33
2	0.24	1.00	0.00	0.62
3	0.00	0.00	1.00	0.00
4	0.33	0.62	0.00	1.00

(b) T = 539 K
Folding tube	1	2	3	4	5	6	7	8	9
1	1.00	0.65	0.87	0.73	0.61	0.79	0.26	0.82	0.78
2	0.65	1.00	0.37	0.85	0.25	0.29	0.35	0.28	0.89
3	0.87	0.37	1.00	0.56	0.71	0.97	0.15	0.95	0.50
4	0.73	0.85	0.56	1.00	0.46	0.55	0.38	0.37	0.80
5	0.61	0.25	0.71	0.46	1.00	0.75	0.11	0.61	0.40
6	0.79	0.29	0.97	0.55	0.75	1.00	0.09	0.88	0.38
7	0.26	0.35	0.15	0.38	0.11	0.09	1.00	0.02	0.31
8	0.82	0.28	0.95	0.37	0.61	0.88	0.02	1.00	0.47
9	0.78	0.89	0.50	0.80	0.40	0.38	0.31	0.47	1.00

Another observation from Fig. 8 is that at the higher temperature T = 539 K, there is a clear correlation between J(α) and P(α), i.e. J(α) ∝ P(α). The plot of J(α) and P(α) at this temperature shows that the correlation coefficient R-squared ≈ 0.7 (Fig. S13). Such correlation between J(α) and P(α) is not observed at the lower temperature T = 465 K.

We have identified the conformational species that folds through the slow folding tube at the lower temperature. The average structure of the slow folding population adopts a hairpin-like conformation stabilized by between 5 and 7 nonnative hydrogen bonds. It also contains a nonnative hydrophobic core featuring Trp6-Arg16 stacking. It is found that the same compact conformation is also sampled by the ultra-long MD trajectory in explicit solvent, but in explicit solvent, these conformations are not metastable. In contrast, their lifetime is ~ 500 ns with the AGBNP implicit solvent model.

The results using the MSM-REMD trajectory at the lower temperature reflects the increased ruggedness in the free energy landscape of the unfolded ensemble at the lower temperatures with the AGBNP implicit solvent model, and a more hub-like partitioning of the unfolded state ensemble, in which slow folding populations and fast folding populations folding independently. At the higher temperature however the MSM-REMD results are more qualitatively similar to those observed using the MSM-MD model (compare Fig. 4 and the right half of Fig. 8).

Discussion

In this study we have focused on kinetics within the unfolded state ensemble and its influence on folding, which is less well understood compared with other aspects of protein folding. We begin with the following observations: First, the sampling of the unfolded states in the ultra-long MD simulation shows good convergence (Fig. S5). Second, the kinetic properties observed in the direct MD simulation are well reproduced by the Markov state model constructed from the MD simulation: The folding passage times, transit times, unfolded state dynamics and folding pathways obtained from the 208 μsec MD simulation and 64 millisecond stochastic MSM-MD simulation are in good agreement (Table 1 and Fig. 6).

The analysis of the MD and MSM-MD data suggests that the unfolded population of Trp-cage mixes well before folding. The relaxation time of the autocorrelation function for the radius of gyration and the principal components are ≤ 40 ns, which are much faster than the folding time ~ 5 μs. The experimentally determined time scales for large scale motions in unfolded proteins have been reported in several studies ^58–61. Using laser-temperature jump Sadqi et al. found that the hydrophobic collapse of the acid-denatured 40-residue BBL occurs on a ~ 60 ns time scale ⁵⁸. Using single-molecule spectroscopy Schuler and coworkers found that the chain reconfiguration time for the unfolded, 70-residue cold shock protein (Csp) was approximately 100 ns ^59,61. The orders of magnitude for the relaxation times for the radius of gyration calculated in the present study for the 20-residue Trp-cage are consistent with those measured for the somewhat larger polypeptides BBL and Csp.

Additional evidence of significant mixing within the unfolded state ensemble comes from the fact that the folding rates are independent of where the folding is initiated from within the unfolded basin and the extensive overlaps among the unfolded state populations which fold along different pathways. The strong correlation between folding passage times and the fraction of the unfolded nodes visited before each MD folding transitions also reflects the absence of major internal barriers in the unfolded basin (Fig. 3).

To further analyze how the kinetics within the unfolded state affects folding, we have studied a simple 5-state model (Fig. S14a), in which two unfolded nodes 1 and 2 have very different microscopic escape rates k₁₃ and k₂₄, with k₁₃/k₂₄ = 10. We examine how the rates of the fast folding tube α and slow folding tube β are affected by changes in the U-state interconverting rate k₁₂. The simulation shows that the tube folding rates k_α and k_β strongly depend n the rate of transition within U-state (Fig. S14b). When the transition rate within U-state k₁₂ is small relative to the microscopic escape rates k₁₃ and k₂₄, the unfolded populations on nodes 1 and 2 fold independently with very different k_α and k_β respectively governed by the intrinsic escape rates k₁₃ and k₂₄, producing bi-exponential folding time distributions (Fig. S15). As k₁₂ increases, the difference between the k_α and k_β decreases monotonically. When k₁₂ is comparable to or faster than k₁₃ and k₂₄, the two tube folding rates k_α and k_β converge to the overall folding rate k_tot (Fig. S14b and Fig. S15).

On the basis of the simple model results and using the concept of P_α introduced earlier, we can write expressions for the folding rates k(α) when mixing within the unfolded free energy basin is much slower or much faster than folding (see Table 3). The tube folding rate k_α has the simple, general expression ${\text{k}}_{\mathrm{\alpha }}=\frac{{\text{J}}_{\mathrm{\alpha }}}{{\text{P}}_{\mathrm{\alpha }}}$, where the tube flux is obtained from transition path theory ${\text{J}}_{\mathrm{\alpha }}={\sum }_{\text{i}\in \text{U},\text{j}\notin \text{U}}{\text{k}}_{\text{ij}}{\text{p}}_{\text{i}}^{\text{ep}}{\text{p}}_{\text{j}}^{\text{fold}}$^30,31. In the fast exchange limit the folding rate along a folding tube becomes ${\text{k}}_{\mathrm{\alpha }}\approx \frac{{\text{J}}_{\text{total}}}{{\text{P}}_{\text{total},\text{U}}^{\text{eq}}}\equiv {\text{k}}_{\text{tot}}$, which is the same for all the folding tubes, independent of the intrinsic rates (k₁₂ and k₂₄). In the limit of slow exchange within the unfolded basin, the result is ${\text{k}}_{\mathrm{\alpha }}=\frac{{\text{J}}_{\mathrm{\alpha }}}{{\text{P}}_{\mathrm{\alpha },\text{U}}^{\text{eq}}}$, where ${\text{P}}_{\mathrm{\alpha },\text{U}}^{\text{eq}}$ is the unfolded population locally associated with tube α. In this regime k_α depends on the escape rates from the local population ${\text{P}}_{\mathrm{\alpha },\text{U}}^{\text{eq}}$. While rates along individual folding tubes are modulated by the rate of U-state mixing, the k_tot, which is the simple average of folding events per unit time (also the same as the inverse of the mean first passage time), is constant and can be written as the weighted average of k_α: ${\text{k}}_{\text{tot}}=\frac{{\text{J}}_{\text{total}}}{{\text{P}}_{\text{total},\text{U}}}=\frac{{\text{J}}_{\mathrm{\alpha }}+{\text{J}}_{\mathrm{\beta }}}{{\text{P}}_{\text{total},\text{U}}}={\text{k}}_{\mathrm{\alpha }}\frac{{\text{P}}_{\mathrm{\alpha }}}{{\text{P}}_{\text{total},\text{U}}}+{\text{k}}_{\mathrm{\beta }}\frac{{\text{P}}_{\mathrm{\beta }}}{{\text{P}}_{\text{total},\text{U}}}$.

Table 3.

Results of k_α, P_α, and J_α for folding tube α, determined from studying a simple folding model (Fig. S13) (neglecting the small intermediate state population).

	kα	Pα	Jα
General	$$\frac{{\text{J}}_{\mathrm{\alpha }}}{{\text{P}}_{\mathrm{\alpha }}}$$	$\frac{\sum _{\text{i}\in \text{U}}\text{t}(\text{i}\mid \mathrm{\alpha })}{{\text{T}}_{\text{total}}}$	$\sum _{\begin{array}{l}\text{i}\in \text{U},\text{j}\notin \text{U},\\ \text{j}\in \mathrm{\alpha }\end{array}}{\text{k}}_{\text{ij}}{\text{p}}_{\text{i}}^{\text{eq}}{\text{p}}_{\text{j}}^{\text{fold}}$
Fast U-State mixing (funneled folding landscape)	$$\frac{{\text{J}}_{\text{total}}}{{\text{P}}_{\text{total},\text{U}}^{\text{eq}}}$$	$$\frac{{\text{J}}_{\mathrm{\alpha }}}{{\text{J}}_{\text{total}}}{\text{P}}_{\text{total},\text{U}}^{\text{eq}}$$
Slow U-state mixing (hub folding landscape)	k13	${\text{p}}_{\text{1}}^{\text{eq}}$	${\text{k}}_{\text{13}}{\text{p}}_{\text{1}}^{\text{eq}}$
	k24	${\text{p}}_{\text{2}}^{\text{eq}}$	${\text{k}}_{\text{24}}{\text{p}}_{\text{2}}^{\text{eq}}$

We now apply these insights to interpret the results of Trp-cage folding obtained from the MSM-MD model. As shown in Fig. 4, for the results from the stochastic simulations on the MSM-MD kinetic network, P_α ∝ J_α and k_α ≈ constant. Comparing with Table 3, we can see that such behavior is consistent with the scenario of significant U-state mixing.

The result that under the fast exchange condition the folding kinetics is single-exponential was first pointed out by Ellison and Cavagnero in an insightful study on the role of unfolded state kinetics ¹⁶. The authors studied different types of folding energy landscapes using simple kinetic models and concluded that under the condition of fast exchange in the unfolded basin, it is not possible to determine the microscopic rate constants for different parallel folding routes by a simple experiment in bulk solution. They also observed that the folding flux along a given route is controlled by the intrinsic escape rate along that route. These results agree well with our analysis of the Trp-cage folding kinetics and the simple model. As we show in the Table 3 here, the flux for a folding route is determined by the product of intrinsic rate and the equilibrium population of the unfolded region from which the folding route originates.

The results for P_α, J_α and k_α calculated using the MSM-REMD model (Fig. 8) reveal the temperature dependence of the unfolded states landscape: at low temperature, the landscape contains a deep basin whose population folds through a slow folding tube only, and does not exchange with other regions of the unfolded ensemble; at higher temperature, there is considerable mixing between the slow folding population and the rest of the unfolded basin, which is reflected in the overlap factor Ω(α,β) (Table 2). The relationships between J_α and P_α at the different temperatures provide additional evidence for the greater mixing within the unfolded basin at higher temperature. We have shown that a strong correlation between J_α and P_α is a signature for significant mixing in the unfolded state relative to folding (Table 3), here we look at J_α and P_α obtained from the MSM-REMD model. At T = 465 K, there is little correlation between J_α and P_α; however at T = 539 K, a stronger correlation between the two quantities emerges (R² ≈ 0.7, Fig. S13). This suggests that at the higher temperature, the unfolded state landscape becomes substantially smoother and this allows for more rapid exchange between the different folding tube populations. The MSM-REMD result at the higher temperature is qualitatively similar to the results we obtained at ambient temperature using the MSM-MD model based on the ultra-long MD trajectory.

We now examine our results in the light of the insightful paper by Bicout and Szabo,⁵ who studied different folding landscapes by modeling the protein dynamics in conformational space as diffusion under a spherically symmetric potential. They showed that the folding kinetics on both a golf-course landscape (Levinthal) and funnel landscape² is single exponential, which arises from the entropic barrier to folding. They also showed that to get such two-state behavior a folding trajectory on these landscapes needs not explore most of the unfolded states before folding.⁵ Our results for the Trp-cage folding are consistent with theirs: for the single exponential, two-state folding behavior of Trp-cage, a trajectory typically explores ~ 27 % of the unfolded space before it folds (Fig. 3).

Finally, we discuss our results from the perspective of the kinetic hub model of folding introduced by Pande.^34,53,54,62 In this model, the folded state F acts as a hub, so that most paths which connect pairs of unfolded states U1 and U2 pass through F. Hub like behavior also appears to imply that the unfolded state partitions into subspaces which largely fold along different pathways.¹⁴ However, as we have reported in this paper, we find no evidence of a kinetic partitioning of the U state space into regions which mostly fold along different pathways. Dickson and Brooks⁶³ introduced a hub score to quantify the hub-like character of a network; the hub score for (U1,U2) corresponds to the fraction of trajectories starting at U1 which pass through native state F before reaching U2. We have calculated the distribution of hub scores for the MSM-MD network constructed from the Shaw trajectory and obtained an average hub score of 0.88. Such a high hub score is not inconsistent with the observation of single exponential folding kinetics of Trp-cage and the rapid mixing within its unfolded state. It is simply a manifestation that on a funnel landscape, because of the energetic bias towards the native state, two sufficiently separated unfolded states will be connected by pathways which include folding events. It is not clear therefore how the hub score can be used to distinguish a rugged landscape from a smooth folding funnel.

Conclusions

An important problem in protein folding is to understand the relationship between the structural heterogeneity and kinetics within the unfolded free energy basin and the folding kinetics. We have investigated the unfolded state kinetics and folding pathways of the miniprotein Trp-cage using (1) a 208 μsec MD trajectory in explicit solvent; (2) Markov state model simulations based on the ultra-long MD trajectory; and (3) a Markov state model constructed from replica exchange molecular dynamics simulations in implicit solvent over a wide temperature range. Using stochastic simulations and transition path theory we have explored the kinetics of the unfolded state ensemble and studied its impact on the kinetics of folding. By comparing the folding behavior observed in the fully atomistic Trp-cage simulations with the kinetics in a simple 5-state folding model, we have obtained a relationship between the rate of mixing in the unfolded state and the folding kinetics along individual pathways (tubes). Here the main result is that the conformational mixing in the unfolded state modulates the apparent protein folding rates by affecting the waiting times for folding along different routes. When this mixing is comparable to or faster than folding, the folding rates associated with different folding routes converge to the same value which is independent of the intrinsic rates along any given route; despite the presence of multiple folding routes with non-uniform barriers, the folding kinetics is essentially single exponential. In the slow exchange limit, the folding rate of along folding route is controlled by the intrinsic rates along the route; In this case the different unfolded populations fold independently and the overall folding kinetics can deviate from single exponential.

We have presented results showing that, based on atomistic Trp-cage models in explicit and implicit solvent the Trp-cage unfolded state ensemble does not contain long-lived metastable states; there exists significant mixing in the unfolded state. These include the time scale for chain extension and compaction within the unfolded state, the approximately uniform folding rates among different folding tubes, the extensive overlaps among the unfolded populations associated with the different folding tubes, and the strong correlation between the flux along folding tubes and the unfolded state populations associated with the corresponding tubes. Because of the significant internal mixing of the unfolded state, the probability to fold along any of the multiple folding paths is almost the same regardless of where in the unfolded state the folding is initiated

Analysis of the Markov state model constructed from the temperature replica exchange data provides an opportunity to probe the temperature dependence of the unfolded states kinetics. By studying the results below and above the midpoint of the folding transition, we found that in implicit solvent at low temperature the unfolded state landscape contains a slow folding basin; internally the exchange between the slow folding population and other regions of the unfolded state basin is much slower than folding. Above the folding temperature, the unfolded state landscape becomes less rugged allowing more rapid mixing and considerable overlap among the unfolded populations associated with the different folding tubes.

Our study reinforces and extends the simple kinetic model of Ellison and Cavagnero¹⁶ in providing a physical basis for the apparent two-state, single exponential kinetics exhibited by many proteins with heterogeneous folding pathways. The current work makes use of Markov state kinetic network models built from atomic simulations, stochastic simulations on the network and transition path theory to analyze how kinetics within the unfolded state affects folding rates. For the models we have studied the unfolded state of Trp-cage is well mixed, and the rate of exchange within the unfolded state ensemble is comparable to or faster than the folding rate. We emphasize that Trp-cage is a small system and its kinetics may not be representative of the folding of larger and more complex proteins. It would be interesting to apply the computational tools and the concepts of P_α and the overlap matrix introduced in the present study to investigate the folding mechanisms of proteins with different native topology and more complex unfolded state kinetics.