Quantifying Waddington landscapes and paths of non-adiabatic cell fate decisions for differentiation, reprogramming and transdifferentiation

Abstract

Cellular differentiation, reprogramming and transdifferentiation are determined by underlying gene regulatory networks. Non-adiabatic regulation via slow binding/unbinding to the gene can be important in these cell fate decision-making processes. Based on a stem cell core gene network, we uncovered the stem cell developmental landscape. As the binding/unbinding speed decreases, the landscape topography changes from bistable attractors of stem and differentiated states to more attractors of stem and other different cell states as well as substates. Non-adiabaticity leads to more differentiated cell types and provides a natural explanation for the heterogeneity observed in the experiments. We quantified Waddington landscapes with two possible cell fate decision mechanisms by changing the regulation strength or regulation timescale (non-adiabaticity). Transition rates correlate with landscape topography through barrier heights between different states and quantitatively determine global stability. We found the optimal speeds of these cell fate decision-making processes. We quantified biological paths and predict that differentiation and reprogramming go through an intermediate state (IM1), whereas transdifferentiation goes through another intermediate state (IM2). Some predictions are confirmed by recent experimental studies.

1. Introduction

Embryonic stem (ES) cells are pluripotent. They can proliferate to maintain their pluripotency by self-renewing processes and differentiate into a variety of cell-lineages under certain conditions. Recently, research has shown that the cellular reprogramming of somatic cells to induced pluripotent stem cells or the transdifferentiation between different cell types can be realized by manipulating a few key genes [1–6]. These results provide possibilities for stem cell models to be applied in regenerative medicine. However, the molecular mechanisms involved in cellular differentiation and reprogramming and the optimal reprogramming pathway remain unknown. This demands a systematic and global approach to investigate underlying gene regulatory networks involving marker genes characterizing different cell types and reciprocal regulations between them.

Cells receive external noise from inhomogeneous environments and intrinsic noise from the fluctuations of the low molecular copy number (inherent stochasticity of biochemical processes such as transcription and translation processes) [7,8]. In addition, gene state fluctuations from the binding/unbinding of the regulatory proteins to the promoters can be significant for gene expression dynamics. A remarkable feature of ES cells is the large cell-to-cell variation in the expression level of NANOG and other stem cell marker genes, showing their phenotypic heterogeneity, which can be crucial to the differentiation process of ES cells [9,10]. Conventionally, the binding/unbinding of the regulators to the genes was assumed to be significantly faster than the synthesis and degradation of the gene products, the proteins (adiabatic limit) [11,12], which is often observed in prokaryotic cells such as bacteria. However, in eukaryotic cells, the effective binding/unbinding process can be comparable or even slower than the corresponding synthesis and degradation of proteins (non-adiabatic limit) owing to, for example, the slow entry of regulators to the cell nucleus, transcription initiation or epigenetics of DNA methylation and histone modification. Non-adiabatic effects can introduce new timescales and induce important changes, such the appearance of non-trivial stable states and generating additional fluctuations other than those generated by intrinsic and extrinsic sources [13–23].

The epigenetic landscape concept was proposed by Waddington [24] to explain the development and differentiation process of cells as a metaphor, which provided a qualitative picture with which to explain the dynamics governing cell development. This picture has been quantitatively realized via investigation of the global nature of the network based on the probabilistic landscape framework [23,25–29]. The state space of the underlying gene regulatory networks is vast. For example, if the network has N genes and each gene has M different expression levels, then the total number of possible states is M^N. Therefore, the state space is composed of states with the combinations of all the possible expression levels of each gene, forming different expression patterns (such as ES marker gene NANOG and OCT4) of the cell and characterizing different cellular phenotypes. Although the number of possible states is huge, the number of phenotypes are often finite. In other words, not all the states have equal probability of appearing. Using the landscape framework, cell types are represented by basins of attraction on the landscape, which reflect the probability of appearance of different cell types. Attractor states have lower potential or higher probability and represent biological functional states or phenotypes. So, biological processes, such as cellular differentiation or lineage commitment, can be understood as the transition from one attractor to another in the state space of the underlying gene regulatory networks. By quantifying the topography of the potential landscape, the transition rates and paths, we can explore the global stability, kinetic speeds and the associated processes of cell fate decision-making.

We will explore the underlying landscape of a stem cell developmental and differentiation network with nine core gene nodes, from both adiabatic and non-adiabatic perspectives, by studying the underlying regulation dynamics and uncover the functional mechanism of transitions for differentiation, reprogramming and transdifferentiation. When the effective binding/unbinding speed ω decreases, the landscape experiences a transformation from bistable attractor states with stem cell and differentiated cell states to multi-stable attractor states with stem cell and other different cell states, including differentiated states, intermediate states and metastable substates. This indicates that non-adiabatic effects promote the appearance of more differentiated cell types and provides a natural explanation for the heterogeneity observed in the experiments [9,10], whereas the conventional adiabatic approach cannot usually lead to the distribution of multiple states. Heterogeneous distribution provides a window for quantifying the underlying structures through statistics of basins and metastable basins of the Waddington landscape from experimental measurements. When mutual activation or repression regulation strength decreases, the differentiation process proceeds from favouring a stem cell state to favouring a differentiated cell state via fast binding/unbinding in the adiabatic case, which reflects changes in the topography of the underlying landscape. This gives a quantitative Waddington downhill landscape for development controlled by changes in regulation. Regulatory changes that occur during developmental processes have been implied in experiments investigating the transcription factor, KLF4 [30]. The downhill trend of the Waddington landscape as a result of regulation timescale changes (slower) is preserved even in the non-adiabatic case to a large extent. This shows that both regulation strengths and regulation timescales can be used to quantify the downhill direction and shape of Waddington landscapes of development and differentiation. The transition rates between different attractors are correlated with the topography of the landscape via interposed barrier heights and serve as the quantitative measure for global stability and kinetic speed of cell fate decision-making processes from one cell type (cell fate attractor) to another. We found the optimal speeds of these cell fate decision processes for differentiation, reprogramming and transdifferentiation. Based on analysis of the kinetic paths, we provide quantitative predictions on the pathways for differentiation, reprogramming and transdifferentiation. We quantified biological paths and predict that differentiation and reprogramming go through an intermediate state (IM1), whereas transdifferentiation goes through another intermediate state (IM2). Some of our predictions are validated by experimental studies. Other predictions will be tested in future experiments. Through analysis of the underlying landscape, we can uncover the mechanisms involved in differentiation, reprogramming and transdifferentiation. Our predictions regarding the biological paths can be used to guide the design of new differentiation or reprogramming tactics.

2. Results and discussion

2.1. Epigenetic landscape

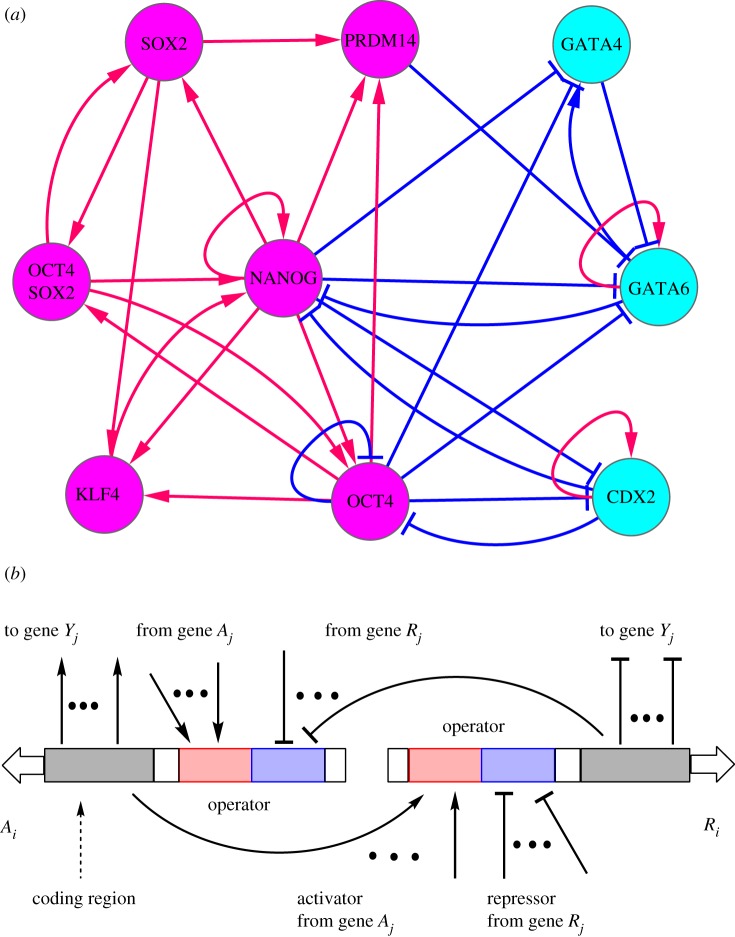
Several studies have been undertaken to investigate the landscape and path of cell fate decision processes based on the corresponding gene regulatory network [25–27,31]. An underlying gene network of human ES cells was explored [31] via a literature search. The underlying gene regulatory wiring is the basis for quantifying the landscape and paths for differentiation, reprogramming and transdifferentiation. Here, focusing on the core cellular developmental marker genes and key transcription regulations [31–33], we constructed an ES cell network comprising nine nodes after undertaking a literature search and integrating previous known networks, as shown in figure 1a.

Figure 1.

The wiring diagram for the stem cell developmental network including nine core gene nodes and their interactions (arrows represent activation and short bars represent repression) (a). The magenta nodes represent six marker genes for the pluripotent stem cell state (NANOG and OCT4 as major ES marker genes), and cyan nodes represent three marker genes for the differentiation state, in which GATA6 is the marker gene of primitive endoderm (PE) state and CDX2 is the marker gene of TE (trophectoderm) state. (b) Illustration of the computation model considering gene binding/unbinding reactions for the nine core node stem cell network. Arrows represent activation, and short bars represent repression. A represents activator genes, and R represents repressor genes. Y represents any genes (activator or repressor). Red regions represent operators for activation, and blue regions represent operators for repression.

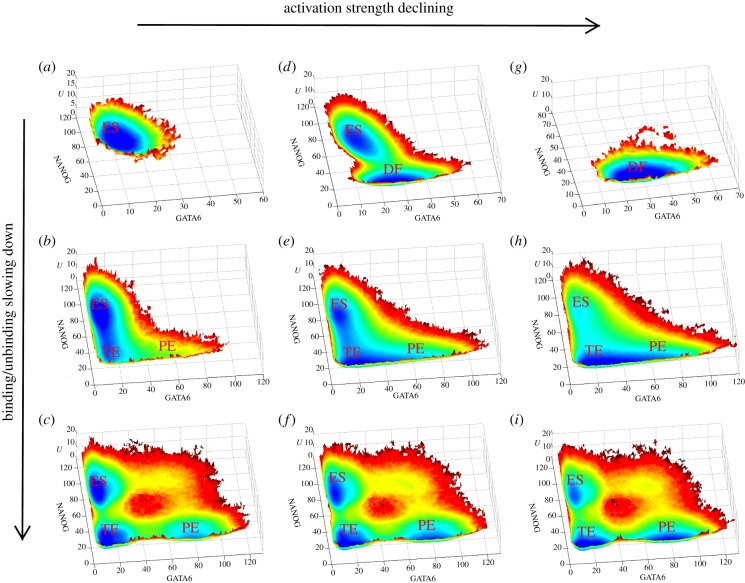
Following the stochastic modelling procedure outlined for our model (see section Materials and methods), we acquired stochastic dynamic trajectories of the stem cell developmental gene regulatory networks with nine core genes represented by nine variables. As a result of the statistical analysis, we obtained the steady-state probability distribution, and further the potential landscape, according to U = −lnP_ss [13,21,23,25–27,34–40]. Here, P_ss is the steady-state probability distribution in the state space of relative gene expression levels. Figure 2 shows the landscape projection in two gene expression variable state space in terms of variable GATA6/NANOG at different binding/unbinding speeds ω (ω = 1000, 1, 0.01 separately from top row to bottom row) as well as different mutual activation strengths f_B (f_B = 120, 60, 0 separately from left column to right column). The vertical axis represents the potential landscape U, and the horizontal axis represents the expression level of GATA6 and NANOG. Here, NANOG is a major stem cell marker, with high NANOG expression representing more stemness, whereas GATA6 and CDX2 are two differentiation markers, with high GATA6 or CDX2 representing higher differentiation. The combinations of high stem (differentiation) cell marker expressions and low differentiation (stem) cell marker expressions produce stem (differentiation) cell states (attractors), whereas any other combinations produce intermediate states. Differentiation (reprogramming) can be quantitatively represented on the landscape by the transition from a ES stem cell (differentiation) attractor to a differentiation (ES stem cell) attractor.

Figure 2.

Landscape picture with respect to gene GATA6/NANOG for the stem cell network at different binding/unbinding speeds ω as well as different activation strength f_B. The binding/unbinding speed ω is decreased from top to bottom (ω = 1000 for the (a,d,g), ω = 1 for the central row and ω = 0.01 for the bottom row). The activation strength is decreased from left to right (f_B = 120 for (a–c), f_B = 60 for (d–f), and f_B = 0 for (g–i)). ES represents stem cell attractor state (high NANOG/low GATA6/low CDX2). DF represents differentiation attractor state. PE and TE separately represent primitive endoderm attractor state (low NANOG/high GATA6/low CDX2) and trophectoderm attractor state (low NANOG/low GATA6/high CDX2). Other parameters are specified as: k = 1 (degradation), 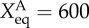, , 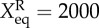f_A = 10, f_R = 60.

Figure 2 provides a quantitative Waddington landscape with two possible cell fate decision mechanisms (horizontal direction and vertical direction), where different cell types are quantitatively represented by the potential basins on the landscape. The horizontal direction gives a differentiation mechanism owing to the change of regulation strength. We can see that, in the adiabatic case (ω = 1000, figure 2ad,g) with the mutual activation strength f_B (representing the strength of mutual activation between major ES marker genes, see Materials and methods for parameter details) decreased, the landscape changes from a monostable attractor (ES stem cell preferred, f_B = 120, figure 2a), to a bistable attractor (ES and differentiation state coexist, f_B = 60, figure 2d), and finally to another monostable state (differentiation cell state preferred, f_B = 0, figure 2g). This demonstrates that when the mutual activation strength decreases, the evolution of differentiation proceeds from stem cell preferred to differentiated cell states preferred as reflected by changes in the topography of the underlying landscape [23,25–27] for fast binding/unbinding in the adiabatic case. This is the quantified Waddington landscape for differentiation and development resulting from regulation. As we can see, the downhill direction of the Waddington landscape is quantitatively represented by the regulation strength. The gene state starts from the stem cell basin (preferred) state, and as a result of regulations and stochastic fluctuations evolves to the differentiation preferred cell basin. In non-adiabatic limits (ω = 0.01, figure 2c,f,i), similar trends are maintained by the landscape, indicating that when the mutual activation strength is high, the ES state is preferred (figure 2c) and when the mutual activation strength is low, the differentiation states (splitting to primitive endoderm (PE) state and trophectoderm (TE) state) are preferred (figure 2i). However, the dominance of the ES state at large f_B or differentiation states at small f_B is not as prominent as in the adiabatic case. This is because non-adiabaticity can promote the appearance of more cell types with more heterogeneity. Thus, the dominant states are not as prominent as in the adiabatic case.

Meanwhile, we found another way to formalize cell fate commitment. Along the vertical direction (central column in figure 2), we can see that when the regulator–gene binding/unbinding speed, ω, decreased from 1000 to 0.01, the landscape changed from bistability to multi-stability. Under adiabatic conditions (fast gene binding/unbind switch, ω = 1000), the landscape exhibited a bistable shape (figure 2d), where the two stable states respectively represent the ES stem cell state and the differentiation state (DF). Increasing the non-adiabaticity or slowing down the effective regulator–gene binding/unbinding (ω decreased), we found that the differentiation attractor gradually splits into two new attractors. Biologically, these two new attractors (two new differentiation states) correspond directly to the PE state (PE state in figure 2f, with low NANOG expression, high GATA6 expression and low CDX2 expression) and the TE state (TE state in figure 2f, with low NANOG expression, low GATA6 expression and high CDX2 expression) [33]. Looking specifically at the evolution of the vertical direction, we see that the first column (figure 2a–c) indicates that by increasing the non-adiabaticity (slowing down of effective binding/unbinding) the cell has the potential to reach the final differentiation state (TE and PE) from the original ES state. The second column (figure 2d–f) shows that non-adiabaticity can promote the occurrence of more differentiated cell types. Therefore, both columns provide quantified downhill Waddington landscapes for differentiation along the effective binding speed direction. As we can see, the downhill direction of the Waddington landscape is quantitatively represented by the binding speed. The gene state starts from the stem cell basin (preferred) state, and through binding speed changes and stochastic fluctuations it evolves gradually to the more differentiation-preferred cell basins. One can argue whether or not the regulation timescales change significantly during differentiation. Owing to the heterogeneity among individual cells [9,10], the distributions of regulation timescales seem natural. Although the timescales do not change significantly, the individual subfigures, figure 2b–i, with fixed binding/unbinding speeds clearly show the quantified downhill Waddington landscapes. The third column (figure 2g–i) shows that differentiated cell states can differentiate to more cell types under non-adiabatic conditions, and they have the potential to be reprogrammed to the ES state by increasing non-adiabaticity as reflected by the shallow ES attractor (figure 2i).

From the corresponding landscape in GATA6/CDX2 expressions (see electronic supplementary material, figure S1), we can see the same transformation process for attractors on the landscape with increasing non-adiabaticity. We can see there are four attractors on the landscape of the electronic supplementary material, figure S1d. Here, the high GATA6/high CDX2 attractor is an intermediate state, corresponding to the IM2 state in figure 3 or figure 4. We will analyse the effects of the two intermediate states in the section on dynamical transition paths (figures 3 and 4). In figure S1d, the two-dimensional projection from high dimensional state space (52 dimensions) will miss information and can have the same state with different natures (the same values in two-dimensional variables but different in values of other 50 variables). Therefore, the low GATA6/low CDX2 attractor from the two-dimensional projection represents both the ES stem cell state and another intermediate state (IM1 in figure 3 or figure 4). We can see that the intermediate states, as well as two new differentiation states, appear only under non-adiabatic conditions with more heterogeneity.

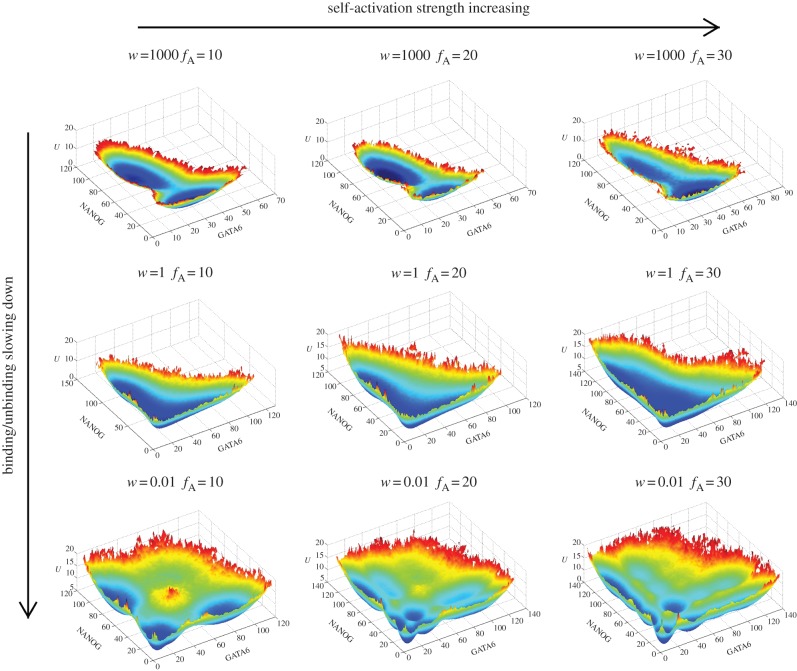
Figure 3.

Changes of landscape topography of nine core node gene regulatory network of stem cell development at different binding/unbinding speeds ω when the activation regulation (class A activation, self-activation for both ES markers and differentiation markers) strength changes. We can see with binding/unbinding speed ω decreased, the bistable landscape gradually evolves to have multi-stable attractors. Parameters are specified as: k = 1 (degradation), X_eq^A = 600, X_eq^A = 2000, f_R = 60 and f_A = 10, 20, 30 separately for the first column, second column and third column.

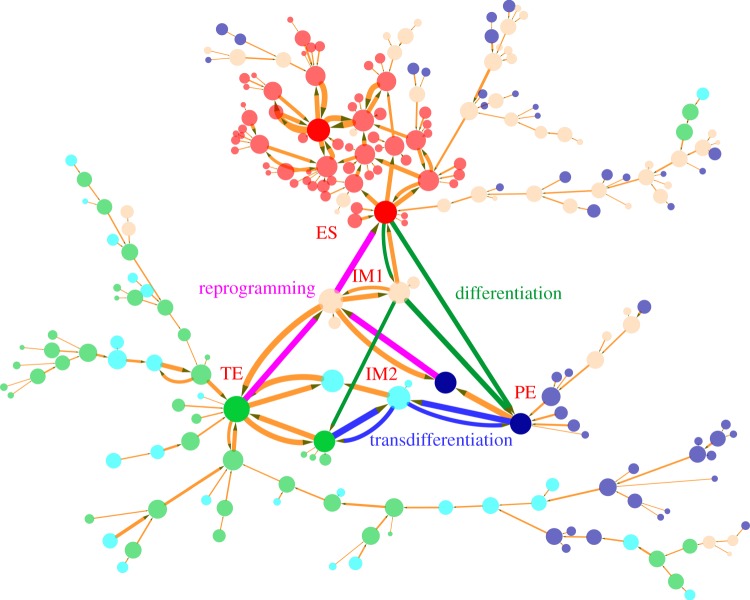
Figure 4.

Differentiation, reprogramming and transdifferentiation represented by 234 nodes (every node denotes a cell state, characterized by expression patterns of the nine marker genes) and 263 edges (transition paths) for slow regulatory binding/unbinding when ω = 0.01. The sizes of nodes and edges are proportional to the occurrence probability (or potential in the landscape) of the corresponding states and paths, respectively. Red nodes represent states that are closer to stem cell ES states in terms of gene expression pattern, and blue nodes and green nodes separately represent states that are closer to PE and TE (two different differentiation states, marked respectively by GATA6 and CDX2). The green and magenta paths denote kinetic paths for differentiation and reprogramming respectively, and blue paths represent transdifferentiation between the PE differentiation state and the TE differentiation state. IM1 and IM2 separately denote intermediate state 1 (low NANOG/low GATA6/low CDX2) and intermediate state 2 (low NANOG/high GATA6/high CDX2). Here, we set a probability cut-off to decrease the number of states and paths appearing on the figure, i.e. we demonstrate only the states and paths with higher probability.

Therefore, our results clearly reflect the effects of non-adiabaticity on the cellular developmental process, which promotes the appearance of multiple differentiation states (PE and TE) and intermediate states. This provides another cellular differentiation or reprogramming mechanism induced by non-adiabaticity. Recently, slow (non-adiabatic) NANOG switching was suggested to mediate distinct cell fate decisions [9,10,23,33]. However, it is worthwhile noting that the network used for the studies before [9,10,23,33] includes some hypothetical regulation links, such as GATA6 and CDX2 mutually repressing each other, and the acquired double differentiation state were marked separately by the expression of GATA6 and CDX2. The possibility that the mutual repression leads to the occurrence of double stable differentiated states cannot be completely precluded because mutual repression is a source of bistability. In our studies, mutually repressed GATA6 and CDX2 links are not used in the core network, because, as yet, there is supporting experimental evidence. We also obtained the double differentiation states. Therefore, our results indicate that the occurrence of double differentiation states (one differentiation state becoming two differentiation states) can be purely due to the increase in non-adiabaticity or the slowing down of the gene binding/unbinding speed rather than due to direct regulation links.

We quantified the Waddington landscape for differentiation and reprogramming of a core gene regulatory network [25,26]. A dynamic Bayesian network (DBN) method was used to explore the underlying gene regulatory network of hESC [31] and a bistable landscape emerges. Based on the underlying gene regulatory network [31], our previous work [27] uncovered the potential landscape and dynamic paths for cellular differentiation and reprogramming of human stem cells in the adiabatic case with fast regulatory binding to the gene. In this work, we explored the network landscape from the non-adiabatic perspective, by looking at the changes to the speed of regulator–gene binding/unbinding.

Therefore, we obtained Waddington landscapes in both directions (regulation strength and regulation timescale) shown in figure 2. Both result in bias from the stem cell state towards the differentiated states. This provides the direction or time arrow of the development. The timescale changes appear to produce more substate basins, thus indicating a possible mechanism for the heterogeneity observed in the experiments.

In addition, the mutual repression regulation strength, f_R, was also changed to investigate its influence on the topography of the landscape (see electronic supplementary material, figure S2). We found that under non-adiabatic limits (third row), when f_R is large the ES state is preferred and when f_R is small, the differentiation states (splitting to PE and TE) are preferred. This might be because increasing mutual repression (most of the repression in the network are mutual repression) is advantageous to the ES state, because many ES marker genes self-activate each other. Therefore, decreasing the repression strength of regulations may represent another mechanism of differentiation dynamics, characterized by the ES attractor becoming less stable and differentiation attractors (PE and TE) becoming more stable on a landscape under non-adiabatic limits.

We also changed the self-activation strength for both the ES marker and the differentiation marker (figure 3) to explore the impact on the landscape topography. We can see that at slow regulatory binding/unbinding (non-adiabatic limits, third row), the landscape of larger self-activation is different from that of lower self-activation regulation. More basins of attractions appear on the landscape. This indicates the appearance of more cell types. Many of them are shallower basins and they are often clustered in the state space. These basins of attractions are often metastable and can represent cell types or cell subtypes (smaller and shallower basins representing cell subtypes within larger and deeper basins representing cell types). The metastable basins and stable basins of cell types and subtypes that emerge from non-adiabaticity provide a possible mechanism for the heterogeneous distribution of the gene markers in development and differentiation [9,10]. On the other hand, by experimentally measuring the heterogeneous distribution, one can infer the structure of the underlying landscape topography such as basin distribution, sub-basin statistics, etc. In this way, we can use experiments to explore the global mechanisms of differentiation and reprogramming. We see that the cell might control the number of differentiation cell types by changing the self-activation strengths for both the ES marker and the differentiation marker.

We can see that the parameter changes will influence the shape of the landscape, and can be explained well (changing self-activation strength in figure 3, changing repression strength in the electronic supplementary material, figure S2 and changing the equilibrium constant in the electronic supplementary material, figure S3). This validates the robustness of the model.

2.2. Dynamical transition paths for differentiation, reprogramming and transdifferentiation

In order to demonstrate the cell states and the transitions between different cell types in the complete state space, we projected the expression level of the nine marker genes to binary states (in total 2⁹ cell states). For example, the stem cell ES state is represented by the binary number 1 1 1 1 1 1 0 0 0 (respectively characterizing expression level of nine marker genes, 1 for high expression, 0 for low expression). Here, the nine marker genes correspond to the six stem cell ES marker genes: OCT4, SOX2, NANOG, SOX2, KLF4, PRDM14, and three differentiation marker genes: GATA4, GATA6 and CDX2. In the same way, the PE differentiation state is denoted by 0 0 0 0 0 0 1 1 0, and the TE differentiation state is denoted by 0 0 0 0 0 0 1 0 1. Figure 4 shows the differentiation, reprogramming and transdifferentiation process under non-adiabatic conditions (ω = 0.01, f_R = 60, f_A = 10, f_B = 60) represented by 234 cell states (nodes, characterized by expression patterns of the nine marker genes) and 263 transition paths (edges) between the different cell states (produced by Cytoscape v. 3.0.0 [41], see the electronic supplementary material, for methods acquiring transition paths). The sizes of the nodes and edges are respectively proportional to the probability of the corresponding states and transition paths. Red nodes represent states that are closer to the stem cell ES state in terms of gene expression patterns (two deep red nodes represent two major stem ES states). Blue nodes (two deep blue nodes represent two major differentiated PE states) and green nodes (two deep green nodes represent two major differentiated TE states) separately represent states that are closer to the PE and TE (two different differentiation states, marked respectively by GATA6 and CDX2) states. In particular, we exhibited the nine dimensional kinetic paths (biological paths). The green and magenta paths denote kinetic paths for differentiation and reprogramming respectively, and blue paths represent transdifferentiation between the PE differentiation state and the TE differentiation state. Additionally, we note that two classes of other high probability states (the light yellow and light blue nodes) exist on the transition path figure. They separately represent two intermediate states, which are low GATA6/low CDX2 (double low, IM1 state) state and high GATA/high CDX2 state (double high, IM2 state).

Figure 4 also provides another landscape perspective for stem cell differentiation, reprogramming and transdifferentiation. Here, the ES stem cell state quantified on the landscape by a basin of attraction has high NANOG, low GATA6 and low CDX2 expressions. The PE differentiation state quantified on the landscape by another basin of attraction has low NANOG, high GATA6 and low CDX2 expressions and TE differentiated state quantified on the landscape by yet another basin of attraction has low NANOG, low GATA6 and high CDX2 expressions. We can see that the major stem cell attractors or basins are surrounded by some smaller sub-basins of high similarity to the stem state but relatively lower probability or higher potential. These sub-basins can jump in and out of the major basins with larger weights and, from there, finally converge to the most stable stem cell attractor (large deep red nodes). The states in the stem cell cluster seem to converge to the major stem cell attractor through the major basins. Substate convergence leads to the major basin. So the picture is much like a funnel from the substate basins to the major basins and finally to the most stable stem cell basins. This shows the robustness of the stem cell state. In the same way, the TE differentiation attractor state (green nodes, bottom left of the figure) and PE differentiation attractor state (blue nodes, bottom right of the figure) are also both characterized by large basins surrounded by a cluster of smaller basins. The smaller substate basins in each cluster can make transitions to their corresponding major basins. Therefore, the states in each cluster seem to converge to the major differentiation attractors. The major attractors then converge to the corresponding most stable differentiated state attractors. This again is analogous to the funnels from the substate basins to the major basins and finally to the corresponding most stable differentiated state basins. It shows the robustness of two differentiation attractor states. The distributed substate basins for stem and differentiated state clusters provide the physical basis for explaining the experimentally observed heterogeneous population distribution of the marker gene expressions.

In addition, focusing on the transition paths, we find that for differentiation and reprogramming processes, cells go through intermediate state 1 (IM1, low NANOG/low GATA6/low CDX2), and for transdifferentiation (transition from PE to TE or from TE to PE) cells go through intermediate state 2 (IM2, low NANOG/high GATA6/high CDX2). For differentiation, we predict that the cell needs to go through the intermediate state 1, before differentiating to either the PE state or TE state. This is consistent with our previous work on cellular differentiation and reprogramming under adiabatic limits [27]. Additionally, except for going through the IM1 state, the cell has another option, which is to undergo direct differentiation (green path from ES to PE, also seen in figure 5) without passing through any intermediate states. This direct differentiation path needs to be confirmed by experiments. For the reprogramming process, we predict that the cell also needs to go through the IM1 state (low NANOG/low GATA6/low CDX2) before reaching the ES state. Recent work has confirmed our prediction [42,43].

Figure 5.

Illustration for major attractors and transition paths of cell fate decisions in non-adiabatic slow binding/unbinding conditions (ω = 0.01). ES represents stem cell attractor state (high NANOG/low GATA6/low CDX2). PE and TE separately represent the primitive endoderm attractor state (low NANOG/high GATA6/low CDX2) and the trophectoderm attractor state (low NANOG/low GATA6/high CDX2). IM1 and IM2 separately denote intermediate attractor state 1 (low NANOG/low GATA6/low CDX2) and intermediate attractor state 2 (low NANOG/high GATA6/high CDX2). It can be seen that both differentiation and reprogramming processes go through the IM1 attractor state, and the transdifferentiation process goes through the IM2 attractor state. In addition, differentiation can also follow a direct path not going through the IM1 attractor state (path from ES to PE).

Regarding cellular transdifferentiation, our prediction is consistent with the results supported by experiments in mouse embryo cardiac fibroblast cells that transdifferentiation may pass through a double positive intermediate state (marker genes for two differentiation states both have high expression levels) [42–44]. Considering that we used different cell developmental and differentiation networks to those used in previous studies [43], this indicates that cells may adopt some common mechanisms in cell fate decision processes for differentiation, reprogramming and transdifferentiation.

At the bottom of figure 4, we can see a side branch, where green nodes (TE states) and blue nodes (PE states) can make mutual transition through cyan nodes (IM2 state). This represents a branch or side pathway for transdifferentiation. In the upper right corner, there is another side branch, where blue nodes (PE states) can transform to red nodes (ES states). This represents a branch or side pathway for reprogramming. In addition, the left branch of the figure represents that TE states (green nodes) and IM2 states (cyan nodes) can transform to each other and eventually approach the major TE stable state (large deep green nodes). These side pathways have lower probabilities than the major pathways discussed.

To display figure 4 in a more understandable way, we provide a corresponding illustration (figure 5), describing major basins of attractors and transition paths on the quantified Waddington landscape of the cell fate decision-making process under non-adiabatic conditions (ω = 0.01). In total, there are five major stable attractor states for the non-adiabatic stem cell network. ES represents the stem cell attractor state. PE and TE separately represent the PE attractor state (high GATA6 expression/low CDX2 expression) and TE attractor state (low GATA6 expression/high CDX2 expression). IM1 and IM2 separately denote intermediate attractor state 1 (low NANOG/low GATA6/low CDX2) and intermediate attractor state 2 (low NANOG/high GATA6/high CDX2). We can see that the differentiation and reprogramming processes both go through IM1 attractor state, and the transdifferentiation processes both go through IM2 attractor state. In addition, differentiation can also be realized directly from the ES attractor state to the PE attractor state (green path from ES to PE) not going through the IM1 attractor state.

We have previously quantified the reprogramming paths for a core gene regulatory network [25,26]. A strategy to find reprogramming recipes was suggested based on DBN methods [31]. Some of the reprogramming recipes found are consistent with experiments. Here, for a different mechanism with non-adiabatic slow regulation binding (regulators binding to the gene), we quantify the kinetic paths for differentiation, reprogramming and transdifferentiation (the transition between different differentiation cell states). The method presented here of quantifying the reprogramming and transdifferentiation paths is general and can be applied to other realistic large underlying gene regulatory networks.

2.3. Kinetic speed from mean first passage time

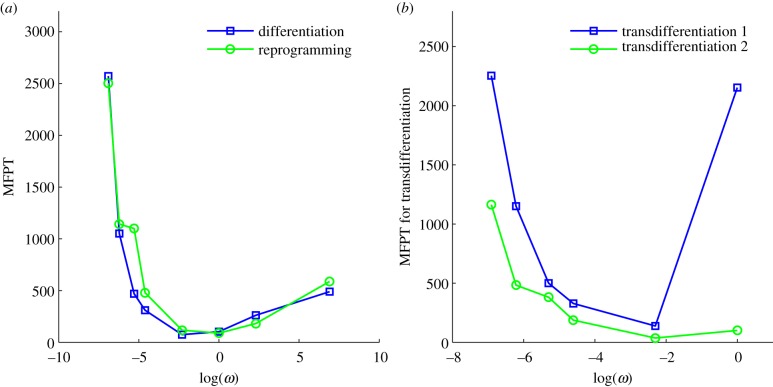
In order to quantify the dynamics of differentiation, reprogramming and transdifferentiation, we further investigated the kinetics or speed of different processes according to the mean first passage time (MFPT), which is shown in figure 6a,b. MFPT reflects the average transition time of the system jumping from one attractor to another attractor in the state space of the gene regulatory network, and therefore can be used to quantify the ability of the cells switching from one cell type to another (for example, from stem cell to differentiated cell in the development and vice versa in the reprogramming). We can see that for differentiation, reprogramming and transdifferentiation, the MFPT (figure 6a,b) first decreases and then increases when the binding/unbinding speed ω increases. Under non-adiabatic conditions (slow binding/unbinding speed ω), the dynamics of the system is controlled by the slow binding/unbinding events because that is the rate limiting step. Therefore, increasing binding/unbinding speed ω will accelerate the kinetics for all transitions of state, including differentiation, reprogramming and transdifferentiation. For large ω values, owing to the frequent binding/unbinding events, the dynamics of the system is determined by the topography of the resulting effective potential landscape. MFPTs are determined by the potential barrier between different cell attractor states. Therefore, at faster binding/unbinding speeds, the MFPT becomes larger with the increase of ω, because the potential barriers between the ES state and the differentiation state (at large ω, only one differentiation state exists) increase, which we can see from the landscape change from figure 2e (ω = 1) to figure 2d (ω = 1000).

Figure 6.

(a,b) The mean first passage time (MFPT) or kinetic transition time for cell type changes through differentiation, reprogramming and transdifferentiation when the binding/unbinding speed ω changes. In (b), transdifferentiation 1 represents MFPT from the TE cell attractor state to the PE cell attractor state, whereas transdifferentiation 2 represents MFPT from the PE cell attractor state to the TE cell attractor state. When ω increases, the MFPT for differentiation, reprogramming and transdifferentiation first decreases, then increases.

This means that the cell has an optimal speed for differentiation, reprogramming or transdifferentiation at a specific speed ω of regulatory binding/unbinding to the gene, which indicates that by changing ω (owing to the change in some epigenetic process such as histone modification, DNA methylation or slow transcription initiation and entry to the cell nucleus, etc.) cells might not only control the appearance of more differentiation states and therefore heterogeneity, but also adjust transition speed among different cell types (differentiation speed, reprogramming speed or transdifferentiation speed). This prediction needs to be confirmed by future experiments, and can be used as a potential guideline to design cellular differentiation, reprogramming or transdifferentiation with optimal speeds.

3. Conclusion

In summary, we developed a model to study epigenetic dynamics and uncovered the underlying landscape of a stem cell developmental network. With slower effective regulatory binding/unbinding to the gene (when the binding/unbinding speed ω is decreased, leading to the increase of non-adiabaticity), the global topography of the landscape of cell development gradually changes from bistability to multi-stability, and therefore we witness the effects of non-adiabaticity (slow binding/unbinding switch) on the appearance of more cellular differentiation types. This provides possible mechanisms for the experimentally observed heterogeneous distribution of gene markers in differentiation and development [9,10]. On the other hand, the experimentally observed heterogeneous distribution allow us to uncover the underlying structure of the Waddington landscape in terms of statistics of stable and metastable basins of attraction representing the emergence of cell types and cell subtypes. We found that when the activation or repression regulation strengths become lower, the evolution of differentiation proceeds from favouring stem cell states to favouring differentiated cell states, which is reflected by the changes in the topography of the underlying landscape [23,25–27] for fast binding/unbinding in the adiabatic case. This trend is largely preserved even in the non-adiabatic case.

Based on the analysis of dynamic transition paths between different phenotypes, we predict that cellular differentiation and reprogramming need to go through a specific intermediate state (IM1, low NANOG/low GATA6/low CDX2), and transdifferentiation between two different differentiation states (PE and TE) needs to pass through another specific intermediate state (IM2, low NANOG/high GATA6/high CDX2 state). Our predictions are consistent with recent experimental studies. Meanwhile, we also propose more experiments regarding the pathways of cell fate decisions-making processes to test these predictions. By calculating MFPT between different cell types, we provide an avenue to acquire information regarding transition rate or kinetic speed for the changes of the cell types through differentiation, reprogramming as well as transdifferentiation, which can be directly tested from the experiments.

It should be noted that the stem cell network we used comprises only certain general biological gene markers and their mutual regulations for stem cell development and differentiation. With more biological details added into the ES developmental network, such as incorporating core marker genes that guide primitive ectoderm to further differentiate into the primary germ layers, it is anticipated that we can discover more intricate mechanisms in cell fate decision processes through exploring potential landscape and kinetic paths. Our work has provided a general framework to explore the landscape and paths of gene regulatory networks from adiabatic and non-adiabatic perspectives. In principle, with enough gene interaction details, one can construct a more comprehensive ES network considering neural differentiation types, endodermal or other differentiation cell types. With these networks constructed, we believe that our landscape and path framework can be used to quantitatively investigate the corresponding differentiation, reprogramming and transdifferentiation processes in terms of other differentiation cell types. Additionally, a recent study reported that OCT4 has a dual function in cell fate decision processes, acting as an important factor for reprogramming and self-renewal [45], but also actively controlling cell state transitions during entry into and exit from the naive pluripotent state [46]. Our current model cannot explain this phenomena. We may need more details regarding gene regulation (more genes and more links between OCT4 and other marker genes) added into the ES network to uncover the mechanism of the dual function of OCT4 from a landscape perspective.

Our approach offers a general way to investigate the global properties—landscape topography, transition rate, kinetic path—of gene regulatory networks using information on interaction directions (activation or repression) from both transcriptional and epigenetic perspectives. In particular, we provide an approach to investigate landscape and biological paths of high dimensional systems under non-adiabatic slow binding conditions often found in eukaryotic cells. Our approach can be applied to other gene regulatory networks or protein networks.

4. Material and methods

4.1. Model for the stem cell developmental network

We constructed an ES cell network comprising nine core nodes by searching the literature and integrating previous known networks, as shown in figure 1a [31–33]. By comparing a human ES cell network [31] and a mouse ES cell network [33], we can see that they have some common core gene regulatory interactions. For example, the main ES marker genes include OCT4, SOX2 and NANOG; the major differentiation marker genes include GATA6 and CDX2; and the dynamics of system is mainly governed by the mutual repression between OCT4 and CDX2 (determining the TE lineage), and mutual repression between NANOG and GATA6 (determining the PE lineage). We extracted these core gene regulatory links and kept some genes, are vital to self-renewal with experimental evidence (KLF4 and PRDM14) [30], and formed our ES network. Some previous work also showed that over-expression of NANOG promotes maintenance of cell pluripotency [32,33,47].

This network includes nine gene/protein nodes and their interactions (totally 30 links including 17 activation links and 13 repression links), in which red arrows represent activation and blue bars represent repression. There are six marker genes for the pluripotency state (iPS state or stem cell state) and three marker genes for the differentiation state, which are separately coloured in purple and cyan. Positive feedback loops between OCT4, SOX2 and NANOG (stem cell marker) maintain their expression to promote continuous ES cell self-renewal. The high expression of NANOG, GATA6 and CDX2 separately characterize the ES cell state, the PE state and the TE state. So, the TE lineage is determined by the antagonism between OCT4 and CDX2, whereas the balance between GATA6 and NANOG determines the PE lineage [33].

The ES marker genes include OCT4, SOX2, NANOG, OCT4SOX2, KLF4, PRDM14, and the differentiation marker includes GATA4, GATA6, CDX2. Previous studies have suggested that the expression of GATA6 in mouse ES cells results in their differentiation into PE [48], and the expression of CDX2 induces ES cells to differentiate into TE [49]. Therefore, we define GATA6 as a PE marker and CDX2 as a TE marker.

Overall, the ES stem cell marker genes and differentiation marker genes have mutually repressed regulation effects, which means that high expression ES marker genes repress the expression of differentiation marker genes, and high expression differentiation marker genes repress the expression of ES marker genes. Some of these genes have self-activation regulations to their own expression, such as NANOG, GATA6, CDX2, etc.

These marker genes constitute a major stem cell gene regulatory network, which orchestrates some important cellular functions, such as cell differentiation, reprogramming and transdifferentiation. For instance, transcription factors OCT4, SOX2 and NANOG play important roles in the early development of cells and in the propagation of undifferentiated ES cells [50]. The proteins OCT4 and FOXD3 are transcriptional regulators expressed in ES cells. Downregulation of OCT4 is an essential requirement during gastrulation for proper endoderm development [51].

Figure 1b provides an illustration of our simulation model. The reactions in the network include degradation reaction, synthesis reaction and binding/unbinding reactions from gene regulation. Assume any gene Y from the network has an activation regulation from gene A and a repression regulation from gene R, then gene Y has six reactions in total, as follows:

Here, X represents protein concentration or relative gene expression level. O_ij represent the status of the promoter. For the gene state index ij, the first index i = 0(1) stands for the activator protein A unbound (bound) to the promoter; the second index j = 0(1) stands for the repressor protein R unbound (bound) to the promoter. 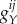is the synthesis rate of the protein Y when the gene Y is in state ij. The parameter k represents degradation rate.

For a network with n nodes and m edges (activation or repression links), there will be (2 × n + 2 × m) reactions in total, where m represents total regulation numbers, and n is the number of nodes. For the current nine-node network, we have 78 reactions, based on which we implemented stochastic simulation [52] to simulate the dynamics of the system.

The prefactor 2 in the rate equations indicates that activator A binds to promoters as a dimer, and 4 indicates that repressor R binds to promoters as a tetramer. We assume that activator A binds to promoters as a dimer, and repressor R binds to promoters as a tetramer. So far, we do not have the corresponding experimental evidence for this assumption. Therefore, this is a general choice of parameters and an assumption. Without other direct experimental results, we believe this is a reasonable assumption. We hope new experiments can be performed soon, upon which the regulation parameters in this mode can be amended. So, the binding rates have the form: 1/2h_An_A(n_A − 1) for the activators, and 1/4! h_Rn_R(n_R−1)(n_R−2)(n_R−3) for the repressors. Here, the binding/unbinding rate of the gene states is defined as: ω_A = f_A/k, ω_R = f_R/k, and the equilibrium constants are: 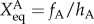, 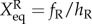. The parameters are set as: the protein degradation rate k = 1, the equilibrium constant, indicating the ratio between unbinding and binding speed, are set as , .

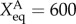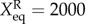In the network, there are two kinds of activation links. One is targeting genes which have both an activation and repression input. For this kind of activation, the activation constant is set f_A = 10 (class A activation). The other activation links target genes that only have activation links (no repression links). For this class of genes, we set the activation constant as f_B = 60 (class B activation), in order to keep the overall synthesis rate for all genes at the same level. The repression constant is set as f_R = 60, and the basal protein synthesis rate is f₀ = 5. Genes have a maximum protein synthesis rate when they are bound by activator A and unbound by repressor R: 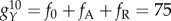. The minimum protein synthesis rate appears when promoters are unbound by activator A and bound by repressor R: 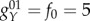. In the same way, the other two classes of synthesis rates are: 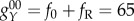(activator off, repressor off), and 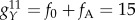(activator on, repressor on). See table 1 for parameters of reactions. For class B activation, we designate the two synthesis rates (high/low) as f₀ = 5 for the activator being off, and f₀ + f_B = 65 for the activator being on. We can find from the network links that the activation regulations for class B (f_B) all belong to the mutual activation between ES marker genes.

Table 1.

Parameter values for the model.

k	f0	fA	fB	fR	ωA = ωR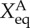
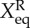1	5	10	60	60	0.01	600	2000

In simulation, the initial protein concentration is set as X_initial = 50 for all nine genes, and the initial promoter state is set as ij = 00 (no activator or repressor bound) for all nine genes.

4.2. The selection of parameters in the model

We first select the parameter regions in adiabatic conditions (fast gene binding/unbinding speed, ω = 1000). The parameter values are chosen according to the following criteria:

• (i) We chose parameter values according to previous studies [21–23] considering non-adiabatic simulation for gene regulatory system.

• (ii) The degradation, activation and repression strength are assumed to be uniform for different variables and have the same magnitude, because, so far, there is no information regarding the regulation strength of stem cell networks; this should come from the detailed biochemistry reactions involved in cellular development. Here, the degradation constant for every gene is set as k = 1, and the protein synthesis rate for every gene is set as f_A = 10 (activation open), f_R = 60 (repression close).

• (iii) Parameters were chosen that satisfied some biological constrains, including producing a stable steady state and either bistability or multi-stability, because the purpose was to explore cellular differentiation, reprogramming and transdifferentiation dynamics (multi-stable states).

In this way, the parameters chosen produced a relatively balanced bistable landscape (figure 2d, ω = 1000, other parameters are as table 1), separately representing the ES state and the differentiation state, under adiabatic conditions (fast gene binding/unbinding speed, ω = 1000). Then, we expanded the same parameter selection to non-adiabatic conditions (vertical direction of figure 2, decreasing ω, corresponding to the change from figure 2d,e, to f). In addition, for horizontal direction, the other parameters were changed in isolation (figure 3: changing self-activation strength; electronic supplementary material, figure S2: changing repression strength; electronic supplementary material, figure S3: changing equilibrium constant) from the default parameter values (table 1) to investigate the effect of these parameters on the landscape.

Funding statement

This work was supported by National Science Foundation.