High-resolution restoration of 3D structures from widefield images with extreme low signal-to-noise-ratio

Significance

Recording 3D fluorescent movies has become a critical tool of modern cell biology. Unfortunately, this requires exposure of the sample to such significant amounts of illumination light that the fluorophores become photobleached and the resultant oxygen radicals can significantly perturb cellular function (phototoxicity). Although widefield microscopy is very light efficient, generating high-quality 3D reconstructions requires removal of out-of-focus light in a process called deconvolution. Unfortunately, most deconvolution methods require high signal-to-noise ratios and are thus incompatible with the very low light levels required for unperturbed in vivo imaging. Here we present a novel deconvolution method that solves this problem, allowing illumination light to be reduced to extremely low levels, resulting in an enabling technology for in vivo imaging.

Abstract

Four-dimensional fluorescence microscopy—which records 3D image information as a function of time—provides an unbiased way of tracking dynamic behavior of subcellular components in living samples and capturing key events in complex macromolecular processes. Unfortunately, the combination of phototoxicity and photobleaching can severely limit the density or duration of sampling, thereby limiting the biological information that can be obtained. Although widefield microscopy provides a very light-efficient way of imaging, obtaining high-quality reconstructions requires deconvolution to remove optical aberrations. Unfortunately, most deconvolution methods perform very poorly at low signal-to-noise ratios, thereby requiring moderate photon doses to obtain acceptable resolution. We present a unique deconvolution method that combines an entropy-based regularization function with kernels that can exploit general spatial characteristics of the fluorescence image to push the required dose to extreme low levels, resulting in an enabling technology for high-resolution in vivo biological imaging.

The study of dynamic processes is an important facet of cell biology research. Fluorescently tagged proteins combined with four-dimensional fluorescence microscopy, which records 3D image information as a function of time, provide a powerful framework for studying the dynamics of molecular processes in vivo. One of the most crucial challenges in 4D fluorescence microscopy is to ensure that normal biological function is not significantly perturbed as a result of the high doses of illumination (phototoxicity) incurred during 4D imaging. Recent work indicates that the maximal photon dose that avoids biological perturbation is 100- to 1,000-fold lower than that typically used for in vivo imaging (1). Dose limitations are even more challenging, given the desire to densely sample in time or to record over extended periods, especially in the context of analyzing multiple subcellular components via multiwavelength imaging.

Under normal imaging conditions, widefield microscopy combined with image restoration using deconvolution methods provides an excellent modality for multiwavelength 4D imaging as it makes very efficient use of the illuminating photons. However, its effectiveness, in particular its ability to resolve subcellular detail sufficiently in the presence of noise, is limited by the performance of the deconvolution method. Such limitations can seriously degrade image quality at the low signal levels required for unperturbed in vivo imaging. The noise behavior of the deconvolution algorithm is determined by the efficiency of the noise stabilization term, known as the regularization functional. In particular, the functional’s ability to discriminate the noise-related high frequencies from weak high frequencies in the signal ultimately determines the final resolution of the deconvolution. Currently used noise-stabilization techniques are largely based on ad hoc formulations and perform poorly, leading to a serious loss of resolution at the low signal-to-noise ratios required to maintain the illumination at safe levels during multiwavelength 4D imaging. Surmounting this problem would dramatically increase the amount of biological data that could be safely acquired, paving the way for a much deeper understanding of the dynamics of biological processes.

We propose a unique deconvolution method that uses a regularization functional constructed using an entropy-based formalism that is tailored to exploit general spatial characteristics of the fluorescence images combined with the more robust use of second-order derivatives in the regularization functional. This entropic-based regularization suppresses large amounts of noise while at the same time preserving the essential details. Hence the method brings out details that are nearly invisible in the raw extremely noisy images and yields a substantially improved resolution. Using several datasets of fixed samples recorded at high and low doses, we quantitatively study the performance of our method, using Fourier shell correlation methods, and demonstrate that entropy-regularized deconvolution (ER-Decon) reveals considerably more detail of the underlying structure compared with existing methods.

Results

Mathematical Formulation of the Method.

Deconvolution is performed as a minimization task with the cost to be minimized being a weighted sum of (i) a data fidelity term measuring the goodness of the fit to the data, (ii) a functional to enforce smoothness (noise suppression), and (iii) a term to promote positivity. Mathematically, the minimization problem is stated as

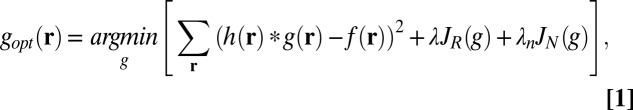where 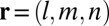represents the 3D pixel index, is the measured 3D widefield image, 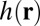is the 3D point spread function (PSF), is the functional for enforcing smoothness, which we call the regularization functional, and is the functional for enforcing positivity. Here, 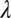is the regularization weight, which will allow a trade-off between the data fidelity and smoothness. Although the data fidelity term could be either quadratic as in the above equation or nonquadratic, nonquadratic data-fitting methods (2–6) are not practical on large datasets.

A smoothness-enforcing functional (hereafter referred to as the smoothness functional) is typically composed of derivatives because derivatives work as cost-effective high-pass filters, complementing the frequency support of the microscope’s transfer function. The earliest work that used derivatives constructed the smoothness functional as the sum of squares of the image gradients (7). The main advantage in minimizing the sum of squares is that the cost can be expressed in Fourier space and the solution can be obtained in a single step. Unfortunately, such methods are notorious for their low resulting resolution. As an improvement, many recent methods use the absolute value of derivative either directly (8, 9) or indirectly in the form of transforms containing built-in derivatives (10) and are considered to be superior to quadratic regularization methods (known as 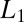or total variation methods). Even though there is no theoretical proof for their superiority, it is generally believed that their improved performance stems from the fact that the weaker penalty of minimizing the absolute value allows some high derivative points, whereas quadratic minimization tends to forbid high derivative points. The main problem is that most of the practical methods use first derivatives and hence the solution takes the form of piecewise constants when the noise is high. This is due to the fact that minimizing first derivatives does not give sufficient freedom for natural intensity variations of fluorescence images. Although this problem can be alleviated by using second-order derivatives, there are no practical numerical methods for handling the resulting complexity although there has been a recent attempt (11).

Our goal in this paper is to develop a method powered by (i) an improved and much more robust second-derivative–based regularization functional and (ii) a unique problem-specific computational method that can handle complexity resulting from using the second derivatives in regularization. The improved robustness of the regularization functional originates from two modifications that we propose to commonly used forms. To elaborate in more mathematical terms and to lead to the proposed modifications step by step, let be the digital filters yielding discrete implementation of all possible second-order derivatives. Their exact form is given in SI Text. Define

The standard quadratic regularization functional can be expressed as

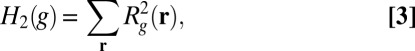whereas the more robust regularization functional can be written as

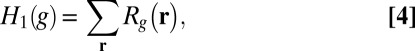which has been recently recognized to yield high-resolution restoration of images (8, 9, 12). As mentioned before, the main reason for the superiority of 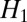is that 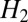forbids large derivative values, whereas 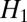allows few points to have large derivative values, thereby better matching the typical distribution of derivative values in images. This effect is commonly known as the sparsifying effect of 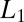regularization. Even though regularization has been applied for restoration of fluorescence images (8, 11), it does not exploit any specific properties of fluorescence images.

We first observe that, in fluorescence images, the percentage of points having nonnegligible derivative magnitudes is much lower than that in general images. Also, among the points that have nonnegligible derivative values, the ratio of high-magnitude derivative points vs. intermediate-magnitude derivative points is much higher compared with more generic images. Hence, using a weighting function that becomes flatter at high values will better preserve the intensity variations in fluorescence images. We propose to use

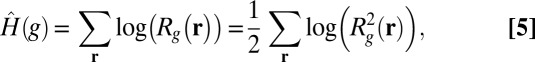which is flatter than 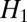at high values of derivative magnitude. To avoid a logarithm of zero, we modify it as

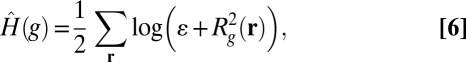where 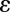is a small positive number. It is expected that this logarithmic weighting will have a more pronounced sparsifying effect and be better suited for restoring intensity variations in fluorescence images.

The second proposed modification is based on the following observation: In fluorescence images, compared with general types of images, high-intensity points are more sparsely distributed and are mostly colocalized with high-magnitude derivative points. Hence, under the sparsifying effect of the logarithm, including the intensity as well as the derivative magnitude will better capture the image patterns. Hence we modify 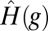as

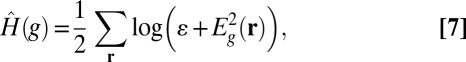where 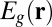is given by

Although one could include a separate weighting factor to distinguish the two terms inside the square root, based on deconvolution experiments, this seemed unnecessary. As we demonstrate experimentally, these two modifications will lead to a significant improvement in the output resolution. In SI Text, we interpret the difference between 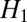and in an entropy minimization viewpoint and explain why 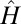is better suited for fluorescence images.

To complete the development of the deconvolution method, J_R in Eq. 1 should be replaced by 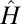of Eq. 7, and, J_N should be explicitly specified. We construct J_N as follows:

where

Hence the deconvolution problem becomes

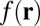Through reconstruction trials, we found that an appropriate choice is , assuming that has been normalized to the range [0,1] . An algorithm to solve the above minimization problem is given in SI Text and Figs. S1 and S2. We name our method ER-Decon. Note that and 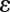are the only data-dependent user-adjustable parameters, with λ affecting smoothness and 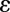most affecting restoration of weak intensities. Ideally, both of these parameters should be optimized for each class of problem.

Experimental Validation.

We validate the performance of the ER-Decon method on datasets with high levels of noise and compare it to two well-established modern methods that have the potential to perform well in the presence of significant noise: the Huygens constrained maximum-likelihood method from Scientific Volume Imaging and DeconvolutionLab’s wavelet-based deconvolution (10).

To quantitatively assess the performance of each method, we cross-validate the restoration obtained from low-dose data by correlating it with data from the identical fixed specimen imaged at high dose. To quantify the correlation at different levels of resolution, we use the Fourier shell correlation routinely used in the cryo-electron microscopy field, 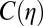, to measure the agreement between the low- and high-dose results at various levels of resolution, 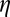. To define the correlation, let 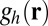and be the deconvolved images obtained from high- and low-dose measured images, respectively. Let 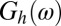and 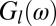be their Fourier transforms, where 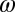is the 3D frequency vector. Then the correlation computed within the spherical shell of radius 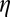in Fourier space is given by

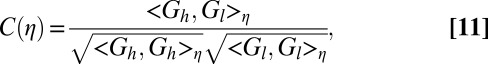where

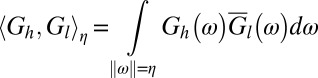with denoting the modulus of its vector argument. Regardless of the deconvolution method, we optimized all parameter settings, choosing the minimum amount of smoothing required to obtain a deconvolved output without any background oscillations. Further, we set the number of iterations to 100.

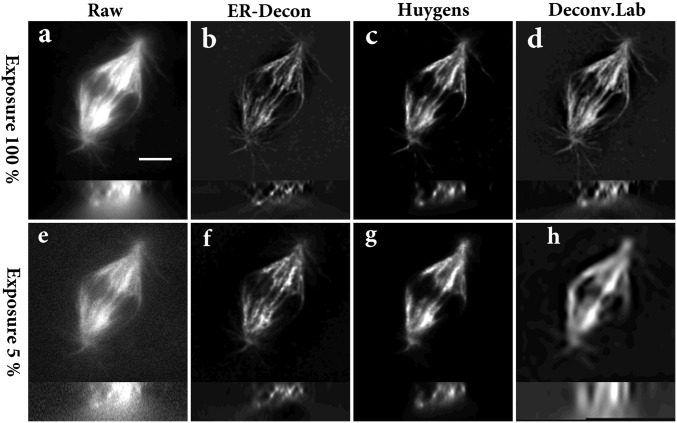
In the first biological experiment, we imaged immunolabeled mitotic spindles of fixed Drosophila S2 cells (Methods) in which the image stacks were acquired with dose levels differing by a factor of 20. Deconvolution results are given in Fig. 1, where in each image the upper part represents an xy section and the lower part represents an xz section for each of the different methods. It is clear that ER-Decon performs best at both dose levels. Although the resolution yielded by ER-Decon from the high-dose image is noticeably better than that by the other two methods, the superiority of ER-Decon is much more pronounced at the low-dose levels. In particular, ER-Decon’s output from the low-dose raw image resolves almost all of the microtubules, whereas many have merged together in the Huygens and DeconvolutionLab results. Note that for a new type of sample, optimization of parameters for ER-Decon typically involves scanning through three or four values for each of the two parameters. 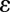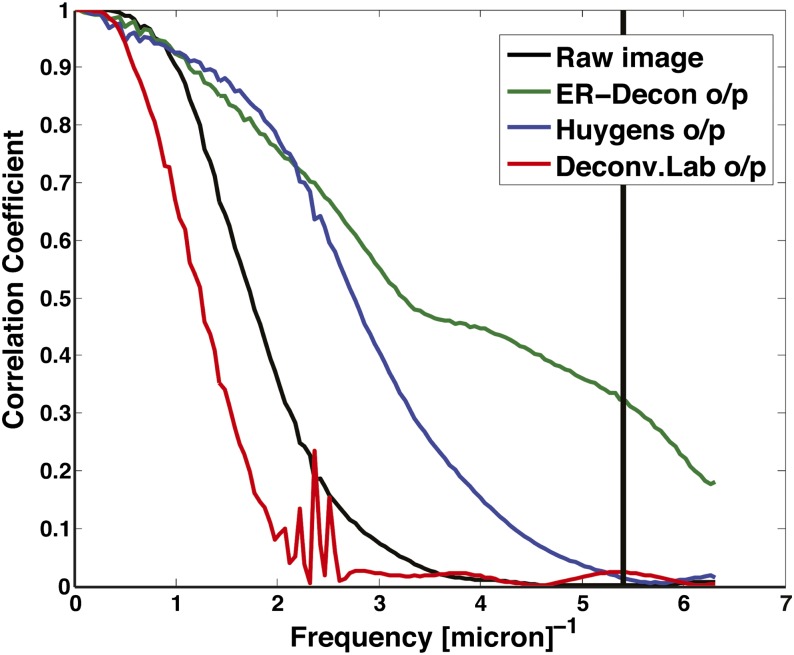Typically, the optimal value of the parameter appears to be inversely proportional to 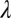, and hence a full 2D grid search is rarely necessary. Ongoing effort is aimed at simplifying this process even further. Fig. 2 shows the corresponding Fourier shell correlation plots clearly demonstrating that ER-Decon achieves considerably higher correlation even at the cutoff frequencies.

Fig. 1.

Deconvolution results for Drosophila spindle. (A and E) High- and low-dose raw images; (B and F) ER-Decon output from A and E; (C and G) Huygens’ output from A and E; (D and H) DeconvolutionLab’s output from A and E. In each image, the upper part is a lateral section, and the lower part is a vertical section. (Scale bar: 4 µm.) ER-Decon’s parameters: λ = 0.05, 3 (B and F); ε = 0.01, 0.001 (B and F).

Fig. 2.

Fourier shell correlation between high- and low-dose images. Correlation plots for the Drosophila spindle displayed in Fig. 1. The vertical line is the xy theoretical resolution limit.

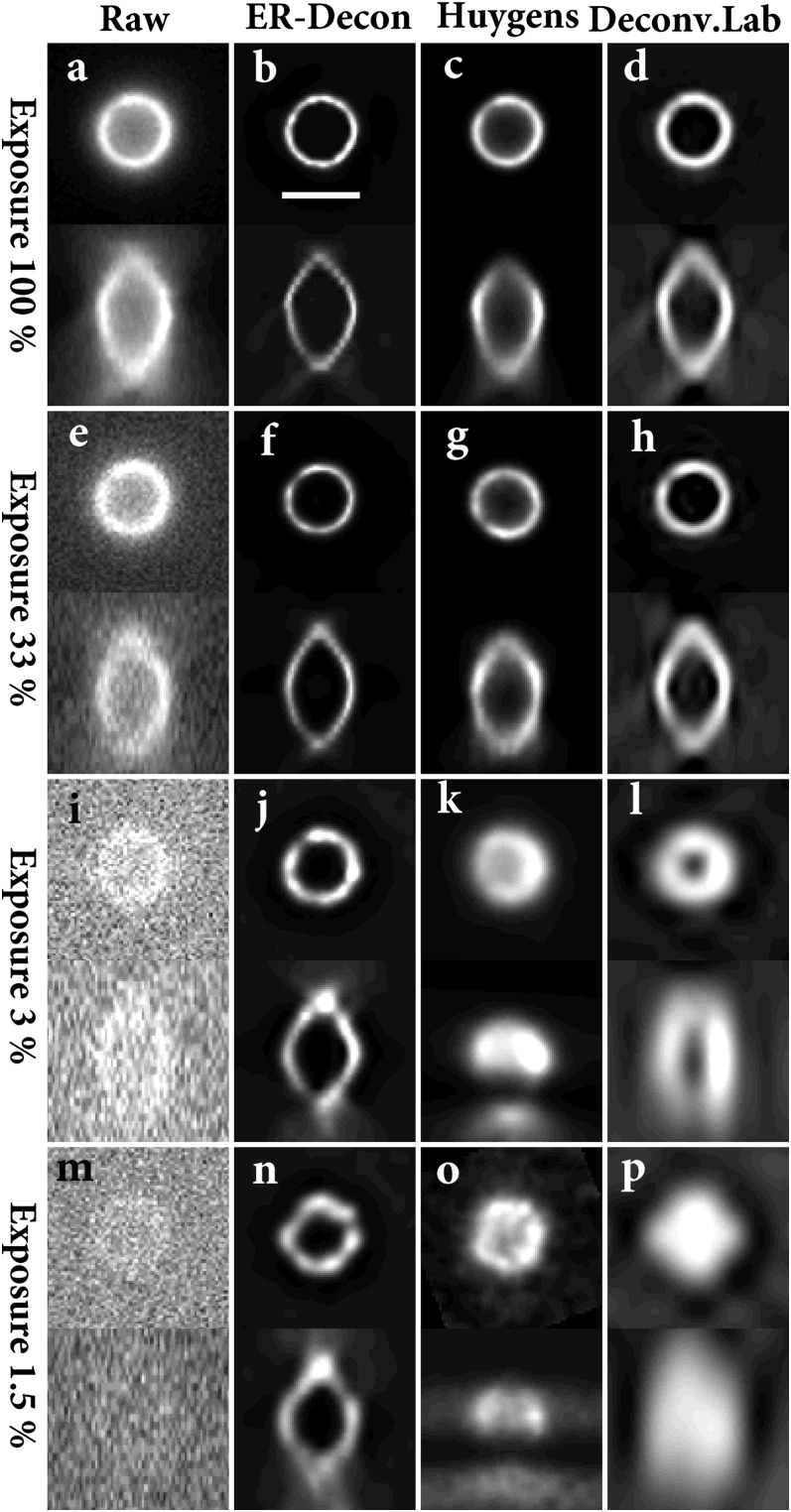
In the second experiment, we imaged green fluorescent protein (GFP)-labeled yeast vacuoles, where the yeast strain was obtained from the GFP library (13). The cells were fixed and mounted as described in Methods and image stacks were acquired with four different dose levels (1.5%, 3%, 33%, and 100% of highest intensity). As shown in Fig. 3, ER-Decon again provides a significantly improved resolution at all dose levels. As before, the most striking improvement is at the lowest dose, where ER-Decon clearly resolves the shell structure of the vacuole even though the structure is completely obscured in the raw image. By contrast, the other methods fail to clearly resolve the shell structure.

Fig. 3.

ER-Decon (B, F, J, and N) output from A, E, I, and M; Huygens' output (C, G, K, and O) from A, E, I, and M; DeconvolutionLab's output (D, H, L, and P) from A, E, I, and M. (Scale bar: 2 µm.) ER-Decon’s parameters: λ = 0.2, 8, 200, 650 (B, F, J, and N); ε = 0.01, 0.001, 0.0001, 0.00001 (B, F, J, and N).

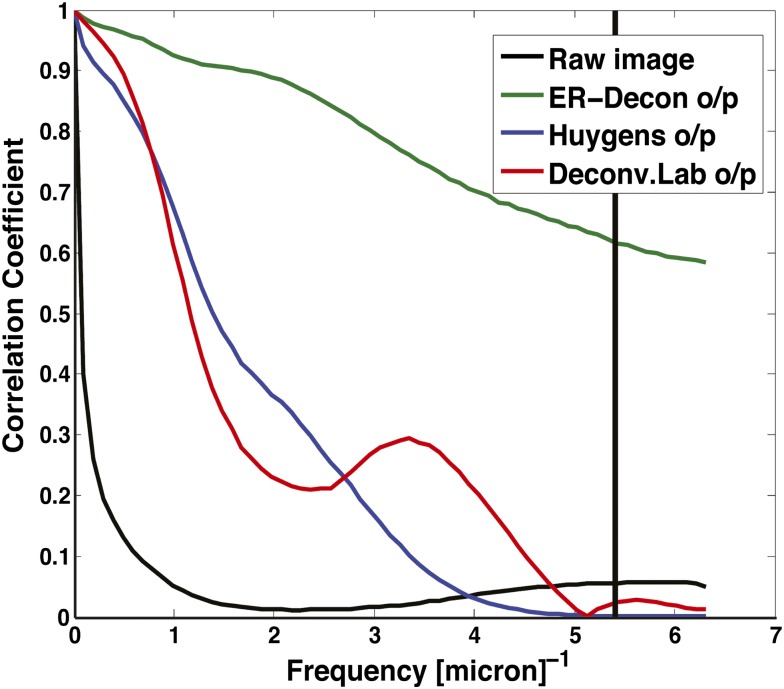
In the third experiment, we imaged GFP-labeled synaptonemal complex protein Zip1 protein filaments (14) in yeast cells (Methods). Emboldened by the previous results, we acquired two stacks with dose levels differing by a factor of 400. It is clear from the deconvolved images (Fig. 4) that the high-dose results of all three methods have comparable resolution, whereas the low-dose results differ significantly. In particular, ER-Decon’s output from the low-dose stack reveals the filamentous structures despite the structure being nearly invisible in the raw images. On the other hand, the results of Huygens and DeconvolutionLab show only blob-like structures. Fig. 5 shows the corresponding Fourier shell correlation plots, from which it is evident that ER-Decon achieves a considerably higher correlation even at the cutoff frequencies.

Fig. 4.

Deconvolution results for a yeast Zip1 filament. (A and E) High- and low-dose raw images; (B and F) ER-Decon output from A and E; (C and G) Huygens’ output from A and E; (D and H) DeconvolutionLab’s output from A and E. (Scale bar: 2 µm.) ER-Decon’s parameters: λ = 0.05, 700 (B and F); ε = 0.01, 0.00001 (B and F).

Fig. 5.

Fourier shell correlation between high- and low-dose images. Correlation plots for the yeast ZIP1 filament displayed in Fig. 4. The vertical line is the xy theoretical resolution limit.

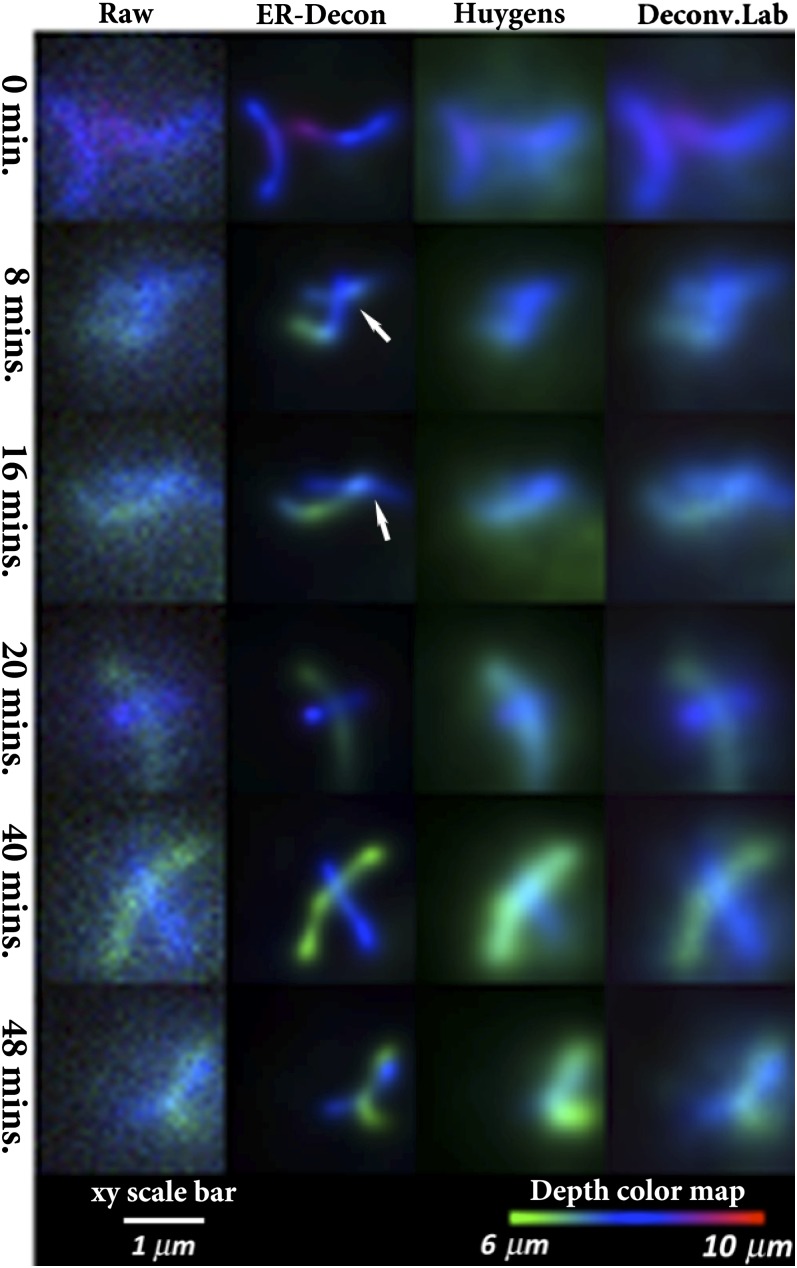
In the final experiment, we imaged Zip1 filaments of live yeast cells undergoing meiotic recombination (Methods). For simplicity in comparison, color-coded z-projections of the raw image sequence and the deconvolved sequences at selected time points are shown (Fig. 6). The images confirm that ER-Decon gives significantly higher resolution on unfixed, live samples. In particular, closely spaced filaments are clearly resolved, whereas the other methods fail to resolve these structures. For example, the upper arrow in Fig. 6 shows a filament traversing from 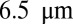depth to 8 µm depth in the ER-Decon output, which cannot be revealed by the other methods. Further, the lower arrow highlights that two filaments in ER-Decon output located at depths 6.5 µm and 7.5 µm are clearly resolved, which again cannot be resolved in the output of the other two methods. Movie S1 demonstrates the superior performance of ER-Decon for all 90 time points.

Fig. 6.

Depth color-coded z-projections of deconvolved live images of yeast Zip1 filaments. Upper arrow points to a filament in ER-Decon output traversing from 6 µm depth to 8 µm depth, which cannot be resolved from the outputs of the other methods. Lower arrow points to two filaments in ER-Decon output located at depths 6.5 µm and 7.5 µm, which again cannot be resolved from the output of the other two methods. ER-Decon’s parameters: λ = 12; ε = 0.001.

It should be emphasized that our method is applicable to any kind of imaging system as long as a PSF is available, and one can expect the same kind of relative improvement in resolution. Considering computational complexity, our method takes less than 1 h to deconvolve images of size 512 × 512 × 32.

Discussion

Multiwavelength 4D live cell imaging is an invaluable tool for understanding the complex interrelationships among various molecular components of live cellular processes. However, to draw reliable conclusions from observations, it is important to ensure that normal cell functioning is not disrupted as a result of the illumination. Due to phototoxicity caused by light-generated oxygen radicals, it is challenging to ensure that illumination does not alter the biochemical processes while imaging in 4D, as it involves higher levels of accumulated illumination dose especially in multiwavelength imaging. To fully avoid this problem, it appears necessary to reduce the illumination intensity by 100- to 1,000-fold compared with levels conventionally used (1). This, in turn, leads to severe loss of resolution due to high levels of the resulting noise, thereby hindering the accurate study of live cell dynamics. Hence, it is important to optimize every component of the imaging system such that the resolution is maximized for a given illumination dose level or, equivalently, the dose level required for ensuring a certain resolution is minimized. From this viewpoint, here we have addressed the computational part of a widefield imaging system, the deconvolution.

To maximize the resolution resulting from deconvolution, we optimized the noise stabilization term, the regularization functional, because it solely determines the obtainable resolution. We constructed a regularization functional that is specifically tailored for spatial characteristics of fluorescence signals and uses appropriately weighted second derivatives to achieve robust behavior. This contrasts with other deconvolution methods that use general-purpose regularization functionals, using first derivatives. We named this method ER-Decon because we constructed the regularization functionals using an entropy-based formalism.

Even though widefield deconvolution has long been a topic of research, ER-Decon is a significantly improved method designed to exploit very general spatial characteristics of fluorescence images, using an entropic formulation. As a result, it is able to distinguish between spatially correlated weak signal high frequencies and random noise far better than the other methods, and hence its output resolution differs from that of the existing methods by an unusually high magnitude. More specifically, there are three factors that make ER-Decon different from other methods and that combine to provide the improved performance: (i) The method uses second derivatives to provide sufficient freedom from fluorescence intensity variations, contrasting with other 3D image restoration methods that use first derivatives; (ii) it combines the image intensity with the derivative magnitude to capture patterns of intensity variations routinely found in fluorescence images; and (iii) it uses logarithmic weighting on the combined derivative and intensity magnitudes to better adapt to the relative distribution of high-derivative and high-intensity points found in fluorescence images. As a consequence, ER-Decon can reveal unprecedented structural detail in data with extremely low levels of signal. This means that ER-Decon can enable the study of dynamic cellular processes at unique exposure levels, thereby opening unique possibilities in cell biology research.

Methods

Fixed Drosophila Spindle.

Schneider S2 cells were cultured in Schneider’s Drosophila medium supplemented with 10% (vol/vol) heat-inactivated FCS (Gibco BRL) and penicillin/streptomycin. Drosophila S2 cells were plated for 3 h on a 35-mm glass-bottom Delta T dish (Bioptechs) coated with Con A (Sigma Aldrich) to promote cell spreading. Cells were fixed with −20 °C methanol for 20 min, rehydrated in PBS, and then blocked with 3% (wt/vol) BSA in PBS/0.1% Triton X-100. Anti–α-tubulin antibodies (mouse DM1 ; Sigma Aldrich) were diluted into blocking solution (1:200) and applied to fixed cells for 1 h followed by extensive washing with PBS/0.1% Triton X-100. Fluorescent secondary antibodies (Alexa 488-conjugated anti-mouse; Invitrogen) were used at a final dilution of 1:500 in blocking buffer. Samples were mounted in PBS, 50% (vol/vol) glycerol, 2% (wt/vol) propyl gallate solution as an antifading agent.

Fixed Yeast Vacuoles.

The yeast strain used was obtained from the GFP library (13) and carries a marker for the limiting membrane of the vacuole (MATa, his3 1, leu2 0, met15 0, ura3 0, VPH1-GFP::HIS3). Five-milliliter liquid YPAD cultures were inoculated with this strain and cultured at 30 °C for approximately 24 h. By this point, the cells have begun a diauxic shift, and vacuole morphology tends to become more fused and spherical. Cells were fixed using paraformaldehyde as described in the next section, and aliquots of cell culture were mounted on microscope slides, using Con A-treated coverslips. Samples were imaged on the OMX microscope (University of California, San Francisco), using a 100× 1.49NA APO TIRF oil-immersion Olympus objective.

Fixed Yeast Zip1 Filaments.

The yeast strain yCA90 is a MATa/MATa diploid in the BR1919-19B background (15). The genotype is zip3::LYS2/zip3::LYS2 zip1::LEU2/ ZIP1-GFP(700) lys2/LYS2 and is homozygous for his4-260, leu2-3,112, ura3-1, ade2-1, thr1-4. Strains were sporulated in 10 mL of 2% potassium acetate at 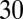°C for 15 h before 1 mL was pelleted and resuspended in 4% formaldehyde, pH 7.0, in PBS. Cells were fixed for 15 min and washed twice with 1× PBS, pH 7.0. A total of 4.6 µL of suspended cells was imaged under a 22 × 22 coverslip coated with 0.1 mg/mL Con A.

Live Yeast Zip1 Filaments.

Two milliliters of diploid Zip1-GFP yeast strains was grown for 20 h at 30 °C in YPD media. Cells were spun down and transferred to 10 mL 2% potassium acetate to sporulate for 12–14 h at 30 °C. Cells were plated in a Delta T dish (Bioptechs) coated with 0.1 mg/mL Concanavalin A (Sigma) and spun at 3,000 rpm for 5 min to adhere cells to the dish. Two milliliters of 2% potassium acetate at 30 °C was added to the dish to cover the cells. Cells were imaged at 30 °C on the OMX microscope.