Model-driven optimization of multicomponent self-assembly processes

Significance

The molecular organization of semiconducting molecules is extremely important for the performance of functional organic materials in electronic devices. The processing of these materials often leads to multiple assembly pathways toward different types of molecular organizations. Hence, directing the assembly process toward the desired type of organization requires many trial-and-error optimization steps. In this paper, we introduce an approach to optimize these self-assembly processes. Based on experiments with a system that assembles into 1D helices in solution, we have developed models to describe the dynamics of multicomponent self-assembly processes. These models simulate the experimental data very well and allow us to understand and avoid, or alternatively attenuate, the entrapment of materials in nonequilibrium assemblies.

Abstract

Here, we report an engineering approach toward multicomponent self-assembly processes by developing a methodology to circumvent spurious, metastable assemblies. The formation of metastable aggregates often hampers self-assembly of molecular building blocks into the desired nanostructures. Strategies are explored to master the pathway complexity and avoid off-pathway aggregates by optimizing the rate of assembly along the correct pathway. We study as a model system the coassembly of two monomers, the R- and S-chiral enantiomers of a π-conjugated oligo(p-phenylene vinylene) derivative. Coassembly kinetics are analyzed by developing a kinetic model, which reveals the initial assembly of metastable structures buffering free monomers and thereby slows the formation of thermodynamically stable assemblies. These metastable assemblies exert greater influence on the thermodynamically favored self-assembly pathway if the ratio between both monomers approaches 1:1, in agreement with experimental results. Moreover, competition by metastable assemblies is highly temperature dependent and hampers the assembly of equilibrium nanostructures most effectively at intermediate temperatures. We demonstrate that the rate of the assembly process may be optimized by tuning the cooling rate. Finally, it is shown by simulation that increasing the driving force for assembly stepwise by changing the solvent composition may circumvent metastable pathways and thereby force the assembly process directly into the correct pathway.

Self-assembled nanostructures often are considered to be in fast exchange with their molecular building blocks (1). Although this is true for highly dynamic systems, the assembly of more rigid systems—i.e., systems most often used in applications—have relatively slow dynamics and are often not in equilibrium (2–5). The long lifetime of the resulting assemblies allows the hierarchical construction of functional nanostructures from self-assembly of multiple components, because aggregates formed in earlier steps will not reequilibrate after addition of subsequent components. Via this approach, 1D multisegment nanorods (6) have been assembled, as have supramolecular electronic structures containing different types of wires (7) and p–n junctions (8). Slow self-assembly dynamics also play a critical role in the processing of organic materials such as bulk heterojunction solar cells. For example, prolonged annealing often is required to obtain optimal morphologies of electron donor and acceptor components (9–11). A drawback of the slow monomer exchange dynamics, however, is that the molecular components may get trapped easily in metastable off-pathway assemblies that hamper assembly along the correct pathway, a phenomenon known as pathway complexity (12). Hence, obtaining the desired supramolecular morphology often is nontrivial, and many variables, including solvent composition, concentration, temperature, and preparation methodology, have to be optimized to obtain the correct molecular architectures (13, 14).

The presence of kinetically controlled self-assembly pathways clearly emphasizes the necessity of developing kinetic models that take into account the growth mechanism and pathway complexity leading to a diversity of various aggregate morphologies. Such a model-driven approach is common in synthetic biology, in which it aids the development of systems that can, for instance, control gene expression (15–18). Typically, a kinetic model is developed first that includes all modular elements and the interactions among them. Next, to identify the most critical parameters that have to be optimized to achieve the targeted function, the combinatorial design variable space of the model is mapped by running many simulations with different parameter combinations.

Inspired by this forward engineering approach, we computationally screen self-assembly strategies that circumvent formation of metastable aggregates and thereby optimize the rate of self-assembly into thermodynamically stable aggregates. First, a molecular model system is introduced consisting of two different molecules that coassemble into 1D helical aggregates. Next, the coassembly is studied experimentally under thermodynamic and kinetic control, and a model is developed to analyze the coassembly kinetics in detail. Simulations reveal the initial formation of metastable structures that buffer free monomers and thereby slow the formation of the thermodynamically stable assemblies. In the third part, we analyze the temperature-dependent entrapment of monomers in these assemblies. The competition exerted by the metastable pathway is found to be highly dependent on the cooling rate applied, and we develop a temperature-dependent kinetic model to rationalize this behavior. Based on the resulting insights into the coassembly pathways, methodologies are proposed and assessed by simulation to circumvent these metastable pathways during the aggregation process while providing the fastest route to the desired structure. Alternatively, this strategy allows the design of methodologies to obtain the kinetically favored assemblies if required. Finally, we outline the importance of this model study for the future design of functional self-assembled materials.

Results and Discussion

Molecular Model System: The Coassembly of Two Different Monomers.

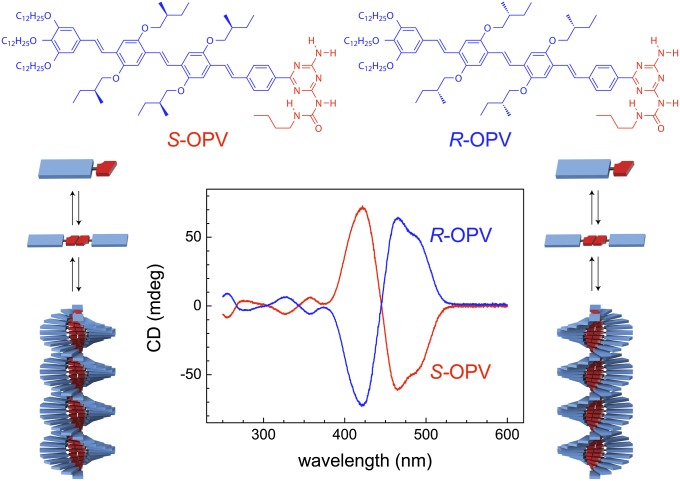
We have selected as a model system the coassembly of R- and S-chiral oligo(p-phenylene vinylene)-ureidotriazine (OPV; Fig. 1). OPVs are known to form hydrogen-bonded dimers that assemble via a nucleated, cooperative growth mechanism into helical stacks that may be probed by CD spectroscopy (19, 20) (SI Appendix, Fig. S2). The assembly of the pure components in methylcyclohexane results in opposite Cotton effects typical of the formation of right- and left-handed R- and S-OPV helices, respectively. To investigate their coassembly, “majority-rules” experiments are performed, which assess the capability of the major enantiomer to amplify its chirality by forcing all assemblies in the system to take over its preferred helicity (21). Solutions of R- and S-OPV (200 µM) are mixed at 20 °C in different ratios characterized by the enantiomeric excess ee, which equals the difference between the molar fractions of R- and S-OPV. The resulting anisotropy factor Δε/ε (460 nm) depends linearly on ee, indicating the lack of chiral amplification (Fig. 2A). However, annealing above the critical temperature of elongation T_e at which all helices are disassembled, followed by slow cooling (1 °C/min) back to 20 °C, strongly influences the relation between Δε/ε and ee. For ee <–0.2 and ee >0.2, Δε/ε is now saturated and equals the anisotropy factor corresponding to the excess enantiomer in its pure form. The strong chiral amplification obtained upon annealing and subsequent cooling implies that initial mixing of the assemblies at 20 °C does not result in notable monomer exchange; hence, the net helicity equals the weighted sum of the helicities of homoaggregates consisting of R- and S-OPV monomers only. Annealing results in disassembly of enantiopure aggregates, after which the monomers can mix upon cooling, resulting in chiral amplified heteroaggregates.

Fig. 1.

Molecular structures and CD spectra of S- and R-chiral OPV. Both enantiomers assemble via a nucleated growth mechanism into helical stacks with left-handed (S-OPV) and right-handed (R-OPV) helicity.

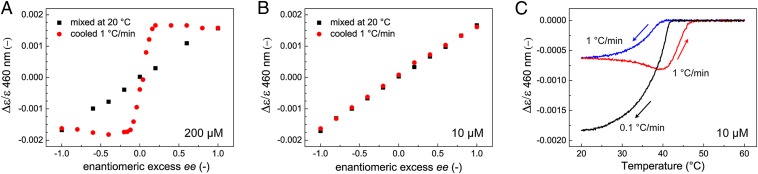
Fig. 2.

Majority-rules experiments to assess amplification of chirality for mixtures of R- and S-OPV in methylcyclohexane. For both high (200 μM, A) and low concentrations (10 μM, B), no chiral amplification is obtained after mixing the assemblies at 20 °C. Heating to 80 °C, well above the elongation temperature T_e, and cooling at 1 °C/min to 20 °C yields only chiral amplification at 200 μM. (C) For a 10-μM OPV solution (ee = –0.3), chiral amplification is obtained only upon cooling at 0.1 °C/min, whereas cooling and heating at 1 °C/min result in a large hysteresis.

The majority-rules experiment also is performed at a lower concentration of 10 µM (Fig. 2B), and again, no chiral amplification is observed upon mixing the assemblies at 20 °C. Also after annealing above T_e and subsequent cooling (1 °C/min) no chiral amplification is observed. To investigate whether this absence of chiral amplification is related to kinetic phenomena, a 10-µM OPV solution with ee = –0.3 is cooled and subsequently heated at a rate of 1 °C/min (Fig. 2C). Indeed, a large hysteresis is obtained, and only cooling at a much slower rate from the molecular dissolved state (0.1 °C/min) results in a Δε/ε-value indicating chiral amplification. Detailed analysis of UV-Visable spectra and fluorescence lifetime measurements reveals that upon cooling at 1 °C/min, all monomers are coassembled into aggregates containing both S- and R-OPV (SI Appendix, Figs. S3 and S4). From this, we thus conclude that fast cooling results in metastable aggregates that display no chiral amplification.

These metastable coassemblies bear a relation with the assembly of enantiopure OPV. Previous studies showed that S-OPV monomers assemble fast into metastable P*-type helices and subsequently form stable M-type helices, whereas R-OPV forms, vice versa, metastable M*-type helices before the slower assembly into stable P-type helices (12).

Analysis of Coassembly Kinetics.

To unravel the origin of the metastable aggregates that appear in the coassembly of S- and R-OPV, we develop a deterministic kinetic model that approximates a previously developed stochastic simulation algorithm for majority-rules kinetics (21). The coassembly model, schematically depicted in Fig. 3A, describes the assembly of both types of monomers in left-handed M-type and right-handed P-type helical stacks. Nucleation occurs by association of two monomers into M- and P-type nuclei. Further elongation of the stacks occurs via stepwise monomer association, with association rate constant a. In contrast to the stochastic simulations, the exact monomer sequence of each aggregate is not considered, which greatly decreases computational time. Hence, to describe the dissociation of the two different monomers from M- and P-type stacks, the dissociation probabilities of S- and R-chiral monomers are computed from the ratio of both monomers present in the respective aggregate type. Monomer dissociation is described with rate constant c; for dissociation of monomers from their nonpreferred aggregate helicity, this dissociation rate constant increases with a mismatch penalty factor MMP.

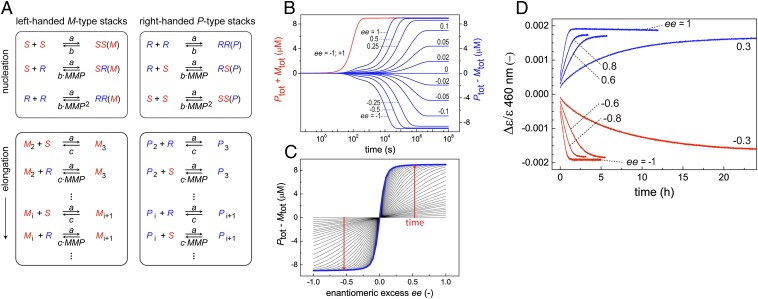
Fig. 3.

Analysis of the coassembly kinetics of two different monomers. (A) Schematic representation of the coarse-grained kinetic model describing the nucleated assembly of R- and S-chiral monomers in P- and M-type helical stacks, with a mismatch penalty factor MMP for R-chiral monomers in M-type stacks and S-chiral monomers in P-type stacks. (B and C) The time-dependent development of net helicity (P_tot – M_tot) and total assembled material (P_tot + M_tot) simulated with different values of ee and an MMP of 1.1. The rate of chiral amplification decreases as the ee approaches 0 (parameters: a = 4 × 10⁴ M^–1⋅s^–1; b = 400 s^–1; c = 0.04 s^–1; c_tot = 10 μM). (D) The rate of chiral amplification is strongly dependent on the ee, as shown by kinetic experiments in which Δε/ε is followed in time at 20 °C for OPV solutions with different ee-values that have been cooled from above the T_e to 20 °C (8 °C/min, 10 μM).

Simulations with the coassembly model, starting with a mixture of R- and S-chiral monomers in different ratios, show that the time-dependent net helicity (P_tot – M_tot), defined as the difference in concentration of monomers present in P- and M-type aggregates, strongly depends on ee and has a minimum rate at ee-values close to zero (Fig. 3B). Under steady-state conditions, the calculated net helicity as a function of ee is comparable to the experimentally observed chiral amplification curve, assuming an MMP of 1.1. However, during equilibration, the net helicity initially depends linearly on the ee, indicating a nonamplified state (Fig. 3C). Congruently, the equilibration of the total assembled material (P_tot + M_tot) is much faster than the equilibration of the net helicity, supporting the fact that during the initial stages of the assembly process, aggregates are formed that do not contribute to chiral amplification. Detailed analysis shows that initially part of the monomer pool assembles into aggregates with a helicity corresponding to the minority enantiomer and that the kinetic stability of these aggregates becomes larger if the ee approaches 0 (SI Appendix, Fig. S5). Hence, the subsequent conversion into the stable aggregate type is delayed at smaller ee values, resulting in a slower rate of chiral amplification for less enantiopure systems.

The strong dependence of the chiral amplification rate on the ee, as predicted by the coassembly model, is verified by kinetic experiments. OPV solutions (10 µM) with different ee-values are cooled from above the T_e to 20 °C at 8 °C/min, and subsequently the increase of Δε/ε is followed in time (Fig. 3D). In agreement with previous chiral amplification studies (22, 23), the ee has a large effect on the annealing kinetics. Slower rates are obtained for less enantiopure compositions, as predicted by the model.

Temperature-Dependent Entrapment of Monomers in Metastable Assemblies.

The majority-rules experiments at a low concentration of 10 μM show that fast cooling results in metastable assemblies that fail to display chiral amplification and contribute to the strong hysteresis observed. To further corroborate the role of these metastable assemblies in the hysteresis, the influence of cooling rate on the coassembly of R- and S-OPV is assessed. An OPV solution (10 μM, ee = –0.3) is cooled from above the T_e to 0 °C at different cooling rates: 1 °C/min, 8 °C/min, and via quenching of the solution in an ice bath. Thereafter, the evolution of the amplified state is probed by CD at 20 °C (Fig. 4A). Surprisingly, a maximum rate in net helicity is observed after rapid quenching, whereas a significantly slower rate is observed after cooling at 1 °C/min. This counterintuitive effect cannot be explained by an aggregation mechanism in which monomers assemble via a single pathway, as in this case longer reequilibration times would be expected for faster cooling rates (SI Appendix, Fig. S6). A possible way to rationalize these kinetic results is via the buffering of monomers into parallel operating, kinetically controlled pathways, comparable to the metastable assemblies that appear in the simulations with the coassembly model (Fig. 3). During slow cooling (i.e., 1 °C/min), free monomers get entrapped into these pathways, and hence a slower assembly into thermodynamically favored aggregates that contribute to chiral amplification occurs.

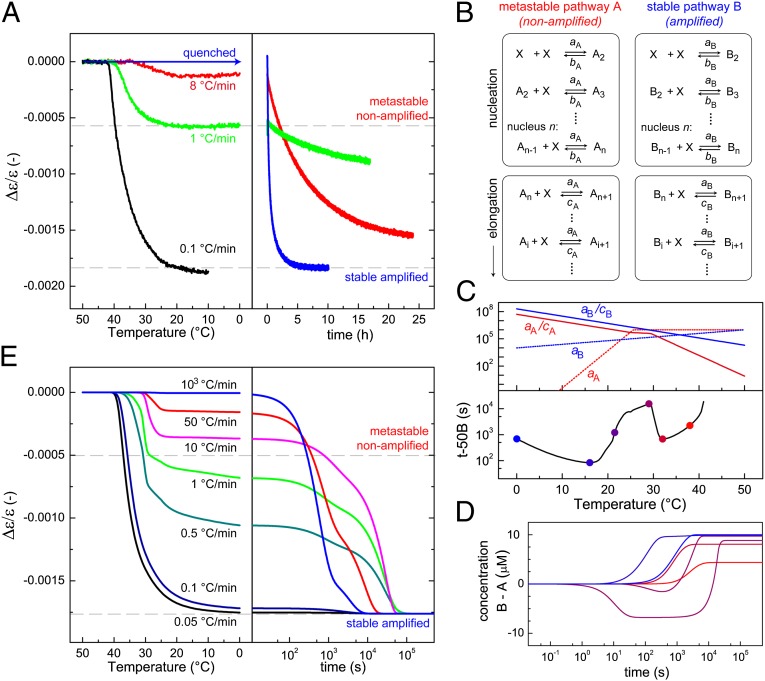
Fig. 4.

Experiments under kinetic control reveal that the competition for free monomer exerted by the metastable assembly pathway is strongly temperature dependent. (A) Temperature-dependent net helicity of an OPV solution (10 μM, ee = –0.3) upon cooling from above T_e to 0 °C with different rates (Left). During subsequent equilibration at 20 °C, faster rates are observed after higher cooling rates (Right). (B) Schematic representation of the kinetic model describing the parallel assembly of a kinetically controlled pathway A and a slower pathway B resulting in thermodynamically stable aggregates. Both pathways compete for the same monomer X. (C) Influence of temperature on rate constants used in simulations (Upper) and simulated assembly time of stable B-type assemblies (Lower). (D) Time-dependent assembly in metastable A-type and thermodynamically favored B-type assemblies, simulated at different temperatures (color coding corresponds to colored dots in C). (E) Simulated temperature-dependent assembly of free monomer into metastable (Δε/ε-value of –0.0005) and stable assemblies (Δε/ε-value of –0.0018) upon cooling (Left). Subsequent equilibration kinetics at 20 °C (Right) reveal the slowest rate after cooling at intermediate cooling rates as a result of the entrapment of monomers in metastable assemblies.

In the coassembly model, all monomer association reactions are described with the same rate constant a, independent of the helicity of the aggregate. This results in the initial appearance of aggregates that show no chiral amplification, as well as the correct prediction of the relation between ee and the rate of chiral amplification. However, it should be noted that previous studies on the assembly of enantiopure OPV revealed a fast, kinetically controlled assembly of both enantiomers into their nonpreferred helical types, i.e., an M*-type helix for R-OPV and a P*-type helix for S-OPV. Upon coassembly of S- and R-OPV, both enantiomerically related monomers also are incorporated in these metastable aggregates, meaning that S-OPV slowly assembles into the kinetically controlled M*-type helix that initially is formed by R-OPV and thereby increases its stability. Analogously, R-OPV slowly stabilizes the metastable P*-type helix that initially is formed by S-OPV. As a result, the stability of the metastable heteroaggregates, as well as the rate constants that describe the association and dissociation of both monomers to these assemblies, depends on the exact composition of the aggregate. Effectively, this results in multiple, parallel operating metastable pathways that compete with the thermodynamically controlled heteroaggregates for available monomers. Giving an exact description of all these assembly pathways by further expanding the coassembly model is possible but will introduce many additional constants that would complicate further analysis. Therefore, we analyze the system by applying a simplified kinetic model that describes the nucleated assembly of one monomer X into a single metastable pathway A that shows no chiral amplification and one stable pathway B that does show chiral amplification.

The model—previously introduced in ref. 12—describes both assembly pathways as a sequence of monomer dissociation and association reactions (Fig. 4B). Monomer association is described with rate constants a_A and a_B for the metastable and stable pathway, respectively. The higher thermodynamic stability of aggregates in pathway B is reflected by a_B/c_B > a_A/c_A, with rate constants of monomer dissociation c_B and c_A for pathways B and A. We note that in the kinetic experiments, after rapid quenching, a Δε/ε-value of –0.001 is reached within 20 min, whereas it would take more than a day to reach this Δε/ε-value after cooling at 1 °C/min (Fig. 4A). This indicates that metastable assemblies sequester monomers most effectively in intermediate temperature regimes. Hence, the assembly of metastable assemblies is assumed to be faster than the stable pathway (i.e., a_A > a_B) only for temperatures above 20 °C (Fig. 4C).

Simulations with the kinetic model, based on the temperature dependency of the various rate constants, as depicted in Fig. 4C, indeed reveal that metastable assemblies appear only above 20 °C (Fig. 4D). As a result, the assembly of thermodynamically stable aggregates, characterized by the time at which 50% of its conversion is completed (t-50B), slows significantly above 20 °C. Using the kinetic model and the temperature-dependent rate constants, we simulate the assembly of free monomers during cooling from 50 °C to 0 °C with different temperature ramps (Fig. 4E). In the simulations, a Δε/ε-value of –0.0005 is assigned to metastable A-type assemblies and a Δε/ε-value of –0.0018 to stable B-type assemblies. The resulting cooling curves reveal for slow cooling the direct formation of thermodynamically stable aggregates (Δε/ε ∼ –0.0018); for fast cooling, no assembly; and for intermediate cooling rates, kinetically controlled assemblies (Δε/ε ∼ –0.0005), in agreement with our experimental results. Moreover, simulation of the subsequent equilibration kinetics at 20 °C yields the slowest rate for intermediate cooling rates, such as 1 °C/min. These simulations demonstrate that upon cooling with intermediate temperature ramps, monomers are sequestered efficiently in metastable assemblies that are formed easily above 20 °C. This buffering of free monomers significantly slows their reassembly into the thermodynamically stable aggregates at room temperature. For a concentration of 200 μM, however, cooling at a rate of 1 °C/min is slow enough to yield chiral amplification as the assembly process starts off at a higher temperature at which the fast association allows direct formation of amplified assemblies (SI Appendix, Fig. S7). At a concentration of 10 μM, cooling with this temperature ramp yields the metastable state; hence, the self-assembly process continues during the subsequent heating step, as experimentally observed in Fig. 2C and simulated in SI Appendix, Fig. S8.

Optimizing Assembly Processes to Circumvent the Metastable State.

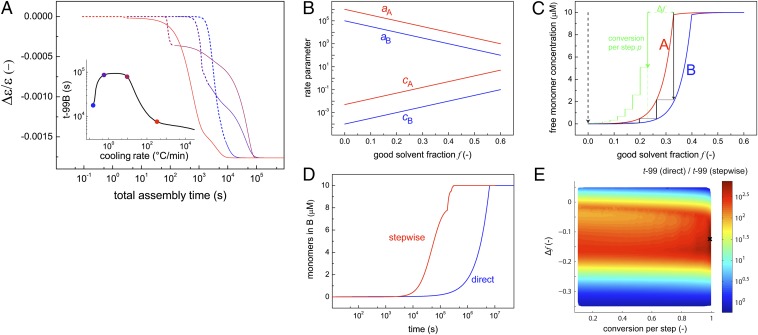
Because the slowest assembly rate of the stable aggregates is obtained by using intermediate cooling rates, the assembly process may be optimized by (i) decreasing the cooling rate such that the monomers can assemble directly into the thermodynamically stable pathway at elevated temperatures or (ii) rapidly quenching the molecularly dissolved monomers from a high temperature. To demonstrate this, we assess by simulation how the cooling rate influences the rate at which the stable aggregates appear. Using the temperature-dependent two-pathway model (Fig. 4B), we calculate the time at which 99% conversion of the equilibrium Δε/ε-value is obtained, corresponding to the thermodynamically stable aggregate (Fig. 5A). Indeed, optimum assembly times are obtained by using slow and fast cooling rates.

Fig. 5.

Optimizing the overall rate of assembly processes to avoid entrapment of monomers in metastable pathways. (A) Analogous to the temperature-dependent assembly simulations in Fig. 4E, Δε/ε is followed in time during (i) cooling with different cooling rates from 42 °C to 20 °C (dashed curves) and (ii) subsequent equilibration at 20 °C (solid curves). (Inset) Total assembly time at which 99% of the equilibrium Δε/ε-value at 20 °C is obtained (t-99B) vs. the cooling rate. (B) In the stepwise assembly methodology, a destabilizing (good) cosolvent is applied, which decreases the monomer association rate and increases the monomer dissociation rate. (C) Equilibrium free monomer concentration for metastable (A) and stable assemblies (B) vs. good solvent fraction f. To circumvent the initial formation of metastable assemblies, the assembly starts at f = 0.33, and f is decreased stepwise to f = 0 (black lines). The vertical lines indicate the different assembly steps, the horizontal lines the decrease of f. (D) The formation of stable assemblies B via the stepwise assembly is significantly faster compared with direct assembly of free monomers at f = 0 (dotted arrow in C). (E) To optimize the stepwise assembly, the method to decrease f stepwise is modified by adjusting (i) the conversion per step p and (ii) the factor Δf (Δf = –0.1 for green lines in C). The influence of p and Δf on the assembly rate is characterized by the time at which the total conversion into the stable assemblies is 99%: t-99 (direct)/t-99 (stepwise). Ten thousand different parameter sets are assessed. The highest rate [t-99 (direct)/t-99 (stepwise) = 744] is found with p = 0.99 and Δf = –0.12 (×).

Besides tuning the cooling rate, the assembly of a system in which metastable pathways buffer the molecular building blocks also may be optimized by adjusting solvent conditions. Typically, the addition of a destabilizing cosolvent (i.e., good solvent) decreases the rate of monomer association and increases the rate of monomer dissociation, as shown in Fig. 5B (24). To demonstrate by simulation how this effect may be used to circumvent metastable pathways, we first analyze the equilibrium free monomer concentration for both the kinetically and thermodynamically controlled pathways independently as a function of the volume fraction of a good solvent f, assuming a total monomer concentration of X equal to 10 μM. In the example shown in Fig. 5C, the stable assemblies are formed below f = 0.40 and the metastable assemblies below f = 0.33.

Simulating the assembly of free monomers at this concentration without the presence of a destabilizing solvent (f = 0) results in the sequestering of monomers in metastable assemblies, which subsequently slows the formation of the stable aggregates (SI Appendix, Fig. S9). To circumvent the initial formation of metastable assemblies, we attempt by simulation an alternative methodology in which the assembly of free monomers dissolved in a good solvent (corresponding to f = 1) is initiated by changing the solvent composition such that the total yield of metastable assemblies is zero (i.e., f = 0.33). After equilibration, further assembly is induced by decreasing f such that the concentration of free monomers that remain from the first step just equals the concentration of monomers required for the formation of metastable assemblies at this new f-value. In this way, the formation of metastable assemblies also is avoided during the second assembly step. Upon repeating this stepwise approach of lowering the fraction of good solvent, a full conversion of all monomers into stable assemblies is obtained in the pure solvent (f = 0) at the sixth step. The advantage of this stepwise assembly approach is demonstrated clearly by the fact that the rate is 21 times faster compared with the direct assembly of free monomers by changing the solvent fraction from f = 1 to f = 0 in a single step (Fig. 5D).

To optimize this stepwise assembly strategy further, we analyze the combinatorial design variable space by investigating the influence of (i) the conversion per step p and (ii) the applied method to decrease f every step. In the example described above, f is decreased such that the concentration of free monomers remaining from the previous step equals the critical monomer concentration required for the formation of metastable assemblies (black lines in Fig. 5C). However, to optimize the process, the decrease in f per step is varied by adding a factor Δf for every step (green lines in Fig. 5C). Ten thousand different parameter sets for p and Δf are assessed, in the range p = [0.1, 1] and Δf = [–0.35, 0.05]. For all parameter sets, the simulated assembly rate obtained via stepwise decreasing f to zero is compared with the rate of direct assembling by changing the solvent fraction from f = 1 to f = 0 in a single step. A maximum rate is obtained with p = 0.99 and Δf = –0.12, well beyond the critical f-value at which metastable assemblies initially appear (i.e., Δf = 0) and hampering the formation of thermodynamically stable assemblies (Fig. 5E). Nevertheless, these conditions yield a Pareto optimal situation that is a tradeoff between the buffering of free monomers in metastable assemblies, which increases upon lowering the fraction of good solvent, and the monomer association rate, which increases upon decreasing f. This example clearly emphasizes that finding the optimal self-assembly route involves the optimization of multiple parameters, which can be done only by computationally analyzing the full combinatorial design variable space. Experimental verification of this stepwise assembly methodology by decreasing the amount of cosolvent would require techniques such as spin coating, which is less practical for the OPV model system. Therefore, we now are focused on applying this optimization strategy to electronic active materials useful for devices.

Conclusions

Kinetic experiments combined with detailed simulations on the coassembly of the R- and S-chiral enantiomers of OPV reveal the appearance of multiple parallel-operating self-assembly pathways. The resulting pathway complexity enables metastable aggregates to exert their influence on the total coassembly process, as entrapment of the chiral monomers results in a slow assembly of the thermodynamically stable coassemblies. Because the kinetic stability of these metastable aggregates increases if the ratio between both chiral monomers approaches one, the coassembly rate is highly dependent on the enantiomeric excess of the monomer pool.

Competition between different nanostructures via cross-talk of parallel-operating self-assembly pathways results in counterintuitive phenomena with important consequences. For example, if a certain preparation protocol results in entrapment of monomers in metastable nanostructures, subsequent conversion to a nanofiber morphology with increased stability is much slower compared with the situation in which monomers can assemble directly into the most stable aggregate morphology. Kinetic studies can identify parallel-operating assembly pathways and, more importantly, yield information on which of the pathways are under kinetic control. For example, self-assembly of a π-conjugated monomer resulting in short fibers with limited length might be the result of entrapment in kinetically controlled off-pathway aggregates. However, these short fibers also may be the result of incomplete assembly of monomers in the thermodynamically controlled pathway, because fast solvent evaporation may effectively freeze in nanostructures as a result of the slow monomer association rate compared with the rate of evaporation. In the first case, the rate may be optimized by the addition of a cosolvent that destabilizes the metastable pathway with respect to on-pathway aggregates, whereas in the second case, a stabilizing solvent or a higher concentration is required to increase the assembly rate into the stable structure.

Model-driven optimization provides a practical approach to the design of preparation protocols to circumvent spurious, metastable self-assembled nanostructures. Especially if multiple components are involved in the assembly process, alternative pathways likely will occur. Combining simulations and experiments, we demonstrate that the competition exerted by metastable assembly pathways may be highly temperature dependent, providing a unique handle to tune the assembly process by optimizing the cooling rate. More generally, if the driving force for self-assembly, e.g., the fraction of poor solvent, is increased in a stepwise manner such that entrapment of monomers in metastable pathways is avoided, the assembly rate may be improved significantly. We note that a comparable stepwise approach now is applied widely in the self-assembly of DNA origami (25–28), in which temperature or solvent annealing steps often are applied to direct the assembly toward the desired structures by optimizing the differential stability between on- and off-pathway nanostructures.

In this study, the two monomers used in the coassembly of helical nanostructures are enantiomers; hence, they experience the same mismatch penalty in their nonpreferred assembly type. However, the phenomena observed in this study generally are applicable to the assembly of multiple building blocks. For instance, nanofibers used in tissue engineering often include bioactive epitopes, together with molecules that provide mechanical strength to the material (29, 30). In bulk heterojunction solar cells, the functional properties are highly dependent on the supramolecular organization of the molecular components, e.g., fullerene and poly(3-hexylthiophene). Although these materials do not really coassemble but rather phase separate, both molecular components have mutual interactions and their concomitant aggregation processes compete for available space (31). Perhaps for this reason, manipulating the aggregation pathways by adding cosolvents such as 1,8-diiodooctane has a strong effect on the resulting morphology of organic devices (32–34).