Nonequilibrium dynamics of helix reorganization observed by transient 2D IR spectroscopy

Significance

Exploration of the helix–coil transition, a fundamental aspect in protein conformational dynamics, remains controversial, with published timescales differing by more than two orders of magnitude. We report measurements of the temporal evolution of local structural parameters within a helix, exploring the free energy landscape near but not initially at the equilibrium conformational distribution. The model helical peptide was constrained with a photosensitive cross-link that can be released in tens of picoseconds upon laser irradiation. Transient 2D IR spectroscopy was used to record structural snapshots of bond distance and bond angle during formation of a single helical turn in an already-nucleated helix upon photorelease. This nonequilibrium approach permits access to transient structures that are averaged out in standard methods.

Abstract

The relaxation of helical structures very close to equilibrium is observed via transient 2D IR spectroscopy. An initial distribution of synthetically distorted helices having an unnatural bridge linking the 10th and 12th residues of an alanine-rich α-helix is released to evolve into the equilibrium distribution of α-helix conformations. The bridge constrains the structure to be slightly displaced from the full α-helix equilibrium near these residues, yet the peptide is not unfolded completely. The release is accomplished by a subpicosecond pulse of UV irradiation. The resulting 2D IR signals are used to obtain snapshots of the ∼100-ps helical conformational reorganization of the distorted dihedral angle and distance between amide units at chemical bond length-scale resolution. The decay rates of the angle between the dipoles, dihedral angles, and distance autocorrelations obtained from molecular dynamics simulations support the experiments, providing evidence that the final helix collapse conforms to linear response theory.

The concept of a rugged free energy surface and the mechanism of how a protein explores that space are longstanding questions (1–3) influencing all aspects of conformational dynamics, ranging from ligand exchange and enzyme activity to protein folding and unfolding. Although in principle one may imagine defining answers from molecular dynamics (MD) simulations to questions regarding specific local steps along such surfaces, there are few experimental approaches that can directly measure the time evolution of distributions of microscopic structural parameters throughout such explorations. Nonetheless, the dominant principles of protein dynamics are beautifully illustrated by an immense theoretical effort that was summarized (4) and exposed recently by experiments on ligand recombination dynamics (5–7), fluctuations in enzyme activity (8), single-molecule FRET experiments (9, 10), and downhill folding (11), all of which measure some coarse-grained aspect of the microscopic fluctuations.

The helix–coil transition is one of the most basic examples of peptide folding; therefore, considerable experimental and theoretical investigation already has been dedicated to investigating such structural searches (12–16). Qualitatively, helix formation is predicted to initiate from infrequently formed single-helix turn structures, which promote rapid development of the remaining turns of the helix (12–15, 17, 18). The equilibrium folding kinetics thus is dominated by the mean existence time of states that have failed to initiate. The current work provides a direct measure of a feature of α-helix conformation dynamics that is independent of the intrusive rate-determining nucleation period involved in helix folding. Prior helix folding experiments demonstrated that helix relaxation occurs with exponential time constants on the order of hundreds of nanoseconds, which may be affected by peptide length, temperature, viscosity, ionic strength, and steric effects of side chains. These experiments have used the vibrational spectra of backbone amides, as well as fluorescence of aromatic side chains or attached chromophores (13, 19, 20). Two-state models (13, 16, 19) extended to include helix propagation, known as kinetic zippering (14, 15), also have been used to infer and extract microscopic nucleation and/or propagation rates from macroscopic relaxation times. “Zipper” dynamics, however, are not seen directly in nanosecond T-jump experiments, although the timescale to make consecutive helix turns has been modeled by combinations of theory and experiment to be on the order of tens to hundreds of picoseconds (14, 15, 17). In addition, stretched exponential kinetics have been observed in T-jump experiments (19, 21, 22). There also have been reports of helix conformational kinetics that are much faster than the conventional T-jump time constants of hundreds of nanoseconds to milliseconds (20, 23). Recently, a helix turn propagation time constant of 51 ns was found for an alanine-based peptide (24), which is much slower than that obtained from the zipper model. What remains, is to bring this earlier work, which used linear kinetic equations, into relation with these more recent results. However, no direct conclusion about the structural rearrangements involved or required in forming a helix turn within a partially formed helix structure has been exposed in any of these relaxation experiments. Helices and “kinked” helices play integral roles in both protein structure and function, serving as nucleation points for protein folding (25) or offering conformational flexibility to modulate biological processes such as signal transduction (26) and ligand binding (6, 7).

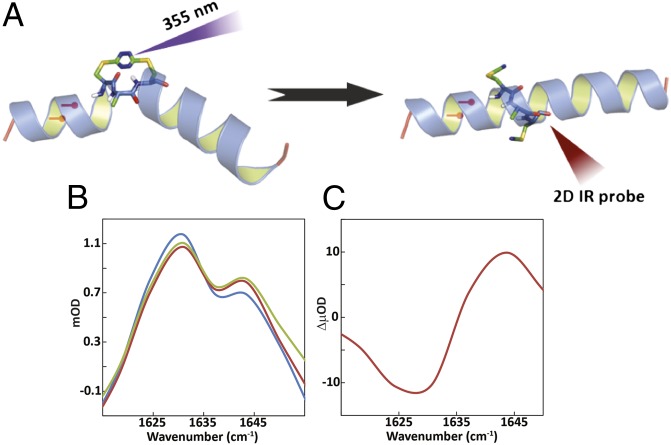
In this paper, we report measurements of the time evolution of structural local parameters of a helix exploring the free energy landscape close to equilibrium. The experiment begins by attaching an unnatural bridge, the S,S-tetrazine phototrigger (27, 28), linking two Cys residues introduced at the 10th and 12th positions of an alanine-rich α-helix (29). This bridge (Fig. 1A) prohibits the helix from folding into the helical equilibrium distribution. Instead, the bridged peptide adopts distinct equilibrium structures, which represent the initial ensemble for our optical triggering experiment. Nonetheless, the bridged structure distribution must be similar to that of the native helix at equilibrium, because the short helices on either side of the bridge are well formed, as judged from the CD spectra and the infrared spectrum of the amide I band (SI Appendix). We therefore consider that the release of the constraint will permit measurement of the relaxation of a very slightly displaced conformational distribution to the equilibrium α-helical conformation. This situation is analogous to the final steps of protein folding that occur once the conformations have already surmounted any free energy barrier, and all molecules in the ensemble will follow paths leading to the equilibrium folded state. The process should be similar to certain stages of “downhill folding” (11), although in the example presented here, the perturbed state is very close to equilibrium.

Fig. 1.

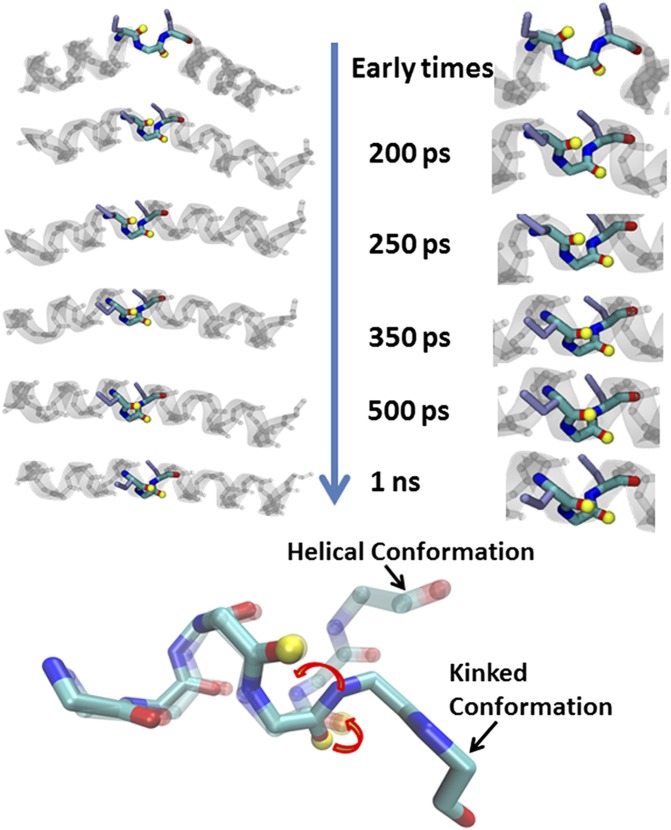
(A) Schematic representation of S,S-tetrazine phototriggering. The S,S-Tet-AKA peptide (AcHN-YGAKA-AAAKC-ACAKA-AAAKA-AAAG-COONH₂) adopts a kinked helix conformation, based on constrained MD simulations. The position of the ¹³C=¹⁸O labels in S,S-Tet-AKA_A5*/A6* is shown in red. The full structure of the constrained region is shown to highlight the orientation of the ¹³C=¹⁸O labels in S,S-Tet-AKA_C10*/A11*. Photolysis releases the S,S-tetrazine constraint to yield the bis-SCN-AKA peptide. (B) Diagonal traces of 2D IR spectra through peak maximum before release (blue), after a 500-ps delay (red), and 1 ns after release (green). (C) Spectrum of the difference between 2D IR traces before and 500 ps after release.

Only a few transient 2D IR studies on biomolecules have been performed, demonstrating the capability of measuring equilibrium relaxation processes after temperature jumps (30) as well as hydrogen bond dynamics in a β-turn (31). The experiments reported here directly record a bond distance and bond angle change associated with helix formation from a photochemically initiated distribution that is slightly shifted from equilibrium. By constraining the center of an α-helix with an S,S-tetrazine linker, a structural perturbation is introduced that may be comparable with the distortion caused by a proline residue (32). Because the stability of the monomeric α-helix depends strongly on the number of consecutively repeating helical turns (12, 33), we chose an initial structure consisting of a preformed helix and introduced a small distortion associated mainly with one helical turn in the central region. After photochemical release of the S,S-tetrazine constraint, the structural reorganization (34, 35) is examined by means of the transient 2D IR of ¹³C=¹⁸O isotopically edited amide I modes (36, 37) in selected regions of the peptide close to where the changes are expected to occur. These transient 2D IR spectra yield structural snapshots of the local peptide structure (34, 35) evolving toward equilibrium (38). We thus ask several questions with these experiments: What are the specific structural movements along the reorganization pathway of the single helical segment? Is there a cascading effect of structural motions, driving the kink toward the end of the helix to generate the native conformation? Do the ends of the helix ever sense the perturbation in the middle, or is the reorganization completely local? Does linear response theory properly account for the relaxation? How successful are equilibrium and nonequilibrium MD simulations in reproducing the relaxation measurements?

Results and Discussion

First, we comment on the photochemistry of the tetrazine phototrigger. The cysteine residues clamping the tetrazine become unreactive C_β-SCN groups after photocleavage and the backbone carbonyl absorptions are modified. The resulting carbonyl bands of the photoproduct of a model dicysteine tetrazine appear with a time constant of 10 ps (39); and the C_β-SCN production for the CAC model peptide unit (SI Appendix) occurs within 67 ps. Thus, the photochemistry of the tetrazine–peptide system certainly is completed within 67 ps, and the peptide very likely is freed to relax within 10 ps.

Transient 2D IR Reveals Helix Reorganization.

The transient 2D IR experiments of the unlabeled AKA tetrazine-containing peptide (S,S-Tet-AKA) in d₃-trifluoroethanol (d₃-TFE) are consistent with a structural evolution toward the fully α-helical conformation. The d₃-TFE solvent was used to increase solubility and overall helical propensity (40). The 2D IR spectrum of the unlabeled version of S,S-Tet-AKA in d₃-TFE is shown in Fig. S2D at 500 ps and 1 ns after photolysis (SI Appendix). The changes are small but significant. The similarity in the diagonal traces (defined as the line passing through the peak maximum parallel to the diagonal, ω_t = ω_τ) after 500 ps and 1 ns, suggest that the structural changes plateau on this timescale. There is a signal increase around 1,640 cm^–1, a typical helical band location for the alanine-rich AKA peptides in TFE (21, 41), indicating that the helical content is increasing before 500 ps. The signal increase at higher frequency and the decrease at lower frequency are more obvious from the 2D IR diagonal traces (Fig. 1 B and C). The cross-peak between the band at 1,582 cm^–1 from a tyrosine side chain (42) and the backbone amide I band disappears by 1 ns, suggesting that the photorelease causes the side chain to reorient, breaking the interaction with the backbone.

Isolating Specific Backbone Regions with ¹³C=¹⁸O Labels.

The results with the isotopically substituted versions are much more structurally distinct. When S,S-Tet-AKA is isotopically edited with ¹³C=¹⁸O at residues Cys10 and Ala11 (i.e., S,S-Tet-AKA_C10*/A11*), both amide I vibrations are isotopically down-shifted 60 cm^–1, which strongly reduces their coupling with those of the other carbonyls (34, 36, 37). The 2D IR spectra and traces of the S,S-tetrazine tripeptide model system, with isotopic labeling of the linked region similar to that found in the S,S-Tet-AKA_C10*/A11*, exhibit one absorption band, indicating the two labeled transitions overlap (SI Appendix). As demonstrated previously (34, 35, 37, 43), the location, polarization, and line width of such a composite amide I band may be used to determine structural parameters in ∼2-ps snapshots, recorded over a nanosecond range of delays. To examine the site-specific structural changes on photorelease of the AKA peptide, two labeled peptides were designed and constructed: one with the double label contained in the nearest-neighbor pairs of residues Ala5 and Ala6 (i.e., S,S-Tet-AKA_A5*/A6*), far from the kink and toward the N terminus, and a second peptide, S,S-Tet-AKA_C10*/A11*, with the labeled pair within the kinked region to afford structural information on residues distorted by the unnatural S,S-tetrazine bridge.

Although only one peak arising from the isotopic labels is observed in the FTIR of the S,S-Tet-AKA_A5*/A6* peptide, two diagonal bands at 1,585 and 1,597 cm^–1 are seen in the 2D IR spectrum as a result of the increased spectral resolution (SI Appendix, Figs. S1 and S6). These bands are excitonic transitions formed from the amide I modes involving a pair of residues spatially separated by approximately one helix turn from the kink. They show equivalent diagonal 2D IR trace spectra through all optical delay times, which implies that these residues do not undergo any significant structural change as a result of the photolysis (SI Appendix, Fig. S6). The measurements, however, indicate that these two modes are coupled to each other, based on the distinct changes in their antidiagonal width and relative peak intensities with different polarization conditions (44–47). The peak separation remains the same at all optical delays for both polarizations. These results can be modeled as a simple exciton as described below.

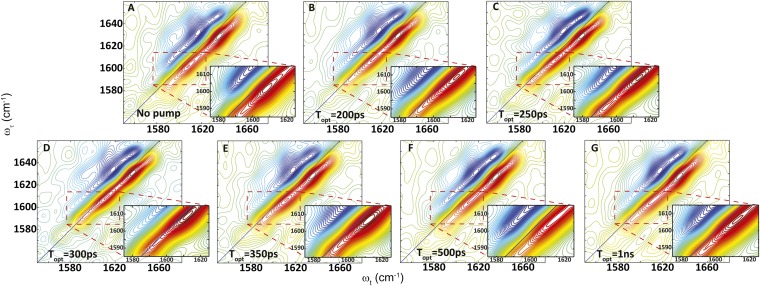
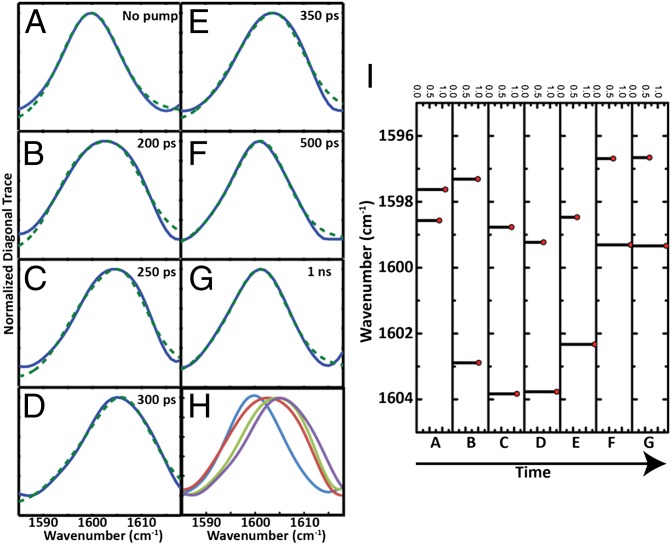
On the other hand, the transient 2D IR spectrum of the S,S-Tet-AKA_C10*/A11* peptide in d₃-TFE exhibits very different spectra and responses to photolysis than S,S-Tet-AKA_A5*/A6* (Figs. 2 and 3). Although two absorption bands are observed in the region between ω_τ = 1,580 and 1,620 cm^–1 of the transient 2D IR spectrum, the lower-frequency peak at ω_τ = 1,582 cm^–1 and ω_t = 1,590 cm^–1 due to a tyrosine side chain does not change appreciably with optical delays, and is not discussed further. The other band located around ω_τ = 1,600 cm^–1 exhibits significant photolysis-induced changes in peak position and spectral width (Fig. 2), which are most evident from the 2D IR diagonal traces (Fig. 3). Based on the 2D IR spectral signatures of the labeled amide transitions observed for S,S-tetrazine tripeptide model systems (SI Appendix), this band is expected to encompass the overlapping transitions of the ¹³C=¹⁸O labeled Cys10 and Ala11, which contain the required structural information (Figs. 4 and 5). A frequency upshift of 7.5 cm^–1 occurs over the first 300 ps after photolysis of S,S-Tet-AKA_C10*/A11*, followed by a slight decrease to a fixed value (3 cm^–1 up-shifted) after 500 ps. The 2D IR spectral width of the diagonal 2D IR traces of this band increases by 5 cm^–1 from the starting constrained configuration and then decreases until about 500 ps delay, whereupon a constant value is reached. The spectral width was fit to exponential decay with a time constant of 97 ± 7 ps (Fig. 4).

Fig. 2.

Transient 2D IR spectra of S,S-Tet-AKA_C10*/A11* in d₃-TFE with (A) no optical pump and (B) 200-ps, (C) 250-ps, (D) 300-ps, (E) 350-ps, (F) 500-ps, and (G) 1-ns optical delay.

Fig. 3.

Exciton modeling of S,S-Tet-AKA_C10*/A11* in d₃-TFE. (Left) Normalized diagonal 2D IR trace (blue) and the fitting to the exciton model (dotted green) (A) with no optical pump and (B) 200 ps, (C) 250 ps, (D) 300 ps, (E) 350 ps, (F) 500 ps, and (G) 1 ns after release. (H) Overlay of normalized diagonal 2D IR traces for (blue) A, (red) B, (green) C, and (purple) D. (I) The peak position and relative intensity from the exciton model fitting of diagonal 2D IR traces for conditions A through G, with delay time increasing as shown.

Fig. 4.

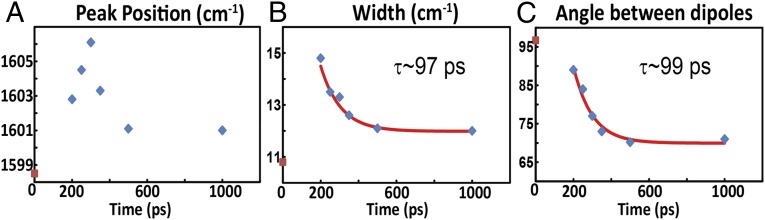
Experimental properties obtained for the isotope-labeled region from 2D IR spectra of S,S-Tet-AKA_C10*/A11* in d₃-TFE photolyzed at T_opt = 0. (A) Peak position and (B) width of experimental 2D IR diagonal traces as a function of the optical delay. (C) Angle between the dipoles obtained from fitting to the exciton resonance pair model. The red curves are the fitted exponential decays. The red points correspond to the data with no optical pump.

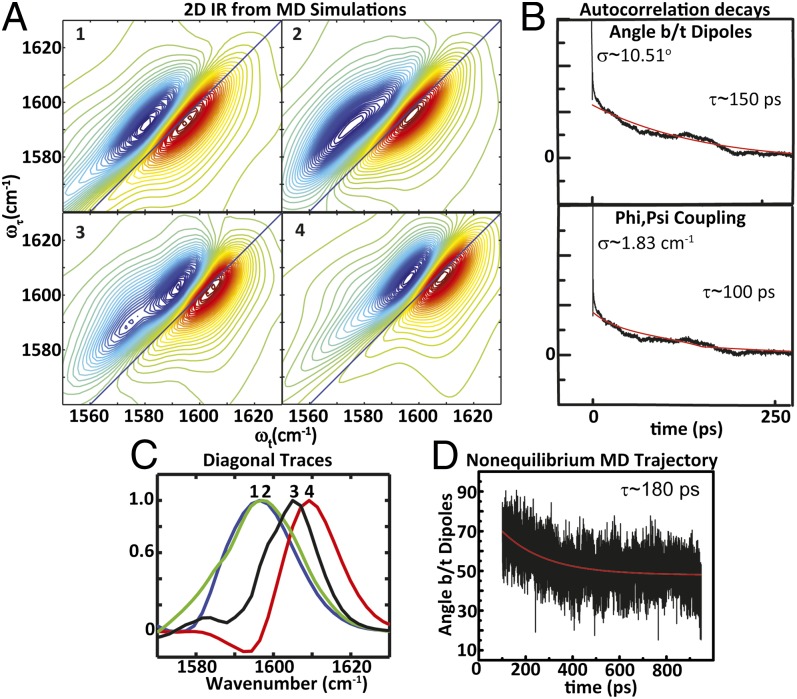
Fig. 5.

(A) Simulations of 2D IR spectra computed from MD trajectories of (1) constrained equilibrium structures, nonequilibrium structures over an interval of (2) 100–200 ps and (3) 200–300 ps, and (4) helical equilibrium structures. (B) Autocorrelation decays of the angle between dipoles and phi,psi coupling obtained from equilibrium MD simulations of helical trajectories for 4 ns. (C) 2D IR diagonal traces obtained from simulated data for 1 (blue), 2 (green), 3 (black), and 4 (red). (D) Decay of the angle between dipoles from mean nonequilibrium MD trajectory.

Heating effects are expected to play a minor role in these experiments for several reasons. The solvent heating effects would result in a temperature rise of the irradiated volume of less than 1 K based on the excitation pulse energy and the optical densities of the S,S-tetrazine chromophore used here (48). Also, the S,S-tetrazine chromophore is inscribed within the peptide through the sulfur atoms of the incorporated Cys residues. The vibrational energy relaxation therefore is minimized by the heavy atom effect (28). Experimental evidence demonstrating that heating does not contribute to the observed changes in the spectra of the carbonyls may be observed from a single labeled ¹³C=¹⁸O-Ala tripeptide (SI Appendix, Fig. S4). Both the experimental width and the position of the 2D IR diagonal traces show no change upon photolysis.

Helical Structure Is Present Throughout Photolysis.

For the S,S-Tet-AKA_A5*/A6* peptide, a simple exciton model permitted determination of the coupling from the peak separation of ∼13 cm^–1 (SI Appendix), corresponding to an intermode coupling of 6.5 cm^–1, a value expected from previous measurements for helical nearest neighbors (49, 50). The ratio of the estimated integrated absorptions of the two underlying bands I₊ and I_– defines an average angle between the transition dipoles of θ = 70 ± 5° or the supplement 110 ± 5° from the exciton relationship I₊/I_– = (1 + cos θ)/(1 – cos θ). Importantly, the coupling strength of 6.5 cm^–1 and the angle of 70° do fall within the range of values established for nearest neighbors within a helical structure based on phi/psi coupling maps (51, 52), but the 110° angle lies outside the helical region known to be present for the equilibrium structure from the CD spectrum and from here on is neglected. These results indicate that in the neighborhood of Ala5/6, the peptide maintains the helical propensity after the photorelease of the S,S-tetrazine bridge linking Cys10 and Cys12, and that no long-range effects of photolysis are sensed. Importantly, MD simulations for the S,S-tetrazine–constrained equilibrium structure distribution, as well as those for the nonequilibrium trajectories, successfully generate results that are confirmed by these experiments.

A Resonance Pair Model Uncovers Structural Change Within the Constrained Region upon Photorelease.

The experimental 2D IR traces of the S,S-Tet-AKA_C10*/A11* peptide were fitted to an exciton resonance pair model (34) in which a shift in the peak position and the changes in width are determined by a combination of the exciton splitting and the relative intensities of the exciton transitions (Fig. 3). The exciton states originate from interactions between the localized ν = 0 → 1 transitions of the neighboring amide I modes. Two transitions are not seen separately in this case, because the backbone distortion from the helical structure of the constrained region, as supported by detailed NMR analyses of a model tripeptide (SI Appendix), results in the coupling being significantly less than the 6.5 cm^–1 observed for S,S-Tet-AKA_A5*/A6*. Such couplings have been calculated and tabulated repeatedly as functions of the dihedral angles around the amide bonds (51, 52). Moreover, the nonlinear response functions we used for computation of the 2D IR spectra were the typical, well-tested 2D IR responses in the frequency domain (34, 35) (SI Appendix). When either residue of the Cys10/Ala11 pair was edited isotopically in analogous tripeptide models of the linked region, the ¹³C=¹⁸O vibrational frequency was 1,598 cm^–1 (SI Appendix, Fig. S4). The frequency of the unphotolyzed S,S-Tet-AKA_C10*/A11* also was 1,598 cm^–1, which therefore corresponds to the uncoupled zero-order frequency of the resonance pair. As the experimentally observed frequency and width change, the angle between the dipoles determined from the least-squares fits of the diagonal traces of the 2D IR decreases significantly (Fig. 4). During this process of fitting the diagonal traces through the 2D IR responses, the uncoupled frequency, 1,598 cm⁻¹, obtained from S,S-Tet-AKA_C10*/A11* before photolysis, was used as an initial starting condition. Each diagonal trace then was least-squares fitted by varying the center frequency of the distribution, the coupling strength, and the angle between the dipole vectors of amide modes. The time constant of the decrease in this angle, ∼99 ps, matches well with the decay time of the experimental width. The implication is that rotation around the angle between the dipoles directly affects the coupling and, as a result, the experimental widths. This change will be shown to correspond to a rotation around the psi angle, which is reproduced by the MD simulations.

Capturing Structural Changes Observed in 2D IR Experiments with MD.

Equilibrium distributions of the constrained and helical AKA_A10C/A12C peptides and nonequilibrium trajectories were obtained (SI Appendix). The constrained AKA peptide was constructed using harmonic constraints representing the S,S-tetrazine molecule because of the lack of force-field parameterization. From the structures acquired from the MD trajectories, a distribution of frequencies was obtained by using an empirical amide I vibrational map (53), with the coupling between nearest-neighbor amides determined from a coupling map (51) for the computed phi,psi angles. Given the uncoupled frequencies, the coupling constants, and the angle between the dipoles, the 2D IR spectral distributions could be simulated by applying the same exciton resonance pair model used to fit the experimental diagonal traces. The simulated 2D IR spectra and diagonal traces computed from the molecular dynamics simulations of the constrained, released peptide (taking structure distributions from 100-ps intervals from the MD simulation: 100–200 ps, etc.) and the helical structural distributions (Fig. 5) follow a trend similar to the one observed in the experiment. The peak maximum becomes frequency up-shifted by ∼12 cm^–1 upon release of the constraint. From the nonequilibrium MD trajectories, the simulated 2D IR traces show an increase in peak maximum position over the structural distributions obtained from 100–200 ps, 200–300 ps, etc. until 500–1,000 ps, at which the 2D IR trace shows a slight 2-cm^–1 decrease. The width initially increases when comparing the constrained and the released peptide, followed by a decrease as the width approaches the helix distribution (Fig. 5C). As such, the experimental data support these trends and suggest that the MD simulations accurately capture the structural changes. The exponential decrease in the angle between the dipoles of the nonequilibrium trajectories, upon release, has a decay time of 180 ps (Fig. 5D). The nonequilibrium trajectory was performed for a total duration of 10 ns. Compared with the initial transition, no significant changes were observed in the distribution of the angle between the dipoles, coupling, or psi angle after 500 ps (SI Appendix, Fig. S8). The constrained structure from the MD trajectory starts with an angle between the dipoles of 90°, which decreases to 50°. The change in this angle, as well as the decay constant, is on the same order of magnitude as those determined from the experimental diagonal traces. As a measure of the helix relaxation, the correlation decay of the rmsd of the nonequilibrium MD trajectory, using a reference minimized helical structure of the AKA_A10C/A12C peptide, is 148 ps, which is within reasonable agreement with the observed spectral changes (SI Appendix).

Rotation Around Psi Dihedral Angle.

The distribution of the distances and angles between the dipoles and the couplings resulting from the phi,psi map for the constrained and helical equilibrium simulations show significant overlap. The mean value for the angle between the dipoles is 110° for the constrained structure, which is in reasonable agreement with both the initial condition determined from the experimentally observed coupling in the S,S-Tet-AKA_C10*/A11* peptide and the NMR structure of an S,S-tetrazine tripeptide model system (SI Appendix). This angle decreases to a mean value of 50° at the helical equilibrium distribution. A comparison of the constrained and the helical equilibrium MD structures reveals that the mean coupling, obtained from the phi,psi map, increases from 0 to 5 cm^–1. The mean distance shows only an ∼0.2-Å decrease. The autocorrelation decays obtained from MD trajectories for the angle between dipoles and the couplings of the helical equilibrium simulation are on the order of 100–150 ps (Fig. 5B). The decay times of these fluctuations, along with the correlation decay of the rmsd (determined to be 113 ps) computed with respect to a mean helical AKA_A10C/A12C structure for the helical equilibrium MD simulation, are a measure of the helical relaxation within the ensemble. The timescales of the helical relaxation also correlate with the spectral changes observed in the 2D IR experiment. Thus, MD simulations may be drawn upon to acquire some important structural parameters during helix reorganization. For instance, no significant variation is seen between the constrained and the helical structure distributions for the phi dihedral angle (C′-N-C^α-C′). The psi dihedral angle (N-C^α-C′-N), on the other hand, undergoes a significant change between the constrained and the helical distributions (Fig. 6). Such a motion would cause the coupling to vary significantly during relaxation, which is consistent with the experiments and nonequilibrium MD trajectories.

Fig. 6.

Representations of the backbone rotation around the psi angle (arrows) of the labeled amides (yellow tops) in the distorted constrained region upon release of tetrazine to reform the helical turn.

Conclusions

We thus obtain from the data a molecular picture of the fast structural changes for the designed constrained S,S-Tet-AKA as the peptide proceeds toward the equilibrium ensemble in response to release of the phototrigger. The initial condition was selected and defined through synthesis such that a small perturbation was made to a single helical turn while maintaining the helix on both ends (Figs. 1A and 6). The constrained S,S-Tet-AKA structure would be located somewhere on the downhill side of the free energy barrier to helix folding. Upon release of the constraint, the 2D IR spectra provide a glimpse into the conformational reorganization that occurs as the peptide proceeds toward equilibrium. Key motions along the reaction coordinate are deduced from these experiments. The peptide reorganization toward the full α-helical conformational equilibrium does not involve movements that push the kink along the chain toward the ends of the peptide. Moreover, the peptide also does not irreversibly unfold before proceeding toward the native helical conformation. Rather, the central region, where the small perturbation to the helical structure had been enforced by the constraint, undergoes a local structural change following photorelease, which we track by changes in the dihedral angle psi. A simple rotation around the psi dihedral angle is detected that allows recovery of the helical structure. Although the propagation times for helices have been estimated from experiments to be on the order of tens of nanoseconds (24), the structural movements presented here on the picosecond timescale reflect the changes due to secondary structure-impeded rotation around a single dihedral angle. The simulations by Brooks and coworkers (18) come close to reproducing our correlation times. Indirect estimates of the rates of helix propagation arising from zipper models (15), as well as these simulations, suggest that propagation times after nucleation are on the order of hundreds of picoseconds.

In summary, 2D IR, in conjunction with phototriggering, has permitted acquisition of picosecond snapshots of helix relaxation. The reorganization of the helix near the perturbed region is tracked by sensing the rotation about the psi dihedral angle. Fast structural changes are observed directly through the changes in the spectral widths and peak positions of the transient 2D IR spectra as the structural change proceeds along the reaction coordinate. Importantly, the timescales of the spectral changes, which may be related to specific structural parameters determining the molecular movie, are reproduced successfully by the MD simulations. Moreover, the simulated equilibrium time autocorrelations of the angle between the dipoles, the distance between the two dipoles, and the dihedral angles all agree well with the observed parameters, suggesting the conformational kinetics are well described by linear response theory.

Methods

Peptide Synthesis.

A fragment-coupling approach was used to construct the S,S-Tet-AKA peptide, as well as the isotopically edited versions. The synthetic details are described in SI Appendix.

2D IR Spectroscopy.

After generation of mid-IR pulses (54), the IR pump beam is transmitted through either a home-built acoustic–optic modulated pulse shaper or a Mach-Zehnder interferometer to create a narrow-band pulse or a pair of pulses, respectively, for the 2D IR measurements. The 2D IR probe pulses were preceded by a 700-fs pump pulse at 355 nm with 7 µJ of energy to generate the photorelease of the tetrazine constraint. More details of the 2D IR experiment may be found in SI Appendix (Fig. S1).

MD Simulations.

MD simulations were carried out using the Nanoscale Molecular Dynamics (NAMD) program (version 2.5 b1) (55) and the CHARMM22 force field (56). The MD simulations are described further in SI Appendix.