Active impedance metasurface with full 360° reflection phase tuning

Abstract

Impedance metasurface is composed of electrical small scatters in two dimensional plane, of which the surface impedance can be designed to produce desired reflection phase. Tunable reflection phase can be achieved by incorporating active element into the scatters, but the tuning range of the reflection phase is limited. In this paper, an active impedance metasurface with full 360° reflection phase control is presented to remove the phase tuning deficiency in conventional approach. The unit cell of the metasurface is a multiple resonance structure with two resonance poles and one resonance zero, capable of providing 360° reflection phase variation and active tuning within a finite frequency band. Linear reflection phase tuning can also be obtained. Theoretical analysis and simulation are presented and validated by experiment at microwave frequency. The proposed approach can be applied to many cases where fine and full phase tuning is needed, such as beam steering in reflectarray antennas.

The reflection phase control for electromagnetic (EM) wave impinging on a surface is important in both fundamental EM research and device technologies. Many phenomena and applications are related to the reflection phase control, such as EM propagating mode to surface mode conversion¹, anomalous reflection²,³,⁴, EM wave absorber⁵, high impedance surface and artificial magnetic conductor⁶,⁷, reflectarray antennas⁸,⁹,¹⁰, beam forming and beam scanning antennas¹¹,¹²,¹³,¹⁴, phase shifters¹⁵, etc. In most of these applications, full reflection phase control with a range of 360° is often desired.

As is well known, a perfect electric conductor (PEC) surface or a perfect magnetic conductor (PMC) surface provides 180° or 0° reflection phase, respectively. The EM wave reflection can be modeled as transmission line shorted or opened at the terminal, as illustrated in Fig. 1. The impedance metasurface is a generalized concept with 0° ~ 360° designable reflection phase, as depicted in Fig. 1¹⁶. It is commonly realized by a planar reflective board composed with textured metamaterial structure. The transmission of such a board is null, and all the incident wave energy are reflected or absorbed. Hence, this kind of board can be characterized uniquely by either reflection coefficient or impenetrable surface impedance. With specifically designed unit cell in the planar metamaterial structure, arbitrary reflection phase distribution can be realized. However, its characteristics are fixed once the metasurface is fabricated¹,².

Figure 1. EM wave reflection by different surfaces.

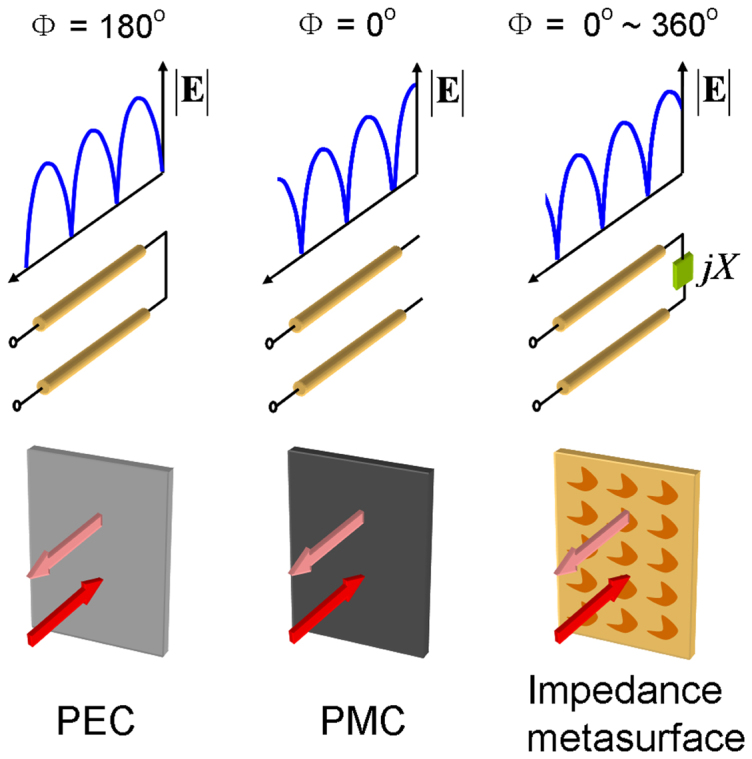
Transmission line model and reflection phase Φ of PEC, PMC and impedance metasurface.

The impedance metasurface usually has dispersive surface impedance with respect to frequency. By integrating tunable component or material into the surface, the dispersive surface impedance can be shifted in frequency domain, providing tunable reflection phase within a certain frequency band. The tunable component includes temperature tuned phase change material, graphene, active microwave elements such as the varactors, mechanical tuning, etc, depending on the usage frequency regime⁴,⁵,¹¹,¹²,¹³,¹⁵. This useful feature can be applied to develop new devices with flexible tunabilities, e.g. active beam scanning in reflectarray antennas¹².

However, in order to have full control of the reflection phase, tunable impedance surface with full 360° phase tuning range is often desired within a frequency band. This feature in fact allows arbitrary reflection phase tuning. Conventional tunable impedance metasurface, such as tunable mushroom structure, usually involves single resonant structure in the unit cell, and therefore suffers the deficiency in phase tuning range¹². As shown by the either curve in Fig. 2, the typical reflection phase of the impedance surface composed of the unit cell with single resonance loaded with varactor decreases from 180° to −180° monotonically. The phase changes rapidly around 0° where parallel resonance takes place in the unit cell, but approaches ±180° asymptotically. This phase curve can be shifted when the resonance frequency is changed by controlling the tunable component (e.g. the varactor shown in Fig. 2) in the unit cell. Thus the reflection phase can be actively tuned, especially within the frequency band across which the parallel resonance shifts, as illustrated by the phase tuning range in Fig. 2. Due to the finite tuning range of the parameters of the practical active component, such as the junction capacitance of the varactor, the shift of the resonance frequency and the reflection phase curve is always finite. On the other hand, the asymptotic behavior of the reflection phase at ±180° always exists in conventional structures with single resonance. Hence, these two issues give rise to the tuning deficiency problem that 360° full phase tuning range usually can not be achieved, as illustrated in Fig. 2.

Figure 2. Phase tuning deficiency in the conventional tunable impedance metasurface.

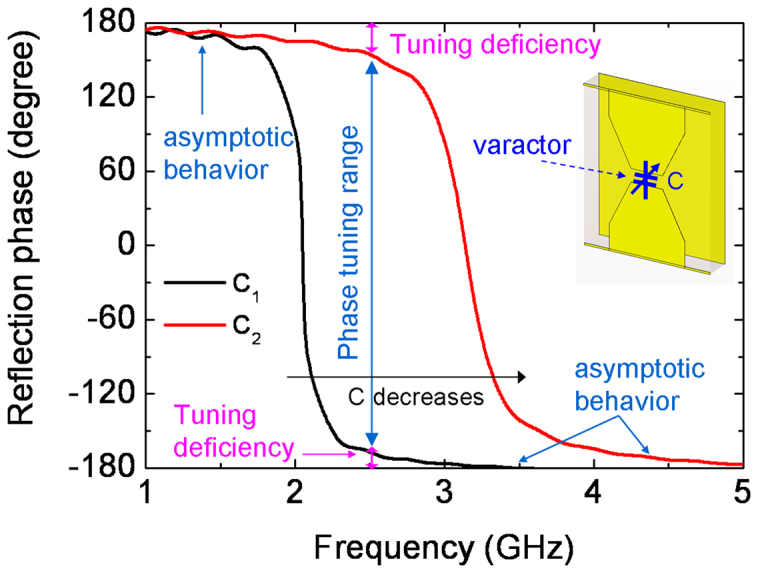
C₁ and C₂ correspond to different varactor capacitance. Inset shows the unit cell of conventional tunable impedance surface with a front metallic bow tie shaped patch connected by a varactor in the middle and an entire metallic sheet at the back of a dielectric substrate.

In this paper, an approach for full 360° reflection phase control is presented. The proposed metasurface employs multiple resonance structure with two resonance poles and one resonance zero in between. Owing to the impedance change with frequency predicted by the Foster impedance theorem, the reflection phase varies continuously by 360° within a finite frequency band without the asymptotic behavior. Therefore, 360° full tuning range can be obtained as long as the frequency spectrum can be shifted larger than the above mentioned finite frequency band, by controlling the varactors capacitance in the proposed impedance metasurface.

Results

Structure and surface impedance

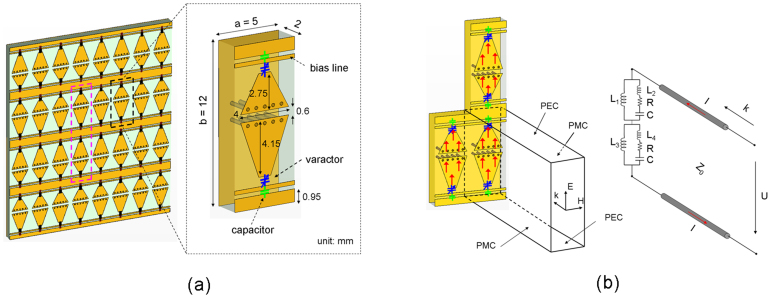
The proposed metasurface comprises electrically small unit cells which are arranged periodically in a two dimensional plane. The unit cell is marked by the pink dash rectangle, and the half unit cell enclosed by the black dash rectangle is enlarged in the right part, as shown in Fig. 3(a). The whole unit cell is the half unit cell plus its mirror image in the vertical direction. The half unit cell is composed of two metallic trapezoidal patches on the top layer of the dielectric substrate and a full metal sheet on the bottom layer. Two thin horizontal bias lines connect to the upper and lower patches through varactors, while another thick horizontal line connects to the thin lines through fixed chip capacitors. This forms serial capacitor connection to reduce the total capacitance. The metals on the top and bottom layers are electrically connected by several vias, forming dual parallel resonant tanks in series. Due to the mirror symmetry between the two half unit cells in the unit cell, the induced electric current on the two parts are symmetric to each other but with same direction under the normal incidence case, as illustrated by the current distribution on the trapezoidal patches in Fig. 3(b). Because each half unit cell is symmetric in the horizontal direction, the induced electric current on the neighboring half unit cells in the horizontal direction is mirror symmetric too under normal incident case. Understanding this point, for a vertically polarized incident wave, we only need to analyze a single half unit cell with two opposite perfect electric boundaries and two opposite perfect magnetic boundaries according to the image theory¹⁷, as shown in Fig. 3(b). It should be noted that since each half unit cell is asymmetric in the vertical direction, PEC boundary conditions can not be used if the two half unit cells are not mirror symmetric in the unit cell. These boundary conditions actually constitute a special waveguide loaded with the half unit cell at the termination. The fundamental mode of such a waveguide is the plane wave with zero cut off frequency. The second order mode is either TE or TM mode, which depends on the property of the boundary with larger width in the waveguide cross section. The cut off wavelength of the second order mode is equal to the double width of the wider boundary. Hence, when the period of unit cells in the surface is smaller than the half operation wavelength, only plane wave can propagate, and all the high-order modes are evanescent. These high-order modes are nothing but the high-order spatial Floquet harmonics under plane wave normal incidence. The evanescent field is localized around the unit cell, and stores the reactive energy. Because the evanescent field together with the incident and reflected plane wave field have to meet the boundary conditions of the half unit cell structure, the evanescent field determines the reflection phase of the reflected plane wave. As a result, we can define the effective surface impedance Z_s to characterize the metasurface. When the period goes to zero, the evanescent field or high-order modes become weaker such that the field at the metasurface is more homogenous. As a result, the impedance metasurface consisting of periodic unit cells would be more like a homogeneous surface. This is known as the effective medium approximation. Under this limiting case, the electric field 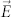and magnetic field 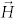satisfy 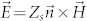at the surface, where 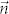denotes the unit vector of the surface normal.

Figure 3. The proposed tunable impedance metasurface.

(a) Schematic of the metasurface and enlarged half unit cell with dimensional parameters. The unit cell is enclosed by the pink dash rectangle. (b) The half unit cell with periodic boundary conditions is equivalent to the infinite board. The red arrow represents the current distribution with mirror symmetry. The half unit cell can be modeled as parallel resonant tanks in serial, and the boundary condition can be modeled as the transmission line.

Circuit model

When there is only a propagating plane wave mode and all the high-order modes are cut off, the field in the cross section is static. Hence, the waveguide can be regarded as a dual electric conductor transmission line, where the two opposite perfect electric boundaries function as the conductors and the other two perfect magnetic boundaries as the insulator since they don't conduct electric current. If the unit cell is also much smaller than the operation wavelength, it can be modeled as the electric circuit. The metallic part should be modeled as inductor because the high frequency current flowing on it produces quasi static magnetic field. In Fig. 3(b), L_1,3 represents the inductance coming from the ground plane, and L_2,4 represents the inductance of the small and large trapezoidal patches on the top layer with vias in the half unit cell. The varactor and chip capacitor are modeled as the capacitor C_1,2. Therefore, the EM property of the proposed periodic surface can be analyzed using circuit theory, as shown in Fig. 3(b). The half unit cell behaves as the termination load of the transmission line. The load impedance Z_l is determined by

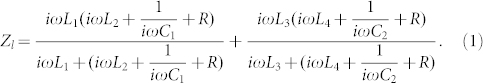The characteristic impedance of the transmission line is calculated as Z₀ = U⁺/I⁺. U⁺ and I⁺ are calculated as U⁺ = E⁺b and I⁺ = H⁺a, where a and b are the width and height of the half unit cell, as shown in Fig. 3(a). The U⁺ and I⁺ are proportional to the amplitude of the forward propagating E⁺ and H⁺ field respectively due to the plane wave feature. As a result, Z₀ = U⁺/I⁺ = ηb/a, where η is the plane wave impedance. Similarly, the surface impedance of the proposed periodic structure is related to the load impedance as Z_s = Z_la/b. The reflection coefficient can be calculated by using either circuit parameters Z₀, Z_l or field parameters η, Z_s because of the proportional relation.

360° reflection phase variation and tuning

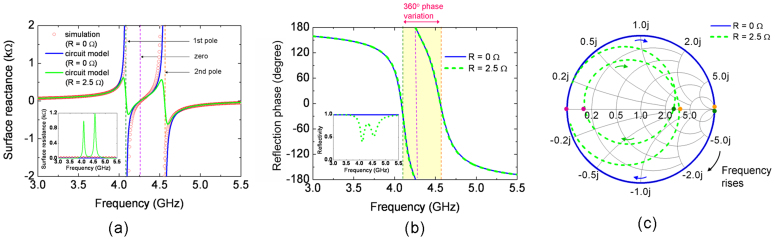
In order to obtain 360° reflection phase tuning range, we introduce two parallel resonance poles into the half unit cell, as illustrated in the circuit model of the half unit cell in Fig. 3(b). The surface impedance of the unit cell, which has only a reactance part for the lossless case R = 0, is plotted in Fig. 4(a) using the equation (1). The element parameters are obtained by fitting the circuit model results to the full wave simulation. The reactance has two parallel resonance poles at 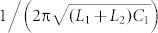and 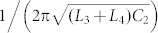, and one serial resonance zero in between. The reactance grows monotonically with frequency, and changes between inductive and capacitive at resonance poles and zero, obeying the Foster impedance theorem. The real part of the surface impedance is zero in lossless case. The surface impedance retrieved from the simulated S₁₁ using an EM full wave solver is also shown in Fig. 4(a) for comparison. Good agreement is observed between the simulation and circuit model results, indicating that the circuit model correctly captures the physics of the half unit cell. The simulation details can be found in the Methods section.

Figure 4. Surface reactance and the reflection of the metasurface.

(a) Surface reactance of the proposed full phase control metasurface. The inset shows the surface resistance. (b) Reflection phase of the proposed structure. The inset shows the reflectivity. (c) Loci of the surface impedance or reflection coefficient with respect to frequency on the Smith chart.

When a plane wave is impinging normally on the proposed periodic surface, the reflection coefficient can be calculated as 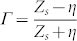. The results are plotted in Fig. 4(b). At the two resonant poles, the circuit impedance of the half unit cell is infinite so that the reflection phase is 0°. At the resonance zero, the circuit impedance of the half unit cell is zero, hence the reflection phase is ±180°. Away from these three resonance frequencies, the circuit impedance of the unit cell changes smoothly from infinitely large capacitive reactance to zero and from zero to infinitely large inductive reactance. Therefore, the reflection phase varies from 0° to −180° and then from 180° to 0° continuously with the frequency. The total phase variation is 360°, as marked in the yellow region in Fig. 4(b). The reflectivity is unity due to lossless assumption. This reflection behavior can also be understood on the Smith chart. Because of the unity reflectivity, the loci of the reflection coefficient or surface impedance are located on the circle with unity radius, as depicted by the blue line in the Smith chart in Fig. 4(c). The green and yellow points represent the corresponding impedance at the resonant poles, and the purple point represents that at the resonant zero. As the frequency increases, the surface impedance locus moves along the blue circle from the green point to the yellow one, producing a full 360° phase variation.

We have just shown that a continuous phase spectrum from 0° to 360° is confined within a finite frequency range without any asymptotic effect. By tuning the capacitor C integrated in the unit cell as shown in Fig. 3(a), the resonance poles and zero can be shifted synchronously so that the 360° phase variation region shifts accordingly. Since the frequency band for this region is finite, 360° full reflection phase tuning can be achieved at a certain frequency band as long as the frequency shift is larger than the frequency band of the full phase variation region.

For practical realization, energy dissipation in the device and components is unavoidable. In the proposed impedance metasurface, the energy loss includes the dielectric loss, metallic loss and varactor PN junction loss. These losses not only absorb the incident EM energy so as to degrade the energy efficiency of the proposed surface but also may destroy the full phase tuning capability of the surface. Among them, the PN junction loss has the largest influence on the reflection phase and magnitude under most cases. The dielectric loss can be reduced by using low loss substrate. The PN junction loss is due to the PN junction resistance, which is modeled as the resistor R in the circuit model.

Fig. 4(a) also shows the surface impedance under lossy case with R = 2.5 Ω, which is the common value to the varactors in the market. Unlike the lossless case, the surface reactance is not infinitely large around the resonance poles, while the surface resistance exhibits resonance peaks at the poles as shown in the inset of Fig. 4(a). From equation (1), we have

where m, n = 1, 2 or 3, 4 at the resonance poles with the high Q approximation. Here, we let C₁ = C₂ = C. It is known from equation (2) that the surface impedance becomes nearly resistive at the resonance poles. Furthermore, the smaller R is, the larger the surface resistance is at the resonance pole. As long as the surface resistance is larger than the wave impedance, 0° reflection phase can still be achieved at the poles, as depicted by the green dot line in Fig. 4(b). However, if the R is so large that the surface resistance is less than the wave impedance, the reflection phase will be 180° rather than 0° at poles. Under this case, our analysis shows that the continuous 360° phase variation will be destroyed. Moreover, the reflectivity at the poles depends on how large the surface resistance is compared with the wave impedance. Larger surface impedance, i.e. smaller R, will lead to higher reflectivity so that the energy loss is small, as can be seen by comparing the two reflectivity curves for different R values in the inset of Fig. 4(b). At the resonance zero located between the two poles, the surface reactance is zero and the surface resistance can be approximated as

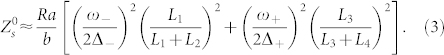for 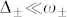and high Q case, where 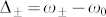, and ω_± and ω₀ are frequencies of the upper or lower pole and zero, respectively. When 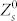is smaller than the wave impedance in free space, which is generally satisfied, the reflection phase will be 180°. Furthermore, smaller 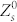, i.e. smaller R, will result in higher reflectivity according to the wave reflection formula. At other frequencies than the resonance poles and zero, the surface reactance changes from large capacitive impedance to large inductive impedance through zero continuously, as shown by the green line in Fig. 4(a). For the case of small R so that 0° and 180° reflection phase can be achieved at the poles and zero respectively, the continuous 360° phase variation is obtained, as shown by the dash curve in Fig. 4(b). However, if R is too large, 0° or 180° reflection phase can not be achieved at poles or zero, leading to the phase gap so that the phase variation is smaller than the full 360°.

The loss effect on the surface performance can be illustrated more clearly by the loci of the surface impedance as a function of frequency on the Smith chart, as depicted by the green dash line in Fig. 4(c). The green and yellow points represent the surface impedance at the resonance poles, and the purple point corresponds to the resonance zero. These points are on the real axis because the total reactive energy is null at resonance. Small R corresponds to large surface resistance at resonance poles and small surface resistance at resonance zero according to equation (2) and (3). When R is small so that the reflection phase is 0° at poles and 180° at zero, the green and the yellow points are located at the positive real axis, and the purple point at the negative real axis. Moreover, these points are farther away from the origin for smaller R, resulting in lower energy dissipation. As the frequency rises, the surface impedance changes from the green point to the purple one, and then to the yellow one along the green dashed line. The phase variation is full 360°. From the above analysis, it can be concluded that under the lossy case, the maximum energy loss occurs at the resonance poles, which is roughly proportional to R for R ~ 0; and full 360° phase variation can be achieved so far as R is small.

In practical applications, such as beam steering reflectarray antennas, the linear phase variation with respect to frequency is important to achieve wide band operation without aperture phase distortion¹⁸. In the Supplementary Information, we show that the proposed design can easily provide tangent like surface reactance so as to realize linear reflection phase variation of more than 360° with respect to frequency. The linear phase bandwidth can be designed by control the separation between the two poles. It is also shown that in a certain frequency band, the reflection phase can be tuned by 360° without the degradation of the phase linearity to frequency. In the Supplementary Information, we also studied the oblique incidence case. It shows that the full phase control can still be obtained for P- and S-polarized oblique incident waves of 45° at least.

Experimental verification

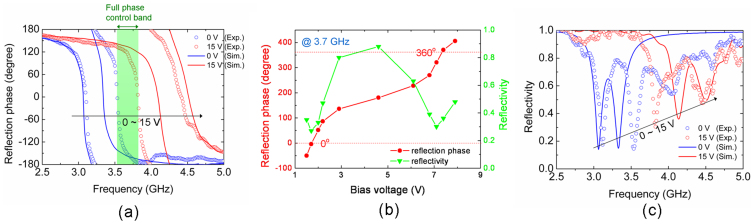
The measured reflection coefficient at 0 V and 15 V bias voltages are plotted in Fig. 5. Simulation results related to the same biasing are given for comparison as well. It is observed in Fig. 5(a) that full 360° phase variation is achieved at both 0 V and 15 V bias voltages. The measured resonance poles are a little different from the simulated ones. This could be due to the various tolerances in measurement, such as calibration, imperfect electrical connection between TEM cell and the sample, etc. By tuning the bias voltage, the reflection phase curve can be shifted by a frequency range larger than the 360° phase variation band. Hence, any frequency point within the band marked by green region will experience 360° phase change when the bias voltage varies between 0 V and 15 V. In other words, the reflection phase can be tuned to take arbitrary value within this frequency band. This full phase control band is delimited by the upper pole at 0 V and the lower pole at 15 V. Fig. 5(b) shows the full phase tuning at 3.7 GHz in the experiment as an example. It can be seen that 360° phase tuning can be achieved perfectly by controlling the bias voltage easily.

Figure 5. Experimental results.

Measured and simulated (a) reflection phase and (c) reflectivity with different bias voltage on the varactor. (b) Full phase tuning at 3.7 GHz in the experiment.

Fig. 5(c) shows the measured and simulated reflectivity. At each bias voltage, the reflectivity curve has two minimums at the resonance poles due to 0° reflection phase such that the electric field is much enhanced at the surface and the energy loss is therefore increased dramatically. This problem can also be seen at the two reflectivity minimums accompanying the 0° and 360° reflection phase in Fig. 5(b) as well. This is a long standing problem with any impedance surface exhibiting 0° reflection phase¹². From equation (2), one solution is to reduce the resistance in the varactor as much as possible so as to keep the surface resistance sufficiently large.

Discussion

Mushroom structure is one conventional approach for the reflection phase tuning¹². It has one resonance pole in the unit cell so that its phase variation is accompanied by asymptotic behavior when approaching ±180°. The linear phase usually occurs within ±90°, whose gradient is controlled by changing the ratio between unit cell inductance and capacitance. In addition, since the 360° phase variation extends for a very wide bandwidth, it is difficult to realize full phase control at any frequencies with the mushroom structure. Our structure employs dual resonant poles in a half unit cell, which provides tangent like surface reactance variation so as to achieve more than 360° linear reflection phase with respect to frequency. By incorporating active element into the structure such as the varactor diode, 360° full phase control can be achieved as presented above. Furthermore, the linear phase frequency bandwidth or gradient of the linear phase part can be designed by changing the separation between the two poles. By shifting the two poles, we can obtain 360° linear phase tuning over a certain frequency band, which is useful for beam steering applications where linear phase variation to frequency is important.

An active impedance metasurface with full 360° reflection phase control is proposed and experimentally validated at microwave frequency. By arranging the two asymmetric half unit cells with mirror symmetry in each unit cell of the metasurface, the whole impedance surface exhibits two resonance poles and one zero in between. Hence, 360° reflection phase variation is confined within the finite frequency band delimited by the two poles. Through tuning the varactors capacitance integrated in the unit cells, the reflection phase response is shifted by a range larger than the frequency band between the two poles, producing a frequency region where the reflection phase can be tuned within full 360° freely. Low losses or small R in the metasurface will not disturb the full 360° reflection phase tunability, but only incurs some reduction of the reflection amplitude, as in any other tunable impedance surfaces. It is shown that varactor with smaller junction resistance is preferred to reduce the absorption. Linear phase can be achieved due to the tangent like surface reactance. It can also be tuned by 360° within a certain frequency band without distortion of linearity. Currently, the proposed structure only works for single polarization of the incident wave, but may be improved to work for both orthogonal polarizations by using identical structures in orthogonal directions¹⁹. The proposed approach can be applied where full phase fine tuning is needed, such as beam steering reflectarray antennas. With geometrical scalability, this concept can be further applied at terahertz or optical regimes by using standard lithography and replacing the varactor with semiconductor thin film structure integrated with the resonant structures as realized in Ref. 20.

Methods

Sample fabrication and numerical simulation

With the prediction of the circuit model, we optimize the half unit cell with the PEC-PMC boundary conditions using the full wave EM solver, and practically fabricate the prototype sample for experimental verification. The optimized dimensions of the half unit cell are shown in Fig. 3(a). The substrate is low loss F4B board with the permittivity of 2.2. Each half unit cell contains two 0.5 pF capacitors and two SMV1231-079 varactors. The 0.5 pF capacitors are in serial with the varactors in order to reduce the total capacitance so as to decrease energy loss at poles, as can be seen in equation (2). In the simulation, the varactor is modeled as the variable capacitance in serial with a 2.5 Ω resistor and a 0.7 nH inductor in order to include the energy loss and parasitic inductance of the varactor. The capacitance can be varied from 0.466 pF to 2.350 pF according to the varactor's data sheet. With the PEC-PMC boundary conditions, we only need to simulate single half unit cell to characterize the proposed surface, as shown in Fig. 3(b). However, the unit cell boundary conditions should be used in the study of oblique incidence case.

Transverse EM (TEM) cell

In the experiment, we use the TEM cell to characterize the reflection coefficients of the prototype sample, as demonstrated in Fig. 6. TEM cell is an efficient way to characterize the periodic structures²¹,²²,²³. The TEM cell consists of a metallic ground plane, and a conducting strip above it. The TEM cell can be regarded as a microstrip line, which is tapered at the two ends to match the characteristic impedance of the feed cable. The TEM cell can generate nearly homogenous plane wave with 377 Ω wave impedance to mimic the plane wave in free space. Furthermore, the conducting strip and the ground plane behave as the imaging plane to duplicate the half unit cell along the direction normal to the TEM cell ground plane. Therefore, it is only necessary to fabricate a row of the half unit cell for measurement by using TEM cell. This measurement configuration is equivalent to the free space measurement method where one horn antenna transmits EM wave onto the whole sample board and the other one picks up the reflected signals to calculate the reflection coefficients²⁴.

Figure 6. Experiment setup.

TEM cell is used to produce nearly plane wave onto the sample. A row of the half unit cells is fabricated which as wide as the conducting strip of the TEM cell.

Measurement

In the experiment, the TEM cell is terminated by a match load at one end to absorb any transmitted waves. Ideally, the transmitted wave is zero. The prototype sample contains 9 half unit cells. It is placed in the TEM cell as shown in Fig. 6. System calibration is carried out before the measurement of the sample. A copper strip with the identical size as the prototype sample is placed where the sample will be placed later. The reflection signal of the copper strip in this environment are measured and recorded using the vector network analyzer, and used as the reference signal to calculate the real reflection coefficient of the sample. This method assumes that the TEM cell is perfectly matched to the feed cable. The upper and lower bias lines shown in Fig. 6 are connected to the same positive DC voltage, and the middle bias line connected to ground.

Author Contributions

B.O.Z. and Y.F. initiated the research. B.O.Z. did the theoretical analysis, and developed the device concept and design. B.O.Z. and J.Z. did the experiment. B.O.Z. and Y.F. wrote the manuscript. Y.F. supervised the project.

Supplementary Material

Supplementary Information

Supplementary Information to Manuscript