Abstract
The purpose of this study is to investigate the effect of exenatide on glycemic control following two administration routes in a streptozotocin/nicotinamide (STZ/NA)-induced diabetic rat model and to develop a pharmacodynamic model to better understand disease progression and the action of exenatide in this experimental system. Two groups of STZ/NA-induced diabetic rats were treated for two weeks with 20 µg/kg/day of exenatide, either by continuous SC infusion or twice daily SC injections. Disease progression was associated with slower glucose utilization. Fasting blood glucose was significantly reduced by 30 mg/dL in both treatment groups at the end of two weeks. A subsequent IV glucose tolerance test (IVGTT) confirmed an improved glucose tolerance in both treatment groups; however, overall glycemic control was similar between groups, likely due to the relatively low and short-term drug exposure. A population indirect response model was successfully developed to simultaneously describe STZ/NA-induced disease progression, responses to an IVGTT, and exenatide effects on these systemic challenges. The unified model includes a single set of parameters, and the cumulative area under the drug-receptor concentration curve was used as a unique driving force to account for systemic effects long after drug elimination.
Keywords: type 2 diabetes, exenatide, pharmacokinetics, pharmacodynamics, mathematical modeling
INTRODUCTION
Type 2 diabetes mellitus is a progressive metabolic disease associated with chronic hyperglycemia. The incidence and prevalence continue to increase, and in 2010, 18.8 million people in the US were diagnosed with diabetes, 90–95% of which are type 21. The causes of type 2 diabetes are not well understood, but abnormal β-cell function resulting in relative insulin deficiency and resistance is a hallmark2. Although diverse conventional pharmacological agents are available for the treatment of type 2 diabetes, incretin mimetics appear capable of long-term improvement in β-cell function3.
The first incretin-mimetic, exenatide, was originally isolated from the saliva of the Gila monster lizard (Heloderma suspecturm)4. It is a 39-amino acid peptide, sharing 53% sequence homology with the glucagon-like peptide-1 (GLP-1)5. Exenatide is less susceptible to degradation by dipeptidyl pepdidase-4, and therefore has a longer half-life and enhanced potency as compared to GLP-16, 7. Binding of exenatide to the GLP-1 receptor leads to multiple biological effects, including glucose-dependent stimulation of insulin secretion, glucose-dependent suppression of glucagon secretion, slowing of gastric emptying, reduction of food intake and body weight, and protection of β-cells8, 9.
An extended release formulation of exenatide (BYDUREON™) was approved by the FDA in 2012. Patients receiving this new formulation had greater reduction in HbA1c than those given the immediate release formulation of exenatide twice daily10. The aim of our study was to investigate the effect of exenatide administered as a continuous subcutaneous (SC) infusion, which provides long-term exposure analogous to the new formulation, or by twice-daily SC injection in a streptozotocin-nicotinamide (STZ/NA)-induced diabetic rat model. This disease model is characterized by moderate stable hyperglycemia, glucose intolerance, and reduced pancreatic insulin stores, and shares a number of syndromes with type 2 diabetes patients11. The disease progression and drug effect on fasting glucose and glucose tolerance challenge were evaluated and a population pharmacodynamic model was developed to further characterize the mechanisms of exenatide action.
METHODS
Animals
Male Sprague-Dawley (SD) rats, weighing 300–325 g, were purchased from Harlan (Indianapolis, IN). All rats were maintained under 12-h light/dark cycle and were allowed free access to standard pellet diet and water. Before the start of the study, all rats were acclimatized for one week. Studies were carried out in accordance with the protocol that was approved by the Institutional Animal Care and Use Committee of the University at Buffalo, SUNY.
Experimental Procedure
The timeline for the experimental design is shown in Figure 1. Diabetes was induced on Day 0 by intraperitoneal injection of STZ/NA11. Briefly, after an overnight fast (5:30 pm – 9:30 am), all rats were given a single intraperitoneal injection of NA (Sigma-Aldrich Co., St. Louis, MO; 110 mg/kg in normal saline), followed after 15 min by STZ (Sigma-Aldrich Co., St. Louis, MO; 60 mg/kg in 0.1 M citrate buffer, pH 4.5). One week later, fasting blood glucose was measured on three occasions. Animals with glucose concentrations greater than 130 mg/dL and less than 180 mg/dL, and mild weight loss were selected for further study. Drug administration (exenatide or saline) was initiated on Day 13 and continued for two weeks. Rats were divided into three groups: (1) The first treatment group (n=5) received SC injection of exenatide (10 µg/kg, GenScript Inc., Piscataway, NJ) in the back twice daily (9:30 am and 5:30 pm); (2) the second treatment group (n=6) received continuous SC infusion of exenatide (20 µg/kg/day); (3) the control group (n=6) received SC infusion of saline. The SC infusion was delivered using Alzet osmotic pumps (Model 2002, flow-rate 0.5 µL/h, DURECT Corp., Cupertino, CA) that were implanted subcutaneously between rat shoulder blades under isoflurane anesthesia. Fasting blood glucose was measured every 4–5 days. Two blood samples were collected from the saphenous vein in the SC infusion group for measuring exenatide plasma concentrations. On Day 25, all rats underwent right jugular vein cannulation under isoflurane anesthesia. On Day 27, an intravenous glucose tolerance test (IVGTT) was performed for all groups after an overnight fast. Glucose (2.78 mmol/kg) was intravenously injected and glucose and insulin were measured at −60, −20, −10, 5, 10, 15, 20, 30, 45, 60, and 120 min.
Figure 1.

Schematic representation of the experimental design.
Analytical Assays
Blood glucose was measured using a BD Logic blood glucose meter (BD Medical, Franklin Lakes, NJ). Exenatide was measured using a commercial ELISA kit (Phoenix Pharmaceuticals, Burlingame, CA); and the linear range was from 0.08 to 0.86 ng/mL (19.1–205 pM). Plasma insulin was measured using a commercial rat ELISA kit (Millipore Corporation, Billerica, MA); the range was 0.2 to 10 ng/mL. All procedures strictly followed the protocols provided by manufacturers.
Pharmacokinetic Model
Exenatide exhibits nonlinear pharmacokinetics in rats, which has been attributed to limited capacity and high-affinity binding to the GLP-1 receptor. A target-mediated drug disposition (TMDD) model was used to describe the pharmacokinetics (PK) of exenatide in diabetic Goto-Kakizaki rats12. Similarly, a TMDD model with an integrated Michaelis-Menten function for nonlinear absorption kinetics was used to investigate interspecies differences in preclinical PK parameters and for predicting exenatide disposition in humans13. According to the diagram in Figure 2, the model can be described by the following equations:14
| Eq. 1 |
| Eq. 2 |
| Eq. 3 |
| Eq. 4 |
| Eq. 5 |
Figure 2.
The final PK/PD model used to charactereize exenatide after two-week treatment in STZ/NA-induced diabetic rats. represents area under the drug-receptor complex concentration-time curve. fdisease(kout, t) represents the change in kout over time as a function of disease state.
The absorption kinetics of exenatide after SC injection is nonlinear and was previously well described using a Michaelis-Menten function, where Vmax represents the maximum absorption rate and Km is the amount of exenatide at the absorption site (SC) when the absorption rate is half of Vmax. The Input in Eq. 1 is either a constant zero-order infusion rate constant or the δ-Dirac function for rapid SC injection. Free exenatide (C) in the central compartment binds to free receptor (R) to form the drug-receptor complex (RC). The second-order association rate constant kon and first-order dissociation rate constant koff are used to describe binding processes. Free exenatide also can distribute to and from a peripheral compartment (AT) with first-order rate constants, kpt and ktp. There are two pathways for exenatide elimination: free drug can be eliminated directly from the central compartment with the first-order rate constant kel and RC can also be internalized and degraded (kint) by receptor-mediated endocytosis. The free receptor is assumed to undergo turnover, with zero-order production rate constant (ksyn) and first-order degradation rate constant (kdeg). ksyn is a secondary parameter which is equal to the product of kdeg and Rtot(0) (the concentration of receptor at baseline). The PK profiles of SC infusion and SC injection were simulated using the parameters obtained from a prior analysis13. The simulated profile for SC infusion was compared to the measured concentrations for SC infusion group.
Pharmacodynamic Model
An indirect response model was proposed to characterize glycemic changes in this chemical-induced diabetic rat model (Figure 2):
| Eq. 6 |
| Eq. 7 |
This model includes the zero-order glucose production rate constant kin and first-order glucose elimination rate constant kout to define glucose turnover. The onset of diabetes in STZ/NA-induced diabetic rats was attributed to an impaired ability to utilize glucose. Therefore, a change in kout was used to explain the increasing glucose and kd was used as the rate constant for kout degradation (Eq. 7). As glucose concentrations usually stabilize after one or two weeks, the kout was assumed to reach a plateau koutss. In treatment groups, various approaches were tested and the cumulative area under the drug-receptor concentration-time curve serving as the driving force to stimulate glucose utilization was chosen as the final one to describe the drug effect. S is the stimulation index of drug effect on glucose utilization, Input is the product of the Doseglu at the time of the glucose IV challenge (2.78 mmol/kg) and the δ-Dirac function, and Vglu is glucose volume of distribution. All parameters were shared across the three groups and all data were fitted simultaneously.
Data Analysis
The PK profiles of exenatide were simulated without inter-animal variability using parameters estimated in a previous study (Table 1 from13). Glucose baselines of each group were fixed to measured values. The individual blood glucose profiles from three study groups were analyzed simultaneously using ADAPT 5 (Biomedical Simulations Resource, University of Southern California, Los Angeles, CA) with the maximum likelihood expectation maximization method. The variance model was Vi = (σ · Y)2, where Vi is the variance of the ith data point, σ is the variance model parameter, and Y is the ith predicted value from the PD model. Model selection was based on visual inspection of curve fitting, Akaike information criterion, confidence of parameter estimation, and goodness of fit.
Table 1.
Parameters used to simulate exenatide pharmacokineticsa
| Parameter (units) | Description | Value |
|---|---|---|
| Vc (L) | Central volume of distribution | 5.08×10−2 |
| kel (hr−1) | Elimination rate constant for free exenatide | 2.50 |
| kpt (hr−1) | Distribution rate constant | 1.56 |
| ktp (hr−1) | Distribution rate constant | 1.62 |
| kdeg (hr−1) | Degradation rate constant for free receptor | 9.3 ×101 |
| kint (hr−1) | Rate constant of internalization for complex | 1.43×10−1 |
| kon (pM−1·hr−1) | Second-order association rate constant | 1.02×10−3 |
| koff (hr−1) | First-order dissociation rate constant for rat | 3.12×10−3 |
| Rtot (pM) | Receptor concentration at baseline | 5.20×103 |
| Vmax (pmol·hr−1) | Maximum absorption rate for rat | 1.48×104 |
| Km (pmol) | Amount of exenatide when absorption rate is half of the max | 3.41×104 |
From Chen et al.13
RESULTS
Exenatide Pharmacokinetics
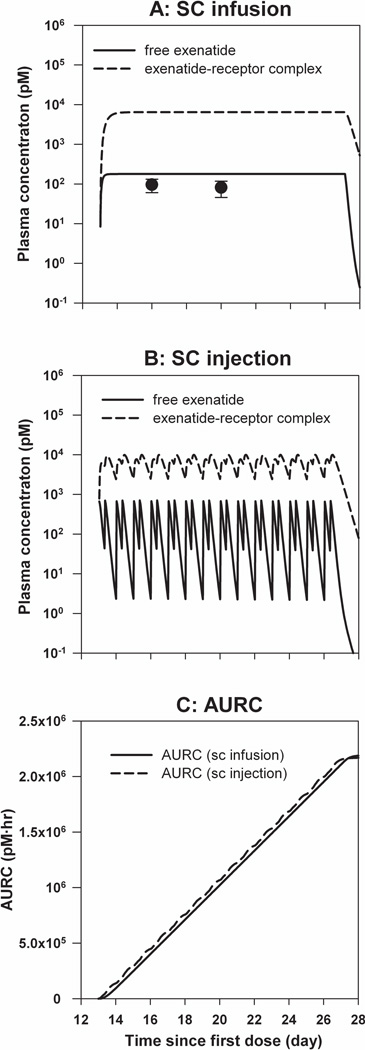
The simulated steady-state blood exenatide concentration after continuous SC infusion was slightly greater than measured values (Figure 3A). In Figures 3A and 3B, solid lines represent free exenatide concentrations, and dashed lines show concentrations of exenatide–receptor complex, which are approximately 40-fold greater than free exenatide concentrations. The dosing intervals for the twice-daily regimen (dosed at 9:30 am and 5:30 pm) are much longer than the exenatide half-life (2.4 hrs after SC injection)7, and therefore accumulation of exenatide was not expected (Figure 3B). The cumulative areas under the drug-receptor concentration-time curves, which were used as the pharmacodynamic effect driver for both administration routes, are shown in Figure 3C. The simulated AURCs after SC infusion and SC injection were nearly superimposable.
Figure 3.
Simulated pharmacokinetic profiles of exenatide. A) Free exenatide and drug-receptor complex profiles following continuous SC infusion (20 µg/kg/day). Symbols are mean measured concentrations (±SD), and lines are model-predicted profiles. B) Free exenatide and drug-receptor complex profiles following multiple SC injections (10 µg/kg twice daily). C) Cumulative AURC during 2-week exenatide therapy. Solid line is simulation of AURC following continuous SC infusion and dashed line is simulated AURC following multiple SC injections.
Pharmacodynamics
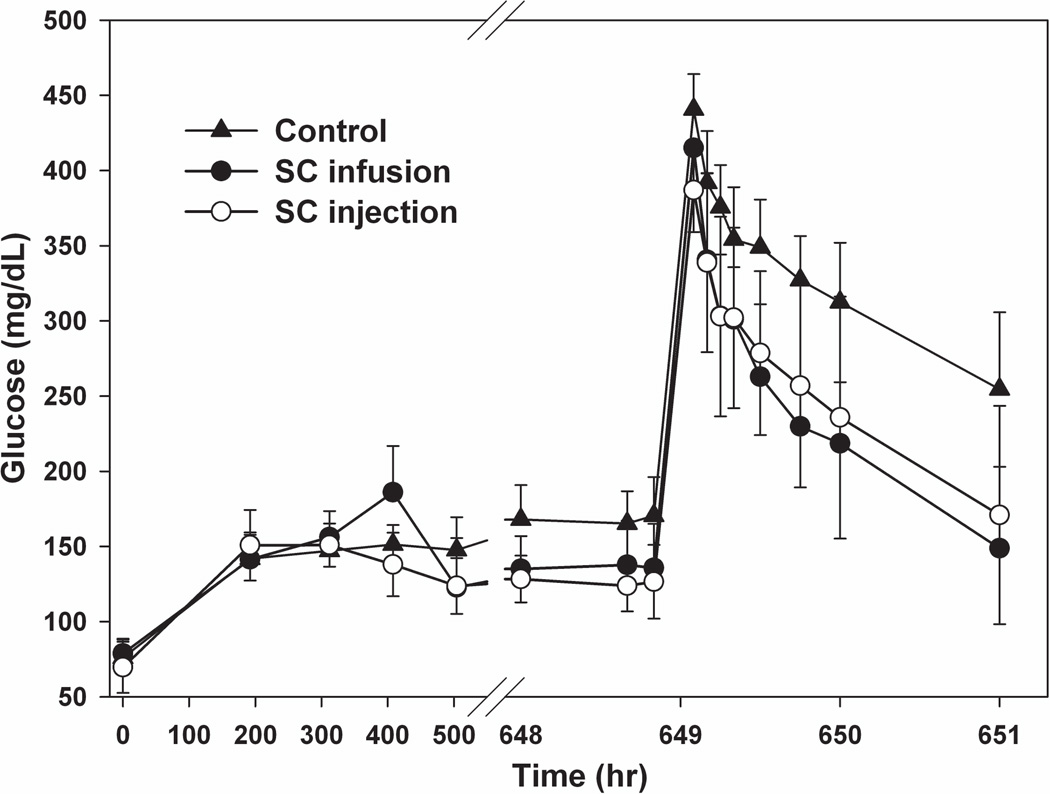
The mean fasting blood glucose was 70–80 mg/dL in healthy SD rats and increased to around 150 mg/dL in one week after the induction of diabetes (Figure 4). At the end of the two-week drug regimen, the fasting blood glucose in both treatment groups decreased by 30 mg/dL, which was significantly less than the control group (p<0.05). However, the fasting blood glucose in both treatment groups was unexpectedly similar. The slight increase in glucose around the 400-hr time-point may be caused by a stress response to the implantation of osmotic pump15 or experimental error. In order to compare glucose tolerance among the three groups, glucose concentrations during the IVGTT were normalized to baseline values (figure not shown). Glucose tolerance improved with blood glucose concentrations significantly lower at 45, 60 and 120 mins in treatment groups (p<0.05). Nevertheless, the time courses of glucose after IV glucose injection for the two exenatide treatment groups were almost superimposable. Fasting insulin concentrations did not change during disease progression or during drug treatment (data not shown). Following the IVGTT, insulin concentrations were sustained around fasting concentrations (0.5–0.9 ng/mL), and thus, insulin was not included in the PD analysis.
Figure 4.
Fasting blood glucose and IVGTT in STZ/NA-induced diabetic rats. Symbols represent measured glucose concentrations (±SD) for the control group—▲, and the SC infusion—● and SC injection—○ groups.
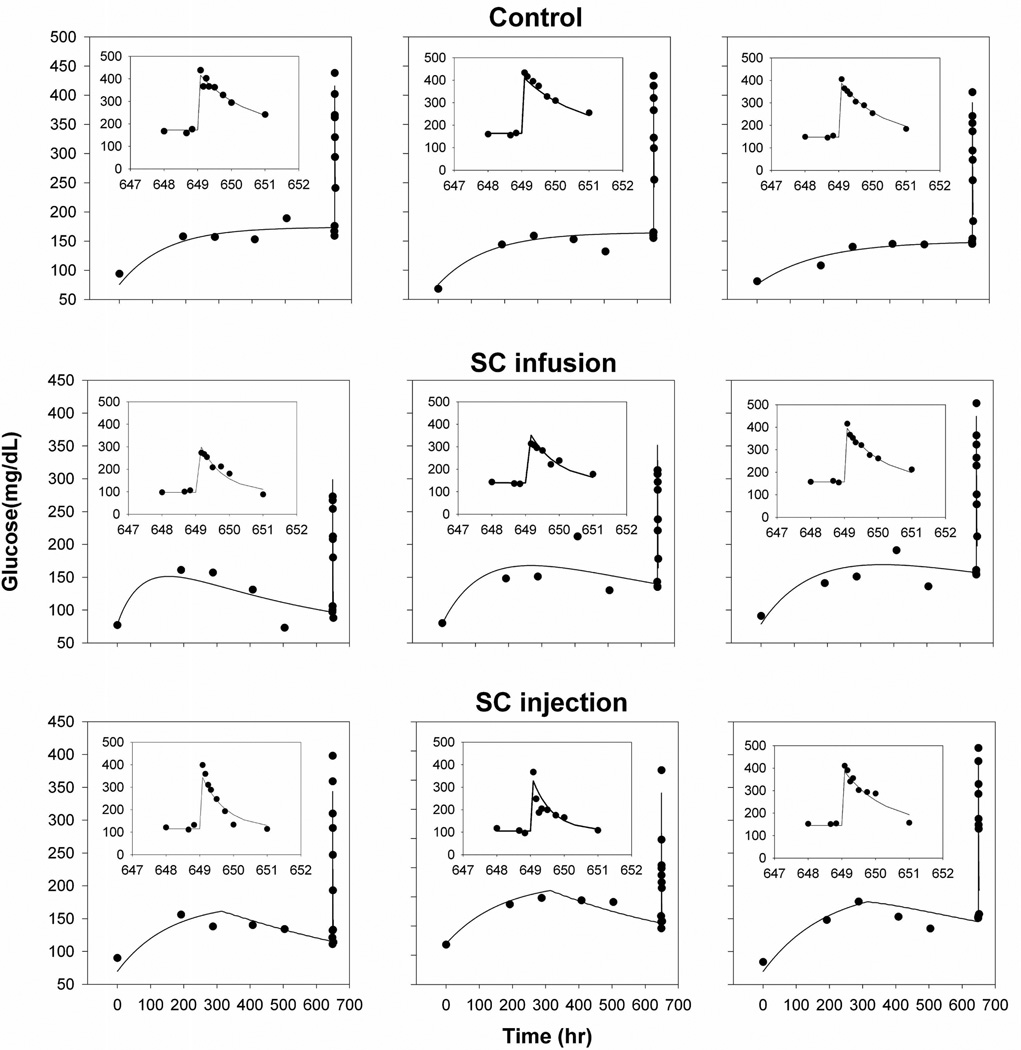
The final model (Figure 3) was fitted to all groups simultaneously and parameters were independent of the route of administration. The modified indirect response model adequately characterized both fasting glucose concentrations and IVGTT profiles. The measured and model-fitted glucose profiles of three representative animals from each group are shown in Figure 5 (goodness-of-fit plots can be found in the online Supplemental Materials). The effect of exenatide on glucose regulation is triggered once free exenatide binds to free GLP-1 receptor, and the concentration of the exenatide-receptor complex was used to stimulate the removal of glucose instead of free exenatide concentration. The improvement in glucose tolerance for the SC injection group during the IVGTT, when there is essentially no drug in the body, supports the selection of the cumulative AURC instead of the drug-receptor complex concentration as the driving force to stimulate the removal of glucose. The estimated parameters and inter-subject variability terms are summarized in Table 2. All population mean parameters were estimated with good precision and comparable with literature reported values16, 17. The estimated volume of distribution of glucose is equivalent to a literature reported value (0.201 L/kg) when pooled data were analyzed and thus fixed in the final model. Inter-subject variability terms were not precisely estimated for all parameters (Table 2), which might result from the relatively small study population.
Figure 5.
Glucose concentration-time profiles for 3 representative animals from each treatment group. Symbols are individual experimental data and solid lines are model fitted profiles. Insets show fitting results of the IVGTT on a shortened time-scale.
Table 2.
Final pharmacodynamic model-estimated parameters
| Parameter | Definition | Mean | %RSE | IIV%a | %RSE |
|---|---|---|---|---|---|
| kd (hr−1) | Degradation rate constant of kout | 5.73×10−3 | 30.7 | 44.4 | 76.9 |
| kout0 (hr−1) | Glucose elimination rate constant at baseline | 1.66 | 28.7 | 36.1 | 120 |
| koutss (hr−1) | Glucose elimination rate constant at steady state | 6.19×10−1 | 25.8 | 30.1 | 60.2 |
| S (nM−1·hr−1) | Stimulation index of drug effect on glucose utilization | 2.02×10−4 | 34.4 | 44.4 | 92.4 |
| Glucose baseline_CG (mg/dL) | Glucose baseline for control group | 76 (fixed) | NAb | NA | NA |
| Glucose baseline_T1 (mg/dL) | Glucose baseline for SC infusion group | 79 (fixed) | NA | NA | NA |
| Glucose baseline_T2 (mg/dL) | Glucose baseline for SC injection group | 70 (fixed) | NA | NA | NA |
| Vglu (L/kg) | Volume of distribution of glucose | 2.01×10−1 (fixed) | NA | NA | NA |
| σ | Proportional residual error | 1.21×10−1 | 6.59 | NA | NA |
IIV%, inter-individual variability
NA, not applicable.
DISCUSSION
The pharmacokinetics and pharmacodynamics of exenatide have been extensively investigated in animals and in humans and are assumed to be dependent on binding to the GLP-1 receptor in all species6. Exenatide exhibits multiple clinical effects including dose-dependent reduction in HbA1c, fasting blood glucose, postprandial glucose, and body weight18, 19. A new extended-release formulation (BYDUREON™) shows efficacy in type 2 diabetes and may be more convenient for patient compliance20. In this study, we sought to determine whether continuous SC infusion or multiple acute SC injections of exenatide would result in differences in disease progression or glucose tolerance in STZ/NA-induced diabetic rats. In addition, a population-based PD model was developed to simultaneously characterize glucose dynamics and to quantitatively assess any potential changes in exenatide pharmacology following the two routes of administration.
The performance of the TMDD model (Figure 2) for describing the nonlinear kinetics of exenatide was consistent with prior studies12,13. The slight discrepancy might be attributed to measurement error (relatively low drug concentration) or the fact that parameters were obtained from a prior study with different experimental settings and dose range. Some drug may have been lost during the loading procedure into the osmotic pumps; however, a bioavailability term was not incorporated into the model based only on two sample points. The concentration of the drug-receptor complex was greater than free drug, with steady-state target occupancy around 97% (calculated as RC/[RC+C]). Thus, the 2-fold greater prediction in free drug concentration would have little influence on the prediction of the exenatide-receptor complex concentrations, which was used as the driver for the PD model.
STZ-NA induction of diabetes is a well-developed and useful animal model. However, the doses of STZ and NA vary across studies, which may result in inconsistencies in the severity of diabetes11,21,22. For example, we evaluated different dose combinations of STZ and NA in a pilot study, and the fasting blood glucose increased up to 170 mg/dL after 3 days by injection of 50 mg/kg STZ and 110 mg/kg NA and returned to baseline around one week later. The doses of 60 mg/kg STZ with 110 mg/kg NA were finally selected. The mean fasting glucose increased to around 150 mg/dL after induction among the three groups (Figure 4). In contrast, the fasting plasma insulin did not change before or after induction of diabetes (data not shown), which is consistent with prior studies23.
At the end of the two-week exenatide treatment regimens, fasting blood glucose concentrations for both routes of administration decreased to similar values, and contrary to expectations, the time courses of glucose following the IVGTT were superimposable (Figure 4). A four-week SC infusion of exenatide resulted in a dose-dependent reduction in blood glucose concentrations in mice on standard and high-fat diets (24 nmol/kg/day vs. 300 pmol/kg/day)9. Our relatively low dose (20 µg/kg/day, 4.7 nmol/kg/day) and short duration of therapy may explain the lower response and lack of differences between routes of administration. Our final steady-state free exenatide concentration (96 pmol/L) was less than model-estimated SC50 values for its insulinotropic effects − 960 pmol/L in high-fat/streptozotocin-induced diabetics rats24 and 1290 pmol/L in GK rats12. In a prior study, a pronounced reduction in HbA1c was not observed until the last two weeks of a six-week treatment in fatty Zucker rats25. A comparison between once weekly and twice daily treatment was evaluated clinically, and the reduction of HbA1c was distinguishable between the two groups after 10 weeks of therapy10.
Glucose-insulin homeostasis is controlled by multiple factors, and diverse mathematical models have been developed to quantitatively describe the PK/PD properties of antidiabetic drugs26. The effects of exenatide on glucose-insulin homeostasis under hyperglycemic clamp conditions in healthy and type 2 diabetic subjects were successfully quantified with a modified minimal PD model; however, PK was assumed to be linear owing to a lack of PK data27. An integrated TMDD-PD model was derived to quantitatively describe the acute effect of exenatide on the glucose-insulin system in Goto-Kakizaki rats12. Disease progression is an important element in diabetes models and quantification of the type 2 diabetes disease progression by modeling approaches can facilitate the understanding of type 2 diabetes and drug effects. Post and colleagues proposed a series of indirect response models to emulate disease progression with altered synthesis or elimination parameters28. Ultimately, type 2 diabetes disease progression was attributed to a time-dependent change in the removal or utilization of glucose. In our study, STZ/NA-induced diabetes progression was characterized with a decreasing first-order glucose elimination rate constant (kout) controlled by the rate constant kd after the onset of diabetes and the final steady-state value kout,ss. The initial value kout0 was estimated at 1.66 hr−1, which is slightly less than a previously reported value (2.67 hr−1)29, probably due to the slower rate of glucose turnover in the fasting state. A more complex mechanism-based model was developed to describe the disease progression in Goto-Kakizaki rats and two components, progressive worsening of insulin resistance and gradual deterioration of β-cell function were included in the model30, 31.
The indirect response model has served as a platform for describing mechanisms of action of diverse antidiabetic drugs32. Based on the multiple actions of exenatide, such as simulation of insulin secretion, inhibition of glucagon secretion, and induction of satiety, both indirect response models II and IV could be justified. Indirect response model IV was eventually selected based on model fitting criteria (Methods). After the IVGTT, the production of glucose may be inhibited by the high concentration of glucose itself; hence the elimination rate of glucose could reflect the ability of the body to utilize glucose, which was gradually altered by exenatide over two weeks. Our final modeling approach is unique in co-modeling disease progression, drug treatment, and the IVGTT simultaneously. The final model successfully integrates major determinants of this response system, including: target-mediated drug disposition, chemically induced disease progression, and the indirect effect of the drug on glucose homeostasis. Although model refinements are needed (e.g., more dose levels and longer duration of treatment), the model framework could be extended to study the short- and long-term effects of other compounds acting through this incretin pathway.
Traditional PK/PD models often utilize drug concentrations to directly or indirectly alter a biomarker. However, improved glucose tolerance was observed in the multiple SC injection group, despite the fact that exenatide would be eliminated before the IVGTT. This supported the use of the cumulative AURC as the driving force for stimulating glucose utilization instead of the drug-receptor concentration (RC). It is common to use a secondary pharmacokinetic parameter such as cumulative area under the concentration-time curve (AUC) to investigate PK/PD relationships in long-term studies. For instance, the long-term hypoglycemic effect of gliclazide was related to net gliclazide exposure (AUC) using an Emax relationship33. The prior model of exenatide dynamics in Goto-Kakizaki rats included an insulin compartment that was driven by free exenatide concentrations12. GLP-1 stimulation of insulin after a glucose challenge has also been modeled using the Adair two binding site model29. Although such models include both capacity and sensitivity parameters, the Hill function was replaced with a simple linear stimulation factor S in our final model (Eq. 6) due to the limited dose range.
A disadvantage of the selected model is that in the absence of a capacity term, the glucose concentration could decrease to unlikely low values if the drug was continually administered at high doses. Multiple dose levels might allow for the deconvolution of drug efficacy and potency from the linear stimulation coefficient. Future studies should include greater dose levels and longer treatment periods to further test whether SC infusion is superior to multiple SC injections. The mode of exenatide action was simplified owing to the lack of glucose-stimulated insulin secretion. The present study design is insufficient for evaluating the multiple mechanisms by which exenatide influences glucuose-insulin homeostasis. Furthermore, the cumulative AURC function will not decrease at later times, and hence will not describe the eventual washout of the drug effect.
In conclusion, the effects of exenatide in STZ-NA-induced diabetic rats were evaluated for two administration routes and glucose dynamics for fasting blood glucose and the IVGTT were similar, which may result from the relatively low daily dose and short duration of treatment. A population-based pharmacodynamic model well described the exenatide effects on both fasting glucose during disease onset and the IVGTT following drug treatment. A single model structure and parameter set were identified, and further research is needed to determine whether this PK/PD model could be extended to other exenatide studies in other animal models of type II diabetes.
Supplementary Material
Acknowledgements
This study was funded, in part, by NIH Grant GM57980 and the University at Buffalo, SUNY Center for Protein Therapeutics.
References
- 1. http://diabetes.niddk.nih.gov/dm/pubs/statistics/#dud.
- 2.Lebovitz HE. Type 2 diabetes: an overview. Clin Chem. 1999;45(8 Pt 2):1339–1345. [PubMed] [Google Scholar]
- 3.Drab SR. Incretin-based therapies for type 2 diabetes mellitus: current status and future prospects. Pharmacotherapy. 2010;30(6):609–624. doi: 10.1592/phco.30.6.609. [DOI] [PubMed] [Google Scholar]
- 4.Eng J, Kleinman WA, Singh L, Singh G, Raufman JP. Isolation and characterization of exendin-4, an exendin-3 analogue, from Heloderma suspectum venom. Further evidence for an exendin receptor on dispersed acini from guinea pig pancreas. J Biol Chem. 1992;267(11):7402–7405. [PubMed] [Google Scholar]
- 5.Goke R, Fehmann HC, Linn T, Schmidt H, Krause M, Eng J, Goke B. Exendin-4 is a high potency agonist and truncated exendin-(9–39)-amide an antagonist at the glucagon-like peptide 1-(7–36)-amide receptor of insulin-secreting beta-cells. J Biol Chem. 1993;268(26):19650–19655. [PubMed] [Google Scholar]
- 6.Gallwitz B. Exenatide in type 2 diabetes: treatment effects in clinical studies and animal study data. Int J Clin Pract. 2006;60(12):1654–1661. doi: 10.1111/j.1742-1241.2006.01196.x. [DOI] [PubMed] [Google Scholar]
- 7.Parkes DJC, Smith P, Nayak S, Rinehart L, Gingerich R, Chen K, Young A. Pharmacokinetic actions of exendin-4 in the rat: comparison with glucagon-like peptide-1. Drug Development Research. 2001;53:7. [Google Scholar]
- 8.Parkes DG, Pittner R, Jodka C, Smith P, Young A. Insulinotropic actions of exendin-4 and glucagon-like peptide-1 in vivo and in vitro. Metabolism. 2001;50(5):583–589. doi: 10.1053/meta.2001.22519. [DOI] [PubMed] [Google Scholar]
- 9.Arakawa M, Ebato C, Mita T, Hirose T, Kawamori R, Fujitani Y, Watada H. Effects of exendin-4 on glucose tolerance, insulin secretion, and beta-cell proliferation depend on treatment dose, treatment duration and meal contents. Biochemical and Biophysical Research Communications. 2009;390(3):809–814. doi: 10.1016/j.bbrc.2009.10.054. [DOI] [PubMed] [Google Scholar]
- 10.Drucker DJ, Buse JB, Taylor K, Kendall DM, Trautmann M, Zhuang D, Porter L. Exenatide once weekly versus twice daily for the treatment of type 2 diabetes: a randomised, open-label, non-inferiority study. Lancet. 2008;372(9645):1240–1250. doi: 10.1016/S0140-6736(08)61206-4. [DOI] [PubMed] [Google Scholar]
- 11.Masiello P, Broca C, Gross R, Roye M, Manteghetti M, Hillaire-Buys D, Novelli M, Ribes G. Experimental NIDDM: development of a new model in adult rats administered streptozotocin and nicotinamide. Diabetes. 1998;47(2):224–229. doi: 10.2337/diab.47.2.224. [DOI] [PubMed] [Google Scholar]
- 12.Gao W, Jusko WJ. Pharmacokinetic and Pharmacodynamic Modeling of Exendin-4 in Type 2 Diabetic Goto-Kakizaki Rats. Journal of Pharmacology and Experimental Therapeutics. 2010;336(3):881–890. doi: 10.1124/jpet.110.175752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen T, Mager DE, Kagan L. Interspecies modeling and prediction of human exenatide pharmacokinetics. Pharm Res. 2013;30(3):751–760. doi: 10.1007/s11095-012-0917-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mager DE, Jusko WJ. General pharmacokinetic model for drugs exhibiting target-mediated drug disposition. J Pharmacokinet Pharmacodyn. 2001;28(6):507–532. doi: 10.1023/a:1014414520282. [DOI] [PubMed] [Google Scholar]
- 15.Balcombe JP, Barnard ND, Sandusky C. Laboratory routines cause animal stress. Contemp Top Lab Anim Sci. 2004;43(6):42–51. [PubMed] [Google Scholar]
- 16.Raman M, Radziuk J, Hetenyi G., Jr Distribution and kinetics of glucose in rats analyzed by noncompartmental and compartmental analysis. Am J Physiol. 1990;259(2 Pt 1):E292–E303. doi: 10.1152/ajpendo.1990.259.2.E292. [DOI] [PubMed] [Google Scholar]
- 17.Gopalakrishnan M, Suarez S, Hickey AJ, Gobburu JV. Population pharmacokinetic-pharmacodynamic modeling of subcutaneous and pulmonary insulin in rats. J Pharmacokinet Pharmacodyn. 2005;32(3–4):485–500. doi: 10.1007/s10928-005-0008-4. [DOI] [PubMed] [Google Scholar]
- 18.Kolterman OG. Synthetic Exendin-4 (Exenatide) Significantly Reduces Postprandial and Fasting Plasma Glucose in Subjects with Type 2 Diabetes. Journal of Clinical Endocrinology & Metabolism. 2003;88(7):3082–3089. doi: 10.1210/jc.2002-021545. [DOI] [PubMed] [Google Scholar]
- 19.Poon T, Nelson P, Shen L, Mihm M, Taylor K, Fineman M, Kim D. Exenatide improves glycemic control and reduces body weight in subjects with type 2 diabetes: a dose-ranging study. Diabetes Technol Ther. 2005;7(3):467–477. doi: 10.1089/dia.2005.7.467. [DOI] [PubMed] [Google Scholar]
- 20.Blevins T, Pullman J, Malloy J, Yan P, Taylor K, Schulteis C, Trautmann M, Porter L. DURATION-5: exenatide once weekly resulted in greater improvements in glycemic control compared with exenatide twice daily in patients with type 2 diabetes. J Clin Endocrinol Metab. 2011;96(5):1301–1310. doi: 10.1210/jc.2010-2081. [DOI] [PubMed] [Google Scholar]
- 21.Kumar EKD, Janardhana GR. Antidiabetic activity of alcoholic stem extract of Nervilia plicata in streptozotocin-nicotinamide induced type 2 diabetic rats. Journal of Ethnopharmacology. 2011;133(2):480–483. doi: 10.1016/j.jep.2010.10.025. [DOI] [PubMed] [Google Scholar]
- 22.Yamabe N, Kang KS, Zhu BT. Beneficial effect of 17β-estradiol on hyperglycemia and islet β-cell functions in a streptozotocin-induced diabetic rat model ☆. Toxicology and Applied Pharmacology. 2010;249(1):76–85. doi: 10.1016/j.taap.2010.08.020. [DOI] [PubMed] [Google Scholar]
- 23.Tahara A, Matsuyama-Yokono A, Nakano R, Someya Y, Shibasaki M. Hypoglycaemic effects of antidiabetic drugs in streptozotocin-nicotinamide-induced mildly diabetic and streptozotocin-induced severely diabetic rats. Basic Clin Pharmacol Toxicol. 2008;103(6):560–568. doi: 10.1111/j.1742-7843.2008.00321.x. [DOI] [PubMed] [Google Scholar]
- 24.Li XG, Li L, Zhou X, Chen Y, Ren YP, Zhou TY, Lu W. Pharmacokinetic/pharmacodynamic studies on exenatide in diabetic rats. Acta pharmacologica Sinica. 2012;33(11):1379–1386. doi: 10.1038/aps.2012.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Young AA, Gedulin BR, Bhavsar S, Bodkin N, Jodka C, Hansen B, Denaro M. Glucose-lowering and insulin-sensitizing actions of exendin-4: studies in obese diabetic (ob/ob, db/db) mice, diabetic fatty Zucker rats, and diabetic rhesus monkeys (Macaca mulatta) Diabetes. 1999;48(5):1026–1034. doi: 10.2337/diabetes.48.5.1026. [DOI] [PubMed] [Google Scholar]
- 26.Landersdorfer CB, Jusko WJ. Pharmacokinetic/pharmacodynamic modelling in diabetes mellitus. Clin Pharmacokinet. 2008;47(7):417–448. doi: 10.2165/00003088-200847070-00001. [DOI] [PubMed] [Google Scholar]
- 27.Mager DE. Exendin-4 Pharmacodynamics: Insights from the Hyperglycemic Clamp Technique. Journal of Pharmacology and Experimental Therapeutics. 2004;311(2):830–835. doi: 10.1124/jpet.104.069765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Post TM, Freijer JI, DeJongh J, Danhof M. Disease system analysis: basic disease progression models in degenerative disease. Pharm Res. 2005;22(7):1038–1049. doi: 10.1007/s11095-005-5641-5. [DOI] [PubMed] [Google Scholar]
- 29.Cao Y, Gao W, Jusko WJ. Pharmacokinetic/Pharmacodynamic Modeling of GLP-1 in Healthy Rats. Pharm Res. 2011 doi: 10.1007/s11095-011-0652-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gao W, Bihorel S, DuBois DC, Almon RR, Jusko WJ. Mechanism-based disease progression modeling of type 2 diabetes in Goto-Kakizaki rats. J Pharmacokinet Pharmacodyn. 2011;38(1):143–162. doi: 10.1007/s10928-010-9182-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cao Y, Dubois DC, Sun H, Almon RR, Jusko WJ. Modeling diabetes disease progression and salsalate intervention in Goto-Kakizaki rats. J Pharmacol Exp Ther. 2011;339(3):896–904. doi: 10.1124/jpet.111.185686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jusko CB, La WJ. Pharmacokinetic/Pharmacodynamic Modelling in Diabetes Mellitus. 2008 doi: 10.2165/00003088-200847070-00001. [DOI] [PubMed] [Google Scholar]
- 33.Frey N, Laveille C, Paraire M, Francillard M, Holford NH, Jochemsen R. Population PKPD modelling of the long-term hypoglycaemic effect of gliclazide given as a once-a-day modified release (MR) formulation. Br J Clin Pharmacol. 2003;55(2):147–157. doi: 10.1046/j.1365-2125.2003.01751.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.