Diversity and Similarity of Motor Function and Cross-Bridge Kinetics in Papillary Muscles of Transgenic Mice Carrying Myosin Regulatory Light Chain Mutations D166V and R58Q

Abstract

Mechanical properties of skinned papillary muscle fibers from transgenic mice expressing familial hypertrophic cardiomyopathy associated mutations D166V and R58Q in myosin regulatory light chain were investigated. Elementary steps and the apparent rate constants of the cross-bridge cycle were characterized from the tension transients induced by sinusoidal length changes during maximal Ca²⁺ activation, together with ATP, ADP, and Pi studies. The tension-pCa relation was also tested in two sets of solutions with differing Pi and ionic strength. Our results showed that in both mutants, the fast apparent rate constant 2πc and the rate constants of the cross-bridge detachment step (k₂) were smaller than those of wild type (WT), demonstrating the slower cross-bridge kinetics. D166V showed significantly smaller ATP (K₁) and ADP (K₀) association constants than WT, displaying weaker ATP binding and easier ADP release, whereas those of R58Q were not significantly different from WT. In tension-pCa study, both D166V and R58Q mutations exhibited increased Ca²⁺ sensitivity and less cooperativity. We conclude that, while the two FHC mutations have similar clinical manifestations and prognosis, some of the mechanical parameters of cross-bridges (K₀, K₁) are differently modified, whereas some others (Ca²⁺-sensitivity, cooperativity, k₂) are similarly modified by these two FHC associated mutations.

1. INTRODUCTION

Familial hypertrophic cardiomyopathy (FHC) is an autosomal dominant disease with clinical features of left ventricle and interventricular septum hypertrophy, myofibrillar disarray, and interstitial fibrosis [1, 2]. FHC is considered to be the leading cause of sudden cardiac death (SCD) in otherwise healthy individuals, including young athletes [1, 3]. Molecular genetic studies have defined FHC as a disease of the sarcomere, as it can be caused by mutations in any of the major sarcomeric proteins, including the β-myosin heavy chain (β-MHC), myosin binding protein C (MyBP-C), α-tropomyosin (α-Tm), troponin T (TnT), troponin I (TnI), troponin C (TnC), α-actin, titin, as well as myosin’s regulatory (RLC) and essential (ELC) light chains [4].

Myosin II is a well-known dimeric motor protein located in muscle cells that converts chemical energy stored in ATP into mechanical work by interacting with actin-containing thin filaments [5]. In addition to two heavy chains that form the head, neck, and tail domains, myosin also contains two pairs of light chains, RLC and ELC [6, 7] that are bound to myosin’s neck region called the lever arm [8]. Apart from the role of stiffening the neck region to support its lever arm function, RLC and ELC together can communicate directly with the active site to influence cross-bridge kinetics that contribute to force production [9]. The interaction of the RLC with the motor domain of myosin is critical for energy transduction process: the transition of the myosin cross-bridge from a pre-power stroke to the post-power stroke configuration [10]. Previous work also suggests that the myosin RLC plays an important role in the cross-bridge cycling kinetics [11].

Ventricular myosin RLC belongs to the super family of EF-hand Ca²⁺ binding proteins. One of the FHC associated RLC mutants, D166V, identified by Richard et al. (mistakenly labeled as D166L) [12, 13], occurs at the last amino acid residue of the human cardiac RLC and the negatively charged and polar aspartic acid (D) residue is replaced by the hydrophobic valine (V) [14]. D166V lies in the “elbow” of the myosin lever arm, the region of the myosin heavy chain that in the crystal structure makes a sharp bend and interacts with the N and C termini of the RLC [14]. Another RLC mutation, R58Q, identified by Flavigny et al. [15], occurs at the much conserved arginine (R) residue of RLC [16], which is replaced by glutamine (Q). It locates in the immediate extension of the exiting helix of the RLC's Ca²⁺-Mg²⁺ binding site (residues 37–48). This mutation, associated with a typical form of hypertrophic cardiomyopathy, causes increased left ventricular wall thickness and abnormal electrocardiograph findings with no mid-cavity obliteration. Multiple cases of sudden cardiac death have been found in the patients carrying this mutation [15, 17]. The location map of D166V and R58Q were published previously [18].

The FHC-linked D166Vand R58Q mutations are similar in their poor prognosis and SCD at a young age. However, their effects on the cardiac muscle motor function and each step of the cross-bridge cycle, as well as the correlation between their effects in vitro and clinical manifestations in humans are not well understood. In this report, we comprehensively investigated for the first time the effect of these two mutations on myosin motor function based on the cross-bridge model consisting of 6 elementary steps [19] by using the skinned papillary muscle fibers from transgenic (Tg) mice expressing human cardiac D166V and R58Q mutations. Papillary muscle fibers from Tg wild type (WT) mice carrying human ventricular RLC were used as controls. The experimental methods included sinusoidal length changes at varying frequencies, chemicals change, and analysis of the concomitant tension time course in terms of exponential processes. By studying the effects of MgATP (abbreviated as ATP hereafter), phosphate (Pi), and MgADP (abbreviated as ADP hereafter), we characterized 6 elementary steps of the crossbridge cycle. We found that: 1) both mutants produced smaller 2πc than WT, which corresponds to slower cross-bridge kinetics compared with WT; 2) both mutants raised the Ca²⁺ sensitivity of tension; 3) both mutants produced smaller rate constant of the cross-bridge detachment step (k₂); and 4) the association constants for ATP (K₁) and ADP (K₀) to the myosin head as well as equilibrium constant of the detachment step (K₂) was significantly smaller in D166V than in WT, whereas no changes in these parameters were observed in R58Q-fibers.

2. MATERIALS AND METHODS

2.1. Muscle fiber preparations

Tg mouse groups that carry human ventricular RLC (WT) and two mutants, D166V and R58Q, were generated at the University of Miami as previously described [14, 20]. All animal studies conducted were in accordance with institutional guidelines and protocols approved by the Animal Care and Use Committee (ACUC). The University of Miami has an Animal Welfare Assurance (A-3224-01, effective July 11, 2007) on file with the Office of Laboratory Animal Welfare (OLAW), National Institutes of Health. In this study, we used ~4 month old D166V mice (L4 expressing 95% transgene), 5–8 month old R58Q mice (L8 expressing 100% transgene and L9 expressing 90% transgene). The 4–8 month old WT (L2 expressing 100% transgene) were used as controls.

Muscle fibers were prepared as described [21]. Briefly, the hearts were quickly removed from mice after euthanasia and rinsed with ice-cold 0.9% NaCl. Papillary muscle strips, ~1 mm in diameter and ~2.5 mm in length, were dissected in ice-cold solution that contained 10⁻⁸ M Ca²⁺, 1 mM Mg²⁺, 7 mM EGTA, 2.5 mM MgATP²⁻, 15 mM creatine phosphate (Na₂CP), 30 mM BDM, 15% glycerol, and 20 mM MOPS; ionic strength (IS) adjusted to 150 mM with K-propionate, and pH to 7.0. After dissection, the strips were transferred to the same solution mixed with 50% glycerol (storage solution), and incubated for 1 h on ice. Then the strips were transferred to fresh storage solution mixed with 1% Triton X-100 for 24 h at 4 °C. The strips were finally transferred to a fresh storage solution without Triton, kept at −20°C, and shipped to Iowa on ice. The strips were subjected to mechanical studies between 2 days and 6 weeks after the shipment.

2.2. Experimental procedure

On the day of the experiment, fibers about 1 mm in length and 100 µm in diameter were dissected and mounted on the experimental apparatus by attaching their ends to two stainless-steel hooks with a small amount of nail polish. One hook was connected to a length driver, and the other to a tension transducer. Fibers were then soaked for a few minutes in the relaxing solution followed by further skinning for 20 min in the relaxing solution that contained 1% Triton X-100. Fibers were then washed in the relaxing solution and their length was adjusted to remove the slack.

Each preparation was tested in the standard activating solution (see Table 1 for solution compositions), followed by studies of pCa (7.0-4.4 in 0 Pi solution and 7.0-4.55 in 8Pi solution), ATP (S: 0.05–10 mM), Pi (P: 0–30 mM), and ADP (D: 0–3 mM) to determine the kinetic constants of the elementary steps based on the six-state cross-bridge model (Scheme 1). At the end of the experiment, the standard activation was repeated to measure the tension reproducibility and then rigor solution was applied to the fibers. All experiments were performed at 20°C. The creatine kinase (CK) concentration in the activation solutions was 160 U/ml; the adequacy of the CK concentration was determined empirically (see Results).

Table 1.

Compositions of solutions used for mechanics experiments.

Ingredient (mM)	Na- skinning solution	K-skinning solution	Storage solution	Relaxing	Standard activating solution	8Pi pCa solution	0Pi pCa solution
DTT	2	2	2	-	-		-
BDM	30	30	30	-	-	-	-
NaOH	28	-	-	-	-	-	-
Glycerol	-	-	6,000	-	-	-	-
K2CaEGTA	-	-		-	6	6b	7b
H4EGTA	10	10	10	6	-
Na2H2ATP	7	7	7	7	6.1	6.1	2
Na2CP	-	-	-	-	15	15	15
HK2PO4 + H2KPO4a	-	-	-	8	8	8	-
MgAc2	2	2	2	2	6.6	6.6	3
NaAc	118	-	-	41	12.8	12.8	-
KAc	-	118	118	70.5	53.5	65.5	66
KCl	-	-	-	-	12	-	-
KOH	10	38	38	~19	17.5	18.33	14
MOPS	10	10	10	10	10	10	10
CK (U/ml)	-	-	-	-	160	160	160

^aEquimolar mixture (8 mM is the total concentration).

^bthe total concentration of K₂CaEGTA and H₄EGTA. Ionic strength (IS) of all solutions is 200 mM, and pH is adjusted to 7.0 ± 0.02 by KOH, except for the Na-skinning solution which was adjusted by NaOH. pCa of the standard activating solution is 4.55, and [Mg²⁺] 1 mM. Ac: acetate; CP: creatine phosphate; Pi: phosphate; CK: creatine kinase.

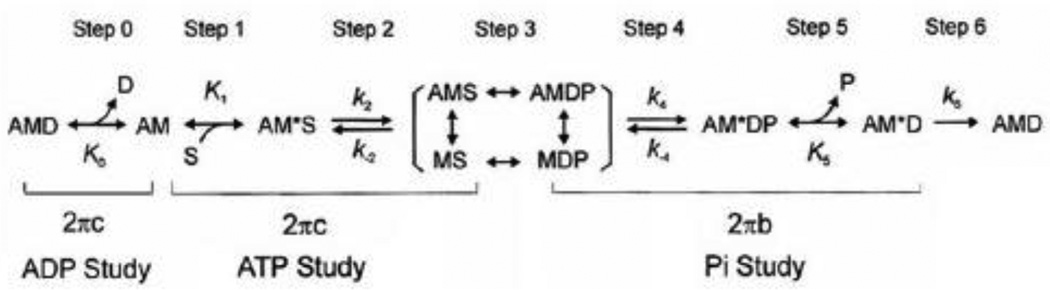
Scheme 1.

Elementary steps of the cross-bridge cycle in striated muscle fibers. In this scheme, force is generated at step 4 as demonstrated by experiments using rabbit psoas muscle fibers with sinusoidal analysis [29], pressure-release experiments [32], and caged Pi experiments [33]. Step 0: ADP release; Step 1: ATP binding; Step 2: Cross-bridge detachment and possibly recovery stroke; Step 3: ATP cleavage followed by cross-bridge attachment; Step 4: Force generation; Step 5: Pi release; Step 6: Work performance (filament sliding). A=Actin, M=Myosin, D=ADP, S=ATP, P=phosphate. K₁: ATP association constant (mM⁻¹); k₂: Rate constant of cross-bridge detachment; k₋₂: Rate constant of reverse detachment; K₂=k₂/ k₋₂= Equilibrium constant of cross-bridge detachment; k₄=Rate constant of force generation; k₋₄=Rate constant of reverse force generation; K₄=k₄/ k₋₄=Equilibrium constant of force generation; K₅=Pi association constant; 2πb=apparent rate constant of delayed tension (process B); 2πc=apparent rate constant of fast tension recovery (process C).

2.3. Sinusoidal analysis

At the tension plateau, the muscle length was oscillated with digitally synthesized sine waves of 17 frequencies (f) sequentially (0.25–250 Hz) at a small amplitude (0.125% of L₀). This frequency range corresponds to 0.64–640 ms in time domain analysis. The experiments were controlled by a 386 computer equipped with a 16 bit digital-to-analog converter, the signal from which moved the length driver. Both tension and length time courses were simultaneously digitized with two 16 bit analog-to-digital converters and recorded by the same computer. The complex modulus data Y(f) were calculated as the ratio of stress change to strain change at each frequency. Y(f) was fitted to Eq. 1, and the parameters (2πb, B, 2πc and C; b<c) of two exponential processes B and C were extracted [22, 23]

$$Y(f)=H-\frac{Bfi}{b+fi}+\frac{Cfi}{c+fi}$$ (1)

where $i=\sqrt{-1};2\pi b$ (rate constant of the delayed tension) and 2πc (rate constant of fast tension recovery) are the apparent rate constants of processes B and C, respectively. B and C are their respective magnitudes (amplitudes), and H is a constant that represents the elastic modulus at zero frequency. The elastic modulus extrapolated to infinite (∞) frequency is defined as Y_∞=H−B+C, where Y_∞ corresponds to phase 1 of step analysis. Y_∞ is loosely called “stiffness” in muscle mechanics literature. Process B corresponds to phase 3 of step analysis, which is a medium frequency-exponential delay when the muscle generates oscillatory work. Process C corresponds to phase 2, which is a high-frequency exponential advance when muscle absorbs work. These parameters were studied as functions of [ATP], [Pi] and [ADP] to deduce the kinetic constants of elementary steps of the cross-bridge cycle. A detailed description of the sinusoidal analysis method was published previously [22].

2.4. Statistics

All data were expressed as mean ± standard error (SE). One-way ANOVA was applied to determine the significance of the difference among different groups of muscle preparations, with post-hoc range tests (least significant difference, LSD) which tests pair wise multiple comparisons. A significant difference was defined as P ≤ 0.05, and a highly significant difference as P ≤ 0.01.

3. RESULTS

The purpose of this study was to further explore the mechanism of myosin RLC mutation-induced changes in cardiac muscle contraction. The kinetic constants (association constants and rate constants) of elementary steps in the cross-bridge cycle were deduced by sinusoidal analysis on skinned papillary muscle fibers from the left ventricles of Tg mice expressing FHC-linked mutations D166V and R58Q. The results were compared with WT.

3.1. Standard activation

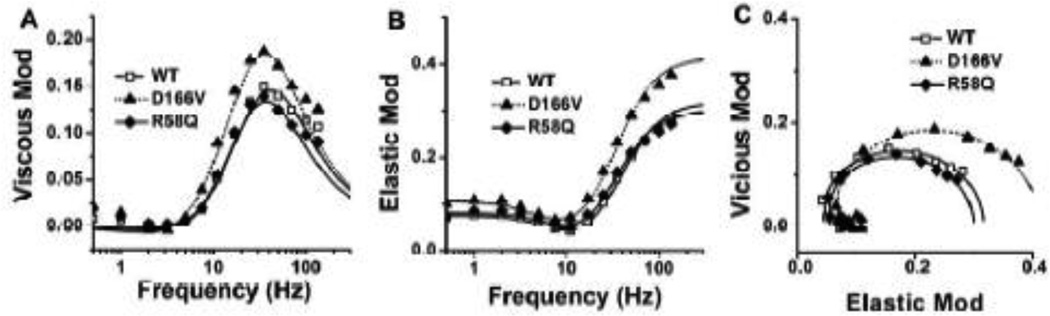
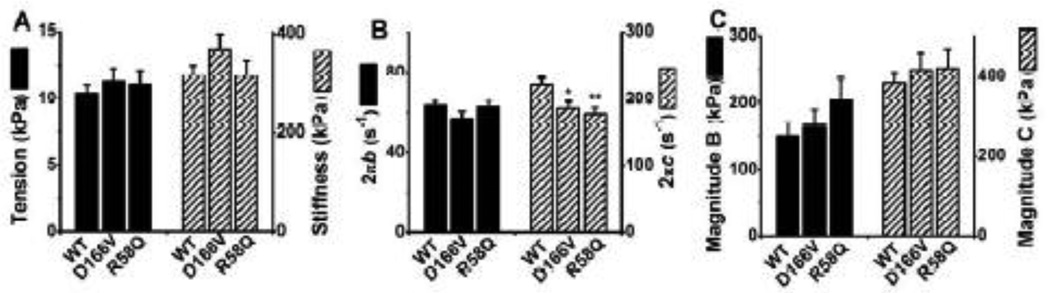
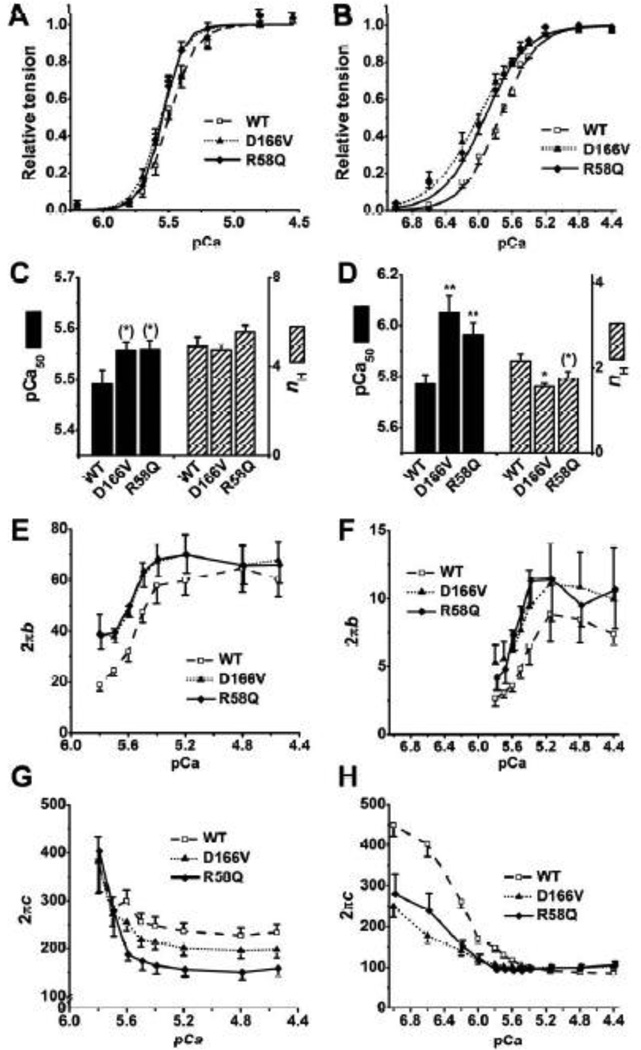
The complex modulus Y(f) is a frequency response function of the muscle tension change to the length change, and consists of two components: the viscous modulus (imaginary component of Y(f)) and the elastic modulus (real component of Y(f)). The results are plotted as the viscous modulus vs. frequency (Fig. 1A), the elastic modulus vs. frequency (Fig. 1B), and the viscous modulus vs. elastic modulus (Nyquist plots) (Fig. 1C) for 3 mouse groups. Data were fitted to Eq. 1, the best-fit curves are shown in Fig. 1, and the apparent rate constants 2πb and 2πc together with their magnitudes (B and C) were extracted. Each Nyquist plot (Fig. 1C) shows two contiguous semicircles, hence the complex modulus can be resolved into two exponential processes, B and C (Eq. 1), with process C faster than process B (b < c). The apparent rate constants 2πb and 2πc, their magnitudes, and the isometric tension and stiffness measured during the standard activation are compared among 3 genotypes (Fig. 2). There were no significant differences among mutants and WT when tension or stiffness is compared (Fig. 2A). The rate constant 2πb, and magnitude parameters B and C were not significantly different among different fiber groups (Fig. 2B and C). However, the rate constant 2πc was significantly smaller in both mutants than in WT (Fig. 2B).

Fig. 1.

The complex modulus data averaged from the first standard activations of individual experiments. Data were plotted as (A) viscous modulus [= Imag Y(f)] vs. frequency, (B) elastic modulus [= Real Y(f)] vs. frequency, and (C) viscous modulus vs. elastic modulus (Nyquist plot) (WT, n = 31; D166V, n = 20; R58Q, n = 24). Continuous curves represent Eq. 1 using best-fit parameters.

Fig. 2.

(A) Tension (T_max) and stiffness (Y_∞), (B) the apparent rate constants, and (C) magnitude parameters of exponential processes of the standard activation comparing three muscle groups. These data are deduced by fitting the complex modulus data to Eq. 1. Error bars represent standard errors (SE). **P≤0.01, *0.01<P≤0.05, (*) 0.05<P≤ 0.1 when compared with WT. The same conventions are used in all figures. WT, n = 31; D166V, n = 20; and R58Q, n = 24.

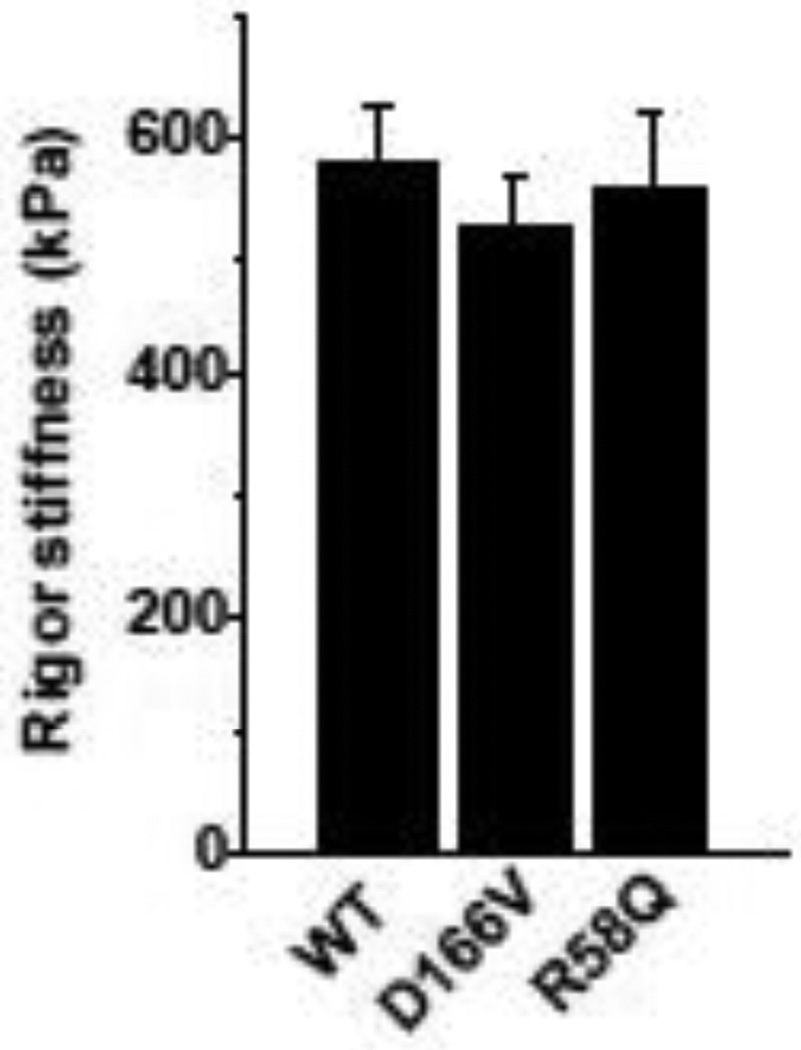
3.2. Rigor stiffness

Rigor stiffness was measured at 100 Hz and is plotted in Fig. 3. There were no significant differences in rigor stiffness among all muscle groups studied.

Fig. 3.

Rigor stiffness. WT, n = 31; D166V, n = 20; R58Q, n = 24.

3.3. pCa study

To characterize the Ca²⁺ sensitivity of tension (pCa₅₀) and cooperativity (n_H), we studied the effect of different concentrations of Ca²⁺ ranging from pCa 7.0 to 4.4. These pCa solutions contained 8 mM Pi, hence named 8Pi solutions and IS was 200 mM. Other group of investigators used solutions that contained 150 mM IS without Pi for their pCa-tension studies [14, 20, 24]. This solution, named 0Pi solution, was also studied in parallel with the 8Pi solution in the current report. The compositions of the solutions are listed in Table 1. The experiments were performed from low [Ca²⁺] to high [Ca²⁺], and results were fitted to the Hill equation:

$$\mathit{\text{Tension}}=\frac{T_{\text{max}}}{1+{\left(\frac{C{a}_{50}}{[C{a}^{2+}]}\right)}^{n_H}}$$ (2)

where T_max is the maximum tension developed at saturating [Ca²⁺], Ca₅₀ is the Ca²⁺ dissociation constant, and n_H is the cooperativity among regulatory proteins, which includes Tn, Tm, actin, and possibly myosin. In particular, pCa₅₀=−log₁₀Ca₅₀, which indicates Ca²⁺ sensitivity of tension.

At maximal Ca²⁺, the addition of 8 mM Pi reduces isometric tension to ~0.5× by decreasing the number of strongly attached cross-bridges [25–27]. Both mutants exhibited the trend of larger pCa₅₀ than WT in the 8Pi solution (0.05 < P ≤ 0.1) (Fig. 4C) and the difference between mutant vs. WT fibers became more significant in the 0Pi solution (P < 0.01) (Fig. 4D). In 0Pi solution, a decrease in n_H was found significant in D166V (P < 0.01) and close to significant in R58Q (0.05 < P ≤ 0.1) compared to WT (Fig. 4D), but this trend was not found in the 8Pi solution (Fig. 4C).

Fig. 4.

pCa study in 8Pi and 200 mM IS solutions in A, C, E, and G; and in 0Pi and 150 mM IS solutions in B, D, F, and H. A and B: pCa-tension plots. The continuous curves represent Eq. 2 using best-fit parameters. C and D: Ca²⁺ sensitivity (pCa₅₀) and cooperativity (n_H). E and F: pCa-2πb plots. G and H: pCa-2πc plots. A, C, E, and G: WT, n = 10; D166V, n = 6; R58Q, n = 6. B, D, F, and H: WT, n = 17; D166V, n = 10; R58Q, n = 10.

The apparent rate constants 2πb and 2πc at varying Ca²⁺ concentrations were also determined from the complex modulus data and plotted in Fig. 4E–H. 2πb and 2πc changed in the opposite directions: 2πb increased and 2πc decreased as [Ca²⁺] was increased in both sets of solutions. When isometric tension was < 5%, the modulus data were noisy, hence 2πb and 2πc could not be resolved at this low level of activation. In the absence of Pi, the magnitude B was much smaller than that in 8 mM Pi solutions and disappeared at pCa ≥ 6.0 (Fig. 4F). We also noticed that 2πb in 8Pi solutions was ~6 times larger, and 2πc was ~2 times larger than their respective values in 0Pi solutions (note a difference in scales in the ordinate in Fig. 4E and F). We further found that 2πb in D166V and R58Q was larger than that in WT at pCa ≥ 5.5 in both sets of solutions (P ≤ 0.05) (Fig. 4E and F); 2πc in R58Q was significantly smaller than that in WT when pCa ≤ 5.6 in the 8Pi solution (P < 0.01) (Fig. 4G); D166V and R58Q produced profoundly smaller 2πc than WT at pCa ≥ 5.6 (P < 0.01) in 0Pi solution, but no significant difference at pCa ≤ 5.5 (Fig. 4H).

3.4. ATP study

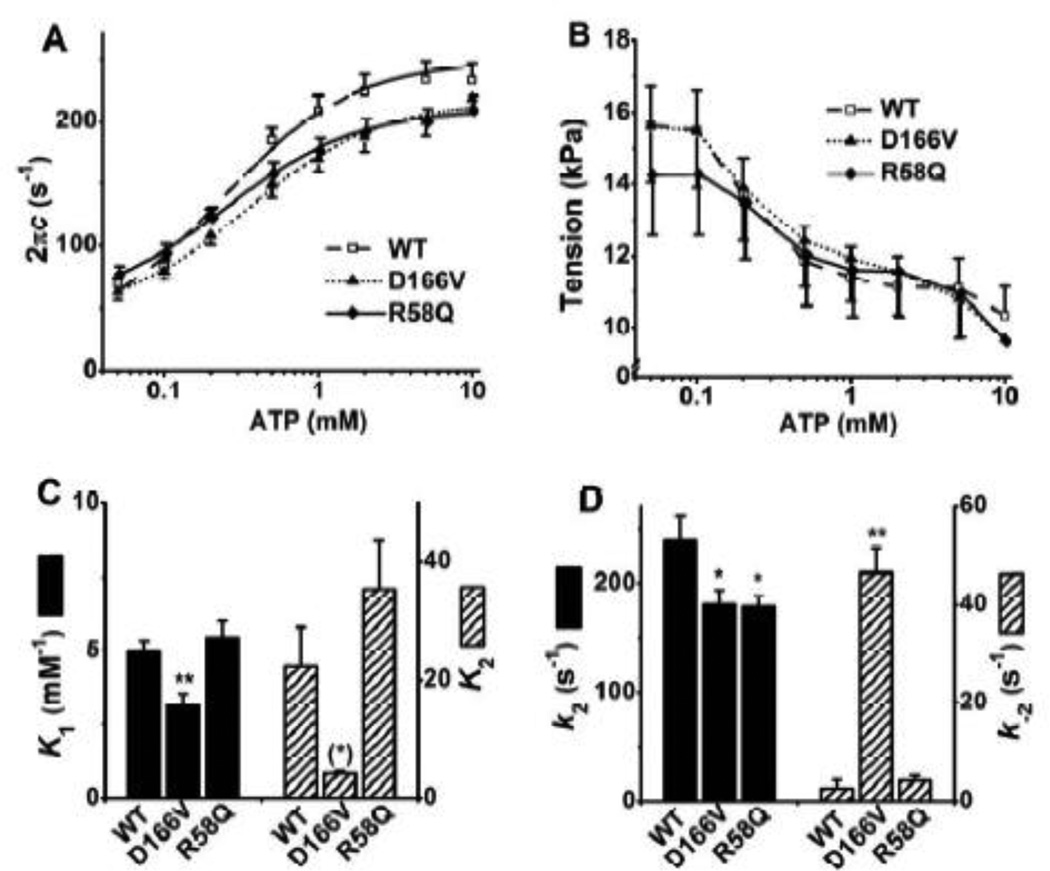
In this study, different concentrations of ATP (0.05, 0.1, 0.2, 0.5, 1, 2, 5, and 10 mM) were applied and exponential process C was studied to examine whether the kinetic constants of ATP binding (step 1) and cross-bridge detachment (step 2) were affected by RLC mutants. [Pi] was kept at the physiological level of 8 mM so that the adequate number of cross-bridges are distributed among the AMD, AM, AM*S and detached (Det) states, where A=actin, M=myosin, D=ADP, and S=ATP (Scheme 1). The resolution of process C is better under this condition than at lower Pi concentrations, because process C primarily represents steps 0–2. Fig. 5 A shows the apparent rate constant 2πc plotted against [ATP]. This relationship is hyperbolic (sigmoid in the semi log scale): 2πc increases with an increase in [ATP] from 0.05 mM to 1 mM and saturates by 10 mM. The data were fitted to Eq. 3 (Eq. 3 of [28]) that was based on Scheme 1, where S represents [ATP], D represents [ADP], and D₀ is the contaminating ADP concentration.

$$2\pi c=\frac{K_{1}S}{1+K_0(D+D_0)+K_{1}S}{k}_2+k_{-2}$$ (3)

The apparent rate constant 2πc in mutants were significantly smaller than that in WT from 0.5 to 5 mM [ATP] (Fig. 5A). The tension at each [ATP] was similar among different types of fibers (Fig. 5B). The ATP dependence of 2πc was fitted to Eq. 3, and the kinetic constants surrounding step 1 (K₁) and step 2 (k₂ and k₋₂) were deduced. The ATP association constant (K₁) in D166V was significantly smaller than that in WT (~60% of WT), whereas that of R58Q was similar to WT. D166V exhibited significantly smaller k₂ (forward rate constant of the cross-bridge detachment step 2), and significantly larger k₋₂ (reverse rate constant step 2) than those of WT (Fig. 5D). These resulted in a smaller K₂ (=k₂/k₋₂: equilibrium constant of cross-bridge detachment step) than that in WT without much significance (P = 0.071), because of relatively large standard error associated with k₋₂. R58Q likewise exhibited significantly smaller k₂ than that of WT, but k₋₂ was not any different from WT (Fig. 5D), which resulted in a slightly larger K₂ compared with WT without significance.

Fig. 5.

(A) Plots of 2πc (rate constant of process C, the fast tension recovery) vs. [ATP], (B) isometric tension vs. [ATP], (C) Equilibrium constants of steps 1 and 2, and (D) the rate constants of step 2 (cross-bridge detachment) in the ATP study. The continuous curves in (A) represent Eq. 3 with best-fit parameters. WT, n = 25; D166V, n = 15; R58Q, n = 18.

3.5. Pi study

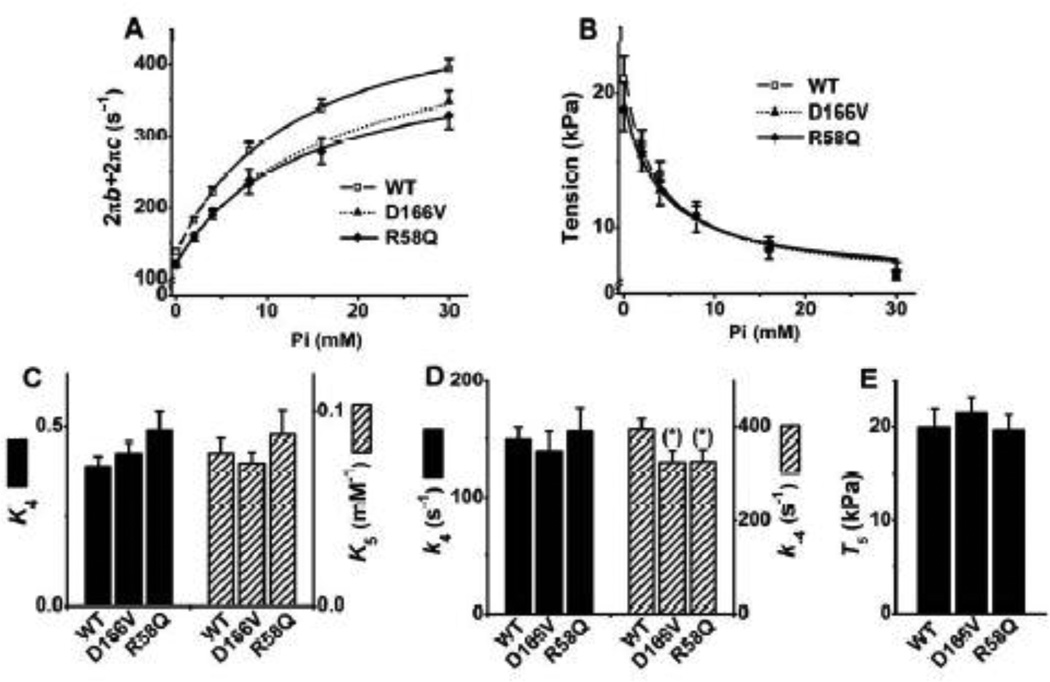
Different concentrations of [Pi] (0, 2, 4, 8, 16, and 30 mM) were applied to study the effects of [Pi] on exponential processes B and C, and isometric tension. The purpose of the Pi study was to investigate the effects of RLC mutants on force generation step 4 and Pi-release step 5 (Scheme 1). Fig. 6A shows the sum of the two apparent rate constants (2πb + 2πc), and Fig. 6B shows tension, plotted as functions of [Pi]. These relationships are hyperbolic. They were fitted to Eq. 4 (Eq. 14 in [29]) and Eq. 5 (Eq. 5. in [30]), which were derived based on cross-bridge Scheme 1:

$$2\pi b+2\pi c=Q+\frac{K_{5}P}{1+K_{5}P}{k}_{-4}$$ (4)

$$\mathit{\text{Tension}}=T_5{X}_5+T_6{X}_6=T_5(X_5+X_6)=\frac{T_5(K_{5}P+1)}{1+(1+1/K_4)K_{5}P}$$ (5)

where X₅ and X₆ represent the probabilities of cross-bridges in the AM*DP and AM*D states, respectively. T₅ is the tension supported by AM*DP, and T₆ is the tension supported by AM*D. AM*DP is a collision complex between Pi and AM*D. It is assumed that T₅ = T₆, because the conformation of a protein cannot change instantly with the collision complex formation [31], and previous data were consistent with this idea [29, 31–33]. T₅ is proportional to tension/cross-bridge. T₅ was not significantly different among mutants (D166V: 19.6 ± 1.7 kPa; R58Q: 19.4 ± 2.0 kPa) and WT (21.5 ± 1.7 kPa) (Fig. 6E), indicating that tension/cross-bridge is similar in all groups of muscle fibers. k₋₄ (Fig. 6D: rate constant of the reverse force generation step 4) and K₅ (Fig. 6C: Pi association constant) were first determined by fitting the rate constant data to Eq. 4 (Fig. 6A). Then, based on this K₅, the tension data were fitted to Eq. 5 (Fig. 6B) to determine K₄ (Fig. 6C: equilibrium constant of force generation step) and T₅ (Fig. 6E). Continuous curves represent the best fit data to Eqs. 4 (Fig. 6A) and 5 (Fig. 6B).

Fig. 6.

(A) Plots of 2πb+2πc (2πb: rate constant of process B, the delayed tension), (B) isometric tension, (C) equilibrium constants of steps 4 (Force generation) and 5 (Pi release), (D) the rate constants of step 4, and (E) tension generated by strongly attached cross-bridges (T₅) in the Pi study. The curves in (A) represent Eq. 4, and the curves in (B) represent Eq. 5 with best-fit parameters. WT, n = 26; D166V, n = 16; R58Q, n = 21.

Both mutants exhibited significantly smaller apparent rate constants (2πb+2πc) in all [Pi] tested, but similar tension at each [Pi], among all groups of fibers. K₅ was not significantly different among different fiber groups (Fig. 6C), indicating that the Pi release step is not affected by the mutations. k₋₄ in mutants was slightly smaller in both mutants than that in WT (Fig. 6D), but k₄ was not different, hence the corresponding equilibrium constant (K₄=k₄/k₋₄) was not much different among fiber groups (Fig. 6C). The tension (T₅) supported by the AM*DP (isomerized form of AMDP) and AM*D states is plotted in Fig. 6E. Consequently, there is no difference in tension supported by each cross-bridge among fiber groups tested.

3.6. ADP study

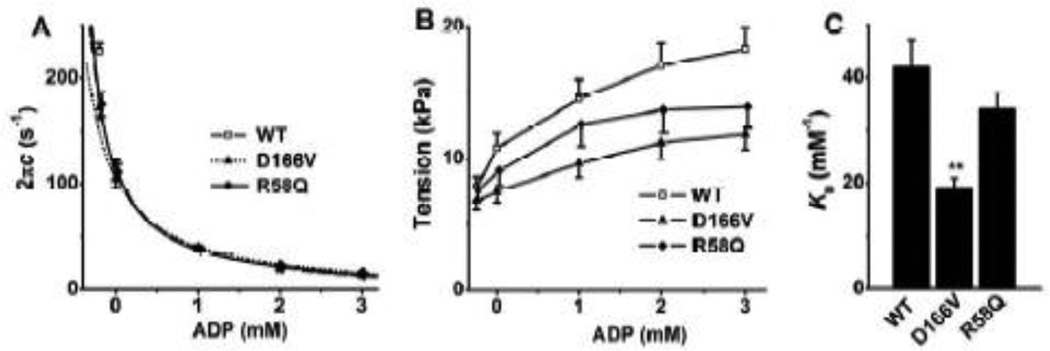
To characterize the association constant (K₀) of ADP to cross-bridges, the effect of ADP on process C was studied. The apparent rate constant 2πc (Fig. 7A) and tension (Fig. 7B) are plotted against [ADP]. As seen in these plots, the rate constant 2πc decreased and the tension increased as [ADP] increased in all groups of muscle fibers. By fitting the data from Fig. 7A to Eq. 3, K₀ was deduced. Here we used K₁, k₂, and k₋₂ derived from the ATP study, and S = 2 mM (experimental condition).

Fig. 7.

(A) Plots of 2πc (rate constant of process C) vs. [ADP], and (B) isometric tension vs. [ADP], and (C) the ADP association constant (K₀). The continuous curves in (A) represent Eq. 3 with best-fit parameters. WT, n = 20; D166V, n = 15; R58Q, n = 15.

During the ADP study, 00D solution (leftmost points in Fig. 7A and B), which contained CP and CK but no A₂P₅ or ADP, was first applied to the fiber, followed by the 0D solution, which contained no CP, CK, or ADP, but A₂P₅. The purpose of these two solutions was to find out the extra ADP concentration (D₀) in the 0D–3D solutions. D₀>0 because of ADP contamination in ATP, and continuous hydrolysis of ATP in fibers. In the 00D solution, the rate constant 2πc was somewhat larger (Fig. 7A), and tension was slightly less (Fig. 7B) than those in the 0D solution, demonstrating that [ADP] in the 0D solution was not negligible and finite. Thereafter, the 1D, 2D and 3D solutions were applied sequentially. D166V and R58Q exhibit significantly smaller 2πc than that of WT only at 00D. Tension generated at each ADP concentration was less in D166V than in WT (1–3D) (Fig. 7B) but similar in R58Q with WT. Extrapolating the 2 πc data versus [ADP] (Fig. 7A, continuous curves) allowed us to determine the contaminating ADP concentration in the 0D–3D solutions: D₀ was 0.28 ± 0.03 mM in WT, 0.30 ± 0.05 mM in D166V and 0.20 ± 0.02 mM in R58Q. This extra [ADP] (D₀), which resulted from ATP hydrolysis by muscle fibers and from ADP contamination present in ATP, was taken into consideration when deducing K₀, and as shown in Eq. 2. K₀ of D166V was significantly less than that of WT, but K₀ of R58Q was not significantly different from WT (Fig. 7C).

3.7. Cross-bridge distribution

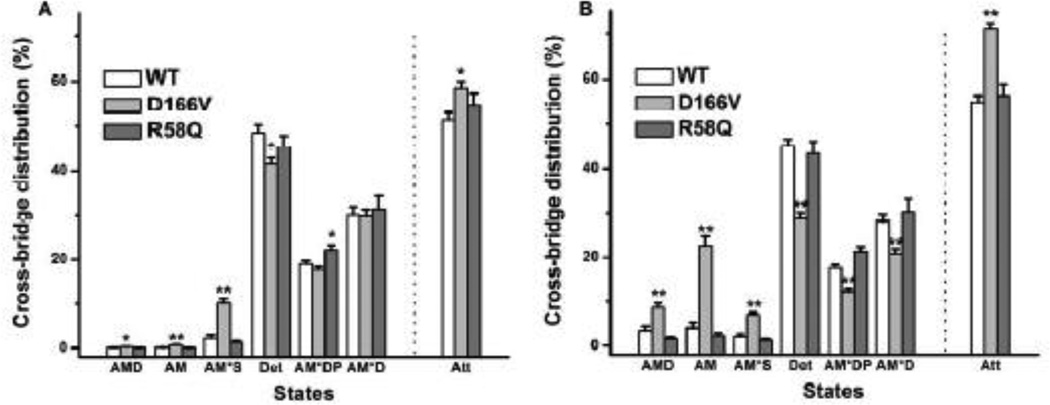
Based on Eqs. 7– 13 of [34], the cross-bridge distribution among 6 states in Scheme 1 was calculated and plotted at the standard activating condition when [ATP] is saturating at 5 mM (Fig. 8A), and at the condition when [ATP] is limiting at 0.1 mM (Fig. 8B). The plots also include the sum of all strongly attached states and labeled as Att, where Att=1−Det. When [ATP] is saturating (Fig. 8A), D166V shows significantly more cross-bridge distribution at the strongly attached state (Att), hence less in the Det state. The cross-bridge distribution at AMD, AM and AM*S is larger in D166V than in WT. In contrast, not many differences are found between R58Q and WT, except that more cross-bridges are distributed at the AM*DP state. When [ATP] is limiting (Fig. 8B), the differences between D166V and WT is more enhanced, including more cross-bridge distribution at Att than WT, which are caused by more distribution at the AMD, AM, AM*S states. The cross-bridge distribution at AM*DP and AM*D in D166V is much less than those in WT.

Fig. 8.

The cross-bridge distribution was calculated based on Eqs. 7–13 of [59] at the standard activating condition (S=5 mM, P=8 mM, D=0.01 mM) in (A) and at the ATP limiting condition (S=0.02 mM) in (B). WT, n = 13; D166V, n = 13; R58Q, n = 11. Det: detached state, including all detached states (MS, MDP) and “weakly attached” states (AMS, AMDP) and shown in brackets in Scheme 1; Att, the sum of strongly attached states (AMD, AM, AM*S, AM*DP, and AM*D).

3.8. Adequacy of CK concentration

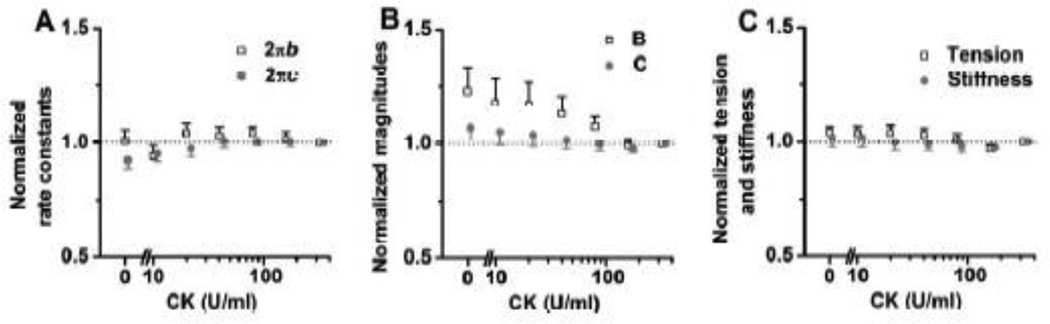
To examine the adequacy of the ATP regenerating system, we tested different CK concentrations (0, 10, 20, 40, 80, 160, and 320 U/ml) at 1 mM MgATP and 8 mM Pi, and studied their effects on the apparent rate constants (Fig. 9A), magnitudes (Fig. 9B), and isometric tension and stiffness (Fig. 9C); these results were normalized to their respective values at 320 U/ml CK. 1 mM MgATP was chosen, because the rate constants change sensitively at this concentration. We didn't find any significant changes among different concentration of CK except the bigger magnitude B at 0–40 U/ml CK than that at 320 U/ml. There were slight but noticeable deviation on rate constant 2πc at [CK] ≤ 10 U/ml, and magnitude B at ≤ 40 U/ml (Fig. 9B). Consequently, we chose [CK] of 160 U/ml, which was sufficient and adequate, and did not have any significant influence on parameters we studied.

Fig. 9.

The effect of different concentrations of CK (0, 10, 20, 40, 80, 160 and 320 U/ml). A: 2πb- and 2πc-[CK] plot; B: magnitude (B and C)-[CK] plot; C: tension- and stiffness-[CK] plot. In each experiment, the values are normalized by those at 320 U/ml. The averages and SE at 320 U/ml CK for each parameter were as follows: 2πb: 35.9 ± 4.4 s⁻¹; 2πc: 225 ± 17 s⁻¹; magnitude B: 113 ± 21 kPa; magnitude C: 457 ± 76 kPa; tension: 11.0 ± 1.6 kPa; stiffness: 417 ± 68 kPa). n = 8.

4. DISCUSSION

The current study investigated tension, stiffness, and the rates and equilibrium constants of six elementary steps of the cross-bridge cycle (Scheme 1) in two FHC-linked RLC point mutations D166V and R58Q, and results were compared to WT. These mutations are similar in their clinical manifestations and prognosis. Through sinusoidal length change experiments combined with chemical changes applied to skinned papillary muscle fibers, we found that some parameters were affected in the same way, but some others were affected in a different way in two mutants. The parameters affected in the same way include Ca²⁺ sensitivity (increase), cooperativity (decrease), and the cross-bridge detachment rate k₂ (decrease). The parameters affected in a different way include nucleotide binding constants (K₀ and K₁), which were attenuated in D166V but invariant in R58Q compared to WT. In D166V, the rate constant of reverse detachment step (k₋₂) was significantly increased, whereas the equilibrium constant of this step (K₂) was somewhat decreased compared to WT. Neither parameter changed in R58Q.

4.1. Sinusoidal analysis

Sinusoidal analysis is unique in that the length oscillation induces a chemical oscillation as a result of modification of the rate constants, thus tension is a result of the resonance between the length change and the chemical change. Hence this analysis method is capable of extracting information on elementary chemical reactions taking place in muscle preparations. If there was some viscoelasticity at the fiber ends, our analysis would readily detect it at a particular frequency by resonance, which we have not found. The effect of the extra viscoelasticity even if it existed is cancelled out when we correct the data (usually against rigor preparations; see Appendix 1 of [22]). We change many experimental parameters (concentrations of ATP, ADP, Pi, ionic strength; temperature) in cardiac muscles [35, 36], which also should discriminate the viscoelasticity if present. Furthermore, in our previous study [37], we have found the tension to stiffness ratio are similar to others [38, 39], which demonstrates that the contribution of the damaged ends (if existed) should be very small.

4.2. Age dependent changes, malignancy, and isometric tension

The age of the WT mice used in the current study was 4–8 months old, which covered the age of D166V mice (4 months old) and R58 mice (5–8 months old). We did not find any difference in results in the WT mice when compared between 4 months and 5–8 months of age. We have chosen to examine relatively young D166V and R58Q mice, before the onset of the structural abnormalities, to elucidate the early events which ultimately result in pathologic FHC phenotypes. The characterization of the Tg mouse models as well as Tg protein expression levels and the histopathology studies on D166V [14] and R58Q [20] have previously been reported. Tg mice, expressing ~95% D166V mutant of the human ventricular myosin RLC, were shown to result in profound changes. Severe fibrotic lesions were found at ~17 months of age, but no obvious histopathology phenotype was found in ~7 and ~11 months old mice [14]. Similarly, myofibrillar disarray and abnormal clustering of nuclei were observed in the hearts of 17.5 months old R58Q mice, but not in mice under 12.5 months of age [20]. With R58Q mice, an increase in ventricular wall thickness during diastole were observed at 15 months, but not at ~8 months [40]. These findings suggest the pathological changes in muscle structure of the mutated mice appear at the older age.

Maximal tension and average force per cross-bridge in skinned papillary muscle fibers from D166V mice were found significantly decreased compared with WT mice [14, 41]. A significant reduction in isometric tension was also found in R58Q, both by in vitro frictional loading assay [42, 43] and in skinned papillary muscle fibers [20, 24, 41]. However, in the current study, no decrease in the active tension or force/cross-bridge (T₅) under saturating Ca²⁺ was found in either D166V or R58Q model. The different age or gender of mice didn’t result in differences in tension and/or kinetics in R58Q [20, 24], which suggests that the age difference is not the reason for R58Q. However, we still cannot rule out the influence of the age in D166V. The D166V mice (7 ± 1 months old) used in the previous study [14] were older than the ones used in the current study (3.9 ± 0.6 month old). The severe fibrotic lesions were found in D166V mice at ~17 months, but not in younger mice (≤ 11 months old) [14], demonstrating the age dependent development of hypertrophic phenotype in D166V mice.

4.3. Difference between the present and previous studies

The most apparent difference between the present study and previous studies is the solution composition used to activate muscle fibers: 0 mM Pi and 150 mM IS were used in previous studies [14, 20, 24, 41], whereas more physiological 8 mM Pi and 200 mM IS were used in the current study. Muscle fibers produce larger tension at 0 mM Pi and 150 mM IS (20–25 kPa with our observations) than at 8 mM Pi and 200 mM IS (10–12 kPa, Fig. 2A). The addition of 8 mM Pi reduces ~40% isometric tension (Fig. 6B), and a 50 mM increase in IS reduces ~15% isometric tension [44]. The different method we applied to measure the fiber diameter may also contribute to the lower level of tension we observed. In our experiments, we averaged the thickest and thinnest portions of the fibers to determine their diameters, which might result in overestimated cross-sectional areas. These are the main reasons for the lower tension observed in our report compared to previous reports (30–40 kPa) [45]. However, the method applied in this work may only affect the absolute values of tension and stiffness, leaving the relative changes between WT and mutants not affected. The solutions used in the current study also reflect more physiological conditions, because the intracellular [Pi] in contracting cardiomyocytes is reported to be 4–9 mM [46]. There are no available data on IS of cardiomyocytes, but in skeletal muscle cells, it was reported to be ~215 mM [47]. The difference in maximal tension between mutants and WT muscle groups seems to be augmented in the lower IS solution without Pi, however, this may not be physiologically relevant.

In the in vitro motility assay, which is performed at an extremely low IS (~58 mM), R58Q and WT showed no difference in the unloaded actin filament velocity, the unloaded duty ratio, and the regulated thin filament velocity [43]. However, by using a frictional loading assay, R58Q reconstituted myosin showed a significant reduction in isometric tension compared to WT [43]. Contractile properties are sensitive to the environmental factors, which vary with the load, the energetic need, the stress imposed on fibers, ionic strength, and the temperature [48].

4.4. pCa study: Ca sensitivity, cooperativity, and rate constants

A large increase (P < 0.01) in Ca²⁺ sensitivity (pCa₅₀) of tension was found in D166V and R58Q mice in the 0 Pi and 150 mM IS solutions (Fig. 4B and D), which are consistent with previous findings [14, 20, 49]. The increase was much smaller (0.05 < P < 0.1) in the 8 Pi and 200 mM IS solutions (Fig. 4A and C). Both the absence of Pi and the decreased IS contribute to the increased pCa₅₀ and the larger difference in the calcium sensitivity between mutant and WT fibers. This is presumably due to enhanced myosin binding to actin in 0 mM Pi and enhanced Ca²⁺ and myosin bindings to the thin filament at 150 mM compared to the 8 mM Pi and 200 IS conditions [50].

With our experience, the change in pCa₅₀ is not always present when compared between different solutions (0 mM Pi vs. 8 mM Pi). In Tm mutants E40K (FDC), E54K (FDC), and D175N (FHC), pCa₅₀ does not differ from WT in the 8 mM Pi solution, whereas pCa₅₀ changed significantly in 0 mM Pi solution [51, 52]. In Tm mutants V95A and E180G (FHC), pCa₅₀ increases in both solutions [51]. Fibers under the non-physiological conditions are expected to perform differently, therefore, it is important to carry out experiments under the physiological condition if the objective is to find out physiological significance.

The cooperativity (n_H) indicates the tightness of coupling between the Tn complex, Tm, actin, and myosin, in addition to the number of Ca²⁺ binding sites in the regulatory unit [50]. n_H was significantly less in D166V and slightly less in R58Q (no significance) than in WT in the 0 mM Pi solutions (Fig. 4B and D), but was not significantly different at 8 mM Pi solutions (Fig. 4A and C). One previous study has found that n_H of R58Q fibers was slightly smaller (without significance) than that of WT by measuring the ATP hydrolysis rate [20]. Both the increase in pCa₅₀ and the decrease in n_H will make the heart more difficult to relax resulting in diastolic failure [14, 20, 42]. The more significant changes in D166V compared to R58Q also suggest that the D166V may cause more serious disease phenotype than R58Q. The fact that n_H is 2–3× larger in 8Pi solutions (Fig. 4A) than in 0Pi solutions (Fig. 4B) indicate the coupling between regulatory proteins is more tight in the 8 mM Pi and 200 mM IS solutions (where less cross-bridges are attached) than in 0 mM Pi and 150 mM IS solutions, suggesting that the primary elements to determine n_H are the regulatory proteins, and the primary force is the electrostatic interaction to stabilize these couplings.

4.5. Comparison to the two-state cross-bridge model

Based on the two-state model of Brenner [53], the cross-bridge detachment rate g was found decreased in D166V fibers compared to WT [14]. The 6–7 months old Tg-D166V mouse myofibrils showed a decrease in both attachment and detachment rates during isometric contraction as measured by polarized fluorescence [54]. However, it is important to note that the cross-bridge detachment rate (g) in previous studies [14, 54] is different from the cross-bridge detachment rate (k₂) measured in our study. The former was based on the two-state model [53], and the rate constant g was calculated by taking the ratio of ATPase/force/[myosin], hence it is a composite of several elementary steps. The latter was based on the six-state model [55, 56] and k₂ was deduced by studying the ATP effect on 2πc (Eq. 3). There has been no other study that characterized 6 elementary steps of cross-bridge cycle by using the muscle fiber system.

4.6. Cross-bridge kinetics

The slower cross-bridge kinetics in D166V and R58Q found in the current study is consistent to previous findings in D166V [54] and R58Q [24]. Previous studies used myofibrils, with the thin filament labeled by fluorescent rhodamine conjugated phalloidin, and the two-state model was used to analyze the results. The current study is based on a more realistic six-state model, many more parameters have been measured, and the method used (small amplitude length change) was not invasive. Our results, showing that the cross-bridge detachment rate (k₂) was smaller in the mutants compared with WT (Fig. 5D), indicate slower cross-bridge kinetics in D166V and R58Q fibers. The slower k₂ is the main reason why 2πc is slower in mutants than in WT (Fig. 5A).

In our experiments, we found that the nucleotide association constants (K₀ and K₁) were smaller in D166V than in WT (Figs. 5C and 7C), but this was apparently not the case with R58Q. It has been reported that both ATP association and ADP release rates influence the shortening velocity [57, 58]; ADP release rate may have a limiting effect on the cross-bridge detachment step [57].

It is interesting to consider how the difference between D166V and R58Q can account for the difference in their clinical symptoms. A previous investigation has found that the ATP hydrolysis rate observed in D166V showed a significant decrease (22%) compared to WT [14]. Because the hydrolysis is driven by the ATP binding, our finding of the decreased ATP association constant K₁ in D166V is consistent with the decreased ATP hydrolysis rate. At the same time, the significantly decreased equilibrium constant of the cross-bridge detachment step K₂ in D166V also accounts for the decreased ATP hydrolysis rate. When the ATP supply is limiting, the decrease in K₁ and K₂ results in an increase in the cross-bridges at the AMD, AM, and AM*S states, which in turn decreases the cross-bridge number in the AM*DP and AM*D states (Fig. 8B). Because the step 6 is limiting the ATP hydrolysis rate, it can be related to the AM*D state by Eq. 6 [59]:

$$(\text{ATPase})=k_6[\mathrm{A}{\mathrm{M}}^{*}\mathrm{D}]$$ (6)

where k₆ is the rate constant of step 6, which is the slowest step in the cross-bridge cycle. k₆ represents elastic recoil of the series compliance, and not likely be affected by the mutation. Thus, ~22% decrease in the ATP hydrolysis rate and the decrease in the cross-bridge distribution at AM*D state by ~24% found in D166V (Fig. 8B) are consistent. Consequently, the reduced nucleotide binding constants (K₀, K₁) in D166V results in less efficient usage of ATP which may cause an hypertrophic cardiomyopathy (HCM) phenotype. The problem may become more severe and significant in ischemia, in which inadequate supply of oxygen would result in an inadequate ATP production.

The two mutants had minor influence on the kinetics of the force generation step 4 and Pi release step 5 (Fig. 6C–E). The rate constant (k₋₄) of the reverse force generation step were slightly smaller in both mutants than in WT, but the equilibrium constant K₄ did not change significantly among different fiber groups. These results suggest that the FHC phenotype in D166V is triggered by the ATP binding step, and not by the force generation step.

5. SUMMARY

The early events of FHC-associated mutations, D166V and R58Q of myosin RLC are investigated by using Tg mice. These mutations have similar clinical manifestations and prognosis in humans, and affect muscle contractile mechanisms through the common pathway of increased [Ca²⁺] sensitivity of force and altered cross-bridge kinetics. Both mutant mice decreased apparent rate constant of fast tension recovery, and slowed the cross-bridge detachment step contributing to FHC-related diastolic dysfunction phenotypes. In D166V, but not in R58Q, the nucleotide binding was weakened, which may result in less efficient energy usage during contraction. The active tension in D166V and R58Q fibers were not much different from WT when tested in fully physiological conditions of 8 Pi and 200 IS. This study comprehensively determined the elementary steps of the cross-bridge cycle and underlined the effect of FHC mutations on myosin cross-bridge kinetics in skinned fibers to better understand the mechanism of FHC.

HIGHLIGHTS.

• ▸FHC mutations D166V and R58Q of myosin RLC were investigated in Tg mouse models
• ▸Papillary muscles were characterized by sinusoidal analysis with ATP, ADP & Pi study
• ▸Tension, stiffness, and rigor stiffness did not differ from the wild type
• ▸Both mutants showed slower crossbridge detachment rate and increased Ca²⁺ sensitivity
• ▸D166V but not R58Q exhibited weaker ATP binding and faster ADP release