A Computational Study of Systemic Hydration in Vocal Fold Collision

Abstract

Mechanical stresses develop within vocal fold (VF) soft tissues, due to phonation-associated vibration and collision. These stresses in turn affect the hydration of VF tissue and thus influence voice health. In this paper, high-fidelty numerical computations are described taking into account fully three-dimensional geometry, realistic tissue and air properties, and high-amplitude vibration and collision. A segregated solver approach is employed, using sophisticated commercial solvers for both the VF tissue and glottal airflow domains. The tissue viscoelastic properties were derived from a biphasic formulation. Two cases were considered, whereby the tissue viscoelastic properties corresponded to two different volume fractions of the fluid phase of the VF tissue. For each case, hydrostatic stresses occurring as a result of vibration and collision were investigated. Assuming the VF tissue to be poroelastic, interstitial fluid movement within VF tissue was estimated from the hydrostatic stress gradient. Computed measures of overall VF dynamics (peak air-flow velocity, magnitude of VF deformation, frequency of vibration and contact pressure) were well within the range of experimentally observed values. The VF motion leading to mechanical stresses within the VFs and their effect on the interstitial fluid flux is detailed. It is found that average deformation and vibration of VFs tends to increase the state of hydration of the VF tissue whereas VF collision works to reduce hydration.

1. Introduction

The myoelastic aerodynamic theory of voice production (van den Berg 1958; Titze 2006) considers true self-oscillation of the vocal folds (VFs) as a dynamic flow-structure interaction (FSI), where the glottal air flow pressure and VF stresses are out of balance instantaneously. This imbalance causes the VFs to move and results in an oscillatory motion as either the air pressure exceeds the restoring force in the VF or vice-versa. This definition of VF self-oscillation sets the context in which the computations in the present paper are performed. The characteristics of self-oscillation, e.g. time-period of oscillation, magnitude of VF vibration and oscillation of flow pressures and velocities are not imposed externally, but are obtained as a result of the coupled system. Computations are conducted with the goal to investigate the role of VF stresses during self-oscillation on VF hydration.

Past studies (Bartlett and Thibeault 2011; Branski et al 2006; Dikkers et al 1993; Gray and Titze 1988; Gray 2000) suggest that voice health and VF function are dependent on the histology of the underlying tissue. Hydration of VF tissue is posited to be beneficial for voice health by helping maintain tissue composition in a healthy state (Tateya et al 2006). Chan and Tayama (2002); Leydon et al (2009); Sivasankar and Leydon (2010) show that systemic and superficial hydration of VF tissue regulate biomechanical, aerodynamic and acoustics indicators of voice health. Miri et al (2012) demonstrate that the hydration state significantly alters tissue biomechanical characteristics.

Vocal health has also been considered to be influenced by mechanical stresses in the VFs, which result from free vibration and collision between the folds. Titze (1994) outlined several contributors to the total mechanical stress and discussed their possible effect on VF tissue damage. Significant research has been conducted to determine contact pressures (Jiang et al 2001; Spencer et al 2006; Tao et al 2006; Verdolini et al 1999), stress tensor components following a choice of coordinate axes (Gunter 2003; Spencer et al 2006) and the coordinate axis invariant von-Mises stress (Gunter 2003).

In this paper, VF systemic hydration is related to vibration induced mechanical stresses in the VF using poroelastic theory (Biot 1941) as suggested by previous research on VF tissue composition (Noordzij and Ossoff 2006). Poroelastic theory considers the interstitial fluid flux as linearly proportional to the hydrostatic stress gradient, where stress gradients result due to VF vibration and collision. However, the problem of determining mechanical stresses in the VF is challenging. Experimental techniques to determine contact pressures on VF surface using pressure sensors (Gunter et al 2005; Verdolini et al 1998) have provided significant insight into the VF deformation response. However, surface pressures do not reveal the hydrostatic stress distribution inside the VF tissue. Digital image correlation has been used to measure superior-surface displacements on vibrating and colliding VFs (Chen and Mongeau 2009; Spencer et al 2006). The resulting strain field is used to estimate stresses on the superior surface using a linear elastic model for the mechanical response of the VFs, and to estimate contact pressures assuming an underlying contact model. Spatial resolution of stresses in the interior (away from the superior surface) and accuracy of the collision model remain the main challenges of this approach.

Computational models of the VFs have been used to directly determine stresses during oscillation and collision. However, complexities in modeling the multi-physics nature of the flow-structure interaction problem has led to research that mostly incorporates simplifications like two-dimensional (2D) geometry, longitudinal uncoupling of VF sections and non-linear stiffening of VF tissue for modeling contact (Dejonckere and Kob 2009; Horáček et al 2005, 2009; Luo et al 2008, 2009; Zheng et al 2009). A related challenge is in solving the glottal airflow. Several studies (Drechsel and Thomson 2008; Krebs et al 2012; Sidlof et al 2011; Triep and Brücker 2010) focusing on the flow across three-dimensional (3D) VFs (either forced or self-oscillating) show that the glottal flow has a rich structure in time and space. Oversimplification of the glottal flow physics (2D geometry, low order flow models) may not yield reliable results in determining VF stresses during self-oscillation (Dejonckere and Kob 2009; Horáček et al 2005, 2009; Luo et al 2008, 2009; Zheng et al 2009).

The phonation process is a strongly coupled fluid-structure interaction problem. Development of solution strategies that incorporate multi-physics capabilities are only beginning to receive the kind of attention reserved for dedicated solvers. Luo et al (2008, 2009); Zheng et al (2010) have implemented monolithic numerical algorithms based on a fully Eulerian description of the combined fluid-structure domain. This methodology has an exciting future as it significantly reduces the required book-keeping and solution interpolation back and forth across the interface between the two distinct physical domains. However, at present it requires meeting afresh challenges particular to the individual domains that have been treated satisfactorily in the dedicated solvers. Contact algorithms and viscoelastic constitutive models are the relevant features in the present context.

Currently, Tao et al (2006) and Zheng et al (2010) are the only studies that simulate self-oscillation of 3D continuum model of VF tissue accounting for collision between opposing VFs. In Tao et al (2006), the VF volume was modeled as a set of coronal layers that were mechanically uncoupled, that is mechanical stresses and strains were discontinuous between adjacent layers. The basic assumption behind this approach is that the anterior-posterior motion of the VF is much smaller compared to the motion in the other two directions. Consequently, the anterior-posterior strains and anterior-posterior stresses are zero. However, a relevant deformation mode of the VFs is that of flexure, due to which anterior-posterior stresses can be significant. On the other hand, in Zheng et al (2010) the effective Reynolds number at which the simulation was conducted is an order of magnitude lower than those of the actual physical problem. Furthermore, the effective stress relaxation factor used in Zheng et al (2010) is several orders of magnitude lower than the biphasic theory treatment of Zhang et al (2008) would suggest. The VF self-oscillation problem is, however, expected to be strongly influenced by viscosity in the fluid and solid domains.

In the present work a computational model is introduced with the following main features: 3D geometry, full Navier-Stokes description for fluid flow with physically representative gas properties, resulting in realistic levels of VF deformation amplitudes and VF collision characteristics. A segregated-solver approach employing commercially-available dedicated computational software is used. A separate coupling code resolves the communication of solution across the code interface. This method has been used successfully for a suite of coupled-physics problems (Bathe et al 1999; Stein et al 2000; Taylor et al 1998; Zhang and Hisada 2001) and leverages the substantial advancement made in simulating problems involving a single physical domain (fluid or structural).

Results from two FSI computations are presented; the computations correspond to a VF tissue under ‘normal’ well hydrated conditions, and another which is only minimally hydrated. For the ‘normal’ VF case, overall exterior characteristics of mean deformation, vibration and collision are compared with experimental observations. Vibration and collision characteristics are analysed in detail, with focus on the internal hydrostatic stress state. The state of stress is analyzed at representative times for a collision-free vibration cycle, and for a cycle with VF collision. The effect of mechanical stresses on VF hydration is demonstrated. Results are discussed in the context of previous experimental and numerical studies.

2. Method

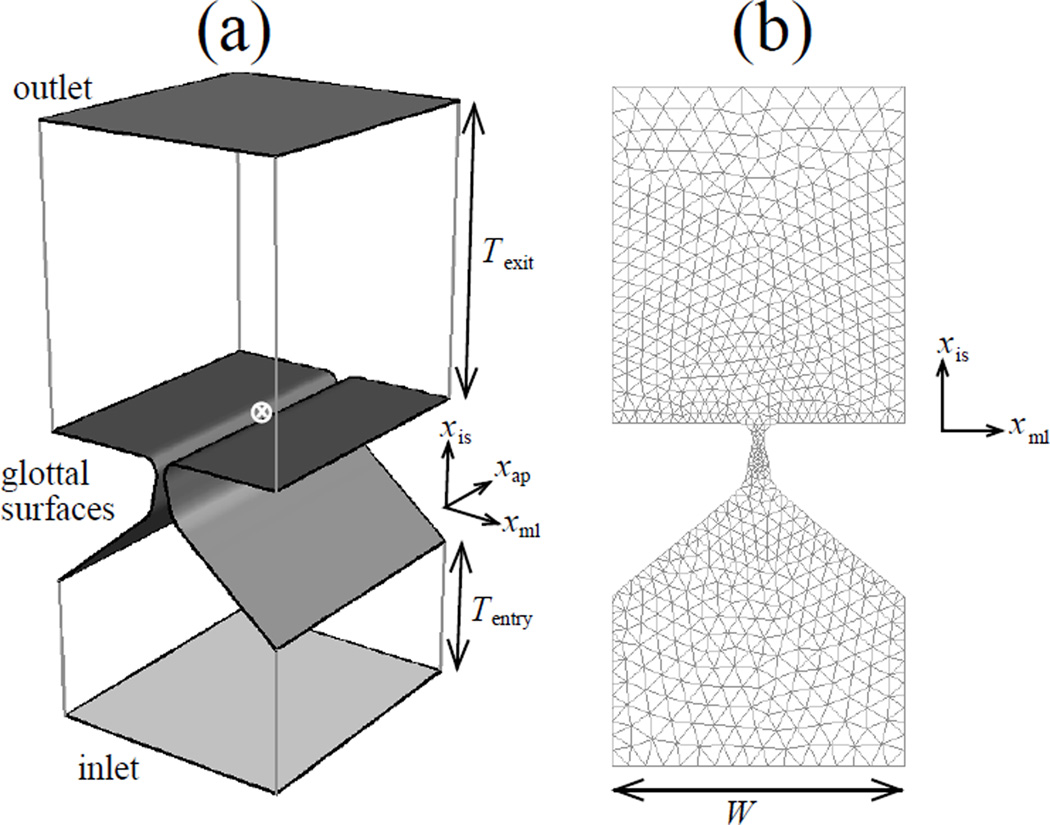
The computational model comprises separate definitions for the continuum regions corresponding to the glottal airflow and the pair of VFs, a contact interaction model for the VFs, and a coupled interaction model between the air (fluid) and tissue (structural) domains. The coordinate system origin for both fluid and structural domains is located at the intersection of the mid-coronal plane, the mid-saggital plane and the VF superior surface (figure 1a). A right-hand coordinate system is fixed by choosing x_is, x_ml and x_ap axes in the inferior-superior, medial-lateral and anterior-posterior directions respectively.

Figure 1.

(a) Geometry of the flow domain volume. The inlet, outlet and glottal flow-structure interaction surfaces appear as shaded. The coordinate system origin (⊗) and coordinate axes (at an offset) are shown. (b) Initial mesh of the flow domain at a coronal section

2.1 Glottal airflow model

The 3D glottal air-tract geometry includes the glottis (region between the folds), and rectangular parallelepipeds corresponding to upstream (inferior) and downstream (superior) channels (figure 1a). Dimensions of the channels are given in table 1. Parts of the boundary of the air-tract that interact with the VFs are identified as glottal surfaces.

Table 1.

Geometric dimensions and constitutive properties of glottal airflow model.

Air-tract Dimensions		Air Properties
Tentry	10.0 mm	pref	101 kPa
Texit	20.0 mm	ρf	1.23 kg/m3
T	10.7 mm	μ	1.79 × 10−4 kg/m·s
L	20.0 mm
W	17.4 mm

The fluid domain mass and momentum conservation equations are written in integral form, in the absence of body forces, for an arbitrary volume of fluid V^f as:

$${\oint }_{\partial (V^{\mathrm{f}})}(\overrightarrow{v}-{\overrightarrow{v}}_{\mathrm{g}})·\mathrm{d}\overrightarrow{S}=0,$$ (1)

$${\rho }_{\mathrm{f}}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_{V^{\mathrm{f}}}\overrightarrow{v}\mathrm{d}V+{\rho }_{\mathrm{f}}{\oint }_{\partial (V^{\mathrm{f}})}\overrightarrow{v}(\overrightarrow{v}-{\overrightarrow{v}}_{\mathrm{g}})·\mathrm{d}\overrightarrow{S}=-{\oint }_{\partial (V^{\mathrm{f}})}p\mathbf{I}·\mathrm{d}\overrightarrow{S}+{\oint }_{\partial (V^{\mathrm{f}})}{\mathit{\tau }}_{\mathrm{f}}·\mathrm{d}\overrightarrow{S}.$$ (2)

Here, v⃗ represents the velocity of the fluid particle at a point with respect to a stationary observer and p is the static pressure measured with respect to an absolute reference pressure p_ref, I is the second-order identity tensor, and τ_f is the stress tensor. The density of the fluid ρ_f is assumed constant (incompressible) following the Boussinesq approximation. Values used for these quantities are given in table 1. The mesh is Eulerian and the velocity of the underlying grid v⃗_g is taken into account. In the finite volume approach variables are typically stored at discrete cell centers. A first order upwinding interpolation scheme is used to determine face values for momentum quantities. A least-square cell-based scheme is used to compute gradients at cell centers from face values. The flow pressure at faces is determined using the pressure staggering option (or PRESTO! scheme).

To solve incompressible flow, a modified form of the SIMPLE algorithm is followed. A guess pressure field is employed, then the momentum equation (2) is advanced using this guess pressure. The resulting velocity field is not divergence-free, a requirement that follows from the continuity equation (1). To make this field divergence-free the required pressure and velocity corrections are prescribed following a predetermined strategy. Instead of the original SIMPLE presciption, the PISO algorithm is employed to relate pressure and velocity corrections, with one additional iteration each for neighbor and skewness correction. The first order implicit scheme is used to discretize all time-derivatives and integrate over a time-increment.

The flow domain is meshed using tetrahedral cells. A mid-coronal cross-section of the initial mesh is shown in figure 1b. During the computation, mesh refinement in the near-glottis region is maintained by using layering and remeshing techniques. Typical edge length in this region is approximately 0.05 mm. The commercially available computational fluid dynamics (CFD) software Ansys/FLUENT is employed to solve the glottal airflow dynamics.

2.2 Vocal fold structural model

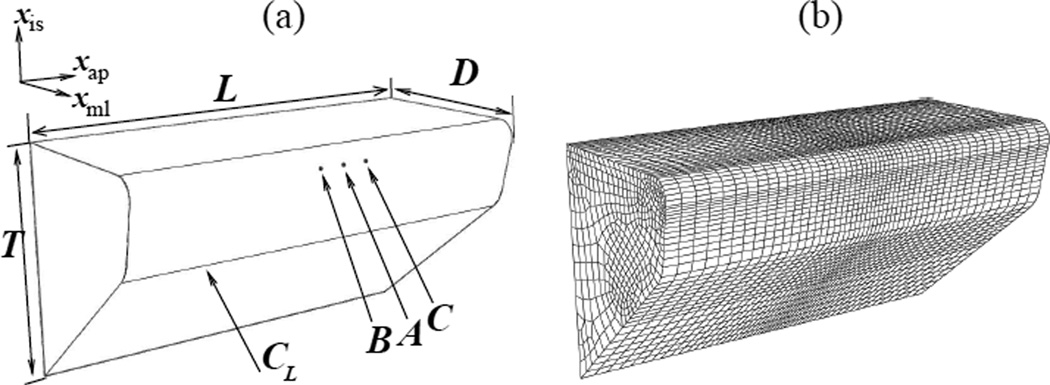
The 3D structural domain comprises a pair of VFs with identical geometry and mesh. The geometry of one of the VFs (left) is shown in figure 2a. Specific dimensions of the VF volume appear in table 2. The geometry follows the M5 canonical model (Scherer et al 2001), with the 2D VF shape pertaining to the M5 definition extruded uniformly through the length L of the VF in the anterior-posterior direction. Reference points A⃗, B⃗ and C⃗ (figure 2) are identified on the medial surface of the left VF to serve as probe locations for contact pressures during VF collision. Point A⃗ lies at (−0.740, −0.294, 0.00) mm. Points B⃗ and C⃗ are located at a distance of 1.20 mm on either side of A⃗ along the anterior-posterior direction. A point A⃗′ is identified on the right VF at (−0.740, 0.294, 0.00) mm.

Figure 2.

(a) Three-dimensional geometry of the left half of the vocal fold (VF) model. The part of the glottal surface that is expected to contact is highlighted as C_L. Locations of reference points A⃗, B⃗ and C⃗ are shown. (b) Hexahedral mesh of the VF model. Note the higher refinement near contact-prone mid-membranous location

Table 2.

Geometric dimensions and constitutive properties of vocal fold models.

Vocal Fold Dimensions		Tissue Properties (I) Well Hydrated		Tissue Properties (II) Minimally Hydrated
L	20.0 mm	E	6.00 kPa	E	6.00 kPa
D	8.40 mm	ν	0.450	ν	0.450
T	10.7 mm	ρs	1070 kg/m3	ρs	1070 kg/m3
dg	0.600 mm	τ1	0.500 s	τ1	0.100 s
dp	0.200 mm	k1, g1	0.670	k1, g1	0.100

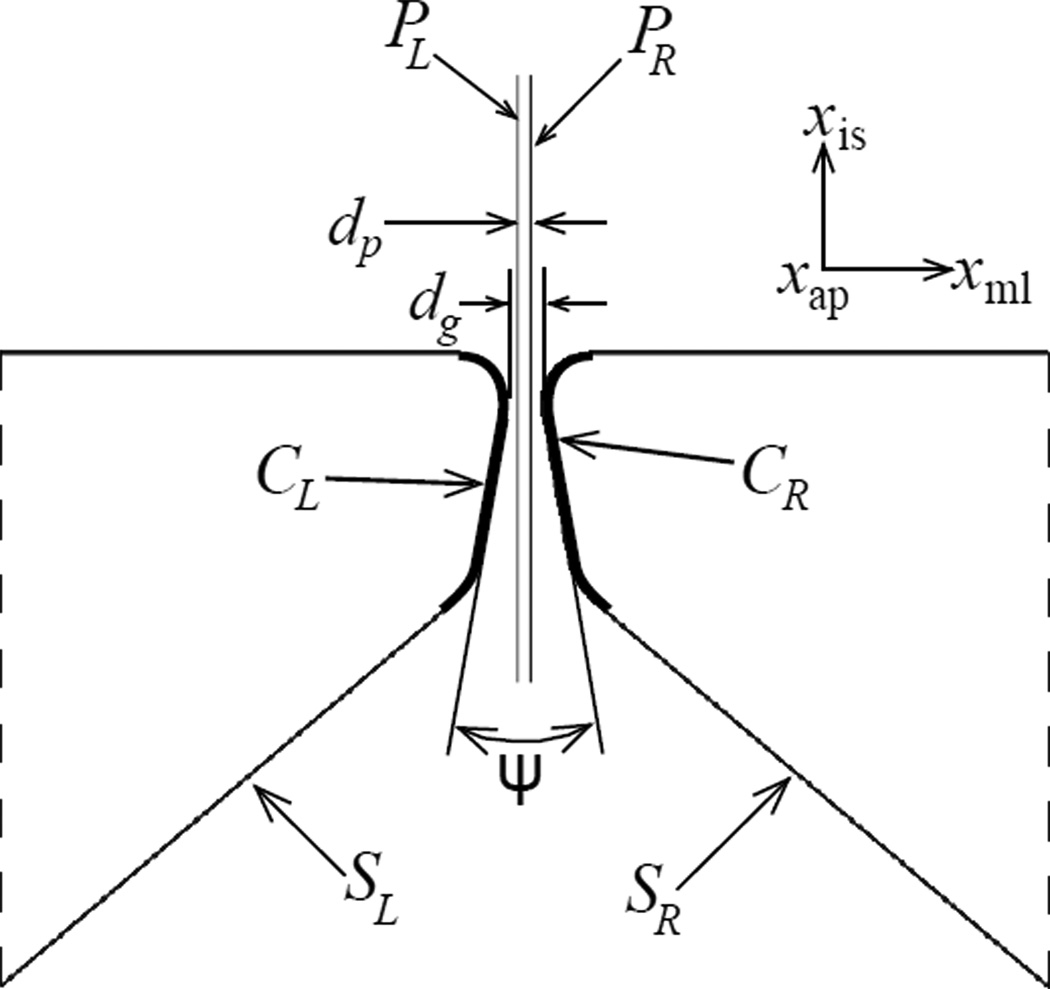
The pair of VFs are assembled as shown in figure 3. The glottal angle is ψ = −20.0° (converging) and the initial separation of the VFs is d_g = 0.600 mm. Note that W = 2D + d_g, and the VF surfaces S_L and S_R sit flush with the flow domain boundary. Parts of the VF exterior surfaces (C_L and C_R) are identified as possible contact surfaces, where the subscripts L and R correspond to left and right VF respectively.

Figure 3.

Mid-coronal cross-section showing initial configuration: rigid planes P_L and P_R separated by distance d_p, the left and right VFs separated initially by at least the gap d_g and located symmetrically on either side of the respective rigid planes, contact surfaces C_L and C_R on respective VFs, initial included glottal angle ψ and flow-structure interaction surfaces S_L and S_R defined on the respective VFs. Coordinate axes are shown offset from the origin for clarity

The structural domain equilibrium equation, in the absence of body forces, is written in the weak form of virtual-work principle as

$${\int }_{V^{\mathrm{s}}}\mathit{\sigma }:\delta {\mathbf{D}}_{\mathrm{v}}\mathrm{d}V={\oint }_{\partial (V^{\mathrm{s}})}{\overrightarrow{\tau }}_{\mathrm{s}}·\delta {\overrightarrow{u}}_{\mathrm{v}}\mathrm{d}\overrightarrow{S}-{\int }_{V^{\mathrm{s}}}{\rho }_{\mathrm{s}}\ddot{\overrightarrow{u}}·\delta {\overrightarrow{u}}_{\mathrm{v}}\mathrm{d}V.$$ (3)

All variables are expressed above in the current, or deformed, configuration. Here σ is the Cauchy stress tensor, τ⃗_s is a externally imposed surface traction, $\stackrel{\ddot{\to }}{u}$ is the local acceleration vector, δu⃗_v is a virtual displacement and δD_v is the corresponding virtual deformation gradient. Symbols ρ_s, V^s and ∂ (V^s) correspond to the density of the tissue, the deformed configuration volume and its bounding surface respectively. In the finite element approach the equation above is first discretized in space using consistent interpolation functions that relate the value of a variable at a point with values at discrete nodes.

The acceleration vector $\stackrel{\ddot{\to }}{u}$ in (3) is used to determine the displacement u⃗ using a time integration scheme. The time integration operator follows the implicit Hilber-Hughes-Taylor α-method (Hilber et al 1977), which allows for numerical damping. The small amount of numerical damping can effectively remove high-frequency noise from the solution. Damping is controlled by the parameter α = −0.41421 of the algorithm.

The commercially available finite element (FE) package ABAQUS is employed to solve the VF dynamics. Both VF volumes are meshed identically. A hexahedral element mesh (using first-order C3D8RH elements from the ABAQUS/Standard library) is used to discretize the VF volumes. Increased refinement near the contact-prone mid-membranous region is present, as shown in figure 2b.

2.3 Contact interaction model

In an ideal contact model, surfaces C_L and C_R would interact. Due to restrictions arising out of numerical algorithm implementation in FLUENT, it is required that the topology of the fluid volume remains unchanged throughout the computation. Therefore, direct contact between surfaces C_L and C_R cannot be considered. Instead, as an approximation of the true contact, a pair of auxiliary rigid planar (2D) surfaces, P_L and P_R, are defined to interact with C_L and C_R respectively. The rigid surfaces P_L and P_R are fixed in space and separated by d_p = 0.200 m. Each rigid plane is meshed identically using rigid R3D4 elements from the ABAQUS/Standard library. The element edge length is uniformly 0.606 mm.

2.4 Boundary and coupling conditions

At any point of time during the computation, the bounding surface of the VFs ∂ (V^s) can be expressed as a union of mutually disjoint surface sets

$$\partial (V^{\mathrm{s}})={[\partial (V^{\mathrm{s}})]}_B\cup {[\partial (V^{\mathrm{s}})]}_C\cup {[\partial (V^{\mathrm{s}})]}_{FSI}.$$ (4)

Here, [∂ (V^s)]_B comprises the lateral (x_ml = ±W /2), anterior (x_ap = L/2) and posterior (x_ap = −L/2) surfaces of the VF. Throughout the computation, all degrees of freedom are constrained for nodes on [∂ (V^s)]_B.

Any point x⃗ ∈ ∂ (V^s) − [∂ (V^s)]_B must satisfy the contact condition

$$|x_{\mathrm{m}\mathrm{l}}|\ge d_{\mathrm{p}}/2,\forall t\ge 0.$$ (5)

Possibly topologically disjoint regions within ∂ (V^s) − [∂ (V^s)]_B (note: ∂ (V^s) − [∂ (V^s)]_B = ∪(S_L, S_R)), for which the equality |x_ml| = d_p/2 is satisfied at a given instant, comprise the surface set [∂ (V^s)]_C referred to in (4). Thus [∂ (V^s)]_C denotes the surface region(s) in active contact, and is always a subset of ∪(C_L, C_R). The remainder of the VF bounding surfaces is denoted by [∂ (V^s)]_FSI.

The displacement condition |x_ml| = d_p/2 on [∂ (V^s)]_C implies that normal surface tractions on [∂ (V^s)]_C are unspecified with the limitation that tensile forces are not allowed. The tangential contact interaction is frictionless, i.e. shear forces are always zero on [∂ (V^s)]_C while there is no constraint on the in-plane displacement.

On [∂ (V^s)]_FSI the following surface traction boundary condition is applied

$${\overrightarrow{\tau }}_{\mathrm{s}}(t)=[-p(t+\mathrm{\Delta }t)\mathbf{I}+{\mathit{\tau }}_{\mathrm{f}}(t+\mathrm{\Delta }t)]·\mathrm{n̂},$$ (6)

where n̂ is the surface normal at a given location on the interface. The terms on the right hand side are obtained from corresponding nodes on the flow domain boundary. The dynamic compatibility condition (6) ensures momentum balance at the FSI interface.

With the above conditions imposed on the VF boundary at time step t, equation (3) can be integrated in time to obtain the displacement and stress fields throughout the VF domain at time step t + Δt. However, equation (6) requires determination of flow variables at t + Δt. The method of determination is given below.

At any time t the flow domain boundary ∂ (V^f) can be composed as a union of mutually disjoint surface sets

$$\partial (V^{\mathrm{f}})={[\partial (V^{\mathrm{f}})]}_B\cup {[\partial (V^{\mathrm{f}})]}_{C\prime }\cup {[\partial (V^{\mathrm{f}})]}_{FSI}.$$ (7)

Here, [∂ (V^f)]_B comprises the flow inlet (x_is = −T − T_entry), flow outlet (x_is = T_exit), and non-moving walls of the entry and exit channels (x_ml = ±W /2 and x_ap = ±L/2) (figure 1a). The pressure at the inlet p_in is varied with time t as

$$\frac{p_{\text{in}}(t)}{p_{\text{max}}}=\{\begin{array}{cc}{(t/T_{\text{ramp}})}^2[3-2(t/T_{\text{ramp}})]\hfill & \forall t\in [0,T_{\text{ramp}}]\hfill \\ 1\hfill & \forall t\in [T_{\text{ramp}},\infty ),\hfill \end{array}$$ (8)

where p_max = 400 Pa and T_ramp = 0.15 s. The pressure at the outlet is constant at 0 Pa. At all times, no slip and no penetration are prescribed on the non-moving walls of the entry and exit channels, i.e. v⃗ = v⃗_g = 0 on x_ml = ±W /2 and on x_ap = ±L/2.

The kinematic compatibility condition, needed to ensure that the moving–deforming regions of flow boundary (∂ (V^f) − [∂ (V^f)]_B) remain coincident with the moving–deforming regions of the VF boundary (∂ (V^s) − [∂ (V^s)]_B), is enforced using a backward difference operator in time,

$${\overrightarrow{v}}_{\mathrm{g}}(t){|}_{\partial (V^{\mathrm{f}})-{[\partial (V^{\mathrm{f}})]}_B}=\frac{{[\overrightarrow{u}(t)-\overrightarrow{u}(t-\mathrm{\Delta }t)]}_{\partial (V^{\mathrm{s}})-{[\partial (V^{\mathrm{s}})]}_B}}{\mathrm{\Delta }t}.$$ (9)

Simultaneously, no slip and no penetration condition (v⃗ = v⃗_g) is imposed on (∂ (V^f) − [∂ (V^f)]_B). Further, we define [∂ (V^f)]_FSI as that part of the flow-domain boundary which remains coincident with [∂ (V^s)]_FSI, and [∂ (V^f)]_C′ is defined by its coincidence with [∂ (V^s)]_C. It is important to note that material surface regions are exchanged between [∂ (V^s)]_C and [∂ (V^s)]_FSI over time (for e.g. [∂ (V^s)]_C = ∅ in the fully open state) and this results in corresponding exchange of surface sets between [∂ (V^f)]_C′ and [∂ (V^f)]_FSI.

With the above boundary conditions on the flow domain (requiring solid domain solution u⃗ only at instants t and t − Δt), equations (1) and (2) are integrated to obtain flow velocity and pressure at time step t + Δt. The surface traction (−pI + τ_f) · n̂ at t + Δt is then computed and substituted back into (6). This updates the solid domain solution to t + Δt. Using the solid domain solution at instants t and t + Δt in (9) to obtain v⃗_g (t + Δt) on ∂ (V^f) − [∂ (V^f)]_B the flow solution can be obtained at step t + 2Δt. The time integration of the coupled domain proceeds accordingly.

Equations (6) and (9) define the weak-coupling approximation employed in the present model. The surface traction (−pI + τ_f) · n̂ at t + Δt is used to compute the surface traction τ⃗_s at t. As a result of staggered approach, the displacement of the solid domain boundary is ahead of the fluid domain boundary by a single increment. The error introduced due to the mismatch in displacements is considered to be small compared to the magnitude of the total displacement integrated over time. The coupling software MpCCI is used to effect the transfer of solution variables between ABAQUS and FLUENT. The time-increment used to integrate the balance equations in both FLUENT and ABAQUS is identical to the solution exchange increment used by MpCCI. In the present computation a constant increment Δt = 0.020 ms was used.

2.5 Constitutive relationships

The constitutive relation for the fluid (air) follows a Newtonian incompressible fluid prescription,

$${\mathit{\tau }}_{\mathrm{f}}=\mu [\nabla \overrightarrow{v}+{(\nabla \overrightarrow{v})}^T],$$ (10)

where μ is the dynamic viscosity. Properties of air corresponding to STP are used (table 1).

For the VF tissue a viscoelastic constitutive relation is used to define the stress-strain response,

$$\mathit{\sigma }(t)={\int }_0^{t}2G(t-t\prime )\mathit{ė}\mathrm{d}t\prime +\mathbf{I}{\int }_0^{t}K(t-t\prime )\mathrm{\epsilon ̇}\mathrm{d}t\prime ,$$ (11)

where e is the deviatoric part of the strain, and ε is the volumetric part. The second-order identity tensor is denoted by I. Functions G and K correspond to time-dependent shear and bulk moduli defined by a single-term Prony series

$$G(t)=\frac{E}{2(1+\nu )}[1-g_1+g_1\text{exp}(-t/{\tau }_1)],K(t)=\frac{E}{3(1-2\nu )}[1-k_1+k_1\text{exp}(-t/{\tau }_1)],$$ (12)

where E is the instantaneous small-strain elastic modulus of the VF tissue. The properties E, g₁, k₁ and τ₁ are given numerical values such that the single-phase viscoelastic VF tissue behaves similar to a biphasic material as considered by Zhang et al (2008). The Poisson’s ratio of the VF tissue ν is given a value close to the incompressibility limit of 0.50, and its density ρ_s is set close to that of water at STP (table 2).

In Zhang et al (2008) the stress within VF tissue – defined as a one-dimensional (1D) linear biphasic material of initial length L – due to an applied displacement at one end

$$u(L,t)={\epsilon }_0\{\begin{array}{cc}t/T_0,\hfill & 0\le t\le T_0=0.01\mathrm{s}\hfill \\ 1,\hfill & t\ge T_0,\hfill \end{array}$$ (13)

while the other end is fixed (u(0,t) = 0) is given by

$$\sigma (t\ge T_0)=\frac{H_A{\epsilon }_0}{L}+\frac{H_A{\epsilon }_0}{L}\left[2e^{-{\pi }^{2}k{H}_{A}t/L^2+{\pi }^{2}k{H}_B}\right(\frac{L^2}{T_0{\pi }^{2}k{H}_A})\times (1-\frac{{\varphi }^f}{{\varphi }^s}\frac{{\pi }^{2}k{H}_B}{L^2+{\pi }^{2}k{H}_B}\left)\right(e^{T_0{\pi }^{2}k{H}_A/L^2+{\pi }^{2}k{H}_B}-1\left)\right],$$ (14)

where only the first term is retained for the sake of simplicity. Here, H_A = λ_s + 2μ_s and H_B = (λ_f + 2μ_f) (ϕ^s/ϕ^f)² are respectively the moduli of the solid and fluid phases in terms of the usual elastic constants (solid) and viscosity coefficients (fluid), ϕ^s and ϕ^f are the volume fractions of the solid and fluid phases respectively and k is the hydraulic permeability of the solid phase. For water, λ_f = −2μ_f /3 (Schlichting 1989).

For the displacement condition (13), the stress on a VF tissue defined as an equivalent single-phase viscoelastic solid is found by integrating (11) to be

$$\sigma (t\ge T_0)=\frac{E{\epsilon }_0}{L}[1-k_1+(\frac{k_1{\tau }_1}{T_0})(e^{T_0/{\tau }_1}-1)e^{-t/{\tau }_1}].$$ (15)

Expressions (14) and (15) are equivalent under two limits. In the first case, assuming a fluid volume fraction typical of a well hydrated VF tissue ϕ^f = 70% (Hanson et al 2010; Phillips et al 2009), with hydraulic permeability k in the range given in literature (Zhang et al 2008; Tao et al 2009), and L equal to the VF length (as in table 2), it follows that π²kH_B ≪ L². This limit is modeled by parameters of model I (table 2). In the second case, assuming a minimally hydrated VF tissue ϕ^f → 0, it follows that π²kH_B ≫ L². Model II property values in table 2 simulate VF tissue in this limit.

A detailed and fundamental treatment of accuracy concerns regarding various parts of the computational FSI model can be found in appendix C.

3. Results

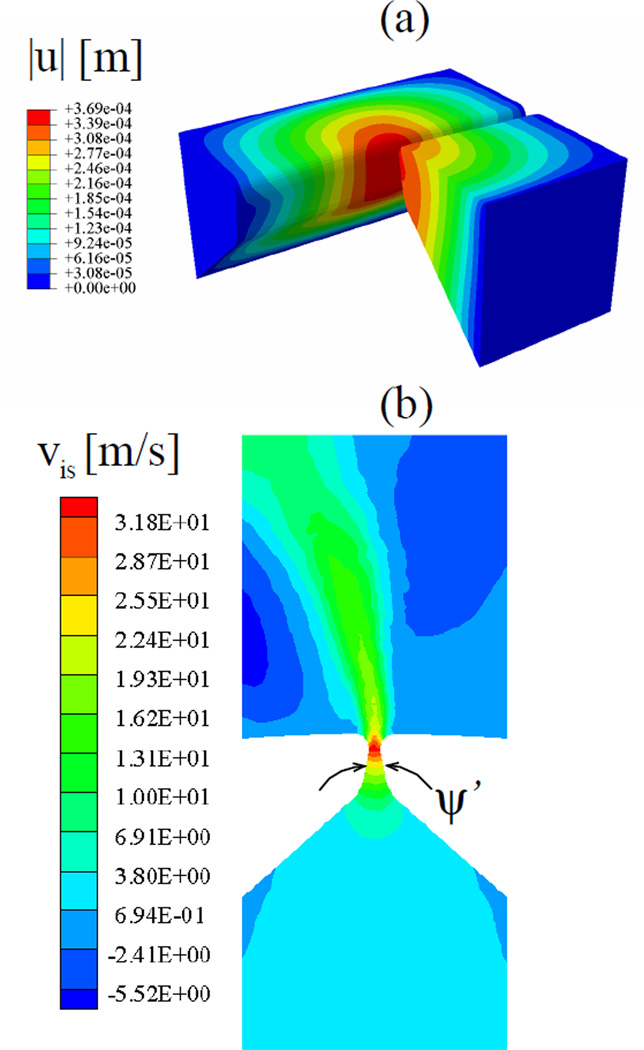
It must be noted that the time-independent elastic modulus E and Poisson’s ratio ν of the VF tissue is identical for models I and II. Therefore both models have identical in vacuo eigenfrequencies, the first of which is 47 Hz. However, in the FSI computations, the frequency of vibration is an outcome of the coupled model, and differences are expected between the models. Computational results are presented first for the computation with tissue parameters representing a hydrated tissue (model I). An FSI computation over a physical duration of 286 ms is presented.¹ During the ramp phase, the VFs deform from their rest state, thereby bulging upward (figure 4a). The overall mean deformation of the VFs are nearly symmetric to each other. Vibrations (in t ≥ T_ramp) occur around this mean state.

Figure 4.

At t = T_ramp (model I): (a) contours of displacement magnitude corresponding to the mean deformed shape, (b) contours of inferior-superior component of glottal airflow velocity on the mid-coronal section.

Figure 4b depicts a typical flow field in the mid coronal section of the model I before vibration onset. Considering the mid-coronal section in the mean deformed state (figure 4a), the included angle between the VFs is ψ = 20.8°, only slightly increased when compared to the rest state (ψ = 20.0°). Flow measurements over a large range of included glottal angles with rigid models having M5 geometries were reported in Fulcher et al (2010). These authors suggests that for a converging case of ψ = 20.0°, the flow pressure near location A⃗ (the glottal exit) is less than that at the flow domain outlet. The pressure difference between glottal exit and outlet is about 10% of the pressure difference between the inlet and outlet. Therefore, the maximum pressure drop occurs between the inlet and glottal exit and is approximately 1.1p_max. Bernoulli’s theorem is expected to be valid up to the glottal exit, which is close to the site of flow separation that results in the glottal jet. Thereby, the approximate relation holds,

$$1.1p_{\text{max}}\approx \frac{1}{2}{\rho }_{\mathrm{f}}(q_2^2-q_1^2),$$ (16)

where q₁ and q₂ are average flow speeds through the inlet and glottal exit sections respectively. Mass continuity dictates that the mass flow rate at every cross-section perpendicular to the streamwise direction must be identical,

$$ṁ={\rho }_{\mathrm{f}}{A}_1{q}_1={\rho }_{\mathrm{f}}{A}_2{q}_2,$$ (17)

where A₁ and A₂ are the respective cross-section areas at the inlet and glottal exit. The mean opening between the VFs at mid-coronal plane d̄ ≃ 2|x_ml (A⃗)| = 0.732 mm. Thereby A₂ can be approximated as Ld̄, assuming a rectangular opening. Using (16) and (17), it can be shown that

$${ṁ}^2=\frac{2{\rho }_{\mathrm{f}}(1.10p_{\text{max}})A_1^2{A}_2^2}{A_1^2-A_2^2}$$ (18)

relating the mean mass flow rate with the inlet pressure. The estimated mean mass flow rate from this simple model is 0.480 g/s.

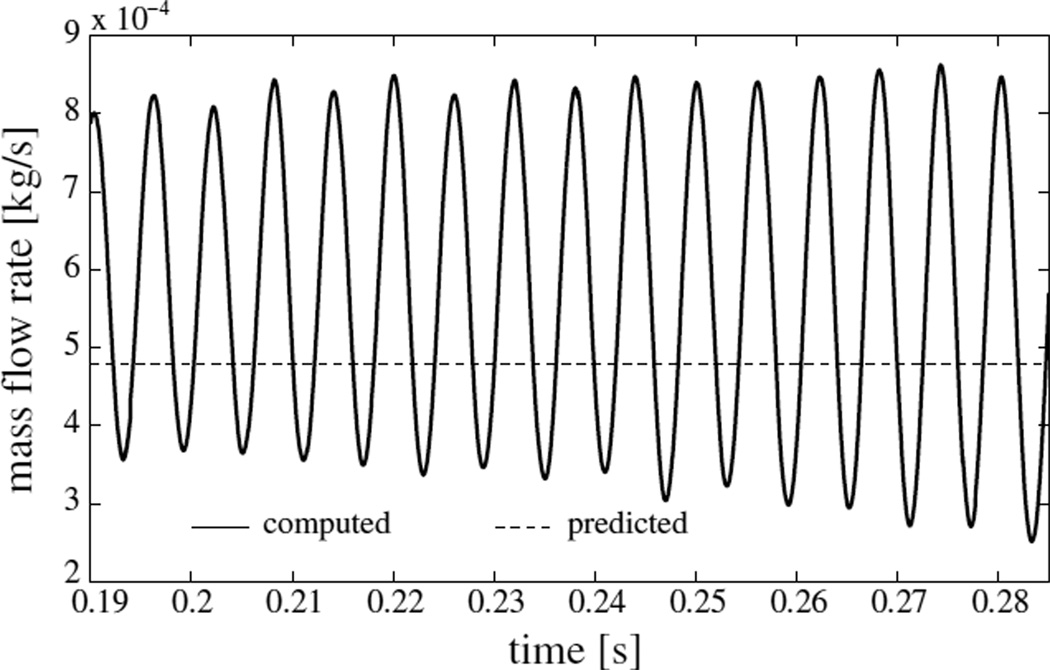
The computed mass flow-rate at the inlet in dependence of time is shown in figure 5. The computed mass flow rate averaged over the cycles shown is ṁ_computed = 0.575 g/s. The corresponding computed average volume flow rate of 471 ml/s. While the Reynolds number varies with time, the average mass flow rate based Reynolds number is Re = ṁ_computed/Lμ ~ 1600. The peak centerline velocity component in the x_is direction was found to be ~ 31 m/s.

Figure 5.

Comparison of computed mass flow rate in dependence of time (solid line) and its predicted mean value using Bernoulli’s theorem (16) (dashed line) for model I

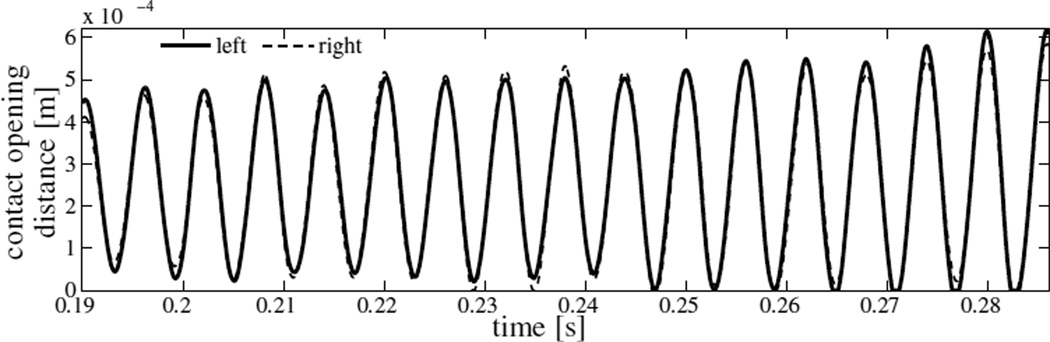
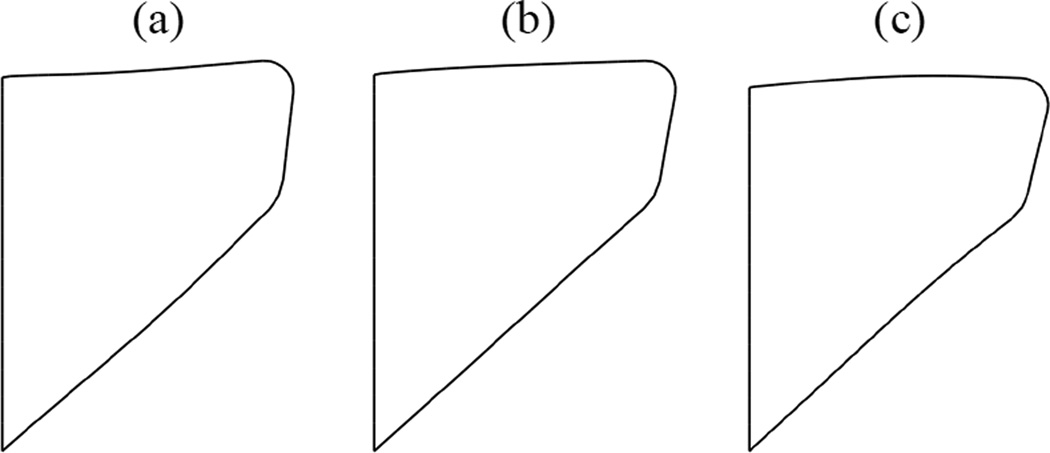
The post-ramp motion of the VFs develops in time to be soon dominated by a single frequency oscillation. This is also evident from the fluctuations in flow rate shown in figure 5. The time variation of distance between point A⃗ on the left VF and the plane P_L is plotted in figure 6 for t ≥ 0.19 s. The three-dimensionality of the computed flow is evident in figure 6. Slight differences between the medial-lateral motion of the left and right VFs are perceptible which can be attributed to the unequal distribution of flow pressure on the left and right VFs. The frequency of vibration is deduced by considering time elapsed between successive peaks in time history and is found to be 167 Hz. The frequency remains nearly constant throughout the computation (SD 1.16%). At three instants of a collision-free vibration cycle, in particular, at t = 0.19626 s, 0.19772 s and 0.19920 s, the mid-coronal sections of the left VF are shown in figure 7. These instances correspond to, respectively, the maximum open state, the mean state, and the least open (or closed) state. Approximating the motion of the right VF to be symmetric, the corresponding included glottal angles (ψ) at these instants are 13.1°, 20.1° and 26.9°, respectively. Though the glottal angles remain convergent, there is significant change in the degree of convergence over the vibration cycle. The amplitude increases with time such that after some cycles it is large enough to result in collision. As seen in figure 6, collision becomes well-established in the cycle beginning at t = 0.27986 s.

Figure 6.

Contact opening distance in dependence of time (model I): solid line, at reference point A⃗ on left vocal fold; dashed line, at point A⃗′ on right vocal fold

Figure 7.

Glottal angle changes during each phonatory cycle (model I). Deformed shapes of the mid-coronal section at three different instants corresponding to: (a) maximum open state at t = 0.19626 s, (b) mean state at t = 0.19772 s and (c) maximum closed state at t = 0.19920 s.

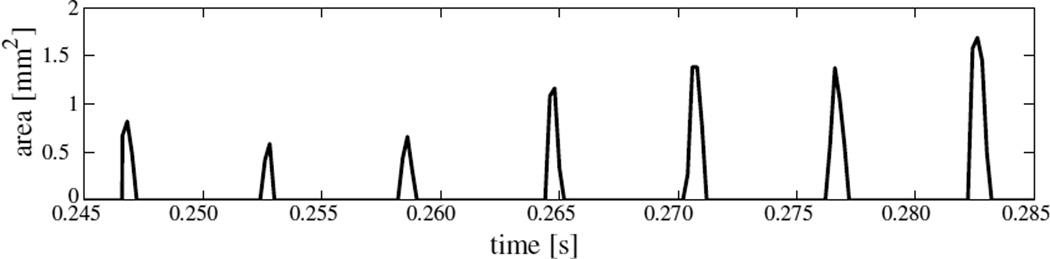
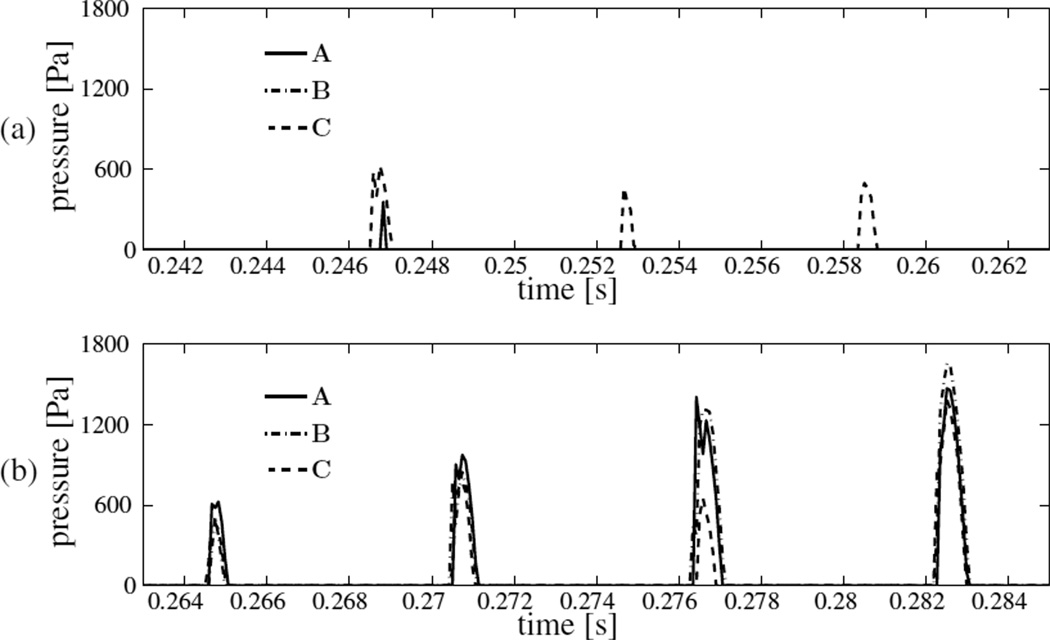
Figure 8 shows the time variation of the area of the left VF under contact for seven consecutive collision cycles. The three-dimensionality of the airflow noted earlier includes an anterior-posterior asymmetry in VF deformation, and thereby VF collision. The asymmetry also causes different contact pressures at B⃗ and C⃗. Contact area being a global measure does not capture this asymmetry, but is seen clearly in the contact pressure history figure 9. The asymmetry develops over subsequent cycles, in that the location of contact pressure peak within a cycle changes between A⃗, B⃗ and C⃗. The within-cycle peak contact pressure computed at A⃗ is found to be between 0.3 kPa and 1.5 kPa. The duration within which the left VF contacts with the plane P_L at A⃗ (in each cycle) – when expressed as a percentage of the cycle time – is at most 13.4%. This corresponds to an open quotient of at least 86.6%.

Figure 8.

Time history of area of the left VF rigid plane P_L during seven consecutive collision cycles (model I)

Figure 9.

Time history of contact pressures (model I) predicted at locations A⃗, B⃗ and C⃗ of the left VF through (a) three consecutive collision cycles, and (b) four subsequent cycles

Hydrostatic stress is defined

$${\sigma }_H=\frac{1}{3}{\sigma }_{kk},$$ (19)

where σ_ij is the Cauchy stress tensor σ written in the Einstein notation. The repeated index in (19) denotes a summation. Biot’s poroelastic theory (1941) specifies that the solid and fluid constituents of the poroelastic VF tissue exert an equal, opposite and non-zero force on each other. The theory employs Darcy’s law to relate this non-zero force, given by the gradient of hydrostatic stress, to the interstitial fluid flux

$$\overrightarrow{q}\propto \mathbf{\nabla }{\sigma }_H,$$ (20)

where q⃗ is the flux vector of the interstitial fluid. Instantaneous interstitial fluid flux fields are determined, and transport of pore fluid over time due to its motion is neglected. Thereby, local hydraulic permeability and fluid volume fraction are assumed constant, and can be absorbed into any multiplicative constant associated with (20).

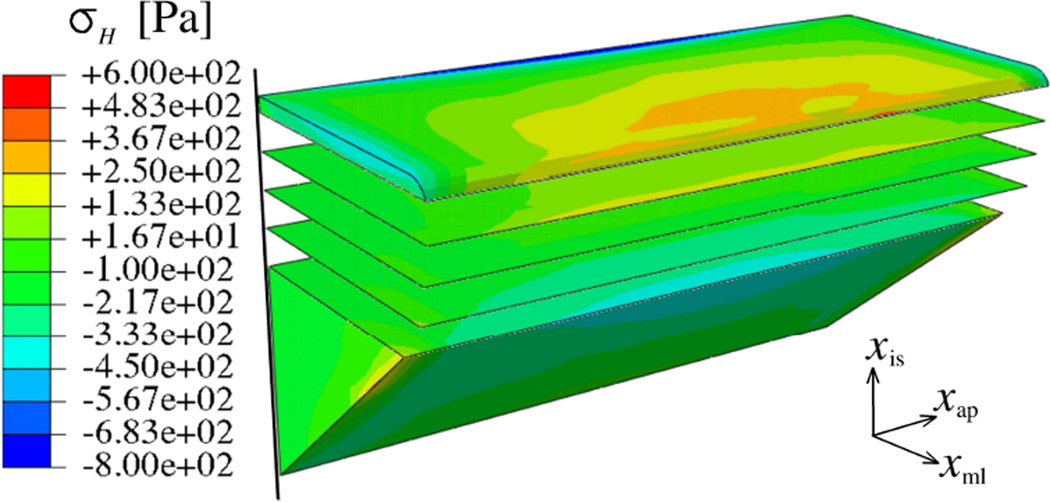
With respect to figure 6, consider one typical vibration cycle free of collision (from t = 0.19626 to t = 0.20212) and one vibration cycle with fully developed collision (from t = 0.27986 s to t = 0.28578 s). The distribution of hydrostatic stress at t = 0.19772 s, i.e. the mean vibration state, is shown in figure 10. The contours of σ_H are given at several inferior-superior cross-sections of the left VF. It is found that the levels of σ_H are rather independent of the anterior-posterior location in the VF, and thus anterior-posterior gradients are small. This is in contrast to the distribution of the hydrostatic stress on the medial-lateral plane.

Figure 10.

At t = 0.19772 s (model I), distribution of hydrostatic stress on several transverse planes (1 mm intervals)

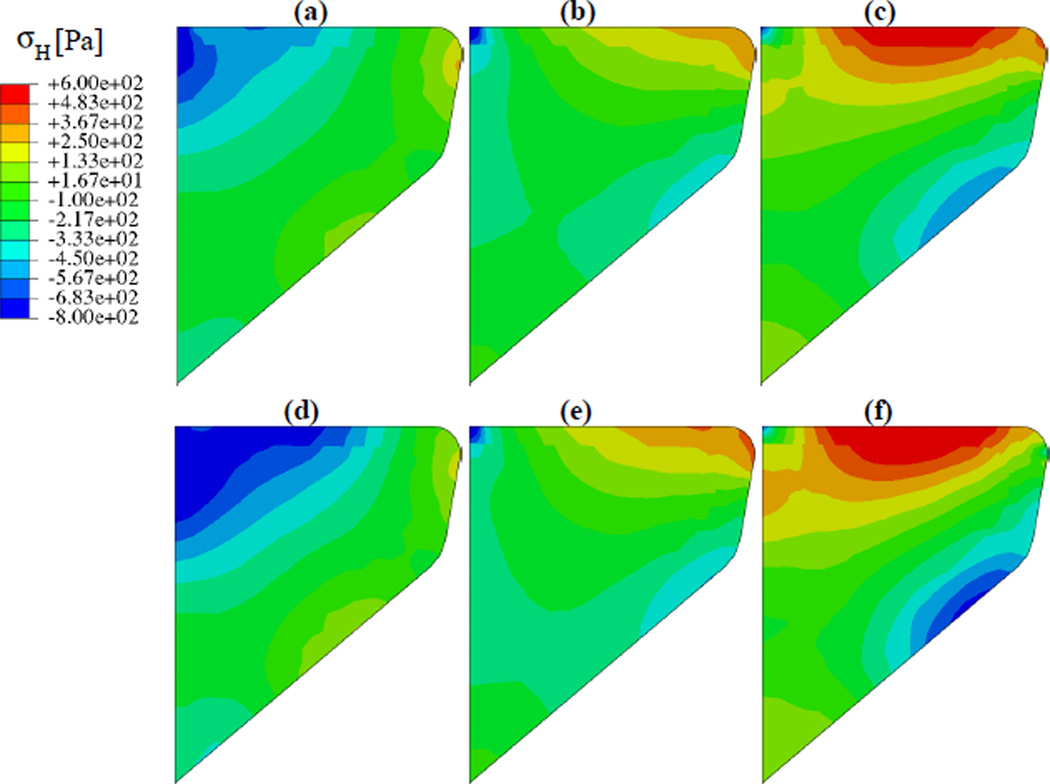
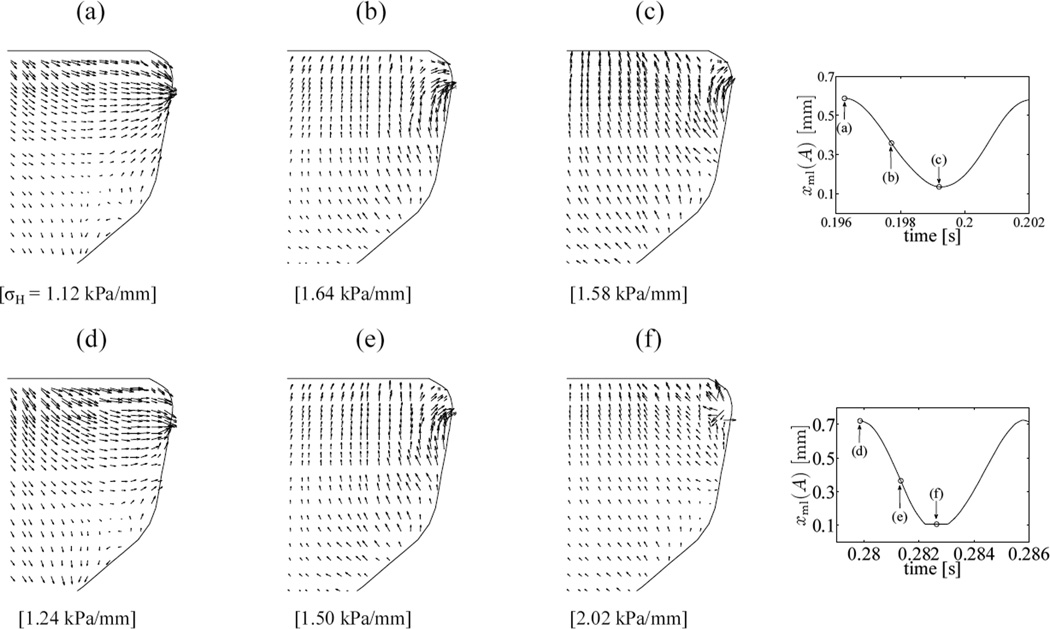
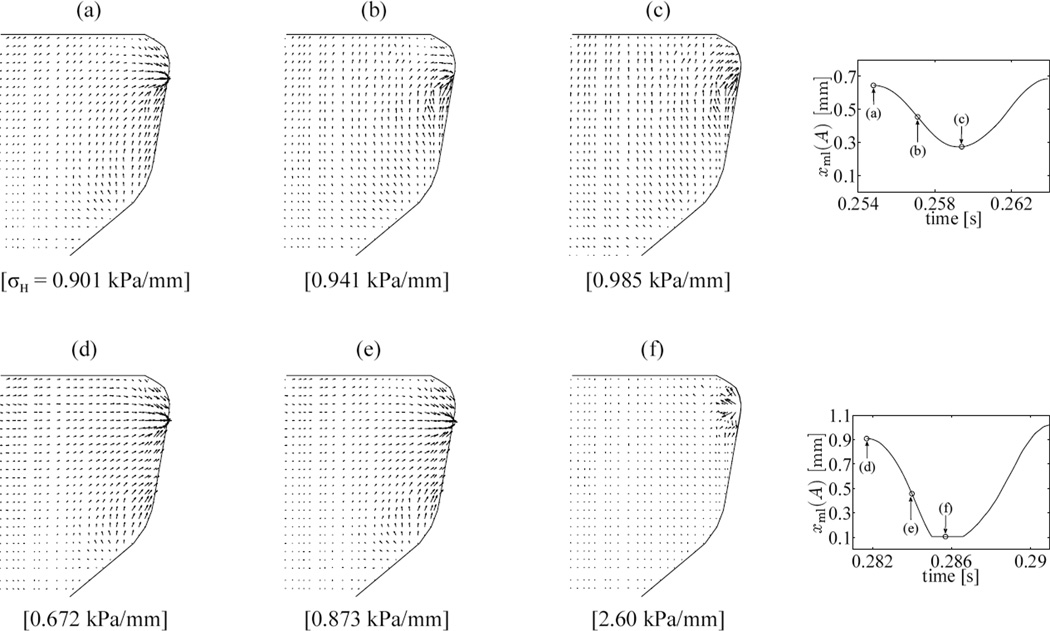
Figure 11a–c show the distribution of hydrostatic stresses on the mid-coronal plane at the maximum open, mean, and closed states of the free-vibration cycle (t = 0.19626 s, 0.19772 s and 0.19920 s). Figure 11d–f shows hydrostatic stress contours on the mid-coronal plane at corresponding states of the cycle with VF collision: maximum open at t = 0.27986 s, mean state at 0.28134 s, and closed at 0.28264 s. The hydrostatic stresses change significantly over the mid-coronal plane. Local hydrostatic stress gradients ∇σ_H, proportional to interstitial flux vectors q⃗, are visualized over a selected region of the mid-coronal plane (figure 12) close to the VF medial surface. The anterior-posterior component of ∇σ_H and q⃗ are neglected in the following as their magnitude is significantly less than that of the in-plane gradient. For each instant considered, the maximum of the vector magnitudes is used to normalize the hydrostatic stress gradient vectors at the given instant. The vectors also represent normalized instantaneous interstitial fluid flux vectors at the corresponding time instants. In figures 12a–c, the largest gradient vector is always directed towards the medial surface, and its magnitude changes by about 46 % between its maximum and minimum values during the cycle. It is thereby inferred that the predominant gradient is caused by the mean deformation of the VF. Indeed, this large gradient is substantial in the mean states of both the vibration and collision cycle (figures 12b,d). Comparing the open and closed states of the cycle without contact (figures 12a,c), a secondary interstitial fluid flux is apparent. This flux is aligned approximately along the inferior-superior axis and switches sense every half-cycle. In the open state, the superior surface is in relative compression, and this directs the interstitial fluid inferiorly. The situation is reversed in the closed state, and flux vectors point superiorly. This secondary fluid flux is understood to be associated with vibration. Comparing figures 12a,d the arrows directed away from the superior surface are found to be larger in the collision cycle case. This is expected since the amplitude of vibration is larger in the collision cycle, causing the magnitude of the secondary flux (relative to the rather constant mean flux) to be larger during the collision cycle. Figure 12f shows a strong tertiary interstitial fluid flux. This flux is associated with VF surface collision, which modifies the hydrostatic stress state locally. This interstitial fluid flux component is large in magnitude (about 63 % larger than the maximum flux in the open state) directed opposite to the primary fluid flux direction, i.e. away from the medial surface during collision. The influence is limited spatially to within a zone surrounding the location of collision (see figure 12c,f), and temporally to within the duration the particular location is in contact. Outside this spatio-temporal zone interstitial fluid flux characteristics resemble those of a free-vibration cycle.

Figure 11.

Hydrostatic stress contours on the mid-coronal plane (reference configuration) in model I: (a–c) open, mean and closed instants in free-vibration cycle starting at t = 0.19626 s; (d–f) open, mean and closed instants in cycle with collision starting at t = 0.27986 s. Note contour levels are identical to those in figure 10

Figure 12.

Instantaneous vectors of hydrostatic pressure gradients on mid-coronal plane for model I (reference configuration). Vector lengths are normalized by the maximum gradient magnitude of each subplot. (a–c) Open, mean and closed instants in free-vibration cycle starting at t = 0.19626 s. (d–f) Open, mean and closed instants in cycle with collision starting at t = 0.27986 s. Values in braces indicate the magnitude of largest instantaneous hydrostatic stress gradient

Results from the FSI simulation considering properties of a minimally hydrated tissue (model II) are presented below. Only some select variables are detailed herein that emphasize the contrast with respect to the hydrated tissue (model I). The mean opening between the VFs at the mid-coronal plane and the mean mass-flow rate are d̄ = 0.852 mm and ṁ_computed = 0.676 g/s respectively. The frequency of vibration for model II is 108 Hz, the peak contact pressures are in the range 0.5–2.0 kPa and open quotients are at least 75.5 %.

The hydrostatic stress gradient derived interstitial fluid flux vectors are considered at instants 0.25480 s, 0.25710 s and 0.25940 s that represent fully open, mean and maximum closed states respectively within a collision-free vibration cycle of model II. For respective states within a cycle with collision, instants 0.28170 s, 0.28400 s and 0.28570 s are considered. The normalized interstitial fluid flux vectors are shown in figure 13(a)–(c) and (d)–(f) respectively for the collision-free cycle and the cycle with collision. The cycles are selected such that the amplitudes of vibration about the mean are comparable to those in corresponding cycles in figure 12 (model I).

Figure 13.

Instantaneous hydrostatic pressure gradients on mid-coronal plane for model II (reference configuration). Vector lengths are normalized by the maximum gradient magnitude of each subplot. (a–c) Open, mean and closed instants in free-vibration cycle starting at t = 0.25480 s. (d–f) Open, mean and closed instants in cycle with collision starting at t = 0.28170 s. Values in braces indicate the magnitude of largest instantaneous hydrostatic stress gradient

Comparison of figures 12 and 13 indicate that the overall fluid flux directions were not altered by changing the tissue properties. However, significant changes in the spatial distribution of flux magnitudes are found. For the free vibration conditions, the magnitude of flux is significantly reduced for all instances considered (−19 %, −42 %, −37 % for the open, mean and closed states, respectively), with the strongest reduction occurring at the mean state. Furthermore, the flux magnitudes are less equally distributed spatially in the minimally hydrated state with the highest flux rates highly concentrated closely to the medial plane.

For the vibration conditions with contact, the magnitude of flux strength is reduced for the open and mean instances only (−45 %, and −42 %, respectively), but is increased (+28 %) for the contact instance. Again, the flux magnitudes are found to be are less equally distributed spatially in the minimally hydrated state with the highest flux highly concentrated closely to the medial lateral plane. This finding is especially true for the contact state where the local flux away from the medial plane highly dominates.

4. Discussion

The present study documents FSI computations of VF vibrations under realistic conditions. For computations considering a hydrated tissue (model I), the average mass flow rate based Reynolds number was found to compare well with Re ~ O(10³) measured in physical experiments (Alipour and Scherer 1995; Cranen and Boves 1985; Triep and Brücker 2010). The computed peak centerline velocity component in the xis direction is typical of measured values in experiments (Erath and Plesniak 2006; Pelorson et al 1994). The computed average volume flow rate is well within the 80 – 750 ml/s range measured in experiments using excised larynges and physical replicas of VFs (Alipour and Scherer 1995; van den Berg et al 1957; Cranen and Boves 1985; Erath and Plesniak 2006, 2010; Triep et al 2005) and computed using numerical models (Scherer et al 2001; Thomson et al 2005; Triep and Brücker 2010). The three-dimensional development of the computed glottal jet was also observed in experiments (Krebs et al 2012; Triep and Brücker 2010). The frequency of vibration as computed falls within the range of realistic phonation frequency (George et al 2008; Morris and Brown Jr. 1996; Titze 2006; Zhang et al 2006). The vibration amplitude is in the range of measured values (Alipour et al 2001; Baer 1981; George et al 2008). The computed peak contact pressures were in the range of measured (Gunter et al 2005; Jiang and Titze 1994; Spencer et al 2006; Verdolini et al 1999) and computed values (Chen 2009; Gunter 2003; Horáček et al 2005). The computed open quotients were at the higher end of the 28 – 93% range observed in experiments (Hanson et al 1990; Henrich et al 2005; Verdolini et al 1998). For the minimally hydrated tissue condition (model II) the above variables were also found to be within the range of values measured in experiments. However, it was evident that a change in the underlying tissue characteristics could result in significantly different vibration characteristics even when the airflow conditions were kept identical. In particular, it was found that a minimally hydrated VF tissue vibrated with a lower frequency than the well hydrated tissue. The mean opening between the VFs during vibration was also higher for the minimally hydrated case, which perhaps explains the higher mean volume air flow rate through the glottis compared to the hydrated case.

The average air flow rate, which remains constant post ramp, was compared with Bernoulli’s approximation for steady flow. The flow during free-vibration and collision cycles is not steady in a strict sense. However, the so-called quasisteady approximation has been found to hold for the glottal air-flow (McGowan 1993). The quasisteady approximation states that the instantaneous flow field though a vibrating glottis is not significantly altered if the deformation of the glottis is frozen in time. The physical implication of the approximation is that at any instant the constriction in the glottal channel provides a larger flow acceleration relative to the time- dependent VF motion. Mathematically, this means that the time-derivative of velocity potential in the unsteady Bernoulli equation (Batchelor 2010) is relatively small compared to the other terms. The 18.0 % difference between the computed and approximated values of average flow-rate is possibly due to the fact that the unsteady effects are not entirely negligible.

Coupled flow-structure interaction problems can be classified in terms of their coupling strength. The coupling strength can be loosely understood as a measure of the influence of the flow-structure interaction on the overall behavior of either domain. The problem of a flag fluttering in the wind is a highly coupled problem (Argentina and Mahadevan 2005). Ignoring the flow-structure interaction changes the outcome in each domain. The “added mass” concept is a well-known measure of coupling strength (van Brummelen and Geuzaine 2010; Förster et al 2007; Zhang and Hisada 2004). It has been noted that due to the added mass effect, numerical solutions of highly-coupled interaction problems using the staggered approach with segregated solvers are susceptible to numerical instability. A variety of factors, viz. density ratio of structure and fluid, material viscosity and stiffness, size of time increment, affect the stability of computing a coupled FSI problem. In fact, if the fluid is incompressible, a segregated problem will always become unstable in a finite number of time increments (Förster et al 2007). The instability in the computed FSI solutions presented in this paper cause the fluctuation amplitude of displacement and stresses to grow with time for both cases considered. This limitation is inherent in a segregated approach. In an ideal case, a finite but stable amplitude of vibration is likely to be observed. However, in the present case the instability is weak. A rough estimate of the amplitude growth rate can be obtained from figure 6. The amplitude of vibration (about the mean distance ~ 0.25 mm) for the first cycle is ~ 0.2 mm. Assuming the mean to be identical for the last cycle the fluctuation amplitude is ~ 0.37 mm, i.e. and increase of ~ 1.8 times over 15 vibration cycles. Therefore, on an average, the amplitude of vibration increases by ~ 3.9% between subsequent cycles. The time-constant associated with this growth rate is much smaller than the vibration period. As the VF vibration amplitude increases, the fluctuation in the flow rate is also found to increase, at a rate which is indistinguishable from the rate of increase of VF vibration amplitude. This implies that flow rate fluctuation remains linearly proportional to the VF vibration amplitude. Further, throughout the computation the average flow rate and mean VF vibration amplitude remains steady. It can be argued that the present computation determines the state of stress in an experimental model with identical geometry, material properties and average flow rate. Such a determination is possible by selecting a particular computed cycle for which the flow-rate fluctuation amplitude matches the experimentally measured flow-rate fluctuation amplitude. For this specific computed cycle, the VF motion would match that of the experiment. The state of stress corresponding to this particular cycle is hence physically relevant.

The problem of unstable response is also relevant because the onset of phonation is in itself a instability event. Phonation onsets when the transglottal pressure difference goes above a certain value. This value, or phonation threshold pressure (PTP), is a function of the dynamical system (tissue properties, geometry, boundary conditions, etc.). Although in the VF FSI problem the density ratio of structure and fluid and structural stiffness are favorable in mitigating the role of numerical instability, it is difficult to reliably predict physical instability (onset) in the presence of numerical instability. Therefore the phonation onset problem is not addressed in this paper. This is not a shortcoming because the phonation onset problem is independent of the problem of determining stresses that develop in a readily self-oscillating VF post the onset. For transglottal pressure difference above PTP, the frequency and amplitude of vibration in self-oscillation are not externally imposed conditions; rather they appear as part of the solution. This is highlighted in the present computations where the two models considered have significant differences in frequencies of vibration and average deformation, although their in vacuo eigenfrequencies based on the instantaneous elastic properties are identical.

The FSI computation framework employed in this paper allows for detailed determination of the spatial and temporal evolution of stresses in the interior of the VFs. In particular, hydrostatic stresses and their gradients are considered. The poroelastic nature of VF tissue motivates the use of hydrostatic stress gradients to determine the flux at which interstitial fluid flows relative to the solid matrix. Distribution of hydrostatic stress at three representative instants (corresponding to open, mean and closed states) of free-vibration cycles and collision cycles were presented for the two VF tissue characteristic states (well hydrated and minimally hydrated). These results underline the following implications on the interstitial fluid flux within the VF tissue:

1. Interstitial fluid flux along a coronal plane is typically stronger that out of it. This is because the hydrostatic stress gradients in the anterior-posterior direction were found in general to be weaker compared to those in the mid-coronal plane.

2. Within the mid-coronal plane, the sense of the gradient in the mean state dictates that interstitial fluid is driven strongly and continuously towards the medial surface of the folds. This is likely to hold for other nearby coronal planes as well, as gradients of hydrostatic stress in the anterior-posterior direction are small.

3. A secondary interstitial fluid flux is aligned approximately along the inferior-superior axis and switches sense every half-cycle. The strength of this flux scales with the magnitude of vibration around the mean state. It aids in the uniform distribution of interstitial fluid throughout the VF volume.

4. A tertiary interstitial fluid flux results from collision at the VF surface. The collision-induced flux operates only within a zone surrounding the location of collision (see figures 12c,f and 13c,f), and while the particular location is in contact. This flux component is directed against the mean deformation induced primary flux.

The degree of severity of collision can be quantified through the extent of the spatiotemporal zone of influence of reversed interstitial fluid flux, and also the magnitude of change in stress caused by collision. The extent of the spatio-temporal domain of influence of collision is in turn determined by the specific phonation conditions. For example, by changing the initial pre-phonatory distance between the VFs, the fraction of cycle-time for which contact occurs and the spatial depth of influence is modified, while keeping vibration amplitude and mean deformation constant. Open quotients smaller than those computed in this paper, and well-within the experimentally observed range, can be expected to result in more severe collision. The effect of moderate collision (as considered here) on the interstitial fluid flux is strong relative to the mean flux. Collision can thereby be expected to play an effective role in removing fluid from the medial surface.

The differences between figures 12 and 13 highlight the effect of tissue viscoelastic properties, and thereby its hydration state. Specifically comparing the maximum open state in the collision-free cycles in figures 12a and 13a, respectively, it is observed that the increase in stress gradient magnitude near the medial surface as compared to the rest of the mid-coronal section is even higher in the minimally hydrated than in the well hydrated state. This is true in general for other states when the mid-coronal section is not in active contact. In the minimally hydrated state collision-induced stresses are seen to play a stronger role in further dehydrating the VF tissue compared to the well hydrated state. A plausible biomechanical implication is that low hydration of VF tissue can lead to even higher levels of dehydration leading to potential tissue damage. Such implications could be investigated in future through carefully designed experiments. Although it is not reasonable to draw definitive conclusions regarding VF biomechanics based solely on present computations, it must be emphasized that specific quantitative comparisons such as the above can only be made by conducting FSI computations presented herein, and cannot be determined from simplified models considering gross pressure differences in the system.

The interstitial fluid flux in Darcy’s equation (20) is, strictly speaking, proportional to the gradient of that part of the total hydrostatic stress (σ_H) which is supported by the fluid constituent. The fluid-supported hydrostatic stress, as fraction of the total stress, changes with time. Therefore, it can be argued that the proportionality in (20) includes a time-dependent factor. Indeed, in Zhang et al (2008) it was shown that this time-dependence is given by an exponential decay (see figure 7 in Zhang et al 2008). The time-constant for the exponential decay is given by τ₁, whereas the time period of vibration is 1 / f. For models I and II the ratio of the time-scales 1 / (fτ₁) is 1.20 % and 9.26 % respectively. This ratio is representative of the percentage decay in fluid-supported stress, as a fraction of the total stress, within a single cycle of vibration. Therefore, the stress on the fluid constituent effectively remains a constant fraction of σ_H. This implies that comparison of interstitial fluid flux derived from (20) is a close measure of the fully coupled problem.

It is important to highlight the modeling challenges accompanying FSI computation of phonation. Firstly, the present modeling framework accounts for collision between the VFs during true FSI. To accomplish this within the limitations on computational modeling capabilities, true contact between the VFs was avoided. Instead contact is enforced at a finite but small distance d_p. The effect of this difference compared to the real situation (d_p = 0), on the development of local collision effects and the development of overall FSI is discussed in appendices A and B respectively. In Shurtz and Thomson (2012) it was demonstrated, using a two-dimensional computational model, that the VF dynamics had negligible sensitivity to the choice of d_p in the range considered. Both models I and II can be compared with that in Shurtz and Thomson (2012) by considering the quantity d_p / d_g. In the present case d_p / d_g = 0.33 was within the range of d_p / d_g (from 0.01 to 0.50) considered by Shurtz and Thomson (2012). Thereby Shurtz and Thomson (2012) support the arguments made in appendices A and B.

Another important aspect of the current framework, and in particular with respect to the VF tissue constitutive relations, is that realistic viscoelastic properties were used and that a full 3D geometric description was included. Deformation asymmetry in the anterior-posterior direction, absent in 2D models reported in literature, emphasizes the importance of three-dimensionality. In agreement with Erath et al (2011b,a), the asymmetry in the air flow and the jet attachment in the medial–lateral direction (Coanda effect) did not result in significant asymmetry of deformation between the left and right VFs. In the airflow model, the dynamic viscosity of air was considered at its realistic value. Consequently, the Reynolds number of the flow turned out to be representative of experimental FSI conditions. The Reynolds number determines length and time scales of dynamic events in a laminar flow, and Buckingham’s Pi-theorem stipulates that it is impossible to determine a single scaling factor that can be applied to both air flow and tissue properties and yet keep unchanged the relevant non-dimensional numbers of the fully coupled flow-structure interaction system (Erath and Plesniak 2010). In this light, modifying the Reynolds number in FSI computation of phonation removes the correspondence between dynamics of the computational model and the physical system it attempts to model.

The results present quantitative data on the dynamic state of stresses inside a pair of VFs with realistic 3D geometry and tissue properties obtained during flow-induced vibration and collision. Validation with a carefully designed experimental replica is the best way to resolve any questions regarding the physical relevance of the results presented herein. In the paper it was shown that, wherever such a comparison is possible, the results from the computation do agree with measurements made on similar experimental models.

5. Conclusion

This paper contributes to the current literature on VF modeling in two ways. Firstly, a modeling methodology is presented that simulates vocal fold self-oscillation and contact under conditions representative of experimental investigations. The computed results obtained on the VF exterior (surface displacements, flow rate, contact pressure) were shown to be well within experimental observations. This lends support to the validity of the proposed model approach. The second important outcome, the focus of this study, is the detailed determination of the stress state in the VF interior and its consequences on systemic hydration. Considering the hydrostatic stress gradient, motivated by questions regarding systemic hydration of VF tissue, the interstitial fluid flux in the VF interior was mapped on a representative coronal plane. Dominant modes of interstitial fluid flux were identified, and the motion characteristics that cause them were hypothesized. It follows that phonation without VF collision leads to a state of stress that tends to distribute interstitial fluid to the actively vibrating (medial, superior, inferior) regions of the VFs. Thereby, collision-free phonation exercise is expected to be conducive towards increasing hydration in the VF tissue in the average sense. Elliot et al (1995) found that subjects regularly reported a better voice condition after a warm-up session. Typical warm-up exercises (O’Connor 2012; Voice and Swallowing Institute 2012) comprise singing in a softly-produced voice, uttering vowels and a general avoidance of pressed vocal configurations. On the other hand, previous studies (Solomon and DiMattia 2000) have found that the effect on voice competence measures (for example, PTP) due to tasks demanding higher voice intensity can be offset by increased hydration of the VFs. Hanson et al (1990) found that increased voice intensity is associated with lower open quotients, whereas Verdolini et al (1998) found that decrease in open quotient was related to increase in contact stresses measured on the VF surface. These observations taken together indicate that, from the perspective of vocal health, increase in severity of collision is detrimental, whereas the avoidance of excessive collision is beneficial. A biomechanical explanation for these clinical findings is given in the present paper.

Appendix A

Error in collision characteristics due to contact enforcement condition

In this section, the the error in determining VF stresses due to the particular value of d_p used is discussed. Note that the rigid planes interact with the VFs only during the collision cycles. Thus, only for collision cycles, can the stress distribution in the VFs have an error due to non-zero d_p.

For the purpose of comparison, the physical scenario is approximated by the hypothetical case d_p = 0. This case is an approximation of the physical scenario because the motion of the left and right VFs are not strictly symmetric. Although such a case cannot be computed by the model (due to limitations mentioned earlier), it allows systematic comparison with the computed case.

In the fully-developed collision cycle, beginning at t = 0.27986 s, the VFs approach each other, collide with the respective rigid planes, and move apart until they reach the maximum open state at t = 0.28578 s. If at t = 0.28578 s the rigid planes are instantaneously repositioned at x_ml = 0 (such that d_p = 0) for the successive cycle, the collision characteristics are modified in two ways. Firstly, a smaller area of the VF surfaces collide, and secondly, within this reduced collision-influenced region, the compression depth is itself reduced by a distance equal to d_p / 2.

From the biomechanics standpoint, the decreases in contact area and contact depth imply that the volume over which collision influences interstitial movement is overestimated in the computation. In particular, the tertiary interstitial fluid flux due to collision is expected to be weaker in the physical scenario (compared to the computation). However, the primary and secondary interstitial fluid flux modes (due to mean deformation and vibration, respectively) are identical to the computation.

Appendix B

Estimate of error in FSI due to contact enforcement condition

It may be recalled that the rigid planes never interact directly with the flow domain. A non-zero d_p influences the flow solution as it modifies the movement of the VF surfaces during collision cycles. Thereby, as computed, the FSI can contain an error due to the presence of the rigid planes. A global measure of the error in FSI can be obtained by considering energy quantities, and is estimated below.

For comparison, following the discussion in appendix A, the hypothetical d_p = 0 case is considered to represent the physical scenario. In particular, consider the time-instant of maximum closure within a physical collision cycle. To move the deformed VF surface in the physical scenario such that it matches the deformed VF shape as computed at a corresponding instant, work will need to be done on the VFs. Part of this work is stored in the VFs as excess strain energy up to the instant of maximum closure, while some energy is lost to VF viscoelasticity.

The excess strain-energy gained by the VFs can be estimated as follows. The medial–lateral extent of the VF at rest is D = 8.40 mm. At the instant of maximum closure, each VF in the computation is stretched by a distance d_p / 2 = 0.100 mm more in the medial–lateral direction at the mid-coronal section. Hence the difference between the physical and computed average strain in the medial–lateral direction is d_p / 2D = 0.0119. The difference in strain-energy density (between computation and the physical situation) is proportional to (d_p / 2D)² = 1.42 × 10⁻⁴. The maximum area of the left VF coming under contact in the cycle beginning at t = 0.27986 s was computed to be A_c = 1.69 mm². The excess strain-energy is thus approximately EA_cD(d_p / 2D)² = 12.5 × 10⁻⁹ J. Assuming an identical value for the right VF, this corresponds to an error of 0.132 % relative to the average strain-energy in the VFs during the computed cycle (~ 19 × 10⁻⁶ J). The average strain-energy in the VFs is a measure of the average energy transferred from the flow to the VFs. Therefore, the error in the energy transfer from the flow to VFs during the half-cycle (maximum opening to maximum closure) is also approximately 0.132 %. This is also an estimate of how much the flow solution is affected due to the non-zero d_p condition.

It must be emphasized that beyond the instant of maximum closure, the VFs lose strain energy as they revert to the maximum open state. In doing so, all of the excess strain energy gained in the closing phase is lost in the opening phase of the collision cycle. Thus the error estimated above does not contribute to any global accummulation or loss of energy in the flow domain over successive cycles.

For constant amplitude harmonic motion, the viscoelastic losses in each cycle will be identical; specifically, this loss equals the (constant) area under the non-linear stress-strain curve integrated over the volume of the viscolastic solid. Hence, the graph of viscoelastic dissipation with time for constant amplitude motion is linear when averaged over cycle time. From the computation the viscoelastic losses with time can be explained by a linear dependence up to 99.95 %. As noted previously, the VFs in the computation demonstrate vibration with the amplitude slightly increasing with time. Accounting for the slight increase of vibration amplitude, increases the r² correlation to 99.99 %. Hence, it can be concluded that collision has a limited (less than 0.01 %) effect on viscoelastic losses. Moreover, during the entire collision cycle considered in appendix A, the average energy lost to VF viscoelasticity (~ 6 × 10⁻⁶ J) was computed to be approximately 1 /3-rd of the average strain energy during the same cycle. This further limits the role collision plays in determining global energy transfer during FSI (less than 0.0033 %). The effect of non-zero d_p on the global development of FSI (mediated through differences in collision characteristics between the computation and the physical scenario) cannot be larger than the effect of collision itself.

Appendix C

Accuracy considerations

C.1 Mesh independence of contact model

For the solid domain, the mesh design can be compared to models of Hertz contact analysis. In particular, for the prediction of the maximum value of contact pressures in the center of the contact a finite element model is not significantly mesh sensitive. The present model employs a mesh with an element size ratio to radius of curvature ratio (as approximated by the circle defined by the vocal fold anterior and posterior ends and the contact point) of 0.218 mm to 251 mm (i.e. less than 0.0869 %). This is in good agreement with typical meshes employed for contact analysis e.g. ABAQUS 6.11 User Manual where the element size to radius of curvature ratio is approximately 5 %.

C.2 Airflow model

To test the accuracy of the mesh for the airflow model, a model with 2D geometry and containing only the flow domain was created. The geometry of the VF wall was identical to that in Scherer et al (2001). Specifically, it had identical thickness T and depth D as the model in this paper, but the opposing glottal walls had an included angle of 10° and were diverging. The VF walls were considered rigid and static. The mesh for the 2D model was identical in refinement to a coronal section of the full 3D model considered in the present study. A steady-state flow solution was considered, and the solution was compared with data from Scherer et al (2001). For example, for a transglottal pressure difference of 294 Pa (or 3 cm water) the model predicts a maximum pressure drop (with respect to the inlet) of 436 Pa which occurs at the glottal entrance. This is in good agreement with Scherers value of 421 Pa (less than 3.42 % difference).

C.3 Flow-structure coupling model

The accuracy of the numerical scheme was verified by analyzing the elastic cantilever benchmark model in Walhorn (2002). The results predicted by the present code set-up were found to be in agreement with data given in Walhorn (2002). For example, the dominant frequency of vibration at the beam tip and its corresponding amplitude were reported to be 4.21 Hz and 1.68 mm, respectively, in Walhorn (2002). Here, these quantities were computed as 4.10 Hz and 1.94 mm, respectively.

C.4 Computation of interstitial fluid flux vectors

Stress gradients were determined on the mid-coronal plane and shown in figure 12 (section 3). To calculate the gradients, and generate the interstitial fluid flux vector plots, the following method is employed. Nodes located on the mid-coronal section in the reference (un-deformed state) are considered, and their coordinates are recorded. At a given instant, hydrostatic stress values at the nodes are interpolated from the element values using the C3D8RH formulation (ABAQUS Theory Manual). A structured rectangular 2D grid is defined on the un-deformed mid-coronal surface. This grid is slightly more refined than the original hexahedral grid. A linear interpolation scheme is used to determine hydrostatic stress values over the finer grid from the nodal values. A central difference scheme is used to determine derivatives of hydrostatic stress in the inferior–superior ∂σ_H / ∂x_is and medial–lateral ∂σ_H /∂x_ml directions at each grid point. In the last two steps (interpolation on to a finer grid, and computing spatial derivatives) the un-deformed nodal coordinates are used.

Determination of stresses in each element at a particular instant is carried out by the Hilber-Hughes-Taylor algorithm, which is at least second-order accurate in time. The shape functions corresponding to C3D8RH elements are linear with respect to spatial coordinates; thus the interpolation of elemental stress values to nodes is first-order accurate with respect to element length. Linear interpolation of nodal values to the structured rectangular grid is again first-order accurate with respect to grid-size which is smaller than the local element length. The central difference scheme used to determine spatial derivatives (stress gradients) is second-order accurate. Thus the combined accuracy of the interstitial fluid flux vectors is at least first-order with respect to element size and second-order with respect to time increment.