Estimating overall exposure effects for zero-inflated regression models with application to dental caries

Abstract

Zero-inflated (ZI) models, which may be derived as a mixture involving a degenerate distribution at value zero and a distribution such as negative binomial (ZINB), have proved useful in dental and other areas of research by accommodating ‘extra’ zeroes in the data. Used in conjunction with generalized linear models, they allow covariate-adjusted inference of an exposure effect on the mixing probability and on the mean for the non-degenerate distribution. However, these models do not directly provide covariate-adjusted inference for the overall exposure effect. Focusing on the ZINB and zero-inflated beta binomial (ZIBB) models, we propose an approach that uses model-predicted values for each person under each exposure state. This ‘average predicted value’ (APV) method allows covariate-adjusted estimation of flexible functions of exposure group means such as the difference or ratio. A second approach considers a log link for both components of the ZINB to allow a direct approach to estimation. We apply these new methods to a study of dental caries in very low birth weight adolescents. Simulation studies show good bias and robustness properties for both approaches under various scenarios. Robustness diminishes when there is exposure group imbalance for a covariate with a large effect.

1 Introduction

Zero-inflated (ZI) models have become an increasingly popular tool to account for ‘extra’ zeros in data, and have been used in many areas of application, including dental health, medicine, and economics. Zero-inflated models are comprised of a mixture of a standard probability distribution, such as Poisson, and a degenerate distribution at 0. It is convenient, though not necessary, to characterize the resulting distribution as involving two (latent) populations, sometimes referred to the ‘susceptible’ and the ‘non-susceptible’ populations. One popular version, suitable for unbounded counts, is the zero-inflated Poisson (ZIP) model.^1,2 Despite the use of the mixture, in some applications this model may provide an inadequate fit to the data due to extra-Poisson dispersion. An attractive alternative is the zero-inflated negative binomial (ZINB) model. The negative binomial part of the model provides an extension of the Poisson distribution and accounts for over-dispersion by assuming that the Poisson mean follows a gamma distribution. ZIP and ZINB models have been used by researchers in a number of areas of application, including dental caries research.^3–5

For bounded counts, available models include the zero-inflated binomial (ZIB) and the zero-inflated beta-binomial (ZIBB).⁶ The latter allows for over-dispersion by assuming the binomial ‘event’ probability to have a beta distribution. The ZIBB, though not yet widely used, would appear to be an appealing model for dental caries, as it would utilize a known upper bound in the count. In particular, the number of teeth is a biological upper bound for the DMFT (number of decayed, missing, or filled teeth), a popular measure of the extent of dental caries.

In zero-inflated models, covariates may be accounted for by using a pair of regression models, one model (usually logistic regression) for the probability of being susceptible (‘susceptible probability’), and the other model (loglinear regression for ZIP and ZINB, logistic regression for ZIBB) for the mean of the susceptible population. Typically, distinct regression parameters are used for the two regression functions, though a ‘shared parameter’ approach has also been proposed.⁷ Commonly, the two models are fit simultaneously using maximum likelihood.

Much of the zero-inflated model literature has been focused on model fit, including fit for extended zero-inflated models involving, for example, random effects for clustered and longitudinal data,^8–11 and semiparametric regression.^{12, 13} A related area of focus has been score tests for zero-inflation.^14–17 Considerably less attention has been given to the problem of assessing the overall effect of a predictor variable, for example, a treatment or exposure, on the response variable. Typically, papers presenting results from a zero-inflated regression analysis show separate exposure effect estimates for the susceptible probability and for the susceptible population mean.^{3, 18} However, in clinical trials and observational studies of an exposure the primary interest is typically in the comparison between treatment or exposure groups based on the overall mean, possibly adjusted for baseline covariates. For such studies, zero-inflated models are primarily of interest for providing a good fit to the data, in which case the mixture distribution may be viewed as describing a single population, rather than literally interpreted as comprising two populations. In fact, a number of researchers have questioned the applicability of the two population interpretation for their data or for any situation not involving structural zeros.¹⁸ Mwalili et al.,⁵ for example, considered it implausible that there was a subpopulation within their study sample that was truly immune to dental caries. They noted that, while the two-population interpretation provides a convenient explanation of zero-inflated models, it is equally valid to consider the zero-inflated distribution as applying to a single population.

Inference for the overall mean for the ZIP model was considered by Böhning et al.³ They suggested two simple approaches to obtain confidence intervals for the overall mean for a population. Yau and Lee,⁹ considering a ZIP regression model with random effects, provided an estimate and confidence interval for the overall mean at a specified set of covariate values. However, these approaches did not address inference for an overall treatment effect while adjusting for covariates. Moulton et al.⁷ noted that overall inference was possible using a two degrees of freedom test that, for two exposure groups, would simultaneously test for an effect of exposure on the susceptible probability and for a difference in means between the exposed and non-exposed groups given susceptible. However, this test is not directed at the overall mean (and is not equivalent to testing for an overall mean difference) and does not provide an estimate of the magnitude of the overall effect.

This paper presents two new methods for assessing an overall mean exposure effect in the context of zero-inflated regression models. Because accounting for over-dispersion in the (susceptible group) count component of the model is often found to be important, we will focus on the ZINB and ZIBB (as opposed to ZIP and ZIB) models. In the first approach, which we refer to the average predicted value (APV) method, estimated overall means are calculated as an average over individual predicted response values under each exposure status. The approach in this paper represents an extension of a method used by a number of previous authors. The method, also referred to as ‘model-based standardization’,¹⁹ was used by Greenland²⁰ for estimation of a relative risk, Bender et al²¹ to compare the number needed to treat between groups based on a logistic regression model, Austin²² for estimating the odds difference assuming a logistic regression model, and Zou¹⁹ who considered the risk difference and risk ratio for probit, logistic, and extreme value regressions. The method was described by the latter author as one of “predicting counterfactuals”, as it uses predicted responses for the unobserved as well as the observed exposure state for each individual. An advantage of the APV method exploited by previous researchers is that it can be applied to various functions of the group proportions (for example, the risk difference and risk ratio). However, previous implementations of the APV method were confined to binary responses in standard regression models for binary data, while the present paper applies the approach to count data using the relatively complex zero-inflated models. In the present context, the APV method can be used to estimate various desired functions of group means, including the ratio and difference. Variance estimation is possible using the delta method or a bootstrap resampling technique.

The second method presented in this paper uses log-linear models for both the binary and the count components of the ZINB model. This approach allows inference for the ratio of group means in a direct manner as this function is no longer dependent on covariates. Again, either the delta method or bootstrap approach may used for variance estimation. An apparent drawback of this second approach is that the log link function is less suitable for a binary response variable than the logistic function.

The remainder of this paper is organized as follows. In the next section we describe the two new approaches for inference on overall exposure effects in the ZINB and ZIBB models. In Section 3, we apply the new methods to a study of dental caries in very low birth weight (VLBW) and normal birth weight (NBW) adolescents. In Section 4, we present a simulation study that compares the alternative methods in terms of bias, efficiency, and coverage of confidence intervals. Section 5 provides concluding remarks.

2 Estimation of overall effects in zero-inflated models

2.1 Zero-inflated count models

We will focus on two distributions for y, the (count) response for an individual: the zero-inflated negative binomial (ZINB) and the zero-inflated beta-binomial (ZIBB) distribution. Zero-inflated distributions may be derived as a mixture of two latent subpopulations: one (‘susceptible’) with responses distributed as negative binomial (with mean λ, say) and the other (‘non-susceptible’) with responses equal to zero with probability 1. The mixing probability, specifically, the probability of being in the ‘susceptible’ population, is denoted as ψ. Then, the ZINB probability function may be written as:

$$P(y;\psi ,\lambda ,\phi )=\{\begin{array}{ll}(1-\psi )+\psi nb(y;\lambda ,\phi )\hfill & \text{for}y=0\hfill \\ \psi nb(y;\lambda ,\phi )\hfill & \text{for}y>0\hfill \end{array}$$ (1)

where

$$nb(y;\lambda ,\phi )=\frac{\mathrm{\Gamma }(y+1/\phi )}{y!\mathrm{\Gamma }(1/\phi )}{\left(\frac{1}{1+\phi \lambda }\right)}^{1/\phi }\times {\left(\frac{\lambda }{1/\phi +\lambda }\right)}^y$$

is the negative binomial probability function with mean λ and dispersion parameter φ. The mean of y is then μ = ψλ. The negative binomial mean (λ) and the ‘susceptible’ probability (ψ) may in turn be modeled as functions of covariates. Conventionally, a logistic regression model is used for ψ and a log-linear regression model for λ (corresponding to the canonical link functions). We write these models as

$$\text{logit}({\psi }_i)={\alpha }_0+{\alpha }_1{x}_i+{\mathit{\alpha }}^{\prime }{\mathit{w}}_{i}ln({\lambda }_i)={\beta }_0+{\beta }_1{x}_i+{\mathit{\beta }}^{\prime }{\mathit{w}}_i$$ (2)

where α₀, α₁, β₀ and β₁ are unknown parameters, α and β are unknown parameter vectors, x_i is the exposure or treatment indicator (equal to 1 if exposed, 0, otherwise), and w_i is a vector of observed covariate values for individual i with response y_i (i=1,…, n). It is not necessary to use the same covariates for the two models, but is done here for ease of presentation. It is common and often scientifically sensible to include the treatment indicator, as well as appropriate prognostic factors, in both component models. We assume that the y_i are independent, so that the likelihood function may be written as the product of individual probability functions (1) where individual parameters ψ_i and λ_i are replaced using the appropriate functions of regression parameters given by (2).

For bounded counts, it may be of interest to use a distribution such as beta-binomial instead of the negative binomial. Like the latter, the beta-binomial distribution can accommodate over-dispersion, and therefore will often be preferred in dental applications to the binomial distribution. Allowing for zero-inflation leads to the zero-inflated beta-binomial distribution (ZIBB),⁶ whose probability function may be written as:

$$P(y;\psi ,n,\lambda ,\phi )=\{\begin{array}{ll}(1-\psi )+\psi bb(y;n,\lambda ,\phi )\hfill & \text{if}y=0\hfill \\ \psi bb(y;n,\lambda ,\phi )\hfill & \text{if}y>0\hfill \end{array}$$ (3)

where

$$bb(y;n,\lambda ,\phi )=\frac{\left(\begin{array}{c}n\\ y\end{array}\right)\left\{{\prod }_{k=0}^{y-1}(\lambda +k\phi )\right\}\left\{{\prod }_{k=0}^{n-y-1}(1-\lambda +k\phi )\right\}}{\left\{{\prod }_{k=0}^{n-1}(1+k\phi )\right\}},$$

n is the specified maximum count, λ is the probability of an event (for example, DMFT for a given tooth), and φ is a dispersion parameter. Here the mean count is obtained as μ = ψ n λ. As with ZINB, we can model the susceptible probability (ψ) and the probability of an event for susceptibles (λ) as a function of covariates, in this case, using logistic regression for both models. The above regression models for ZINB and ZIBB may be used directly to obtain predicted counts for specified covariate values. However, our goal for both the ZINB and ZIBB models is to do inference on the overall mean count, in particular, to compare means between groups.

2.2 Average predicted value approach

The first method will be referred to as the average predicted value (APV) approach. This approach may be flexibly applied to estimate any function of the overall response means for the two exposure groups while adjusting for covariates. The first step in the approach involves the calculation of the model-predicted responses (for example, μ̂ = ψ̂λ̂ for the ZINB model) for each person (possibly confined to a designated reference population), both if the person were exposed and if the person were not exposed, and where the other covariates are fixed at the person’s observed values. Note, of course, that each person is either exposed or not exposed, so that one of these predicted values will represent a counterfactual response. For discrete covariates, we can simply calculate the predicted response, if exposed and if not exposed, for each distinct set of covariate values in the covariate space. For continuous covariates, we may, alternatively, obtain predictive functions of the covariates for both the exposed and unexposed states. The mean for a given exposure status is then obtained as the average of the predicted values (or integral of the predictive function) over the covariate distribution for the chosen reference population (for example the exposed group). The exposure effect may then be defined as an appropriate function of the two means, for example, the ratio or difference.

To present this approach formally, we let F(w) be the joint distribution function for the covariate vector w in the reference population. Then the average difference in predicted responses is

$${\theta }_D\equiv \int [E(y\mid x=1,\mathit{w})-E(y\mid x=0,\mathit{w})]dF(\mathit{w})$$ (4)

where the integral (possibly multivariate) is over the covariate space for w. The proposed approach to inference uses a regression model (such as ZINB or ZIBB as discussed above) to determine the predicted values of y given the covariates. When the covariates (w) are discrete, then the integral in (4) may be written as a sum. For either categorical or continuous covariates, a model for the typically unknown, and possible multivariate, distribution function, F(w), must be chosen (in conjunction with a choice of the covariate space). For categorical covariates, it will often be reasonable to assume a multinomial distribution based on the observed categories. In some cases, alternative covariate spaces, for example obtained from model smoothing, may be of interest. For continuous covariates, an appropriate continuous distribution (such as normal or multivariate normal) can be chosen, in which case, parameter values must be estimated. Then, estimation of θ_D may proceed by integrating over the estimated distribution of the covariates (w), possibly using a numerical integration technique. Alternatively, the distribution can be non-specified and the empirical distribution function used. This amounts to summing over the observed multivariate covariate values (possibly for a subgroup representing the reference group). We will consider an implementation of the parametric approach (i.e., integrating over an assumed distribution for w) in our simulation study (Section 4). However, our emphasis in this paper is on the empirical approach (averaging over the empirical distribution function). A further description of the empirical approach, as applied to the zero-inflated regression models, follows.

For the ZINB regression model (2), the expected (or ‘predicted’) value for an individual with observed covariate values w_i and (possibly counterfactual) exposure status x, would have the form

$$E(y_i\mid x,{\mathit{w}}_i)={\text{logit}}^{-1}({\alpha }_0+{\alpha }_{1}x+{\mathit{\alpha }}^{\prime }{\mathit{w}}_i)exp({\beta }_0+{\beta }_{1}x+{\mathit{\beta }}^{\prime }{\mathit{w}}_i).$$ (5)

To estimate θ_D (4) we use the expression in (5) plugging in estimated regression parameter values following the fit of the model (2) to the whole sample. A predicted effect of exposure x for individual i is obtained as E(y_i | x=1,w_i) − E(y_i | x=0,w_i). An estimate of the mean difference (4) is then obtained by averaging over the empirical distribution function of the covariates (w), possibly for a subsample representing a reference group (denoted by G with sample size n_G). Thus, our estimate of the mean difference for the ZINB model becomes:

$${\widehat{\theta }}_D=\frac{1}{n_G}{\sum }_{i\in G}{\text{logit}}^{-1}({\widehat{\alpha }}_0+{\widehat{\alpha }}_1+{\widehat{\mathit{\alpha }}}^{\prime }{\mathit{w}}_i)exp({\widehat{\beta }}_0+{\widehat{\beta }}_1+\widehat{{\mathit{\beta }}^{\prime }}{\mathit{w}}_i)-{\text{logit}}^{-1}({\widehat{\alpha }}_0+{\widehat{\mathit{\alpha }}}^{\prime }{\mathit{w}}_i)exp({\widehat{\beta }}_0+{\widehat{\mathit{\beta }}}^{\prime }{\mathit{w}}_i).$$ (6)

The expression in (6) has the form of the well-known standardization formula²³ as used for stratified analysis. However, the standard approach to a stratified analysis uses observed differences for the exposed versus non-exposed group from each subpopulation (stratum), whereas the present approach uses model predicted values, which are calculable even if there are no representatives for one of the exposure groups for a given set of covariate values. To the extent that there is a lack of overlap in the distribution of the covariates for the two exposure groups, this approach will involve some degree of extrapolation beyond the multivariate support of the data.

An alternative function of possible interest would be the ratio of response means for the exposed versus unexposed groups. Here the APV estimand would be the ratio of expected values, θ_R ≡ ∫[E(y|x = 1, w)dF(w)/∫ E(y|x = 0, w)]dF(w), which can be estimated given model (2) as

$${\widehat{\theta }}_R={\sum }_{i\in G}{\text{logit}}^{-1}({\widehat{\alpha }}_0+{\widehat{\alpha }}_1+{\widehat{\mathit{\alpha }}}^{\prime }{\mathit{w}}_i)exp({\widehat{\beta }}_0+{\widehat{\beta }}_1+{\widehat{\mathit{\beta }}}^{\prime }{\mathit{w}}_i)/{\sum }_{i\in G}{\text{logit}}^{-1}({\widehat{\alpha }}_0+{\widehat{\mathit{\alpha }}}^{\prime }{\mathit{w}}_i)exp({\widehat{\beta }}_0+{\widehat{\mathit{\beta }}}^{\prime }{\mathit{w}}_i).$$ (7)

The variances for θ̂_D and θ̂_R can be estimated via the delta method. For w consisting of a small number of cells, this may be accomplished easily by writing out the function of parameters (as given in (6) or (7)), and using, for example, the ‘estimate’ statement in SAS Proc NLMIXED. With continuous covariates it becomes cumbersome to write out the function, but the derivatives can be derived in order to obtain the delta method estimate. This approach, particularly with multiple continuous covariates, can be tedious. An alternative approach is to obtain variance estimates via bootstrap resampling.²⁴ The bootstrap approach has the potential additional advantage of allowing the computation of confidence intervals without requiring a distributional assumption, such as normality, for the estimator. Under the assumed models, the APV estimators of the mean ratio or difference, being functions of the maximum likelihood estimates of the regression coefficients, are themselves maximum likelihood estimators and therefore consistent. Note that in the special case in which the logit function for the susceptible probability involves only an intercept term, the overall mean model (5) reduces to a loglinear model (with intercept adjusted for the zero inflation). In this case, the mean ratio (exposed versus non-exposed) is easily obtained as log β₁.

2.3 Direct (log-log model) approach

Next we consider a simple alternative to the average predicted response approach. Instead of using a logistic regression model for the susceptible probability, we use a loglinear model. We thus assume the set of models

$$ln({\psi }_i)={\alpha }_0+{\alpha }_1{x}_i+{\mathit{\alpha }}^{\prime }{\mathit{w}}_{i}ln({\lambda }_i)={\beta }_0+{\beta }_1{x}_i+{\mathit{\beta }}^{\prime }{\mathit{w}}_i$$ (8)

which we refer to for convenience as the ‘log-log model’. (In a similar vein, we will refer to model (2) as the ‘logit-log’ model and the model for ZIBB as ‘logit-logit’). Using the log link for both regression models provides an overall exposure effect that does not depend on the covariate values. Specifically, we can obtain the ratio of the overall means (exposed versus non-exposed groups) as

$${\theta }_{RL}\equiv \frac{{\mu }_1}{{\mu }_0}=\frac{exp({\alpha }_0+{\alpha }_1+{\mathit{\alpha }}^{\prime }{\mathit{w}}_i)exp({\beta }_0+{\beta }_1+{\mathit{\beta }}^{\prime }{\mathit{w}}_i)}{exp({\alpha }_0+{\mathit{\alpha }}^{\prime }{\mathit{w}}_i)exp({\beta }_0+{\mathit{\beta }}^{\prime }{\mathit{w}}_i)}=e^{{\alpha }_1+{\beta }_1}.$$ (9)

The mean ratio, θ_RL, is directly estimable from the fit of the model (8) by plugging regression estimates for α₁ and β₁ into the simple expression on the right hand side of (9). This provides the estimate, θ̂_RL = e^{α̂₁+ β̂₁}. The delta method estimate of the variance of θ̂_RL is readily obtained, for example using the ‘estimate’ statement in SAS Proc NLMIXED.

The log-log model approach has the advantage of simplicity. However, it is limited to inference on the ratio of means, whereas the APV approach is flexible in the specification of the functions of the means, allowing, as shown above, inference for both the difference and ratio of means. An obvious potential limitation of the log-log model is that the log function may not be the canonical, or even an apparently suitable, link function for some distributions. For example, when modeling the susceptible probability in the ZINB model, or either component in the ZIBB model, the logit link is preferred to the log link, because the mean in these cases is restricted to the range 0 to 1, while the loglinear model may produce predicted probabilities greater than 1. For the goal of inference for the overall mean, however, it remains to be studied, in real data and in simulations, whether this apparent inadequacy in the model translates into a practical problem.

It might appear to be of interest to apply the APV approach to the ZINB/log-log model. However, it turns out that the resulting estimand, whether using the parametric (integration) or the empirical (summation) approaches for averaging over the covariates, reduces algebraically to the direct approach estimand (9). This result is easily shown and a brief proof is provided in the Appendix.

3 Application to Dental Data

Our motivating example comes from a study of dental caries in VLBW and NBW adolescents.²⁵ The subjects were previously recruited in a cohort study that followed them from birth and assessed various psychosocial factors as well as demographic variables.²⁶ The dental study involved a clinical assessment at around age 14, providing the DMFT score and other dental outcomes. In the original study, the NBW (control) group was selected in order to obtain similar distributions to the VLBW group for key baseline (‘stratification’) variables, namely, race, socioeconomic status (SES), and sex. Therefore, it is sensible to use the VLBW (‘exposed’) children as the reference group, although the distribution for the three stratification variables would be expected to be similar in the two groups. The original study separated the VLBW infants into groups with and without brochopulmonary dysplasia; however, we have combined these two groups for present purposes. The analysis (complete case) sample sizes were 139 and 85 for the VLBW and NBW groups, respectively.

A primary study objective was to compare the mean DMFT for VLBW versus NBW adolescents, while controlling for race (African American versus other), SES (low versus high) and sex. To compare alternative approaches, we fit the following models: 1) normal distribution (with standard linear regression model), 2) Poisson (loglinear model), 3) negative binomial (loglinear model), 4) ZIP/logit-log model, 5) ZIP/log-log, 6) ZINB/logit-log, 7) ZINB/log-log model, and 8) ZIBB/logit-logit model. For the ZIBB model, an upper bound of 28 was used for DMFT, corresponding to the maximum possible number of affected teeth. Goodness of fit for each model was evaluated using the Akaike Information Criterion (AIC), the Bayesian Information Criterion (BIC), and a Pearson chi-square test. The latter compared empirical versus predicted frequencies across DMFT categories (0, 1, 2,…, 9, >9). The predicted frequencies were marginal, that is, calculated as a weighted average over strata-specific predicted values. Following, Rose et al.¹⁸ we used the number of categories minus one (that is, 10) degrees of freedom for the chi-square tests. This approach essentially assumes that parameter values are known. A refined approach, taking into account parameter estimation in the degrees of freedom might be possible but is not available. Simply subtracting the number of estimated model parameters is not a suitable approach, particularly as we are predicting the marginal counts (and for some models the number of parameters is as high as the number of categories).

From Table 1, we see that according to all goodness-of-fit criteria, the last three models (ZINB/logit-log, ZINB/log-log, and ZIBB/logit-logit) are superior to the first five models. Furthermore, the last three models show adequate fit according to the chi-square statistic whereas the first five models (with the possible exception of the negative binomial model) do not. The last three models appear to be very close in fit according to AIC and BIC. Interestingly, the ZINB model with log-linear regression functions for both the susceptible probability and the susceptible mean (‘ZINB/log-log’) is best according to both AIC and BIC. For example, AIC for ZINB/log-log is 809.2, slightly better than ZINB/logit-log (AIC = 811.3) and ZIBB (AIC = 811.1). We also considered a log-log model for ZIBB, as such a model would appear to be possible and have the potential advantages noted above. However, we were not able to obtain convergence using this model for the dental data.

Table 1.

Goodness-of-fit statistics for alternative models fit to the dental data (DMFT responses). All regression models included an exposure indicator (VLBW versus NBW) and control covariates (race, SES, and sex). Smaller is better for AIC and BIC.

Model	Parameters	AIC	BIC	Pearson’s χ2	p-value (χ2)
1. Normal	5	1087.9	1091.3	58.36	< 0.001
2. Poisson	5	1072.9	1090.0	432.24	< 0.001
3. Negative Bin	6	821.6	842.0	17.03	0.074
4. ZIP (logit-log)	10	855.8	890.0	35.60	< 0.001
5. ZIP (log-log)	10	853.9	888.0	35.76	< 0.001
6. ZINB (logit-log)	11	811.3	848.8	4.10	0.94
7. ZINB (log-log)	11	809.2	846.7	4.07	0.94
8. ZIBB (logit-logit)	11	811.1	848.6	7.17	0.71

The above results indicate that the data show significant zero inflation, as the ZIP and ZINB models provide a better fit than the Poisson and negative binomial models, respectively. We note, for example, that the marginal predicted frequency of zeros under the ZINB model is 107 (or 48% of the sample), the same as the observed number of zeros. Of that number, the contribution (that is the marginal predicted frequency of zeros) of the negative binomial component of the ZINB model is only 21, indicating a ‘zero-inflation’ (or marginal predicted frequency of non-susceptibles) of 107 – 21 = 86. In addition, there is significant over-dispersion, as indicated by the superior fit for the negative binomial and ZINB models compared to the Poisson and ZIP models, respectively. Although the ZIBB takes into account the biological upper bound for DMFT, it does not appear to have an advantage in fit over the ZINB models, possibly because the observed maximum (and mean) DMFT is considerably lower than the biological maximum, and thus biologically impossible DMFT values have very low predicted probabilities under the ZINB models. The standard linear regression model provides a poor fit, with considerably higher (worse) AIC and BIC values than the other models. Figure 1 shows the predicted frequencies for the ZINB/logit-log and ZIBB models against the histogram of observed frequencies for the DMFT counts.

Figure 1.

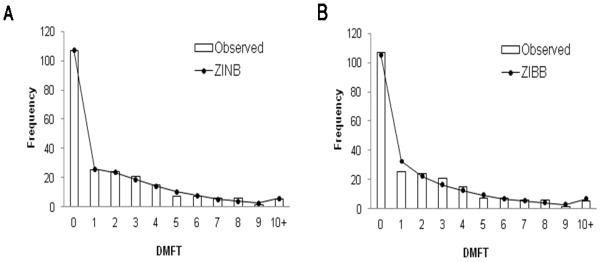
Observed and predicted frequencies for each number of DMFT, using the dental data. Predicted values are from the ZINB/logit-log (A) and ZIBB/logit-logit (B) models.

Next, we used the three models that provide a good fit to the dental data (namely, ZINB/logit-log, ZINB/log-log, and ZIBB/log-log) to assess the effect of exposure (VLBW versus NBW) on the overall mean DMFT. We wished to assess both the difference in means and the ratio of the means for the exposed versus non-exposed groups. For the ZINB/logit-log and ZIBB/logit-logit models, the APV approach was used for both the difference and the ratio of means. For the ZINB/log-log model, the direct approach, which allows inference for the ratio but not the difference in means, was used.

Table 2 shows the results of inference for the difference and the ratio of exposure group means for the three models. The table includes the estimated mean difference (mean for VLBW minus mean for NBW), the standard error (estimated via the delta method), and the Wald test p-value of the null hypothesis of the mean difference equal to 0. It also has the estimated mean ratio (mean for VLBW over the mean for NBW), standard error, and Wald test p-value of the null hypothesis of the mean ratio equal to 1. The estimated mean differences for the ZINB/logit-log and ZIBB/logit-logit models (adjusting for covariates) are −0.62 and −0.58, respectively, thus showing a lower mean DMFT for VLBW than NBW adolescents; however, this difference is not statistically significant by either method. The estimated mean ratio from the ZINB/logit-log model is 0.73; that is, the mean DMFT for the VLBW group is an estimated 0.73 times the mean DMFT for the NBW group, though not statistically significant at the 0.05 α-level (p=0.09). A similar estimate and conclusion is provided by the ZIBB model. For the ZINB/log-log model the estimated ratio is 0.68, showing a more pronounced birth weight effect that is statistically significant (p=0.04). The unexpected finding of a lower estimated mean DMFT for VLBW than NBW adolescents corroborates the results in the primary report on these data.²⁵ The somewhat different results among our alternative approaches suggested the need for simulation studies to help determine the preferred model and method of inference.

Table 2.

Estimated difference and ratio of mean DMFT for the VLBW versus NBW groups controlling for race, SES, and sex. “SE” is the standard error of the estimate and “P” is the p-value for the Wald test of the null hypothesis (difference equal to 0 and ratio equal to 1)

Model	Mean Difference			Mean Ratio
	Estimate	SE	P	Estimate	SE	P
ZINB/logit-log (APV approach)	−0.62	0.38	0.10	0.73	0.13	0.09
ZINB/log-log (direct approach)	-	-	-	0.68	0.12	0.04
ZIBB/logit-logit (APV approach)	−0.58	0.35	0.10	0.75	0.13	0.10

4 Simulation study

4.1 Simulation study design and methods

In this section, we describe our approach to simulation studies intended to further investigate the properties of the proposed methods. Our primary goals were to determine the validity of overall mean ratio estimator using the APV method for the ZINB/logit-log model, as well as robustness of the direct method which assumes the ZINB/log-log model. For comparison, we also considered analogous scenarios in which the ZINB/log-log model is correct. In addition, we wished to study the APV method under the ZIBB/logit-logit model in the situation of a known upper bound to the count response variable, and to investigate the robustness, under this model, of estimates assuming the ZINB model (either logit-log or log-log).

In our first simulation study, we assumed a ZINB/logit-log model. The logistic regression model for the susceptible probability and the loglinear model for the susceptible population mean both included a binary exposure indicator (1 if exposed, 0, otherwise) and a single covariate. The model is thus given as (2) above with α′ = α₂ and β′ = β₂, where α₂ and β₂ are unknown scalar coefficients for the covariate, w. We considered both the case of a continuous and a categorical (binary) covariate. The other parameter that needs to be specified is the negative binomial dispersion parameter, φ.

We considered five scenarios which are distinguished in the magnitude of the effects of the exposure and the covariate on the susceptible probability (corresponding to parameters α₁ and α₂, respectively) and on the mean for the susceptible population (β₁ and β₂, respectively). The scenarios were specified as 1) small exposure and covariate effects (approximating estimates from the dental data); 2) small exposure and large covariate effects; 3) large exposure and small covariate effects; 4) large exposure and covariate effects; and 5) null exposure and small covariate effects. The regression coefficient values used in the simulation study for each of these scenarios are given in Table 3. For the negative binomial model, the dispersion parameter (φ) for each scenario was set to 0.2, 0.5, and 1. The value 0.5 was chosen as it is close to that estimated from the dental data; the other two values were chosen to study the effect of varying values of the dispersion parameter.

Table 3.

Regression coefficient values for intercept, exposure, and covariate (categorical or continuous) for ZINB/logit-log models used in simulation studies

Scenario	Categorical Covariate						Continuous Covariate
	Probability of Susceptible			Mean Susceptible Population			Probability of Susceptible			Mean Susceptible Population
	Int (α0)	Exp (α1)	Cov (α2)	Int (β0)	Exp (β1)	Cov (β2)	Int (α0)	Exp (α1)	Cov (α2)	Int (β0)	Exp (β1)	Cov (β2)
1	0.8	−0.5	−0.1	1.4	−0.1	−0.3	1.2	−0.5	−0.1	1.4	−0.3	−0.01
2	0.8	−0.5	−1.0	1.4	−0.1	−0.6	4.0	−0.5	−0.4	2.0	−0.3	−0.1
3	0.8	−1.0	−0.1	1.4	−0.5	−0.3	1.2	−1.5	−0.1	1.4	−0.5	−0.01
4	0.8	−1.0	−1.0	1.4	−0.5	−0.6	4.0	−1.5	−0.4	2.0	−0.5	−0.1
5	0.8	0	−0.1	1.4	0	−0.3	1.2	0	−0.1	1.4	0	−0.01

In addition, we considered different situations with regard to covariate balance. Specifically, we included a balanced case where, in the binary (0–1) covariate case, each exposure group had a 50% frequency of w=1, and in the continuous covariate case, the expected value of the covariate was 10 and the standard deviation was 2 for each exposure group. In addition, we included two unbalanced cases. In one case, the imbalance ‘favored’ the exposure; specifically, in the binary covariate case, the frequencies of w=1 were 75% in the exposed group and 25% in the unexposed group, and in the continuous covariate case, the expected values of the covariate were 10 in the exposed group and 7 in the unexposed group with a standard deviation of 2 in both groups. In the other unbalanced case, the imbalance favored non-exposure; that is, the above proportions/means were used with the groups switched.

For each scenario and type of covariance balance, 5000 simulated datasets were generated. Sample sizes of 200 (100 per exposure group) and 2000 (1000 per exposure group) were used. The exposure indicator and covariate were generated independently for individuals within each dataset and between datasets using pseudorandom number generators in SAS/IML (SAS System, Version 9.2). In the case of a binary covariate, the randomization was constrained to assure the targeted balance in the covariate levels over the two exposure groups. In the continuous case, the covariate was generated independently from a normal distribution. The response variates were then generated independently according to the ZINB distribution with regression model (2) given the individual exposure and covariate values.

The true value for the ratio of means is defined by the function on the right hand side of (7) with the true coefficients in place of the estimates. We denote this quantity, representing a sample version of θ_R, as MR (mean ratio). In the simulations studies, MR was either equal to θ_R, in the case with a categorical covariate (because the empirical distribution of w in this case is the same as the true distribution), or a close approximation (for a continuous covariate). For comparison, in the continuous covariate case, we also calculated true values by integrating over the true (normal) distribution of the covariates. Integration was carried out using the “quad” function in SAS/IML, which uses an adaptive (Romberg-type) numerical integration technique. Note that the true value was fixed over the simulations in the binary covariate case, due to the imposed balance, but could vary over simulations in the continuous covariate case. In the latter case, for use in tables, a summary ‘true MR’ was calculated as the average MR over the simulated data sets for each scenario.

For each dataset the competing methods (that is, the APV method assuming ZINB/logit-log or the direct method assuming ZINB/log-log) were used to estimate the ratio in overall means for the exposed versus unexposed groups, and to construct a 95 percent confidence interval for the ratio. From the simulations, we calculated the average estimate of the mean ratio (EMR); the average percent error (PE = 100 x (EMR – MR)/MR), a measure of relative bias; the standard deviation (SD) of EMR; the average estimated standard error (SE) of EMR; and the coverage probability (CP, percent of simulated datasets for which the 95 percent confidence interval for MR covered the true value). For comparison, in the continuous covariate case, we also computed the APV estimator by integrating over the distribution of the covariate using the numerical integration method described above. The covariate distribution was (correctly) assumed to be normally distribution, but with parameters estimated from the exposure (reference) group data.

In a second simulation study, we assumed a ZIBB/logit-logit model. As before, we included a single binary exposure variable and a single (either continuous or binary) covariate. We examined similar scenarios to those described above for ZINB. The regression coefficient parameter values used in this simulation study are given in Table 4. The ZIBB dispersion parameter was set at φ =1/9, 1, and 9 (with 1/9 chosen as a value close to that estimated from the dental data). In this second study, we compared several approaches for estimating the overall exposure effect: the APV method assuming ZIBB/logit-logit (the correct model in this case), the APV method under ZINB/logit-log, and the direct approach assuming ZINB/log-log. The same simulation statistics listed above for the ZINB model were obtained.

Table 4.

Regression coefficient values for intercept, exposure, and covariate (categorical or continuous) for ZIBB/logit-logit models used in simulation studies

Scenario	Categorical Covariate						Continuous Covariate
	Probability of Susceptible			Mean Susceptible Population			Probability of Susceptible			Mean Susceptible Population
	Int (α0)	Exp (α1)	Cov (α2)	Int (β0)	Exp (β1)	Cov (β1)	Int (α0)	Exp (α1)	Cov (α2)	Int (β0)	Exp (β1)	Cov (β2)
1	0.8	−0.5	−0.1	−1.8	−0.1	−0.4	1.6	−0.5	−0.1	−0.1	−0.1	−0.2
2	0.8	−0.5	−1.0	−1.8	−0.1	−0.8	4.0	−0.5	−0.4	1.5	−0.1	−0.4
3	0.8	−1.0	−0.1	−1.8	−0.5	−0.4	1.6	−1.5	−0.1	−0.1	−0.5	−0.2
4	0.8	−1.0	−1.0	−1.8	−0.5	−0.8	4.0	−1.5	−0.4	1.5	−0.5	−0.4
5	0.8	0	−0.1	−1.8	0	−0.4	1.6	0	−0.1	−0.1	0	−0.2

4.2 Simulation study results

We focus on results for the continuous covariate case; results for the categorical case are similar and are therefore not presented. We note that for both the true estimands and the APV estimators, calculated values based on the empirical approach (which sums over the empirical distribution function of the covariate) are very close (usually within 0.001) to the values obtained by integrating over the (estimated) normal distribution of the covariate. The results are thus provided only for the former approach. Table 5 gives the results for the first simulation study in the case of n = 100 per group and dispersion parameter equal to 0.5. We see over all five scenarios that the APV method under the true (ZINB/logit-log) model produces a small positive bias in its estimation of the mean ratio. In particular, the average percent error (PE) is less than 3.1% for all five scenarios in the balanced case and is less than 6.0% when there is imbalance in the covariate between the two groups. The average estimated standard errors were found to be slightly lower than the true (simulation) values, and thus, the coverage probabilities of 95 percent confidence intervals slightly lower than the nominal level, though still within 2% for most scenarios. We note that a small number of simulated data sets did not provide estimates due to lack of convergence. This occurred only a few times for both the APV and direct methods in the simulations with n = 100 per group, and did not occur for n = 1000 per group.

Table 5.

Simulation statistics for the estimated mean ratio for the APV (ZINB/logit-log model) and direct (ZINB/log-log model) methods on data generated from the ZINB/logit-log model (φ = 0.5) with continuous covariate, n = 100 per group

Scenario	Balance*	True Mean Ratio (MR)	APV (logit-log) Approach					Direct (log-log) Approach
			Ave Est MR	Ave PE (%)	SD of Est MR	Ave SE	CP (%)	Ave Est MR	Ave PE (%)	SD of Est MR	Ave SE	CP (%)
1	B	0.575	0.588	2.17	0.143	0.139	93.9	0.588	2.28	0.144	0.139	93.9
2		0.590	0.601	2.00	0.155	0.149	93.5	0.602	2.08	0.162	0.150	92.3
3		0.239	0.245	2.67	0.082	0.078	91.8	0.245	2.74	0.082	0.078	92.0
4		0.265	0.273	3.09	0.093	0.088	92.0	0.269	1.64	0.095	0.089	90.6
5		1.000	1.024	2.38	0.222	0.217	94.0	1.024	2.43	0.224	0.216	94.1
1	E	0.575	0.603	4.88	0.176	0.172	93.8	0.603	4.93	0.175	0.170	94.0
2		0.590	0.615	4.27	0.176	0.173	94.0	0.604	2.50	0.181	0.165	92.6
3		0.239	0.251	5.08	0.094	0.092	92.2	0.251	5.26	0.094	0.091	92.4
4		0.265	0.276	4.29	0.102	0.099	92.5	0.262	−1.19	0.102	0.091	88.9
5		1.000	1.033	3.26	0.279	0.273	93.4	1.022	2.17	0.267	0.258	93.2
1	U	0.596	0.623	4.38	0.169	0.167	94.3	0.609	2.11	0.172	0.169	93.6
2		0.655	0.675	3.04	0.168	0.168	93.7	0.641	−2.16	0.187	0.168	88.9
3		0.265	0.277	4.67	0.097	0.093	92.2	0.267	0.87	0.097	0.093	90.9
4		0.370	0.384	3.89	0.112	0.105	93.3	0.324	−12.2	0.111	0.098	80.6
5		1.000	1.040	3.97	0.268	0.258	93.9	1.034	3.44	0.274	0.261	93.4

^*B = balanced covariate, E = unbalanced favoring exposed, U = unbalanced favoring unexposed

For the direct (log-log) method, the average percent error is less than 3% for all five scenarios in the balanced case and less than 6.0% when there is imbalance in the covariate between the two groups favoring exposed. Standard errors tend to be slightly underestimated and coverage probabilities somewhat lower than, but usually within a few percent of, the nominal level. However, in the unbalanced case favoring unexposed, the average percent error (in absolute value) is relatively high (−12.2%) in the case of large exposure and covariate effects (Scenario 4). The standard error is also markedly underestimated in this case and the coverage of the 95% confidence interval is only around 80%.

When the sample size per group is increased to 1000 (Table 6), the APV approach shows very low bias (less than 1%) and good coverage (within 2 percent) for all scenarios. In contrast, the direct approach has relative biases of up to 12 percent in the unbalanced situations as before. In the case of a binary covariate, on the other hand, the properties of the direct approach are better, with relative bias less than 3% and coverage within 3 percent of the nominal level for all scenarios (results not shown).

Table 6.

Simulation statistics for the estimated mean ratio for the APV (ZINB/logit-log model) and direct (ZINB/log-log model) methods on data generated from the ZINB/logit-log model (φ = 0.5) with continuous covariate, n = 1000 per group

Scenario	Balance*	True Mean Ratio (MR)	APV (logit-log) Approach					Direct (log-log) Approach
			Ave Est MR	Ave PE (%)	SD of Est MR	Ave SE	CP (%)	Ave Est MR	Ave PE (%)	SD of Est MR	Ave SE	CP (%)
1	B	0.575	0.576	0.14	0.044	0.043	94.5	0.577	0.27	0.044	0.043	94.6
2		0.590	0.591	0.17	0.046	0.046	95.6	0.602	1.99	0.048	0.047	94.8
3		0.239	0.240	0.29	0.024	0.024	94.8	0.24	0.40	0.024	0.024	95.0
4		0.265	0.266	0.14	0.027	0.027	94.6	0.266	0.12	0.028	0.028	94.6
5		1.000	1.001	0.08	0.067	0.067	94.7	1.001	0.07	0.067	0.066	94.5
1	E	0.575	0.577	0.34	0.051	0.052	94.7	0.582	1.15	0.051	0.052	95.0
2		0.590	0.592	0.42	0.053	0.053	94.8	0.547	−7.28	0.050	0.047	79.5
3		0.239	0.240	0.47	0.027	0.028	94.8	0.242	1.24	0.028	0.028	95.0
4		0.265	0.267	0.46	0.030	0.030	95.4	0.234	−11.9	0.026	0.025	71.5
5		1.000	1.005	0.49	0.082	0.082	95.1	1.003	0.26	0.079	0.080	95.0
1	U	0.596	0.600	0.53	0.050	0.050	94.7	0.59	−1.07	0.051	0.051	93.7
2		0.655	0.657	0.18	0.049	0.049	94.6	0.649	−0.95	0.057	0.053	92.5
3		0.265	0.265	0.27	0.029	0.028	94.3	0.258	−2.64	0.029	0.028	92.3
4		0.370	0.372	0.42	0.032	0.032	94.6	0.336	−9.10	0.036	0.031	72.9
5		1.000	1.004	0.40	0.078	0.077	94.8	1.005	0.49	0.081	0.080	94.7

^*B = balanced covariate, E = unbalanced favoring exposed, U = unbalanced favoring unexposed

We also considered ZINB/log-log as the true model in scenarios with a single binary covariate. In this case, the relative performance of the APV (logit-log) and direct (log-log) methods are essentially reversed from the previous results (results not shown). Note that the continuous covariate case was not considered here, as the loglinear model could then produce predicted susceptible probabilities greater than 1.

Not surprisingly, as the dispersion parameter increases, the variances and small sample biases increase. At the smallest value (φ = 0.2) the nonconvergence rate was somewhat increased; of course, in practice, a small estimated value for the ZINB dispersion parameter would suggest that the zero-inflated Poisson may be a preferred model. The relative performance of the APV and direct methods for other dispersion parameter values are similar to that seen for the presented results (for φ = 0.5) and therefore are not shown here.

The second simulation study examined different estimators of the overall mean ratio under the ZIBB/logit-logit model; results for dispersion parameter equal to 1/9 are presented here. The APV method based on the ZIBB/logit-logit (correct) model provides relative biases of less than 3% in the balanced case and less than 6% in the unbalanced case for all scenarios with n = 100 per group, and less than 1% for all scenarios with n = 1000 per group (results not shown). Fitting the ZINB/logit-log model to these data and using the APV method results in relatively small positive biases of less than 4.2% in the balanced covariate case and less than 7.1% in the unbalanced case for n=100 per group with a continuous covariate (Table 7). As before, standard errors are somewhat underestimated and coverage probabilities are lower than the nominal level. For n=1000 (Table 8), the relative bias in the balanced case is less than 2% and the coverage of confidence intervals is within 0.5% of the nominal (95%) level. For the unbalanced case, the relative bias is still less than 4% and coverage of confidence intervals within 2.5% of the nominal level for all scenarios.

Table 7.

Simulation statistics for the estimated mean ratio for the APV (ZINB/logit-log model) and direct (ZINB/log-log model) methods on data generated from the ZIBB/logit-logit model (φ = 1/9) with continuous covariate, n = 100 per group

Scenario	Balance*	True Mean Ratio (MR)	APV (logit-log) Approach					Direct (log-log) Approach
			Ave Est MR	Ave PE (%)	SD of Est MR	Ave SE	CP (%)	Ave Est MR	Ave PE (%)	SD of Est MR	Ave SE	CP (%)
1	B	0.752	0.774	2.82	0.179	0.174	94.0	0.769	2.22	0.181	0.175	93.6
2		0.758	0.782	3.14	0.207	0.198	93.5	0.766	1.09	0.240	0.202	88.5
3		0.296	0.307	3.62	0.098	0.095	92.2	0.299	0.98	0.097	0.093	91.2
4		0.318	0.331	4.14	0.123	0.114	91.5	0.299	−5.55	0.123	0.108	84.7
5		1.000	1.024	2.35	0.216	0.211	94.8	1.024	2.42	0.220	0.212	94.7
1	E	0.752	0.773	2.70	0.204	0.196	93.1	0.770	2.28	0.204	0.191	92.4
2		0.758	0.771	1.68	0.205	0.193	92.5	0.786	3.74	1.858	0.204	86.2
3		0.296	0.310	4.50	0.110	0.103	91.6	0.302	1.78	0.109	0.099	90.2
4		0.318	0.323	1.83	0.118	0.109	90.9	0.287	−9.52	0.139	0.100	79.1
5		1.000	1.034	3.41	0.250	0.246	94.0	1.025	2.51	0.245	0.233	93.3
1	U	0.784	0.821	4.75	0.190	0.189	95.2	0.788	0.56	0.201	0.194	93.1
2		0.844	0.878	4.00	0.183	0.167	94.1	0.805	−4.68	0.247	0.199	83.8
3		0.340	0.364	7.04	0.109	0.107	94.6	0.328	−3.47	0.106	0.103	89.4
4		0.462	0.481	4.10	0.118	0.113	94.2	0.350	−24.4	0.122	0.101	64.3
5		1.000	1.028	2.80	0.232	0.234	94.1	1.029	2.94	0.249	0.235	93.1

^*B = balanced covariate, E = unbalanced favoring exposed, U = unbalanced favoring unexposed

Table 8.

Simulation statistics for the estimated mean ratio for the APV (ZINB/logit-log model) and direct (ZINB/log-log model) methods on data generated from the ZIBB/logit-logit model (φ = 0.5) with continuous covariate, n = 1000 per group.

Scenario	Balance*	True Mean Ratio (MR)	APV (logit-log) Approach					Direct (log-log) Approach
			Ave Est MR	Ave PE (%)	SD of Est MR	Ave SE	CP (%)	Ave Est MR	Ave PE (%)	SD of Est MR	Ave SE	CP (%)
1	B	0.752	0.759	0.82	0.055	0.054	94.8	0.755	0.38	0.055	0.054	94.5
2		0.759	0.765	0.76	0.061	0.061	95.0	0.775	2.02	0.081	0.063	87.3
3		0.296	0.301	1.49	0.030	0.03	94.8	0.294	−0.81	0.029	0.029	93.5
4		0.319	0.324	1.61	0.037	0.035	94.5	0.305	−4.39	0.037	0.035	89.2
5		1.000	1.002	0.18	0.066	0.065	94.5	1.002	0.19	0.066	0.065	94.5
1	E	0.752	0.751	−0.13	0.060	0.06	94.4	0.743	−1.29	0.059	0.058	93.4
2		0.759	0.755	−0.59	0.062	0.06	93.5	0.620	−18.3	0.063	0.051	28.7
3		0.296	0.296	−0.19	0.033	0.031	93.4	0.284	−4.09	0.031	0.029	89.4
4		0.319	0.317	−0.65	0.037	0.034	92.5	0.228	−28.5	0.029	0.025	10.5
5		1.000	1.003	0.27	0.073	0.074	95.3	0.990	−1.04	0.070	0.070	94.2
1	U	0.784	0.795	1.40	0.057	0.056	95.3	0.769	−1.85	0.060	0.059	92.9
2		0.844	0.857	1.45	0.052	0.051	94.6	0.872	3.26	0.082	0.068	89.4
3		0.340	0.352	3.47	0.032	0.032	94.5	0.323	−5.09	0.032	0.031	88.6
4		0.464	0.472	1.81	0.035	0.035	94.9	0.391	−15.6	0.050	0.033	40.8
5		1.000	1.003	0.28	0.066	0.066	95.3	1.016	1.61	0.072	0.072	95.1

^*B = balanced covariate, E = unbalanced favoring exposed, U = unbalanced favoring unexposed

For the direct approach (assuming the ZINB/log-log model), the average percent error (in absolute value) for n=100 per group is less than 6% for all five scenarios, but is as high as 25% when there is imbalance in the continuous covariate (Table 7). We note that there were two extreme mean ratio estimate values (of the order of 10¹⁵ or greater) obtained for the direct approach in the unbalanced covariate case. These values were removed from the overall statistics provided in the table. For n=1000 per group (Table 8) the average percent error (in absolute value) of the direct estimator is up to 4% in the balanced case and up to 29% in the unbalanced case, both occurring for Scenario 4 (high exposure and covariate effects). The cases of high percent error also tend to have substantially under-estimated standard errors and low coverage of confidence intervals. The results for a categorical covariate (not shown) are somewhat better with an average percent error for the direct method of less than 3% in the balanced case and less than 8% in the unbalanced case for n = 100 per group, and less than 1% in the balanced case and less than 5% in the unbalanced case for n = 1000 per group.

Similarly to the ZINB model results, as the ZIBB dispersion parameter increases, the finite sample bias and variance increases. The relative performance of the APV and direct methods for other dispersion parameter values (φ = 1 and 9) are similar to that for φ = 1/9. These results and others not shown here are available upon request.

5 Discussion

In this paper, we have studied the use of zero-inflated models for comparing overall response means between groups (exposures or treatments) while controlling for baseline covariates, as is often of interest in both clinical trials and observational studies. Zero-inflated models are appealing because of their ability to account for ‘extra’ zeros, relative to standard models such as Poisson and negative binomial, allowing them to often provide a good fit to count data from dental and other studies.

The first proposed method, the ‘average predicted value’ (APV) approach, involves the comparison of model-predicted response values for each individual under both the exposure and no-exposure conditions. A similar approach, as we discussed in the introduction, has been used by previous researchers in other contexts. However, the present paper generalizes this approach and extends it, apparently for the first time, to zero-inflated models. As we have sought to reveal, the APV approach is very flexible, being applicable to any zero-inflated regression model as well as other models not presented here. Other models of interest for zero-inflated data include the hurdle model²⁷ and mixture models²⁸, possibly extended to more than two subpopulations. In addition, the APV approach can be used for inference on any specified function of group means, such as the ratio or difference. We presented two version of the APV approach: one (‘parametric’) integrates the predicted function with respect to the covariates over their assumed parametric distribution, and the other (‘empirical’) sums over the empirical distribution of the covariates. The latter approach, which was emphasized in this paper, has several advantages: 1) it avoids distributional assumptions regarding the covariates; 2) it is computationally simple; and 3) it provides exposure effect estimates that are very close to that of the parametric approach when the model for the latter is correct, even for modest sample sizes (as shown in our simulation studies using normally-distributed covariates).

Upon the request of a referee, we conducted further simulation studies of the ZINB/logit-log model involving two covariates. In these scenarios, the two component models (logit and loglinear) either had the same covariates or one different covariate. The common covariate was either balanced or unbalanced and the second covariate was balanced across exposure groups. The covariates were generated as normally distributed and mutually independent. Both the empirical and parametric (integration) versions of the APV method were readily extended to these multiple covariate cases. The former used the same expression as before (7), possibly with different covariates (w) for the two models. The parametric approach integrated over the (correctly specified) multivariate normal distribution for the covariates (with estimated means and variances). The pattern of results and overall conclusions were quite similar to the single covariate case, and detailed results are therefore not included here but are available upon request.

In many situations, the variance of the estimated exposure effect can easily be obtained using the delta method (as was used in the present study). However, a bootstrap approach may be preferred in more complex situations. Our simulation studies showed low bias for the APV estimator under the correct (ZINB or ZIBB) model, even for the case of an unbalanced continuous covariate. However, there was a tendency of the delta method to underestimate standard errors (resulting also in under-coverage of confidence intervals) for relatively small sample sizes (n = 100 per group). The method based on the ZINB/logit-log model still does well when the true model is ZIBB. The small biases found appear to be due more to the difference in the shape of the functions (beta binomial versus negative binomial) than the fact than the negative binomial distribution ignores the upper bound of the count. This is seen by the very low bias found when we fit the ZINB model to data generated from a truncated ZINB distribution (results not shown here).

The second proposed method (the ‘direct’ approach) utilizes loglinear models for both components of the zero-inflated model. The primary appeal of this approach is its simplicity. Under the ‘log-log model’, the ratio of means is readily obtained as a function of the regression coefficients for exposure that does not involve the covariates. However, this approach is not applicable for other functions that may be of interest, such as the difference in group means. In addition, it is only applicable to certain zero-inflated models, for example ZINB, but not others such as ZIBB.

Both of the proposed methods were applied successfully to our dental data, corroborating previous results²⁵ that showed an unexpected negative (though, at best, marginally statistically significant) relationship between VLBW (versus NBW) and dental caries (DMFT). In light of our simulation studies, the fact that the results for the APV (ZINB/logit-log) and direct (ZINB/log-log) approaches were not greatly different may be due to the fact that the covariates (as assured by design) were fairly well balanced across the exposure groups in the dental study data.

An interesting finding of our simulation studies is that even when the loglinear regression function is incorrect (that is, the susceptible probability for the ZINB model follows a logistic regression rather than loglinear model), the direct approach in the case of a balanced covariate appears to provide valid inference for the overall mean ratio, and is also fairly robust if the true model is ZIBB/logit-logit. However, in the case of an unbalanced covariance this method can be substantially biased, particular when the covariate has a large effect on the outcome. Note that we consider the logit-log, a priori, as more plausible than the log-log model, as it provides the appropriate range restriction for the susceptible probability. However, when the log-log model is correct, as may be obtained in the case of categorical or bounded continuous covariates, then the results described above are essentially reversed for the APV (logit-log) and direct (log-log) estimators. It is therefore useful to note that either estimator appears to do well, even if an incorrect model choice is made, in the case where the covariate is balanced across exposure groups. Despite their being balanced, it is important to include any prognostic covariates in nonlinear models^29,30 such as those considered in the present paper; thus, our proposed methods are relevant in the balanced as well as unbalanced covariate cases.

In conclusion, we recommend the APV as an appropriate and flexible method for estimating covariate-adjusted overall exposure effects based on the ZINB (logit-log) and ZIBB (logit-logit) models. The direct (log-log model) approach may have a role as a quick and easy method for estimating the mean ratio in the case of a balanced covariate or when there is reason to suppose that the log-log model is correct. Further work is needed to study possible improved variance estimates for APV estimators for small samples.

Appendix: Demonstration of equivalence of estimands for the log-log model

Here we show that the APV approach to defining the mean ratio estimand, when applied to the ZINB/log-log model, produces the same estimand as the direct approach (9). This result obtains regardless of the distribution of w, thus for either the empirical distribution function (over a finite reference population G) or an assumed parametric (large reference population) distribution function for w.

For the empirical approach,

$$\begin{array}{l}{\theta }_R={\sum }_{i\in G}exp({\alpha }_0+{\alpha }_1+{\mathit{\alpha }}^{\prime }{\mathit{w}}_i)exp({\beta }_0+{\beta }_1+{\mathit{\beta }}^{\prime }{\mathit{w}}_i)/{\sum }_{i\in G}exp({\alpha }_0+{\mathit{\alpha }}^{\prime }{\mathit{w}}_i)exp({\beta }_0+{\mathit{\beta }}^{\prime }{\mathit{w}}_i)\\ =exp({\alpha }_0+{\alpha }_1+{\beta }_0+{\beta }_1){\sum }_{i\in G}exp\{({\mathit{\alpha }}^{\prime }+{\mathit{\beta }}^{\prime }){\mathit{w}}_i\}/exp({\alpha }_0+{\beta }_0){\sum }_{i\in G}exp\{({\mathit{\alpha }}^{\prime }+{\mathit{\beta }}^{\prime }){\mathit{w}}_i\}\\ =exp({\alpha }_1+{\beta }_1).\end{array}$$

For the parametric approach, the result is shown in a similar manner with the sum replaced by an integral (with respect to w, over an arbitrary distribution function F(w)). These results also hold where the two component models involve different covariates.