Testing for departures from additivity in mixtures of perfluoroalkyl acids (PFAAs)

Abstract

This study is a follow-up to a paper by Carr et al. that determined a design structure to optimally test for departures from additivity in a fixed ratio mixture of four perfluoroalkyl acids (PFAAs) using an in vitro transiently-transfected COS-1 PPARα reporter model with a mixing ratio that is based on average serum levels in NHANES subjects. Availability of information regarding potential for additivity of PFAAs in mixtures is critically important for risk assessors who are concerned with the ability of the compounds to affect human health and impact ecological systems. It is clear that exposures are not to single compounds, but to mixtures of the PFAAs. This paper presents the results from the data collected using the design from Carr et al. along with subsequent analyses that were performed to classify the relationships among mixtures of PFAAs. A non-linear logistic additivity model was employed to predict relative luciferase units (RLU), an indicator of PPARα activation. The results indicated a less than additive relationship among the four PFAAs. To determine if the possible “antagonism” is from the competition among or between carboxylates and sulfonates, four different binary mixtures were also studied. There was a less than additive relationship in all four binary mixtures. These findings are generally similar to two other reports of interfering interactions between PFAAs in mixtures. The most conservative interpretation for our data would be an assumption of additivity (and lack of a greater than additive interaction), with a potential for antagonistic interactions.

1. Introduction

The single-chemical effects of perfluoroalkyl acids (PFAAs) have been extensively studied and a range of toxicological endpoints have been reported following exposure in laboratory studies and wildlife, as reviewed in (Lau et al., 2007). These outcomes include immunotoxicity, hepatotoxicity, hormonal effects, and developmental toxicity. The mechanism of action for the biological effects of the PFAAs remains largely unknown, but activities mediated through the peroxisome proliferator activated receptor alpha (PPARα) have been considered key steps in the induction of liver tumors in the rat (Kennedy et al., 2004; Klaunig et al., 2003). PPARα was also shown to be necessary to mediate the developmental toxicity induced by perfluorooctanoic acid (PFOA) and perfluorononanoic acid (PFNA) in the mouse (Abbott et al., 2007; Wolf et al., 2010). Exposure to PFOA or PFNA throughout gestation in CD-1 or 129S1 strains of mice resulted in high rates of neonatal mortality in the first few hours or days after birth (Abbott et al., 2007; Wolf et al., 2010). However, in PPARα knockout mice, the neonatal mortality, growth deficits and developmental delay were not observed after exposure to PFOA or PFNA (Abbott et al., 2007; Wolf et al., 2010). These studies in mice suggested an important role for PPARα in mediating responses to PFAA compounds. There is also considerable evidence that PFAAs modify expression of genes that are directly regulated by PPARα (Abbott et al., 2012; Rosen et al., 2007, 2008, 2009). To further support that PPARα is involved in mediating effects of PFAAs, a recent study characterized the patterns of expression of PPAR receptors in developing human fetal tissues and effects of PFOA on fetal and postnatal mouse gene expression in nine different tissues (Abbott et al., 2010, 2012).

The ability of PFAA compounds to activate PPARα has also been demonstrated using transiently transfected COS-1 cells (Wolf et al., 2008, 2012). In those studies, a luciferase reporter was used to compare the ability of members of the PFAA family of compounds to activate mouse or human PPARα and it was revealed that the carbon chain length and functional moiety (carboxylate or sulfonate) of the compound influenced the responsiveness and that mouse PPARα was more responsive that human PPARα. This in vitro approach thus provides a valuable means to evaluate the potential interactions of various PFAAs in a mixture paradigm.

The biological effects described for individual PFAA compounds have led to an increased interest in the effect of the combinations of PFAAs. PFAAs are classified into two categories – carboxylates and sulfonates. The purpose of this report is to test the hypothesis that the single chemical data can be combined in an additivity model that may be used to predict their in vitro response from an environmentally relevant mixture of the PFAAs. For this investigation, two compounds with longer half-lives were selected from each group. From the carboxylates, PFOA and PFNA and from the sulfonates, perfluorooctane sulfonate (PFOS) and perfluorohexane sulfonate (PFHxS). All four of these PFAA chemicals have been detected in the U.S. general population at varying degrees in the NHANES biomonitoring program (Kato et al., 2011). In vitro data were previously published for each of these four compounds individually (Wolf et al., 2008). The present study extends the investigation for a fixed-ratio mixture for these four compounds as well as several binary mixtures.

2. Methods

2.1. Experimental data

In vitro data were collected for activation of mouse PPARα by Wolf et al. (2008) at varying concentrations (0 μM-100 μM) for each compound (i.e., PFOA, PFNA, PFOS, and PFHxS), tested on at least two transient transfection assays performed on different dates using COS-1 cells, as per common laboratory practice in measuring PPARα activation (Wolf et al., 2008). A concentration of 250 μM was also evaluated for PFOS, and these data were used in the analysis. Using biomonitoring data from the NHANES 2005–2006 dataset, a relevant mixing ratio was determined that represented the average proportion of each of the four PFAAs from human serum. Using the mixing ratio and the single chemical data, a model under the assumption of additivity was estimated and used to determine a local D-optimal design for a mixture study that would be robust to model misspecification since a design for a nonlinear model is dependent specification of model parameters a priori (Carr et al., submitted for publication). A D-optimal design is one that chooses dose locations in order to minimize the variance of the parameter estimates. In other words, the design lends itself to more precise estimation of the dose-response curves. The optimal design included 7 dose groups: 0, 20, 40, 50, 80, 100, and 200 μM, (combined total concentration of the 4 compounds). In experiments for this study, data were generated for a mixture of all 4 compounds and for selected binary mixtures of the compounds. The mixture data (expressed as Relative Luciferase Units, RLU) were collected under the same methods as the single chemical data (as described in Wolf et al., 2008) and experimental design details specific to the 4 compound and binary mixtures follow.

2.1.1. Mixture of 4 compounds

In vitro data were collected for activation of mouse PPARα following exposure to a mixture of PFOA, PFNA, PFOS, and PFHxS. The mixture and individual compounds were tested on 96-well plates with three replicate plates per assay and 3 independent assays total (each at different dates using cells of a different passage number). There were 7 dose groups (0, 20, 40, 50, 80, 100, and 200 μM) and each concentration was present in 8 wells on each plate. The total sample size for each dose is 72 (3 assays × 3 plates × 8 wells per plate = 72). Each plate also included a positive control Wy14643 at 10 μM and its vehicle, DMSO, with 4 wells for each of these controls. The plate also included the individual compounds at the concentrations present in the 100 μM mixture with 8 wells for each individual compound.

2.1.2. Binary mixtures

In vitro data were collected for activation of mouse PPARα following exposure to selected binary mixtures (PFOA:PFNA, PFOS:PFHxS, PFOA:PFOS, and PFNA:PFOS). As described for the 4 compound mixture studies, the mixtures were tested on 96-well plates with 3 replicate plates per assay and 3 independent assays total (each using cells at a different passage number). Binary mixtures were tested across a range of 9 concentrations in which the pair of compounds being tested was held at the previously determined mixing ratio, while the total concentration increased. As shown in Table 1, the range for the total concentration varied between the binary pairs. Each binary mixture assay included 4 wells of DMSO and 4 of WY14643, 8 wells of the water control, 8 wells of each mixture dose, and 8 wells of each individual compound at the concentration of that compound in the highest total dose.

Table 1.

Concentration of each compound and total dose (μM) in the binary mixture medium.

1	PFOA	1.9	3.8	5.7	7.6	9.5	11.4	15.2	22.8
	PFNA	0.6	1.2	1.8	2.4	3.0	3.6	4.8	7.2
	Total dose	2.5	5.0	7.5	10.0	12.5	15.0	20.0	30.0
2	PFOS	8.5	42.7	85.3	128.0	170.7	213.3	255.9	341.4
	PFHxS	1.5	7.3	14.7	22.0	29.3	36.7	44.1	58.6
	Total dose	10.0	50.0	100.0	150.0	200.0	250.0	300.0	400.0
3	PFOS	7.7	15.4	23.1	30.8	38.6	46.2	61.7	77.1
	PFOA	2.3	4.6	6.9	9.2	11.4	13.8	18.3	22.9
	Total dose	10.0	20.0	30.0	40.0	50.0	60.0	80.0	100.0
4	PFOS	22.9	45.7	68.6	91.4	114.3	137.1	160.0	182.9
	PFNA	2.2	4.3	6.5	8.6	10.8	12.9	15.1	17.1
	Total dose	25	50	75	100	125	150	175	200

2.1.3. Mixtures of 4 compounds and binary mixtures

Data for the DMSO and WY14643 present on each plate were excluded as was previously done in the analysis by Wolf et al. (2008). In addition, as per the methods from Wolf et al. (2008), outliers were excluded based on an r-student value of + −2.6, which corresponds to a two-sided p-value of 0.01. The residual values were the result of a fixed effects linear model that accounted for concentration and plate.

2.2. Outcome variable

The outcome of interest was relative luciferase units (RLU), which was calculated by standardizing the observed luciferase value from the Luciferase reporter assay kit (Promega) to the average of the control group (water) for each plate (Wolf et al., 2008). This artificially forced the mean of the control group to have a RLU value of 1. A log₁₀ transformation was used in the model to accommodate the skewness in the data – i.e., log₁₀(RLU). Through the transformation, the mean value of the control group is approximately 0 (log₁₀(1) = 0).

2.3. Statistical analysis

Following the single chemical required (SCR) method of Casey et al. (2004), a test of additivity for each fixed ratio mixture was conducted. Specifically, a nonlinear logistic model was fit to the data which allows for a sigmoidal dose-response shape between log(RLU) and the mixture dosages. The predicted dose response curve for each mixture was estimated using single chemical data in a nonlinear logistic additivity model. The test of additivity for each mixture is equivalent to a test of coincidence between the two corresponding dose-response curves. Details are provided in the appendix. Figures for all models are given to demonstrate model shape and fit.

3. Results

3.1. Four chemical mixture

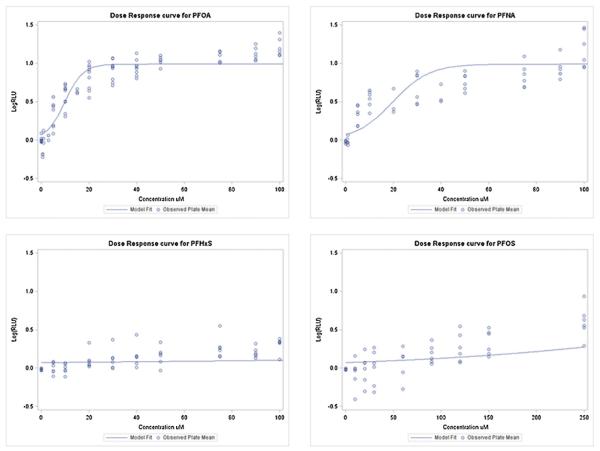
Fig. 1 contains the observed single chemical plate means and the plot of the mean predicted LogRLU at each dose group. The model fit was adequate for the whole concentration range for PFOS and PFHxS. For the remaining two PFAAs, the model fits well in the active region and an initial plateau, but there appears to be a slight increase after the plateau. The model used is restricted to a single active region and single plateau and therefore cannot fully capture this pattern. Because the primary interest in toxicological research is the lower concentration range (more relevant exposure ranges), the slight misspecification of the model in this region was deemed acceptable. Fig. 2 contains the estimated mean curve for the mixture data along with the observed plate means for the mixture data. The model fit was adequate for the mixture data and the LogRLU was adequately predicted. A simultaneous plot of the two curves is given in Fig. 3 for comparison. It is clear from the plot that the two curves have different slopes, which is confirmed by the test of coincidence (F_3,35 = 123.46, p-value < 0.0001). This test indicates that there is a significant difference in the slopes and therefore the mixture data violate the assumption of additivity as estimated from the single chemical data. Looking at Fig. 3, it can be seen that the departure from additivity is in the less than additive direction. By looking at the binary mixtures we will be able to determine if this is caused by the combination of carbonates and sulfonates or a more general competition for PPARα. The parameter estimates are given in Table A1 in Appendix.

Fig. 1.

Single chemical model fit from additivity model.

Fig. 2.

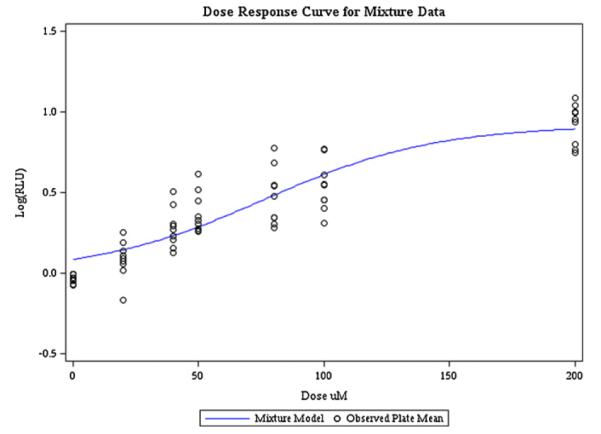
Mixture model fit under additivity assumption.

Fig. 3.

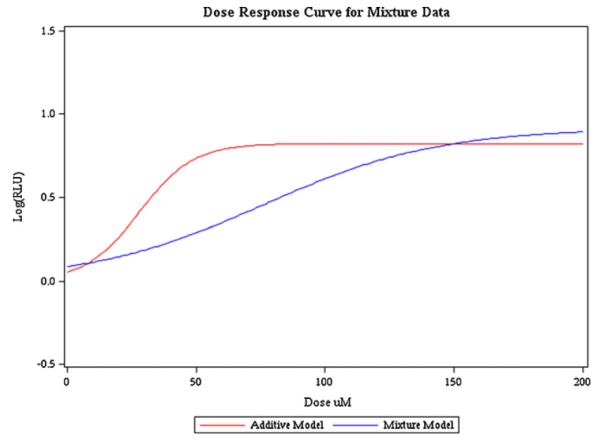
Simultaneous plot of models with and without additivity assumption.

3.2. Binary mixtures results

The binary mixture models were fit simultaneously with the additive data. As described above, the binary mixture data were used to estimate the slope and plateau parameter for the binary mixture model; the single chemical data were used to estimate the slope and plateau parameter for the additive model, and the complete data (binary mixtures and single chemical data) were used to estimate the intercept and random effect associated with the plate variation.

Using the same relative mixing ratio present in the four-chemical mixture for pairs of chemicals, the additive slopes were estimated. Table 2 lists the new mixing ratios.

Table 2.

Binary mixtures ratios and test results.

Mixture components	Ratio	Test
		F 2,62	p-value
PFOA, PFNA	76:24	46.9	<0.0001
PFOS, PFHxS	85:15	11.57	<0.0001
PFOS, PFOA	77:23	8.92	0.0004
PFOS, PFNA	92:8	10.86	<0.0001

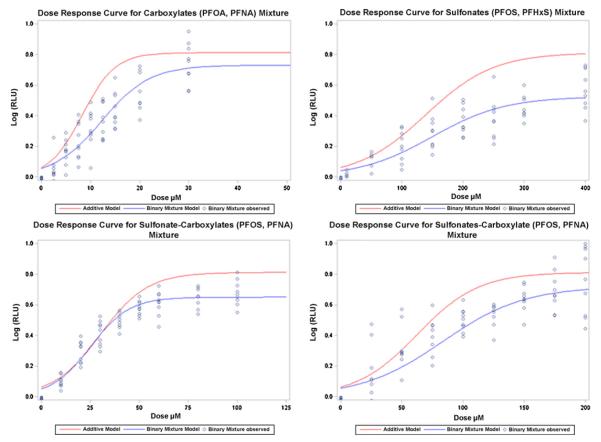
In each of the four mixtures, a test of coincidence was performed to determine if there was departure from additivity. The results are given in Table 2. For illustrative purposes, plots of all four mixtures are given in Fig. 4 (both under the additive assumption and the predicted mixture model along with the observed mixture data to show model fit). The curves in all four plots demonstrate a departure from additivity. The departure from additivity is deemed less than additive since a higher dose of the mixture is needed to reach the same outcome value as with the additive mixture. For parameter estimates, see Table A2 in Appendix.

Fig. 4.

Binary mixture plots.

4. Discussion

The results from the binary mixtures indicate that the less than additive responses seen in the mixture of all four PFAAs may be inherent in PFAAs and not due to the combination of carboxylates and sulfonates, as suspected. This could be due to the competition of the 4 PFAAs for the same receptor, PPARα. While the occurrence of less than additive responses is typically thought of as a change in a slope parameter, in the non-linear setting we are working in, the plateau parameter is directly related to the slope and vice versa. It seems as though the plateau parameter is responsible for more of the departure from additivity than the slope parameter. That is, if the models were fit only in the response region (i.e. before the plateau), the two mixtures may be deemed additive.

The study of interactions of PFAA mixtures is clearly important for evaluation of risk for exposed human and wildlife populations. However, there is very little information available and we could only find two other studies that experimentally evaluated PFAA mixtures. The first of these studies (Wei et al., 2009) tested the effects of PFAA mixtures on gene expression in primary cultured hepatocytes of rare minnows using a custom cDNA microarray. PFOA, PFNA, PFOS, perfluorodecanoic acid (PFDA), perfluorododecanoic acid (PFDoA), and 8:2 fluorotelomer alcohol (FTOH 8:2) were evaluated individually and in four mixture formulations. Their mixture ratios were based on reported environmental levels (15 mg/L combined concentration). PFOA and PFOS were present at equal levels in one mixture, whereas in two other mixtures PFOA and PFOS represented 50% of the PFAAs, respectively. Analysis of gene expression in the exposed hepatocytes revealed different patterns of effects on gene expression for the carboxylates compared to PFOS or 8:2 FTOH. It was of interest that patterns of effects on gene expression for the PFOA- or PFOS-dominant mixtures, and in the PFOA:PFOS mixture, were not detected in the responses to the individual compounds. These data were believed to support an interpretation that co-exposure to PFOA and PFOS, together or in combination with other PFAAs, trigger distinctly different functions and activate multiple cellular responses, distinct from those that may occur following exposure to a single PFAA. This seems to be a reasonable assumption as the effects of PFAA exposure undoubtedly occur at multiple levels, including effects on metabolism, signal-transduction, and transcriptional and post-transcriptional regulation of gene expression. The complexity of the levels of responses complicates the interpretation of the responses to mixtures of PFAAs, particularly if single exposures and mixtures elicit different profiles of cellular response. Although this study was conducted in cultured fish hepatocytes, a differential response to mixtures is similar to the findings of the present study in which we report an interaction between PFAAs that affects responsiveness to PPARα activation. The second study that we found dealt with combined toxicity of PFOA and PFOS and used a bioluminescent cyanobacterial toxicity test to compare interactions of PFOA and PFOS with other pollutants, using a Combination-Index method to evaluate binary, ternary and multicomponent mixtures (Rodea-Palomares et al., 2012). A binary mixture of PFOA and PFOS was reported to have “an antagonistic interaction across the whole range of effect levels” and this was believed to explain the finding that these compounds also generally interacted antagonistically with the other pollutants tested.

Although these aquatic models are very different from the mammalian COS-1 transiently transfected PPARα model used to generate the data for our mixtures, it is very interesting that both models report antagonistic interaction between PFOA and PFOS. Caveats for interpreting our data, and limitations that should be noted, include (1) the fact that these data are based on an in vitro model for activation of PPARα and may not necessarily reflect the outcomes in an intact animal model; (2) this is a mouse, not human, PPARα reporter; (3) the NHANES mixing ratio, although appropriate for investigating a particular mixture that reflects the serum levels of PFAAs in the general population in the US, may not necessarily reflect the levels or compounds found in all nationalities, in specific highly exposed populations, or be representative of mixtures found in wildlife. It is also important to remember that other PFAA compounds can be found in the environment and that the pharmacokinetics that affect body burdens differ for the various perfluorinated compounds and across species (Lau, 2012).

In summary, our study of the interactions between PFAAs using an in vitro transiently-transfected COS-1 PPARα reporter model with an NHANES-based mixing ratio suggested a less than additive relationship in a mixture of four PFAAs, and an apparent interference between the PFAAs for activation of PPARα in the binary mixtures. However, if models were fit only in the low-dose response region the mixtures may be deemed additive. These findings are generally similar to two other reports of interfering interactions between PFAAs in mixtures. Availability of information regarding potential for additivity of PFAAs in mixtures is critically important for risk assessors who are concerned with the ability of the compounds to affect human health and impact ecological systems. It is clear that exposures are not to single compounds, but to mixtures of the PFAAs. The most conservative interpretation for our data would be an assumption of additivity (and lack of a greater than additive interaction), with a potential for antagonistic interactions.

Appendix A. Modeling details

The definition of additivity (i.e., zero interaction) used here is given by Berenbaum (1985) and can be related to the isobologram for a combination of chemicals (e.g., Loewe and Muischnek, 1926; Loewe, 1953) through the interaction index. That is, in a combination of c chemicals, let E_i represent the concentration/dose of the ith component alone that yields a fixed response, y₀, and let x_i represent the concentration/dose of the ith component in combination with the c agents that yields the same response. According to this definition of additivity if the substances combine with zero interaction, then

$$\sum _{i=1}^c\frac{x_i}{E_i}=1.$$ (1)

If the left-hand side of (1), termed the interaction index, is less than 1, then a greater than additive relationship can be claimed at the combination of interest. If the left-hand side of (1) is greater than 1, then a less than additive relationship can be claimed at the combination. This definition of additivity is a general form for dose-addition. It should be pointed out that use of the toxic equivalency factor (TEF) approach assumes common dose-response slopes across the chemicals under study; the general dose-addition definition of (1) does not require such an assumption.

In short, a nonlinear additivity model that is algebraically equivalent to Berenbaum’s definition of additivity was used to predict the response from a fixed-ratio mixture. Mixture data were experimentally generated using an experimental design with statistically important characteristics: a D-optimal design robust to model (i.e., additivity model) misspecification (Carr et al., submitted for publication). This report presents the results from testing the hypothesis of additivity for the specified fixed-ratio mixture of the four PFAAs and four binary mixtures.

Preliminary analyses indicated the variance of the response log(RLU) (denoted Y) remained constant with increased mean response. Thus, in subsequent analyses, we assume Var(Y) = τ. There was indication of a plate effect which was accounted for in two ways – (1) by standardizing to the mean of the control group and (2) by allowing for correlation between observations on the same plate through a random coefficients model. Since there is often correlation among observations from the same plate, observations within a plate were assumed to have variance, ω and observations from different plates were assumed to be independent. Preliminary analyses indicated that the dose-response relationship differed slightly from plate to plate and therefore suggested the use of a random coefficients model.

There was evidence of a significant correlation between data from the same plate, which was accounted for with the random plate effect (p-value = 0.0003). The correlation between observations on the same plate is estimated by the intraclass correlation, ω/(ω + τ). Individual plates are assumed to be independent from each other.

A.1. Model: four-chemical mixture

The nonlinear logistic function was used to model the mean log(RLU) (μ) and is algebraically equivalent to the interaction index set to 1, i.e.

$$\mu =\frac{\gamma }{1+\exp (-({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_3{x}_3+{\beta }_4{x}_4\left)\right)}$$ (2)

where x₁, x₂, x₃, and x₄ are the concentration in (μM) for PFOS, PFOA, PFNA, and PFHxS, respectively. Through algebraic steps, the model in (2) can be shown to be equivalent to the equation in (1), i.e., the model in (2) is an additivity model in the sense of the definition of dose addition used in isobolograms and as described by Berenbaum (1985):

$$\begin{array}{cc}\hfill & \mu =\frac{\gamma }{1+\exp \left(-\left({\beta }_0+\sum _{j=1}^4{\beta }_j{x}_j\right)\right)}\hfill \\ \hfill & 1+\exp \left(-\left({\beta }_0+\sum _{j=1}^4{\beta }_j{x}_j\right)\right)=\frac{\gamma }{\mu }\hfill \\ \hfill & \exp \left(\left({\beta }_0+\sum _{j=1}^4{\beta }_j{x}_j\right)\right)=\frac{\gamma -\mu }{\mu }\hfill \\ \hfill & {\beta }_0+\sum _{j=1}^4{\beta }_j{x}_j=\log \left(\frac{\mu }{\gamma -\mu }\right)\hfill \\ \hfill & \sum _{j=1}^4{\beta }_j{x}_j=\log \left(\frac{\mu }{\gamma -\mu }\right)-{\beta }_0\hfill \\ \hfill & \sum _{j=1}^4\frac{{\beta }_j{x}_j}{\log (\mu ∕(\gamma -\mu \left)\right)-{\beta }_0}=1\hfill \\ \hfill & \sum _{j=1}^4\frac{x_j}{\left(\log \right(\mu ∕(\gamma -\mu ))-{\beta }_0)∕{\beta }_j}=1\hfill \\ \hfill & \sum _{j=1}^4\frac{x_j}{E_j}=1\hfill \end{array}$$

Using this definition of additivity, the form of the joint model for the jth plate is:

$$\begin{array}{cc}\hfill {\mu }_{\mathit{addj}}& =\frac{{\gamma }_{\mathit{add}}+{\phi }_j}{1+\exp (-({\beta }_{0,\mathit{add}}+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_3{x}_3+{\beta }_4{x}_4\left)\right)}\hfill \\ \hfill {\mu }_{\mathit{mixj}}& =\frac{{\gamma }_{\mathit{mix}}+{\phi }_j}{1+\exp (-({\beta }_{0,\mathit{mix}}+{\theta }_{\mathit{mix}}\times t\left)\right)}\hfill \end{array}$$

where x₁, x₂, x₃, and x₄ are the concentrations (in μM) for PFOS, PFOA, PFNA, and PFHxS, respectively. For the additive model using a fixed ratio, $\left[\begin{array}{c}\hfill x_1\hfill \\ \hfill x_2\hfill \\ \hfill x_3\hfill \\ \hfill x_4\hfill \end{array}\right]=\left[\begin{array}{c}\hfill a_1\hfill \\ \hfill a_2\hfill \\ \hfill a_3\hfill \\ \hfill a_4\hfill \end{array}\right]\times t$ where a_i represents the proportion of the ith chemical in the mixture and t represents the total molar concentration for the mixture. The additive portion of the model can therefore be simplified by substituting θ_add = ∑β_i × α_i. The weights, a_i, were estimated from biomonitoring data from NHANES (2005–2006). From a previous analysis, the weights were estimated to be: 0.64, 0.19, 0.06 and 0.11 for PFOS, PFOA, PFNA and PFHxS, respectively (Carr et al., submitted for publication). The simplified form of the model for the jth plate is:

$$\begin{array}{cc}\hfill {\mu }_{\mathit{addj}}& =\frac{{\gamma }_{\mathit{add}}+{\phi }_j}{1+\exp (-({\beta }_{0,\mathit{add}}+{\theta }_{\mathit{add}}\times t\left)\right)}\hfill \\ \hfill {\mu }_{\mathit{mixj}}& =\frac{{\gamma }_{\mathit{mix}}+{\phi }_j}{1+\exp (-({\beta }_{0,\mathit{mix}}+{\theta }_{\mathit{mix}}\times t\left)\right)}\hfill \end{array}$$

This joint model includes the random effect for each plate, φ_j, to take into account the correlation of the data within each replicate plate. This random effect is assumed to be normally distributed with a mean of 0 and a variance denoted ω. This model combines the data to estimate the variance components ω and τ. The single chemical data are used in the estimation of γ_add, β_0,add, θ_add. The mixture data are used to estimate γ_mix, β_0,mix, θ_mix.

Unknown model parameters in the model were estimated using an Adaptive Gaussian Quadrature criterion in PROC NLMIXED with the Dual Quasi-Newton algorithm in SAS (version 9.2).

Table A1.

Parameter estimates for joint four chemical mixture with and without assumption of additivity.

Parameter	Estimate	Standard error	t value	p-value	95% confidence interval
γadd	0.825	0.045	18.2	<0.0001	0.733	0.917
β0,add	−2.672	0.088	−30.4	<0.0001	−2.851	−2.493
θadd	0.096
β1 (PFOS)	0.019	0.002	12.5	<0.0001	0.016	0.022
β2 (PFOA)	0.324	0.015	22.0	<0.0001	0.294	0.354
β3 (PFNA)	0.326	0.018	18.1	<0.0001	0.289	0.362
β4 (PFHxS)	0.022	0.002	11.1	<0.0001	0.018	0.026
γmix	0.917	0.073	12.6	<0.0001	0.769	1.066
β0,mix	−2.253	0.099	−22.8	<0.0001	−2.453	−2.053
θmix	0.030	0.002	16.9	<0.0001	0.026	0.033
τ	0.028	0.001	34.9	<0.0001	0.027	0.030
ω	0.042	0.011	4.0	0.0003	0.021	0.064

The assumption of additivity was assessed using a three parameter test of coincidence:

$$\begin{array}{cc}\hfill & H_0:{\gamma }_{\mathit{add}}={\gamma }_{\mathit{mix}}\hfill \\ \hfill & {\beta }_{0,\mathit{add}}={\beta }_{0,\mathit{mix}}\hfill \\ \hfill & {\theta }_{\mathit{mix}}={\theta }_{\mathit{add}}\hfill \end{array}$$

An F-test with 3 numerator degrees of freedom was used to evaluate departures from additivity.

A.2. Model: binary mixtures

In order to further assess the relationship among the PFAAs, four binary mixtures were experimentally evaluated and analyzed. The binary mixtures included a set of carboxylates (PFOA with PFNA), a set of sulfonates (PFOS with PFHxS) and two mixtures of the two subclasses (PFOS with PFOA and PFOS with PFNA). These experiments were performed in order to determine if any interactions that are detected could result from the combination of the carboxylates and the sulfonates, with a possible less than additive relationship between carboxylates and sulfonates in the same mixture, and a potentially additive relationship among the carboxylates and among the sulfonates. The binary mixtures maintained the original relative ratio and are described further in Table 1. A joint model was fit to estimate the model under additivity and to estimate the dose-response relationship among the binary mixtures. The random effect for the plate and the intercept parameter were estimated using the entire dataset, whereas the additive parameters only used the single chemical data and the binary mixture parameters were estimated using the corresponding binary mixture data. The form of the model for a given plate (j) is given by:

$$\begin{array}{cc}\hfill {\mu }_{\mathit{addj}}& =\frac{{\gamma }_{\mathit{add}}+{\phi }_j}{1+\exp (-({\beta }_0+{\theta }_{\mathit{add}}\times t\left)\right)}\hfill \\ \hfill {\mu }_{\mathit{carbj}}& =\frac{{\gamma }_{\mathit{carb}}+{\phi }_j}{1+\exp (-({\beta }_0+{\theta }_{\mathit{carb}}\times t\left)\right)}\hfill \\ \hfill {\mu }_{\mathit{sulf}j}& =\frac{{\gamma }_{\mathit{sulf}}+{\phi }_j}{1+\exp (-({\beta }_0+{\theta }_{\mathit{sulf}}\times t\left)\right)}\hfill \\ \hfill {\mu }_{\mathit{osoaj}}& =\frac{{\gamma }_{\mathit{carb}}+{\phi }_j}{1+\exp (-({\beta }_0+{\theta }_{\mathit{osoa}}\times t\left)\right)}\hfill \\ \hfill {\mu }_{\mathit{osnaj}}& =\frac{{\gamma }_{\mathit{osna}}+{\phi }_j}{1+\exp (-({\beta }_0+{\theta }_{\mathit{osna}}\times t\left)\right)}\hfill \end{array}$$

This joint model includes the random effect for each plate, φ_j to take into account the correlation of the data within each replicate plate. This random effect is assumed to be normally distributed with a mean of 0 and a variance denoted ω. This model combines the data to estimate β₀ and the variance components ω and τ. The single chemical data are used in the estimation of γ_add and θ_add. The binary mixture data are used to estimate their corresponding slope and plateau parameters (γ and θ). In order to assess the interaction among the binary mixtures, four 2-degree-of-freedom tests of coincidence will be calculated (i.e., coincidence of the slope and plateau parameter between the additivity models and the corresponding mixture model). Each will be of the form:

$$\begin{array}{cc}\hfill H_0:& {\gamma }_{\mathit{add}}={\gamma }_{\mathit{mix}}\hfill \\ \hfill {\theta }_{\mathit{add}}& ={\theta }_{\mathit{mix}}\hfill \end{array}$$

For each of the binary mixtures: θ_add = ∑β_i × α_i.

Table A2.

Binary mixtures results.

Parameter	Estimate	Standard error	t value	p-value
β0	−2.50	0.051	−49.28	<0.0001
γadd	0.81	0.037	22.05	<0.0001
γpfoa,pfna	0.73	0.059	12.26	<0.0001
γpfos,pfhxs	0.53	0.059	8.9	<0.0001
γpfos,pfoa	0.65	0.056	11.44	<0.0001
γpfos,pfna	0.72	0.058	12.54	<0.0001
β1 (PFOS)	0.02	0.001	14.82	<0.0001
β2 (PFOA)	0.30	0.011	28.18	<0.0001
β3 (PFNA)	0.30	0.014	21.33	<0.0001
β4 (PFHxS)	0.02	0.002	12.04	<0.0001
θpfoa,pfna	0.20	0.009	22.43	<0.0001
θpfos,pfhxs	0.02	0.001	14.75	<0.0001
θpfos,pfoa	0.10	0.004	23.86	<0.0001
θpfos,pfna	0.03	0.002	21.73	<0.0001
τ	0.02	0.0005	47.37	<0.0001
ω	0.03	0.005	5.25	<0.0001

Table A3.

Binary mixture ratios, parameter estimates and test results.

Mixture components	Ratio	Additive model		Mixture model		Test
		β	γ	β	γ	F2,62	p-value
PFOA, PFNA	76:24	0.303	0.81	0.208	0.73	46.9	<0.0001
PFOS, PFHxS	85:15	0.018	0.81	0.017	0.53	11.57	<0.0001
PFOS, PFOA	77:23	0.083	0.81	0.100	0.65	8.92	0.0004
PFOS, PFNA	92:8	0.040	0.81	0.033	0.72	10.86	<0.0001

A.3. Results: four-chemical mixture

There was a significant intraclass correlation among observations from the same plate, which was estimated to be 0.6. The rest of the parameter estimates for the additive model are given in Table A1. As state before, this model combines the data to estimate the variance components ω and τ. The single chemical data are used in the estimation of γ_add, β_0,add, θ_add. The mixture data are used to estimate γ_mix, β_0,mix, θ_mix (Table A3)

A.4. Results: four-chemical mixture

The results for the four-chemical mixture are given in Table A2. The complete data are used to estimate β₀ and the variance components ω and τ. The single chemical data are used in the estimation of γ_add and θ_add. The binary mixture data are used to estimate their corresponding slope and plateau parameters (γ and θ).

Recall that the additive portion of the model fit five parameters (four slope parameters and a new plateau parameter). So, while the slope parameter may be greater than the additive model slope, it does not necessarily indicate a “greater than additive” relationship. Both the slope and the plateau need to be considered to determine if there is a greater than or less than additive relationship. For example, the mixture of PFOS and PFOA, the additive slope parameter is estimated to be 0.083 while the binary mixture model has an estimated slope of 0.1, which is greater than the additive slope. However, the plateau parameters for these two models are also very different: the plateau for the mixture is much lower than the additive mixture. This is an indication of a less than additive relationship, which can be seen more clearly in Fig. 4.