Abstract
The speed of computations in neocortical networks critically depends on the ability of populations of spiking neurons to rapidly detect subtle changes of the input and translate them into firing rate changes. However, high sensitivity to perturbations may lead to explosion of noise and increased energy consumption. Can neuronal networks reconcile the requirements for high sensitivity, operation in low-noise regime and constrained energy consumption? Using intracellular recordings in slices from rat visual cortex we show that layer 2/3 pyramidal neurons are highly sensitive to minor input perturbations. They can change their population firing rate in response to small artificial excitatory postsynaptic currents (EPSCs) immersed in fluctuating noise very quickly, within 2–2.5 ms. These quick responses were mediated by generation of new, additional action potentials, but also by shifting spikes into the response peak. In that latter case, the spike count increase during the peak and the decrease after the peak cancelled each other, thus producing quick responses without increases of total spike count and associated energy costs. The contribution of spikes from one or the other source depended on the EPSC timing relative to the waves of depolarization produced by on-going activity. Neurons responded by shifting spikes to EPSCs arriving at the beginning of a depolarization wave, but generated additional spikes in response to EPSCs arriving towards the end of a wave. We conclude that neuronal networks can combine high sensitivity to perturbations and operation in low-noise regime. Moreover, certain patterns of on-going activity favor this combination and energy-efficient computations.
Keywords: rat neocortex, slices, population coding, response speed, signal detection time
INTRODUCTION
Accumulating evidence suggests that cortical networks use sparse code for representing sensory stimuli and processing. Sparseness means that information is encoded by activity of a small sub-population of neurons, and often in a few, temporally precise spikes (Theunissen 2003; Olshausen, Field 2004; Wolfe et al., 2010). Examples of sparse coding in the brain range from representation of visual objects and scenes, sounds, and somatosensory information in respective sensory cortices (e.g. Olshausen, Field 1996; Lewicki 2002; Brecht, Sakmann 2002) and odors in the olfactory bulb (Spors, Grinvald 2002), to feedback projections from motor to sensory cortices (Petreanu et al 2012) and decision-making networks of parietal cortex (Harvey et al 2012). Although occasionally cortical synapses can be strong (Miles, Wong 1983; Volgushev et al., 1995; Galarreta, Hestrin 2001; Song et al., 2005; Lefort et al., 2009; Ikegaya et al., 2013), the vast majority of connections between cortical neurons are weak. To achieve sparse coding using these weak connections, neurons should be sensitive to subtle changes of their inputs. Indeed, recent studies showed that neocortical neurons are highly sensitive to even minor perturbations at their inputs (London et al., 2010; Tchumatchenko et al., 2011; Ilin et al., 2013). Moreover, neurons can change their firing rate in response to small amplitude current steps embedded in the fluctuating input very fast, on the scale of 1–2 ms (Tchumatchenko et al., 2011; Ilin et al., 2013). However, in a system built of highly sensitive elements any perturbation, including noise, may be amplified, leading to a “noise explosion” (London et al., 2010). High level of noise would necessitate the use of strong signals for communication between neuronal ensembles and create unfavorable conditions for temporal coding, thus forcing the use of rate coding (London et al., 2010). It would also lead to increased energy consumption, which is an important constraint on processing abilities of the brain (Attwell, Laughlin 2001; Lennie 2003; Harris et al., 2012). It remains unclear, whether high sensitivity to perturbations is compatible with operation in low-noise regime that favors sparse temporal coding. Here we show, using intracellular recordings in slices from rat visual cortex that layer 2/3 pyramidal neurons can respond to small artificial EPSCs by changing their population firing rate very quickly, within ~2 ms after the EPSC onset. Quick increase of the firing rate was produced by generation of new, additional action potentials but also by shifting spikes into the response peak. Neurons typically responded by shifting spikes to EPSCs arriving at the beginning of a depolarization wave. Because these responses did not lead to an increase of total spike count, they would not lead to an explosion of firing, an increase of noise and related energy costs in the system. We conclude, that neuronal networks can combine both, high sensitivity to perturbations and operation in low-noise regime, and that certain patterns of on-going activity are especially favorable for this combination and for energy-efficient computations.
MATERIALS and METHODS
All experimental procedures used in this study were in accordance with National Institutes of Health regulations. Experimental protocols were approved by the Institutional Animal Care and Use Committee of University of Connecticut. In vitro intracellular recordings were made in slices of rat visual cortex. The details of slice preparation and recording were similar to those previously used (Volgushev et al., 2000; Tchumatchenko et al., 2011; Ilin et al., 2013). The Wistar rats (P21–P28, Charles River or Harlan, USA) were anaesthetized with isoflurane (Baxter, USA), decapitated, and the brain was rapidly removed. One hemisphere was mounted onto an agar block and 350μm thick coronal slices containing the visual cortex were cut with a vibrotome (Leica, Germany) in ice cooled oxygenated solution. After cutting, the slices were placed into an incubator where they recovered for at least one hour at room temperature before transferring them in to the recording chamber. The solution used during the preparation of the slices had the same ionic composition as the perfusion/extracellular solution. It contained (in mM) 125 NaCl, 2.5 KCl, 2 CaCl2, 1 MgCl2, 1.25 NaH2PO4, 25 NaHCO3, 25 D-glucose and was bubbled with 95% O2 and 5% CO2. In some experiments synaptic transmission was blocked by adding 25 μM APV, 5 μM DNQX and 80 μM PTX to the extracellular solution. Chemicals were obtained from Sigma-Aldrich or Tocris.
Recordings were made with the slices in submerged conditions at 28–32°C. Temperature in the recording chamber was monitored with a thermocouple positioned close to the slice, 2–3mm from the recording site. Whole-cell recordings using patch electrodes were made from layer 2/3 pyramidal neurons, selected under visual control using Nomarski optics and infrared videomicroscopy. The patch electrodes were filled with K-gluconate based solution (in mM: 130 K-Gluconate, 20 KCl, 4 Mg-ATP, 0.3 Na2-GTP, 10 Na-Phosphocreatine, 10 HEPES) and had a resistance of 4–6MΩ. Recordings were performed using the bridge mode of Axoclamp-2A (Axon Instruments, USA) or Dagan BVC-700A (Dagan Corporation, USA) amplifier. After amplification and low-pass filtering at 10 kHz, data were digitized at 20kHz and fed into a computer (Pentium4; Digidata 1440A interface and pCLAMP software, Molecular Devices).
Fluctuating current for injection into a neuron ση(t) was synthesized to mimic the effect produced in the soma by numerous balanced excitatory and inhibitory synaptic inputs (Destexhe, Pare 2003). η (t) was an Ornstein-Uhlenbeck process with zero mean, unit variance and correlation time τI=50 ms, and σ was the standard deviation of the resulting background current noise, scaled to achieve membrane potential fluctuations of ~15–20 mV amplitude. Membrane potential fluctuations produced by the injected current were similar to those recorded in neocortical neurons in vivo (Azouz, Gray 2000; Destexhe, Pare 2003; Volgushev et al., 2003, 2006). Each realization of the noise current was injected either as “noise only”, or with artificial EPSCs added at a rate 1/s (Fig. 1B,C). aEPSCs were synthesized with rise time 1ms, decay time 10ms and peak amplitude of 20pA. During current injection, a DC current was added if necessary to maintain desired firing rate of ~4–5 Hz in most of experiments or ~1 Hz in some experiments as indicated. All currents were injected into the soma through the whole-cell recording pipette. Current injections lasted 46s, and were separated by a recovery period of 60–100s.
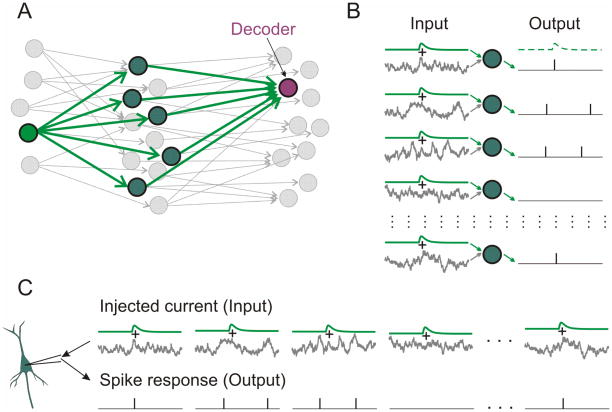
Figure 1. Experimental paradigm: How to study population encoding in slices.
A: A scheme of three-layer network of neurons. Green arrows show divergent connections from one first-layer neuron (“source neuron”) onto neurons of the second layer which converge on a third-layer neuron (“decoder”). Other neurons and connections are shown in gray.
B: Input to each second-layer neuron consists of individual fluctuating noise and a common EPSCs produced by an action potential in the source neuron. Population firing of these neurons provides synaptic input to the decoder neuron in layer three.
C: In experiment, artificial EPSCs (aEPSCs) immersed in different episodes of fluctuating noise are injected in a cell sequentially. This mimics population encoding from B.
Processing
Data were processed offline in Matlab (The Mathworks, Natick, MA). Spikes were detected in membrane potential traces as positive zero crossings. Spike timings were used for constructing PSTH histograms, and for estimating EPSC detection probability.
The probability of EPSC detection was quantified using a theoretical decoder (Tchumatchenko et al., 2011; Ilin et al., 2013) that reports a change in the input when the population firing rate exceeds the 95% quantile of the pre-signal distribution. The probability of detection was estimated as function of time interval T (from 0.4 ms to 10 ms after the EPSC onset), for populations of N=300, N=1000 and N=3000 neurons using bootstrap analysis and calculated from theoretical distributions. For bootstrap analysis, we composed 100 trial sets of N=300 (or 1000, or 3000) randomly selected sweeps. For each time interval T we first used all 100 trial sets to calculate distribution of spike counts during pre-signal interval T and defined 95% quantile of this distribution. Next, for each trial set, we determined whether the spike count in the interval T after the EPSC onset fell outside the 95% quantile of the pre-signal distribution. The number of trial sets, which fulfill this condition, provides an estimate of the probability for a population of N neurons to detect the EPSC within time T after its onset. The whole procedure was then repeated 30 times for N=300 (or 1000 or 3000) neurons to obtain results shown as open circles in Fig. 2D.
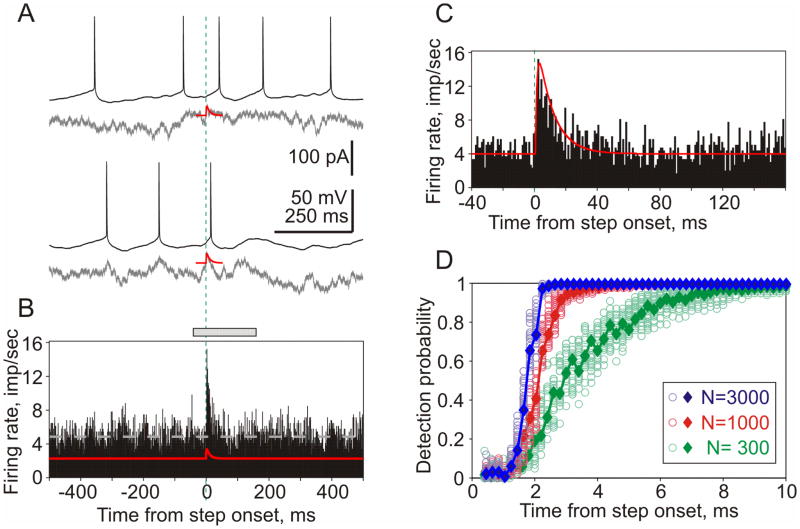
Figure 2. Rapid detection of small EPSCs in population firing.
A: Responses of a neocortical neuron to injection of two episodes of fluctuating noise current (gray traces) with immersed small aEPSCs (red).
B: Firing rate changes of a neuronal population in response to injection of fluctuating current with immersed aEPSCs (red trace). Data from 11 neurons; total of N=2959 repetitions. Bin 1 ms. Dashed gray line shows averaged firing rate (4.84 imp/sec).
C: Zoom in of response peak, a portion the histogram indicated by gray bar on top of B. Green vertical dashed lines in A–C show EPSC onset.
D: Probability of EPSC detection by populations of 300, 1000 and 3000 neurons vs. time. Results of bootstrapping (circles) and theoretical curves (diamonds, solid lines).
Theoretical curves of detection probability were calculated as follows. The distribution of the number of spikes in a window of length T after the signal onset Dpost and the distribution of the number of spikes in a window of the same length before signal onset Dpre were modeled as two independent binomial distributions with N equal to the number of neurons (N=300 or N=1000 or N=3000), and success probabilities Ppost (after EPSC onset) and Ppre (before EPSC onset), respectively. The success probabilities Ppost and Ppre were estimated using data from all recordings as average probabilities of spikes, that is
The theoretical detection probabilities were then computed as the probability that a Binomial distribution B(N,Ppost) exceeds the 95% quantile of a Binomial distribution B(N,Ppre), that is
with FB(N,Ppost) and F−1B(N,Ppre) denoting the distribution and quantile function of a Binomial random variable with parameters N and P, respectively. Distributions and quantiles were computed using the Matlab programs binoinv and binocdf.
Significance of an increase or decrease of spike count in responses to injection of fluctuating currents with immersed aEPSCs as compared to responses to currents without EPSCs was calculated based on a one-sided version Welch’s t-test. Spike count was considered significantly (p<0.05) increased (decreased) if the lower (upper) bound of the one-sided confidence interval for the difference of the mean spiking rate was above (below) zero.
RESULTS
We used an established approach to study firing rate responses of neuronal populations (Silberberg et al., 2004; Tchumatchenko et al., 2011; Ilin 2013). Consider a population of independent neurons receiving input from one common fiber (Fig. 1A). Each neuron of the population has a unique pattern of background activity (“noise”) which is different from other neurons, but also receives an input from a common fiber, which is the same for all neurons in the population (Fig. 1B). Background activity in each neuron is mimicked by injecting fluctuating noise current, which is different for different cells, and common input is mimicked by introducing a common signal, an artificial EPSC (aEPSC) injected in all neurons. Recording from all neurons of the population simultaneously (Fig 1B) is mathematically equivalent to successive recording of responses of several cells to the signal immersed in different realizations of the fluctuating noise (Fig. 1C). Averaging the successively recorded responses provides an estimate of the population response, whereby the number of repetitions is equivalent to the number of neurons in the population (Silberberg et al., 2004).
Figure 2A shows membrane potential responses to the injection of two different realizations of fluctuating noise with immersed aEPSC. PSTH constructed using spikes from N=2959 such responses exhibits a clear peak at the aEPSC onset (Fig. 2B,C). The firing rate changes sharply, within ~2 ms after the aEPSC onset. A theoretical decoder that reports a change in the input if the population firing rate exceeds 95% quantile of the pre-signal distribution (Ilin et al., 2013), can report the change of firing rate of a population of N=1000 or N=3000 neurons very quickly, within 2–2.5 ms (Fig. 2D). With decreasing the size the population to N=300, the time required for detection increases to about 5–6 ms (Fig. 2D, green). The high sensitivity of neocortical neurons to aEPSCs described above is consistent with recent in vivo (London et al., 2010) and in vitro (Tchumatchenko et al., 2011) results. Also the quantification of the detection speed of aEPSCs and its dependence on the size of neuronal population are in agreement with recent reports on quick detection of small DC current steps by populations of neocortical neurons in vitro (Tchumatchenko et al., 2011; Ilin et al., 2013).
However, high sensitivity of neurons to input perturbations and high speed of firing rate responses to subtle changes of the input may have undesirable effects on operation of neuronal networks. Generation of new spikes in response to any additional EPSC may lead to amplification of random perturbations and thus to “noise explosion” in the system (London et al., 2010) and respective increase of energy consumption. It remains unclear how these undesirable effects are counteracted in neuronal networks. One possibility here is to change timing of spikes, so that APs that are about to be generated sometime during the next few dozens of ms, will be actually generated earlier, upon arrival of an additional EPSC. In this scenario, EPSC would still produce a peak in the population firing rate, but it will not lead to additional spikes and related undesirable network effects. This “redistribution” hypothesis predicts that (i) after the EPSC-produced peak the firing rate will decrease below the average, and (ii) number of spikes in the histogram peak will be higher than total increase of the spike count.
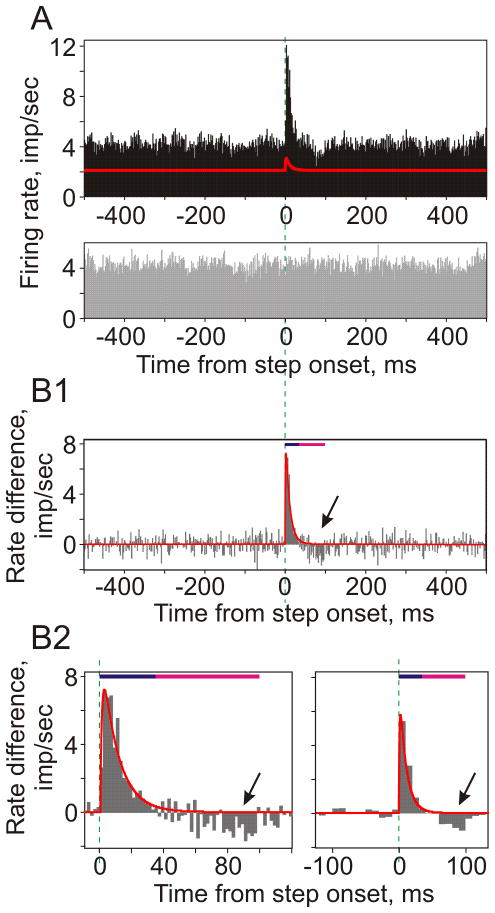
To test these predictions, we injected neurons with pairs of fluctuating currents: one sweep consisting of fluctuating noise with aEPSCs immersed in it, as in the experiments described above, and the other sweep in a pair containing the same fluctuating noise only, without aEPSCs. Figure 3A shows firing rate changes of a large population of neurons (N=12105, mean firing rate 4.2 Hz) in response to injection of fluctuating noise with (black) and without (gray) an immersed aEPSCs. Because injections of fluctuating current induce reliable and reproducible spike responses in neocortical neurons (Mainen, Sejnowski 1995), the difference between the two histograms (Fig. 3B) provides an estimate of the firing rate change caused by the addition of aEPSCs relative to control. The difference histogram demonstrates that, first, the shape of the histogram peak (0–35 ms after the aEPSC onset) reproduces precisely the shape of the injected aEPSC. Second, it reveals a decrease of the firing rate after the peak during 35–100 ms after the aEPSC onset (oblique arrows in Fig. 3, B1–B2). The decrease of population firing rate stands out clearly in the zoom-in of the response and with a bigger bin size (Fig. 3, B2). It indicates that some of the spikes generated in noise-only condition did not appear during 35–100 ms of responses to aEPSCs immersed in noise. Moreover, increase of total spike count in responses to injection of noise with aEPSCs as compared to noise-only (Nnew=781 spikes) was less than number of spikes in the peak (0–35 ms, Npeak=1146 spikes). Thus, response peak was composed of action potentials originating from two sources. Out of 1146 spikes in the response peak, about two thirds were “new”, or “additional” spikes, which would not be generated in response to injection of noise current without an aEPSC (Nnew=781, or 68% of Npeak=1146). The remaining one third of the response peak was composed of “shifted” spikes, i.e. those that would be generated in response to noise-only injection, but an addition of an aEPSC changed their timing shifting them into the response peak (Nshifted= Npeak − Nnew =365, or 32% of Npeak=1146). The effect of shifting spikes into the response peak by an addition of aEPSC was also clearly present in experiments with a lower rate of background firing (1.1 Hz, Nshifted=229, or 22% of Npeak=1065). These results are consistent with the above predictions of the redistribution hypothesis.
Figure 3. Transient firing rate response to small aEPSCs is produced both by generation of additional APs and shifting the „existing“ spikes.
A: Firing rate changes of a large neuronal population (data from 17 neurons, N=12105 repetitions; bin 2 ms) in response to injection of fluctuating current with immersed aEPSCs (top), and responses to the same fluctuating current but without EPSCs (gray histogram, bottom).
B: Difference between population firing induced by injection of fluctuating current with and without aEPSCs, calculated using data from A. Red line shows aEPSC, scaled to match the amplitude of histogram peak. Bottom panels show zoom-in of the peak region (left) and histogram with 10ms bin (right). In all three histograms, dark blue bars show duration of aEPSC and the histogram peak (0–35ms), magenta bars show period of decreased firing (arrows, 35–100ms).
What determines whether response to an EPSC is composed of added or shifted spikes? To address this question we exploited the fact that the peak of the population response reproduces precisely the shape of aEPSC (Fig. 3). This allowed us to specify for the following analysis two intervals: one that included the peak (0–35 ms after aEPSC onset), and another one that included the trough of the firing rate response (35–100 ms). Generation of additional action potentials in response to EPSC would produce a histogram peak that is not followed by a decrease of the firing rate below the mean. In contrast, shifting spikes into the peak would lead to firing rate decrease after the peak. In the next series of experiments, we have repeatedly injected in 5 neurons 45 pairs of episodes of fluctuating noise with or without immersed aEPSC (Fig. 4A). Each pair of episodes was injected 110 times. For each pair we computed difference histograms (Fig. 4B). Note that histograms in each column are computed using responses to multiple injections of the same realization of the fluctuating current. For this reason, noise-only histograms are not flat and difference histograms in Fig. 4B do not reproduce the aEPSC shape. However, because the firing rate response of a population of neurons receiving independent fluctuating input reproduces reliably the aEPSC shape (Fig. 3), we have used the defined above windows to calculate changes in spike count during the response peak (0–35 ms, dark blue bar in Fig. 4B, bottom) and during the trough (35–100 ms, magenta bar in Fig. 4B, bottom). Figure 4B illustrates 4 types of difference histograms. Histograms of the first type expressed an increase of the firing rate during 0–35 ms after the aEPSC onset (p<0.05), followed by a comparable decrease of the firing rate below the mean level during 35–100 ms interval (Fig. 4B, left column). The histogram peak was thus produced by shifting the spikes that would occur later in responses to noise-only current injection. In histograms of the second type, increase of the firing rate during 0–35 ms was not followed by a significant decrease during the 35–100 ms interval, indicating that aEPSC led to generation of additional spikes, not present in responses to noise-only injection (Fig. 4B, second column). In histograms of the third type the peak was followed by firing rate decrease, but the decrease was of a smaller magnitude than the peak. We interpreted this as an indication that both additional and shifted spikes contributed to the peak (Fig. 4B, third column). Finally, type four histograms show little EPSC-related firing rate changes. In fact, on most of such occasions neither injection of noise-only current nor injection of noise with aEPSCs evoked spikes during the specified intervals (Fig. 4B, right column).
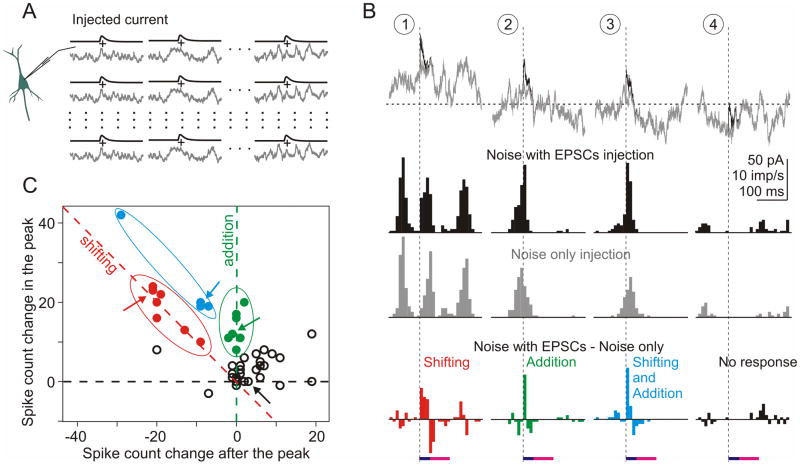
Figure 4. Differential contribution of added and shifted spikes to the histogram peak.
A: Experimental paradigm. A set of 45 different episodes of fluctuating noise with or without immersed aEPSCs were injected in neurons repeatedly (N=110 repetitions).
B: Examples of 4 (out of 45) episodes of the injected currents and firing rate responses. Gray traces of noise without aEPSCs are superimposed on black traces with immersed aEPSCs, vertical dashed lines show aEPSC onset. Horizontal dashed line shows DC current (0.255 nA) used to achieve target firing rate of 4 to 6 imp/sec.
Histograms show firing rate responses to the injected currents with (black) or without (gray) immersed EPSCs, and their difference (colored histograms). Horizontal bars on the bottom show measuring windows corresponding to the duration of aEPSC/histogram peak (dark blue, 0–35 ms), and the period of decreased firing (magenta, 35–100 ms), same as in Fig. 3B. For each of the 45 difference histograms, number of spikes was measured in these windows.
C: Spike count in the peak (0–35 ms) vs. spike count after the peak (35–100 ms) of 45 difference histograms. Red symbols (n=7) show cases when spikes were “shifted” to produce histogram peak: spike number increase in the histogram peak was balanced by the decrease after the peak. Green symbols (n=7) show cases in which the histogram peak was produced by additional, “new” spikes: spike count was increased in the peak but did not change after the peak. Blue symbols (n=4) show cases with both added and shifted spikes. Open symbols show remaining (n=27) cases. Arrows indicate data for 4 episodes from B.
Scatter plot in Fig. 4C shows results of this analysis for all 45 episodes. Each point represents data for one pair of noise episode, with the spike count change in the peak (0–35 ms after the aEPSC onset) plotted against spike count change during 35–100 ms interval. Note that calculations were made using the difference histograms, so spike count values can be negative. When the histogram peak was produced by shifting spikes, i.e. the increase in spike count during the peak was compensated by the decrease in spike count in 35–100 ms interval (type 1 histogram), data points are located at or around the negative-slope diagonal (red dashed line in Fig. 4C). When the peak was produced by added spikes (type 2 histogram), respective data points are located around the ordinate (green dashed line in Fig. 4C). Data points located between the negative-slope diagonal and the ordinate represent cases in which the histogram peak was composed of both added and shifted spikes (histogram type 3).
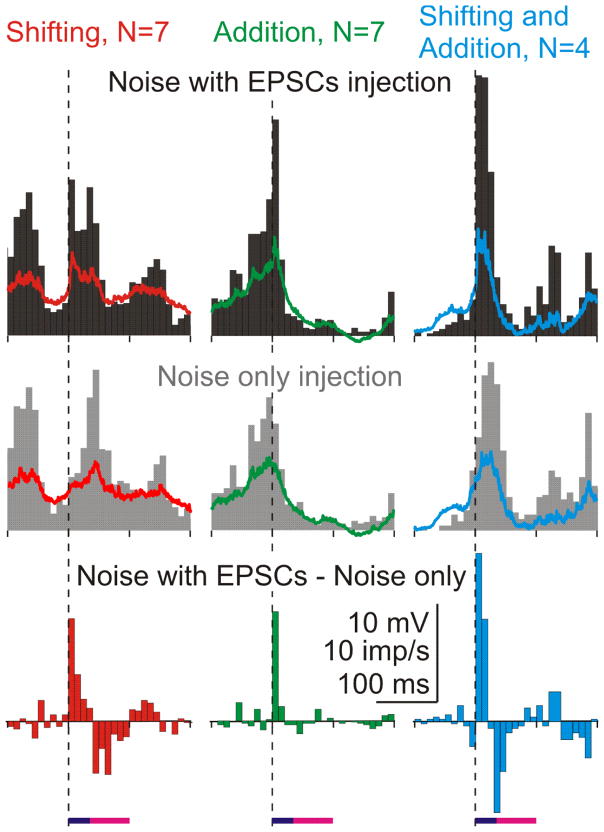
We argued that the reason why an EPSC leaded to additional spikes in some cases but shifted spikes into the peak in the other cases may lay in the difference between patterns of the ongoing membrane potential fluctuations at which EPSCs arrived. To test this conjecture, we have selected N=7 cases in which the histogram peak was produced by shifted spikes, N=7 cases in which the peak was formed by additional spikes, and N=4 cases in which both added and shifted spikes contributed to the peak (red, green and blue points, delineated within ellipses of respective color in Fig. 4C). For each of the three groups, we computed the PSTHs and averaged traces of the membrane potential (Fig. 5). The pattern of background activity was clearly different for the three groups. When aEPSCs arrived at the beginning of a depolarizing wave and associated increase in population firing, they shifted the spikes into the response peak (Fig. 5, left column). When arrived towards the end of a depolarizing wave, aEPSCs evoked additional spikes (Fig. 5, middle column). Arriving in the middle of the activity wave, aEPSCs shifted spikes and evoked additional ones (Fig. 5, right column). Thus, the pattern of on-going activity determines whether additional spikes will be generated in response to an EPSC, or whether a neuron will respond by shifting the spikes, without net increase of the firing rate.
Figure 5. Relative contribution of added and shifted spikes to response peak depends on the pattern of background activity.
Firing rate changes in episodes in which response peak was composed of shifted spikes (n=7, left column), added spikes (n=7, middle column) and a combination of shifted and added spikes (n=4, right column). Responses to injection of fluctuating noise with aEPSCs, noise only, and their difference. Averaged membrane potential traces are superimposed on the respective histograms. Dashed vertical lines show onset of aEPSCs.
DISCUSSION
Results of the present study show that populations of cortical neurons are highly sensitive to even minor perturbations of their input, and can change their firing rate very quickly, within 2–2.5 ms in response to small EPSCs. Quick firing rate responses to EPSCs were mediated by (1) generation of new, additional action potentials, and (2) shifting spikes into the peak, so that increased spike count during the response peak was compensated by the decrease of the number spikes that occur after the peak. The contribution of spikes from one or the other source to the response peak depended on the EPSC timing relative to the pattern of on-going activity.
The high sensitivity of neocortical neurons to small aEPSCs is consistent with recent results reported for neurons of other types and/or from other cortical regions (London et al., 2010; Tchumatchenko et al., 2011). In pyramidal neurons from layer 5 of rat barrel cortex in vivo, injection of subtle artificial EPSCs (~25 pA amplitude) led to detectable change of neurons’ firing. Moreover, action potentials induced in a single neuron by depolarizing pulses, led to a measurable change of the population firing of neighboring neurons (London et al., 2010). In layer 3 pyramidal neurons from rat visual cortex in vitro, injection of small current steps immersed in fluctuating noise led to clear changes in population firing which could be detected quickly, on a ms time scale (Tchumatchenko et al., 2011; Ilin et al., 2013). Prior data also showed that neocortical neurons connected via strong synapses (~180 pA amplitude) can communicate fast (Galarreta, Hestrin 2001), and that few strong connections may define preferred pathways for transmission of sensory information in neocortical networks (Lefort et al., 2009; Teramae et al 2012; Ikegaya et al., 2013). Our results extend these findings, showing that populations of neocortical neurons can respond to small EPSC-shaped signals immersed in fluctuating noise by changing their firing rate quickly, within ~2 ms after the aEPSC onset. This demonstrates that weak synaptic connections can effectively influence neuronal firing and thus propagation of signals in neocortical networks. Moreover, neocortical neuronal ensembles are able to communicate fast, on a ms-time scale, using weak signals. High sensitivity for subtle changes of the input and the ability to communicate fast using weak signals are vital features for sparse encoding in cortical networks (Olshausen, Field 1996; Theunissen 2003; Olshausen, Field 2004; Wolfe et al., 2010).
Downside of the high sensitivity is that any perturbation, including noise, can lead to firing rate changes. In multilayer networks consisting of highly sensitive elements this may lead to amplification of signal-irrelevant events leading to “noise explosion” (London et al., 2010), runaway firing and eventually to an over-excitation in the system. These effects would have devastating consequences for operation of neural networks. Increased noise would lead to a degradation of signal-to-noise ratio, demanding stronger signals for processing. Increased firing rate and demand for stronger signals would lead to dramatic increase of energy consumption. Generation of each action potential is associated with a chain of energy demanding processes, such as restoration of ionic gradients disturbed by currents involved in initiation and propagation of the action potential, transmitter release and postsynaptic currents, that totally account for about ~50% to ~70% of energy consumption in the cortex (Attwell, Laughlin 2001; Lennie 2003; Harris et al., 2012; Howarth et al., 2012). These undesirable consequences may take place when neurons respond to changing inputs by generation of additional action potentials. Explosion of activity can be prevented by inhibition: ample evidence indicates that cortical neuronal networks operate in a balanced regime (van Vreeswijk, Sompolinsky, 1996; Okun, Lampl 2008; Ozeki et al., 2009). Our results indicate an additional mechanism that helps to prevent explosion of noise and metabolic costs of computations in neuronal networks. When firing rate responses to EPSCs are mediated by shifting spikes into the response peak, these problems do not occur at all. Because net number of spikes generated by a population of neurons does not change, neither the noise in the system, nor energy consumption would increase. Rather, the response will be manifested as redistribution of the neuronal activity, so that refined firing pattern will incorporate information about the EPSC and its timing.
In our experiments, ~1/3 of the response peak in the PSTH was due to shifted spikes. How does spike timing can be shifted? We argued that when neuron is about to generate a spike in response to injection of fluctuating noise, addition of an EPSP may advance the timing of the spike initiation, thus “shifting” it into the response peak. Once spike is generated, it raises the threshold for generation of further spikes, thus leading to a trough in the histogram after the response peak. This interpretation is consistent with in vivo data showing that action potential threshold is influenced by the history of membrane potential changes during few dozens of ms, and cell firing during ~1 s preceding the spike (Azouz, Gray 1999; Henze, Buzsaki 2001).
The contribution of shifted vs. added spikes to the response peak depended on the pattern of ongoing activity. Activities of neuronal ensembles across various brain regions and states express distinct temporal structure, examples ranging from hippocampal theta-rhythm during active exploration (Buzsaki 2006) or responses to sensory stimuli (e.g. Volgushev et al., 2003) to slow sleep waves (Steriade, Timofeev, 2003; Chauvette et al., 2011). Activation of a single inhibitory neuron can completely shunt action potential generation or shift its timing in pyramidal neurons in the hippocampus (Cobb et al., 1995; Miles et al., 1996). Our present results show that excitatory inputs, activated at certain phases of on-going rhythm, can also produce a clear, detectable change of the firing rate mediated by changing the timing of action potentials, without generation of additional spikes. In this regime, despite high sensitivity of neurons to input perturbations (Galarreta, Hestrin 2001; London et al., 2010; Tchumatchenko et al., 2011), noise level would remain low, as would the metabolic costs of neuronal computations (Attwell, Laughlin 2001; Lennie 2003; Harris et al., 2012). Redistribution of discharges of neuronal populations rather than generation of additional spikes may be one mechanism of refinement of firing pattern of neuronal ensembles – a desirable feature for a multitude of neural functions that rely on precise timing of spikes, such as spike timing dependent synaptic plasticity (Caporale, Dan 2008), or effective temporal coding in sensory processing (Gray, Singer 1989; Singer 1999).
Acknowledgments
We are grateful to Marina Chistyakova, James Chrobak and Harvey Swadlow for comments on the manuscript. Supported by grant from the RFBR to AM and grant R01MH087631 from the NIH and start-up funds from University of Connecticut to MV and.
ABBREVIATIONS
- AP
action potential
- EPSC
excitatory postsynaptic current
- aEPSC
artificial excitatory postsynaptic current
- PSTH
peristimulus time histogram
References
- Attwell D, Laughlin SB. An energy budget for signaling in the grey matter of the brain. J Cereb Blood Flow Metab. 2001;21:1133–1145. doi: 10.1097/00004647-200110000-00001. [DOI] [PubMed] [Google Scholar]
- Azouz R, Gray CM. Cellular mechanisms contributing to response variability of cortical neurons in vivo. J Neuroscience. 1999;19:2209–2223. doi: 10.1523/JNEUROSCI.19-06-02209.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azouz R, Gray CM. Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. Proc Natl Acad Sci U S A. 2000;97:8110–8115. doi: 10.1073/pnas.130200797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brecht M, Sakmann B. Dynamic representation of whisker deflection by synaptic potentials in spiny stellate and pyramidal cells in the barrels and septa of layer 4 rat somatosensory cortex. J Physiology. 2002;543:49–70. doi: 10.1113/jphysiol.2002.018465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G. Rhythms of the brain. Oxford University Press; 2006. p. 448. [Google Scholar]
- Caporale N, Dan Y. Spike timing-dependent plasticity: A Hebbian learning rule. Ann Rev Neurosci. 2008;31:25–46. doi: 10.1146/annurev.neuro.31.060407.125639. [DOI] [PubMed] [Google Scholar]
- Chauvette S, Crochet S, Volgushev M, Timofeev I. Properties of slow oscillations during slow-wave sleep and anesthesia in cats. J Neurosci. 2011;31:14998–15008. doi: 10.1523/JNEUROSCI.2339-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cobb SR, Buhl EH, Halasy K, Paulsen O, Somogyi P. Synchronization of neuronal activity in hippocampus by individual GABAergic interneurons. Nature. 1995;378:75–78. doi: 10.1038/378075a0. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Pare D. The high-conductance state of neocortical neurons in vivo. Nat Rev Neurosci. 2003;4:739–751. doi: 10.1038/nrn1198. [DOI] [PubMed] [Google Scholar]
- Galarreta M, Hestrin S. Spike transmission and synchrony detection in networks of GABAergic interneurons. Science. 2001;292:2295–2299. doi: 10.1126/science.1061395. [DOI] [PubMed] [Google Scholar]
- Gray CM, Singer W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc Natl Acad Sci USA. 1989;86:1698–1702. doi: 10.1073/pnas.86.5.1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris JJ, Jolivet R, Attwell D. Synaptic energy use and supply. Neuron. 2012;75:762–777. doi: 10.1016/j.neuron.2012.08.019. [DOI] [PubMed] [Google Scholar]
- Harvey CD, Coen P, Tank DW. Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature. 2012;484:62–68. doi: 10.1038/nature10918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henze DA, Buzsaki G. Action potential threshold of hippocampal pyramidal cells in vivo is increased by recent spiking activity. Neuroscience. 2001;105:121–130. doi: 10.1016/s0306-4522(01)00167-1. [DOI] [PubMed] [Google Scholar]
- Ikegaya Y, Sasaki T, Ishikawa D, Honma N, Tao K, Takahashi N, Minamisawa G, Ujita S, Matsuki N. Interpyramidal spike transmission stabilized the sparseness of recurrent network activity. Cerebral Cortex. 2013;23:293–314. doi: 10.1093/cercor/bhs006. [DOI] [PubMed] [Google Scholar]
- Ilin V, Malyshev A, Wolf F, Volgushev M. Fast computations in cortical ensembles require rapid initiation of action potentials. J Neurosci. 2013;33:2281–2292. doi: 10.1523/JNEUROSCI.0771-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefort S, Tomm C, Sarria JCF, Peterson CCH. The excitatory neuronal network of the C2 barrel column in mouse primary somatosensory cortex. Neuron. 2009;61:301–316. doi: 10.1016/j.neuron.2008.12.020. [DOI] [PubMed] [Google Scholar]
- Lennie P. The cost of cortical computation. Neuron. 2003;13:493–497. doi: 10.1016/s0960-9822(03)00135-0. [DOI] [PubMed] [Google Scholar]
- Lewicki MS. Efficient coding of natural sounds. Nat Neurosci. 2002;5:356–363. doi: 10.1038/nn831. [DOI] [PubMed] [Google Scholar]
- London M, Roth A, Beeren L, Haeusser M, Latham PE. Sensitivity to perturbations in vivo implies high noise and suggests rate coding in cortex. Nature. 2010;466:123–127. doi: 10.1038/nature09086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ. Reliability of spike timing in neocortical neurons. Science. 1995;268:1503–1506. doi: 10.1126/science.7770778. [DOI] [PubMed] [Google Scholar]
- Miles R, Toth K, Gulias AI, Hajos N, Freund TF. Differences between somatic and dendritic inhibition in the hippocampus. Neuron. 1996;16:815–823. doi: 10.1016/s0896-6273(00)80101-4. [DOI] [PubMed] [Google Scholar]
- Miles R, Wong RK. Single neurones can initiate synchronized population discharge in the hippocampus. Nature. 1983;306:371–373. doi: 10.1038/306371a0. [DOI] [PubMed] [Google Scholar]
- Okun M, Lampl I. Instantaneous correlation of excitation and inhibition during ongoing and sensory-evoked activity. Nat Neurosci. 2008;11:535–537. doi: 10.1038/nn.2105. [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. 1996;381:607–609. doi: 10.1038/381607a0. [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Sparse coding of sensory inputs. Curr Opin Neurobiol. 2004;14:481–487. doi: 10.1016/j.conb.2004.07.007. [DOI] [PubMed] [Google Scholar]
- Ozeki H, Finn IM, Schaffer ES, Miller KD, Ferster D. Inhibitory stabilization of the cortical network underlies visual surround suppression. Neuron. 2009;62:578–592. doi: 10.1016/j.neuron.2009.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petreanu L, Gutnisky DA, Huber D, Xu N-L, O’Connor DH, Tian L, Looger L, Svoboda K. Activity in motor-sensory projections reveals distributed coding in somatosensation. Nature. 2012;489:299–303. doi: 10.1038/nature11321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silberberg G, Bethge M, Markram H, Pawelzik K, Tsodyks M. Dynamics of population rate codes in ensembles of neocortical neurons. J Neurophysiol. 2004;91:704–709. doi: 10.1152/jn.00415.2003. [DOI] [PubMed] [Google Scholar]
- Singer W. Neuronal synchrony: A versatile code for the definition of relations? Neuron. 1999;24:49–65. doi: 10.1016/s0896-6273(00)80821-1. [DOI] [PubMed] [Google Scholar]
- Song PLoS Biology. 2005 [Google Scholar]
- Spors H, Grinvald A. Spatio-temporal dynamics of odor representations in the mammalian olfactory bulb. Neuron. 2002;34:301–315. doi: 10.1016/s0896-6273(02)00644-x. [DOI] [PubMed] [Google Scholar]
- Steriade M, Timofeev I. Neuronal plasticity in thalamocortical networks during sleep and waking oscillations. Neuron. 2003;37:563–576. doi: 10.1016/s0896-6273(03)00065-5. [DOI] [PubMed] [Google Scholar]
- Tchumatchenko T, Malyshev A, Wolf F, Volgushev M. Ultrafast population encoding by cortical neurons. J Neurosci. 2011;31:12171–12179. doi: 10.1523/JNEUROSCI.2182-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teramae JN, Tsubew Ym Fukai T. Optimal spoike-based communicationin excitable networks with strong-sparse and weak-dense links. Sci Reports. 2012;2:485. doi: 10.1038/srep00485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theunissen FE. From synchrony to sparseness. Trends Neurosci. 2003;26:61–64. doi: 10.1016/s0166-2236(02)00016-4. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C, Sompolinsky H. Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science. 1996;274:1724–1726. doi: 10.1126/science.274.5293.1724. [DOI] [PubMed] [Google Scholar]
- Volgushev M, Chauvette S, Mukovski M, Timofeev I. Precise long-range synchronization of activity and silence in neocortical neurons during slow-wave oscillations. J Neurosci. 2006;26:5665–5672. doi: 10.1523/JNEUROSCI.0279-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volgushev M, Pernberg J, Eysel UT. Gamma-frequency fluctuations of the membrane potential and response selectivity in visual cortical neurons. Europ J Neurosci. 2003;17:1768–1776. doi: 10.1046/j.1460-9568.2003.02609.x. [DOI] [PubMed] [Google Scholar]
- Volgushev M, Vidyasagar T, Chistiakova M, Yousef T, Eysel UT. Membrane potential and spike generation in rat visual cortical slices during reversible cooling. J Physiology. 2000;522:59–76. doi: 10.1111/j.1469-7793.2000.0059m.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volgushev M, Voronin LL, Chistiakova M, Artola A, Singer W. All-or-none excitatory postsynaptic potentials in the rat visual cortex. European J Neuroscience. 1995;7:1751–1760. doi: 10.1111/j.1460-9568.1995.tb00695.x. [DOI] [PubMed] [Google Scholar]
- Wolfe J, Houweling AR, Brecht M. Sparse and powerful cortical spikes. Curr Opin Neurobiol. 2010;20:306–312. doi: 10.1016/j.conb.2010.03.006. [DOI] [PubMed] [Google Scholar]