Quantitative assessment of flow and electric fields for electrophoretic focusing at a converging channel entrance with interfacial electrode

Abstract

The electric field and flow field gradients near an electrified converging channel are amenable to separating and focusing specific classes of electrokinetic material, but the detailed local electric field and flow dynamics in this region have not been thoroughly investigated. Finite elemental analysis was used to develop a model of a buffer reservoir connected to a smaller channel to simulate the electrophoretic and flow velocities (which correspond directly to the respective electric and flow fields) at a converging entrance. A detailed PTV (Particle Tracking Velocimetry) study using charged fluorescent microspheres was performed to assess the model validity both in the absence and presence of an applied electric field. The predicted flow velocity gradient from the model agreed with the PTV data when no electric field was present. Once the additional forces that act on the large particles required for tracing (dielectrophoresis) were included, the model accurately described the velocity of the charged particles in electric fields.

1 Introduction

Since its inception capillary electrophoresis (CE) has matured into a highly efficient analytical technique amenable to multiplexed, microfluidic separations of compounds and biomolecules from complex samples [1-3]. Despite its advantages, the low concentration sensitivity with typical CE and related techniques remains a major drawback [4]. This has spurred an interest in methods designed to improve sensitivity without compromising the distinguishing benefits of electrophoretic separations.

Many techniques have relied on the equilibrium gradient principle summarized by Giddings [5] to achieve the improved sensitivity. Here, constant forces opposed to a gradient cause a unique and specific equilibrium position to where analytes with similar properties, such as net charge, mass, size, etc., migrate to from all parts of the separation domain. Separation and concentration occur simultaneously and diffusional band-broadening is minimized as restoring forces on both sides of the equilibrium position act to keep the concentration plug focused. Isoelectric focusing (IEF) [6, 7], counteracting chromatographic electrophoresis (CACE) [8], electric field gradient focusing (EFGF) [9], and temperature gradient focusing (TGF) [10], to name a few, have all successfully exploited the equilibrium gradient technique by establishing continuous in-channel gradients to separate analytes serially within the confines of a channel.

Other techniques have been developed to establish a focusing condition near a converging channel entrance where fluid velocity and electric field gradients typically exist. Many of these designs were primarily developed for the purpose of pre-concentrating all analytes for injection into a channel for further electrophoretic separation, and consequently little attention was given to the possibility of separation selectivity at the entrance region [11-13]. Some works, however, explored the feasibility of exploiting the relatively sharp field gradient at the entrance to create a selective focusing condition. Under these conditions, some analytes of a particular electrophoretic (EP) mobility could be excluded from entering the channel and concentrated in an inlet buffer reservoir, while other analytes, with different EP mobilities, pass through to an exit reservoir [14-17]. The separation condition described here is fundamentally different from the techniques that create a continuous gradient to separate analytes serially along the gradient. Rather, this technique is designed to establish a single differentiation zone that would be of little value as a stand-alone separation tool, but could be of significant value in a serial or parallel (array) format where the electric field and detection element of each array unit could be specifically tailored and independently operated to concentrate a chosen category of analytes in bulk solution.

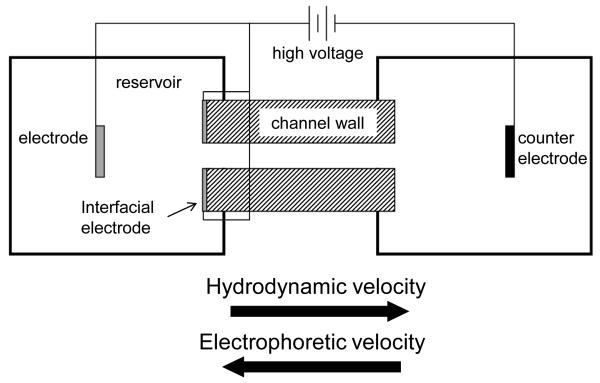
Works to establish the exclusion condition at the entrance have predominantly used traditional CE electrode configurations, where the anode and cathode electrodes are placed in the buffer reservoir away from the channel entrance and exit [14-17]. It is presumed that with this configuration, flow and electric field gradients largely overlap, thereby increasing the complexity of optimizing a discrete, high resolution separation zone at the entrance. Pacheco et al. [18] numerically described the 2D model of an earlier exploratory electrophoretic focusing experiment [19], where an electrode was placed exactly at the reservoir-channel entrance interface with the intent of decoupling the electric field gradient from the flow field gradient by confining the electric field more to the channel (Figure 1). Work using a similar configuration demonstrated qualitative differential behavior at the interface leading to separation and concentration enhancement of small molecules [20] and proteins [21]. However, unlike IEF, CACE, EFGF, and TGF that have been extensively modeled and tested empirically to help improve performance and increase the overall understanding of gradient field separations within a channel [22, 23], little detailed quantitative experimental information exists for the combined effects of the flow and electric field gradients at a channel entrance, particularly where an electrode is in close proximity to the entrance. There is a strong need to confirm or contradict intuitive and theoretical understanding of this entrance area so that any future progress can be built upon a solid foundation.

Figure 1.

Schematic of electrophoretic focusing principle with the interfacial electrode configuration described in this work.

This work uses the velocities of charged particles to investigate the hydrodynamic and electrokinetic effects in the region adjacent to the channel entrance (Figure 1). Both particle image velocimetry (PIV) and particle tracking velocimetry (PTV) studies with charged fluorescent particles have been used to monitor fluid and EP-influenced velocities [24, 25]. A 3D model specific to the fabricated device was developed using finite element analysis software and utilized to simulate the principle of electrophoretic focusing at the channel entrance. In order to assess the particle tracking methodology and the accuracy of a model in predicting hydrodynamic gradients, PTV was first used to measure particle velocities in the device when only hydrodynamic flow was present. Subsequently, varying electric fields were applied to create an electrokinetic force counter to the hydrodynamic force in an effort to evaluate the combined gradient effects. Results showed a non-linear hydrodynamic flow gradient near the channel entrance was accurately described using the model for this specific system. In the same region of interest, stepped increases in the electric field caused decreases in net particle velocities consistent with model simulations.

2 Materials and methods

2.1 Device fabrication

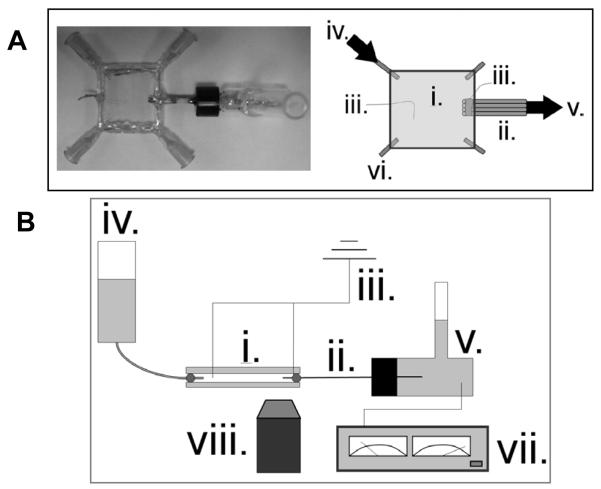
A 144 μL glass plate reservoir was fabricated by placing a 360 μm spacer between two 2 cm glass squares cut from standard microscope slides and epoxying the perimeter (Figure 2A). Four syringe needles with removable caps (Exel International, St. Petersburg, FL, USA) were inserted at each corner to serve as inlets or outlets and to facilitate cleaning when necessary. The cleaved tips of four fused silica capillaries (5 cm in length, 75 μm i.d. 365 μm o.d., Polymicro Technologies, Phoenix, AZ, USA) had a small portion (~0.5 cm) of the polyamide coating removed and were sputter-coated with 30 nm titanium then 50 nm platinum. The sputtered capillary face served as an electrode symmetric to and exactly at the capillary channel entrance. The electrode faces were electrically connected to a platinum wire by aligning the tips parallel to one another and fixing their sputtered sides with silver conducting epoxy. All conducting surfaces with the exception of the electrode faces were coated with standard epoxy to render them electrically nonconductive and nonreactive in solution. The electrode ends of the capillary bundle were inserted and fixed into the fabricated glass plate reservoir and the nonsputtered ends were inserted and fixed into a 2 mL glass outlet vial. A platinum electrode was set 1 cm external to the capillary face electrode in the plate reservoir and a counter electrode was placed in the 2 mL outlet vial.

Figure 2.

(A) Top-view photo and schematic of glass plate device fabricated to image particles near a converging channel with electrode exactly at entrance. Hydrodynamic flow was from left inlet to right outlet. (B) Side-view schematic of experimental setup. A CCD camera attached to an epifluorescence microscope was used to capture fluorescent particle images. (i.) glass plate reservoir (ii.) 4-capillary bundle (iii.) electrode (iv.) inlet (v.) outlet (vi.) additional inlets/outlets (vii.) power supply (viii.) objective

2.2 Particle tracking experiments

Velocimetry data from four identical capillaries connected in parallel were compiled and treated as one dataset for the study. Buffer was prepared to 5 mM using DL aspartic acid (Sigma Aldrich, St. Louis, MO, USA) and18 MΩ water then adjusted to pH 2.80 using 1 M HCl (Mallinckrodt, Hazelwood, MO, USA). Ten microliters of stock sulfated fluorescent polystyrene particles of 1 μm diameter and 505/515 wavelength excitation/emission (Invitrogen, Carlsbad, CA, USA) were diluted to 2 mL with working buffer and sonicated for 15 minutes, yielding a concentration of approximately 2 × 10⁸ particles/mL. Particles had an EP mobility of 3.5 × 10⁻⁴ cm²/(Vs) as determined from previous experiments using similar conditions [26]. The inlet vial, glass plate reservoir, capillary bundle, and outlet vial were preconditioned with 0.1 M HCl for 10 minutes then flushed with the working buffer for 20 minutes by pressurizing the inlet with house nitrogen. Preconditioning [27] and low pH buffer [28] helped limit EOF to simplify flow conditions and quantification of the system. The 2 × 10⁸ particles/mL suspension was introduced into the reservoir by adding 100 μL to 4 mL of working buffer in the inlet vial and pressurizing with nitrogen. The pressurized inflow aided the mixing and uniform particle distribution throughout the reservoir. The final particle concentration in the reservoir was approximately 5 × 10⁶ particles/mL. Pressure was removed, and bulk flow for the experiments was established and controlled using hydrostatic pressure created by keeping the inlet fluid level higher than that of the outlet, forcing particles to flow through the channels (Figure 2B). The average system flow rate of 2.7 nL/s was calculated using the hydrostatic pressure change from the 19 mm fluid level difference [1.9 × 10⁵ g/(ms²)] and total hydrodynamic resistance of the inlet, reservoirs, and channels [6.9 × 10¹⁶ g/(m⁴s)]. It was assumed the flow rate in each of the four capillaries was one-fourth the total flow rate, or 0.68 nL/s, due to flow division common in parallel, like-channel configurations. The duration of the study totaled 19 min, equating to a 1% hydrodynamic flow rate change as a result of inlet and outlet fluid levels changing over time. For the electrokinetic studies, the cathode in the outlet vial was attached to a Bertan Series 225 power supply (Bertan, Hauppauge, NY, USA), and both anodes in the glass plate reservoir were held to ground. Electric potential was applied incrementally from 0-200 V across the channel to create global electric fields ranging from 0-40 V/cm.

Particles were imaged using an Olympus IX70 inverted epifluorescence microscope (Tokyo, Japan) with a 4x, UPlanAPO, 0.16 NA objective and mercury short arc light source. Image acquisition was achieved using a QICAM CCD camera (QImaging, Burnaby, Canada) and Streampix III image capturing software (Norpix, Montreal, Quebec, Canada) set to 45 ms exposure time with an average frame rate of 16 frames per second and 1.8 mm × 1.6 mm imaging region (the minimum required to image all 4 capillaries at once) focused on the longitudinal mid-plane of the 4 capillary entrances. The exposure time of 45 ms remained constant throughout the experiment and was selected during test trials to maximize fluorescence intensity of the particles while simultaneously limiting particle streaks (particle images longer than 5 um) to only a few microns from the channel interface where particle velocities increase rapidly. Images were recorded for a total of 60 s during each measurement, with voltage applied after the initial 10 s in the case of the electrokinetic studies.

2.3 Image analysis

The MTrackJ plugin within ImageJ software (http://rsbweb.nih.gov/ij/) was used to manually track and determine the velocity of the particles. Each particle was cursor-selected throughout each advancing frame assigning it a coordinate that was used to determine distance traveled over the frame interval. For all images, a 100 μm long × 25 μm high region in the reservoir directly adjacent to the center of the channel entrance was selected and only particles moving within this zone were tracked to reduce velocity variations from particles outside the ± 12.5 um centerline region. The microscope objective was focused at the z-plane bisecting the channel, so particles outside the 25 um depth of focus would have a fluorescent diameter greater than 5 μm and would be excluded. A total of 204 particles were tracked over the course of the data collection, with at least 40 in-focus and traceable particles passing through the region of interest during the 0, 50, 100, and150 V trials and 18 for the 200 V trial.

2.4 Model development

The fabricated device used in this study was modeled using COMSOL Multiphysics 4.2 software with the microfluidics module (COMSOL, Inc., Los Angeles, CA, USA). The device materials - liquid, silica glass, and platinum – were selected from the built-in library and assigned to the respective geometric entities. The liquid electrical conductivity was modified to reflect that of the aspartic acid buffer (0.04 S/m) used in the experiments. Ohm’s Law and the Navier-Stokes equation were solved for by assigning Electric Current and Laminar Flow interfaces to the respective domains. Electric potential was assigned to an electrode boundary located 1 mm from the exit in the reservoir, while ground was assigned to the electrode boundary on the capillary face and to an electrode boundary located 1 mm from the entrance in the reservoir. All other boundaries were defined as electrical insulation. Laminar, incompressible flow was assigned to all domains and a no slip condition used for all wall boundaries. The laminar inflow boundary condition was set to a flow rate of 0.68 nL/s to match that of the PTV experiments. A 3.5 × 10⁻⁴ cm²/(Vs) EP mobility (from section 2.2) and global 700 V applied potential (for 3.1) were used to calculate EP velocities.

With the high aspect ratio geometry of the device, the reservoir length (2 cm) and width (2 cm) dimensions were scaled down by a factor of 20, having no noticeable effect on the gradient fields near the channel entrance. Channel length (5 cm) was reduced by a factor of 100, having a linear scaling effect on electric field near the entrance that was easily rescaled after computation. The scaling effects were determined by comparing the simulation results from the original dimensions to the simulation results from several scaled geometries. Scaled dimensions were used to improve mesh quality and computation performance. All other model parameters closely mirrored the fabricated device and experimental conditions.

Before developing the 3D model that more accurately reflected the geometry of the fabricated device, a 2D model (not shown) was developed using the COMSOL program to validate against the similar 2D theoretical development described by Pacheco et al. [18]. As expected, the resulting numerical descriptions of the fields that define the gradient near the channel entrance were reasonably consistent between the different modeling approaches, motivating the expansion of the 2D model to 3D using the COMSOL program.

3 Results and discussion

3.1 Model development and simulated principle of electrophoretic focusing

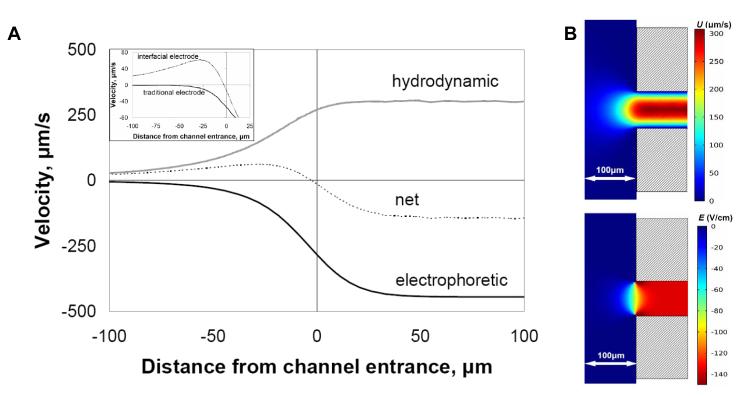
The 3D model was used to generate centerline velocities for comparison with particle tracking data. The resulting 300 μm/s fully-developed flow velocity from the simulation (Figure 3B) was consistent with the centerline velocity calculated using the Poiseuille equation. Beyond the hydrodynamic flow, other critical parameters used in the simulations, and required for electrophoretic focusing within the inlet reservoir, include the globally applied electric field and the EP mobility of the species of interest. When the average EP velocity towards the reservoir becomes equal to the average hydrodynamic velocity towards the channel at any location where x ≤ 0 (denoted in Pacheco et al. as S = 1 locally [18]), the cross-sectionally averaged mass flux of an analyte is zero (including diffusive elements) and a focusing condition occurs. Because average EP mobility of the species remains constant for the given buffer, the focusing behavior could be controlled by varying the hydrodynamic flow and/or electric field. The net velocity plot, which is the sum of two opposing centerline velocities, reached a focusing condition (y = 0) a few microns outside the channel entrance and inside the inlet reservoir (Figure 3A).

Figure 3.

(A) Simulation showing the principle of electrophoretic exclusion at a channel entrance with an electrode exactly at the reservoir-channel interface. The central dashed line represents the net velocity resulting from electrophoretic velocity opposing bulk fluid velocity. (Inset) The net velocity with an interfacial electrode configuration, as described in A, compared to the net velocity profile of a traditional CE configuration, where no interfacial electrode is present. All plots reflect centerline values. (B) Surface plot simulations of fluid velocity, U, from 0.68 nL/s applied flow rate and electric field, E, from 700 V applied potential at a converging channel entrance with interfacial electrode.

The placement of the electrode in the reservoir was examined theoretically. A magnified region of the net velocity profile was examined (Figure 3A – inset) with the electrode placed distal (traditional CE configuration) and at the entrance (Figure 1). Two major effects on the velocity profile were noted when the electrode resided exactly at the entrance. First, the electric field had minimal influence on the net velocity until roughly 25 μm from the entrance. Having an electrode at the entrance and another held at the same potential in the reservoir ensured an almost zero electric field across the reservoir except near the entrance where focusing is designed to occur. Secondly, unlike the traditional CE electrode configuration (Figure 3A – inset, lower black line), there was a much steeper velocity gradient induced by the electric field being confined near the channel entrance, indicating a steeper local gradient in E in the presence of a flow field. This describes a microscale gradient electrophoresis system where bandwidth is inversely proportional to the gradient. The steeper gradient suggests that any resulting concentration profile generated by the focusing condition will be narrower. This is analogous to pH gradients in isoelectric focusing but with steeper gradients and without dynamic range limitations since each interface is designed to differentiate a single species of interest.

3.2 Assessment of hydrodynamic velocity gradient using PTV and simulation

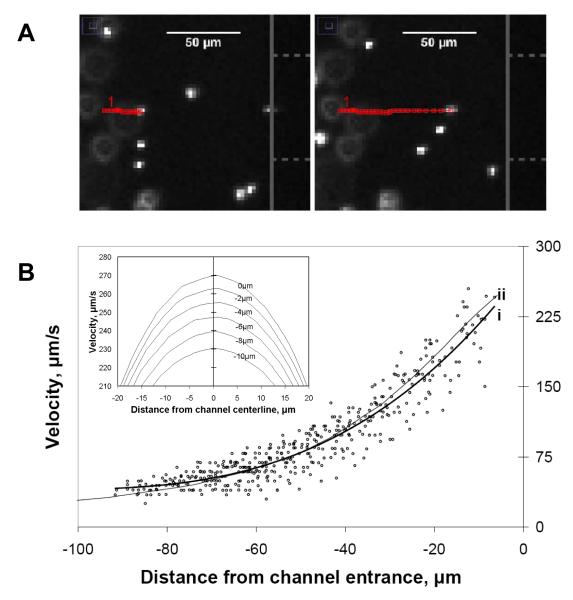
Particle tracking velocimetry was used near the channel entrance in order to evaluate the flow field as compared to the model. As the particles approached the channel entrance along the centerline, the distance between the tracking points over a constant frame interval became larger, indicating a fluid velocity gradient (Figure 4A). In most cases, it was possible to track the particles to within 5 μm of the reservoir-channel interface before they disappeared inside the capillary within the next frame. The velocity trend of the particles in the gradient region agreed with that predicted by the model simulation when no electric field was present (Figure 4B).

Figure 4.

(A) Representative snapshot of manually tracked fluorescent particle moving left to right and approaching channel entrance along centerline. Open (red) squares represent particle location in prior frames. Capillary face and channel are represented by solid vertical line and dashed horizontal lines, respectively, along right edge of panel. The elapsed time between the two snapshots was 0.88 s. (B) Centerline velocity plot of fluorescent particles as they approached the capillary entrance (x = 0) as in A. Line (i) is the best fit for the data points, and line (ii) is the centerline fluid velocity plot from the 3D model. (B - inset). Simulated velocity profiles about the centerline from 0 to −10 um that illustrate velocity variation off the centerline near the channel entrance (applied U = 0.68 nL/s).

Scatter amongst the velocities was mostly attributed to particles several microns off the y- and z- center planes being included in the centerline tracking data. The error associated with the distances off the centerline and near the entrance was predicted using the simulation (Figure 4B – inset). Taking into account the width of the region of interest and the depth of focus of the microscope objective (section 2.3), a ±18% relative standard deviation could be expected in measurements occurring −7.5 μm from the interface.

3.3 Assessment of combined electric field and hydrodynamic velocity gradients using PTV and simulation

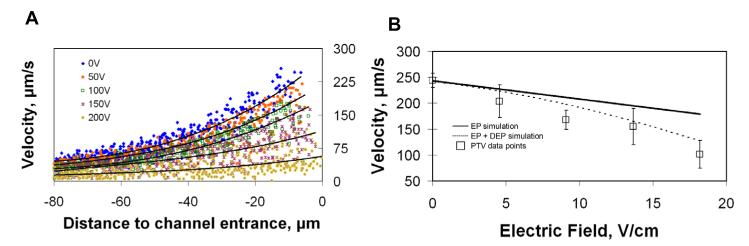
Charged species in the presence of flow and electric gradients near the channel entrance were examined next. With the flow velocity field quantified from the previous section, any change in particle velocity is assumed to be a direct result of the electric field. Hydrostatic conditions were held constant throughout and particle velocity control images were captured before each applied potential. A consistent decrease in net velocity as a result of the increasing electric field was evident (Figure 5A).

Figure 5.

(A) Particle velocities approaching channel entrance (x = 0) along centerline with increasing applied electric potentials. (B) Average velocity of particles in electric fields at −7.5 ± 1.5 μm from channel entrance. Each data point is the mean of 3 to 19 tracked particles with 1 sigma error bars. The solid line represents a simulation where only electrophoretic velocity was considered while the dashed line includes both electrophoretic (EP) and dielectrophoretic (DEP) forces.

To illustrate the relationship between velocity and electric field in this system, a bin −7.5 ± 1.5 μm outside the entrance (where particles were still visible and velocity could be tracked) was chosen (Figure 5B). Using the model and combining the electric field and flow effects at −7.5 μm, an estimated net velocity was calculated for the various applied electric field strengths. The velocities from the experimental data decreased with increased electric field but at a greater slope than the simulation. EOF was not likely the cause of this behavior because preconditioning and low pH buffer (as described in the methods section) severely limited these effects. Additionally, based on the experimental conditions, EOF would have countered the EP velocity making the slope shallower rather than steeper. Dielectrophoresis, on the other hand, was considered a viable explanation for the discrepancy since this force typically has a more pronounced effect at higher electric fields, and since the particles used were known to be polarizable and of an appropriate size to generate a non-trivial force. The dielectric force is proportional to the local electric field gradient squared and particle radius to the third power and is described in detail elsewhere [29, 30]. To examine this possibility quantitatively, the force was calculated within the construct of the 3D model using a dielectrophoretic mobility of −2 × 10⁻⁸ cm⁴/(V²s) (recently published from this laboratory [26]) (Figure 5B). The addition of the dielectrophoretic effects provided an improved fit to the data and was likely a factor. The core flow and electric field effects can still be interpreted from this data, however, as the dielectrophoretic effects are well-studied, quantifiable, and can be considered an artifact as a result of the physical properties of the particles which are required as tracers. Small molecules, peptides and proteins - the putative targets for this system - will have negligible dielectrophoretic susceptibilities.

Though the motivation for the current work was to quantify the gradient region near an entrance rather than demonstrate a full exclusion condition, an earlier proof-of-principle study was carried out with stronger electric fields to verify that a charged substance could be slowed and eventually excluded from entering the channel (supplemental data).

4 Concluding remarks

To begin to investigate and rationally alter an electrified converging flow interface, quantitative models and data must be generated and compared. Using a highly symmetric and traditional interface with an electrode positioned at the entrance, a model was generated and data collected with particle tracers to investigate both the interface and the accuracy of the model. For this interface, the model and data agree and the strategy is validated. This work enables sound device design, like shaping the entrance geometry or placing the electrode at different locations, and similar strategies for models and velocity visualization can be used to optimize separation conditions at a channel entrance.

Abbreviations

PTV

(Particle Tracking Velocimetry)

PIV

(Particle Image Velocimetry)

EP

(Electrophoretic)

DEP

(Dielectrophoresis)

CACE

(Counteracting Chromatographic Electrophoresis)

EFGF

(Electric Field Gradient Focusing)

TGF

(Temperature Gradient Focusing)