Prediction of Preterm Deliveries from EHG Signals Using Machine Learning

Abstract

There has been some improvement in the treatment of preterm infants, which has helped to increase their chance of survival. However, the rate of premature births is still globally increasing. As a result, this group of infants are most at risk of developing severe medical conditions that can affect the respiratory, gastrointestinal, immune, central nervous, auditory and visual systems. In extreme cases, this can also lead to long-term conditions, such as cerebral palsy, mental retardation, learning difficulties, including poor health and growth. In the US alone, the societal and economic cost of preterm births, in 2005, was estimated to be $26.2 billion, per annum. In the UK, this value was close to £2.95 billion, in 2009. Many believe that a better understanding of why preterm births occur, and a strategic focus on prevention, will help to improve the health of children and reduce healthcare costs. At present, most methods of preterm birth prediction are subjective. However, a strong body of evidence suggests the analysis of uterine electrical signals (Electrohysterography), could provide a viable way of diagnosing true labour and predict preterm deliveries. Most Electrohysterography studies focus on true labour detection during the final seven days, before labour. The challenge is to utilise Electrohysterography techniques to predict preterm delivery earlier in the pregnancy. This paper explores this idea further and presents a supervised machine learning approach that classifies term and preterm records, using an open source dataset containing 300 records (38 preterm and 262 term). The synthetic minority oversampling technique is used to oversample the minority preterm class, and cross validation techniques, are used to evaluate the dataset against other similar studies. Our approach shows an improvement on existing studies with 96% sensitivity, 90% specificity, and a 95% area under the curve value with 8% global error using the polynomial classifier.

Introduction

Preterm birth, also known as premature birth or delivery, is described by the World Health Organisation (WHO) as the delivery of babies who are born, alive, before 37 weeks of gestation [1]. In contrast, term births are the live delivery of babies after 37 weeks, and before 42 weeks. According to the WHO, worldwide in 2010, preterm deliveries accounted for 1 in 10 births [1]. In 2009, in England and Wales, 7% of live births were also preterm (http://ons.gov.uk). Preterm birth has a significant adverse effect on the new born, including an increased risk of death and health defects. The severity of these effects increases the more premature the delivery is. Approximately, 50% of all perinatal deaths are caused by preterm delivery [2], with those surviving often suffering from afflictions, caused by the birth. These include impairments to hearing, vision, the lungs, the cardiovascular system and non-communicable diseases; up to, 40% of survivors of extreme preterm delivery can also develop chronic lung disease [3]. In other cases, survivors suffer with neuro-developmental or behavioural defects, including cerebral palsy, motor, learning and cognitive impairments. In addition, preterm births also have a detrimental effect on families, the economy, and society. In 2009, the overall cost to the public sector, in England and Wales, was estimated to be nearly £2.95 billion [4]. However, developing a better understanding of preterm deliveries can help to create preventative strategies and thus positively mitigate, or even eradicate, the effects that preterm deliveries have on babies, families, and society and healthcare services.

Preterm births can occur for three different reasons. According to [2], roughly one-third are medically indicated or induced; delivery is brought forward for the best interest of the mother or baby. Another third occurs because the membranes rupture, prior to labour, called Preterm Premature Rupture of Membranes (PPROM). Lastly, spontaneous contractions (termed preterm labour or PTL) can develop. However, there is still a great deal of uncertainty about the level of risk each factor presents, and whether they are causes or effects. Nevertheless, in [2] some of the causes of preterm labour, which may or may not end in preterm birth, have been discussed. These include infection, over-distension, burst blood vessels, surgical procedures, illnesses and congenital defects of the mother's uterus and cervical weakness. Further studies have also found other risk factors for PTL/PPROM [5], [6]. These include a previous preterm delivery (20%); last two births have been preterm (40%), and multiple births (twin pregnancy carries a 50% risk). Other health and lifestyle factors also include cervical and uterine abnormalities, recurrent antepartum haemorrhage, illnesses and infections, any invasive procedure or surgery, underweight or obese mothers, ethnicity, and social deprivation, long working hours/late nights, alcohol and drug use, and folic acid deficiency.

As well as investigating preterm deliveries, several studies have also explored preterm labour (the stage that directly precedes the delivery). However, in spite of these studies, there is no internationally agreed definition of preterm labour. Nonetheless, in practice, women who experience regular contractions, increased vaginal discharge, pelvic pressure and lower backache tend to show threatening preterm labour (TPL). While this is a good measure, Mangham et al., suggest that clinical methods for diagnosing preterm labour are insufficient [4]. Following a medical diagnosis of TPL, only 50% of all women with TPL actually deliver, within seven days [2]. In support of this, McPheeters et al., carried out a similar study that showed 144 out of 234 (61.5%) women diagnosed with preterm labour went on to deliver at term [7]. This can potentially add significant costs, and unnecessary interventions, to prenatal care. In contrast, false-negative results mean that patients requiring admittance are turned away, but actually go on to deliver prematurely [8].

Predicting preterm birth and diagnosing preterm labour clearly have important consequences, for both health and the economy. However, most efforts have concentrated on mitigating the effects of preterm birth. Nevertheless, since this approach remains costly [1], it has been suggested that prevention could yield better results [9]. Effective prediction of preterm births could contribute to improving prevention, through appropriate medical and lifestyle interventions. One promising method is the use of Electrohysterography (EHG). EHG measures electrical activity in the uterus, and is a specific form of electromyography (EMG), the measurement of such activity in muscular tissue. Several studies have shown that the EHG record may vary from woman to woman, depending on whether she is in true labour or false labour and whether she will deliver term or preterm. EHG provides a strong basis for objective predication and diagnosis of preterm birth.

Many research studies have used EHG for prediction or detection of true labour. In contrast, this paper focuses on using EHG classification to determine whether delivery will be preterm or term. This is achieved by comparing various machine-learning classifiers against an open dataset, containing 300 records (38 preterm and 262 term) [10], using a signal filter and pre-selected features, which are suited to classifying term and preterm records. The results indicate that the selected classifiers outperform a number of approaches, used in many other studies.

The structure, of the remainder, of this paper is as follows. Section 2 describes the underlying principles of Electrohysterography. Section 3 describes how features are extracted from Electrohysterography signals. Section 4 discusses machine learning and its use in term and preterm classification, while section 5 presents the approach taken in this paper. Section 6 describes the evaluation, and Section 7 discusses the results. Section 8 then concludes the paper.

Analysis and Methods

Electrohysterography

Electrohysterography (EHG) is the term given for the recording of electrical activity of the uterus, in the time domain. In order to retrieve EHG signals, bipolar electrodes are adhered to the abdominal surface. These are spaced at a horizontal, or vertical, distance of 2.5 cm to 7 cm apart. Most studies, including [10], use four electrodes, although one study utilizes two [11]. In a series of other studies, sixteen electrodes were used [12]–[17], and a high-density grid of 64 small electrodes were used in [18]. The results show that EHG may vary from woman to woman. This is dependent on whether she is in true or false labour, and whether she will deliver at term, or prematurely.

A raw EHG signal results from the propagation of electrical activity, between cells in the myometrium (the muscular wall of the uterus). This signal measures the potential difference between the electrodes, in a time domain. The electrical signals are not propagated by nerve endings; however, the propagation mechanism is not clear [19]. Since the late 70s, one theory suggests that gap junctions are the mechanisms responsible. Nevertheless, more recently it has been suggested that interstitial cells, or stretch receptors may be the cause of propagation [20]. Gap junctions are groups of proteins that provide channels of low electrical resistance between cells. In most pregnancies, the connections between gap junctions are sparse, although gradually increasing, until the last few days before labour. A specific pacemaker site has not been conclusively identified, although, due to obvious physiological reasons, there may be a generalised propagation direction, from the top to the bottom of the uterus [21].

The electrical signals, in the uterus, are ‘commands’ to contract. During labour, the position of the bursts, in an EHG signal, corresponds roughly with the bursts shown in a tocodynamometer or intrauterine pressure catheter (IUPC). Clinical practises use these devices to measure contractions. More surprisingly, distinct contraction-related, electrical uterine activity is present early on in pregnancy, even when a woman is not in true labour. Gondry et al. identified spontaneous contractions from EHG records as early as 19 weeks of gestation [22]. The level of activity is said to increase, as the time to deliver nears, but shoots up especially so, in the last three to four days, before delivery [23]. As the gestational period increases, the gradual increase in electrical activity is a manifestation of the body's preparation for the final act of labour and parturition. In preparation for full contractions, which are needed to create the force and synchronicity required for a sustained period of true labour, the body gradually increases the number of electrical connections (gap junctions), between cells. In turn, this produces contractions in training.

Before analysis or classification occurs, EHG signals, in their raw form, need pre-processing. Pre-processing can include filtering, de-noising, wavelet shrinkage or transformation and automatic detection of bursts. Recently, studies have typically focused on filtering the EHG signals to allow a bandpass between 0.05 Hz and 16 Hz [24]–[28]. However, there are some that have filtered EHG recordings as high as 50 Hz [19]. Nevertheless, using EHG with such a wide range of frequencies is not the recommended method, since more interference affects the signal.

Feature Extraction from Elecrohysterography

The collection of raw EHG signals is always temporal. However, for analysis and feature extraction purposes, translation, into other domains, is possible and often required. These include frequency representation, via Fourier Transform, [15], [28]–[30] and wavelet transform [24], [27], [30]–[33]. The advantage of frequency-related parameters is that they are less susceptible to signal quality variations, due to electrode placement or the physical characteristics of the subjects [26]. In order to calculate these parameters, a transform from the time domain is required, i.e., using a Fourier transform of the signal. In several of the studies reviewed, in order to obtain frequency parameters, Power Spectral Density (PSD) is used. Peak frequency is one of the features provided within the Term-Preterm ElectroHysteroGram (TPEHG) dataset, used within this paper. It describes the frequency of the highest peak in the PSD. Most studies focus on the peak frequency of the burst, in both human and animal studies, and is said to be one of the most useful parameters for predicting true labour [34]. On the other hand, the study by [10] found medium frequency to be more helpful in determining whether delivery was going to be term or preterm.

Several studies have shown that peak frequency increases, as the time to delivery decreases; generally, this occurs within 1–7 days of delivery [11], [19], [24], [26], [30], [35]. In particular, the results in [28] show that there are, statistically, significant differences in the mean values of peak frequency and the standard deviations in EHG recordings taken during term labour (TL) and term non-labour (TN) and also between preterm labour (PTL) and preterm non-labour (PTN).

In comparison to peak frequency, the TPEHG study [10] found that median frequency displayed a more significant difference, between term and preterm records. When considering all 300 records, the statistical significance was p = 0.012 and p = 0.013, for Channel 3, on the 0.3–3 Hz and 0.3–4 Hz filter, respectively. Furthermore, this significance (p = 0.03) was also apparent when only considering early records (before 26 weeks of gestation), with the same 0.3–3 Hz filter, on Channel 3. The TPEHG study [10] concluded that this might have been due to the enlargement of the uterus, during pregnancy, which would affect the position of electrodes. The placement of the Channel 3 electrode was, approximately, always 3.5cm below the navel. However, as pregnancy progressed, this would mean that the electrode would move further away from the bottom of the uterus (cervico-isthmic section). If a generalised pacemaker area actually exists, and it is at the cervico-isthmic section, then, as pregnancy progresses, its position would move further and further away from the electrode, resulting in a diminished record of the signal. Whether this explanation is true or not, the results of [10] show that, the discriminating capability of median frequency is somehow diminished, after the 26th week.

Amplitude-related EMG parameters represent the uterine EMG signal power, or signal energy. However, a major limitation is that the differences in patients can easily affect these parameters. Patients may differ in the amount of fatty tissue they have, and the conductivity of the skin–electrode interface, which leads to differences in the attenuation of uterine signals [8], [26], [34]. Examples of amplitude-related parameters include root mean square, peak amplitude and median amplitude.

Using the Student's t-test, [10] found that root mean square might be useful in distinguishing between whether the information was recorded early (before 26 weeks of gestation) or late (after 26 weeks). The results obtained are in agreement with [19], [30] and [36], who found that the amplitude of the power spectrum increased, just prior to delivery. This was despite only analysing the root mean square values, per burst, rather than the whole signal. On the other hand, other studies did not find that amplitude-related parameters displayed a significant relationship to gestational age or indicate a transition to delivery (within seven days) [23], [25], [28]. Some of these discrepancies may be due to the differences between the characteristics in the studies: [10] compared records before and after 26 weeks, whereas [25] only examined records after the 25th week; [29] and [35] studied rat pregnancy, in contrast to human pregnancy. The frequency band used in [30] and [19] was also a much broader band than in other studies (0.3–50 Hz; no bandwidth given for [36]), and the studies by [29] and [35] measured per burst, whilst [25] measured the whole signal.

Meanwhile, the TPEHG study [10] could not find any significant difference in root mean squares between preterm and term records. However, [25] did find that the root mean squares, in preterm contractions, were higher (17.5 mv ±7.78), compared to term contractions (12.2 mV ±6.25; p<0.05). The results, from [25], could not find a correlation between root mean squares and the weeks left to delivery. Nevertheless, they do suggest that a greater root mean square value was, for the most part, a static symptom that indicated a woman's dispensation to give birth prematurely. They also found that the root mean square values, within each pregnancy, did increase within a few days of birth.

Overall, the results suggest that there is no significant difference in the amplitude-related parameters between term and preterm deliveries, when taken during labour, or close to it. However, there may be considerable differences earlier on in the pregnancy. This suggests that by the time of delivery, any differences have equalised themselves.

Sample entropy measures the irregularity of a time series, of finite lengths. This method was introduced by [37] to measure complexity in cardiovascular and biological signals. The more unpredictable the time series is, within a signal recording, the higher its sample entropy. The process is based on calculating the number of matches of a sequence, which lasts for m points, within a given margin r. The disadvantage of this technique is the requirement to select two parameters, m and r. However, sample entropy did show a statistical difference between term and preterm delivery information, recorded either before or after the 26th week of gestation, when using any of the filters, but only using the signal from Channel 3 [10].

Term and Preterm Classification

Computer algorithms, and visualization techniques, are fundamental in supporting the analysis of datasets. More recently, the medical domain has been using such techniques, extensively.

Artificial Neural Networks (ANN) have been used in a large number of studies to classify term and preterm deliveries, [11], [38]. They have also been useful for distinguishing between non-labour and labour events [11], [38], irrespective of whether they were term or preterm. Moslem et al. [14] argue that they have been particularly useful in helping to identify important risk factors associated with preterm birth. The global accuracy of these studies varied from between 73% and 97%.

Baghamoradi et al. [39] used the TPEHG database [10] to compare sample entropy with thirty and three cepstral coefficients extracted from each signal recording through sequential forward selection and Fisher's discriminant. A multi-layer perceptron (MLP) neural network classified the feature vectors into term and preterm records. The results indicate that the three cepstral coefficients produced the best classification accuracy, with 72.73% (±13.5), while using all thirty coefficients showed only 53.11% (±10.5) accuracy. Sample entropy performed the worst with an accuracy of 51.67% (±14.6). The results indicate that the sequential forward selection and Fisher's discriminant had the most effect on the accuracy because the thirty coefficients set only presenting a small improvement, in classification accuracy.

Support Vector Machines (SVM) have featured in several studies, which include [12], [13], [14]. Many of them classify contractions into labour or non-labour, using different locations on the abdomen. Majority voting (WMV) decision fusion rules, including a Gaussian radial basis function (RBF), form the basis for classification. The feature vectors include the power of the EMG signal, and the median frequency. The highest accuracy for a single SVM classifier, at one particular location on the abdomen, was 78.4% [12], [13], whilst the overall classification accuracy, for the combined SVM, was 88.4% [14]. Finding the coefficients, for the decision boundary, occurs by solving a quadratic optimisation problem.

The k-NN algorithm has been used by Diab et al. [40] with an emphasis on Autoregressive (AR) modelling and wavelet transform pre-processing techniques. The study focused on classifying contractions into three types using data obtained from 16 women. Group 1 (G1), were women who had their contractions recorded at 29 weeks, and then delivered at 33 weeks; Group 2 (G2) were also recorded at 29 weeks, but delivered at 31 weeks, and Group 3 (G3) were recorded at 27 weeks and delivered at 31 weeks. Classification occurred against G1 and G2 and against G2 and G3 using, the k-NN algorithm combined with the pre-processing method of AR. As well as this, an Unsupervised Statistical Classification Method (USCM), combined with the pre-processing method of Wavelet Transform, was also used. The USCM adopted the Fisher Test and k-Means methods. The wavelet transform, combined with USCM, provided a classification error of 9.5%, when discerning G1 against G2, and 13.8% when classifying G2 against G3. Using AR, the k-NN provided a classification error of 2.4% for G1 against G2 and 8.3% for G2 against G3. In both classifications, the AR and k-NN methods performed better than the USCM. Furthermore, the classification accuracy for G1 and G2 was always lower than the equivalent G2 and G3 classifications. This suggests that it is easier to distinguish between pregnancies recorded at different stages of gestation than it is to distinguish between the time of delivery.

Methodology

Despite the advances, within the last twenty years, in the EHG diagnosis and prediction field, knowledge of the uterus, and its mechanisms, remains relatively poor. This is especially evident when compared to other organs, such as the heart, and to a lesser extent, the gastro-intestinal system [20]. Given this inadequate knowledge, it may be easier to utilise an empirical backward looking, ‘data mining’ or ‘brute force’ approach. This is opposed to a forward-looking, conceptual model approach, in order to find features that best describe pregnancy.

The aim of most studies, in EHG prediction or detection, has been to detect true labour, rather than predicting, in advance, whether delivery will be preterm or term. Furthermore, many of the studies concentrated on a late state in gestation. Even when earlier stages are incorporated, they always only included those with threatened preterm labour. However, the TPEHG dataset is different, as it involves the general population of pregnant women. Therefore, this collection includes fewer records for women who delivered preterm than term.

For term deliveries, true labour only starts within 24 hours. For preterm deliveries, it may start within 7 to 10 days. The change in EHG activity, from non-labour to labour, is dramatic; throughout the rest of the pregnancy, any change in EHG is more gradual. Therefore, classification of records, into preterm and term, is particularly challenging. For this reason, and due to the configuration of the dataset, the study attempts to classify records from an earlier stage, according to whether they will eventually result in term or preterm deliveries.

Fele-Zorz et al. conducted a comprehensive study that compared linear and non-linear signal processing techniques to separate uterine EMG records of term and preterm delivery groups [10]. The EHG records are from a general population of pregnant patients at the Department of Obstetrics and Gynaecology Medical Centre in Ljubljana, gathered between 1997 and 2006. These records are publicly available, via the TPEHG dataset, in Physionet.

The TPEHG dataset contains 300 records (one record per pregnancy). Each recording is approximately 30 minutes long. Records are either recorded early, <26 weeks (at around 23 weeks of gestation) or later,  = >26 weeks (at around 31 weeks). It is not clear why the 26^th week is used as the dividing line for early and late records, however, this is possibly because of significant changes that occur in the 3^rd trimester of pregnancy. Table 1, below, shows the classification of records in the TPEHG dataset.

Table 1. Numbers of Patients in each group.

Terms:	Term Deliveries	Term Deliveries	Preterm Deliveries	Preterm Deliveries	All Deliveries	All Deliveries
Recording Time	Number of records	Mean/Median Recording weeks	Number of records	Median/Median Recording Weeks	Number of records	Mean/Median Recording Weeks
Early	143	22.7/22.86	19	23.0/23.43	162	22.73/23.0
Later	119	30.8/31.14	19	30.2/30.86	138	30.71/31.14
All Recording Time	262	26.75/24.36	38	27.0/25.86	300	26.78/24.43

The recording time relates to the gestational age of the foetus, at the time of the recoding. The classifications of these recordings, as term and preterm deliveries, was made retrospectively, after giving birth, and following the widely used definition of preterm being under a fully completed 37 weeks. Therefore, the four categories of recordings are as follows:

1. Early-Term: Recordings made early, which resulted in a term delivery.

2. Early-Preterm: Recordings made early, which resulted in a preterm delivery.

3. Late-Term: Recordings made late, which resulted in a term delivery.

4. Late-Preterm: Recordings made late, which resulted in a preterm delivery.

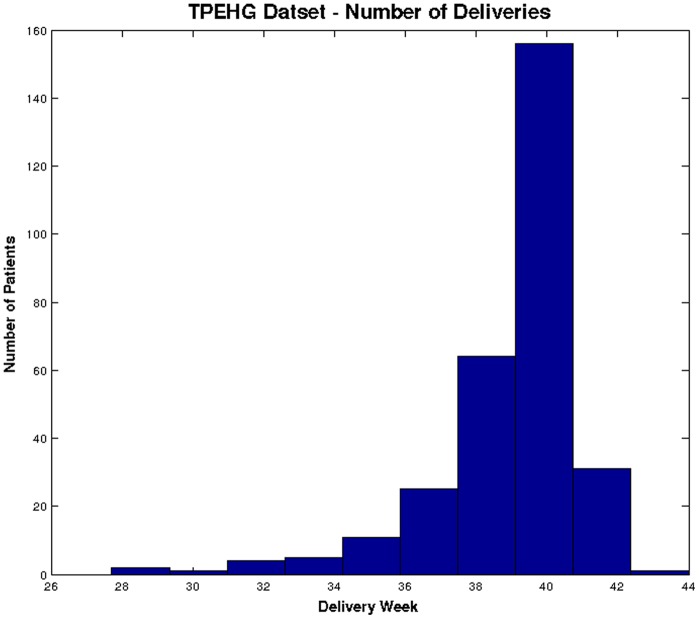
Figure 1 shows the distributions of term and preterm records in the TPEHG dataset, which clearly indicates that the majority of the data are term.

Figure 1. Distribution of deliveries in TPEHG dataset.

In summary, this paper uses 300 records that consist of ‘38’ preterm and ‘262’ term records.

Data Pre-processing

In the TPEHG dataset, the records have a sample frequency of 20 Hz, and 16-bit resolution, with an amplitude range of ±2.5 mV. Before sampling took place, an analogue, three-pole, Butterworth filter, filtered the signal within the range of 1–5 Hz. Signals were recorded simultaneously through three different channels (Channel1, Channel2, and Channel3), via four electrodes attached to the abdominal surface, with the navel at the symmetrical centre.

Fele-Zorz et al. showed that the 0.3–3 Hz filtered signals on Channel 3 is the best filter for discriminating between preterm and term delivery records [10]. The results show that sensitivities (true positives – in this instance preterm records), produced by several of the classifiers, was higher than those produced when other filters were used [10]. However, there was no appropriate filter to remove unwanted artefacts, such as maternal heart rate. Uterine activity has been found to comprise both ‘fast’ and ‘slow’ signals of high and low frequency signals. The fast waves represent the individual electrical signals firing, whilst the slow waves correspond to the resulting mechanical contractions. Slow waves exist between 0.03 and 0.3 Hz, and the fast waves exist between 0.3 and 3.0 Hz. Reference [36] found in a study of 99 pregnant patients, that 98% of uterine electrical activity occurred in frequencies less than 1 Hz, and that the maternal heart rate (ECG) was always higher than 1 Hz. Furthermore, 95% of the patients, measured had respiration rates of 0.33 Hz or less. Therefore, the authors considered that a 0.34–1 Hz bandpass filter removed most of the unwanted artefacts. Several other studies have adopted the same filtering scheme [53]–[54], and [12]. Therefore, in this paper, the raw Channel 3 signal was chosen and filtered using a 0.34–1 Hz filter. This is to coincide with the findings in [10] and [36].

Features Selection

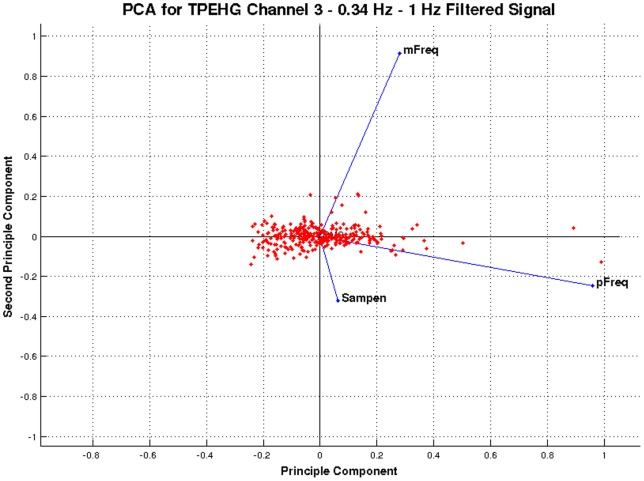
The feature vectors in this paper are generated using four features – root mean squares, peak frequency, median frequency, and sample entropy. The literature reports that Mean frequency and sample entropy have the most potential to discriminate between term and preterm records. However, root mean squares and peak frequencies have had conflicting results. Nonetheless, several studies report that these features are useful for discriminating between term and preterm records. To validate these findings, the discriminant capabilities of each feature are determined using principal component analysis (PCA). Figure 2 shows the PCA for the features extracted from Channel 3 0.34–1 Hz filter signal.

Figure 2. PCA for features extracted from the Channel 3 0.34–1 Hz filtered signal.

As indicated in Figure 2, the horizontal axis shows that the peak frequency is the principal component and has the most discriminant capabilities of the four features considered. This is consistent with the findings in [11], [19], [24], [26], [28], [30], [35]. The vertical axis shows median frequency as the second component with very good discriminant capabilities. This is consistent with the findings in [10]. Sample entropy is the third component and hence considered useful. These findings are broadly consistent with [10], which found a statistical difference between term and preterm records, using sample entropy. Finally, the root mean squares feature resides towards the cross-section of the first and second components, as indicated in Figure 2. This feature has the least discriminative capabilities and again the findings are consistent with [10]. Nevertheless, [25] suggested that the root mean square is a useful feature because, in preterm contractions, it is higher.

In summary PCA, in conjunction with various studies reported in the literature, make a very strong case for the use of peak frequency, median frequency, root mean squares and sample entropy in discriminating between term and preterm records.

Synthetic minority over-sampling

In a two class balanced dataset the prior probabilities will be equal for each. This is not the case for the TPEHG dataset because it is not balanced. There are 262 true negatives (majority class) and 38 true positive values (minority class). Classifiers are more sensitive to detecting the majority class and less sensitive to the minority class and this leads to biased classification [1]. Therefore, given a random sample taken from the dataset, the probability of a classifier classifying a pregnant woman as term will be much higher (87.3%–262/300) than the probability of it classifying a pregnant woman as preterm (12.6%–38/300). This imposes a higher cost for misclassifying the minority (predicting that a pregnant woman is likely to deliver full term only to go home and deliver prematurely) than the majority class, (predicting a pregnant woman will deliver preterm only to go deliver at term).

In order to address this problem, it is necessary to resample the dataset. Various resampling techniques are available, and these include under sampling and over sampling [3]. Under sampling reduces the number of records from the majority class to make it equal to the minor class – in this instance it would mean removing 224 records leaving us with a small dataset. Data in the minority class is generated using oversampling. In this study, the synthetic minority over-sampling technique (SMOTE) is used rather than reducing the dataset further [41].

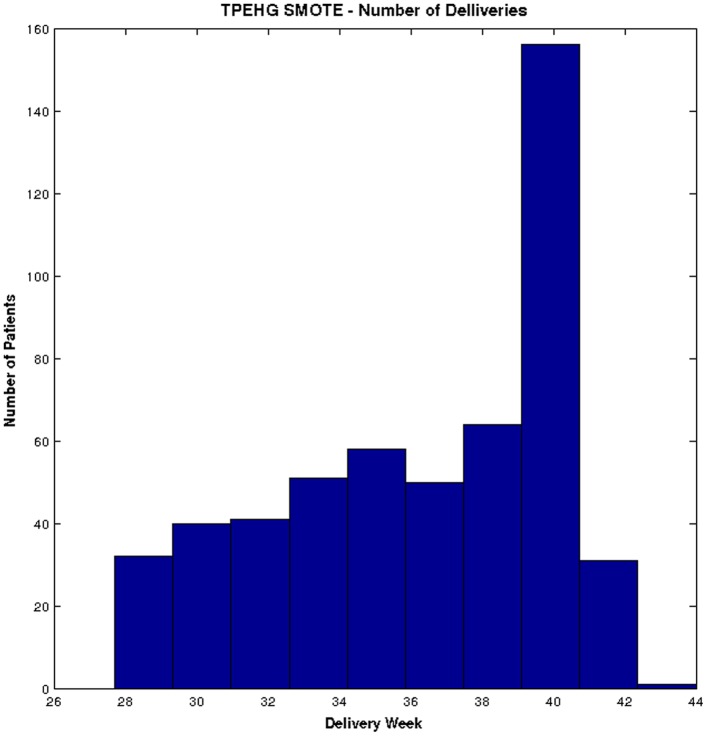
Several studies have shown that the SMOTE technique effectively solves the class skew problem [42]–[47]. Using SMOTE, the minority class (preterm) is oversampled using each minority class records, in order to generate new synthetic records along line segments joining the k minority class nearest neighbours. This forces the decision region of the minority class to become more general and ensures that the classifier creates larger and less specific decision regions, rather than smaller specific regions. In [41] the authors indicated that this approach is an accepted technique for solving the problems related to unbalanced datasets. Figure 3 shows the distribution of term and preterm records, using the SMOTE technique.

Figure 3. Distribution of deliveries in TPEHG dataset after the SMOTE technique is applied.

Figure 3 clearly shows that using the SMOTE technique allows the term and preterm dataset to be more balanced, compared to the original TPEHG dataset.

Classification

Following an analysis of the literature, the study in this paper uses simple, yet powerful algorithms, as shown in Table 2.

Table 2. Summary of Classifiers, Features, Validation Techniques and Sample Sizes used in this study.

Classifiers	Features	Validation	Sample Sizes
Density-Based	Root Mean Squares	Holdout Cross Validation	Original (38 preterm/262 term)
Linear Discriminant Classifier (LDC)	Peak Frequency	k-fold Cross Validation	SMOTE (262 preterm/262 term)
Quadratic Discriminant Classifier (QDC)	Median Frequency	Sensitivity/Specificity	SMOTE Clinical (150 preterm/150 term)
Uncorrelated Normal Density Classifier (UDC)	Sample Entropy	Receiver Operator Curve	Clinical (38 preterm/262 term)
Linear and Polynomial-Based		Area Under the Curve
Polynomial Classifier (POLYC)
Logistic Classifier (LOGLC)
Nonlinear-Based
K Nearest Neighbour Classifier (KNNC)
Decision Tree Classifier (TREEC)
Parzen Classifier (PARZENC)
Support Vector Classifier (SVC)

The classifiers considered in this study include the linear discriminant classifier (LDC), quadratic discriminant classifier (QDC), uncorrelated normal density based classifier (UDC), polynomial classifier (POLYC), logistic classifier (LOGLC), 3-NN (KNNC), decision tree (TREEC), parzen classifier (PARZENC) and the support vector classifier (SVC) [48]. The linear, quadratic and uncorrelated normal density-based classifiers are all density-based classifiers. The LDC is particularly useful when two classes are not normally distributed, and where monotonic transformations, of posterior probabilities, helps to generate discriminant functions. The QDC assumes that the classes are normally distributed with class specific covariance matrices, thus allowing a set of optimal discriminant functions to be obtained. The UDC works in a similar way to the QDC classifier but computation of a quadratic classifier between the classes by assume normal densities with uncorrelated features. The QDC takes decisions by assuming different normal distribution of data that leads to quadratic decision boundaries.

The polynomial and logistic classifiers are linear-based classifiers, which predict class labels based on weighted, linear combination of features or the variables of the objects. The LOGLC computes the classification of a dataset by maximizing the likelihood criterion, using the logistic (sigmoid) function. The POLYC adds polynomial features to the datasets in order to run the untrained classifier. It is possible to construct second order terms, using this classifier. The parzen, decision tree, support vector, and k-nearest neighbour classifiers are nonlinear classifiers. Nonlinear classifiers compute the optimum smoothing parameter between classes in the datasets. Using smoothing parameters without any learning process, produces discrimination. Smoothing parameters may be a scalar, a vector or a matrix with objects and their features. The TREEC classifier uses binary splitting and classes are decided upon the basis of a sequence of decision rules. Quadratic programming optimises the SVC, and non-linearity is determined by the kernel. If an SVM model, uses the sigmoid kernel then it behaves more or less like a two-layer, perceptron neural network. There are four basic kernels, linear, polynomial, radial basis function and sigmoid. In this type of classification, functions map training sets into a higher dimensional space in this type of classifier. It finds a linear separating hyperplane with the maximum margin in the higher dimensional space. The KNNC and PARZENC are similar in the sense that their build-up classifiers still use the training dataset and their parameters, while KNNC classifies the object in a feature space with the nearest training parameters.

Validation Methods

The Holdout Cross-Validation technique is used in this study [49], in which, 80% of the whole dataset is designated for training and the remaining 20% for testing. To maintain generalisation, the training and test sets comprise randomly selected instances from the TPEHG dataset. Since the exact selection of instances, for the training, is random, it is necessary to repeat the learning and testing stage. The average performance obtained from 100 simulations is utilised. This number is considered, by statisticians, to be an adequate number of iterations to obtain an average [50]. After each repetition, the error rate for each classifier is stored and the learning experience of the algorithm wiped so that it does not influence the next test. Producing several repetitions provides average error rates, standard deviations and performance values for each classifier.

The k-fold cross-validation is a validation technique used to estimate the accuracy of the classifiers. In this paper, the results obtained for k-fold validation uses 5 folds and 1 and 100 repetitions respectively. The results are then compared with those from the 80/20 holdout cross-validation approach. Sensitivity (true positives) and specificity (true negatives) measure the predictive capabilities of classifiers in binary classification tests. Sensitivities refer to the true positive rate or recall rate (preterm records). Specificities measure the proportion of true negatives (term records). Sensitivities are considered a higher priority than specificities, in this study. It is important to predict a preterm delivery rather than miss classifying a term pregnancy.

The Receiver Operator Curve (ROC) is a standard technique used to summarise classifier performance based on trade-offs between true positive and true negative error rates [51]. The Area Under the Curve (AUC) is an accepted performance metric that provides a value equal to the probability that a classifier will rank a randomly chosen positive instance higher than a randomly chosen negative one (this obviously assumes that positive ranges higher than negative) [51]. These have been chosen since they are suitable evaluation methods for classifiers, which produce binary output (term or preterm) [52].

The pattern recognition toolbox (PRTools) has been used to implement all of the techniques used in this study.

Results

This section presents the classification results for term and preterm delivery records using the TPEHG dataset. The 0.34–1 Hz filter on Channel 3 is used with 80% holdout technique and k-fold cross-validation. The initial evaluation provides a base line for comparison against all subsequent evaluations, considered in this section.

Results for 0.34–1 Hz TPEHG Filter on Channel 3

This evaluation uses the 0.34–1 Hz filtered signals on Channel 3 with nine classifiers. The performance for each classifier is evaluated, using the sensitivity, specificity, mean error, standard deviation and AUC values with 100 simulations and randomly selected training and testing sets for each simulation.

Classifier Performance

The first evaluation uses the original TPEHG dataset (38 preterm and 262 term). Table 3, illustrates the mean averages obtained over 100 simulations for the sensitivity, specificity, and AUC.

Table 3. Classifier Performance Results for the 0.34–1 Hz Filter.

	Sensitivity	Specificity	AUC
Classifier	Channel 3 0.34–1Hz Filter	Channel 3 0.34–1Hz Filter	Channel 3 0.34–1Hz Filter
LDC	0.0000	0.9807	53%
QDC	0.0000	0.9807	53%
UDC	0.0000	1.0000	52%
POLYC	0.0000	0.9807	61%
LOGLC	0.0000	0.9807	60%
KNNC	0.0000	0.9230	53%
TREEC	0.2857	0.8653	60%
PARZENC	0.0000	1.0000	50%
SVC	0.0000	1.0000	61%

As shown in Table 3, the sensitivities (preterm), in this initial test, are low for all classifiers. This is expected because there are a limited number of preterm records from which the classifiers can learn. Consequently, specificities are higher than sensitivities. More specifically, there are 31 preterm records in the 80% holdout training set. This is a limited number of records for one class. Furthermore, the AUC indicated that all classifiers failed to generate results higher than 61%. This indicates that the classifiers classified most of the instances into the major class, which caused very low sensitivities. Table 4 illustrates the results from a k-fold cross-validation technique, used to improve the results obtained from the holdout method. The results showed that it was not possible to achieve a classification error, lower than the base-rate error of 12.67%.

Table 4. Cross Validation Results for the 0.34–1 Hz Filter.

	80% Holdout: 100 Repetitions		Cross Val, 5 Folds, 1 Repetitions	Cross Val, 5 Folds, 100 Repetitions
Classifiers	Mean Err	SD	Mean Err	Mean Err	SD
LDC	0.1342	0.0127	0.1333	0.1349	0.0045
QDC	0.1355	0.0166	0.1366	0.1421	0.0088
UDC	0.1324	0.0142	0.1366	0.1383	0.0080
POLYC	0.1300	0.0072	0.1300	0.1300	0.0000
LOGLC	0.1324	0.0112	0.1333	0.1322	0.0034
KNNC	0.1707	0.0270	0.1267	0.1312	0.0081
TREEC	0.2135	0.0443	0.1995	0.2183	0.0210
PARZENC	0.1267	0.0000	0.1267	0.1267	0.0000
SVC	0.1267	0.0000	0.1267	0.1267	0.0000

The k-fold cross-validation results, using five folds and both one and one hundred repetitions shows that the k-fold cross-validation approach improved the error rates, for some classifiers. However, these results are not considered statistically significant. Furthermore, the lowest error rates could not be improved below the minimum error rate expected, which is 12.67% (38 preterm/300 deliveries).

Model Selection

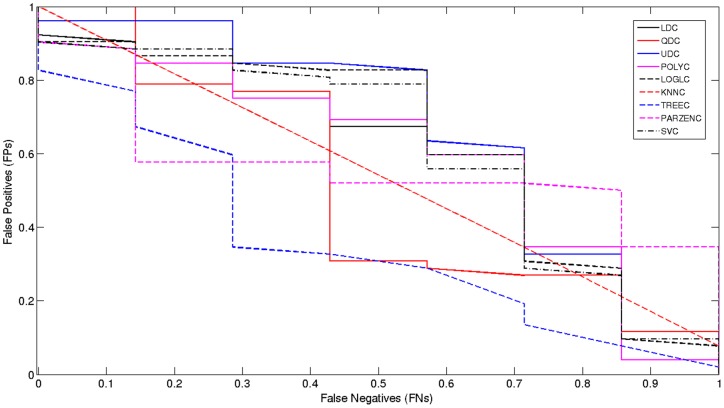
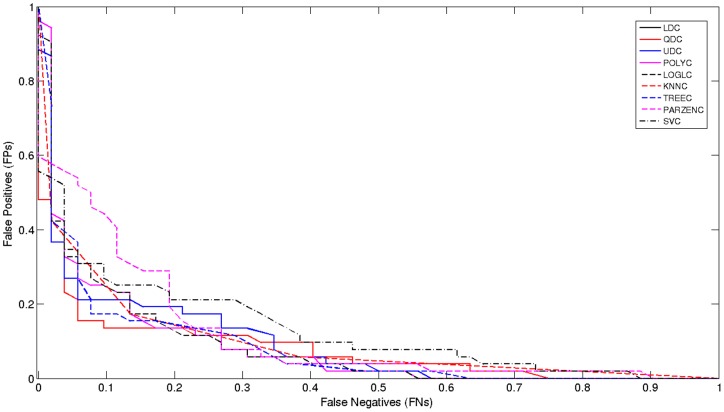
The receiver operator characteristic (ROC) curve shows the cut-off values for the false negative and false positive rates. It has been used for each of the classifiers, using the original TPEHG dataset 0.34–1 Hz filter. Figure 4 indicates that, none of the classifiers performed particularly well. The AUC values in Table 1 support these findings with very low accuracy values.

Figure 4. Received Operator Curve for the 0.34–1 Hz Filter.

The poor results indicate that the classification algorithms do not have enough preterm records to learn from, in comparison to term records. Consequently, sensitivities are low while specificities are high, which in this study are of lower importance. The main issue, in terms of machine learning, is that the dataset is skewed. Although this problem has not been widely reported, in many recent EHG studies, imbalanced data is a common machine-learning problem. As such, re-sampling the classes (with the minority class – in this instance, preterm records) is a conventional way to balance the dataset [53].

Results for 0.34–1 Hz TPEHG Filter on Channel 3 – Oversampled using SMOTE

The 38 preterm records are re-sampled using the SMOTE technique [41]. The SMOTE algorithm allows a new dataset to be generated that contains an even split between term and preterm records (262 each) oversampled using the original preterm records.

Classifier Performance

Table 5 indicates that the sensitivities, for all the algorithms, improved at the expense of lower specificities. In addition, the AUC results showed significant improvements with a value of 89% achieved by the TREEC classifier. The results also show that the AUC values, for all the algorithms, increased. This is encouraging given that sensitivities are more important in this research than specificities. Balancing the dataset increased the classification algorithms ability to predict preterm records. From the previous set of results, we find a 60% increase in sensitivities, a 17% drop in specificities, and a 30% increase in the performance of the TREEC classifier.

Table 5. Classifier Performance Table for Oversampled 0.34–1 Hz Signal.

	Sensitivity	Specificity	AUC
Classifier	Channel 3 0.34–1Hz Filter	Channel 3 0.34–1Hz Filter	Channel 3 0.34–1Hz Filter
LDC	0.8653	0.8076	66%
QDC	0.9230	0.8461	72%
UDC	0.8269	0.8076	72%
POLYC	0.8653	0.8076	86%
LOGLC	0.8653	0.8269	86%
KNNC	0.8653	0.8269	84%
TREEC	0.9038	0.8269	89%
PARZENC	0.5961	0.9615	72%
SVC	0.8076	0.7692	78%

Again, the k-fold cross-validation results are better than the holdout method. This is indicated in Table 6.

Table 6. Cross Validation Results for Oversampled 0.34–1 Hz Signal.

	80% Holdout: 100 Repetitions		Cross Val, 5 Folds, 1 Repetitions	Cross Val, 5 Folds, 100 Repetitions
Classifiers	Mean Err	SD	Mean Err	Mean Err	SD
LDC	0.2132	0.0325	0.2116	0.2064	0.0023
QDC	0.1770	0.0347	0.1811	0.1806	0.0040
UDC	0.2035	0.0328	0.1981	0.2001	0.0018
POLYC	0.2132	0.0325	0.2116	0.2064	0.0023
LOGLC	0.2037	0.0315	0.2118	0.1972	0.0059
KNNC	0.2249	0.0386	0.2594	0.2340	0.0088
TREEC	0.1995	0.0387	0.1944	0.1994	0.0069
PARZENC	0.2499	0.0392	0.2423	0.2461	0.0124
SVC	0.2851	0.0383	0.2899	0.2901	0.0042

The results show that, using the 80% holdout method, several classifiers produce better results. Overall, the mean errors produced, using all of the validation techniques, were significantly lower than the expected error, which is 262/524, i.e. 50%.

Model Selection

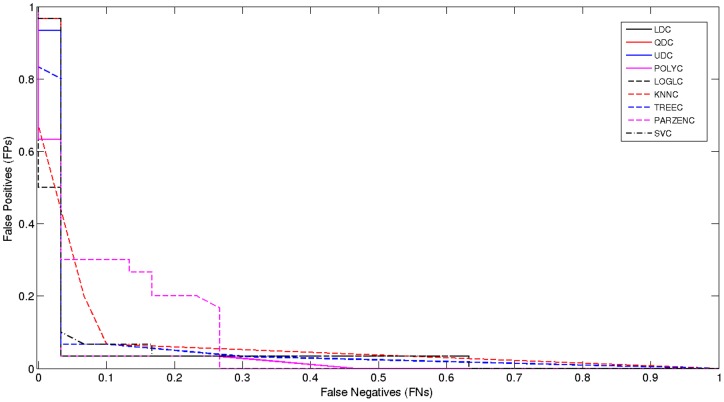
Again, the ROC curve shows the cut-off values for the false negative and false positive rates. Figure 5, below, shows a significant improvement.

Figure 5. Received Operator Curve for Oversampled 0.34–1 Hz Signal.

The results present a strong case for oversampling and indicate that better predictive models are possible for predicting term and preterm records.

Results for 0.34–1 Hz TPEHG Filter on Channel 3 – Oversampling with additional features

In December 2012, Fele-Zorz et al. made additional features available. These features are age, parity (number of previous births), abortions, weight, hypertension, diabetes, placental position, first and second trimester bleeding, funnelling and smoking. Incorporation of the new features, into the original dataset, resulted in the filtration of the dataset. The purpose of this was to remove any noisy data that may have been contained in the additional features. This resulted in a new dataset containing 19 preterm records and 150 term records. The SMOTE algorithm has balanced the dataset, and the classifiers have been re-run.

Classifier Performance (Oversampling with additional features)

Table 7 shows the sensitivity, specificity, and AUC results. These results show that there is a significant increase in sensitivity, specificity and AUC values, due to the utilisation of the additional features. The best classification algorithm is the POLYC classifier. This achieved 97% sensitivity, 90% specificity, and 95% AUC value with 8% global error. From the previous set of results, this shows a 6% increase in sensitivities, 7% increase in specificities, and a 6% increase in the AUC value, while maintaining an 8% global error. Other classifiers also produced very good results, particularly, the LOGLC, KNNC and the TREEC classifiers. All these classifiers produced improvements on the classifications performed on the original TPEHG dataset.

Table 7. Classifier Performance for Oversampled 0.34–1 Hz Signal with additional Features.

	Sensitivity	Specificity	AUC
Classifier	Channel 3 0.34–1Hz Filter	Channel 3 0.34–1Hz Filter	Channel 3 0.34–1Hz Filter
LDC	0.9666	0.9000	70%
QDC	0.9666	0.1666	83%
UDC	0.9666	0.1333	78%
POLYC	0.9666	0.9000	95%
LOGLC	0.9666	0.9000	94%
KNNC	0.9333	0.8000	90%
TREEC	0.9666	0.9000	93%
PARZENC	0.9666	0.5666	59%
SVC	0.9666	0.7000	92%

The performance of k-fold cross-validation was compared with the results obtained from both the 80% holdout method and cross-validation. Table 8 shows that minor improvements are made, using k-fold cross-validation.

Table 8. Cross Validation Results for Oversampled 0.34–1 Hz Signal with additional Features.

	80% Holdout: 100 Repetitions		Cross Val, 5 Folds, 1 Repetitions	Cross Val, 5 Folds, 100 Repetitions
Classifiers	Mean Err	SD	Mean Err	Mean Err	SD
LDC	0.0858	0.0289	0.00800	0.0867	0.0060
QDC	0.3260	0.0780	0.0780	0.3344	0.0216
UDC	0.4162	0.0471	0.0471	0.4289	0.0124
POLYC	0.0858	0.0289	0.0289	0.0867	0.0060
LOGLC	0.0932	0.0301	0.0301	0.0983	0.0062
KNNC	0.1458	0.411	0.0411	0.1522	0.0131
TREEC	0.1127	0.0436	0.0436	0.1178	00.0149
PARZENC	0.2130	0.044	0.0444	0.2067	0.0056
SVC	0.1338	0.0419	0.0419	0.1233	0.0070

The results show that the additional features significantly improve the performance of several classifiers. In particular, the POLYC, LOGLC, KNNC and the TREEC classifiers perform very well. The best classifier is the POLYC with 97% for sensitivity, 90% for specificity, and an AUC value of 95%, with a global mean error of 8%.

Model Selection

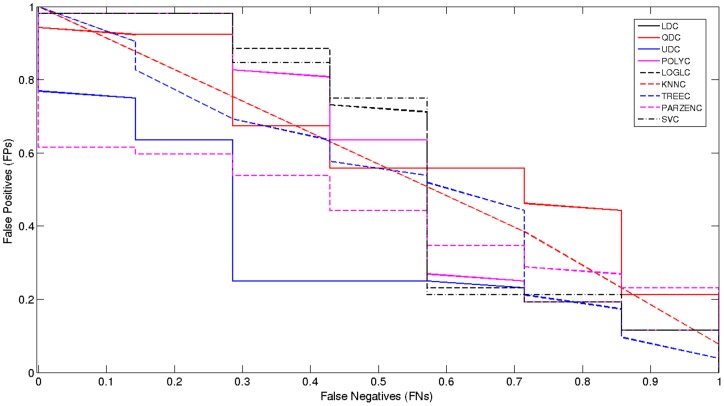
Figure 6 below, shows that there is a significant improvement, compared to the ROC curve illustrated in Figure 5.

Figure 6. Received Operator Curve for Oversampled 0.34–1 Hz Signal with additional features.

Results for Clinical Data Only

In this section, the clinical data by itself is used to classify the term and preterm records. As before, the dataset is balanced using the SMOTE algorithm. The same classification algorithms have also been re-run, on the new 300 record clinical dataset.

Classifier Performance (Clinical Data Only)

Table 9 shows the sensitivity, specificity, and AUC results when using the clinical data only. As it can be seen, the AUC has reduced significantly when using the clinical data by itself. This is an indication that the EHG signals play significant roles in the classification process. The simulation results indicated that the AUC dropped noticeably with a best value achieved by the POLYC and LOGLC classifiers producing a value of 55% only.

Table 9. Classifier Performance for Clinical Data Only.

	Sensitivity	Specificity	AUC
Classifier	Channel 3 0.34–1Hz Filter	Channel 3 0.34–1Hz Filter	Channel 3 0.34–1Hz Filter
LDC	0.0000	1.0000	51%
QDC	1.0000	0.0384	51%
UDC	0.0000	0.9038	52%
POLYC	0.000	1.0000	55%
LOGLC	0.0000	1.0000	55%
KNNC	0.0000	0.9230	50%
TREEC	0.1428	0.8461	52%
PARZENC	0.0000	1.0000	49%
SVC	0.0000	1.0000	53%

The performance of k-fold cross-validation is compared with the results obtained from both the 80% holdout methods. Table 10 shows that the mean errors when using the clinical data only.

Table 10. Cross Validation Results for Clinical Data Only.

	80% Holdout: 30 Repetitions		Cross Val, 5 Folds, 1 Repetitions	Cross Val, 5 Folds, 6 Repetitions
Classifiers	Mean Err	SD	Mean Err	Mean Err	SD
LDC	0.1354	0.0146	0.1399	0.1355	0.0053
QDC	0.8443	0.0338	0.8532	0.8559	0.0073
UDC	0.1953	0.0364	0.1930	0.1939	0.0062
POLYC	0.1278	0.0049	0.1300	0.1272	0.0013
LOGLC	0.1334	0.0139	0.1300	0.1322	0.0053
KNNC	0.1652	0.0289	0.1267	0.1283	0.0028
TREEC	0.2231	0.493	0.2126	0.2362	0.0227
PARZENC	0.1267	0.000	0.1267	0.1267	0.0000
SVC	0.1267	0.000	0.1267	0.1267	0.0000

Using the clinical data only, the mean errors and k-fold values are as expected and they are not considered statistically significant.

Model Selection

Figure 7 shows that, when only using the clinical data, all classifiers have performed significantly worse than previous evaluations.

Figure 7. Received Operator Curve for Clinical Data Only.

Summary of Results

Table 11 and 12 illustrates a summary of the results for all four approaches. As it can be seen, the oversampled dataset, which utilized additional features, provided the best results with a significant increase in sensitivity, specificity and AUC values. In particular, using this method, POLYC has improved significantly.

Table 11. Summary of Classifier Performance for Original TPEHG Dataset and Oversampled Dataset Using SMOTE.

	Original TPEHG dataset			Oversampled using SMOTE
	Sensitivity	Specificity	AUC	Sensitivity	Specificity	AUC
Classifier	Channel 3 0.34–1 Hz Filter	Channel 3 0.34–1 Hz Filter	Channel 3 0.34–1 Hz Filter	Channel 3 0.34–1 Hz Filter	Channel 3 0.34–1 Hz Filter	Channel 3 0.34–1 Hz Filter
LDC	0.0000	0.9807	53%	0.8653	0.8076	66%
QDC	0.0000	0.9807	53%	0.9230	0.8461	72%
UDC	0.0000	1.0000	52%	0.8269	0.8076	72%
POLYC	0.0000	0.9807	61%	0.8653	0.8076	86%
LOGLC	0.0000	0.9807	60%	0.8653	0.8269	86%
KNNC	0.0000	0.9230	53%	0.8653	0.8269	84%
TREEC	0.2857	0.8653	60%	0.9038	0.8269	89%
PARZENC	0.0000	1.0000	50%	0.5961	0.9615	72%
SVC	0.0000	1.0000	61%	0.8076	0.7692	78%

Table 12. Summary of Classifier Performance for Oversampling with Additional Features and Clinical Data Only.

	Oversampling with Additional Features			Clinical Data Only
	Sensitivity	Specificity	AUC	Sensitivity	Specificity	AUC
Classifier	Channel 3 0.34–1 Hz Filter	Channel 3 0.34–1 Hz Filter	Channel 3 0.34–1 Hz Filter	Channel 3 0.34–1 Hz Filter	Channel 3 0.34–1 Hz Filter	Channel 3 0.34–1 Hz Filter
LDC	0.9666	0.9000	70%	0.0000	1.0000	51%
QDC	0.9666	0.1666	83%	1.0000	0.0384	51%
UDC	0.9666	0.1333	78%	0.0000	0.9038	52%
POLYC	0.9666	0.9000	95%	0.0000	1.0000	55%
LOGLC	0.9666	0.9000	94%	0.0000	1.0000	55%
KNNC	0.9333	0.8000	90%	0.0000	0.9230	50%
TREEC	0.9666	0.9000	93%	0.1428	0.8461	52%
PARZENC	0.9666	0.5666	59%	0.0000	1.0000	49%
SVC	0.9666	0.7000	92%	0.0000	1.0000	53%

The results illustrate that using machine learning techniques are encouraging. Within a wider context, this approach might be able to utilise real-life pregnancy data to predict, with high confidence, whether an expectant mother is likely to have a premature birth or proceed to full term.

Discussion

Most studies, in the field of EHG classification, have focused on the diagnosis of true labour. This occurs at the stage when a woman believes, or suspects, she is in actual labour. This study has evaluated the use of a machine learning approach, using records from earlier stages of gestation, to predict term or preterm deliveries.

The initial classifications on the dataset (unbalanced) achieved a high specificity. However, this was at the cost of very poor sensitivity, below 20%. The k-fold cross-validation function was evaluated as a dataset splitting method to determine whether the sensitivities could be improved. However, the small improvements, in the mean error, were not statistically significant. The main problem occurred due to the disproportionate number of term records to preterm records. This causes bias in favour of true negatives or the majority class, as reported in [42]–[47]. The minimum error rate displayed across several of the classifiers, was 12.67%. This initially appeared to be a good error rate. However, the classifiers were simply classifying by minimising the probability of error, in the absence of sufficient evidence to help them to classify otherwise. It appeared as though most of the classifiers were classifying according to the prior probabilities of the classes, in order to minimise the error.

Using the SMOTE technique significantly improved the sensitivity and specificity rates, while maintaining high accuracy in the AUC values. The best classification algorithm was the TREEC classifier, which achieved 90% sensitivity, 83% specificity, and an AUC value of 89% with a 20% global error.

Using the oversampled clinical data the initial publication of the TPEHG dataset was in November 2010. However, in December 2012, clinical data became publically available. The final set of results shows that the overall performance of classifiers is improved further by including the information from the clinical dataset. Nonetheless, more recordings are needed, particularly more clinical information about the patients themselves. This would allow more reliable models to be constructed using the clinical and the EHG signals, which the findings in this paper support.

As it can be shown from Table 7, the Binary Decision Tree produced promising results of 93% accuracy, for the area under the curve, when the extra features are utilised in addition to the EHG signals. This is due to the feature of Binary decision trees, which use the engineering concept of divide and conquer. In this case, the binary decision tree will break down the complex decision-making problem into a collection of simpler decisions, thus providing a solution, which is often easier to interpret and understand. As indicated in Table 7, the best results have been achieved using the polynomial classifier. This is because the polynomial classifier adds polynomial features that can expand the input space, into higher dimensional space where linear seperability is possible.

While the results were very good, several issues were evident in the clinical data. Firstly, while the weight of the patient was provided, there was no information to say how tall they were, thus making it impossible to calculate their body mass index. Other features, such as bleeding, failed to show how often the bleeding occurred, or the amount of bleeding. In another example, the fact that someone smoked would be more informative if the number of cigarettes per day was provided. Nonetheless, while the data was vague, it was decided that the information might still be useful. The results suggest that the additional features further enhance the algorithms capability to separate term and preterm records.

From all the experiments performed, on the oversampled TPEHG dataset, with combined additional features, the POLYC classifier obtained the best result, as can be seen in Table 7. This classifier obtained 97% sensitivity, 90% specificity, a 95% AUC value and a global error of 8%. The LOGLC, and TREEC classifiers produced similar results, with overall AUC values of 94% and 93% respectively.

Generally, this paper produced significantly better results than those in [25], who report a sensitivity of 47%, specificity of 90%, and an overall error rate of 25%. Furthermore, the results have also been an improvement than those reported in [12]–[16], [54]–[58]. However, the findings in [31] produced a much lower error rate of 3.33%±1.3, a sensitivity rate of 100% and a specificity rate of 94%. Diab et al. have used several alternative techniques, including artificial neural networks and autoregressive models. However, it should be noted that the sample size is much smaller than the sample size in this paper (15 preterm and 15 term). The study in [31] also used a different data source, for their 30 records, compared to the TPEHG. Therefore, it is difficult, to make a direct comparison between that study and the study in this paper. Consequently, it is impossible to determine if the higher results are, in fact, better.

Conclusions and Future Work

The rate of premature births has increased globally, which can lead to severe medical conditions and an increase in societal and economical costs. However, a better understanding of preterm births, and a strategic focus on prevention, is likely to improve health outcomes and reduce national healthcare service costs. A strong body of evidence has suggested that the analysis of uterine electrical signals from the abdominal surface (EHG) could provide a viable way of diagnosing true labour, and even predict preterm deliveries.

This paper utilises such EHG signals, within a supervised machine-learning paradigm, to classify term and preterm records. The focus of the paper has been to improve sensitivity rates, as it is more important to predict preterm delivery, as opposed to miss classifying a term pregnancy. As such, using the original TPEHG dataset, the number of preterm records (minority class) was considerably lower than the number of term records (majority class). Since the classifiers do not have enough preterm records to learn from, this led to the original results being quite poor. AUC values were no higher than 61% and, for the majority of the classifiers sensitivity was at 0%. In this instance, using the SMOTE technique, it has been necessary to oversample the preterm records. Oversampling the minority class enables the distribution between the two classes (term and preterm) to be more balanced. This technique significantly improved the results, with a maximum AUC value of 89% and sensitivity rate of 92%. Along with the SMOTE technique, as additional features became available this further improved the results. In this instance, a maximum AUC value of 95% and sensitivities of 97% were achieved. However, using only the clinical data produced significantly poorer results, with a maximum AUC value of 55% and the majority of sensitivities at 0%. As discussed, this could be due to the ambiguity of the clinical data. Nevertheless, these results are encouraging, and the approach shows an improvement on existing studies.

Despite these encouraging results, more in-depth research is still required. For example, regression analysis, using a larger number of classes, would be interesting. This would help to predict the expected delivery, in terms of the number of days or weeks, not just whether a woman is likely to deliver term or preterm.

Future work will evaluate different parameter adjustment settings. In addition, more advanced classification algorithms, and techniques, will be considered, including advanced Artificial Neural Network architectures, such as higher order and spiking neural networks. The investigation, and comparison, of features, such as fractal dimension and cepstrum analysis, autocorrelation zero crossing and correlation dimension, has also not been performed. Future work will investigate these techniques in a head-to-head comparison, with linear methods.

It would also be interesting to run a study in which the classification accuracy of features extracted, per-burst of EMG, are compared against those extracted from the whole record. In such a study, the same signals would be used. However, pre-processing would occur differently. According to the literature review, no such evaluation has been carried out. Future work will also combine signals from the various channels.

Overall, the study demonstrates that classification algorithms provide an interesting line of enquiry, when separating term and preterm delivery records.

Funding Statement

The authors have no support or funding to report.