GIM³E: condition-specific models of cellular metabolism developed from metabolomics and expression data

Abstract

Motivation: Genome-scale metabolic models have been used extensively to investigate alterations in cellular metabolism. The accuracy of these models to represent cellular metabolism in specific conditions has been improved by constraining the model with omics data sources. However, few practical methods for integrating metabolomics data with other omics data sources into genome-scale models of metabolism have been developed.

Results: GIM³E (Gene Inactivation Moderated by Metabolism, Metabolomics and Expression) is an algorithm that enables the development of condition-specific models based on an objective function, transcriptomics and cellular metabolomics data. GIM³E establishes metabolite use requirements with metabolomics data, uses model-paired transcriptomics data to find experimentally supported solutions and provides calculations of the turnover (production/consumption) flux of metabolites. GIM³E was used to investigate the effects of integrating additional omics datasets to create increasingly constrained solution spaces of Salmonella Typhimurium metabolism during growth in both rich and virulence media. This integration proved to be informative and resulted in a requirement of additional active reactions (12 in each case) or metabolites (26 or 29, respectively). The addition of constraints from transcriptomics also impacted the allowed solution space, and the cellular metabolites with turnover fluxes that were necessarily altered by the change in conditions increased from 118 to 271 of 1397.

Availability: GIM³E has been implemented in Python and requires a COBRApy 0.2.x. The algorithm and sample data described here are freely available at: http://opencobra.sourceforge.net/

Contacts: brianjamesschmidt@gmail.com or hyduke@usu.edu

Supplementary information: Supplementary information is available at Bioinformatics online.

1 INTRODUCTION

The extraction and integration of biological knowledge from large, omics datasets is an active area of research (Palsson and Zengler, 2010). Genome-scale metabolic models (GEMs) provide a ‘context for content’ for metabolic information and facilitate interpreting large datasets in terms of the resulting functional state of the network (Feist and Palsson, 2008; Oberhardt et al., 2009). As opposed to an inference-based analysis of omics datasets (Ansong et al., 2013a; Yoon et al., 2011), GEMs enable the calculation of the flux through network reactions (Hyduke et al., 2012; Orth et al., 2010). However, sufficient information to uniquely determine all of the fluxes for network reactions is generally not available (Orth et al., 2010; Reed, 2012).

Constraint-based modeling approaches are useful for calculating network states at the genome scale, establishing bounds of allowed operation of the network from available information (Orth et al., 2010; Reed, 2012). Omics datasets can be used to better constrain the allowed operations of a metabolic network model and improve the accuracy of flux predictions, especially when the regulatory logic of the network is not fully known (Hyduke et al., 2012; Reed, 2012). The value of model-guided analysis of omics data is evident from its application in a variety of contexts in systems biology research (Hyduke et al., 2012). For example, constraint-based models have been used to assess the impact of alternate conditions on growth rate, biofilm formation and other functions that pathogens require to effectively implement a virulence program (Oberhardt et al., 2010; Kim et al., 2013). In the context of mammalian metabolism, constraint-based models have been used to study metabolic alterations in diseases of interest to medical research (Bordbar and Palsson, 2012) and drug development (Schmidt et al., 2013).

Algorithms have been developed and used to automatically constrain GEMs by using a variety of data types, especially transcriptomics and proteomics (Blazier and Papin, 2012). Metabolomics has also been used to develop model constraints (Fleming et al., 2009; Henry et al., 2007; Kümmel et al., 2006; Yizhak et al., 2010) and infer altered reactions from GEMs (Cakir et al., 2006). When isotopically labeled metabolic substrates are used for cellular uptake, GEMs facilitate the calculation of metabolic fluxes directly from metabolomics data (Sauer, 2006). In addition, GEMs can be used with transcriptomics data to infer transcriptional control of cellular metabolites (Patil and Nielsen, 2005).

Metabolomics data can also be used to develop model flux constraints, but using measures of cellular metabolite concentrations to develop model reaction flux constraints requires additional information (Reed, 2012). For example, reaction directionality can be bound by the calculated Gibb’s free energy change of a reaction from metabolite concentrations (or more precisely, activity) (Reed, 2012). However, the free energy change for all reactions in the model often is not available and must be estimated from group contribution theory (Fleming et al., 2009; Henry et al., 2007; Kümmel et al., 2006). Also, free energy varies as a function of cellular pH (Fleming et al., 2009), which might be unknown. Furthermore, the concentration of all reaction participants may not be known. Finally, available metabolomics data may be qualitative or semi-quantitative and may not give the absolute concentration of detected metabolites.

Here, we present an algorithm to enable the integrated functional analysis of intracellular metabolomics data and gene expression microarray data, guided by a GEM. The algorithm, GIM³E (Gene Inactivation Moderated by Metabolism, Metabolomics and Expression), uses metabolomics data to ensure that the detected species are used in the calculated network operating states. Transcriptomics data are used in GIM³E to further constrain the model fluxes. The models created with the GIM³E algorithm report the modeled rate of creation or consumption (turnover) of metabolites. GIM³E can also be implemented with metabolomics data that report the identity of detected metabolites and does not require their absolute concentrations.

We developed and used GIM³E during an investigation of alterations in S.Typhimurium metabolism in ‘rich’ and ‘virulence’ media specifically to combine the broad semi-quantitative metabolomics dataset we developed for this infectious microbe with transcriptomics data (Kim et al., 2013). Our purpose was to better constrain the model and perform an investigation of alterations in the network that was focused on metabolite turnover. Unexpectedly, we discovered alterations in metabolites with previously postulated immunomodulatory roles (Bordbar et al., 2012) and a preferential maintenance of cellular pathways implicated in virulence. However, we did not provide a detailed description of the steps in the algorithm or perform a holistic investigation of the impact of transcriptomic and metabolomic constraints on the conclusions drawn to better validate GIM³E. Therefore, we expand on our previous analysis, detail GIM³E and elucidate the impact of additional omics data sources on the model-guided interpretation of metabolism.

2 METHODS

2.1 Steps in GIM³E

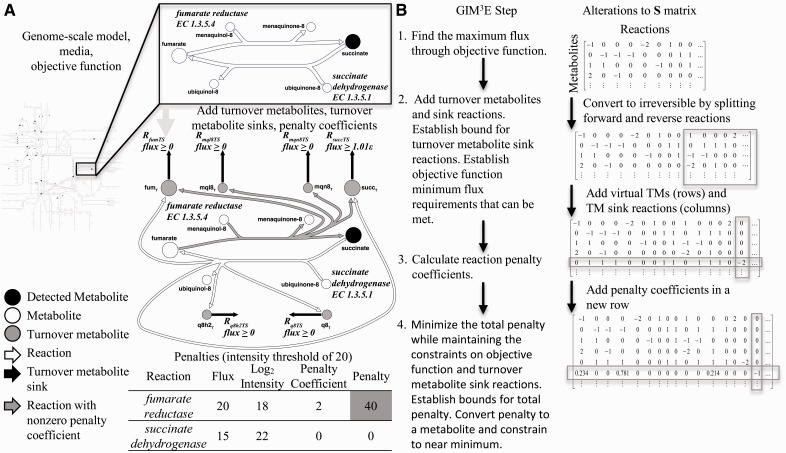
The steps in GIM³E proceed in distinct phases to implement constraints based on the cellular objective as well as metabolomics and transcriptomics data (Fig. 1). Models developed with GIM³E also report the production or consumption (turnover) of metabolites by adding turnover metabolites to the model. Hence, any reaction that produces or consumes metabolite ‘A’ also produces a corresponding ‘turnover’ metabolite, ‘A_T.’ A sink reaction for the turnover metabolite, i.e. ‘R_ATS,’ therefore tracks the flux through the metabolite. The network can then be constrained to use a detected metabolite by imposing a minimum flux requirement for the turnover.

Fig. 1.

GIM³E modifies a genome-scale model of metabolism to incorporate constraints based on metabolomics and transcriptomics data. (A) GIM³E starts with a genome-scale model, allowed nutrient exchanges as defined by the media and an objective function such as biomass production (growth). Metabolomics data are mapped onto the model. Two reactions are shown in more detail to illustrate the manipulations to the model made during execution of the GIM³E algorithm. Turnover metabolites are added as products to each reaction, one turnover metabolite for each reaction substrate or product. A turnover sink reaction is also added for each turnover metabolite. The minimum bound for the turnover sink flux is set to a small positive value if the metabolite was detected. Transcriptomics data were used by calculating penalties for reactions that do not meet a threshold criterion. The inset table demonstrates a sample calculation of the penalty for each reaction assuming a given set of reaction flux values. The total penalty that is subject to minimization is calculated by summing the penalty values for all reactions. (B) Summary of the steps in GIM³E and alterations to the S matrix

As in the previously developed Gene Inactivation Moderated by Metabolism and Expression (GIMME) algorithm (Becker and Palsson, 2008), penalty coefficients are calculated for model reactions based on transcriptomics data. The penalties minimize the degree to which the network uses reactions that have weaker supporting evidence in the data. Manipulations to the stoichiometric S matrix are also shown in Figure 1B. The mathematical description of the steps in GIM³E follows.

1. Determination of objective function bound The GEM is optimized for the selected objective with flux balance analysis (Orth et al., 2010).

Maximize:

(1)

Such that:

(2)

(3)

Here, c is a column vector of objective coefficients, v is a column vector of reaction flux values, S is the stoichiometric matrix, a is a vector of lower bounds for the fluxes and b is a vector of upper bounds for the fluxes. Note that a and b include limits for nutrient uptake, and will vary based on the media. Once the optimal value is determined, a constraint is added to require that the objective maintains a value greater than or equal to some fraction, f, of the optimum objective value, o_opt.

2. Addition of turnover metabolites The model is first converted to an irreversible format that serves two purposes. First, breaking reversible reactions into complementary irreversible pairs is required for the calculation of virtual metabolite turnover. Second, complementary irreversible pairs will be mathematically necessary to calculate a penalty using commercial linear program solvers. A turnover metabolite for each model cellular metabolite is added to each reaction that produces or consumes the corresponding model cellular metabolite. Next, a sink reaction for each turnover metabolite is added. To ensure that detected metabolites are used by the network in valid model solutions, the lower bound on flux through each turnover sink reaction corresponding to a detected metabolite is set to a small positive value limited by the solver’s numerical tolerance (here, 1 × 10⁻⁸). As described previously (Kim et al., 2013), it was not possible to require 100% of optimal growth and also produce all detected metabolites. Therefore, we set f to 0.99 to stay within 1% of the maximum objective value, o_opt.

3. Addition of penalty coefficients Transcriptomics data are used to develop penalties to reduce the use of reactions with lower evidence for expression. Transcriptomics data are particularly useful, as these data generally offer good coverage of the reactions in the genome-scale model. Penalty coefficients are calculated for each model-paired transcript on the basis of intensity by:

(4)

Here, τ_g indicates the transcript-associated penalty coefficient for transcript g. I_g indicates the corrected log₂ intensity for transcript g. I_max indicates the maximum corrected log₂ intensity for all model-paired transcripts in the current media condition being considered. The transcript-associated penalty coefficients are then mapped to model reactions with gene–protein reaction relationships from the reconstruction (Thiele et al., 2011) (e.g. τ_g values are mapped to the elements of φ^irr, a column vector of reaction penalty coefficients).

4. Determination of penalty bound Optimization is performed to minimize the total penalty.

Minimize:

(5)

Such that:

(6)

(7)

(8)

Here, S^irr is the stoichiometric matrix that has been converted to an irreversible format (Fig. 1B) with added turnover metabolites, v^irr is the vector of reaction fluxes, a^irr is a vector of lower bounds for the fluxes, b^irr is a vector of upper bounds for the fluxes and c^irr is the column vector of objective coefficients corresponding to the optimization in Step 1. Note that a^irr will include lower bounds for the turnover sink reactions, which are taken to be 1.01 ε, the solver tolerance. For clarity, a sample penalty calculation is shown in the table in Figure 1A.

Once the best objective function value is determined, a constraint is implemented to require that the penalty maintained a value within some fraction, g, of the minimum value, Φ_min. Because we took f to be 0.99 to remain within 1% of maximum growth, we took g to be 1.01 to remain within 1% of the minimum penalty. Network properties could then be explored while maintaining consistency with the omics data sources and the capacity to meet cellular objectives.

2.2 Conversion to mixed integer linear program

When calculating the turnover flux of a metabolite participating in multiple reversible reactions, the flux of one reaction of each reversible pair should be constrained to 0. An example to illustrate the motivation for this requirement is provided in Supplementary Figure S1. To ensure only one reaction of a reversible pair is used, integer (binary) variables can be incorporated into the model to represent the choice of the forward or reverse reaction for each pair. In this case, a mixed integer linear programming (MILP) problem must be solved. Once we have already established constraints on the penalty and objective function based on the best values, the optimization problem for any linear objective function of interest can be stated as:

Optimize (minimize/maximize):

(9)

Such that:

(10)

(11)

(12)

(13)

With additional constraints for each reversible reaction pair k (of 1, 2, … , K):

(14)

(15)

(16)

(17)

Here, m is the column vector of objective coefficients, r_k is a binary variable that effectively enables just one reaction of forward and reverse reaction pair k, d is a K × 2 matrix with rows that track the indices of the forward and reverse pairs in v_irr and i_forward(k) and i_reverse(k) are functions to respectively map each of the K reaction pairs to the appropriate indices in v^irr. As described in the Supplementary Data, a distinct formulation was required to implement the MILP in COBRApy (Ebrahim et al., 2013).

2.3 Preparation and integration of omics data

The processed omics data used to inform the analysis are available with the GIM³E algorithm (see opencobra.sourceforge.net). Transcriptomics data from 25 microarrays for Salmonella Typhimurium were used (JCVI S.Typhimurium 13k v8 two-channel spotted oligonucleotide microarrays, see SysBEP.org for datalinks). The microarrays offered coverage of >99% of annotated genes (Supplementary Table S1) in our previously published genome-scale model of S.Typhimurium metabolism (Thiele et al., 2011). Intensities were extracted using the limma package for R from Bioconductor on individual channels (Smyth, 2005a, b), background-corrected with the normexp method (Ritchie et al., 2007), normalized using the print-tip LOESS method and adjusted by quantile normalization between the channels and arrays. Median intensities were used for transcripts with multiple probes for the calculation of penalties in Equation (4).

We used published GC–MS metabolomics datasets for S.Typhimurium in log-phase growth in two conditions (Kim et al., 2013), which we have previously described as ‘rich’ (Luria Burtani broth, LB) and ‘virulence’ (acidic minimal medium low in phosphate and magnesium, LPM) media. Virulence medium has been designed for the induction of genes critical for intracellular virulence, as observed in vivo (Aranda et al., 1992; Deiwick et al., 1999; Figueroa-Bossi and Bossi, 1999). We used Kyoto Encyclopedia of Genes and Genomes (KEGG) identifiers assigned to the detected metabolites to speed the matching with metabolites in our consensus reconstruction of S.Typhimurium metabolism (Kanehisa and Goto, 2000; Kanehisa et al., 2011). One challenge in interpreting metabolomics data is the confounding factor of subcellular compartment localization. Unlike more complex eukaryotic organisms with greater compartmentalization, our reconstruction of S.Typhimurium metabolism contains a cytoplasmic and periplasmic space. Therefore, we preferentially paired our metabolomics data with metabolites in the larger more biosynthetically relevant cytoplasmic compartment. The cytoplasmic compartment is also potentially less permeable to the loss of metabolites by diffusive transport processes during sample washing and preparation. Future implementations of GIM³E to analyze more compartmentalized organisms could alter the implementation of turnover metabolites to couple each metabolite across compartments and ensure flux through the metabolite in at least one compartment.

2.4 Effects of penalty and metabolite constraints

Imposition of model metabolite and penalty constraints each alters the allowed solution space. Therefore, three methods were used to characterize the solution space: a characterization of reaction and metabolite accessibility, requirement and relative flux range change. Accessibility was evaluated by testing whether the maximal flux for a given reaction (or metabolite) exceeded the numerical tolerance. Required reactions (and metabolites) were enumerated by constraining the flux for the reaction (or metabolite) of interest to zero and checking whether a solution, given the constraints on the objective (growth), penalty and turnover metabolite sink reactions, could still be found. We describe these reactions and metabolites as ‘required’ as opposed to ‘essential’ to emphasize that not only non-zero growth constraints but also a near optimal growth constraint and constraints based on omics data must be met.

The relative flux range change was previously defined (Kim et al., 2013):

(18)

Here, x_j indicates the relative flux range change for reaction j, r_m,j indicates the width of the flux range for reaction j in condition m and c_m,j indicates the center of the flux range for reaction j in condition m. Note that r_m,j and c_m,j are found by flux variability analysis (Mahadevan and Schilling, 2003). A logical cutoff to use when interpreting the relative flux range change is |x_j| > 1.

We further characterized the importance of correct metabolite identification on the performance of the GIM³E algorithm by quantifying the ability to identify the required metabolites implicated by metabolomics-constrained models created in virulence medium with ‘noisy’ metabolomics data. Noisy metabolomics datasets were created by randomly selecting a subset of detected metabolites and replacing the selected metabolites with random accessible cellular metabolites. Five alternate noisy metabolomics datasets were created for each number of randomized metabolites to determine the average effect of metabolite misidentification. Alternately constrained models were then created for S.Typhimurium in virulence medium using constraints based on the objective and the noisy metabolomics data. The required cellular metabolites were then tested for each of the alternately constrained models. We then characterized which of the required metabolites agreed with the required metabolites determined with the true metabolomics constraints (true positives) and whether new requirements for metabolites with a non-zero flux were introduced (false positives). When scoring true and false positives, metabolites implicated as required by the model without omics constraints were filtered from the comparison.

3 RESULTS AND DISCUSSION

Condition-matched transcriptomic, proteomic and metabolomic data sources were available for S.Typhimurium. Multi-omics data (available from SysBEP.org) gathered in two alternate growth conditions, rich and virulence media (Kim et al., 2013), therefore presented a good opportunity for algorithm validation. The model coverage of these alternate omics datasets is described in Supplementary Table S1. To elucidate the impact of additional constraints derived from omics data on the solution space, we performed a detailed analysis of four alternate models for each condition, using alternate constraints in GIM³E to customize our published genome-scale model of S.Typhimurium metabolism (Thiele et al., 2011). The eight resulting models are described in Table 1.

Table 1.

Required and accessible reactions and metabolites for alternate penalty implementations and metabolomics constraints

Medium	Rich				Virulence
Omics constraints	None	Transcriptomics	Metabolomics	Transcriptomics, metabolomics	None	Transcriptomics	Metabolomics	Transcriptomics, metabolomics
Reactions considereda	2201
Accessible reactions	1517	1517	1517	1517	1483	1483	1483	1483
Required reactions	343	374	355	386	344	377	356	389
Metabolites consideredb	1461
Accessible metabolites	985	985	985	985	971	971	971	971
Required metabolites	420	429	447	456	427	443	456	472

^aAll network (cellular, non-demand) reactions were included.

^bAll model cellular metabolites were included.

3.1 Constraints impact required reactions and metabolites

One method of characterizing the effects of the constraints on the solution space is to enumerate reactions and metabolites that must necessarily carry a nonzero flux for the model to satisfy the constraints. The concept is similar to an analysis of essential genes, whereby an in silico knockout of a gene is evaluated for an impact on the capability for non-zero growth (Joyce and Palsson, 2008). We investigated whether constraining a reaction or metabolite to be inactive (zero flux) resulted in the inability to find a solution that satisfied imposed constraints based on the objective (near optimal growth), as well as transcriptomics (penalty) and metabolomics (turnover metabolite sink reactions) data. To test the impact of the omics data on the required metabolites and reactions, we used four models based on alternate omics constraints: a model with no omics constraints (growth constraints only), a model with transcriptomics-based constraints, a model with metabolomics-based constraints and a model with both transcriptomics and metabolomics constraints. The number of required reactions and metabolites for each model are summarized in Table 1.

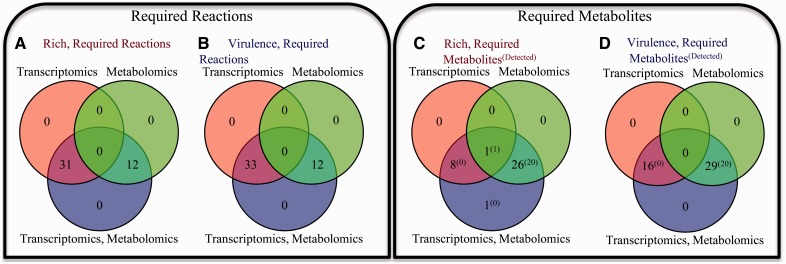
We further contrast the effect of the constraints introduced by omics on the required reactions and metabolites in Figure 2. Here, each panel contrasts the requirements for models constructed from the alternate omics constraints (metabolomics, transcriptomics or both), but not solely due to constraints on growth. For example, in Figure 2C, we show differences between the required metabolites for the three alternatively constrained models in rich media. If transcriptomics data are additionally included to constrain the model, there are nine additional required metabolites. If transcriptomics data are used, there are 27 required metabolites. If both transcriptomics and metabolomics data are used, there are 36 required metabolites. In Figure 2D, we show differences between the required metabolites for the three alternatively constrained models in virulence media. If metabolomics data are included to build and constrain the model, 29 more metabolites are required to be active, 20 of which were directly detected by metabolomics (green and blue circles). Alternatively, if transcriptomics data are included to constrain the model, 16 metabolites are required to be active (red and blue circles). Inclusion of both metabolomics and transcriptomics constraints results in the requirement for all 45 to be active (bottom, blue circle). In general, imposition of constraints based on metabolomics and transcriptomics data results in additional non-redundant constraints on the solution space.

Fig. 2.

Alternate omics constraints result in non-overlapping requirements for valid metabolic network operation. The effects of alternately imposing metabolomics-based constraints (green circle), transcriptomics-based constraints (red circle) or both (blue circle) are contrasted for (A) required reactions in rich medium, (B) required reactions in virulence medium, (C) required metabolites in rich medium and (D) required metabolites in virulence medium

Another feature of GIM³E is that the addition of metabolomics-derived constraints effectively identifies additional metabolites required to provide flux to produce/consume the detected metabolites. For example, in virulence medium, both models created with metabolomics constraints require 29 cellular metabolites be produced/consumed that were not required by the model with transcriptomics but not metabolomics constraints (Fig. 2D and Supplementary Fig. S3). However, only 20 of these metabolites were detected by metabolomics. As described in the Supplementary Data, we performed an enrichment analysis on model metabolites using pathways defined by KEGG. We first performed an enrichment analysis on the required metabolites identified only when using the metabolomics constraints (Supplementary Fig. S4). The most highly enriched pathway in rich medium was pantothenate and coenzyme A (CoA) metabolism (P = 0.0463) and in virulence medium was pyrimidine metabolism (P = 0.0533).

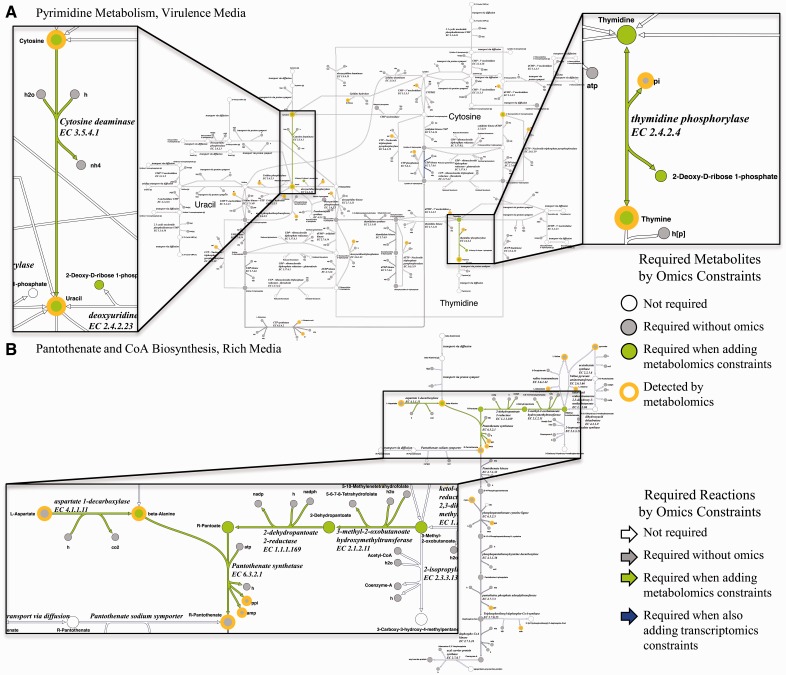
Our results prompted us to explore the impact of omics datasets on the interpretation of pathway-level alterations in metabolism. In Figure 3, we examine the impact of additional omics constraints on required reactions and metabolites, from no omics, to metabolomics, to metabolomics plus transcriptomics. Based on the pathways suggested by the enrichment analysis, we examined pyrimidine metabolism in virulence conditions (Fig. 3A). The general importance of pyrimidine metabolism for S.Typhimurium virulence in vivo has been noted previously (Chaudhuri et al., 2009). Addition of metabolomics to growth constraints suggested an additional reaction, cytosine deaminase, was necessarily active to facilitate the conversion of cytosine to uracil (inset). It has been shown that cytidine and uracil repress cytosine deaminase in S.Typhimurium (West and O’Donovan, 1982). However, the topology and directionality of the pyrimidine synthesis and salvage pathways for uracil (West and O’Donovan, 1982) suggest cytosine deaminase should be expressed for uracil production. Therefore, the inclusion of constraints based on metabolomics ensures pathways are maintained in an active state that might not be suspected from known transcriptional regulatory interactions. We also observed that although only thymine was detected, flux through thymidine also became required with the imposition of metabolomics constraints (Fig. 3A). When available, exogenous thymine can be directly incorporated for DNA synthesis during growth (Friesen, 1968). However, given thymine and thymidine are not available in virulence medium, the result suggests synthesized thymidine is degraded to thymine by thymidine phosphorylase. The metabolic versatility for thymine use may come with the cost of metabolic efficiency in the synthesis of DNA precursors.

Fig. 3.

Impact of omics datasets on the requirements in selected subsystem metabolism for S.Typhimurium. For clarity, the turnover metabolites added by GIM³E are not shown. The inclusion of additional constraints derived from transcriptomics data did not result in additional requirements for reactions and metabolites in the subsystems shown. (A) Requirements for pyrimidine metabolism in virulence medium. (B) Requirements for pantothenate and CoA biosynthesis in rich medium

R-pantothenate (vitamin B₅) is an important nutrient in CoA synthesis, and S.Typhimurium strains deficient in pantothenate synthetase are auxotrophic for pantothenate (Cronan et al., 1982). In rich medium, on the imposition of metabolomics constraints, we observed an enrichment of required metabolites in pantothenate biosynthesis (Supplementary Fig. S4). Constraints on the objective (growth) alone required the conversion of R-pantothenate to CoA (Fig. 3B). Cellular β-alanine was detected by metabolomics, and the addition of metabolomics constraints required the biosynthesis of R-pantothenate and the conversion of l-asparate, 5-10-methylenetetrahydrofolate and 3-methyl-2-oxobutanoate to R-pantothenate. The allowed solution space developed with metabolomics constraints suggests the biosynthetic pathway is active despite availability of pantothenate in the medium.

The addition of transcriptomics constraints to the metabolomics constraints resulted in no new additional metabolite requirements for the pathways shown in Figure 3. Therefore, we wished to further clarify the impact of transcriptomics constraints in addition to metabolomics. We performed the pathway enrichment analysis for metabolites required by metabolomics and transcriptomics constraints, but not required when omics constraints are absent (e.g., all metabolites in the blue circles in Figure 2C andD). Our results confirmed the importance of omics constraints in the interpretation of pantothenate biosynthesis in rich medium (Supplementary Fig. S5). However, the result for virulence conditions did not implicate pyrimidine metabolism with a similar level of significance.

The set of metabolites connected by biochemical conversions implicated as required by metabolomics data in the pantothenate biosynthesis pathway (Fig. 3A) prompted us to investigate the connectivity of metabolites required by the omics datasets. Therefore, we checked for metabolites required by inclusion of metabolomics and also connected by reactions required by the inclusion of metabolomics data. Sets with at least two connected metabolites are shown in Supplementary Figure S6A and B. In addition to the metabolites previously implicated in rich medium in pantothenate and CoA biosynthesis, the analysis uncovered a grouping of metabolites required for urocanate metabolism in virulence medium.

We verified the effect of adding transcriptomics constraints in addition to the metabolomics constraints. Additional sets of connected metabolites were implicated (Supplementary Fig. S6C and D), including intermediates in fatty acid synthesis. Effects of alterations in growth conditions such as temperature, growth phase and medium on the fatty acid composition of bacterial membranes and LPS are well documented (Marr and Ingraham, 1962; Wollenweber et al., 1983). The result suggests a change in requirements from hexadecanoyl to shorter dodecanoyl intermediates on the change from rich to virulence medium. Furthermore, the addition of transcriptomics constraints implicated an additional required reaction set spanning the conversion of 3-phosphoglyceroyl-phosphate to o-phospho-l-serine. Given glycerol is the primary carbon source in virulence medium, the result may indicate a change in metabolism to facilitate the efficient synthesis of cysteine, which can be produced from serine (Kredich and Tomkins, 1966). The result is noteworthy because proteomics measurements have identified a protein s-thiolation switch from glutathione to cysteine when changing from rich to virulence medium (Ansong et al., 2013b).

The requirement that detected metabolites are used in valid model solutions is a new development in GIM³E. Therefore, we wanted to characterize the impact of metabolite misidentification, or noise in the metabolite identification process, on the required metabolites enumerated from the models created with GIM³E (Supplementary Fig. S7). Each identification error reduced the correct identification of true-positive required metabolites by 0.45 (unadjusted R² of 0.85 with all datapoints). Each identification error also increased the number falsely identified required metabolites by 1.72 (unadjusted R² of 0.776 with all datapoints).

3.2 Constraints impact reactions altered between rich and virulence gene-inducing conditions

We also investigated the impact of alternate model constraints on reactions that were increased or decreased with respect to the relative flux range change, as shown in Equation (18) and discussed further in the Supplementary Data, when comparing cellular metabolism in virulence medium to rich medium. Essentially, the relative flux range change reports alterations in the allowed flux through a reaction between conditions. Models with constraints on the objective only (no omics constraints) exhibited the lowest number of reactions with an increased or decreased flux range, 236 of 1587 in Table 2. Integration of transcriptomics constraints shrank the solution space in each condition such that more reactions were necessarily altered in their flux range when comparing between the two conditions, 386 of 1587 reactions. The models created with the GIM³E algorithm can also be used to compute the turnover flux of metabolites, and the integration of transcriptomic constraints also had effects on the calculated turnover flux. The number of metabolites necessarily altered in their flux range increased, from 118 to 271 of 1397, when constraints calculated from transcriptomics data were included. Although the integration of metabolomics constraints had a demonstrated impact on the solution space by increasing the required reactions and metabolites, metabolomics constraints did not have a noticeable impact on the number of reactions or metabolites with an altered flux range.

Table 2.

Effect of the penalty and metabolite constraints on relative flux range

Omics constraints	None		Transcriptomics		Metabolomics		Transcriptomics, metabolomics
Medium	Rich	Virulence	Rich	Virulence	Rich	Virulence	Rich	Virulence
Model genes with penalty	0	0	1258	1258	0	0	1258	1258
Model reactions with penalty	0	0	1996	1996	0	0	1996	1996
Reactions considereda	1587
Increased reactions (X > 1)	70		128		70		128
Decreased reactions (X < −1)	166		258		166		258
Remaining reactions (|X| < 1)	1351		1201		1351		1201
Metabolites consideredb	1397
Increased metabolites (X > 1)	28		74		28		74
Decreased metabolites (X < −1)	90		197		90		197
Remaining metabolites (|X| < 1)	1279		1126		1279		1126

^aModel reactions that were not implicated in loops that could carry flux greater than the solver tolerance in at least one condition were included.

^bAll model cellular metabolites that were not implicated in loops were included.

In the initial application of the GIM³E algorithm, the combined omics data helped elucidate a new possible avenue of host–pathogen interaction by alterations in the flux of metabolites (Kim et al., 2013). To summarize those results here, metabolic models of macrophages (Bordbar et al., 2012), the host cells of S.Typhimurium, and experimental results have demonstrated that individual metabolites can have predicted stimulatory or inhibitory effects on antimicrobial functions such as nitric oxide production. The analysis of S.Typhimurium suggested that metabolites produced or consumed by this pathogen have direct effects on macrophage function through metabolic flux. These results highlight the importance of evaluating omics results in an integrated manner as possible with the GIM³E algorithm. Interestingly, another model-guided investigation of metabolism elucidated the ability of S.Typhimurium to exploit parallel nutrient sources to enhance virulence (Steeb et al., 2013). An important next step to interpret metabolic feedback will be the integrated model-guided analysis of omics datasets from both the host and pathogen.

4 CONCLUSION

The GIM³E algorithm uses metabolomics and transcriptomics data to develop constraints for a GEM. GIM³E requires a cellular objective and condition-matched omics datasets, preferably transcriptomics data with good coverage of model genes and metabolomics data that may be qualitative or semi-quantitative in nature. In our previous investigation, we illustrated the utility of GIM³E to develop biological insights into the cellular metabolism of S.Typhimurium in both rich and virulence media (Kim et al., 2013). Here, we also demonstrate that omics data integrated into the model with GIM³E also yields insight into metabolites and reactions that must be active to be in agreement with model constraints but that are not necessarily detected in the metabolomics experiments. Metabolomics and transcriptomics yielded distinct constraints on the solution space. The calculation of metabolite turnover is an additional benefit of using the GIM³E algorithm, and omics-derived constraints impacted the allowed metabolite turnover flux ranges.