Determination of Relevant Neuron–Neuron Connections for Neural Prosthetics Using Time-Delayed Mutual Information: Tutorial and Preliminary Results

Abstract

BACKGROUND

Identification of functional dependence among neurons is a necessary component in both the rational design of neural prostheses as well as in the characterization of network physiology. The objective of this article is to provide a tutorial for neurosurgeons regarding information theory, specifically time-delayed mutual information, and to compare time-delayed mutual information, an information theoretic quantity based on statistical dependence, with cross-correlation, a commonly used metric for this task in a preliminary analysis of rat hippocampal neurons.

METHODS

Spike trains were recorded from rats performing delayed nonmatch-to-sample task using an array of electrodes surgically implanted into the hippocampus of each hemisphere of the brain. In addition, spike train simulations of positively correlated neurons, negatively correlated neurons, and neurons correlated by nonlinear functions were generated. These were evaluated by time-delayed mutual information (MI) and cross-correlation.

RESULTS

Application of time-delayed MI to experimental data indicated the optimal bin size for information capture in the CA3-CA1 system was 40 ms, which may provide some insight into the spatiotemporal nature of encoding in the rat hippocampus. On simulated data, time-delayed MI showed peak values at appropriate time lags in positively correlated, negatively correlated, and complexly correlated data. Cross-correlation showed peak and troughs with positively correlated and negatively correlated data, but failed to capture some higher order correlations.

CONCLUSIONS

Comparison of time-delayed MI to cross-correlation in identification of functionally dependent neurons indicates that the methods are not equivalent. Time-delayed MI appeared to capture some interactions between CA3-CA1 neurons at physiologically plausible time delays missed by cross-correlation. It should be considered as a method for identification of functional dependence between neurons and may be useful in the development of neural prosthetics.

INTRODUCTION

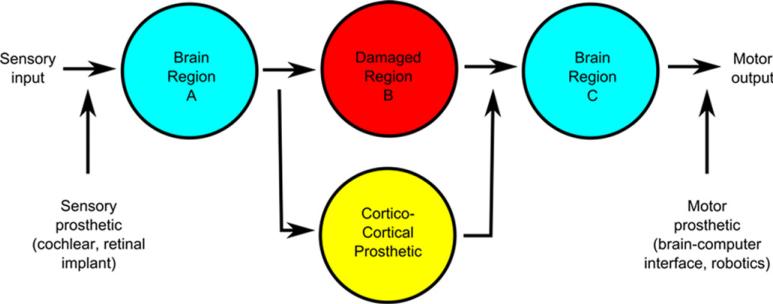
The development of neural prosthetics to replace damaged neural circuitry is an exciting frontier in the biomedical sciences, and several groups of investigators are working on systems that interact with the central nervous system to replace lost function (4). Primarily, these prosthetics are designed for restoration of sensory or motor function. Sensory prosthetics, such as a cochlear implant or artificial retina work by transduction of physical energy into an electrical stimulation of nerve fibers (20, 22, 27). In systems designed to recapitulate motor function, premotor/motor cortical commands are decoded for the control of robotic systems (12, 26, 37). Our group is primarily interested in a third type of prosthetic that functions in a biomimetic manner to recapitulate information transmission between damaged cortical brain regions (2, 3). In such a prosthetic, damaged central nervous system neurons would be replaced with a biomimetic system comprised of silicon neurons with similar functional and computational properties to the replaced neurons. Functionally, these silicon neurons would receive input electrical signals from other neurons and output an appropriate electrical signal to other neurons depending on the computational properties of the replaced, damaged neurons (Figure 1).

Figure 1.

Different neural prosthetic types and their point of insertion along a schematized neural circuit. We are primarily interested in corticocortical prosthetics.

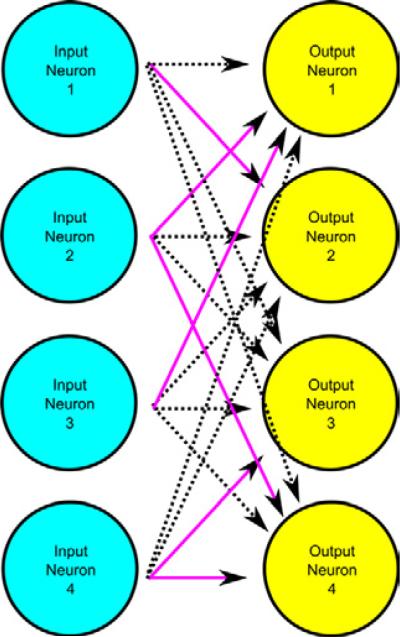
Compared with other types of prosthetics, the design of this type of cortical-to-cortical prosthetic has an additional complexity in that from a large set of possible connections between input and output neurons, one must choose a set of the functionally important connections to model with the prosthetic. As an example, if we take a small system of 100 input neurons with 100 output neurons, the number of possible combinations of connections between these neurons is 2¹⁰⁰, or one followed by 30 zeros. To develop an intuition for the size of this number, imagine a 0.1-mm thick piece of paper. If one were to fold this paper 100 times, the stack would reach from earth to the end of the observable universe. Therefore, to make cortical-to-cortical prosthetics a reality, computational methods must be found to reduce the magnitude of this problem that accurately identify relevant connections (Figure 2). Information theory is becoming widely applied to the analysis of neuronal spike train data (32), and we hypothesized that information theoretic methods such as determination of mutual information (MI) may be applied to this problem.

Figure 2.

Example of identification of relevant neuron–neuron examples. Even in this small 4 × 4 neuron diagram, it becomes apparent that many irrelevant (dashed lines) connections may cloud computational analysis. Relevant connections (solid lines) need to be identified in an efficient manner.

Several advances have been recently made in the rational design of neural prosthetic implants. A multiple-input, multiple-output nonlinear dynamic model of spike-train to spike-train transformations was previously formulated for hippocampal-to-cortical prostheses, and this model has good agreement with experimentally observed output from hippocampal neurons (39). In this model, as in the actual in vivo connectivity, CA3 hippocampal region neuronal activity serves as the “input,” and these neurons connect to CA1 region hippocampal neurons to influence their output. What this means is that the neural prosthetic synthesizes the information contained in axonal outputs from multiple neurons coming into the prosthetic, processes that data in a nonlinear fashion, and comes up with an output spike train. This is similar to what happens physiologically when a neuron processes incoming signals from dendrites, synthesizes them, and converts this into an axonal electrical impulse.

With that in mind, identification of functional dependence among neurons is a necessary component in both the rational design of neural prostheses as well as in the characterization of network physiology, for the simple reason that one must be able to choose which input signals have relevance to the output of any given neuron that the prosthetic is meant to replace. This is especially important in prosthetic design given the computational complexity and large number of possible connections in a physiologically plausible system.

One of the most widely used methods for determining connectivity between two neurons is cross-correlation, a linear technique. To calculate cross-product, one essentially frameshifts the values of two spike trains, multiplies the corresponding values in the spike trains, and adds these values together. The frameshift where this value is maximized is the time delay where there is maximal correlation between these two signals. Cross-correlation, be ing a linear technique, may miss complex, nonlinear interactions between two neurons. Time-delayed MI (TDMI) is a statistical, nonlinear technique that, as we show in the present article, may be better suited to determine connections between two neurons. TDMI works by evaluating correlations between firing rates of two neurons in discrete time periods, but unlike cross-correlation, it does not presuppose a linear, strictly positive, or strictly negative relationship between the two neurons. In our experiment, we evaluated cross-correlation versus MI in actual input (CA3 neuron) and output (CA1neuron) hippocampal activity and determined that MI may, in fact, detect relationships between neurons that is missed by cross-correlation.

This article is intended as first, a tutorial for the neurosurgery community on the concepts of information theory, which has become widely accepted for the analysis of information transmission of neurons. For interested readers, an appendix reviews the mathematical concepts and details involved in this experiment. Second, we report on some of our initial experimental findings that we hope will serve as a springboard for future experimentation.

METHODS

Simulated Data

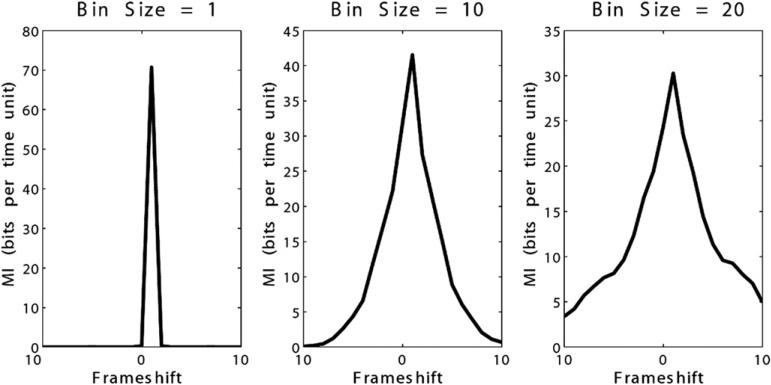
Spike trains from intracranial rat hippocampal recordings as well as simulation data were evaluated with TDMI and cross-correlation. Simulations of positively correlated, negatively correlated, spike trains correlated by mapping functions, independent spike trains, and sine-cosine functions were evaluated by TDMI and cross-correlation. Results for cross-correlation and TDMI were then graphically compared. To evaluate the effect of increasing bin size, the simulation for positively correlated data was performed for bin sizes of 1, 10, and 20 time-units.

A simulated spike train was created by randomly generating 10,000 numbers uniformly distributed between 0 and 1. All values more than 0.98 were represented as a spike, therefore roughly 10 of 500 time points were spikes. For data collected at 2-ms intervals (as our data), this represents a neuron with a 10-Hz firing rate. To create a second spike train, values from the first spike train were mapped to the second spike train based on the simulation type. For simulations of positively correlated data, spike values from the first spike train were directly copied to the second spike train with some frameshift applied. For negative correlations, zeros in the first spike train were represented as ones in the second spike train and vice versa, and again a frameshift was applied. For independent spike trains, two spike trains were randomly generated as previously. MI and cross-correlation were calculated, as explained previously, with bin size of 1. To evaluate the effect of bin size, for the positively correlated simulation, MI was calculated based on the sum of spikes in each bin for bins of size 1, 10, and 20.

For mapping functions, a slightly different approach was taken. We assumed words of four bits, leading to a vocabulary of 16 words (0000–1111). These words were randomly generated from a uniform distribution to create a spike train. A mapping function was then also randomly generated that assigned each of the 16 words to another word within the 16-word vocabulary. Each word in the first spike train was mapped to a word in the second spike train, and a frameshift applied. (This is similar to an encryption substitution cipher.)

For sine and cosine, the functions were evaluated during a period of 1 to 1000 radians at each 0.1 radians. The functions were multiplied by a factor of 10, then 10 was added to the value of the function to maintain positive values for each function. (Positive values of functions for MI calculation are not necessary but facilitated calculation within our computational framework designed for spike trains.) The functions were discretized by rounding the function at each data point to the nearest whole number, and MI and cross-correlation calculated.

Experimental Data

Male Long-Evans rats ranging in age from 200 to 250 days were trained to a criterion of 70% in 100 trial sessions with trial delays of 1 to 30 s, implanted with hippocampal recording arrays (discussed later), and retrained to the same behavioral standard after recovery from surgery. Only animals meeting stringent neural recording conditions, requiring detectable activity from a minimal number (n = 15) of neurons, were retained for experimental purposes. All procedures conformed to National Institutes of Health and Society for Neuroscience guidelines for care and use of experimental animals. The testing apparatus was the same as used in other studies from this laboratory (9, 10, 15) and consists of a 43 × 43 × 53-cm Plexiglas behavioral testing chamber with two retractable levers mounted 3.5 cm above the floor on one wall separated by 14.0 cm center-to-center, positioned to either side of a water trough on the same wall. A nosepoke sensor device was mounted at the same height as the levers in the center of the opposite wall below a cue light. The apparatus was housed in a commercially built sound-attenuated cubicle (Industrial Acoustics Co., Bronx, New York, USA) with speakers for “white noise” (75 db) and house lights to illuminate the chamber for video monitoring.

The delayed non-match to sample (DNMS) task was also the same as described previously (10) and consists of three main behavioral phases: Sample, Delay, and Nonmatch. A trial is initiated at the Sample phase by extension of either the left or right lever, chosen at random. When the “sample lever” is pressed (Sample response), it retracts, initiating the Delay phase of the task, which can be 1 to 30 s in duration (also selected at random). In the Delay phase, the cue light above the nosepoke device on the opposite wall is illuminated, and the animal is required to nosepoke at least once after the delay interval times out. This extinguishes the cue light and extends both levers, signaling onset of the Nonmatch phase and the animal is then required to press the lever opposite to the position of the lever pressed in the Sample phase. Animals received a drop of water (0.04 mL) immediately after a correct response and both levers were retracted for a 10-s intertrial interval, after the next trial initiated by extension of the Sample lever. An error, in which the same lever was pressed in both phases (“Match” response), results in no reward, the levers were retracted and the house lights turned off for 5 s of darkness after which the illuminated intertrial interval continues for 5 s until the start of the next trial. Criterion DNMS performance consisted of 1) 90% correct responding on trials with delays of 1 to 5 s in sessions of 100 to 150 trials with delays ranging from 1 to 30 s and 2) an associated linear, delay-dependent, decrease in accuracy from 85% to 90% correct to 50% to 60% (chance) across trials ranging in delays of 6 to 30 s (9). Data used for the TDMI analysis ranged from 1.5 s before to 1.5 s after each DNMS behavioral event (lever press or nosepoke).

Extracellular single-cell action potential waveforms were isolated and selected for analysis from each of the 32 different recording locations sampled by two bilaterally placed hippocampal array electrodes (9, 16, 17). The recording arrays were configured as two rows of eight 25-mM wires positioned along the longitudinal axis of the hippocampus at 200-mM intervals such that one row has lengths sufficient to sample neurons in CA3 with the other in the CA1 cell layers, providing recordings from eight pairs of CA3/CA1 located electrodes in the same hippocampus. One or at most two distinct action potential waveforms recorded from the tip of each wire were isolated by time–amplitude window discrimination as well as computer-assisted template matching of individual waveform characteristics through a Plexon Multineuron Acquisition Processor (Plexon, Inc.; Dallas, Texas, USA). Activity from separately identified neurons was time stamped along with the behavioral events within each DNMS trial and stored in arrays for online computer processing (discussed later). Only CA1/CA3 pyramidal neurons with firing rates (mean background firing rate 0.25–5.0 Hz) consistent with those previously reported (9, 10, 15), and consistently exhibited the same DNMS behavioral correlate across all test sessions, were included in the analyses. To determine DNMS behavioral correlates, perievent histograms of mean firing rates for each neuron in the ensemble were created and analyzed.

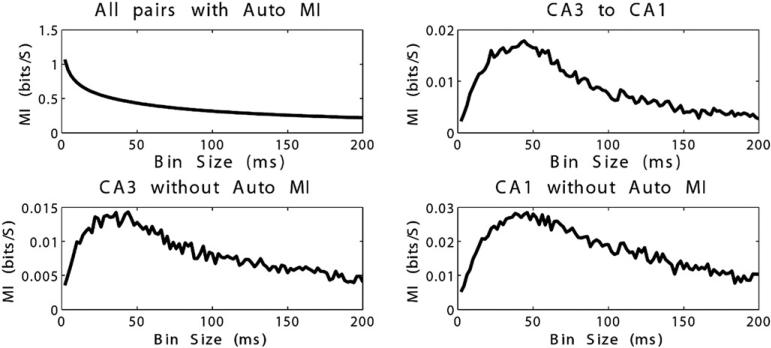
Approximately 300 tasks were performed for each data set and 3 s of data were obtained during each task. In total, 60 data sets from 10 rats were analyzed. Data was processed and spikes detected at a temporal precision of 2 ms where each 2-ms time point either contains a spike (1) or does not (0). Therefore, roughly 450,000 data points were obtained for each neuron–neuron pair, and these data points were merged as dictated by bin size. For example, for a 40-ms bin size, 20 bins of size 2 ms are merged for each data point, giving 22,500 data points for each neuron–neuronpair. MI and cross-correlation were calculated between pairs of CA3 and CA1 neurons by evaluation of spike counts in bins, as described previously. To determine the optimal bin size for analysis, MI for this data set was calculated for bins of 2 to 200 ms in increments of 2 ms. The average MI among all pairs was graphically analyzed to determine an optimal bin width. This process was also performed for CA3/CA3 pairs, CA1/CA1 pairs, and the entire data set (including neurons compared with themselves, or auto MI).

After this preliminary analysis, MI and cross-correlation were calculated for a bin size of 40 ms with time lags from -60 to 60 ms in 2-ms intervals. Positive values indicate information flow from CA3 to CA1. Sampling bias correction of MI was calculated per Panzeri and Treves as described in the Appendix (30).

After this initial calculation, spike bins were randomly shuffled and reassigned for calculation of confidence intervals (CI) for both MI and cross-correlation. Shuffling trials (2000) were performed for each data set and CIs calculated. Statistically significant pairs were identified at the 99% and 99.9% confidence levels, and time lags of maximum MI recorded. MI and time lag of maximum MI were plotted for these significant pairs. The statistically significant pairs as well as the time-lag values of maximum correlation were also calculated for cross-correlation and compared with the results from the TDMI analysis.

RESULTS

Simulated Data

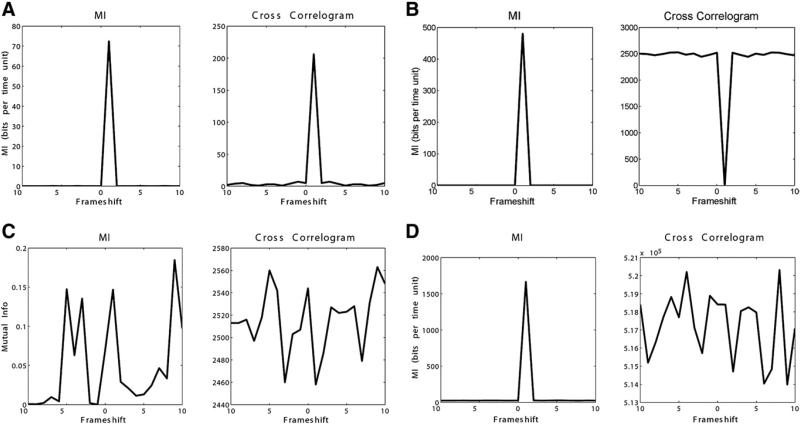
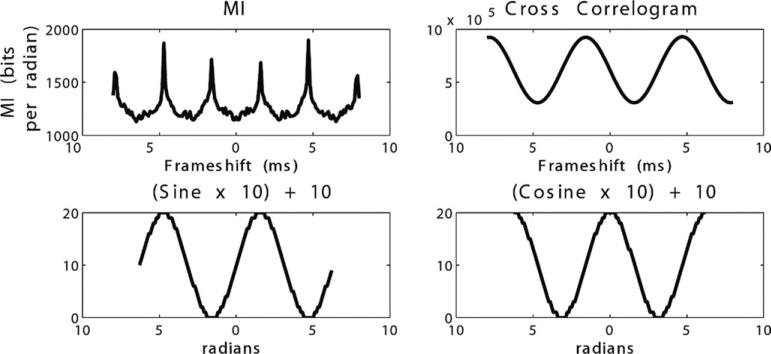
Positively correlated data demonstrated concordant, positive peaks in TDMI and cross-correlation at the appropriate time delay (Figure 3A). Negatively correlated data showed a positive peak in TDMI and a trough in cross-correlation at the appropriate time delay (Figure 3B). TDMI and cross-correlation showed no clear peaks in evaluating independent spike trains (Figure 3C). For sine-cosine, TDMI showed positive peaks at π/2 +/– πn, and cross-correlation showed positive peaks at -π/2 +/– 2πn and troughs at π/2 +/– 2πn (Figure 4).

Figure 3.

(A) Simulation of positively correlated data with frameshift of 1. Concordant peaks seen in time-delayed mutual information (MI) and cross-correlation at the correct frameshift. (B) Simulation of negatively correlated data with frameshift of 1. Peak seen in time-delayed MI and trough seen in cross-correlation at the correct frameshift. (C) Simulation of two independent (no relationship) spike trains evaluated using time-delayed MI and cross-correlation. (D) Mapping (substitution cipher) function between two spike trains with frameshift of 1. Four-bit words in one spike train are directly mapped to four-bit words in another spike train. Peak seen in time-delayed MI at the correct frameshift, and erratic behavior in cross-correlation. Map used was 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 map to 5, 10, 14, 1, 8, 2, 2, 15, 9, 2, 4, 8, 10, 11, 5, 6, respectively.

Figure 4.

Sine-cosine. Time-delayed mutual information (MI) showed positive peaks at π/2 ± πn, and cross-correlation showed positive peaks at -π/2 ± 2πn and troughs at π/2 ± 2πn. Sine and cosine (bottom left, bottom right) scaled by factor of 10 and increased by absolute value of 10 to avoid negative numbers in calculation.

In the evaluation of mapping functions, for maps where there was a trend toward positive or negative correlation of the data, TDMI and cross-correlation behaved similarly to those situations as described previously. However, in cases where there was no clear trend to the mapping, TDMI successfully identified the appropriate time delay with a positive peak where cross-correlation was often erratic. One such example is shown in Figure 3D. No cases were identified where cross-correlation identified the time delay where TDMI did not. Evaluation of increasing bin size on TDMI demonstrated correct identification of the appropriate time delay, with blunting of the peak and decreasing maximum value of MI with increasing bin size. Of note, frameshifts smaller than the bin size were correctly identified (Figure 5).

Figure 5.

Time-delayed mutual information (MI) and effect of bin size. Positively correlated data with bin sizes of 0, 10, and 20 time units. The peak in time-delayed MI is blunted, but present, at the correct frameshift with increasing bin size.

Experimental Data

Analysis of optimal bin sizes for MI calculation between pairs of CA3 and CA1 neurons indicate peak levels of information capture with bins sized between 20 and 60 ms, and a maximum around 44-ms bin width (Figure 6). MI of the entire dataset (including MI of neurons compared with themselves) demonstrated peak information capture with smallest bin sizes (2 ms), which decreased with increasing bin size. This was related to the strong effect of auto-MI in the data set. Analysis of MI among CA3 neurons and among CA1 neurons demonstrated optimal information capture at bin widths comparable to the information capture between pairs of CA3 and CA1 neurons. The average MI was smaller within CA3/CA3 pairs than between CA3/CA1 pairs; however, CA1/CA1 pairs had higher MI than CA3/CA1 pairs. This may indicate significant network effects within the CA1 region. However, it is important to note that this is MI without a time delay, therefore it is not altogether surprising that within-region MI is higher than cross-region MI. Furthermore, CA1 is the output of the circuit, therefore shared inputs from the CA3 region may contribute to this finding. It is also important to note that the average MI within the CA1 region is lower than the most informative CA3 to CA1 TDMI connections (Figure 7).

Figure 6.

Mutual information (MI) versus bin size on experimental data. For the entire system including auto-MI, MI decreases with increasing bin size (top left). In CA3-CA1 interactions, CA3-CA3, and CA1-CA1 excluding auto-MI, MI peaks at bin size of approximately 40 ms before decreasing.

Figure 7.

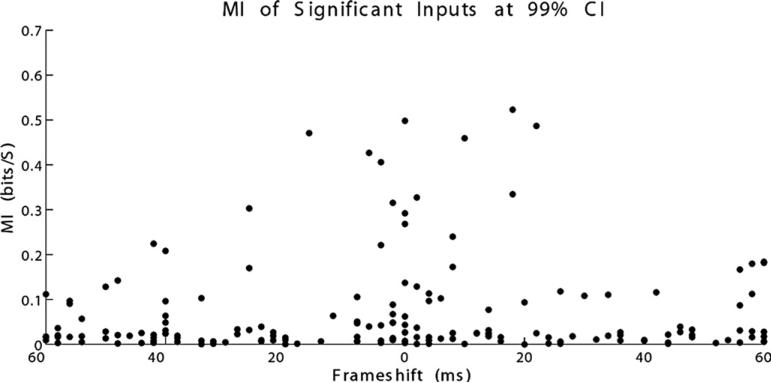
Scatter plot of mutual information (MI) and maximally informative time lag for neuron pairs significant at the 99% confidence interval (CI) level. Maximally informative connections appear to have time lags near 0 frameshift up to around 20 ms of shift.

Pairwise comparisons were made between 7374 pairs of CA3 and CA1 neurons, with a total of 366 CA3 and 363 CA1 neurons in a total of 5643 DNMS trials in 21 separate animal implantations. TDMI and cross-correlation were calculated with a bin width of 40 ms. TDMI identified 2373 significant pairs at the 99% CI and 1725 pairs at the 99.9% CI. Cross-correlation identified 3472 significant pairs at the 99% CI and 2477 at the 99.9% CI (Table 1). At the 99% CI, 1856 pairs or 46.5% [1856 / (2373 + 3472 – 1856]) were concordant. At the 99.9% CI, 1378 or 42.7% were concordant (Table 2).

Table 1.

Significant and Nonsignificant Pairs of CA3/CA1 Neurons at 99% Confidence Interval

	Time-Delayed Mutual Information
	Significant	Nonsignificant	Total
Cross-Correlation
Significant	1856	1616	3472
Nonsignificant	517	3385	3902
Total	2373	5001	7374

Table 2.

Significant and Nonsignificant Pairs of CA3/CA1 Neurons at 99.9% Confidence Interval

	Time-Delayed Mutual Information
	Significant	Nonsignificant	Total
Cross-Correlation
Significant	1378	1099	2477
Nonsignificant	347	4550	4897
Total	1725	5649	7374

Looking at a physiologically plausible interval for direct synaptic transmission from CA3 to CA1 (4–10 ms), TDMI identified 182 and 144 pairs with peak information transmission in this time frame at the 99% and 99.9% CIs, respectively. Cross-correlation identified 178 and 152 pairs at the 99% and 99.9% CIs, respectively. Also, 75 pairs or 26.3% were concordant at the 99% CI, and 69 pairs or 30.4% were concordant at the 99.9% CI (Tables 3 and 4).

Table 3.

Significant and Nonsignificant Pairs of CA3/CA1 Neurons with a 4- to 10-ms Time Lag at 99% Confidence Interval

	Time-Delayed Mutual Information
	Significant	Nonsignificant	Total
Cross-Correlation
Significant	75	103	178
Nonsignificant	107	7089	7196
Total	182	7192	7374

Table 4.

Significant and Nonsignificant Pairs of CA3/CA1 Neurons with a 4- to 10-ms Time Lag at 99.9% Confidence Interval

	Time-Delayed Mutual Information
	Significant	Nonsignificant	Total
Cross-Correlation
Significant	69	83	152
Nonsignificant	75	7147	7222
Total	144	7230	7374

DISCUSSION

Given the intractably large number of neuron–neuron pairs in even a small system of neurons, a neural prosthetic that seeks to recapitulate lost cortical connections must have a method for determining which neuron–neuron connections are significant and which are not. Previously reported data from our group indicate that output spike trains may be reproduced with a high level of accuracy in small systems where relevant connections are known (39). These computation methods are nonlinear in nature. Therefore, determination of relevant connections with a robust, nonlinear framework, such as TDMI, may reduce an intractable computational problem to a tractable one and allow for rational design of cortical prosthetics. Identification of relevant connections with TDMI may allow for application of computational methods to transform input spike trains to output spike trains. Certainly future work will focus on whether this method of selection yields superior results in deriving these transformations.

Simulated Data

With regard to this specific experiment, simulations of functionally dependent neurons evaluated by TDMI and cross-correlation behaved in a predictable fashion with some potentially interesting findings. TDMI, being a statistical measure, will give positive peaks at time lags where statistical dependence exists. No assumptions are made about the nature of the interaction. In addition, values of MI do not give any indication of causality, directionality, or the excitatory versus inhibitory nature of the interaction. For this sort of analysis, one must revisit the probability histogram to evaluate for trends. In addition, unless using a binless strategy or a method for continuous data, MI calculations require data binning and discretizing of data. Cross-correlation, by contrast, is an arithmetic/multiplicative measure of dependence, and although one can infer the nature of an excitatory versus inhibitory interaction, certain higher order interactions may be missed. In addition, the magnitude of a cross-correlation depends on the magnitude of the signals and changes in the signals and not the statistical strength of an interaction. However, cross-correlation does not require discrete values, but generally does require some sort of binning.

Certain points from simulation examples merit special discussion. The simulation using a mapping function indicates that some higher order encoding processes between two neurons may be missed by cross-correlation. The converse case where cross-correlation detects interactions missed by TDMI was not observed, and it is difficult to imagine such a scenario.

It is important to note another point regarding cross-correlation: that the magnitude of the cross-correlation is less important than clearly defined peaks. One may note that the magnitude of the cross-correlation (but not the TDMI) is much higher for Figure 3C (independent, uncorrelated, spike trains) than for Figure 3A. This is because magnitude has simply to do with the summation of the data at a given time-point, which has more to do with the baseline value of a function rather than correlation. MI, however, provides an actual unit (bits), therefore magnitude is important.

The example of sine-cosine is useful in that it elucidates some subtleties of the nature of TDMI. A naïve assumption is that sine predicts cosine at all time lags, and therefore a TDMI plot will be a flat line. However, calculation of these values indicates that this is not the case. A closer examination reveals why. For the simple case where the time delay is π/2, cosine and sine are in phase, therefore each value of cosine exactly predicts the value of sine at that time delay. For example, if cos(t) = 1, sin(t +π/2) = 1, cos(t) = 0, sin(t + π/2) = 0, etc. If you examine the case where the time delay is π/4, one cannot predict sine exactly from the value of cosine. For example, cosine is 0 at – π/2 and π/2. sin(–π/2+π/4) = sin(–π/4) = –πμ2/2, but sin(π/2 + π/4) = sin(3 π/4) = +πμ2/2. Therefore, the ability to predict sine from cosine based on the value of cosine is different at different time delays, therefore TDMI is different at these time lags.

When bin sizes were increased in our simulations, the peaks were blunted, but peaks were identified at the correct time lags. It is worth noting that time lags smaller than the bin size were still able to be identified. This is not intuitively obvious, but also is important because one major consideration in calculation of TDMI is choosing an appropriate bin size. This result suggests that detection of small magnitude time delays is not limited absolutely by bin size.

Experimental Data

In our experimental analysis, some preliminary findings may form the basis for further investigation. The first point is that optimal bin widths for analysis of MI in this experiment appear to be on the order of 20 to 60 ms. This suggests one of two possibilities: 1) that the temporal structure for information transfer among hippocampal neurons is at least of that length, and possibly longer, or 2) 40 ms is an appropriate bin size to capture temporal structure and time delay for information transfer (the optimal bin size analysis was performed at time delay = 0). Analysis of the entire data set shows that, when auto MI is included, information capture is highest at small bin widths, then decreases as bin width increases.

To understand the argument of higher order temporal structure, we can expand on the document analogy presented previously. Assume that we are presented with document A, which is somehow related in content to document B, and we are trying to calculate MI between the two documents. Let us take the situation of a small bin width, for example, one letter. Looking at the situation of comparing document A with itself, it is easy to see that knowing that the letter “a” occurs in one position in the document is enough to know that letter “a” occurs in the same position in the same document. Conversely, it will likely be difficult to establish a statistical dependence between occurrences of given letters in document A with document B. As we expand our bin width to include entire words, however, we may be able to extract meaningful connections between words in document A with words in document B. Looking at bigrams, or two words together, we may be able to extract even more meaning, but we will require more data to draw these conclusions because the number of possible two-word combinations in document A is much larger than the number of possible words. Ignoring the fact that some two-word combinations never occur in the English language, the number of possible two-word combinations is approximately the square of the number of possible words. As we get to the sentence level, we will never have sufficient data to sample all possible sentences in document A and compare those to document B.

For those reasons, it appears that the smallest structure necessary to capture information is around 20 ms, but there may be larger structures present that are simply inadequately sampled. This may be secondary to the time delay necessary for increases or decreases in voltage from incoming spikes to dissipate, or it may be something inherent to the way information is encoded in the hippocampus. Again, this is somewhat confounded because there is a component of synaptic transmission included in that time lag. However, given that analysis of CA3/CA3 and CA1/CA1 pairs yields similar results (Figure 6), it may be more likely that there is spatiotemporal structure to the information encoded by the hippocampus, or it may be secondary to some larger network effect. Other work also suggests that there may be complex spatiotemporal coding within hippocampal spike trains. Theta-phase precession is an example of a well-studied spatiotemporal construct in the hippocampus. Theta-phase precession is a change in spike timing in which the place cell fires at progressively earlier phases of the extracellular theta rhythm as the animal crosses the spatially restricted firing field of the neuron (14, 18, 21, 23, 28, 38). Clearly this is an area of ongoing study, and more work is needed to elucidate the components of this spatiotemporal encoding. This will likely include more sophisticated experimental and information theoretic analysis.

The second interesting point from this experiment is that TDMI may be able to pick up information transfer between neurons in physiologically plausible time frames. Experimental data suggest that an appropriate time delay for synaptic transmission from CA3 to CA1 is in the 4- to 9-ms range (35). Evaluation of TDMI and cross-correlation in the 4- to 10-ms time-lag window suggests that the results are not equivalent. Simulated data further suggests that TDMI may be superior in the evaluation of negatively correlated data or data with complex correlations. Disparity in the results for experimental data is not entirely surprising, as we would expect there to be inhibitory and other complex relationships in the data to which cross-correlation is not sensitive. However, analysis of neuron pairs with highest information rates indicates similarity in the results. Given that MI and cross-correlation give similar results for excitatory, monotonic connections, it would suggest that excitatory, glutamatergic connections from CA3 to CA1 are the ones that exact the most information transfer within the system.

Plots of statistically significant values of MI between CA3 and CA1 neurons compared with time lags showed a fairly broad spread of time lags across significant pairs. However, neurons with highest information rates (>0.3 bits/s) seem to have information peaks between 0 and 20 ms (Figure 7). Again, it is important to point out that, as shown in the simulated data, it is possible to extract meaningful time delays even when the bin size is larger than the time lag.

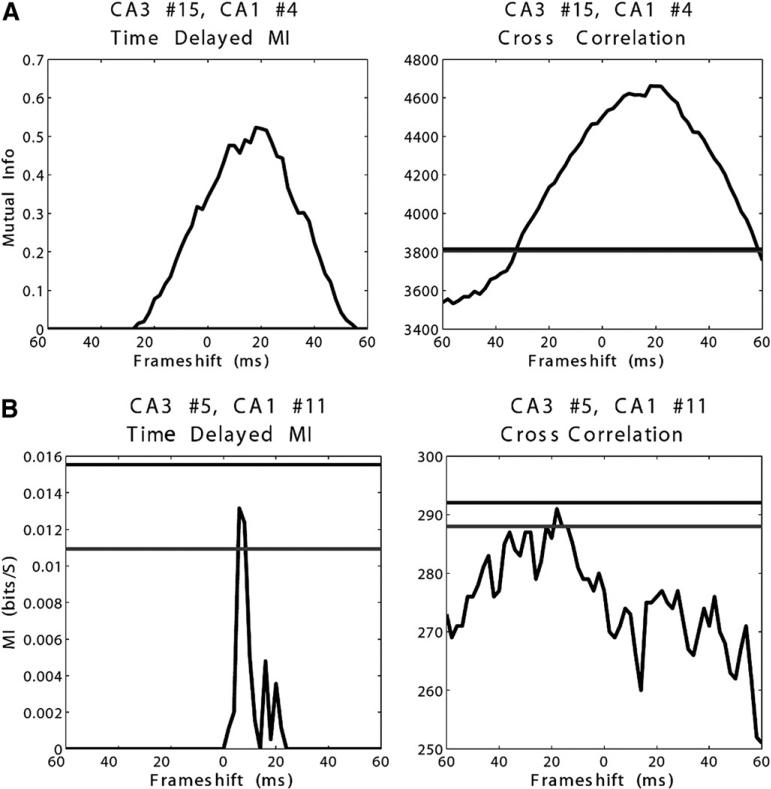
Determination of significant values at broad ranges of time lags may be either related to inadequate methods of calculating significance or of spike train modulation occurring at a broad temporal spread. Using a statistical significance level of 0.995 and calculating 60 separate time lags, we would expect significant values for approximately 1 of every 200 calculations by chance, or a little less than 1 in every 3 neurons. This is close to what we do see, but qualitative examination of highly significant neurons exhibits values of MI well above statistical significance (Figure 8A). Our analysis may benefit from application of a correction factor, such as the Bonferroni correction, as used to correct for evaluating statistical significance in multiple samples. It may also be possible to apply a numerical cutoff for what we consider a sufficient information transfer rate. Obviously, with any analysis of this sort, one may miss physiologically significant connections that are not statistically significant. Figure 8B is an example of a neuron pair significant at the 99% but not 99.9% CI, which appears to have a strong information peak in the physiologically plausible range.

Figure 8.

(A) Example of time-delayed mutual information (MI) and cross-correlation in a CA3-CA1 pair reaching significance. Horizontal lines are 99% and 99.9% confidence intervals (nearly superimposed on this graph). (B) Example of time-delayed MI and cross-correlation in a CA3-CA1 pair with significance level between 99% and 99.9% confidence interval. Horizontal lines are 99% and 99.9% confidence intervals (nearly superimposed on this graph). Time-delayed MI appears to be maximal at a physiologically plausible time-lag, with cross-correlation more difficult to interpret.

Some limitations in TDMI include the need for binning and need for bias correction. In addition, given that neurons receive input from multiple neurons, it is probably worthwhile to consider multiple inputs simultaneously, especially as these interactions may be synergistic or redundant. MI can be calculated for multiple inputs simultaneously; furthermore, synergy and redundancy are information-theoretic quantities, which have been previously defined (33). Addition of each input requires that an additional dimension be added to the probability histogram, and therefore, to populate the table, one needs more data to avoid large bias. Also, computational complexity increases as there are more combinations of neurons that need to be considered. Similarly, given that the spiking behavior of a neuron is likely dependent on some sort of synaptic input summation over a finite time period, it may also be useful to consider multiple time lags simultaneously. Increasing bin size will capture some of that effect, but obviously, detailed characterization of spatiotemporal time patterns will require a more specific analysis.

One experimental point worth mentioning is that we did not subdivide our analysis by the tasks performed. That is, we pooled our analysis for all types of DNMS tasks. This essentially gives us a sense of overall information transfer between neurons and not task-specific information transfer. If one were interested specifically, say, in the information transfer that occurs when a correct choice is made by the animal, the analysis could be easily tailored to answer that question.

In addition, one limitation of TDMI is the inability to determine whether the neurons have correlating activity secondary to information transfer between neurons, or whether there are similar inputs to both neurons, leading them to have similar activity. In this study, we have chosen to discern this by evaluating TDMI in time lags that seem physiologic for information transfer from one brain location to another. Another possible solution espoused by other groups is the use of transfer entropy in physiologic systems (34). Transfer entropy in this system works by evaluating the dependence of one neuron's signal on another neuron's signal and takes into account its own history in the calculation. This attempts to determine directionality in the system and actual information transfer, but consideration of history of both neurons adds complexity to the calculation and requires more data. In future work, we will determine whether this is a feasible approach for our system.

In conclusion, TDMI is an information theoretic tool that can be applied to the evaluation of functional dependence between neurons. Simulations demonstrate superior performance versus cross-correlation, a commonly used method. Although this is a preliminary experimental analysis, two important points arise that may be elucidated by further analysis. First, information theoretic analysis of CA3 and CA1 neurons in the rat hippocampus hints toward a higher order temporal coding structure that should be evaluated in further work. TDMI analysis suggests that the most informative CA3 neurons pass information to functionally dependent CA1 neurons with a time delay on the order of 0 to 20 ms. Second, TDMI and cross-correlation analyses are poorly correlated overall, especially in the 4- to 10-ms range, where synaptic transmission may occur.

Abbreviations and Acronyms

CI

Confidence interval

DNMS

Delayed non-match to sample

MI

Mutual information

TDMI

Time-delayed MI

APPENDIX

Mathematical Concepts of Mutual Information And Cross-Correlation

Consider an experiment where an animal performs memory-related tasks, and we are seeking to evaluate and model connections between CA3 and CA1 neurons for the purposes of neural prosthetic design. Spike trains can be represented as a time series of zeros and ones, where a “one” represents a spike and a “zero” represents no spikes. We can group these ones and zeros into “bins” of some length of time. For purposes of analysis, these bins can either be represented as the sum of the number of spikes in a bin or as a binary “word” representing the pattern of ones and zeros. In this experiment, we will represent each bin as the sum of spikes in that bin. For example, the sequence “10010” is represented as “2.” We can do this for each neuron observed in our experiment for the purposes of determining functional correlations between the neurons.

To do this formally, for a system with n CA3 neurons, we can represent the spikes emitted during the task as a multidimensional array x. Each row, i, represents the response of a single CA3 neuron. Each column j is a temporal window, or bin, of size Δt, such that each element x_i,j of the array represents the number of spikes emitted by CA3 neuron i during temporal window j (41). Δt can be varied parametrically and optimized to the temporal precision of the spike code, meaning we can make the bin bigger or smaller as dictated by the nature of our data. For our system of n CA3 neurons, a task of total time T can be represented by an array of size n × L where L = T/Δt:

$$x=\left[\begin{array}{ccc}\hfill x_{\mathrm{I},\mathrm{I}}\hfill & \hfill \cdots \hfill & \hfill x_{\mathrm{I},\mathrm{L}}\hfill \\ \hfill ⋮\hfill & \hfill x_{i,\mathrm{j}}\hfill & \hfill ⋮\hfill \\ \hfill x_{n,\mathrm{I}}\hfill & \hfill \cdots \hfill & \hfill x_{n,\mathrm{L}}\hfill \end{array}\right]$$

Spikes emitted by m CA1 neurons can be similarly represented by an array y of size m × L where each element y_k,j represents spikes emitted by CA1 neuron k in bin j.

$$y=\left[\begin{array}{ccc}\hfill y_{\mathrm{I},\mathrm{I}}\hfill & \hfill \cdots \hfill & \hfill y_{\mathrm{I},\mathrm{L}}\hfill \\ \hfill ⋮\hfill & \hfill y_{k,\mathrm{j}}\hfill & \hfill ⋮\hfill \\ \hfill y_{m,\mathrm{I}}\hfill & \hfill \cdots \hfill & \hfill y_{m,\mathrm{L}}\hfill \end{array}\right]$$

In this experiment, let us say that we are trying to model spike train transformations from CA3 to CA1 where the spike train output y_k of each CA1 neuron is dependent on some combination of CA3 spike trains, x_i. Before analysis, we do not know to which CA3 neurons is functionally connected to which CA1 neuron, nor do we know to how many it is connected. For a set of CA3 neurons of size n, the number of possible subsets of neurons is 2ⁿ. Intuitively, this can be understood because each element of the set is either present in a given subset or not. As described previously, even for a small system of 100 neurons, one can easily determine why evaluation of these combinations individually is computationally intractable.

Functional Dependence, Cross-Correlation, and Mutual Information

Cross-correlation is a statistical technique used to determine whether two simultaneously recorded neuronal spike trains are functionally dependent. Cross-correlation is a sliding dot product, where two functions are frameshifted in time relative to one another, and then the values of the two functions are multiplied at each of these frameshifts and added together. This is represented by the formula:

$$\left(x^{\star }y\right)\left(\tau \right)=\sum _{t}x\left(t\right)y(t+\tau )$$

Given that cross-correlation is essentially a sliding dot product, it may not be sensitive to complex nonlinear relationships between two spike trains. To identify functional dependence in systems with complex relationships, statistical methods more robust than cross-correlation may be useful. In recent years, information theory has been applied by several groups to provide insight into the complex encodings of neurons (1, 6, 19, 32).

Mutual information (MI) is a method of measuring statistical dependence that can be applied to spike train analysis (32). Typically, it has been used to characterize the response of a set of neurons to some external stimulus, but can easily be modified to characterize information between neurons. To calculate MI we must first define a few related quantities as they apply to our specific problem. As a first step, we define the set of total possible responses of a CA1 neuron as Y. In the previous example, this can be thought of as the number of unique elements in y for each neuron k, which can be simplistically estimated as the set of integers from zero to the maximum number of spikes emitted by neuron k in any bin j from 1 to L. Simply put, we are trying to characterize the number of possible responses for any given neuron in any time bin. For an experiment where we are counting spikes in a bin, it makes sense that the number of possible responses ranges from zero to the maximum number of spikes we observe from that neuron in any time bin. In a situation where we interpret a sequence of length n as a binary number, the number of possible responses is the total number of words of length n over the alphabet {0,1}. The total number of such words is 2ⁿ.

The greater the variability of a response, the more capacity it has to transmit information (8). We can characterize this variability using the concept of entropy (36). The response variability, or response entropy, is defined as:

$$H\left(X\right)=-\sum _{x\epsilon X}P\left(x\right){\log }_{2}P\left(x\right)$$

where P(x) is the probability of response x over all trials in our experiment. The entropy is not a direct measure of information as the entropy of a neuron contains not only the variability due to information transfer but also a component of variability due to noise. Therefore, we must calculate the entropy of the response to a specific stimulus. If there is a high degree of variability in a neuron's response to the same stimulus, the less information we are able to extract about that stimulus from the response. In our case, a specific stimulus is the number of CA3 spikes in the bin correlating to the CA1 response. This quantity, called conditional entropy or noise entropy, is larger in“noisier” neurons. It is defined as:

$$H(X\mid Y)=-\sum _{y\epsilon Y}P\left(y\right)\sum _{x\epsilon X}P(x\mid y){\log }_{2}P(x\mid y)$$

Intuitively, this represents the entropy of a response x given a specific stimulus y, averaged over all y. The amount of information that response conveys about the specific stimulus, or the amount of information knowing the number of spikes in CA1 tells you about CA3, or MI, is the difference between the response entropy and noise entropy:

$$I(X;Y)=H\left(X\right)-H(X\mid Y)=\sum _{y\epsilon Y}P\left(y\right)\sum _{x\epsilon X}P(x\mid y){\log }_{2}P(x\mid y)-\sum _{x\epsilon X}P\left(x\right){\log }_{2}P\left(x\right)$$

Given the relationship between joint and conditional probability:

$$P(x\mid y)=\frac{P(x,y)}{P\left(y\right)},P\left(y\right)>\mathrm{o}$$

And, marginal probability, P(x), is defined as:

$$P\left(x\right)=\sum _{y}P(x,y)$$

We can rewrite MI as:

$$\begin{array}{cc}\hfill & I(X;Y)=\sum _{y\epsilon Y}P\left(y\right)\sum _{x\epsilon X}\frac{P(x,y)}{P\left(y\right)}{\log }_2\frac{P(x,y)}{P\left(y\right)}-\sum _{y\epsilon Y}\sum _{x\epsilon X}P(x,y){\log }_{2}P\left(x\right)\hfill \\ \hfill & =\sum _{y\epsilon Y}\sum _{x\epsilon X}P(x,y){\log }_2\frac{P(x,y)}{P\left(y\right)}-\sum _{y\epsilon Y}\sum _{x\epsilon X}P(x,y){\log }_{2}P\left(x\right)\hfill \\ \hfill & =\sum _{y\epsilon Y}\sum _{x\epsilon X}P(x,y)\left({\log }_2\frac{P(x,y)}{P\left(y\right)}-{\log }_{2}P\left(x\right)\right)\hfill \\ \hfill & =\sum _{y\epsilon Y}\sum _{x\epsilon X}P(x,y){\log }_2\frac{P(x,y)}{P\left(x\right)P\left(y\right)}\hfill \end{array}$$

MI can be interpreted as the average reduction in uncertainty observing a specific response gives us with respect to the stimulus. When log base 2 is used, the units of MI are in bits. Intuitively, one can see that MI is also a measure of statistical dependence between X and Y. In the situation of statistical independence, P(x,y) = P(x)P(y), and MI effectively becomes zero. In addition, MI is a symmetric quantity, that is, I(X;Y) = I(Y;X), and we are interested in knowing what spikes in a given CA3 neuron tell us about the spike train output of a CA1 neuron.

To calculate MI in this experiment, we estimate P(x,y) as the number of times spike counts x and y occur together divided by the total number of data points. This is referred to as the plug-in method. For example, if we have 100 data points, and we see the combination of 3 CA3 spikes and 2 CA1 spikes 5 times in our experiment, P(x = 3,y = 2) = 5/100 = 0.05. Marginal probabilities P(x) and P(y) are obtained by summation of P(x,y) over all y and all x, respectively.

Time-Delayed MI

We know that there is a physiologic time delay in the transfer of information from one brain location to another. These can be both synaptic, namely the time it takes for an electric impulse from one locus to another, and postsynaptic, in this case, referring to the processing time of a postsynaptic CA1 neuron. Optical recording studies of the rat hippocampus suggest that membrane potential changes in CA3 affect changes in membrane potential in CA1 with a delay on the order of 4 to 15 ms (35). With this in mind, calculations of instantaneous MI without acknowledgment of time delay may not accurately represent information transfer in this system. By calculating MI at various time lags, or time-delayed MI (TDMI), one can create a metric analogous to cross-correlation for evaluation of functional dependence. TDMI is defined as (13):

$$I(X,y,\tau )=\sum _{y\epsilon Y}\sum _{x\epsilon X}P(x,y,\tau ){\log }_2\frac{P(x,y,\tau )}{P\left(x\right)P\left(y\right)}$$

where P(x,y,ô) is the probability of P(X = x) at time t and P(Y = y) at time t + ô. In practice, calculation of this metric is similar to calculation of MI as described previously, except that we compare bins of x to bins of y in the past (for negative values of ô) or future (for positive values of ô). TDMI has been used in applications that include analysis of information transport in models of neural networks (11, 42) and analysis of time series of hybrid neurophysiologic data (5). Appendix Figure 1 is a step-by-step illustration of the calculation of TDMI.

Temporal Precision and Bias

Inherent to the calculation of MI is identifying an appropriate temporal precision for the analysis, as alluded to earlier. We will refer to this process as binning, which more specifically refers to grouping spikes into bins of length Δt for the sake of creating our spike-response arrays x and y. Information extracted from a spike train is dependent on the bin size, as demonstrated previously (31). Bins with high temporal precision increase the amount of available data for sampling, but may not capture the temporal coding of the spike train, whereas large bins decrease sample size and may average out temporal information if spike counts are summed within each bin (as opposed to counting different patterns of spikes). As an analogy, imagine if one were analyzing documents to extract information about the topic of the documents.

Analysis of these documents with a bin width of one letter may not tell us much about the document. That is, the number of occurrences of any given letter will likely not tell us much about the topic of the document. Conversely, occurrences of any specific sentence or paragraph among documents will likely be too rare to draw any meaningful conclusion. However, analysis with bins that have a length of the average English word may prove useful. For example, documents with high occurrences of “cat” or “dog” may refer to animals or pets. whereas documents with many occurrences of “tennis” or “baseball” may refer to sports.

Related to the concept of temporal precision is the concept of sampling bias. Given that we must estimate entropies from experimentally determined stimulus-response pairs, we are limited in the amount of data that we are able to acquire. For sample sizes that are small relative to the set of possible responses, estimation of response, stimulus, and stimulus-response probabilities may be inaccurate. Intuitively, if one envisions entropy as a measure of variability, inadequately sampled distributions will appear to have less variability, and therefore, less entropy than if we were able to fully sample the entire distribution of neuron responses. That being said, the response entropy H(R), will be less biased downward than the response entropy given specific stimuli, H(R|S), simply because it will be better sampled looking across all stimuli. This will have a net effect of biasing MI upward.

Multiple methods of bias correction have been proposed (for an excellent review, see Panzeri et al.) (29). In the present study, we have chosen to estimate bias using an asymptotic sampling regime, as described previously (24, 30). In this method, bias is estimated as:

$$BIAS\left[I(S;R)\right]=\frac{\mathrm{I}}{2N\mathrm{I}n2}\left\{\sum _s\left[{\stackrel{‒}{R}}_s-\mathrm{I}\right]-\left[\stackrel{‒}{R}-\mathrm{I}\right]\right\}$$

where N is the total number of trials, R_s is the number of relevant responses for a given stimulus, or roughly the number of responses with nonzero probability observed for a given stimulus, and R is the number of relevant responses over all stimuli. Numbers of relevant responses are estimated using Panzeri-Treves bayesian estimation of relevant responses (30). This is done because the number of relevant responses may be underestimated given limited experimental sample size.

Furthermore, given our goal is to identify functionally dependent pairs of neurons in this study, we have attempted to identify a suitable proxy for statistical significance. Applying a simple numerical cutoff does not seem to be an appropriate method as MI rates are dependent on factors beyond functionally connectivity, including neuron firing rate. Resampling methods have been applied to estimates of information for the purposes of bias calculation (25, 40) and for estimation of CIs in evaluating MI (5, 7). In this method, stimulus-response pairs are shuffled such that stimuli are randomly reassigned to responses and MI is recalculated. After this is done a number of times, confidence bounds can be estimated by evaluating the distribution of the calculated information. Presumably, by reassigning stimulus-response pairs, we are operating under the assumption that the reassigned pairs are independent, and we get a sense of information biases intrinsic to the data.

In the present study, first we will evaluate TDMI and cross-correlation in a set of simulated spike trains to characterize the behavior of these two metrics. After simulation, we seek to elucidate the nature of functional connections between CA3 and CA1 neurons by analysis of experimental data using TDMI. As a consequence, we will also attempt to identify the optimal temporal precision for this analysis, which may provide insight into the spatiotemporal encoding of this system. In addition, we will compare analysis of this system using MI with that of cross-correlation through both application to simulated and experimental data.

Appendix: Figure 1. Schematic of calculation of time-delayed mutual information. (A) Digitization of spike train and binning. Here, bins of size 2 are used, and a 1 unit frameshift is applied. (B) Word count histogram. This example calculates mutual information based on two-bit words, but spike counts may also be used. (C) Joint and marginal probabilities, calculated by division of values in the word count histogram by the total number of words counted. (D) “Plug-in” method of mutual information calculation.