Enhanced size-dependent trapping of particles using microvortices

Abstract

Inertial microfluidics has been attracting considerable interest for size-based separation of particles and cells. The inertial forces can be manipulated by expanding the microchannel geometry, leading to formation of microvortices which selectively isolate and trap particles or cells from a mixture. In this work, we aim to enhance our understanding of particle trapping in such microvortices by developing a model of selective particle trapping. Design and operational parameters including flow conditions, size of the trapping region, and target particle concentration are explored to elucidate their influence on trapping behavior. Our results show that the size dependence of trapping is characterized by a threshold Reynolds number, which governs the selective entry of particles into microvortices from the main flow. We show that concentration enhancement on the order of 100,000× and isolation of targets at concentrations in the 1/mL is possible. Ultimately, the insights gained from our systematic investigation suggest optimization solutions that enhance device performance (efficiency, size selectivity, and yield) and are applicable to selective isolation and trapping of large rare cells as well as other applications.

Introduction

Isolation of rare cells from a mixture remains to be a critical technical challenge in cell biology (Attard and de Bono 2011; den Toonder 2011; Dykes et al. 2011; Osborne 2011; Toner and Irimia 2005). Active methods for cell separation rely on external forces (such as dielectric (Khoshmanesh et al. 2012; Kohlheyer et al. 2008; Salomon et al. 2011), magnetic (Gaitas and French 2011; Kolostova et al. 2011; Zborowski and Chalmers 2011), or acoustic (Agarwal and Livermore 2011; Jeong et al. 2011; Nilsson et al. 2004) to discriminate cells with different sizes. These active methods typically provide excellent separation accuracy, but often offer limited throughput and require complex sample preparation or sophisticated external controls. Another approach is to use immunoselection, relying on selectivity of biological markers (antibodies) (Attard and de Bono 2011; Nagrath et al. 2007; Paterlini-Brechot and Benali 2007). While effective, the approach relies on availability of monoclonal antibodies against markers on cell surface, and is often limited due to morphological variations in cell surface and non-homogeneous expression of surface markers (Rupp et al. 2011). The need to process relatively large sample volumes (5–10 mL) is a compounding challenge (den Toonder 2011). Although there are other methods, such as density gradient centrifugation or filtration, they lack specificity and can be limited due to clogging.

One of the more exciting developments on the microscale in the recent years has been the development of inertial microfluidic approaches for cell sorting (Bhagat et al. 2010a; Bhagat et al. 2010b; Bhagat et al. 2011; Choi et al. 2012; Gossett et al. 2010; Hou et al. 2010; Hur et al. 2010; Hur et al. 2011b; Kuntaegowdanahalli et al. 2009; Lee et al. 2011b; Mach and Di Carlo 2010). These passive systems use curved or spiral channels to manipulate hydrodynamic forces for positioning of cells within the flow stream (Bhagat et al. 2008a; Bhagat et al. 2008b; Bhagat et al. 2008c; Hou et al. 2010; Hur et al. 2011a; Kuntaegowdanahalli et al. 2009). Since no external forces are used, these devices are typically low-cost and easy to integrate into LOC systems. While highly effective at high-throughput separations of multiple cell sizes, these approaches generally lack selectivity for isolation of rare cells, such as circulating tumor cells (CTCs) (Attard and de Bono 2011).

Recently, a number of investigators reported a novel approach for selective isolation and trapping of cells from a mixture in microvortices generated by channel expansions in channel geometry. Sollier et al. (Hur et al. 2011b; Mach et al. 2011; Sollier et al. 2009; Sollier et al. 2010) reported trapping blood cells for high purity plasma extraction. More recently Hur et al. (Hur et al. 2011b; Mach et al. 2011) introduced a highly-parallel system in which particles and cells are trapped and subsequently released on demand. In a parallel, independent work, we reported ultra-sensitive size-based selection of particles in rectangular channel expansions (Zhou et al. 2011). All of these approaches are based on the formation of microvortices by modulating channel geometry. These devices offer multiple promising potential applications, including extraction of plasma from blood and isolation of rare cells. Recent work also proposed an automated on-chip cell labeling to simplify the process and save time (Mach et al. 2011). Isolation of CTCs, which are exceptionally rare, has also been proposed (Vona et al. 2000; Vona et al. 2004). While the described devices were successful in capturing target cells, little in terms of operational parameters has been explored and the mechanics of particle trapping remain unclear.

In this work, we aim to improve our understanding of particle trapping in microvortices by developing a model of selective particle trapping. Design and operational parameters including flow conditions, size of the trapping region, and target particle concentration were explored to better understand the trapping mechanism. The developed model shows that the size dependence property of trapping is characterized by a threshold Reynolds number, which governs the selective entry of particles into microvortices from the main flow. We also examined the recirculating particle behavior in microvortices following entry, as it bears direct influence on the trapping efficiency and the subsequent release of particles. While herein we work with neutrally buoyant particles, the results can be directly extrapolated to cells. Ultimately, our results suggest optimization solutions that enhance device performance (efficiency, size selectivity, and yield) for specific applications.

Trapping of particles

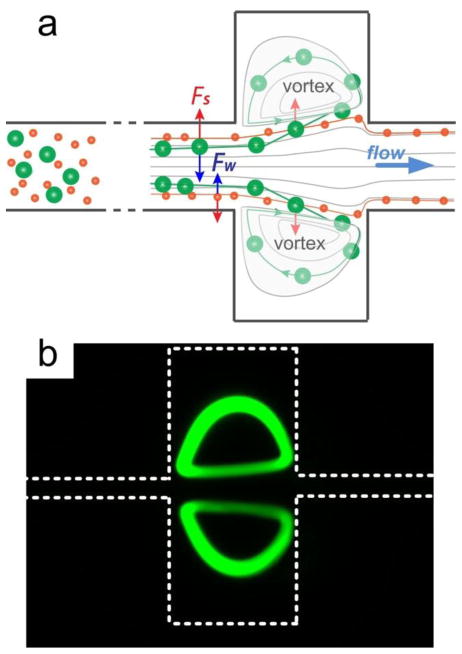
The device operation is based on integration of inertial focusing with microscale laminar vortices to isolate and trap larger cells or particles of interest, with smaller cells/particles passing through the device. This is schematically shown in Fig. 1a. Upstream of the trapping chambers, neutrally buoyant particles (or cells) migrate to distinct equilibrium positions resulting from balance of two counteracting inertial lift forces, the shear-induced inertial lift force (F_S) and the wall-induced lift force (F_W) (Bhagat et al. 2008b; Bhagat et al. 2008c). The shear-induced inertial lift is due to the parabolic nature of the laminar velocity profile in Poiseuille flow and drives particles away from the microchannel center towards microchannel walls. As particles migrate closer to the channel walls, induced asymmetric wake generates a wall-induced lift that pushes them away. These opposing forces cause particles to equilibrate ~0.2D_h away from channel wall (hydraulic diameter D_h = 2WH/(W+H) for a channel W wide and H high). For particles of diameter a to focus in a finite channel length, equilibration occurs for a/D_h> 0.07 (Bhagat et al. 2008b). The net lift force (F_L), which leads to particle migration across streamlines, is strongly dependent on the particle diameter (a) and the flow velocity (U_f) and is expressed as

Fig. 1.

Particle trapping in rectangular microchannels. (a) Two lift forces orthogonal to the flow direction act to equilibrate microparticles near wall in rectangular microchannel upstream from the trapping chambers. The shear-induced lift force F_s is directed down the shear gradient and drives particles toward channel walls. The wall-induced lift force F_w directs particles away from the walls and drives particles toward the channel centerline. The balance of these two lift forces causes particles to equilibrate. At the channel expansion, the fluid is accelerated by the drag force and forms laminar vortices (Moffatt eddies). Since the channel wall is no longer in close proximity, the wall-induced lift force F_w is absent, causing the shear-induced lift force to dominate particle migration into the vortices. The vortices entrain these particles and effectively trap them. (b) Fluorescent image illustrating traces of trapped particles.

$$F_L=\frac{2\rho U_f^2{a}^4}{D_h^2}$$ (1)

where ρ is the fluid density. In microchannels with a square cross-section, after sufficient downstream length particles equilibrate into four positions observed around the channel perimeter due to uniform shear gradient (Matas et al. 2004a, 2004b). In high aspect ratio channels, due to asymmetric shear gradient, these positions can be further reduced to two, centered on the channel height (longer dimension).

At the channel expansion, the fluid is accelerated by the drag force and forms laminar vortices (Moffatt eddies), which entrain particles migrating into them. Once entrained in the vortex, particles follow the flow streamlines and form particle vortices. This is clearly seen from the experimental results (Fig. 1b) that show traces of fluorescent particles forming the vortex. The mechanism of particle migration appears to be initially based on the inertial migration. Since the channel wall is no longer in close proximity, and the wall-induced lift force F_w depends on the distance to the wall δ and scales as F_w ∝ a³/δ (Williams 1994), the particles no longer experience this lift force. In the absence of equilibrium, particle migration is dominated by the shear-induced lift force F_s that is strongly dependent on particle diameter and scales as F_s ∝ a² (Kurose and Komori 1999; Loth and Dorgan 2009; Zhou and Papautsky 2013). Assuming that this force is balanced by the Stokes drag (F_D=3πμaU_L, μ is the fluid viscosity) the lateral migration velocity of these particles scales with particle size as U_L ∝ a. This size-dependent migration drives particles across streamlines toward the laminar vortex, where they become trapped and isolated, rotating in the vortex. It is this size-sensitive trapping feature that leads to the possibility of selective isolation, as particles below the set threshold diameter do not migrate sufficiently far into the chambers to be trapped. The relatively high flow rates necessary to generate vortices actually assist in particle trapping since the shear-induced force scales with $U_f^2$ (Asmolov 1999). Herein, we use experimental results, in conjunction with developed a numerical model, to gain insights and improve understanding of the vortex trapping, with implications for more predictable trapping systems.

Experimental methods

A. Design and fabrication of devices

For this work, we fabricated devices with a single straight high aspect ratio channel for focusing particles upstream of a single trapping chamber. The channel width and length were fixed (W = 45 μm and L = 25 mm), while height was varied (80 μm ≤H ≤ 150 μm). The high AR channel and its length were necessary to ensure complete focusing of particles into two equilibrium positions near channel height centers. A number of configurations were used for the trapping chamber, ranging from 300 μm × 300 μm to 500 μm × 400 μm. The length of channel following the chambers was 1 mm, increasing the total channel length to be of ~26.5 mm. This single inlet/single outlet channel configuration with a single pair of trapping chambers allowed for easy and rapid testing. For increased throughput, the system can be easily parallelized to include multiple channels, and/or multiple chambers.

Devices were fabricated in polydimethylsiloxane (PDMS) using standard soft photolithography. Briefly, we utilized the dry resist film (PerMX 3050 series, DuPont Electronic Technologies) to pattern the microchannels on a 3″ silicon wafer by conventional photolithography and then cast PDMS on the wafer. After 2 hr curing at 80 °C on hotplate, the microchannels were then replicated in PDMS and were bonding to 1″ × 3″ Corning® glass slides (Fisher Scientific) using surface treater (Electro-Technic Products Inc.). The inlet and outlet ports were punched manually using stainless flat head needles.

B. Fluorescence imaging

Experimental validation and quantitative analysis were used to visualize the streams of fluorescently-labeled microparticles flowing in the channel using an inverted epi-fluorescence microscope (Olympus IX71) equipped with a 12-bit CCD camera (Retiga EXi, QImaging). 50 frames of fluorescent images were captured and stacked using ImageJ^® for better visualization of microvortices. Dash lines in pseudo-colored images in this work represent the approximate channel walls. The trapped particles were counted manually from bright-field images captured every 30s after vortex stabilized. Short exposure (10 μs) was used to accurately locate each particle.

Fluorescently-labeled, neutrally buoyant polystyrene particles 6 to 20 μm in diameter were used in this work. Particles were mixed in deionized water at various particle concentrations (5.68 ×10⁵ to 6 particles per mL) for specified investigations. Particles were purchased from a number of vendors, depending on size (Bangs Lab Inc., Polyscience Inc., and Life Technologies Inc.). A 1% v/v of Tween 20 (Fisher Scientific) was added to reduce clogging channels. A 1/16″ PEEK tubing and fittings (IDEX) were used to connect to device ports. A syringe pump (NE-1000X, New Era Pump Systems, Inc.) was used to provide stable flow rates (20 ≤Re ≤ 325) in all particle flow experiments.

C. Numerical models

The microchannels were modeled using a commercial computational fluid dynamics software CFD-ACE+ (ESI Group Inc.). The modeled device geometry consisted of a pair of 300 μm × 300 μm chambers in the middle of a high AR rectangular microchannel (W = 45 μm and H = 90 μm). FLOW module was picked to trace the streamlines within the chambers and unstructured triangle mesh was implemented, creating 3,137,926 cells with size less than 2 μm. The physical properties of water were applied to the fluids participating in the simulation (density ρ= 1000 kg m⁻³ and dynamic viscosity μ = 10⁻³ kg m⁻¹ s⁻¹). Flow rates corresponding to 30≤Re≤300 were specified at the input, while the outlet was set to a fixed-pressure boundary condition. The convergence limit for mass fraction was set to 10⁻⁶. Combinations of x-, y- and z-cut were processed CFD-VIEW to obtain velocity profiles and to trace the fluid vortices within chambers.

Results and discussion

A. Numerical models of particle trapping

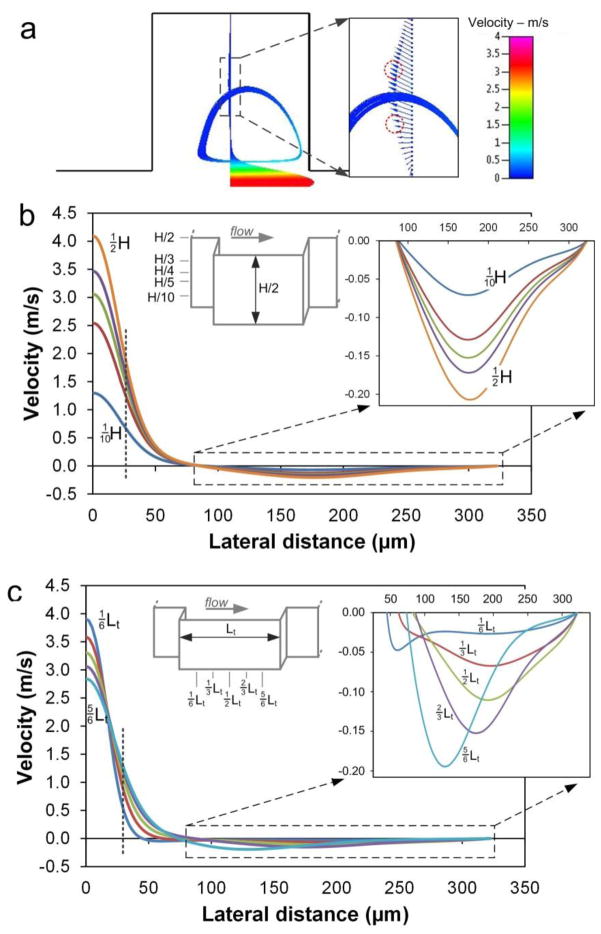
We first investigated particle trapping with 3-D numerical simulations (CFD-ACE+, ESI Inc.), which clearly show formation of microvortices in the expansion region (Fig. 2a). Our models show that the vortex structure is dependent on flow Re, with size increasing with faster flows. Hur et al. (Hur et al. 2011b) reported that with increasing Re, the vortex core progressively shifts toward the center of the reservoir, ultimately expanding to take on the entire reservoir. Our numerical results show that particles experience rapid changes in velocity while entrained in the vortex, with higher velocities near the channel center and the lowest velocities at the back of the vortex (Fig. 2b). Fluid velocity within the microvortex, on the other hand, is substantially smaller (<10%) as compared with the flow in the main channel. This drastic reduction suppresses the lift force for lateral migration (from eq. 1), causing particles to follow the flow streamlines. As particles migrate from the main flow into the vortex chamber, the dominance of the lift force is replaced by the drag force. Hence, particles follow the streamlines under control of the drag force and develop particle vortices. Although the magnitude is significantly smaller, the velocity profile in chambers remains parabolic analogous to that of the main channel (Fig. 2a). This mapping of velocity potentially suggests two particle trajectories (red circles in Fig. 2a) in the chambers as particles following the vortex are at the maximum of the velocity profile and thus migrate down the gradient to either side undergoing shear-induced lift F_s. The downstream evolution of the velocity profile through the chamber shows the slow reduction of the velocity in the main channel, which is expected due to increased cross-section, with progressive increase of the reverse flow velocity in the chambers (Fig. 2c).

Fig. 2.

(a) Traces of streamlines indicating vortices within expansion area. Velocity profile through the chamber exhibits maximum at the vortex trajectory and the heterogeneous velocity direction. Red circles illustrate positions where particle orbits originate. The vortex is in the plane at quarter of channel height (¼H). (b) Velocity profiles (U-component, downstream direction) at different channel heights at ⅔L_t downstream from chamber entrance. Dashed line indicates the upstream channel width. (c) Velocity (U-component) as a function of lateral position at five downstream positions along the chamber length at ¼H. Dashed line indicates position of the upstream channel width. For all panels, Re = 154.

Recent work by Hur et al. (Hur et al. 2011b) revealed through confocal imaging that particles form two vortices in a single chamber, one above the other, suggesting multiple stable orbits that can be occupied by trapped particles. Indeed, our numerical models show these stable particle vortices forming at approximately ¼H and ¾H (Fig. 3a). Plotting flow velocity line profiles at channel bottom, through the stable vortex plane, and channel centerline, reveals a clear inflection point at the center of the vortex where the shear-induced lift force changes direction (Fig. 2b–c). The fluid vortices appear to be non-planar (Fig. 3b), crossing multiple vertical planes and displaying symmetry with respect to the central horizontal plane, indicating equilibrium planes for particles in the expansion chamber. Sideviews of the vortex reveal that some fluid in the main channel is pulled into the chamber from the top, rotating clockwise downward to the central z-plane, and from the bottom, rotating counter-clockwise up to the central z-plane. In this case, particles follow the streamline and proceed into the vortex. Interestingly, our models suggest the outline of the vortices in z-direction (Fig. 3c), indicating two vertically-aligned vortices in each chamber that direct particles from the top and bottom face to the central z-plane. Particles accumulate in the central planes of these intriguing hourglass-type structures.

Fig. 3.

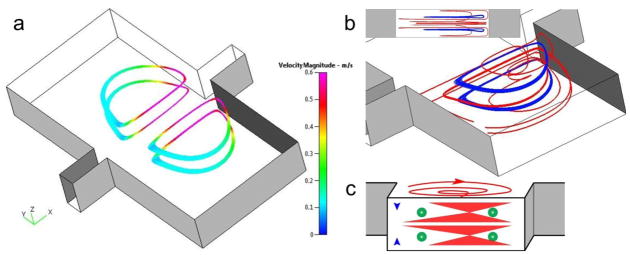
Numerical models suggest four orbits (two z-planes) for particle trapping. (a) The planar orbits symmetrically located in two chambers. The velocity closer to the main channel is higher, with the lowest velocity at the back of the vortex orbit. Flow is from left to right at Re=154. (b) Perspective view and sideview (inset) of the 3-D vortex structure. The trapping orbits (blue) are located at ¼H and ¾H, vertically centered at each of the two vortices (red). (c) The schematic illustration of particle trapping within the vortices.

B. Fluorescent visualization of particle trapping

We investigated formation of vortices by injection of particles of different size. Fig. 4a shows a particle vortex similar in shape to the traces in the numerical model (Fig. 3b), which confirms that drag is dominant. At the center of each vortex, the fluid is stationary. Indeed, we can precisely locate the center (eye) of a particle vortex using an air bubble (Fig. 4b). Since the air bubbles experience minimal centrifugal force due to small density, they migrate down the velocity gradient toward the vortex center upon entering the expansion, as predicted in Fig. 2a. The bright field image in Fig. 4b shows that particles trapped in the vortex recirculate around the air bubble. The air bubbles were observed to remain stationary at the vortex center for at least 30 sec, until completely diffusing into the carrier fluid. This zero velocity together with the bead traces then experimentally demonstrated the formation of low-velocity vortices in chambers.

Fig. 4.

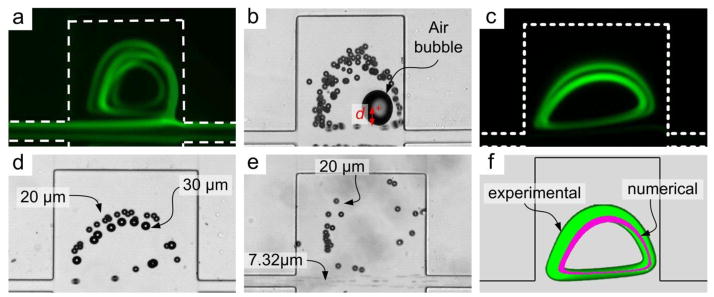
Visualization of particle vortices. (a) Fluorescent traces of the 3D particle vortices at Re=135. Here the straight channel prior to expansions was 1 mm long. (b) Particle recirculation around center of the vortex indicated by a stationary air bubble. d indicates distance between particles entering trapping chamber and the vortex center. (c) Fluorescent trajectories of two particle vortices. (d) Brightfield image illustrating smaller 20 μm diameter particles occupying the larger outer orbit, while the 30 μm diameter particles occupy the tighter inner orbit. (e) Size-selective trapping of 20 μm diameter particles from a mixture with 7.32 μm particles which pass though the device. The concentration ratio (large vs. small particles) was 1:10⁵. (f) Composite image of experimental (green) and numerical (purple) results at Re = 80. The green vortex is the fluorescent trace of 20 μm diameter particles in a 300 μm × 300 μm chamber.

Both particle diameter and Re alter the lateral inertial equilibrium position of particles in a rectangular channel (Matas et al. 2004a; Matas et al. 2004b). Since lateral velocity scales with particle diameter, smaller particles migrate into the trapping chambers at a much slower rate than the larger ones. Hence, smaller particles exhibit a longer distance d (distance relative to the vortex center, as depicted in Fig. 4b) in comparison with the larger particles, even after traversing the trapping chamber length. In contrast, at the same flow velocity, larger particles move across streamlines at a faster rate, enter the vortex and get trapped. Thus, we conclude that d scales inversely with particle diameter a. Previous work (Matas et al. 2004a; Matas et al. 2004b) has also shown that increasing Re shifts the inertial equilibrium position away from the channel centerline, moving particles away from the walls. Higher Re implies faster flow, which reduces time for lateral migration. Thus, d also scales with the flow Re.

An intriguing observation is that in some cases, particles form double orbits. This is clearly evident from particle traces in Fig. 4c. One factor that can cause particles to form multiple orbits is the particle distance d relative to the vortex center. Particles close to the vortex center (small d) tend to occupy the inner orbit, while those further away (large d) tend to occupy the outer orbit. Since larger particles migrate laterally across streamlines at a faster rate and thus exhibit smaller d, they tend to occupy the inner orbit. Conversely, smaller particles migrate slower and thus exhibit a larger d; they tend to occupy the outer orbit at the same flow conditions. Indeed, the bright field image in Fig. 4d demonstrates this preferential orbit selection as 30 μm diameter particles orbit inside the 20 μm diameter particles at Re = 55. Similar observations have been reported by (Mach et al. 2011). These findings lead us to associate this preference with shear-induced lift F_s which is strongly size-dependent. Particles do, however, follow the flow streamlines at low Re, as confirmed by overlaying the ACE+ model results and the experimental data (Fig. 4f), suggesting dominance by the drag force in the vortex.

C. Vortex evolution and threshold Re

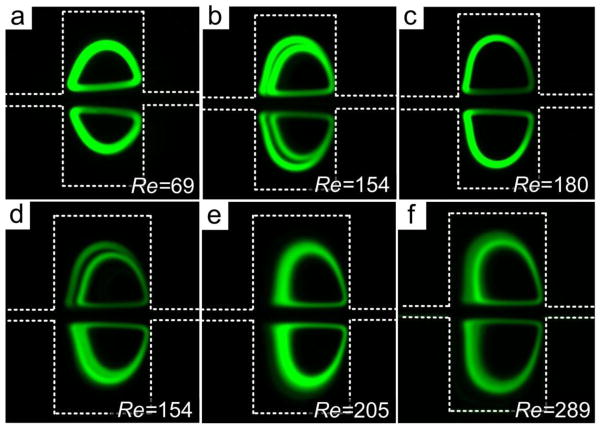
To investigate the vortex formation further, we introduced a suspension of 20 μm particles into the microchannel. We first investigated effects of flow on particle trapping since trapping is influenced by the position of particles in the channel upstream of the trapping chambers and increasing Re tends to push inertial equilibrium positions away from channel wall. The results are shown in Fig. 5. At low Re, the recirculating orbit of the 20 μm diameter particles was small, but the band is thicker due to low velocity. Increasing flow rate to Re =154 lead to formation of two orbits in each chamber; increasing flow further to Re =180 caused the vortex orbit to expanded to a larger size (Fig. 5c). This vortex enlargement could be a result of higher flow velocity that strengthens the centrifugal force pushing particles outward.

Fig. 5.

Evolution of particle orbits corresponding to input Re. (a) Single small orbits at low Re in a 300 μm × 300 μm chamber. (b) Double orbits at intermediate Re. (c) Particles trapped in the large orbit at high Re. The inner particle trajectory is not present in this image. (d) Double orbits in large 400 μm × 400 μm chamber. (e) At higher Re, particles fill in the gap between the double orbits. (f) Distortion of orbits and loss of particles at excessive high Re. In all experiments, 20 μm diameter particles were used; trapping chambers were 300 μm × 300 μm in panels (a)–(c) and 400 μm × 400 μm in panels (d)–(f); microchannel height was 100 μm in all experiments.

Additional experiments were carried out to further explore particle trapping and recirculation in the vortices (Fig. 5d–f). We used larger chambers to show the Re effect more clearly, as more particles could recirculate in the orbits. Again, at Re=154 we observed two orbits. The shape of the orbits was analogous to those in smaller chambers (Fig. 5a–c). Increasing Re first fed more particles into the vortices, as they populated the space between the two orbits. Higher flow velocity in the chamber also distorted the shapes of the orbits, while higher density of particles introduces particle-particle interactions, causing instabilities in particle recirculation. Vertical spread of particles in z-plane may occur, which would undermine the sharpness of the observed orbits.

Excessively high Re (Fig. 5f) further distorted the orbits causing particles to escape, which might be due to the increased centrifugal force. On one hand, high Re could increase the distance d between the particles and the vortex center, as we already discussed. On the other hand, higher Re reduces time available for lateral migration, which further increases d. Hence particles can only occupy the outer orbit. In short, increasing Re can lead to unstable orbits and ultimately lead to loss of particles.

Microvortex formation and structure were found to depend on the flow velocity. Fig. 6 illustrates the evolution of the vortex for 20 μm diameter particles (shown as fluorescent streaks), with formation at Re ~ 70. We term this the threshold Re, denoted as Re_th in this work. Below this threshold value, no particle vortex formation was observed (Fig. 6a). At or above the threshold value, particle vortices evolve. Interestingly, vortices span almost the entire longitudal width of the expansion region, but only half the transverse width. The clear and sharp boundaries of the vortices in Fig. 6b indicate that particles are entrained in a vortex (trapped) in the same horizontal plane. At higher flow rates, vortex boundaries become unclear (Fig. 6c), indicating formation of additional vortices in other vertical planes. At even higher flow rates, the microvortex becomes less stable, exhibiting multiple circulation paths and expanding further into the trapping region. These observations of the vortex structure and symmetry are in agreement with the results of our numerical model (Fig. 3) as well as the recent confocal imaging results (Hur et al. 2011b).

Fig. 6.

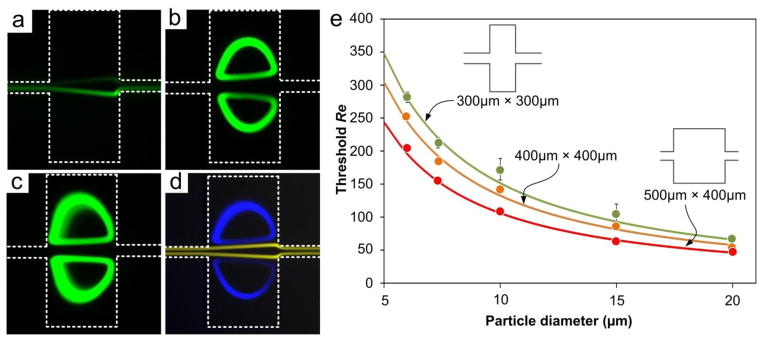
Size dependence of particle trapping. (a) Fluorescent image illustrating no trapping at input Re = 54 for 20 μm diameter particles. (b) Trapping of 20 μm diameter particles at Re = 70. (c) Trapping of 20 μm diameter particles at Re = 160. (d) Superimposed images illustrating trapping of 20 μm diameter particles (blue) and free passage of 15 μm diameter particles (yellow) at Re = 69. The population ratio of the mixture is 1:1000. (c) Characterization of size-dependent trapping by flow threshold Re (Re_th) as a function of particle diameter. The curves represent the calculated Re_th for differently-sized particles. In all experiments, particle concentration of 56,800/mL in 100 μm high channels was used; chamber size in panels (a)–(d) was 300μm×300μm.

Our experiments show that the threshold Re is strongly dependent on the particle diameter and the length of expansion opening (L_t), which can be exploited in order to optimize flow parameters for separation of particles of desired size. For example, Fig. 6d shows blue 20 μm diameter particles trapped (Re_th ~ 70) while the orange 15 μm diameter particles with Re_th ~ 120 pass through. Similarly, in the brightfield Fig. 4e, large particles are recirculating while small beads remain in main flow. We experimentally measured Re_th for particles in multiple channel geometries (Fig. 6e) and found that Re_th exhibits a non-linear dependence on particle size. The exponential change in Re_th for smaller particle sizes a < 10 μm is especially conducive to extraction and trapping of larger particles. For larger particle sizes a > 15 μm, changes in Re_th are small, indicating potential difficulties in selective trapping of larger particles from a mixture. Moreover, Re_th also shows an inverse relation with the opening length. We measured Re_th = 104 for 15 μm particles when L_t = 300 μm. But Re_th reduced to ~63 for L_t = 500. This decrease in Re_th primarily results from the longer opening length that offers more time for particle lateral migration. Hence, the lateral displacement of particles into the chambers may remain the same depending on the interplay of more time and slower lateral-migration velocity, and thus Re_th decreases.

Considering that the lateral migration velocity of particles scales with the flow velocity and particle diameter as $U_L\propto U_f^2{a}^3$ (Bhagat et al. 2008b) one would expect the threshold Reynolds number to scale with the particle diameter as Re_th ∝ a^−1.5. Surprisingly, the empirical evidence in Fig. 6e suggests a weaker scaling of Re_th ∝ a^−1.2. This weaker dependence could due to two facts. On one hand, the velocity profile is no longer constant at the expansion region, which undermines the lateral migration velocity responsible for trapping. On the other hand, the formation of vortices modifies the distribution of local shear rate that dictates the size-dependent migration. More specifically, expression of $U_L\propto U_f^2{a}^3$ could no longer be applicable in the expansion region since it was initially derived from the net force expression for planar Poiseuille flow (Asmolov 1999). These two factors compromise the degree of size dependence.

Based on experimental data, we arrive to an empirical expression for the threshold Re as

$${Re}_{th}=\frac{840000}{L_t\times a^{1.2}}$$ (2)

where the length of expansion opening L_t and particle diameter a are in μm. We note that while only L_t and a are present in the equation, other parameters such as microchannel height and expansion chamber width can also affect Re_th, as we discuss below. The plotted curves appear to be highly consistent with the experimental data. For the same particle, larger expansion shifts the curve downward which means smaller Re_th due to the larger trapping window that offers more time for lateral migration. On the contrary, small L_t increases Re_th due to insufficient time for lateral migration and limited space for particle recirculation. Ultimately, the equation relates the three critical parameters that govern the design of our inertial microfluidic system: the flow conditions, the particle or cell size, and the trapping chamber length. It offers a simple practical guide to design of systems for selective trapping of particles or cells.

The length of the trapping chamber opening L_t can be estimated from equation (2), considering that for 20 μm diameter particles L_t = 72 μm at Re_th = 320 (which is the maximum for our PDMS devices). Nevertheless, practical considerations can further limit the minimum size of the trapping chambers. For example, during experiments, we never observed trapping of 20 μm diameter particles in the smaller 100 μm × 100 μm chambers (L_t = 100 μm). This is likely due to the small size of the opening that offers insufficient time (~19 μs) for migration into the vortices as particles travel downstream. The small chamber size may also lead to increased local particle concentration, leading to strong particle-particle interactions.

While length of opening shows significant effect on Re_th, we found less influence of other dimensions of chambers, such as chamber width (W_t) and channel height (H). Careful comparison of Re_th obtained for different channel heights, we found that taller channels exhibit slightly higher Re_th, for instance Re_th ≈ 85 for H = 100 μm but Re_th ≈ 94 for H = 150 μm for 300 μm × 400 μm chambers for 20 μm diameter particles. This is because the taller channel increases the hydraulic diameter (D_h) which is linearly related to Re (Re = ρU_fD_h/μ). In addition, high aspect ratio of chamber (W_t/L_t > 1) also tends to increase the Re_th. For the 20μm diameter particle, Re_th ≈69 for 300 μm × 300 μm chambers but Re_th ≈ 85 for 300 μm × 400 μm (L_t × W_t) with all other dimensions identical. Possibly the deeper chambers possess more fluid which requires more energy to trigger the recirculation. As a result it requires higher flow rate and thus larger Re_th for trapping to occur.

D. Trapping capacity and enrichment

Although the vortices begin to trap particles upon reaching Re_th, the capture cannot continue indefinitely due to the limited space in the vortex orbits. Consequently, trapping capacity of the chamber is an important parameter to consider. The brightfield time-lapse images in Fig. 7 reveal the progressive trapping of particles. Secondary orbits appear to form after 60s. We counted the number of particles trapped at multiple Re to evaluate the effect of flow rate (Fig. 7e). All the curves were saturated in about 1 min. Interestingly, before the flat saturation region of each curve, there is a small bump indicating oversaturation. These additional particles escape shortly after trapping, and the particle number stabilizes.

Fig. 7.

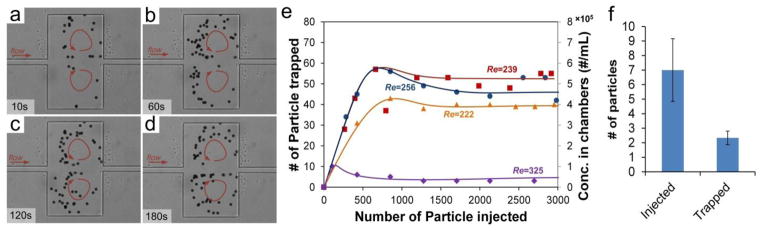
Demonstration of trapping and enrichment of 20 μm particles in 500 μm × 400 μm chambers. (a–d) Timelapse images illustrating progressive trapping. (e) Number of trapped particles as a function of injected particles at various Re. Sample concentration was 568 particles per mL. (f) Results of sensitivity tests at Re = 239. Concentrations as low as 9 particles per 10 mL were used.

Our results show that the capacity exhibits a complex, nonlinear relationship with Re. It first grows as Re increases, and then drops dramatically at excessive Re. For example, the capacity is ~ 50 at Re = 239 but it is less than 10 at Re = 325. The initial increase in capacity could be the result of additional orbits that are created as fast flow empowers the centrifugal force. In addition, high Re modulates the distance between particles and vortex center d to select more orbits as shown in the fluorescent traces in Fig. 5e. However, further increasing in Re extends the d and reduces the chance for particles to enter the chamber. Furthermore, particle-particle interactions become much stronger at high flow velocity. These two facts could result in instable orbits that lead to particle escape. Nevertheless, these results suggest an optimal capacity with respect to Re.

Trapping of particles can lead to tremendous enhancement in concentration. As indicated by the secondary axis in Fig. 7e, concentration of particles in the cavities is calculated to be on the order of 10⁵. Considering that the initial concentration of particles in these experiments was ~568/mL, the enhancement factor is ~1,000×. This substantial enhancement is very promising for isolation of rare cells, where concentrations of 1 per mL is not uncommon. To explore this, we tested this capability using suspension of particles in an extremely-low concentration (9 particles in 10 mL). We found that ~20% of injected particles were observed in the chambers during repeated tests (Fig. 7f), confirming the possibility of 10⁵× concentration enhancement. In addition, this demonstrates the extreme sensitivity of working at a low concentration (<1/mL).

Since recent work (Bhagat et al. 2011) proposed that channel height would affect particle focusing in straight channel, it may also modify the trapping capacity. To test this, we fabricated channels with 100 μm and 150 μm in height and evaluated particle trapping. The results (Fig. 8a) show that taller channels captured more particles. This is not unexpected, as taller channels offer more space in vertical stacking of vortices, helping reduce particle-particle interactions. Based on these results, we would expect shallow channels (e.g., H=50 μm) to further reduce the trapping capacity. Nevertheless, influence of channel height on trapping is weak and does not need to be a major consideration in device design.

Fig. 8.

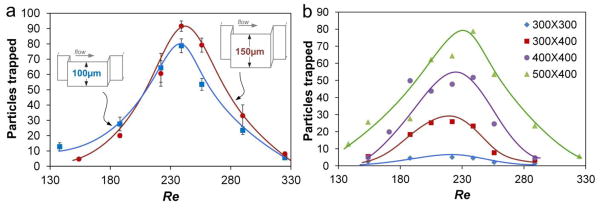
Dimensional effects on trapping capacity. (a) Height effect on the total number of particles trapped. The chamber size was 500 μm ×400 μm. (b) Comparison of the total number of particles trapped vs. Re in chambers of different size. In all experiments, 20 μm diameter particles were used at concentration of 5680 particles/mL.

In addition, Fig. 8a clearly demonstrates the optimal flow Re for trapping, which is the position of peak maximum. This confirms our previous speculation of optimal Re and provides a flexible option to maximize the trapping performance regardless the device design. In the circumstance of handling fragile cells (e.g. CTCs), such curves would help to pick an appropriate flow rate to minimize cell damage while maintaining performance. While these channels share similar optimal Re, unexpectedly, our results of four different devices exhibit the same manifestation (Fig. 8b). This should not be coincidence if comparing channel dimensions. More specifically, the focusing length of the channels may determine the optimal Re as all these devices shared the same straight segment before the chambers (focusing length).

Unlike the manifestation of similar optimal Re, Fig. 8b shows that larger chambers provide more room for particle recirculation. For example, the 500 μm × 400 μm chambers captured as many as 80 particles, while less than 10 were captured by the smallest 300 μm × 300 μm chambers. The increase in trapping occurs with increase in any of the chamber dimension, either L_t or W_t, which permits larger vortices that can accommodate more particles. Comparisons among the first three curves further show that it is more effective to enhance the capacity by increasing W_t rather than L_t. Approximately 300% increase of capacity was achieved by increase W_t from 300 μm (blue) to 400 μm (red) while 200% enhance was made comparing L_t=400 μm (purple) with L_t=300 μm (red).

E. Effects of sample concentration

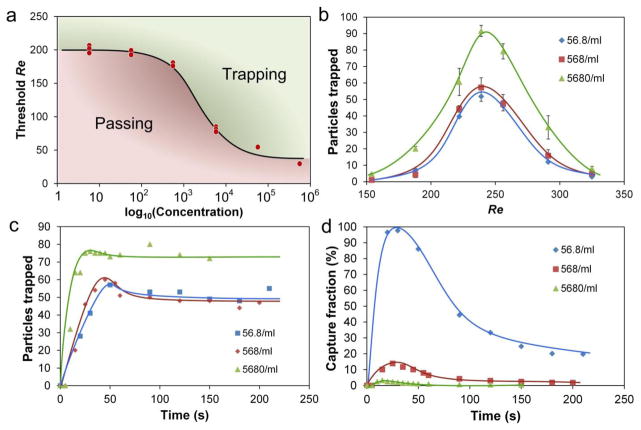
During the experiments, we observed that particle concentration appeared to influence trapping performance, which led us to systematically examine the effect. We used 20 μm particles diluted to concentrations ranging from ~6 particles/mL to ~600,000 particles/mL. Surprisingly, our results indicate a clear dependence of the Re_th on particle concentration (Fig. 9a). At low concentration, the Re_th tends to converge at high value, while increasing concentration tends to lower Re_th. Such characteristic curve suggests that not every position near sidewalls can be trapped. Indeed our numerical results indicate the vortex is expanding from ¼ H to ½ H following the initial reduction as it rotates down from top to central plane (Fig. 3b–c).

Fig. 9.

Effects of particle concentration on (a) threshold Re, (b) capacity, (c) accumulation, and (d) capture efficiency. The trapping chamber size was 500 μm ×400 μm, and 150 μm height. Accumulation and capture efficiency were measured at Re = 239.

The concentration of particles in the sample appears to affects not only the Re_th but also the trapping capacity. As shown in Fig. 9b, decrease of concentration from 5680/mL to 568/mL shifts the curve downward which reduces the capacity. However further decrease from 568/mL to 56.8/mL shows only minor impact on capacity. This non-monotonic trend is similar to the trend for Re_th, which tends to converge at low concentration. Such an interesting correlation between the Re_th and capacity exposes the trapping concept in a practical circumstance of cell isolation, since low Re and high capacity are both desired to minimize cell damage while offering high yield. Analogous to low concentration, we expect the capacity for sample with higher density also converges at the ultimate capability of particle accommodation as implied by the similar Re_th. This up-limit of capacity is mainly due to the finite space of confinement while the down-limit may be resulted from the equilibrium positions of particles in the main channel. Unlike the capacity reduction at low concentration, the optimal Re remains unchanged (Fig. 9b). This is expected as Re is determined by the focusing channel upstream from the chambers, as also suggested in Fig. 8b.

Presenting the particle counts as a function of time (Fig. 9c) indicates that lower concentrations, as one would expect, require longer time to saturate the trapping chambers. However the trapping efficiency acts in different way. Fig. 9d indicates a substantial drop-off after the initial 30 sec in our system with a single trapping chamber (systems with multiple trapping chambers may exhibit a longer saturation time). This finding is important, as it offers insight into the optimal time when the trapping is the most effective. Since cell trapping in these devices is not continuous, but rather is done in a two-step trap-release mode (Mach et al. 2011), the trapping rate suggests when to switch flow rates to transition from trapping to releasing. More specifically, we show herein that concentrations bellow 10²/mL range maximize the performance of the trapping design; the ~60/mL concentration achieves ~98% trapping efficiency. In short, trapping performance is better at low-concentrations, which is highly desirable in applications such as isolation of large rare cells from a bulk mixture for sample preparation.

Not only are we able to effectively trap particles (or cells) at low concentrations, but our results show that we can do so in cases of extreme heterogeneity. In other words, the target particles (or cells) at extremely low concentration can be trapped from a mixture containing a large number of smaller diameter non-target particles (or cells). We have already presented a result in Fig. 6d, demonstrating extraction of 20 μm diameter particles from a mixture with 15 μm diameter beads in the ratio of 1:1,000. In another test (Fig. 4e), we further demonstrated the trapping capability by increasing heterogeneity of the sample suspension to 1:10⁵. When coupled with the ~10⁵× concentration enhancement (as was shown in Fig. 7f), these results reveal the extraordinarily promising selectivity of the approach, suitable for isolation of rare cells that are larger than blood cells (e.g., MCF-7 breast cancer cells) as an enrichment approach in sample preparation for downstream analysis.

Microfluidic systems with parallel arrangement of isolation channels or with downstream sequencing of trapping regions are of great interest in isolation of rare cells. The former can remarkably enhance the throughput, and the latter provides more space for trapping cells in the system. While parallelization scales the throughput directly, the capture efficiency of subsequent trapping regions does not compound linearly with their number. For example, Mach et al. (2011) has shown efficiency of 20% in a device consisting of 80 traps; compared with our results for a single trap under similar conditions (input concentration at ~500 particles/mL,), it is only a ~4% improvement (Fig. 9d). These differences in performance between single and multiple trapping chamber devices we believe stem from the input flow conditions of the downstream trapping region being different from the input conditions of the initial trapping region. Lee et al. (2011a) reported that secondary flow can be present in the channel cross-section following the expansion, which may alter equilibration positions of un-trapped particles. As a result, particles not trapped in the first trapping region may not be captured by the downstream trapping region since focusing of particles to their equilibrium positions near sidewalls is critical to trapping. In addition, local particle concentration at downstream trapping regions decreases as a portion of input particles is captured in the preceding expansions, leading to differences in the threshold Reynolds number. Similarly, the phase diagram of the concentration effect in Fig. 9a is likely to shift in the multiple-trap device. Hence, the results in this work should be extrapolated to the multiple trapping regions with caution.

Distribution of sizes in particles or cell suspensions in real-world samples can also influence performance of the trapping system. Since larger particle size requires a smaller Re_th, size variation in a sample will undermine trapping efficiency as flow will not be sufficiently fast to trap smaller particles. However, efficiency can be improved by increasing the input flow until it reaches the Re_th for the smallest particle size in the sample. The smallest particle size in the sample suspension, in essence, dictates the Re_th of the sample, and the trapping efficiency for that sample. The concentration effect on threshold Reynolds number for a suspension with different sizes is a more complex issue. Excessively high concentrations of particle in a sample introduce particle-particle interactions and significantly increase disturbance of local velocity profile as well as increase effective viscosity of the sample. These factors can significantly affect particle focusing behavior and thus influence particle trapping. Nevertheless our results in this work provide an opportunity to estimate the appropriate Re_th in order to minimize the negative effects associated with sample size variations on trapping performance.

Conclusions

In this work, we successfully demonstrated a simple planar microfluidic structure for size-selective isolation and enrichment of particles in geometrically-generated microvortices. Our numerical models demonstrate the 3D structure of microvortices, which span the entire channel height. In each chamber, the models suggest two hour-glass shaped vortices, with orbits for particle recirculation. Both numerical and experimental results reveal the low-velocity and drag dominance within the chambers. Intriguingly, our results show that recirculating orbit in single plane can differentiate into two, depending on flow condition (Re) and particle diameter (a). The flow Re is found to not only dictate the trapping, but also determine the trapping capacity. We identified the threshold Re (Re_th) which triggers the particle recirculation in the vortices. Based on our experimental data, we proposed an empirical equation to predict Re_th, for particles with different sizes and trapping chambers.

Finally, our results suggest that sample concentration is a critical parameter that can significantly alter device performance, with target concentrations bellow 10² particles/mL offering the best performance. In consideration of separation applications, we experimentally confirmed the feasibility of isolation and enrichment of both extremely low concentration (~1 particle/mL, enrichment factor of 10⁵×) and extraordinarily high selectivity (1:10⁵). The insights gained from our systematic investigation offer improved understanding of the vortex trapping design, permitting a more predicable development of such a platform for a wide range of applications including rare cell isolation.