STRUCTURAL CONNECTIVITY VIA THE TENSOR-BASED MORPHOMETRY

Abstract

The tensor-based morphometry (TBM) has been widely used in characterizing tissue volume difference between populations at voxel level. We present a novel computational framework for investigating the white matter connectivity using TBM. Unlike other diffusion tensor imaging (DTI) based white matter connectivity studies, we do not use DTI but only T1-weighted magnetic resonance imaging (MRI). To construct brain network graphs, we have developed a new data-driven approach called the ε-neighbor method that does not need any predetermined parcellation. The proposed pipeline is applied in detecting the topological alteration of the white matter connectivity in maltreated children.

1. INTRODUCTION

The human brain exhibits one of the most complex networks. This anatomical substrate supports the emergence of the coherent physiological activities in the distant brain regions that make up a functional network [1]. Unlike extensively studied functional brain networks, structural connectivity is not often explored till the introduction of diffusion tensor imaging (DTI) which is often used to investigate the structure of axonal fiber bundles in human brains in vivo.

Recently, there has been an attempt of using cross-correlation of cortical thickness as a way to investigate cortico-cortical connectivity [2, 3]. Besides the cortical thickness, it is possible to correlate other voxel-wise morphometric measures such as the Jacobian determinant (JD) obtained from the tensor-based morphometry (TBM) framework. The JD measures the change in the volume of a voxel in deforming the template brain to match an individual brain [4]. By correlating the JD at different voxels, we can quantify how the local volume in one voxel is correlated to the local volume in other voxels. Thus it can be directly used in constructing the whole brain map of corresponding structures.

In this paper, we propose to construct a structural connectivity map based on the cross-correlation of the JD for the first time. The main advantage of the proposed technique is that it does not require DTI but still able to construct the population specific connectivity maps only using T1-weighted MRI. Since MRI has been extensively collected than DTI so far in clinical applications, it would be highly beneficial if we can exploit this massive database of MRI.

The second advantage is that it can build connectivity maps over the whole brain. While the cortical thickness-based connectivity is restricted to the gray matter only, neural development such as myelination or glial proliferation contributes the white matter volume [5]. Our approach can build a connectivity map of the whole brain enabling such an investigation that involves in the white matter.

The proposed framework is applied to the brain networks of the children who have been maltreated in the early stages of life and have been institutionalized in orphanages in East Europe and China but are now living with adopted families in the USA (Post-Institutionalized; PI). It is known that individuals who experience such an early adversity are at heightened risk for a various mental and physical problems. In the physically abused children, smaller local volume was found in the orbitofrontal cortex, which is known as central to social and emotional regulation [6]. Rodent models show that the chronic stress occurs the cytoarchitectural changes in the frontal cortex [7]. Thus we expect decreased white matter connectivity in the PIs in the regions including the frontal cortex.

2. METHODS

2.1. Subjects and MRI image

T1-weighted MRIs were collected using a 3T GE SIGNA scanner for 32 PI and 33 normal control (NC) subjects. Two groups are matched in terms of age (PI: 11.19 ± 1.73 years, NC: 11.48 ± 1.62 years; T (63)=0.71, p > 0.47). But the gender ratios (girls over all; PI: 0.59, NC: 0.39) and the whole brain volume (PI: 1,808.2 ± 117.6 cm³, NC: 1,690.0 ± 156.4 cm³; T (63)= 3.44, p < 0.001) are different. A study specific template was constructed using symmetric normalization (SyN) through Advanced Normalization Tools (ANTS) [8].

Computational load quadratically increases as the number of nodes increases. Even with 336363 white matter voxels in the template as in this case, there will be total 113140000000 cross-correlations to compute. Thus, to reduce the computational load, the 1mm-resolution JD maps are subsampled at every 5 mm after spatial smoothening with a Gaussian kernel with 3 mm FWHM. Subsequently 2692 nodes are obtained (reduction ratio= 0.0080). This is more than sufficient number of nodes for modeling white matter connectivity and substantially larger than most of connectivity studies that use between 50–100 nodes.

2.2. Partial correlation maps

Fig. 1 illustrates the proposed pipeline. Between 2692 nodes, we link two nodes if the partial correlation of the JDs is statistically signifi-cant at a certain threshold. The JD is defined as the determinant of the displacement gradient matrix ∂U/∂x [4] as

Fig. 1.

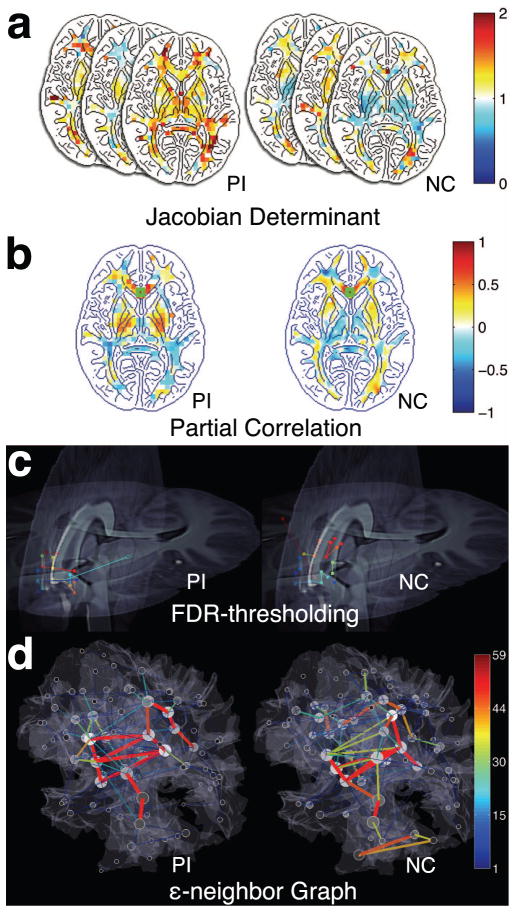
Framework of the proposed analysis applied to post-institutionalized (PI) children and normal control (NC). (a) Jacobian determinant maps of individuals projected on the template. (b) partial correlation maps seeded at the genu (marked with green squares) (c) FDR-thresholding on partial correlation is used to establish edges of the connectivity network. Only edges connecting near the genu are visualized. The different pairings are marked with different colors. (d) The proposed ε-neighbor graphs of connectivity. Only positive correlations are shown here. The gray shading of nodes indicates the node degree. The size of nodes represents the number of nodes that are merged in the ε-neighbor construction.

$$J=det(\mathbf{I}+\partial \mathbf{U}/\partial \mathbf{x})$$ (1)

where U is the displacement matrix and x is the coordinate vector. To remove the possible confounding effect of age, gender and brain volume, we used the partial correlation obtained from fitting general linear models (GLM). Let z = (1, age, gender, volume) be the nuisance covariate vector. Then we modeled the JD on the i-th node as

$$J_i=\mathbf{z}{\lambda }_i+{\epsilon }_i$$ (2)

where λ_i = (λ_i1, …, λ_i4)′ is the unknown parameter vector and ε _i is the correlated zero mean Gaussian noise. The residual of the fit is given by r_i = J_i − zλ̂_i, where λ̂_i are the least-squares estimation. It can be shown that the partial correlation ρ_ij between J_i and J_j while factoring out the effect of the nuisance covariates z is simply given by the correlation between the residuals r_i and r_j [9]. The partial correlation ρ_ij is then estimated using the Pearson correlation as

$${\widehat{\rho }}_{ij}=\frac{\sum r_i{r}_j-\frac{\sum r_i\sum r_j}{n}}{({r_i}^2-\frac{{(\sum r_i)}^2}{n})({r_j}^2-\frac{{(\sum r_j)}^2}{n})}$$ (3)

where n is the number of subjects in each group.

2.3. FDR thresholding of partial correlations

In order to obtain the deterministic network graph, we have thresholded the partial correlations using the false discovery rate (FDR) thresholding. The distribution of correlations can be approximated using the Fisher transform: [10]:

$$z_{ij}=\frac{{tanh}^{-1}({\widehat{\rho }}_{ij})}{\sqrt{1/(n-3)}}~N(0,1).$$ (4)

The null hypothesis H₀ is that there is no link between the nodes i and j, i.e. ρ_ij = 0.

The family-wise error rate (FWER) would be highly inflated with 2692 × 2691/2 possible tests between all nodes. Thus we applied the FDR with q = 0.01 under a weak assumption of dependency. If the resulting FDR-threshold is given by s, the adjacency matrix A = (a_ij ) is given by a_ij = 1 if z_ij ≥ s and a _ij = 0 otherwise, with the diagonal terms a_ii = 0.

2.4. ε-neighbor graph simplification

Though the obtained adjacency matrices via the FDR thresholding are sparse, almost ten thousands edges still encumber biological interpretation. Furthermore, isolated single connections consisting of two nodes are more likely false positives. Therefore, we need to perform a network simplification without distorting underlying network topology. For this purpose, we have adapted the ε-neighbor scheme [11], which was originally applied in constructing network graphs out of numerous white matter tracts obtained from DTI. The algorithm condenses a given complex graph to a much simpler graph iteratively.

From the FDR-thresholding, we obtain collection of significant edges e_i1e_i2 linking two nodes e_i1 and e_i2. Suppose we have constructed the graph 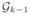using edges e₁₁e₁₂, · · ·, e_k−1,1e_k−1,2 only. Then at the k-th iteration, we construct the graph 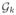using e_k1e_k2 somehow. In order to do this, we need to define the ε-neighbor of a graph. Let us define the distance d(p, 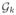) of a node p to the graph 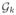as

$$\mathbf{d}(\mathbf{p},{\mathcal{G}}_k)=\underset{\text{q}\in {\mathcal{V}}_k}{min}\Vert \text{p}-\text{q}\Vert .$$ (5)

If d(p, 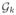) ≤ ε for some radius ε, the node p is called the ε-neighbor of .

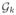Initially the graph 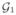= { 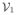, 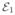} starts with two nodes 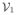= {e₁₁, e₁₂} and a single edge 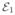= {e₁₁e₁₂}. At the 2nd iteration, we check if the new nodes e₂₁ and e₂₂ are the ε-neighbor of 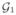. We will merge a new node to the existing node in 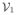if the new node is the ε neighbor of a node in 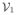. The idea is best illustrated with a toy example given in Fig. 2.

Fig. 2.

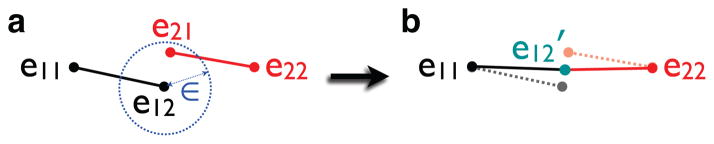
Schematic illustration of the ε-neighbor updating scheme. (a) Initially the graph consists of one edge e₁₁e₁₂ (black). At the next stage, we determine how to connect the new edge e₂₁e₂₂ (red) to the existing graph . The node e₂₁ is within the ε radius (blue) of the node e₁₂. So e₂₁ is the ε-neighbor of and has to be merged with e₁₂. (b) The coordinates of the merged node e₁₂ is updated to e₁₂′ (green) and the new edge e₁₂′e₂₂ is included in .

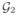Suppose e₂₁ is the ε-neighbor of 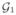. We assume that e₁₂ is the closet node to e₂₁. Then we merge e₂₁ to e₁₂ and update the vertex and edge sets as 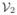= {e₁₁, e₁₂, e₂₂}, 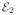= {e₁₁e₁₂, e₁₂e₂₂}. Other possible scenarios are given in [11]. This merging and deletion process is iteratively performed. However, the original ε-neighbor construction method as presented in [11] does not produce a unique graph and it depends on the initial choice of edge set 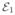. To guarantee the stability, we decided to update the coordinates of the pre-existing node when a merging occurs. In the toy example, the coordinates of e₁₂ are updated to e₁₂′ as

$${{\text{e}}_{12}}^{\prime }\leftarrow \frac{{\text{e}}_{12}{n}_{12}^1+{\text{e}}_{21}}{n_{12}^1+1}$$ (6)

where $n_{ij}^k$ is the total number of nodes that are merged to the existing node e_ij at the k-th iteration. If the merging happens, we have to update $n_{ij}^k$ as well. So we have $n_{12}^2=n_{12}^1+1$. For this study, ε was set to be 21 mm to investigate the connectivity at macro-scale level.

3. RESULTS

The FRD-thresholding produces graphs with 2692 nodes. The ε-neighbor method simplifies the graphs with only 88 nodes and 241 edges for the PIs, and 86 nodes and 276 edges for the NCs. In terms of the number of nodes, the ε-neighbor method achieves the compression rate of 3.27 % while still preserving the overall topological structures in the graphs with 2692 nodes.

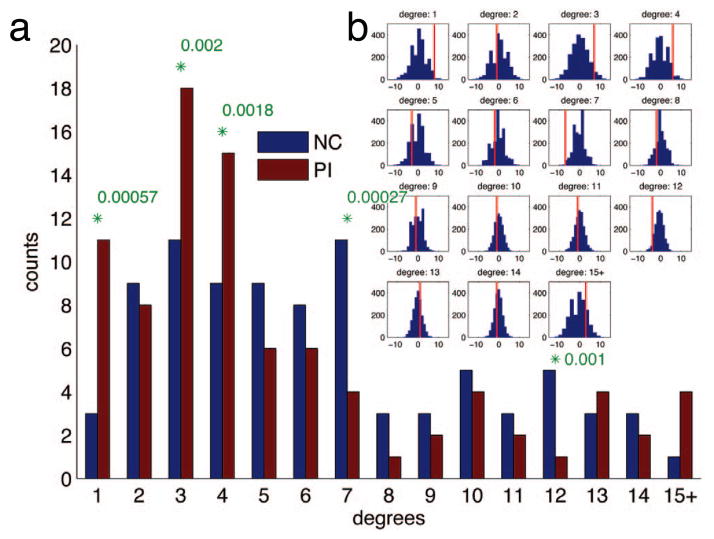
We used the degree of nodes as a discriminating feature between the two groups. The degree distributions of ε-neighbor graphs are shown in Fig. 3. The counts in the high degrees are prone to noise thus those exceeding degree 14 are summed into a single bin [1]. Since the underlying distribution is unknown, the significance was tested using a non-parametric permutation test. We randomly permuted the group identifiers for 2000 times and proceeded with the graph construction procedures. Since we need to perform multiple tests for 15 degree bins simultaneously, Bonferroni correction threshold for an individual test was set at 0.05/15 = 0.0033. There are significantly more nodes with the low degrees (1, 3 and 4) in the PIs than the NCs and more nodes with the high degrees (7 and 12) in the NCs than the PIs. Since the numbers of nodes are expected to be similar across groups, it suggests that the nodes with the high degrees are affected in the PIs resulting more low degree nodes. It also implicates weakened connectivity in the PIs in accordance with the previous literature [7].

Fig. 3.

Permutation tests on degree distributions. (a) Degree distributions. The significant differences between the PIs and the NCs marked with green asterisks with p-values (Bonferroni corrected at α=0.05). (b) The null distribution obtained by 2000 permutation tests. X-axis is for the difference of degrees between the PIs and the NCs. Y-axis is for the number of counts. Red vertical lines note the actual differences.

The anatomical patterns of the ε-neighbor graphs are shown in Fig. 4. While the inter-hemispherical edges connecting homologous sub-cortical regions are commonly found in the both groups, the differences in the edge concentration are observed in the regions that include the cerebellar, the brainstem and the regions around the anterior cingulate gyri. In addition, the extension of the edges that reach to the dorsal lateral prefrontal cortex and the medial temporal cortex seems to be limited in the PIs than the NCs suggesting consistency with the reduced local volume in those regions [6].

Fig. 4.

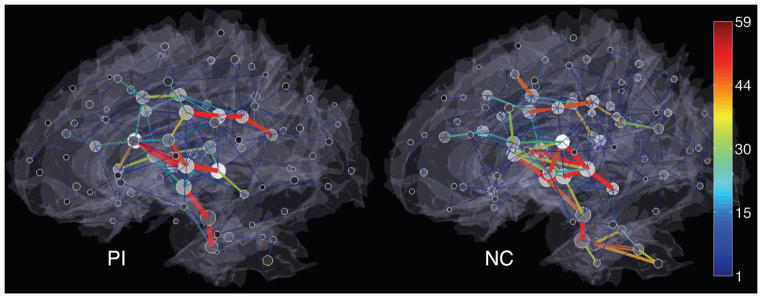
Local connectivity patterns of the ε-neighbor graphs. Only positive correlations are shown in a lateral view. Edges are color-coded by the number of merged connections implying the strength of connections. The gray shading of nodes indicates the degree and the size of nodes represents the number of nodes that are merged.

4. DISCUSSIONS

We have presented a novel structural connectivity mapping technique that uses only T1-weighted MRI. The constructed partial correlation maps (Fig. 1) look very similar to the probabilistic connectivity maps obtained from DTI. Further research is needed for validating the closeness of the partial correlation maps to the probabilistic connectivity maps.

The network graphs showed significantly different degree distributions in the PIs implying abnormal connectivity. The anatomical pattern of the white matter connectivity seems to be locally different across groups. However, it should be more thoroughly validated in a further study.

In this paper, we have mainly focused on developing the connectivity mapping technique via the TBM framework and the ε-neighbor graph simplification.