Improving the Efficiency of Free Energy Calculations in the Amber Molecular Dynamics Package

Abstract

Alchemical transformations are widely used methods to calculate free energies. Amber has traditionally included support for alchemical transformations as part of the sander molecular dynamics (MD) engine. Here we describe the implementation of a more efficient approach to alchemical transformations in the Amber MD package. Specifically we have implemented this new approach within the more computational efficient and scalable pmemd MD engine that is included with the Amber MD package. The majority of the gain in efficiency comes from the improved design of the calculation, which includes better parallel scaling and reduction in the calculation of redundant terms. This new implementation is able to reproduce results from equivalent simulations run with the existing functionality, but at 2.5 times greater computational efficiency. This new implementation is also able to run softcore simulations at the λ end states making direct calculation of free energies more accurate, compared to the extrapolation required in the existing implementation. The updated alchemical transformation functionality will be included in the next major release of Amber (scheduled for release in Q1 2014) and will be available at http://ambermd.org, under the Amber license.

1 Introduction

Free energy calculations¹ have been used for many different applications including relative binding energy calculations for drug design,^2,3 solvation free energy calculations on drug-like molecules,⁴ and determining the free energy change upon mutation of an amino acid in a protein.^5–7 There are many methods for conducting free energy calculations^8–10 ranging from inexpensive, but more approximate methods, such as docking,¹¹ to intermediate methods such as MM/PBSA,^12,13 and finally to expensive, but less approximate methods, such as thermodynamic integration (TI)^14,15 and the multistate Bennett acceptance ratio estimator (MBAR).¹⁶

These latter methods are more expensive for a variety of reasons, including the need for unphysical intermediate states, long simulation times, often complicated setup and analysis and the implementation of the method itself. Work by others has described how to optimize the number of intermediate states, and reduce the simulation time while preserving the accuracy of TI and MBAR methods.^17–19 However, the efficiency of the algorithm used to implement alchemical transformations has not been examined. This paper focuses on a more efficient implementation of alchemical transformations in the Amber²⁰ package. Free energies are calculated from these alchemical transformations using TI or MBAR among other methods.

Amber is a widely used software package for running MD simulations, which has been in development for many years.^21–23 The main software packages for MD simulations in Amber are sander and pmemd. The pmemd module of Amber is a more efficient implementation of some of the features available in sander, focused mainly on better parallel scaling and GPU acceleration.^22–26 In the current release (v12) of Amber, alchemical transformations are only available in sander. We introduce a more efficient implementation of alchemical transformations in pmemd which includes both algorithmic and performance enhancements. This support for alchemical transformations in pmemd will be available as part of the next version of Amber (scheduled for release in Q1 2014).

2 Theory and Methods

2.1 Free Energy Calculations

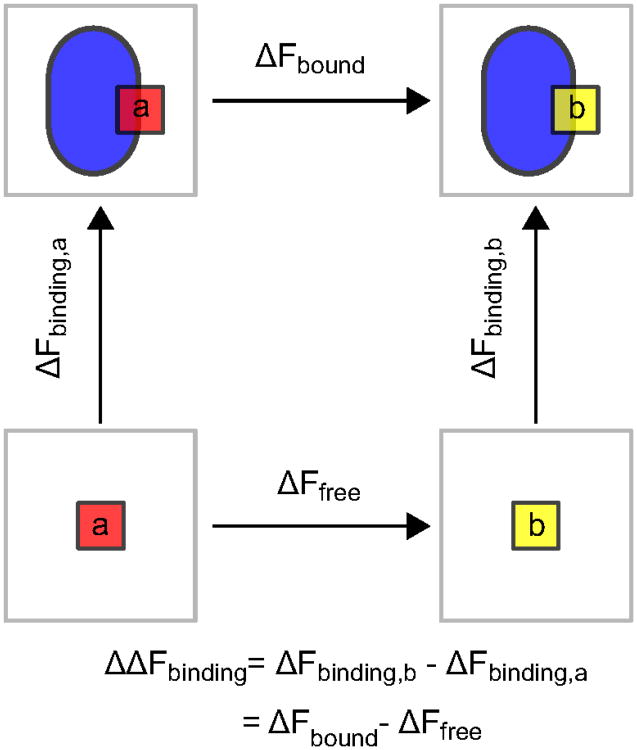
A thermodynamic cycle is often used in free energy calculations in order to make the calculations computationally tractable. These cycles probe the free energy difference between two states using non-physical transformations to connect the initial and final states.² Each segment in the thermodynamic cycle requires a separate simulation. Figure 1 shows an example of a thermodynamic cycle that is used when calculating relative binding free energies. The alchemical transformation of one ligand to another requires less computational time than the direct calculation of the free energy of binding for each ligand. Free energy is a state function, so the relative binding energy will be the same, regardless of which path is used for the calculation.

Figure 1.

Thermodynamic cycle for a relative binding free energy calculation. The vertical arrows show ligand binding (squares) to a protein (blue oval). The horizontal arrows show the alchemical transformations between the two different ligands bound to the protein (top) and free in solution (bottom). Free energy is a state function, so ΔΔF_binding can be calculated using either path.

TI is one method that can be used to calculate the free energy difference for each segment. The free energy is calculated using¹⁴

$$\mathrm{\Delta }F={\int }_0^{1}d\mathrm{\lambda }\langle \frac{\partial U}{\partial \mathrm{\lambda }}\rangle$$ (1)

where ΔF is the free energy difference for a segment, U is the potential energy of the system, and λ is a parameter which varies the potential from the initial state where λ = 0 to the final state where λ = 1. In practice, eq. 1 is integrated numerically, with simulations run at discrete values of λ. In order to determine the error, the correlation time of the $\frac{\partial U}{\partial \mathrm{\lambda }}$ values is determined. Then samples are taken from the complete data set at intervals larger than this correlation time. This subsampling removes correlations in the data, so that the error can be determined using the standard deviation of these values.

Besides TI, free energies can be calculated using MBAR¹⁶ As with TI, this method makes use of the calculated potential energy at various values of λ. However, rather than integrate eq. 1, MBAR uses the additional information of what the potential energy would have been for each configuration calculated at all of the other λ values. To calculate the free energies¹⁶

$${\widehat{f}}_i=ln\sum _{j=1}^K\sum _{n=1}^{N_j}\frac{\mathit{exp}[-u_i(x_{jn})]}{{\sum }_{k=1}^K{N}_k\mathit{exp}[{\widehat{f}}_k-u_k(x_{jn})]}$$ (2)

is solved self consistently for the free energy f̂_i at each λ value using the reduced potential energy u calculated at the all λ values. In practice, eq. 2 can be solved using the freely available pyMBAR program. This program can be downloaded from https://simtk.org/home/pymbar. The statistical uncertainty can also be calculated using pyMBAR. This method has been shown to minimize the variance in the calculated free energies, by making more efficient use of the simulation data.^16,17,27,28 Both TI and MBAR are post processing methods which can be applied to alchemical transformation simulations. In both the sander and pmemd implementations, the extra energies needed for MBAR are calculated during the simulation, with little additional cost compared to an equivalent TI simulation.

The potential energy varies smoothly from the initial to the final state, using linear scaling or softcore terms. The general functional form for the potential energy is

$$U(q,\mathrm{\lambda })=U_{\mathit{\text{common}}}(q)+(1-\mathrm{\lambda })U_{i,\mathit{\text{perturbed}}}(q,\mathrm{\lambda })+\mathrm{\lambda }{U}_{f,\mathit{\text{perturbed}}}(q,\mathrm{\lambda })$$ (3)

where U_common is the potential for the unperturbed atoms, U_i,perturbed and U_f,perturbed are the potentials that correspond to the initial and final states for the perturbed part of the system, and q represents the 3N atomic coordinates. The potentials for the initial and final states may include softcore van der Waals (vdW) and electrostatic (EEL) terms, which improve the efficiency and stability of the simulations.^29–31

These potentials only modify the functional form of the intermediate states; at the initial or final states (end states), the potential energy is calculated using the original vdW and EEL potential terms. A free energy calculation may make use of both softcore potentials in a single-step transformation, or may just use the vdW softcore term in a multi-step transformation, with the free energy associated with removing the charges calculated in separate simulations. Both methods have been used in this work.

2.2 Implementation

In this section, the differences between the current (sander) and new (pmemd) implementations of alchemical transformations are discussed. This discussion applies to both TI and MBAR post processing methods, as the same simulation can be analyzed with both methods.

2.2.1 Existing Implementation

In the current (Amber 12) implementation, which uses the sander MD engine, a separate topology is created for the initial and final states of the system. Effectively, the code starts two simulations, one for the initial state and another one for the final state. For a simulation that does not use softcore potentials, the potential energy is combined using

$$U(q,\mathrm{\lambda })=(1-\mathrm{\lambda })[U_{i,\mathit{\text{common}}}(q)+U_{i,\mathit{\text{perturbed}}}(q,\mathrm{\lambda })]+\mathrm{\lambda }[U_{f,\mathit{\text{common}}}(q)+U_{f,\mathit{\text{perturbed}}}(q,\mathrm{\lambda })]$$ (4)

which is equivalent to eq. 3. Amber uses a pairwise potential, so the above terms describe the pairwise interactions between atoms.²¹ U_common describes the pairwise interactions between atoms that are the same in the initial and final states. U_i,perturbed and U_f,perturbed describe the interactions between the common and perturbed atoms, as well as the interactions among the perturbed atoms. For a simulation that includes softcore potentials, the above equation is modified so that the softcore atoms become decoupled from the rest of the system, while the bonding terms for the softcore atoms remain intact. The potential used for this case is

$$U(q,\mathrm{\lambda })=(1-\mathrm{\lambda })[\frac{1}{1-\mathrm{\lambda }}{U}_{i,\mathit{\text{bsc}}}(q,\mathrm{\lambda })+U_{i,\mathit{\text{nbsc}}}(q,\mathrm{\lambda })+U_{i,\mathit{\text{perturbed}}}(q,\mathrm{\lambda })+U_{i,\mathit{\text{common}}}(q)]+\mathrm{\lambda }[\frac{1}{\mathrm{\lambda }}{U}_{f,\mathit{\text{bsc}}}(q,\mathrm{\lambda })+U_{f,\mathit{\text{nbsc}}}(q,\mathrm{\lambda })+U_{f,\mathit{\text{perturbed}}}(q,\mathrm{\lambda })+U_{f,\mathit{\text{common}}}(q)]$$ (5)

where U_bsc is the potential for the bonded interactions of the softcore atoms and U_nbsc is the potential for the non-bonded interactions including the softcore atoms.³¹

Note that in eqs. 4 and 5 the U_common term is calculated for both the initial and final states. This calculation is redundant, as U_common will always be the same for both states. In typical alchemical free energy calculations, the number of perturbed atoms is small compared to the total number of atoms in the system. In this case, the number of pairwise interactions between common atoms is much larger than the number of pairwise interactions involving the perturbed atoms or softcore atoms. In other words, the calculation of U_common is expensive compared to the rest of the potential calculations needed for the simulation.

The algorithmic efficiency can be quantified by comparing the speed of the free energy calculation, in terms of the number of nanoseconds that can be simulated in a day, to a regular MD simulation (reference simulation) for either the initial or final state using the same number of cores. In the current sander implementation, the calculation is approximately 50% efficient, as there are effectively two simulations running, one for each end state.

The algorithmic efficiency can be improved by only calculating U_common once for each step rather than twice. This reduces the number of terms in the direct calculation, and also reduces the communication overhead between MPI threads. For each step, the forces that correspond to U_common have to be sent across nodes and combined using eqs. 4 or 5. This can be detrimental to the scalability of the program. Only the forces for perturbed atoms need to be communicated and combined. These changes are the basis for the new implementation of alchemical transformations in pmemd. The idea to remove redundant calculations has been implemented in other MD programs, such as Gromacs.³² However, this is the first time that this optimization has been applied in the Amber suite of programs. We also introduce an additional optimization which may be beneficial for vdW-only free energy calculations.

2.2.2 New Implementation

In the new (pmemd) implementation, only one topology is used, which contains the common atoms and the atoms corresponding to the end states. This “merged” topology removes the redundant parameters involving the common atoms, but still contains all of the parameters for the perturbed atoms. In this work a dual topology was used, however the implementation supports both single and dual topology approaches.³³ Creation of this topology is straightforward, and is discussed in the supporting information. Only a single simulation is run, with all of the terms that differ between the end states stored in separate arrays. At the end of each step, these arrays are combined, giving the same results as the sander version. However, the functional form of the potential energy is different, as only one set of calculations is carried out for the common interactions. For simulations without softcore atoms, the functional form is

$$U(q,\mathrm{\lambda })=U_{\mathit{\text{common}}}(q)+(1-\mathrm{\lambda })U_{i,\mathit{\text{perturbed}}}(q,\mathrm{\lambda })+\mathrm{\lambda }{U}_{f,\mathit{\text{perturbed}}}(q,\mathrm{\lambda })$$ (6)

which is the same as eq. 3. For softcore simulations the potential form is

$$U(q,\mathrm{\lambda })=U_{\mathit{\text{common}}}(q)+U_{i,\mathit{\text{bsc}}}(q,\mathrm{\lambda })+(1-\mathrm{\lambda })[U_{i,\mathit{\text{nbsc}}}(q,\mathrm{\lambda })+U_{i,\mathit{\text{perturbed}}}(q,\mathrm{\lambda })]+U_{f,\mathit{\text{bsc}}}(q,\mathrm{\lambda })+\mathrm{\lambda }[U_{f,\mathit{\text{nbsc}}}(q,\mathrm{\lambda })+U_{f,\mathit{\text{perturbed}}}(q,\mathrm{\lambda })]$$ (7)

where the difference between eq. 5 and eq. 7 is that the U_common term is only calculated once per time step and there is no division by λ. This reformulation of the potential energy is more efficient as explained above, and allows softcore simulations to be run at the end states where λ = 0 or λ = 1. For a softcore simulation run using sander, the values of λ cannot be too close to 0 or 1, because the potential energy calculation becomes unstable for low or high λ values when using eq. 5. This can make it difficult to accurately determine the free energy difference since simulations cannot be run at the end states and so the values at the end points have to be obtained by interpolation. One possible work around is to use a method of numerical integration that does not require sampling at the end states which works in most cases but is not always optimal. The new pmemd implementation, however, completely removes any limitations on running at the end states, by using eq. 7 to calculate the potential energy.

2.3 Simulation Details

All of the simulations follow a similar protocol; any details that are specific to a particular system will be described below. The Amber 12 version of sander, patched up to and including bugfix 11, and the modified version of pmemd were used for these calculations. Protein models used the Amber 99SB-ILDN force field,^34,35 with the TIP3P³⁶ model for water. Neutralizing counter-ions, sodium or chloride, were added to each system as needed. Ligands were parameterized using the generalized Amber force field (GAFF)³⁷ for the bonded and vdW parameters. Partial charges for ligands were obtained using RESP³⁸ fitting for the electrostatic potentials calculated using Gaussian03³⁹ at the Hartree-Fock/6-31G* level of theory. A truncated octahedral periodic box was used with a minimum distance of 15 Å between any box edge and any solute atom. Long range electrostatics were calculated using Particle mesh Ewald (PME),⁴⁰ with a 1 Å grid. Short range vdW interactions were truncated at 8 Å with a continuum model long range correction applied for energy and pressure. Hydrogen bonds were constrained with SHAKE⁴¹ for non-water molecules and SETTLE⁴² for water molecules. This allows for the use of a 2 fs time step.

The same initial coordinates were used for both the pmemd and sander simulations. Initial geometries were minimized using 20,000 steps of steepest descent minimization at λ = 0.5. These minimized geometries were then used for simulations at all λ values. The number of λ values used varied between the simulations, and is discussed below. Each simulation was heated to 300 K over 500 ps using the Langevin thermostat,^43,44 with a collision frequency set to 2 ps⁻¹. The Berendsen barostat⁴⁵ was used to adjust the density over 500 ps at constant pressure, with a target pressure of 1 bar and a 2 ps coupling time. 500 ps of constant volume equilibration was followed by five independent 5 ns long constant volume production simulations. Energies were recorded every 1 ps, and coordinates were saved every 10 ps. Production simulations recalculated the potential energy at each λ value every 1 ps for later analysis with MBAR. Reference simulations were run corresponding to the initial and final states for each system. These were standard MD simulations, so the only difference from the above protocol is that options specific to free energy calculations were disabled. Scaling simulations were run for 100 ps at constant volume, starting from the equilibrated alchemical transformation or reference simulation.

Unless otherwise noted, all simulations were run on 16 cores of the SDSC Gordon Compute Cluster, with dual-socket Intel Xeon E5 8-core 2.6 GHz CPUs in each node and QDR InfiniBand interconnects. The current sander implementation requires the core count (MPI tasks) to be a power of two for efficiency while pmemd does not have this restriction. Thus, for ease of comparison, we restricted both calculations to use 16 cores.

2.4 Model Systems

In this work, three types of free energy calculations were used to test the new implementation: the solvation free energy, the relative free energy of binding (simply referred to below as the relative binding energy), and the free energy change due to the mutation of a protein residue.

2.4.1 Solvation Free Energy

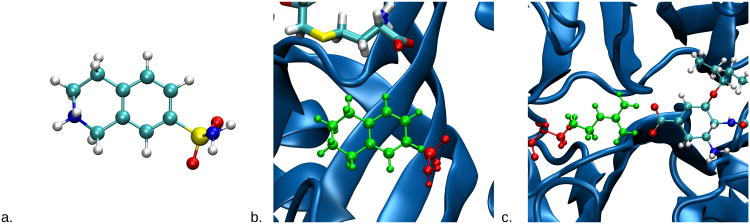
First, we calculated the solvation free energy for an inhibitor of Phenylethanolamine N-methyltransferase (PNMT), which synthesizes epinephrine from norepinephrine.⁴⁹ The initial geometry for the inhibitor, 7-sulfamoyl-1,2,3,4-tetrahydroisoquinolinium, was taken from the crystal structure of human PNMT (PDB 1HNN) chain A.⁴⁹ The structure is shown in Figure 2a. A single chloride ion was added to neutralize the net charge in the system. The atom types and corresponding partial charges are included in the supporting information. The free energy was calculated using

Figure 2.

The model systems used in this study are representative of common free energy transformations. All model systems include explicit solvent, which is not shown for clarity. Part a shows the model for the solvation free energy of the PNMT inhibitor 7-sulfamoyl-1,2,3,4-tetrahydroisoquinolinium. Part b shows the model for the relative binding energy to PNMT (blue) for the same ligand (red) and the related molecule with the sulfamoyl functional group removed (green). The cofactor is shown in licorice and the protein is in the new cartoon representation given by STRIDE.⁴⁶ Part c shows the model for the R371A mutation in the active site of NMD. In green is Arginine 371 and in red is the Alanine mutant. This residue makes a salt bridge with oseltamivir, an inhibitor of NMD. Model images were rendered using the Tachyon module⁴⁷ in visual molecular dynamics (VMD).⁴⁸

$$\mathrm{\Delta }{F}_{\mathit{\text{solvation}}}=F_{\mathit{\text{water}}}-F_{\mathit{\text{gas}}}$$ (8)

where F_water is the free energy of the ligand in water, and F_gas is that of the gas phase ligand. Softcore potentials were used for both vdW and EEL interactions. Nine λ values were used, equally spaced between 0.1 to 0.9. To estimate the error in the resulting free energy caused by omitting the end states, additional simulations were run using the pmemd implementation at λ = 0.0 and λ = 1.0.

2.4.2 Relative Binding Energy

Next, the relative binding energy of two inhibitors of PNMT was calculated. A thermody-namic cycle was used to calculate the free energy. One segment of the cycle is the difference in free energy with the inhibitors bound, and the other segment is with the inhibitors in solution. This is the same cycle that was shown in Figure 1. This system has been studied previously,^50,51 albeit with a different simulation protocol. Initial coordinates for the bound simulation were obtained from the crystal structure of human PNMT (PDB 1HNN).⁴⁹ As in the previous studies,^50,51 the first ligand was 7-sulfamoyl-1,2,3,4-tetrahydroisoquinolinium, the second was 1,2,3,4-tetrahydroisoquinolinium, which is the first ligand with the sulfamoyl moiety removed (Figure 2b). Missing heavy atoms were added using LEaP in AmberTools.²⁰ The cofactor S-adensoyl-L-homocysteine and ligands were parameterized using the protocol described above. The H++ webserver,^52–54 at http://biophysics.cs.vt.edu/H++, was used to determine the protonation states of the Histidine residues.

The free energy was calculated using

$$\begin{array}{c}\mathrm{\Delta }{F}_{\mathit{\text{bound}}}=F_{\mathit{\text{ligand}}2,\mathit{\text{bound}}}-F_{\mathit{\text{ligand}}1,\mathit{\text{bound}}}\\ \mathrm{\Delta }{F}_{\mathit{\text{free}}}=F_{\mathit{\text{ligand}}2,\mathit{\text{free}}}-F_{\mathit{\text{ligand}}1,\mathit{\text{free}}}\end{array}$$ (9)

where “bound” refers to the ligands bound to PNMT and “free” refers to the ligands in water. The bound system had five sodium ions added, and the free system had one chloride ion added to neutralize the net charge. As with the solvation free energy calculation, softcore vdW and EEL potentials were used with the same λ values.

2.4.3 Mutation of a Protein

Finally, the free energy difference between a wild-type and mutant protein was calculated. The protein studied is N1 neuraminidase (NMD), an influenza surface protein, bound to oseltamivir, an anti-influenza drug. NMD has been the subject of structural and theoretical studies.^55–57 Arginine 371, a residue in the active site which interacts directly with the drug oseltamivir, is mutated to Alanine (Figure 2c). This could be used as part of a thermodynamic cycle to determine how this mutation affects drug binding. However, we were only interested in determining the accuracy of our new implementation and so the additional simulations required for a complete thermodynamic cycle were not performed.

The initial coordinates for this system came from the crystal structure (PDB 2HU4) chain A.⁵⁵ All of the Histidine residues were protonated in the ε position. Disulfide bonds were added between Cysteine residues based on the information in the crystal structure. Four neutralizing sodium ions were added to the system.

Unlike the previous simulations, the softcore EEL potential was not used, so the calculation was broken down into three steps. In the first step, the charges on residue 371 were removed. Then, the softcore vdW potential was used to mutate Arginine to Alanine, with no charge on the perturbed atoms. Finally, the charges were restored on the mutated residue. The free energy was calculated using

$$\begin{array}{c}\mathrm{\Delta }{F}_{\mathit{\text{charge}},\mathit{\text{wt}}}=F_{\mathit{\text{wt}},\mathit{\text{no charge}}}-F_{\mathit{\text{wt}},\mathit{\text{charge}}}\\ \mathrm{\Delta }{F}_{\mathit{\text{vdW}}}=F_{\mathit{\text{mut}},\mathit{\text{vdW}}}-F_{\mathit{\text{wt}},\mathit{\text{vdW}}}\\ \mathrm{\Delta }{F}_{\mathit{\text{charge}},\mathit{\text{mut}}}=F_{\mathit{\text{mut}},\mathit{\text{no charge}}}-F_{\mathit{\text{mut}},\mathit{\text{charge}}}\end{array}$$ (10)

where wt denotes the wild-type NMD, and mut denotes the R371A mutant. This multi-step method should give the same results as the single-step method, but there may be cases where it converges more rapidly³⁰ For the charge removal calculations, eleven equally spaced λ values were used, from λ = 0 to λ = 1. For the vdW calculation, the softcore vdW potential was used, with nine equally spaced λ values from λ = 0.1 to λ = 0.9.

2.5 Accuracy and Efficiency Metrics

In order to determine the accuracy and efficiency of our new implementation, we compared the free energies calculated from pmemd simulations to equivalent sander simulations. The deviation between the resulting free energies is

$$|\mathrm{\Delta }\mathrm{\Delta }F|=|<\mathrm{\Delta }{F}_{\mathit{\text{pmemd}}}>-<\mathrm{\Delta }{F}_{\mathit{\text{sander}}}>|$$ (11)

where ΔF_pmemd and ΔF_sander are the free energies calculated from the alchemical transformations simulated using pmemd and sander respectively. The brackets denote an average over independent simulations. The uncertainty in the deviation is

$${\sigma }_{\mathrm{\Delta }\mathrm{\Delta }F}=\sqrt{{\sigma }_{\mathrm{\Delta }{F}_{\mathit{\text{pmemd}}}}^2+{\sigma }_{\mathrm{\Delta }{F}_{\mathit{\text{sander}}}}^2}$$ (12)

where σ_ΔF is the standard deviation of the free energy over independent simulations. We also define ΔF_window as the free energy difference for the alchemical transformation between adjacent λ values. Then eq. 11 is used to calculate |ΔΔF_window|, the deviation between each pair of λ values.

It is well established that a standard MD simulation will run more quickly in pmemd than in sander for the same number of cores.^22,23 The metric used to determine the algorithmic efficiency of the new implementation, as opposed to the raw performance, has to be independent of the absolute speed of the calculation in either program. In this work, the algorithmic efficiency is defined as

$$\text{Algorithmic Efficiency}=\frac{\text{speed of the energy calc.}}{\text{speed of reference calc.}}$$ (13)

where the speed is in ns/day and reference calculations refers to classical MD simulations of the end states for the system being studied. The speed was averaged over all λ values for the free energy calculations and over both end states for the reference simulations. This is the key metric, as it shows which implementation is more efficient, regardless of the absolute speed of the program that it is implemented in. The overall change in performance from both improvements in the algorithmic efficiency and the optimization of the code in pmemd can be quantified with the relative speed (Rel. Speed)

$$\text{Rel. Speed}=\frac{\text{speed of free energy calc. in}\mathit{\text{pmemd}}}{\text{speed of free energy calc. in}\mathit{\text{sander}}}$$ (14)

3 Results and discussion

3.1 Comparison of the Calculated Free Energies

The most important assessment of the implementation is to make sure it is correct. Here we compare the pmemd implementation to the widely used sander implementation since both programs are part of Amber²⁰ and provide equivalent results for standard MD simulations. This makes direct comparison of the results straightforward, as it avoids issues arising from differences in the results due to different algorithms or force field parameters and thus in principal is only limited by convergence of the sampling. As discussed above, most of the free energies were calculated without including the end states due to the limitations in the original sander implementation. For comparison purposes we are thus calculating the free energy difference between two non-physical states λ = 0.1 to λ = 0.9. To estimate the error in the resulting free energy caused by not including the end states, we used the pmemd implementation to run alchemical transformations at the end states for the solvation free energy system. When these end states are included, the free energy decreased by 20 kcal/mol, suggesting that these states are important for correctly calculating the free energy. However, our goal with this work is to compare the sander and pmemd implementations at the λ values that can be used with both implementations.

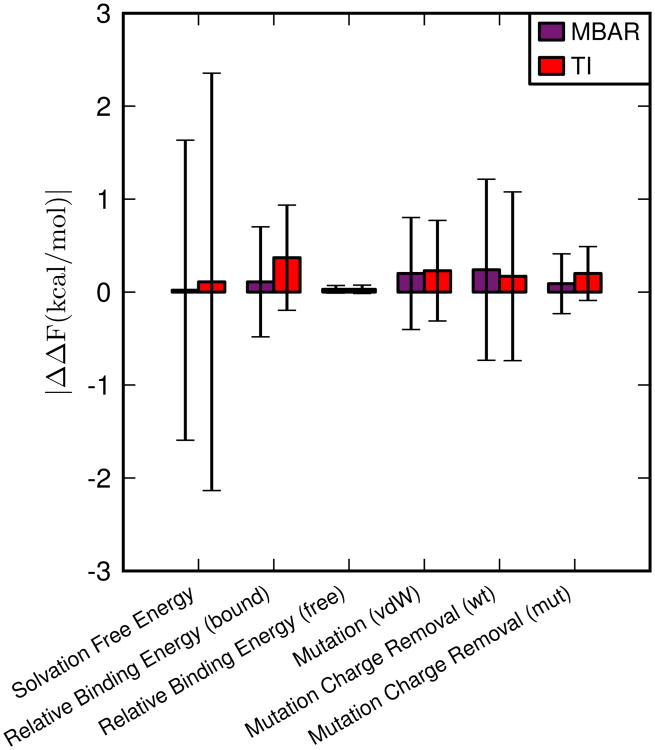
The deviation in the free energies, calculated using eq. 11, is shown in Figure 3. All of the deviations are within 0.5 kcal/mol, with the largest uncertainty calculated for the solvation free energy system. This system is difficult to converge, as it involves complete decoupling of a ligand from the solvent. These results indicate that the implementation of alchemical transformations in pmemd matches the results from the sander implementation.

Figure 3.

The deviation for each model system, defined as the magnitude of the difference between the free energies calculated using pmemd and sander, averaged over five independent simulations (eq. 11). Error bars represent the propagation of the standard deviation of the free energies calculated from independent simulations (eq. 12). The production stage for each window was simulated for 5 ns.

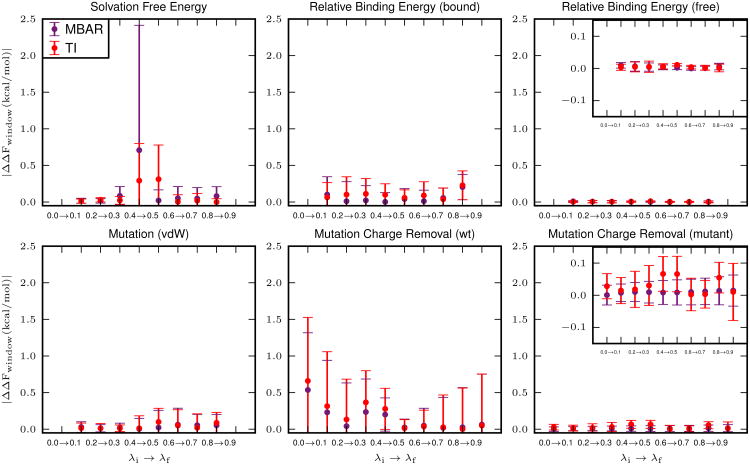
To further examine the deviations in the resulting free energies, |ΔΔF_window|, the deviation for each pair of adjacent λ values, was calculated for each model system as shown in Figure 4. A per window deviation of 0 kcal/mol indicates that the free energy difference between adjacent λ values is the same for the pmemd and sander calculations. All of the differences are under 1 kcal/mol, with the largest deviations found with the solvation free energy and wild type charge removal calculations. These results indicate that the deviations are simply due to small differences in which states were sampled in the pmemd or sander calculations. This issue is inherent to all stochastic simulations, as a simulation with different random velocities will explore different configurations resulting in slightly different free energies.

Figure 4.

The deviation in the free energy, separated into contributions from each pair of adjacent λ values (windows). The free energy for each window describes the free energy change for the non-physical transformation from λ_i to λ_f. Each point represents the deviation in this value calculated from pmemd and sander, averaged over five independent calculations. Error bars represent the propagation of the standard deviation of the free energies calculated from independent simulations (eq. 12). The production stage for each window was simulated for 5 ns.

These model systems are representative of common transformations in free energy calculations. We have shown that the new implementation of alchemical transformations in pmemd reproduces the results from equivalent simulations run with sander. The small deviation in the resulting free energies is due to the stochastic nature of the simulations, where the perturbed atoms explore slightly different regions of phase space in the pmemd and sander simulations.

3.2 Algorithmic Efficiency of the New Implementation

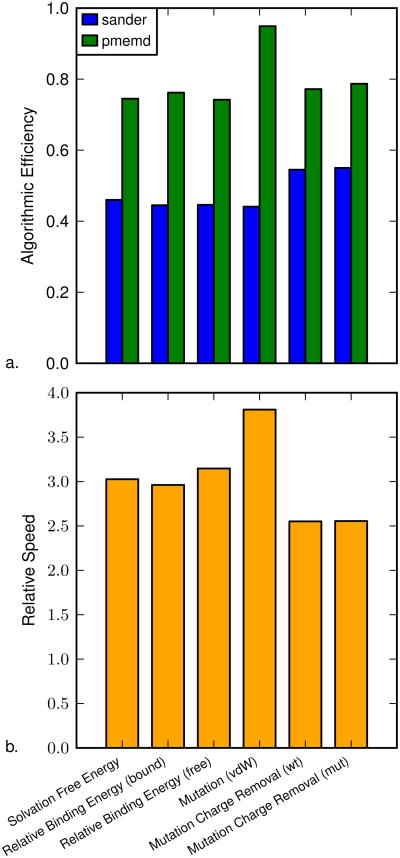
The new implementation of alchemical transformations in pmemd has been shown to produce results equivalent to the original sander implementation. Next, we examined the algorithmic efficiency of the new implementation (Figure 5a). These results show that the original sander implementation is approximately 50% efficient, as expected, while the new pmemd implementation is between 75% and 95% efficient. The range is due to an additional optimization which will be discussed below. This corresponds to a gain in algorithmic efficiency of 1.5 to 2 times over the original implementation.

Figure 5.

Algorithmic efficiency and relative speed for the model systems. Part a shows the algorithmic efficiency of the calculation for the model systems using the original sander and new pmemd implementations. Part b shows the relative speed, which describes how much faster the free energy calculation was using the pmemd implementation.

Much of the algorithmic efficiency gain is due to the removal of the redundant calculation of U_common in eqs. 6 and 7. However, these gains are still limited due to the need to calculate the reciprocal sum for PME⁴⁰ twice, once for each end state. This limitation arises from the non-linearity of the reciprocal sum, so it cannot be decomposed into pairs. In the case of the vdW-only transformation, the mutated residue has had all charges removed, so the value for the reciprocal sum was the same for both end states. In this case, pmemd only calculates the reciprocal sum once, leading to a 20% increase in the algorithmic efficiency of the calculation. This applies to all vdW-only transformations, and will be automatically detected.

Breaking up a free energy calculation into multiple steps may prevent certain convergence issues that can be seen with single-step transformations. However, a multi-step transformation requires three steps, while a single-step transformation requires only one step. The type of transformation to be used will depend on the details of the system under study.³⁰ It may be beneficial to use a multi-step transformation in certain cases, and in these cases, the vdW-only transformation will run more efficiently in pmemd than the other transformations.

The relative speed (Figure 5b) shows that using pmemd over sander reduces the computational cost by a factor of at least 2.5 times regardless of the type of free energy calculation. The additional gain in relative speed seen with the vdW-only transformation is due to the optimization discussed above. The algorithmic efficiency gain depends on the number of atoms that are perturbed between the end states. However, for typical alchemical transformations, only a small number of atoms are perturbed to prevent sampling issues. For these systems, there is a clear benefit in using the new, more efficient, pmemd implementation.

3.3 Scaling of the New Implementation

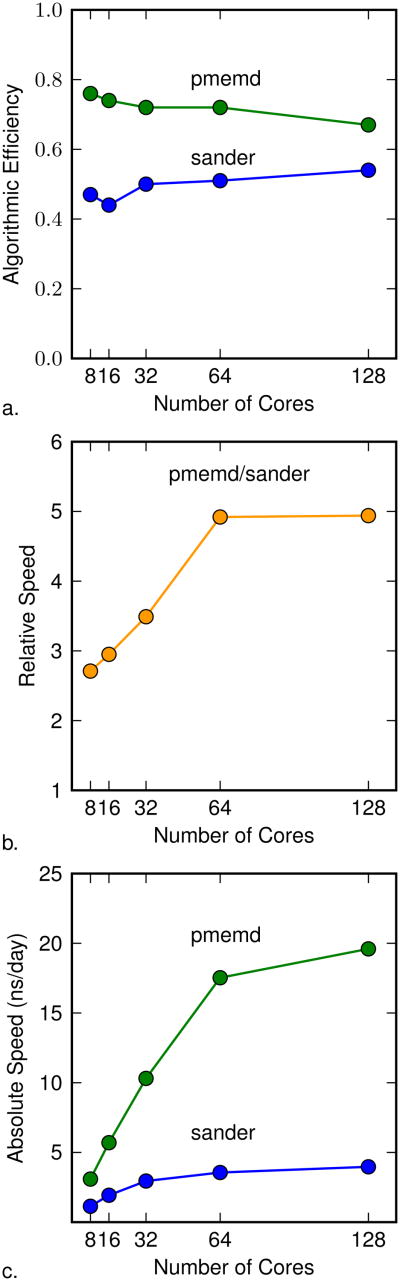
The new implementation in pmemd is more algorithmically efficient, but it is also important to quantify how well it scales to a large number of cores. We addressed this question by looking at the algorithmic efficiency and relative speed for a single λ window run using different numbers of cores. Specifically, we examined the λ = 0.5 window from the bound state relative binding energy calculation.

As shown in Figure 6, the algorithmic efficiency is stable over a large number of core counts, indicating that it is independent of the number of cores. For very large core counts, the speed of the reciprocal sum becomes a limiting factor, causing a small decrease in the algorithmic efficiency for pmemd compared to sander. In the original implementation in sander, the reciprocal sum is calculated for each end state in parallel, using half of the total number of cores. In the new implementation in pmemd, the reciprocal sum is calculated for the end states sequentially, using the total number of cores. This is not as efficient for very large core counts, but is a limitation that arises from the current structure of the parallel code in pmemd. However, the relative speed jumps from three to five times and the absolute speed for pmemd increases more rapidly than sander, indicating that an alchemical transformation simulated using pmemd will use fewer computational resources over a large range of core counts.

Figure 6.

Scaling for the λ = 0.5 point taken from the bound state of the relative binding energy model system. Part a shows the algorithmic efficiency for the original sander and new pmemd implementations as the number of cores is varied. Part b shows the relative speed using pmemd over sander for the same calculation at different core counts. Part c shows the absolute speed of the same calculation in nanoseconds per day at different core counts. Each simulation was run for 100 ps.

These results were determined using the bound state relative binding energy calculation. Similar results would be expected with all of the model systems which include a protein. For the smaller model systems where the ligands were in water, the scaling is not expected to be as efficient due to the small total number of atoms. However, even at low core counts, these systems already run much faster than the larger systems, so additional scaling would not be particularly beneficial for calculating free energies.

4 Conclusions

An efficient method for alchemical transformation calculations has been implemented into the pmemd module of Amber.²⁰ This implementation produces results which are equivalent to those from the original sander program. We show the majority of the improvement in the calculation speed is due to improvements in algorithmic efficiency from the new implementation in pmemd. The new implementation can run softcore calculations at λ = 0 and λ = 1, facilitating direct calculation of free energies without needing to extrapolate the energy at the end states. The interface is very similar to the sander program, and only a few changes are needed in the Amber input files.

The improvements in the algorithmic efficiency and relative speed for alchemical free energy calculations will appeal to many users of Amber. These improvements make more efficient use of computer time, and provide a guide for further improvements in the implementation of free energy calculations. Future work will focus on enabling the use of Graphics Processing Units (GPUs)^24–26 to accelerate alchemical free energy calculations, based on this work in pmemd. Our new implementation will be released publicly as part of the next version of the Amber software.