Impact of Timing of Starting Treatment Following Infection with Application to Initiating HAART in HIV-Positive Patients

Summary

We estimate how the effect of antiretroviral treatment depends on the time from HIV-infection to initiation of treatment, using observational data. A major challenge in making inferences from such observational data is that treatment is not randomly assigned; e.g., if time of initiation depends on disease status, this dependence will induce bias in the estimation of the effect of interest. To overcome this, we develop a new class of Structural Nested Mean Models (SNMMs) to estimate the impact of time of initiation of treatment after infection on an outcome measured a fixed duration after initiation, compared to the effect of not initiating treatment. This leads to a SNMM which models the effect of multiple dosages of treatment on a time-dependent outcome, unlike most existing SNNMs, which focus on the effect of one dosage of treatment on an outcome measured at the end of the study. Our identifying assumption is that there are no unmeasured confounders. We illustrate our methods using the observational AIEDRP (Acute Infection and Early Disease Research Program) Core01 database on HIV. The current standard of care in HIV-infected patients is Highly Active Anti-Retroviral Treatment (HAART). However, the optimal time to start HAART has not yet been identified. The presented new class of SNNMs allows one to estimate how the effect of one year of HAART depends on the time between estimated date of infection and treatment initiation and on patient characteristics. We conclude that HAART substantially affects immune reconstitution in the early and acute phase of HIV-infection.

1. Introduction

The question of when to start therapy in HIV-positive patients is arguably the most pressing issue in HIV research now, and affects the life of millions of HIV-positive individuals. Providing quantitative evidence to inform this debate is challenging, since no clinical trial data are available, and one has to rely on observational data. One statistical challenge in estimating the effect of time of treatment initiation from observational data arises from selection effects/confounding. For example, patients with a steeper decline of CD4+ T-lymphocyte count (a measure of immune function, hereafter referred to as CD4 count) following infection may receive treatment earlier than others, since they have a worse prognosis. Hence, any method must adjust for the confounding factors that impact both (1) time at which treatment is started and (2) the prognosis with respect to the outcome of interest. If these confounders are also predicted by past treatment, as is well-known to be the case for the CD4 count in HIV-positive patients, standard methods, conditioning on the confounders, lead to biased results (Robins et al. (1992), Hernán et al. (2005), Robins et al. (2000), Hernán et al. (2000)). Causal inference methods are necessary.

Structural Nested Mean Models (SNMMs) have already been developed for repeated outcomes, such as those described in Robins (1994) that focus on the effect of one dosage of treatment given data observed immediately before treatment. By contrast, we are interested in the effect of multiple dosages of treatment given in one year. The latter is not simply the sum of the effects of the individual dosages of treatment: these effects are conditional on data observed immediately before the specific dosage, and thus each effect is conditional on a different past. Adding them would require a model for all relevant covariates given past treatment and covariate history, and such a model would likely result in model misspecification and bias (Robins (1986, 1987a,b, 1988, 1989)). SNMMs modeling the effect of multiple dosages at once have been investigated in Lok et al. (2007), but those results are for an outcome measured at the end of the study.

This article proposes methods to investigate how the effect of a fixed duration of treatment, measured after this duration, depends on the time from infection to treatment initiation, using observational data. To be more specific, our effect of interest is the expected difference between the outcome after say X months under the treatment regime “start immediately” versus under the treatment regime “do not treat for X months”, given past observed patient characteristics. To accomodate both time-varying outcomes and the effect of multiple dosages of treatment, we develop a new class of SNMMs. Our assumptions and methods are similar to Robins (1994, 1998), Robins et al. (1992) and Lok et al. (2004, 2007). As for those classical causal inference methods, our identifying assumption is that there is no unmeasured confounding (introduced in e.g. Robins et al. (1992)), and that censoring is not necessarily independent, but only depends on past observed characteristics (Missing At Random, or MAR, introduced in e.g. Robins et al. (1995)). We apply our new class of SNNMs to the AIEDRP data, to estimate the effect of one year of HAART, Highly Active Anti-Retroviral Treatment, in the acute and early stage of HIV-1-infection, and how this effect depends on the time between estimated date of infection and initiation of HAART. Our outcome of interest is the state of the immune system as measured by increase in CD4 count. To date, no clinical trial data exist for this investigation, and one has to rely on observational data.

Although our focus is on the effect of time of initiation of HAART in HIV-positive patients, our methods have broad application to investigations where interest is in the effect of a treatment initiated after a certain duration of some event. The outcome of interest can be any outcome measured after some fixed time following start of treatment.

This article is organized as follows. Section 2 introduces the observational AIEDRP (Acute Infection and Early Disease Research Program) Core01 database, describes what we want to estimate, and why. Section 3 introduces a new class of SNNMs, and describes our estimators as solutions to unbiased estimating equations. Section 4 applies these methods to the AIEDRP data. Section 5 concludes this article with some discussion.

2. Motivating data: impact of timing of starting HAART following infection in HIV-positive patients

Guidelines about when to start HAART in HIV-positive patients have recently undergone several revisions (Hammer et al. (2006, 2008); Thompson et al. (2010); Panel on Antiretroviral Guidelines for Adults and Adolescents (2008 , 2009); ?); WHO Dept. of HIV/AIDS (2010)). Delaying the initiation of HAART has the advantage of postponing the onset of adverse events or drug resistance, but may also lead to irreversible immune system damage. Application of our methods to observational data on treatment initiation will help provide insight into these tradeoffs. Current clinical guidelines regarding HIV-positive patients recommend initiation of HAART when CD4 drops below 350–500; viral load may also play a role in the decision of when to start (Thompson et al. (2010); Panel on Antiretroviral Guidelines for Adults and Adolescents (2011); WHO Dept. of HIV/AIDS (2010)). There is considerable interest in whether treatment at an earlier disease stage may help to preserve immune function (Thompson et al. (2010); Panel on Antiretroviral Guidelines for Adults and Adolescents (2009); WHO Dept. of HIV/AIDS (2010); Phillips and Emery (2009); Wood and Lawn (2009); Kitahata et al. (2009); Sabin and Phillips (2009)). The current interest in using treatment to control epidemic spread heightens interest in these issues, as early treatment can only be ethically justified if it benefits individual patients, regardless of the potential for community-wide benefits (Granich et al. (2009), DeGruttola et al. (2008)). Furthermore, current CDC efforts aim for earlier HIV-diagnoses (Branson et al. (2006)), which, if successful, will increase the need to make such decisions, compared to a setting where most patients are only diagnosed when they have advanced disease.

This paper estimates how the effect of treatment depends on the time from estimated date of infection to treatment initiation. This work will therefore not lead to a recommended CD4 count to start HAART, but rather will provide insight into the response of the immune system on early treatment [[Victor: would you please beef this up? Is it true that this response is unknown and there are no other available data on acute and early infection?]].

We have applied our new class of SNMMs to the observational AIEDRP (Acute Infection and Early Disease Research Program) Core01 database on 1762 HIV-positive patients, diagnosed and followed during acute or early HIV-1-infection. These data arose from a cohort of patients who were followed from soon after the estimated time of infection, and in some cases even from before infection. Our hypothesis is that shorter time from HIV-1-infection to initiation of HAART will be associated with improved immune reconstitution following one year of HAART.

Dates of infection were estimated using a set of rules based on EIA, Western Blot, CD4 cell percentage and viral load (Hecht et al. (2006); Smith et al. (2006)). 1203 patients initiated treatment under follow-up, and 559 did not. Among those who started treatment, 293 and 214 patients did so in the acute and early phases, respectively (defined as < 90 and > 90 days from Estimated Date of Infection), and stayed on treatment for at least one year. In addition, there are 129 patients with at least 3 years of follow-up who did not start treatment within 3 years of infection. Because the large AIEDRP Core01 database has considerable variability in the time of initiating treatment and in characteristics of patients at this time, it is an excellent basis for investigating the impact of timing of treatment on immune reconstitution. There was a broad range of time from infection to treatment initiation (interquartile spread 1.5 to 6 months). The mean time on treatment was about 1.3 years, but about a quarter of the patents were treated for more than 2 years during follow-up. The viral load and CD4 count range at time of treatment initiation was very broad (interquartile spread viral load 17,000 to 400,000 copies and CD4 count 340 to 630 cells/ml). Of note: with CD4 counts between 350 and 500, the recommendations regarding treatment initiation from e.g. Panel on Antiretroviral Guidelines for Adults and Adolescents (2011) are not as firm, and the panel was undecided about patients with a CD4 count above 500. Hence, we are studying the population that is most interesting with respect to the discussion on treatment initiation. As date of start of follow-up visits we took the first visit before or at which both viral load and CD4 count were measured.

The main question we want to answer is how the effect of one year of HAART, measured by increases in CD4 count over a year, depends on the time between the estimated date of infection and treatment initiation. We define this effect more specifically as the expected difference between the outcome after one year under the treatment regime “start HAART immediately” versus under the treatment regime “do not treat this year”, given past observed patient characteristics. This includes a decline in untreated patients and a rise in treated patients, and is similar to an intention-to-treat analysis in a randomized clinical trial, since we have not corrected for treatment stops and interruptions.

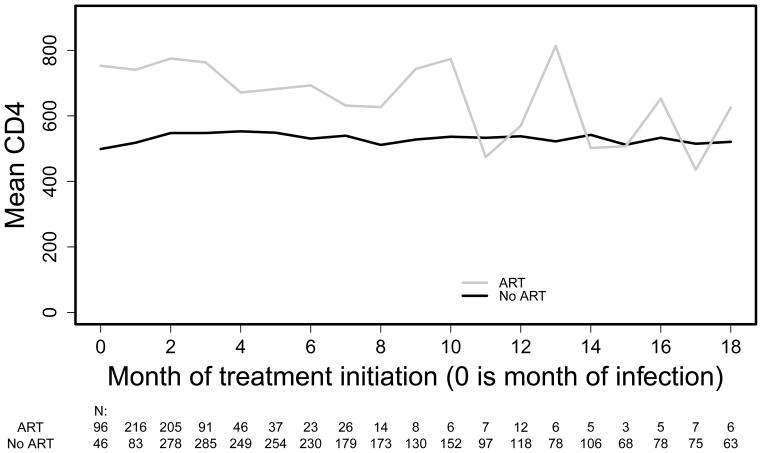
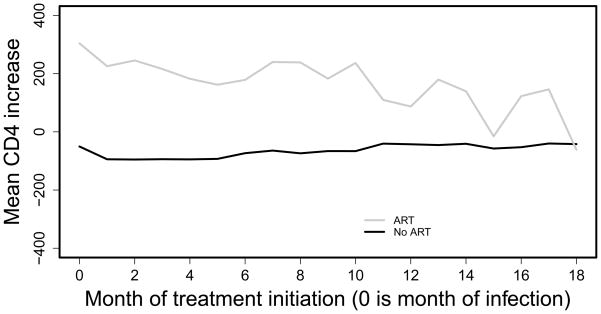
This effect of interest cannot be estimated by simply averaging over patients following these two treatment regimes since, due to the observational nature of the data, there will be confounding by indication: the patients who are treated do not have the same prognosis as the patients who are untreated. This can e.g. be seen in Figures 1 and 2, as follows. Figure 1 displays the unadjusted mean values of CD4 count one year after the start of HAART for patients who start treatment from 0 to 18 months after infection. It also includes the mean CD4 of the comparator group measured at the same times; patients in this group did not start treatment for at least one year after the month of initiation of therapy for the group to which they are compared. We restricted this analysis to patients who had a visit at the month of treatment initiation and 11, 12 or 13 months afterwards. Only those starting treatment within 18 months and their comparators are included in the plot, because the numbers are small for later months. While there are months in which treated patients have even lower mean CD4 increases than those untreated, this very likely results from selection/confounding. This belief is confirmed by a similar naive analysis of increase in CD4 following initiation of HAART, Figure 2: if the treated and untreated had the same initial CD4, the difference between the two lines in Figure 2 should be about the same as in Figure 1. Thus, we need methods to estimate the treatment effect in the presence of confounding by indication.

Figure 1.

mean CD4 count after 1 year, in subjects with visit this month, with and without ART

Figure 2.

mean CD4 count increase after 1 year, in subjects with visit this month, with and without ART

3. Methods

3.1 Setting and notation

Prior to Section 3.5, we assume that all patients are followed monthly, at month 0, 1, …, K + 1, but visits may be missed, also (and especially) in the earliest months of infection. Extension to fixed times τ_k is straightforward. 0, the time origin for analysis, is estimated time of infection. We assume that the outcome, henceforth assumed to be the CD4 count, is measured one year after each of these visits. Y_k is the CD4 count at month k. Ȳ_k is the history of CD4 count until month k. A_k is the treatment at month k. We investigate the effect of a binary treatment A_k, which is either given (coded as A_k = 1) or not (coded as A_k = 0) at each month k. Ā_k is the treatment history until month k. We only consider the impact of starting therapy, and do not consider issues of treatment interruption or compliance; such an analysis is analogous to intent-to-treat in randomized studies. T is the month of treatment initiation, with T = K + 1 if treatment never started. Similarly, L_k are the covariates at month k, and L̄_k is the covariate history until month k. 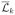is the space in which L̄_k takes its values. We suppose that at each visit month k, treatment decisions A_k are made after L_k is measured and known. Throughout this paper we will suppress the subscript i for patients. $Y_k^{(\infty )}$ is the (counterfactual, not always measured) CD4 count at month k under “no treatment”, and ${\overline{Y}}_k^{(\infty )}$ is the CD4 history under “no treatment” until month k. $L_k^{(\infty )}$ are the covariates at month k under “no treatment”, with history ${\overline{L}}_k^{(\infty )}$. $Y_k^{(m)}$ is the CD4 count at month k under “start treatment at month m”. We assume that observations and counterfactuals on the different patients are independent and identically distributed (Rubin (1978)).

In our application and in clinical practice, Y, A and L will be measured at multiple time points which vary across patients. To get measurements of the outcome for each patient at each month k, we use interpolation, except for visits just prior to onset of treatment, for which we carry the last observation forward. We assume that visits may take place at every month. To account for missed visits, we include the visit pattern as part of the covariates that are measured.

The first subsections assume that full data on all subjects is available; Section 3.5 considers the adaptation of our results to censored outcomes.

3.2 Model

Our model for treatment effect is similar to the model in Lok et al. (2007), but differs in that we consider a different outcome, the CD4 count after one year, for each treatment initiation time:

Definition 3.1

For m ≥ k,

$${\gamma }_m^k({\overline{l}}_m)=E\left[Y_{k+12}^{(m)}-Y_{k+12}^{(\infty )}\mid {\overline{L}}_m^{(\infty )}={\overline{l}}_m,T=m\right].$$ (1)

Note that this is a model for treatment effect, because it compares the outcome under different fixed treatments in the same group of patients. In fact, it is a model for the treatment effect in the treated, since it conditions on the patient starting treatment at month m. This model compares the means, for a patient whose treatment started at month m with covariates l̄_m, of $Y_{k+12}^{(m)}$ and $Y_{k+12}^{(\infty )}$. The former refers to the outcome at month k + 12 had the patient started treatment at month m, and the latter, to the outcome at that month had the patient never started treatment. The model implies that for such a patient, the expected difference between these outcomes is ${\gamma }_m^k({\overline{l}}_m)$. More intuitively, it says that the conditional expectation of the outcome is shifted by ${\gamma }_m^k({\overline{l}}_m)$ if treatment started at month m compared to never starting. Shifts in CD4 greater than 0 imply that treatment is beneficial. Note that for m ≥ k + 12, there is no difference in treatments between $Y_{k+12}^{(m)}$ and $Y_{k+12}^{(\infty )}$; because of Consistency Assumption 3.4 below, ${\gamma }_m^k$ equals zero. Note also that with this definition, the effect on the one-year increase in CD4 since month k is the same as the effect on the CD4 count after one year, because choosing the outcome Y to be CD4 increase since treatment initiation would affect both $Y_{k+12}^{(m)}$ and $Y_{k+12}^{(\infty )}$ the same way. The effect of one year of treatment initiated at month k, given past covariate history l̄_k, in persons initiating treatment at month k, is

$${\gamma }_k^k({\overline{l}}_k).$$ (2)

We will assume a semi-parametric structure. We require:

Assumption 3.2: (Structural Nested Mean Model)

For m = k, …, k + 11, suppose that ${\gamma }_{m,\psi }^k({\overline{l}}_m)$ is a correctly specified model for $E\left[Y_{k+12}^{(m)}-Y_{k+12}^{(\infty )}\mid {\overline{L}}_m^{(\infty )}={\overline{l}}_m,T=m\right]$, with the true parameter equal to ψ₀.

In the following, ψ is always a parameter in ℝ^p.

3.3 The Assumption of No Unmeasured Confounding and the Consistency Assumption

As in Robins et al. (1992), Robins (1994, 1998), Keiding et al. (1999), and Keiding (1999), to distinguish between treatment effect and selection bias, we require the Assumption of No Unmeasured Confounding. This implies that we have information on all factors that both: (1) influence treatment decisions and (2) possibly predict a patient’s prognosis with respect to the outcome of interest. We note that $Y_{k+12}^{(\infty )}$, the outcome at month k + 12 without treatment, is an indication of the patient’s prognosis with respect to the outcome of interest. If there is no unmeasured confounding, treatment decisions at month m (described by A_m) are independent of this unmeasured prognosis $Y_{k+12}^{(\infty )}$, given the observed past treatment and covariate history Ā_m−1 and L̄_m.

Assumption 3.3: (No Unmeasured Confounding - formalization)

$$A_m⫫Y_{k+12}^{(\infty )}\mid {\overline{L}}_m,{\overline{A}}_{m-1}$$ (3)

for m = 0, …, K, where ⫫ means “is independent of” (Dawid (1979)).

Note that the observed outcome Y_k+12 could not play the role of $Y_{k+12}^{(\infty )}$ here, because if treatment affects the outcome, treatment decisions may well affect Y_k+12 (but not $Y_{k+12}^{(\infty )}$).

In order to estimate the effect of treatment, we need the following consistency assumption. Note that if a person is not treated until month k, there is no difference in treatment between Y_k and $Y_k^{(\infty )}$. For this and similar occasions, we assume that then the outcome would have been the same:

Assumption 3.4: (Consistency)

If T ≥ k, $Y_k=Y_k^{(\infty )}$ and ${\overline{L}}_k={\overline{L}}_k^{(\infty )}$. Y ^(T) = Y.

This is a usual consistency assumption for Structural Nested Models.

3.4 Estimation without censoring

The proofs in this section differ from Lok et al. (2007) in that we consider the outcome at different months k+12 since infection, and from Robins (1994) in that we use a different model for treatment effect.

Definition 3.5

On Ā_k−1 = 0̄, for k ≤ K − 11, define

$$H(k)=Y_{k+12}-{\gamma }_T^k({\overline{L}}_T)=Y_{k+12}-{\gamma }_{{\psi }_0,T}^k({\overline{L}}_T).$$ (4)

For the true ψ₀, H_ψ0(k) = H(k). H(k) mimics a counterfactual outcome:

Theorem 3.6: (Mimicking counterfactual outcomes.)

Under Consistency Assumption 3.4, for k ≤ K − 11 and m with k ≤ m ≤ K,

$$E\left[H(k)\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0},A_m\right]=E\left[Y_{k+12}^{(\infty )}\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0},A_m\right].$$

Note that for m ≥ k + 12 this result is trivial, since $H(k)=Y_{k+12}=Y_{k+12}^{(\infty )}$ there. The proof of Theorem 3.6 can be found in the Web-Appendix.

As we will explain now, using Theorem 3.6, models for the treatment process A based on the observed past treatment and covariate history are used as a tool for the estimation of treatment effect, as in, for example, Robins et al. (1992); Robins (1994, 1998); Keiding et al. (1999). Define

$$p(m):=P(A_m=1\mid {\overline{A}}_{m-1}=\overline{0},{\overline{L}}_m),$$ (5)

for m = 0, …, K, the probability of treatment initiation given past observed patient characteristics. p(m) is an unknown that needs to be estimated. Henceforth we assume that p_θ(m) is a correctly specified model for p(m), with θ₀ the true parameter. Specifying a model p_θ(m) for p(m) is potentially easy, since it is a model for the start of treatment in practice, and clinicians may have clear ideas about this process, at least qualitatively. A flexible model that can reflect p(m) is a standard pooled (over patients and visits) logistic regression model: where Ā_m−1 = 0̄ (no treatment before month m) and a visit took place at month m,

$$\text{logit}{p}_{\theta }(m)=\overrightarrow{\theta }·\overrightarrow{f}({\overline{L}}_m),$$

with θ⃗₀ the true (nuisance) parameter vector and f⃗(L̄_m) ∈ ℝ^dimθ a vector depending on L̂_m pre-specified by the data analyst. We assume that treatment can only start at a visit, so that p_θ(m) = 0 unless a visit took place. We estimate the parameters in this model as usual by maximum partial likelihood, resulting in unbiased estimating equations for θ₀.

The idea behind estimation is that under the Assumption of No Unmeasured Confounding 3.3, $Y_{k+12}^{(\infty )}$ does not help to predict treatment initiation given this patient was not treated before month m and given his or her covariate history until month m. H_ψ0(k) has the same conditional expectation as $Y_{k+12}^{(\infty )}$, according to Theorem 3.6. Hence, neither would H_ψ0(k) help to predict treatment initiation given this same history. So, one can add αH_ψ0(k) to the pooled logistic regression model, and look for α̂(ψ) = 0. This approach is intuitively appealing since the “true α” should be zero. This can be done by using standard software using e.g. a grid search; this was conjectured in ?Robins (1998), proved in Lok (2008), and explained in a partial likelihood context in Lok (2007). As we will see later, we will not need this intuition or grid search for estimation, since we will restrict to models γ which are linear in ψ. Therefore, we will only need the following theorem (it turns out that the grid search solves estimating equations like these, as explained in e.g. Lok (2008)):

Theorem 3.7: (Unbiased estimating equations)

Suppose that Consistency Assumption 3.4 and the Assumption of No Unmeasured Confounding 3.3 hold. Consider any ${\overrightarrow{q}}_m^k:{\overline{\mathcal{L}}}_m\to {\mathbb{R}}^p$, k = 0, …, K − 11, m = k, …, k + 11, which are measurable, bounded, and vector-valued. Define Then

$$E\sum _{k=0}^{K-11}\sum _{m=k}^{k+11}{\overrightarrow{q}}_m^k({\overline{L}}_m)H(k)1_{{\overline{A}}_{m-1}=\overline{0}}{1}_{\mathit{visit}}(m)(A_m-p(m))=0,$$

with 1_visit(m) the indicator of whether a visit took place at month m. Thus if p_θ(m) and γ_ψ are correctly specified (parametric) models for p (m) and γ, then

$$P_n\sum _{k=0}^{K-11}\sum _{m=k}^{k+11}{\overrightarrow{q}}_m^k({\overline{L}}_m)H_{\psi }(k)1_{{\overline{A}}_{m-1}=\overline{0}}{1}_{\mathit{visit}}(m)(A_m-p_{\theta }(m))=0,$$

stacked with the estimating equations for θ₀, with P_n the empirical measure $P_{n}X=1/n{\sum }_{i=1}^n{X}_i$, are unbiased estimation equations for both the parameter ψ and the (nuisance) parameter θ. The ${\overrightarrow{q}}_m^k$ here are allowed to depend on ψ and θ, as long as they are measurable and bounded for (θ₀, ψ₀).

The proof of Theorem 3.7 can be found in the Web-Appendix. In general, when estimating ψ of dimension dimψ, one would choose a number of dimψ estimating equations of the form of Theorem 3.7, by specifying q⃗ of dimension dimψ. We will return to specifying q⃗ in Section 4.

We could have included terms with m ≥ k+12. However, for those, there is no power to estimate ψ₀. Where 1_Āk+11=0̄ equals 1, H_ψ(k) = Y_k+12, a function of L̄_k+12, and hence such a term is of the form

$${\overrightarrow{q}}_{m,\psi }^k({\overline{L}}_m)1_{{\overline{A}}_{m-1}=\overline{0}}{1}_{\mathit{visit}}(m)(A_m-p_{\theta }(m)),$$

which has expectation 0 for each ψ and the true θ₀: conditioning on L̄_m, Ā_m−1 fixes all factors except for (A_m − p (m)), which has conditional expectation 0.

3.5 Estimation in the presence of censoring

We need to include censoring by end of follow-up in our framework, since patients can be lost to follow-up in practice. Write C_k = 0 if a patient is uncensored at month k, and C_k = 1 otherwise. We will use Inverse Probability of Censoring Weighting (IPCW) to handle censoring (see e.g. Hernán et al. (2005) or Robins et al. (1995)). Following those authors, we suppose that censoring is Missing At Random (MAR):

Assumption 3.8: (Missing At Random (MAR))

$$(\overline{L},\overline{A})⫫C_{k+1}\mid {\overline{L}}_k,{\overline{A}}_k,{\overline{C}}_k=\overline{0}.$$

Under this assumption, censoring may depend on past observed data. However, it states that censoring is independent of future patient characteristics and future treatments (had they been observable) given past observed data. Like those previous authors, we also need a Positivity Assumption, to assure that data are available for estimation. As usually done with Inverse Probability of Censoring Weighting, we henceforth assume that (Ȳ, Ā, L̄) takes values in a discrete space.

Assumption 3.9: (Positivity)

Suppose that P(C̄_K = 0̄, Ā = ā, L̄ = l̄) > 0 if P(Ā = ā, L̄ = l̄)> 0.

Then we have the following extension of Theorem 3.7:

Theorem 3.10: (Unbiased estimating equations with censoring)

Suppose that the conditions of Theorem 3.7, MAR Assumption 3.8 and Positivity Assumption 3.9 hold. Write

$${EE}_m^k(\psi ,\theta )={\overrightarrow{q}}_m^k({\overline{L}}_m)H_{\psi }(k)1_{{\overline{A}}_{m-1}=\overline{0}}{1}_{\mathit{visit}}(m)(A_m-p_{\theta }(m)).$$

Then

$$P_n\sum _{k=0}^{K-11}\sum _{m=k}^{k+11}{EE}_m^k(\psi ,\theta )1_{{\overline{C}}_{k+12}=\overline{0}}{\left(\prod _{p=k+1}^{k+12}P(C_p=0\mid {\overline{L}}_{p-1},{\overline{A}}_{p-1},{\overline{C}}_{p-1}=\overline{0})\right)}^{-1}=0$$

is an unbiased estimation equation for both the parameter ψ and the (nuisance) parameter θ.

The proof of this Theorem can be found in the Web-Appendix.

3.6 Fitting the models and asymptotics

In the estimating equations of Theorem 3.10, we still have the expression P (A_m = 1|L̄_m, Ā_m−1 = 0̄), which is hard to estimate directly in the presence of censoring. The following Lemma solves that issue:

Lemma 3.11

Under Missing At Random Assumption 3.8,

$$P(A_m=1\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0},{\overline{C}}_m=\overline{0})=P(A_m=1\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0})$$

on {Ā_m−1 = 0̄, C̄_m = 0̄}.

The proof of this Lemma can be found in the Web-Appendix.

Fitting a model γ_ψ can thus be done as follows. If one uses e.g. also a standard pooled logistic regression model for the censoring probabilities, with true parameter η₀, one can fit this model first, resulting in η̂. Then, one can fit a model for the treatment initiation probabilities θ̂ using Lemma 3.11, which allows one to estimate the treatment initiation probabilities using the observed data, using standard software for logistic regression, e.g. SAS PROC LOGISTIC.

To facilitate calculating ψ̂, we have the following corrolary of Theorem 3.10:

Corollary 3.12

If γ is linear in ψ, this approach leads to a linear restriction on ψ once the parameter θ has been estimated. This leads to a closed form expression for ψ̂.

This follows immediately from Theorem 3.10, since if γ is linear in ψ, H_ψ is linear in ψ. This closed form expression for ψ̂ facilitates estimation, since such linear restrictions can be solved using e.g. SAS PROC IML.

If one models both censoring and for treatment initiation with pooled logistic regression models, the resulting estimators η̂ and θ̂ are zeroes of unbiased estimating equations of the form P_nG = 0. With many other models this will be the case as well. Then, the approach outlined above leads to the same estimators as stacking the resulting estimating equations for η₀, θ₀, and ψ₀ from Theorem 3.10, and solving for η̂, θ̂, and ψ̂. This follows since the estimating equations for η and θ do not depend on the other parameters and completely identify η̂ and θ̂. Stacking the estimating equations leads to joint unbiased estimating equations for the joint parameters (θ₀, ψ₀, η₀). Thus, the resulting estimators are just solutions to unbiased estimating equations P_nG = 0. Because of extensive theory about unbiased estimating equations of the form P_nG = 0 (see e.g Van der Vaart (1998)), they are, under regularity conditions, consistent and asymptotically normal. One can use the sandwich estimator of the asymptotic variance, but this would require estimating covariances for the estimating equations of η₀, θ₀ and ψ₀. Instead, we implemented the bootstrap, for all 3 parameters (η, θ, ψ) at the same time.

4. Impact of Time to Start HAART on Immune Reconstitution: the AIEDRP Core 1 Database

In our application, described in Section 2, our main interest is in how the effect of one year of HAART depends on the time between estimated date of infection and initiation of treatment. As outcome, we focus on the CD4 increase one year after starting treatment. We used the AIEDRP data described in Section 2. We assume that all visits are recorded in the database and discuss approaches to relaxing this condition in the discussion. Central to our analysis was the ability to adjust for confounding in the initiation of treatment; we considered as confounders: time-varying measurements of CD4 count, viral load, month of treatment initiation, time since the last visit, and demographic factors (and functions of these).

To adjust for confounding by indication and informative censoring, we have applied the analysis method described in Section 3. Initially we assumed that for m = k, …, k + 11,

$${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}m+{\psi }_3{m}^2)(k+12-m),$$ (6)

with (k + 12 − m) the duration of treatment from month m to month k + 12, is a correctly specified model for treatment effect γ (Definition 3.1). This specification says that the effect of starting treatment at month m, as compared with no treatment, on the outcome measured at month k + 12, depends linearly on the duration of treatment, k+12−m. The coefficient may depend in a quadratic way on the month the of treatment initiation m.

To fit this model, first, we fitted pooled logistic regression models for treatment initiation and censoring as explained in Section 3.6. Then, applying Theorem 3.10, we chose ${\overrightarrow{q}}_m^k=0$ for m ≠ k and

$${\overrightarrow{q}}_k^k({\overline{L}}_k)=(12-E[Tr(k,k+12)\mid {\overline{A}}_k=\overline{0},{\overline{L}}_k]){\left(\begin{array}{ccc}1& k& k^2\end{array}\right)}^{\top },$$

to get 3 estimating equations for ψ after estimation of θ. Here, Tr(k, k + 12) is the number of months of treatment between month k and 12 months later; e.g., if a patient started treatment at month 3, Tr(2, 14) = 11: of all months between 2 and 14, this patient was treated for 11 months. We estimated the conditional expectations in a prior regression step; in fact, we first estimated the relevant conditional probability of Tr(k, k + 12) being non-zero using SAS PROC LOGISTIC and then PROC REG to get the estimated conditional expectation given that Tr(k, k + 12) is non-zero, restricting the dataset to A_k−1 = 0̄ because we only needed those values with this choice of q, see Theorem 3.10. We did the fitting with only A_k = 0 but saved residuals for all patients by using the WEIGHT statement in SAS, weighting only those patients who have A_k = 0. It can be shown that, under stricter conditions and if there is no censoring, this choice of q⃗ is optimal within the class of estimating equations that set ${\overrightarrow{q}}_m^k=0$ where k ≠ m (Lok and Robins (2010); deriving this is beyond the scope of the current article). Note that any choice of q here is valid; this choice was made with a goal of gaining efficiency. Notice that, although we used estimated parameters in our choice of q⃗, the relevant unbiased estimating equations for those parameters can again be thought of as stacked with our original estimating equations as described in Section 3.6, so consistency and asymptotic normality still hold, also if we mis-specify the parameters in the fit of q⃗ (of course, as long as the assumptions described in Section 3 are satisfied). Finally, notice that with this initial model (6),

$$H_{\psi }(k)=Y_{k+12}-({\psi }_1+{\psi }_{2}T+{\psi }_3{T}^2)Tr(k,k+12).$$

We fitted the model by solving the resulting linear estimating equations for ψ̂ in Theorem 3.10 (with θ̂ and η̂ replacing the true parameters), as described in Section 3.6. We used SAS PROC IML.

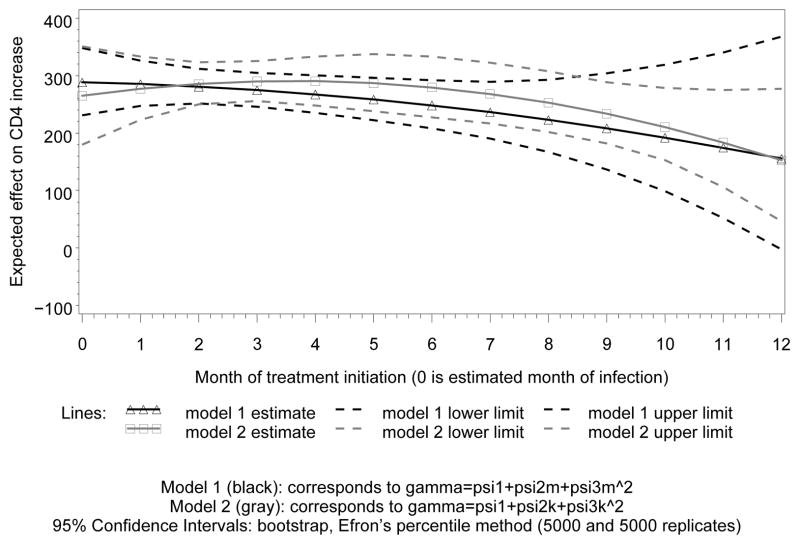
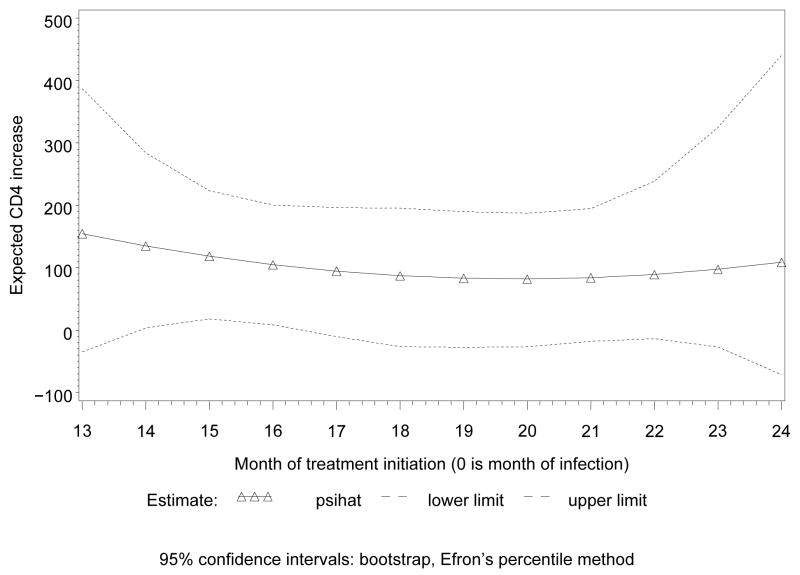
Figure 3 displays the result of fitting this model for the earlier treatment initiation times, in the gray lines. For each displayed month, these are estimates for the difference in CD4 increase over the next year between the treated and untreated groups, after adjustment for confounding. We did separate analyses for the first and the second year from estimated date of infection, Figures 3 and 4, respectively, because we have much more data in the first year; fitting a single model would put most weight on the data from this year, and estimates for the second would largely be extrapolation. As could have been expected, the difference between untreated and treated patients increases after adjustment for confounding. This probably reflects confounding by indication in the naive analysis. The (pointwise) confidence intervals in Figures 3 and 4 were obtained by bootstrap, using Efron’s percentile method (see e.g. Van der Vaart (1998)).

Figure 3.

effects of 1 year of treatment on CD4

Figure 4.

effects of 1 year of treatment on CD4; 3 parameters

The parameter estimates, along with bootstrap confidence intervals, for this initial model are displayed in Table 1. As expected, treatment increases CD4 count. The trend supports benefit of earlier treatment, but the confidence intervals show that the evidence to support this trend is not strong.

Table 1.

estimates, 95%-CIs, and Z-scores (bootstrap, 5000 replicates) of parameters for year 1.

Model: ${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}m)(k+12-m)$
parameter	estimate	95%-CI	Z-score	p-value
ψ1	24.90	(22,28)	14.2	<.0001
ψ2	−0.73	(−1.5,0.1)	−1.7	0.08
Model: ${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}m+{\psi }_3{m}^2)(k+12-m)$
parameter	estimate	95%-CI	Z-score	p-value
ψ1	24.02	(19,29)	9.5	<.0001
ψ2	−0.19	(−2.6,2.1)	−0.2	0.87
ψ3	−0.06	(−0.3,0.2)	−0.5	0.64
Model: ${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}k)(k+12-m)$
parameter	estimate	95%-CI	Z-score	p-value
ψ1	25.35	(21,30)	11.7	<.0001
ψ2	−0.66	(−1.5,0.2)	−1.5	0.12
Model: ${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}k+{\psi }_3{k}^2)(k+12-m)$
parameter	estimate	95%-CI	Z-score	p-value
ψ1	22.08	(15,29)	6.1	<.0001
ψ2	1.18	(−2.1,4.5)	0.7	0.48
ψ3	−0.16	(−0.4,0.1)	−1.2	0.24
Model: ${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}m+{\psi }_3{m}^2+{\psi }_{4}k)(k+12-m)$
parameter	estimate	95%-CI	Z-score	p-value
ψ1	22.60	(15,30)	5.9	<.0001
ψ2	−1.22	(−6.0,3.5)	−0.5	0.61
ψ3	−0.07	(−0.3,0.2)	−0.5	0.59
ψ4	1.16	(−3.4,5.6)	0.5	0.61
Model: ${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}m+{\psi }_3{m}^2)(k+12-m)+{\psi }_4{(k+12-m)}^2$
parameter	estimate	95%-CI	Z-score	p-value
ψ1	12.24	(−55,84)	0.4	0.72
ψ2	−0.19	(−2.6,2.1)	−0.2	0.87
ψ3	−0.06	(−0.3,0.2)	−0.4	0.65
ψ4	0.91	(−4.6,6.0)	0.3	0.73
Model: ${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}m+{\psi }_3{m}^2)(k+12-m)+{\psi }_4{\mathit{lvl}}_m(k+12-m)$
parameter	estimate	95%-CI	Z-score	p-value
ψ1	18.97	(3.5,36)	2.3	0.02
ψ2	−0.10	(−2.5,2.2)	−0.1	0.93
ψ3	−0.06	(−0.3,0.2)	−0.5	0.64
ψ4	5.34	(−11,21)	0.6	0.52
Model: ${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}m+{\psi }_3{m}^2)(k+12-m)+{\psi }_4{\mathit{lvl}}_m$
parameter	estimate	95%-CI	Z-score	p-value
ψ1	13.38	(−21,42)	0.1	0.94
ψ2	0.06	(−2.5,2.5)	0.0	1.00
ψ3	−0.07	(−0.3,0.2)	0.0	1.00
ψ4	13.66	(−22,59)	0.0	0.97

Alternatively, we could assume that again, the treatment effect depends linearly on the duration of treatment, but with a coefficient depending in a quadratic way on the time the outcome is measured, k+12:

$${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}k+{\psi }_3{k}^2)(k+12-m).$$ (7)

For this model, we chose ${\overrightarrow{q}}_m^k=0$ for m ≠ k and

$$\left(\begin{array}{c}12-E\left[Tr(k,k+12)\mid {\overline{A}}_k=\overline{0},{\overline{L}}_k\right]\\ (12k-E[\mathit{TTr}(k,k+12)\mid {\overline{A}}_k=\overline{0},{\overline{L}}_k])\\ (12k^2-E[T^{2}Tr(k,k+12)\mid {\overline{A}}_k=\overline{0},{\overline{L}}_k])\end{array}\right).$$

Using the same techniques as for model (6), this leads to the black lines in Figure 3. We conclude that although these models cannot both be true, they lead to similar conclusions regarding how the effect of one year of treatment depends on month of treatment initiation.

Possibly, the mean effect of treatment also depends non-linearly on the duration of treatment. In that case, one could add terms like ψ₄(k + 12 − m)², or have the non-linear term also depend on month of treatment initiation. The mean effect of treatment may also depend on covariates, like log viral load, resistance mutations, and regimen used. To incorporate these, one can extend the model by including terms like ψ₄lvl_m(k + 12 − m), if the mean effect depends on the log viral load (lvl). We chose some function of (k + 12 − m), the duration of treatment between month m and month k + 12, since the duration of treatment may well predict its effect. If, for example, the treatment effect only depends on the log viral load at treatment initiation for the first month of treatment, one might add terms like ψ₄lvl_m. We fitted some different 4-parameter models, with model (6) as the basic model and adding different fourth-parameter specifications. The dataset was not rich enough to fit more than 4 parameters, as can be seen from the confidence intervals in Table 1.

To fit these 4-parameter models, we proceeded as above. To find a good choice of q⃗, first consider a more elaborate model:

$${\gamma }_{m,\psi }^k({\overline{L}}_m)=({\psi }_1+{\psi }_{2}m+{\psi }_3{m}^2)(k+12-m)+{\psi }_{4}k+{\psi }_5{(k+12-m)}^2+{\psi }_6{\mathit{lvl}}_m(k+12-m)+{\psi }_7{\mathit{lvl}}_m,$$ (8)

for m = k, …, k+11. Similar to the choice of q⃗ for model (6), for model (8) we would use ${\overrightarrow{q}}_m^k=0$ for m ≠ k and

$${\overrightarrow{q}}_k^k({\overline{L}}_m)=\left(\begin{array}{c}12-E[Tr(k,k+12)\mid {\overline{A}}_k=\overline{0},{\overline{L}}_m]\\ 12k-E[\mathit{TTr}(k,k+12)\mid {\overline{A}}_k=\overline{0},{\overline{L}}_k]\\ 12k^2-E[T^{2}Tr(k,k+12)\mid {\overline{A}}_k=\overline{0},{\overline{L}}_k]\\ 12k-kE[Tr(k,k+12)\mid {\overline{A}}_k=\overline{0},{\overline{L}}_k]\\ {12}^2-E[Tr{(k,k+12)}^2\mid {\overline{A}}_k=\overline{0},{\overline{L}}_k]\\ 12{\mathit{lvl}}_k-E[{\mathit{lvl}}_{T}Tr(k,k+12)\mid {\overline{A}}_k=\overline{0},{\overline{L}}_k]\\ {\mathit{lvl}}_k-E[{\mathit{lvl}}_T{A}_{k+11}\mid {\overline{A}}_k=\overline{0},{\overline{L}}_k]\end{array}\right).$$

To get a choice of q⃗ for a 4-parameter model, we selected the corresponding rows of this q⃗. As for the 3-parameter models above, these 4-parameter q⃗ are optimal in the absence of censoring within the class of estimators with ${\overrightarrow{q}}_m^k=0$ for m ≠ k. For model (8),

$$H_{\psi }(k)=Y_{k+12}-({\psi }_1+{\psi }_{2}T+{\psi }_3{T}^2+{\psi }_{4}k+{\psi }_{5}Tr(k,k+12)+{\psi }_6{\mathit{lvl}}_T)Tr(k,k+12)-{\psi }_7{\mathit{lvl}}_T{A}_{k+11}$$

For all 4-parameter models, H_ψ can be found by setting all other parameters in this expression to 0. We did not estimate the effect of CD4 count at time of treatment initiation because increase in CD4 count in the three years after initiating treatment seems to be largely independent of pre-treatment CD4 count (Lok et al. (2010)).

Table 1 displays the estimated parameters with bootstrap confidence intervals also for these 4-parameter models as well as for the 2- and 3-parameter models, for the first 12 months. [[Victor: I was thinking about adding approximate p-values for the parameters by inverting the bootstrap confidence intervals, and then based on that deciding which of these 4-parameter models should be preferred. Do you think that makes sense? One of the referees wanted to know what model should be preferred, and I think that is a reasonable question.]] [[Some words here about the direction of the nonsignificant results: is the treatment effect larger for patients with a larger viral load? I will have to re-do Table 1 given that we prefer model (6) rather than the model we had before, model (7).]]

5. Discussion

This paper extends the Structural Nested Mean Models (SNMMs) from Lok et al. (2007), which describe the effect of multiple dosages of treatment, to an endpoint that varies with time. Robins (1994) did this for the usual SNMM, describing the effect of one dosage of treatment. We have applied this new method to the AIEDRP Core01 database on patients with recent HIV-infection.

We assumed a Structural Nested Mean Model for the way in which treatment affects the outcome of interest. We identified a large class of unbiased estimating equations for the effect of treatment on immune reconstitution after one year of treatment. For our analysis, we chose the optimal estimator within the class with ${\overrightarrow{q}}_m^k$, the free quantity in the estimating equations, equal to 0 for m ≠ k, thus avoiding a lot of mis-specification of nuisance parameters had we chosen the optimal estimator itself. Our choice may not be optimal, but turned out to behave much better than a naive initial choice. Additional estimating equations for models with more parameters can be chosen by stacking the extra estimating equations that are described in Section 4. Note that any choice of ${\overrightarrow{q}}_m^k$ leads to consistent, asymptotically normal estimates; the choice determines just precision. We are continuing to explore properties of other estimators, including doubly robust ones, see e.g. Lok and Robins (2010).

We investigated the effect of having started treatment, regardless of whether it was maintained for a year. It would also be of interest to study the effect of HAART assuming that it is maintained for a year. Enough treatment options are available now to make this a conceivable counterfactual. In order to do the estimation, we could proceed as in the current paper, but censor patients once they go off their initiated treatment. This most likely introduces informative censoring, which can be accommodated as described in Section 3.5. Currently available information is not sufficiently precise to carry out such analysis; additional data must be collected to address this issue.

In order to apply our methods, we have interpolated the outcome variables if data before and after the time of interest were available, so that we could assume that full data are available until the time of censoring. This may lead to bias, and it would be of interest to develop methods that avoid this. In order to predict treatment intitiation, we have carried the last observation forward if data on specific covariates was missing at the time of the visit. This may be reasonable, given that physicians most likely do not have more information on those covariates either, and we included the time since the last visit in the covariates.

To weaken the Assumption of No Unmeasured Confounding, one could consider applying methods from e.g. Robins et al. (1999) or Robins (1998). Also, we assumed that all visits are recorded in the database. If that were not the case one could construct a database with monthly records, carrying predictors of treatment forward and interpolating outcomes, and assume that treatment can be started at every month. p_θ(k) then predicts a visit with treatment initiation (A_k = 1). In addition, while the method we describe is based on interpolation to get outcome measurements for each month k, one could also make use of splines fit to data on CD4 count increase or other outcomes of interest.

We based our analysis on a time scale of months since estimated date of infection. This may not be a real limitation, since in any case, the actual date of infection is generally unknown. Extension of our approach to investigate the treatment effect as a function of the date of infection itself, that is, to incorporate uncertainty in estimated infection times, is an interesting topic for future research. If interval estimates were obtained, one could sample from an assumed distribution with mean and variance taken as the point estimates. For each resample, one could obtain estimates of the effect of treatment on CD4 increase as well as variance estimates for these estimated effects. Using the methods of Little and Rubin (1987), one might obtain point estimates from these resamples as well as interval estimates that take into account the uncertainty in infection time. This may need to be done with special care since there may be additional confounding issues: e.g. CD4 cell percentage was used to estimate the date of infection, and CD4 cell percentage may also be predictive of the treatment effect we are estimating.

The methods in this paper can easily be adapted to any situation where a treatment process gives rise to a counting process N(t), t ∈ [0, τ], e.g. counting the number of treatment changes up to time t. A model for this treatment process can be a tool to estimate the effect of treatment, as p(k) in our paper. If the treatment process is only measured at 0 = τ₀ < τ₁ < … < τ_K = τ, one can assume that N only jumps at 0 = τ₀ < τ₁ < … < τ_K = τ, too. In our application, the counting process N would take the value 0 until treatment starts, and the value 1 once treatment has started.

The model specification for the treatment effect of interest is rather arbitrary. Therefore, we have also included 4-parameter models. In addition, we have included two different 3-parameter models, see Section 4 and Figure 3. Both 3-parameter models lead to similar results regarding the dependence of the treatment effect on initiation time. More experience with model specification in clinical practice needs to be developed, since this is largely unexplored territory. In addition, in future work we plan to develop tests for model misspecification using ideas about overidentification tests, using that we have more potential unbiased estimating equations than parameters.

It would also be of interest to extend the models to include continuous time measurements of Ā and L̄; such inclusion would make timing of visits more flexible. However, preliminary efforts suggest that such an approach requires additional assumptions: aside from some regularity conditions, one may have to assume that there is no jump in outcome after one year of treatment, and that there is no instantaneous treatment effect. Also, one may need to assume a parametric model for treatment initiation, e.g. a time–dependent Weibull proportional hazard model. Properties of our estimators using a Cox proportional hazards model for treatment initiation have not been proven, even in the setting of an outcome measured at the end of the study or a survival outcome. For the latter situation, however, Lok (2001) proved that this model leads to unbiased estimating equations, though not of the form P_nX, and this approach has been applied in e.g. Robins et al. (1992), Keiding et al. (1999), and Keiding (1999).

WEB-APPENDIX Impact of Timing of Starting Treatment Following Infection with Application to Initiating HAART in HIV-Positive Patients

This Web-Appendix has the proofs of the theorems and the lemma.

Proof of Theorem 3.6

We prove this theorem by backward induction, for k fixed, starting with m = K and ending with m = k. Basis: m = K. We distinguish between A_K = 0 and A_K = 1. First, A_K = 0. Under L̄_K, Ā_K−1 = 0̄, A_K = 0, $Y_{k+12}^{(\infty )}=Y_{k+12}$ because this person is never treated and Consistency Assumption 3.4, and H(k) = Y_k+12, too, since T ≥ K +1 so that ${\gamma }_T^k$ is zero. Next, for A_K = 1, Ā_K−1 = 0̄ and A_K = 1 is the same as T = K. Moreover, because of Consistency Assumption 3.4 and the definitions of H(k) and γ,

$$\begin{array}{l}E\left[H(k)\mid {\overline{L}}_K={\overline{l}}_K,T=K\right]=E\left[Y_{k+12}-{\gamma }_K^k({\overline{l}}_K)\mid {\overline{L}}_K={\overline{l}}_K,T=K\right]\\ =E\left[Y_{k+12}^{(K)}-{\gamma }_K^k({\overline{l}}_K)\mid {\overline{L}}_K^{(\infty )}={\overline{l}}_K,T=K\right]\\ =E\left[Y_{k+12}^{(\infty )}\mid {\overline{L}}_K^{(\infty )}={\overline{l}}_K,T=K\right].\end{array}$$

Another application of the Consistency Assumption replaces ${\overline{L}}_K^{(\infty )}$ by L̄_K again, finishing the proof for m = K.

Induction step

we show that if the theorem holds for m + 1, it also holds for m. We distinguish between A_m = 1 and A_m = 0. First, A_m = 0. Because of the induction hypothesis,

$$E\left[H(k)\mid {\overline{L}}_{m+1},{\overline{A}}_m=\overline{0},A_{m+1}\right]=E\left[Y_{k+12}^{(\infty )}\mid {\overline{L}}_{m+1},{\overline{A}}_m=\overline{0},A_{m+1}\right].$$

The result for A_m = 0 follows because E[H(k)|L̄_m = l̄_m, Ā_m−1 = 0̄, A_m = 0] is the expectation of the left hand side of this given L̄_m = l̄_m, Ā_m = 0̄, and similarly for the right hand side.

Next, consider A_m = 1. Note that then, Ā_m−1 = 0̄, A_m is the same as T = m. Hence, because of the definition of H(k) and Consistency Assumption 3.4,

$$\begin{array}{l}E\left[H(k)\mid {\overline{L}}_m={\overline{l}}_m,T=m\right]=E\left[Y_{k+12}-{\gamma }_m^k({\overline{L}}_m)\mid {\overline{L}}_m={\overline{l}}_m,T=m\right]\\ =E\left[Y_{k+12}^{(m)}-{\gamma }_m^k({\overline{L}}_m)\mid {\overline{L}}_m^{(\infty )}={\overline{l}}_m,T=m\right]\\ =E\left[Y_{k+12}^{(\infty )}\mid {\overline{L}}_m^{(\infty )}={\overline{l}}_m,T=m\right],\end{array}$$

where for the last equality we used Definition 3.1 of γ. Another application of the Consistency Assumption finishes the induction step, and hence the proof of the theorem.

Proof of Theorem 3.7

We can leave out the visit-indicator since if there is no visit at month m and treatment did not start before, A_m = p(m) = 0. We show that each term has expectation 0.

$$\begin{array}{l}E\left({\overrightarrow{q}}_m^k({\overline{L}}_m)H(k)1_{{\overline{A}}_{m-1}=\overline{0}}(A_m-p(m))\right)=E\left(E\left[{\overrightarrow{q}}_m^k({\overline{L}}_m)H(k)1_{{\overline{A}}_{m-1}=\overline{0}}(A_m-p(m))\mid {\overline{L}}_m,{\overline{A}}_{m-1},A_m\right]\right)\\ =E\left({\overrightarrow{q}}_m^k({\overline{L}}_m)E[H(k)\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0}]1_{{\overline{A}}_{m-1}=\overline{0}}(A_m-p(m))\right)\\ =E\left({\overrightarrow{q}}_m^k({\overline{L}}_m)E[H(k\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0})]1_{{\overline{A}}_{m-1}=\overline{0}}(A_m-p(m))\right)\\ =E\left(E\left[{\overrightarrow{q}}_m^k({\overline{L}}_m)E[H(k)\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0}]1_{{\overline{A}}_{m-1}=\overline{0}}(A_m-p(m))\mid {\overline{L}}_m,{\overline{A}}_{m-1}\right]\right)\\ =E\left({\overrightarrow{q}}_m^k(L_m)E[H(k)\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0}]1_{{\overline{A}}_{m-1}=\overline{0}}E[A_m-p(m)\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0}]\right)=\overrightarrow{0},\end{array}$$

where for the third equality we use Theorem 3.6 together with the Assumption of No Unmeasured Confounding 3.3, and for the fifth equality we use that the expression includes the factor 1_Ām−1=0̄.

Proof of Theorem 3.10

We show this for the product starting at p = 1 instead of k + 1, which suffices because the extra factors can be incorporated in ${\overrightarrow{q}}_k^m$ when Ā_k−1 = 0̄; the latter is the only value of interest since ${EE}_k^m$ includes 1_Ām−1=0̄. So, first, note that because of Theorem 3.7

$$\begin{array}{l}0=E({EE}_k^m({\psi }_0,{\theta }_0))=E\left({EE}_k^m({\psi }_0,{\theta }_0)\frac{E\left[1_{\{{\overline{C}}_{k+12}=\overline{0}\}}\mid {\overline{L}}_{k+12},{\overline{A}}_{k+12}\right]}{P({\overline{C}}_{k+12}=\overline{0}\mid {\overline{L}}_{k+12},{\overline{A}}_{k+12})}\right)\\ =E\left(E\left[{EE}_k^m({\psi }_0,{\theta }_0)\frac{1_{\{{\overline{C}}_{k+12}=\overline{0}\}}}{P({\overline{C}}_{k+12}=\overline{0}\mid {\overline{L}}_{k+12},{\overline{A}}_{k+12})}\mid {\overline{L}}_{k+12},{\overline{A}}_{k+12}\right]\right)\\ =E\left({EE}_k^m({\psi }_0,{\theta }_0)\frac{1_{\{{\overline{C}}_{k+12}=\overline{0}\}}}{P({\overline{C}}_{k+12}=\overline{0}\mid {\overline{L}}_{k+12},{\overline{A}}_{k+12})}\right),\end{array}$$

where for the second equality we use that because of Positivity Assumption 3.9 we are not dividing by 0, for the third equality we use that ${EE}_k^m({\psi }_0,{\theta }_0)$ and the conditional probability are L̄_k+12, Ā_k+12-measurable, and for in the last equality we use the Law of Iterated Expectations. Next, note that under MAR,

$$\begin{array}{l}P({\overline{C}}_{k+12}=\overline{0}\mid {\overline{L}}_{k+12},{\overline{A}}_{k+12})=\prod _{p=1}^{k+12}P(C_p=0\mid {\overline{L}}_{k+12},{\overline{A}}_{k+12},{\overline{C}}_{p-1}=\overline{0})\\ =\prod _{p=1}^{k+12}P(C_p=0\mid {\overline{L}}_{p-1},{\overline{A}}_{p-1},{\overline{C}}_{p-1}=\overline{0}).\end{array}$$

Proof of Lemma 3.11

On {Ā_m−1 = 0̄, C̄_m = 0̄}, the conditioning events are not null events with probability 1. Hence

$$\begin{array}{l}P(A_m=1\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0},{\overline{C}}_m=\overline{0})=\frac{P(A_m=1,{\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0},{\overline{C}}_m=\overline{0})}{P({\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0},{\overline{C}}_m=\overline{0})}\\ =\frac{P(A_m=1,{\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0}){\prod }_{p=1}^{m}P(C_p=0\mid A_m=1,{\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0},{\overline{C}}_{p-1}=\overline{0})}{P({\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0}){\prod }_{p=1}^{m}P(C_p=0\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0},{\overline{C}}_{p-1}=\overline{0})}\\ =P(A_m=1\mid {\overline{L}}_m,{\overline{A}}_{m-1}=\overline{0})\frac{{\prod }_{p=1}^{k}P(C_p=0\mid {\overline{L}}_{p-1},{\overline{A}}_{p-1}=\overline{0},{\overline{C}}_{p-1}=\overline{0})}{{\prod }_{p=1}^{m}P(C_p=0\mid {\overline{L}}_{p-1},{\overline{A}}_{p-1}=\overline{0},{\overline{C}}_{p-1}=\overline{0})}\end{array}$$

because of Missing At Random Assumption 3.8.