Combining Individual-Based Modeling and Food Microenvironment Descriptions To Predict the Growth of Listeria monocytogenes on Smear Soft Cheese

Abstract

An individual-based modeling (IBM) approach was developed to describe the behavior of a few Listeria monocytogenes cells contaminating smear soft cheese surface. The IBM approach consisted of assessing the stochastic individual behaviors of cells on cheese surfaces and knowing the characteristics of their surrounding microenvironments. We used a microelectrode for pH measurements and micro-osmolality to assess the water activity of cheese microsamples. These measurements revealed a high variability of microscale pH compared to that of macroscale pH. A model describing the increase in pH from approximately 5.0 to more than 7.0 during ripening was developed. The spatial variability of the cheese surface characterized by an increasing pH with radius and higher pH on crests compared to that of hollows on cheese rind was also modeled. The microscale water activity ranged from approximately 0.96 to 0.98 and was stable during ripening. The spatial variability on cheese surfaces was low compared to between-cheese variability. Models describing the microscale variability of cheese characteristics were combined with the IBM approach to simulate the stochastic growth of L. monocytogenes on cheese, and these simulations were compared to bacterial counts obtained from irradiated cheeses artificially contaminated at different ripening stages. The simulated variability of L. monocytogenes counts with the IBM/microenvironmental approach was consistent with the observed one. Contrasting situations corresponding to no growth or highly contaminated foods could be deduced from these models. Moreover, the IBM approach was more effective than the traditional population/macroenvironmental approach to describe the actual bacterial behavior variability.

INTRODUCTION

Since risk analysis emerged as the internationally recognized framework to improve food control systems, many risk assessments were published that evaluated the probabilities and severities of adverse health effects resulting from the exposure of consumers to pathogenic microorganisms present in foods. This is especially the case for the food-borne pathogen bacterium Listeria monocytogenes. Its ubiquitous nature and its ability to multiply in many foods during chilled storage fostered the development of quantitative microbial risk assessment aimed at ranking foods according to risk or predicting the impact of management options (1–6).

The assessment of the microbial behavior of the pathogen is of the highest importance when performing these quantitative assessments, since listeriosis cases are predominantly linked to the consumption of highly contaminated foods (2), and the variability of this behavior is of paramount importance in the context of exposure assessment (7, 8). The major sources of variability affecting microbial responses in foods are the initial contamination level, the variability in processing factors, the variability in food characteristics and in the storage conditions, and the biological variability, i.e., the variability of microbial behavior.

For several years, it has been accepted that the accurate prediction of the behavior of food-borne pathogens contaminating food with a few cells requires a single-cell approach, taking into account the variability of individual cell lag times, since this variability will strongly influence the lag phase duration of the bacterial population (9–13). More recently, studies also emphasized the need to take into account the single-cell growth probability when assessing the behavior of these food-borne bacteria (14–17). These observations were used to implement individual-based probabilistic approaches to assess the bacterial growth in food (18–20).

Published microbial quantitative risk assessment studies take into account the variability of food characteristics by measuring physicochemical properties of foods, e.g., pH and water activity, on relatively large food portions, i.e., 10- or 25-g portions (21, 22). These measurements expressing the between- and within-batch variability of product characteristics are then used to run stochastic models describing the growth of food-borne bacteria (19, 22). To our knowledge, this variability was never described at a microscale level in a risk assessment framework to assess the impact of the microenvironment surrounding individual bacterial cells.

A survey performed by Rudolf and Scherer (23) showed that a higher incidence of L. monocytogenes was observed in European soft and semisoft red smear cheeses made from pasteurized milk (8.0%) than in cheeses manufactured from raw milk (4.8%), illustrating the significance of postprocess contamination and the role of the ripening facilities and the environment of dairy plants. This postprocess contamination leads to a contamination of the surface of cheese with a few cells. Recently published models described the behavior of high inocula of L. monocytogenes in cheeses during ripening according to the location of contaminating cells in the core or on the rind (24, 25). These models are useful to simulate the behavior of large populations of L. monocytogenes in cheese during ripening in dynamic conditions, but the physicochemical characterization of the product at a macroscale level and the high inoculum do not allow the variability of bacterial behavior at the individual cell level to be assessed.

In this study, we investigated the variability of pH and water activity (a_w) on the surface of smear soft cheese at a microscale level to characterize the microenvironment surrounding the bacterial cells. An individual-based modeling (IBM) approach was used to describe the variability of the growth of L. monocytogenes on the cheese surface. This approach was also compared to more traditional macroscale and population approaches to considering variability.

MATERIALS AND METHODS

Overview of the experimental design.

Smear soft cheese (Munster) was obtained from a local manufacturer near Strasbourg in the French geographical area corresponding to the cheese appellation. The cheeses are made with pasteurized milk, weigh 200 g, and have a diameter of 11 cm. Curds are salted 2 days after the beginning of the process and are stored at 16°C and 93% relative humidity for 3 days. The cheeses are then ripened in a maturing cellar at 13.5 ± 0.5°C and 98% relative humidity for approximately 25 days. During ripening, the cheeses are washed two times (at 9 to 10 and 13 to 14 days of age) with a smearing solution spread on the surface using a circular, rotating brush. The surface of the cheese is irregular and displays hollows and crests.

The physicochemical characteristics of cheese surfaces and their temporal and spatial variability were characterized during ripening with three different batches (1 to 3). Models describing the variability of pH and a_w at micro- and macroscale levels were derived from these measurements. The growth of L. monocytogenes in homogeneously blended and irradiated cheese also was studied to adjust predictive microbiology models to smear soft cheese (maximum specific growth rate [μ_opt] and population initial physiological state characteristic [K]). Three kinds of cheese, exhibiting different pH/a_w combinations, were used to estimate these growth parameters.

The environmental and microbiological models were then used to predict the behavior of low or high inocula of L. monocytogenes on the surface of cheeses of different ripening ages. Cheeses coming from batches 2 and 3 and artificially contaminated on the surface with approximately 10 and 1,000 L. monocytogenes cells were used to validate model predictions. Cheese surfaces were previously irradiated to eliminate indigenous microflora and avoid microbiological interactions not taken into account in current models. Since physicochemical characteristics of cheese surfaces were frozen by irradiation and cheeses were in a steady state during the storage, cheeses of different ages were sampled during ripening in batches 2 and 3 to obtain cheeses exhibiting different pH levels for the validation step. Inoculated cheese surfaces were enumerated after storage under laboratory conditions at 15°C, and observed distributions of L. monocytogenes counts were compared to simulated ones with the IBM/microenvironmental and population/macroenvironmental approaches.

Physicochemical characteristics of smear soft cheese.

pH and a_w of cheese surfaces were measured during ripening from 2-day-old curds to ripened cheeses after approximately 30 days of storage. The macro- and microscale pH and a_w were determined for three batches (1 to 3) and on three cheeses at each measurement time. For microscale measurements, different locations of the cheese surface were examined to reveal potential spatial effects.

(i) Macroscale pH of cheese.

The pHs of cheese surfaces were determined with a pH meter (HI pH 213; Hanna Instruments, Tanneries, France) according to the FD V04-035 standard (26). The pH meter was equipped with a combination pH electrode (HI 1131B; Hanna Instruments, Tanneries, France) calibrated with pH 4.01 and 9.18 buffer solutions (Schott Glas, Mainz, Germany). Measurements were performed on analytical portions consisting of 5 g of cheese surface homogenized in 5 ml of deionized water.

(ii) Microscale pH of cheese.

The microscale pH of cheese surfaces was determined with a miniaturized 50-μm-diameter pH electrode (Unisense, Aarhus, Denmark). The microelectrode was manipulated with a micromanipulator (Unisense, Aarhus, Denmark), and the position of the electrode on the cheese surface was watched with binocular glasses. For each 11-cm-diameter cheese surface, the pH was measured at five different radius locations (0.7, 3.6, 4.3, 4.7, and 5 cm). For each radius, five measurements were performed in hollows and five were performed on crests.

(iii) Modeling the pH variability.

The increase of cheese pH with time during ripening was described by the following logistic-type equation:

$$pH\left(t\right)=p{H}_f-\frac{p{H}_f-p{H}_i}{1-\exp \hspace{0.17em}\left(-R\right)+\exp \hspace{0.17em}\left(-R+kpH\cdot t\right)}$$ (1)

where pH(t) is the cheese pH at time t (in days), pH_i and pH_f are the asymptotic initial and final pH, respectively, R is a constant expressing a lag in the pH increase, and kpH is the specific rate of pH increase (day⁻¹).

For the microscale level, the pH of each cheese surface microlocation was assumed to follow the model described in equation 1, and a random between-microlocation variability was assumed. Normal distributions were used to describe the variability of each parameter of the model in equation 1 (i.e., pH_i, pH_f, and kpH). Evolution of the microscale pH for each batch was then modeled with a nonlinear mixed-effect model, and parameter distributions were estimated by computing the maximum likelihood estimators using Monolix software (www.monolix.org; Lixoft). Expectations of the initial pH, mpH_i, and of the rate of pH increase, mkpH, were dependent on the location on the cheese surface, and the following equations were proposed to describe these relationships:

$$mp{H}_i=p{H}_{i0}-0.004\cdot r^2$$ (2)

where pH_i0 is the asymptotic initial pH when the radius on the cheese surface location, r (in cm), is equal to 0, and

$$mkpH=\{\begin{array}{cc}kp{H}_0+0.0018\cdot \exp \hspace{0.17em}\left(r\right)& for\hspace{0.17em}hollows\\ kp{H}_0+0.0012\cdot \exp \hspace{0.17em}\left(r\right)& for\hspace{0.17em}crests\end{array}$$ (3)

where kpH₀ is the approximate specific rate of pH increase when the radius on the cheese surface location, r (in cm), is equal to 0.

(iv) Macroscale water activity of cheese.

The a_w of cheese surfaces was determined with a dew-point analyzer (FA-st/1; GBX Scientific Instruments, Romans sur Isere, France) according to the ISO 21807 standard (27) after calibration with a saturated solution of K₂SO₄. Three samples of 12.6 cm² (4-cm diameter) were obtained per cheese surface, and the results were regarded as replicates of the a_w value for the cheese under consideration.

(v) Microscale water activity of cheese.

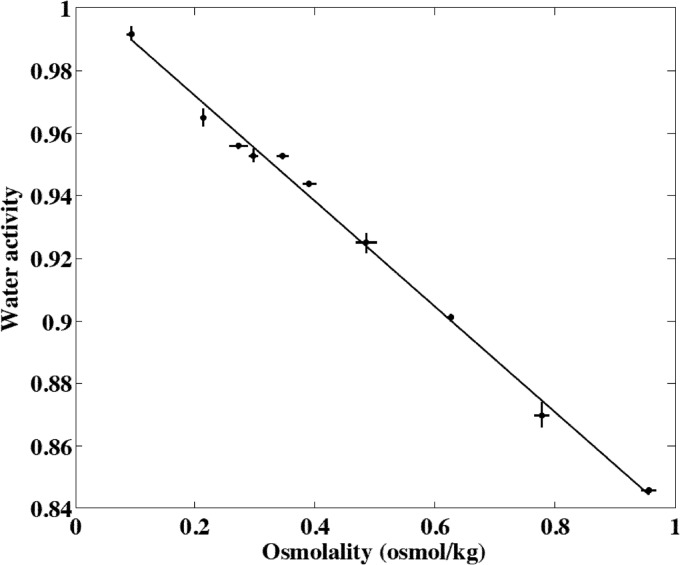
The microscale a_w of cheese surfaces was estimated using a cryoscopic micro-osmometer (Osmomat 030; Gonotec, Berlin, Germany). Cheese extracts were prepared by mixing 100 mg of cheese with 300 μl of deionized water. The mixture was blended, centrifuged (2,000 rpm for 5 min), and then allowed to stand at room temperature for 1 h. The osmolality of the cheese extract solutions was measured in the intermediate phase (28). First, a calibration curve linking the osmolality of cheese extracts to the a_w measured with the dew-point analyzer was established. Ten artificial samples of cheese were made by adding and mixing NaCl or water with natural cheese. These artificial samples exhibited a_w ranging from 0.85 to 0.99 (Fig. 1). For each sample, 10 measures were performed with the cryoscopic micro-osmometer, and four a_w values were obtained with the dew-point analyzer. The relationship between a_w and osmolality, Osm (osmol kg⁻¹), is shown in Fig. 1, and we used linear model II (major axis) regression (29) to estimate the calibration curve:

$$a_w=1.006-0.169\cdot Osm$$ (4)

Fig 1.

Relationship between the osmolality and the water activity of artificial samples of cheese mixed with NaCl or water. Points represent the means from observations, and error bars represent two standard deviations for 10 replicated experiments for osmolality and 4 replicated experiments for water activity.

For each cheese surface, the microscale a_w was measured in the center, at the intermediate radius, and near the edge. For each location, 5 or 10 100-mg samples were analyzed, and each osmolality measurement was performed in duplicate.

(vi) Modeling the water activity variability.

The following random factors were identified to explain the variability of the microscale a_w of the cheese surface: the factors termed “surface” and “location,” with the location factor nested within the surface factor. The factor surface described the between-surface variability of a_w from one cheese surface to another one. The factor location described the within-surface variability of a_w. The random effects of these factors followed normal distributions centered on 0 with standard deviations σ_surface and σ_location, respectively. For the macroscale level, only the factor surface was considered. The parameters were estimated by computing the maximum likelihood estimators using R software (www.R-project.org; R Development Core Team) and the lme4 package (https://r-forge.r-project.org/projects/lme4/2010).

Growth of L. monocytogenes in smear soft cheese. (i) Bacterial strain and culture conditions.

Strain LM14 of L. monocytogenes (serotype 4b; isolated from the environment of a meat industrial plant and a reference strain of the French program in predictive microbiology; Sym'Previus [www.symprevius.org]) was used throughout the study. Stock cultures were kept frozen at −80°C on cryobeads (Technical Service Consultants Ltd., Lancashire, United Kingdom).

Cryobeads were incubated at 37°C for 16 h in brain heart infusion (BHI; Oxoid, Dardilly, France). These first cultures were diluted to obtain an initial bacterial concentration of approximately 10⁴ CFU ml⁻¹, and second cultures were performed for 8 h at 37°C. These second cultures were then diluted as described for the first ones, and the last cultures were performed in BHI at 15°C for 64 h to obtain approximately 10⁸ cells ml⁻¹ in the late log phase. Appropriate dilutions of these cultures were filtered through 9-cm-diameter hydrophobic membranes with a pore size of 0.45 μm (Millipore, Molsheim, France). The membranes were then used to artificially contaminate cheese portions by applying the membranes to cheese surfaces. The initial contamination was controlled by adjusting the bacterial concentration of the filtered suspensions. This technique was preferred to the usual protocol performed with bacterial suspensions to avoid altering the microlocal cheese environment (especially the a_w).

(ii) Growth parameters in irradiated cheese.

Whole cheeses of different ripening durations were blended to obtain homogeneous matrices with various physicochemical characteristics. Three cheeses with the following pH/a_w characteristics were obtained: 5.12/0.964, 5.81/0.962, and 6.56/0.986. The cheeses were irradiated at 15 kGy with an electron accelerator (Vivirad High Voltage; Aérial, Illkirch, France) to eliminate the technological microorganisms avoiding potential bacterial interactions and achieving unchanging matrices during storage. Cheeses were homogeneously contaminated with L. monocytogenes cells filtered on membranes to approximately 10² CFU g⁻¹, and whole cheeses were divided into 10-g samples stored at 15°C for 25 days. The L. monocytogenes population was periodically enumerated by homogenizing 10-g portions in buffered peptone water (BPW; Oxoid, Dardilly, France) with a stomacher blender (AES, Bruz, France). Appropriate 10-fold dilutions were plated onto Oxford agar (Biokar Diagnostics, Beauvais, France). At least 15 measurement points were obtained for each growth curve, and enumerations were performed in triplicate at each measurement time.

Growth parameters were estimated from growth kinetics by fitting the model of Baranyi and Roberts (30) with the nlinfit subroutine of Matlab R2011b software (The Matworks Inc., Natick, MA, USA):

$${\log \hspace{0.17em}}_{10}\left(N\right)={\log \hspace{0.17em}}_{10}\left(N_{\max \hspace{0.17em}}\right)-{\log \hspace{0.17em}}_{10}\left\{1+\frac{{10}^{{\log \hspace{0.17em}}_{10}\left(N_{max}\right)-{\log \hspace{0.17em}}_{10}\left(N_0\right)}-1}{1-\exp \hspace{0.17em}\left(-{\mu }_{max}\cdot lag\right)+\exp \hspace{0.17em}\left[-{\mu }_{max}\cdot \left(lag-t\right)\right]}\right\}$$ (5)

where N is the bacterial concentration (CFU g⁻¹) at time t (h), N_max is the maximum cell concentration (CFU g⁻¹), N₀ is the initial cell concentration (CFU g⁻¹), μ_max is the maximum specific growth rate (h⁻¹), and lag is the lag time (h).

The effect of storage temperature and food characteristics on μ_max and lag is described by a multiplicative function with interactions (31, 32) derived from cardinal and square-root models:

where X_min, X_opt, and X_max are the minimal, optimal, and maximal temperature, pH, and water activity, respectively, for growth. The cardinal values obtained by Augustin et al. (31) for L. monocytogenes were used in this study, i.e., T_min = −1.72°C, T_opt = 37°C, T_max = 45.5°C, pH_min = 4.71, pH_opt = 7.1, pH_max = 9.61, a_w, _min = 0.913, a_{w, opt} = 0.997.

The maximum specific growth rate, μ_max, is calculated according to the following equation:

$${\text{μ}}_{\text{max}}={\text{μ}}_{\text{opt}}\cdot \text{γ}(T,\hspace{0.17em}pH,\hspace{0.17em}{a}_w)$$ (7)

where μ_opt is the maximum specific growth rate when T, pH, and a_w are set to their optimal values. This optimal growth rate is dependent on the food matrix, and estimates obtained were representative of the cheese used in this study. The initial physiological state of the bacterial population used in these experiments was expressed by the product (19, 33) of the following equation:

$$K=\hspace{0.17em}{\mu }_{max}\cdot lag$$ (8)

The growth parameters μ_opt and K were assumed to be representative of validation experiments performed afterwards with artificially contaminated cheese surfaces, and then they were used to perform growth predictions.

(iii) Behavior of L. monocytogenes on irradiated cheese surfaces.

Surfaces of 11 cm in diameter of smear soft cheese were artificially contaminated with L. monocytogenes with cells filtered on membranes to obtain approximately 10 and 1,000 cells per surface. Two batches (2 and 3) were used, and cheeses were sampled during the ripening period after 5, 12, and 19 days of storage for the first batch (2) and after 7 and 12 days of storage for the second batch (3). Cheeses were irradiated at 15 kGy, and 20 cheeses were contaminated with each initial level. Afterward, the cheeses were stored in a laboratory incubator at 15°C for 11 to 21 days depending on the ripening age of cheeses. Cheeses were not washed during this storage to avoid the redistribution of bacterial cells on the surface, and they were wrapped in plastic bags to avoid dehydration. The sterility of cheese was checked after irradiation. Enrichment was performed in tryptone soy broth supplemented with 0.6% yeast extract (TSBye; Oxoid, Dardilly, France) for 7 days at 20°C. TSBye was then plated on tryptone soy agar (TSA; Oxoid, Dardilly, France) to confirm the absence of bacterial or fungal colonies. Moreover, the pH of irradiated cheese control samples was measured during the storage length to check the stability of physicochemical characteristics.

L. monocytogenes populations were enumerated by homogenizing the whole cheese surfaces in BPW and plating adequate dilutions on Compass Listeria agar (Biokar Diagnostics, Beauvais, France). In the absence of a visible colony, i.e., counting below the enumeration threshold (140 CFU surface⁻¹ for batch 2 and 14 CFU surface⁻¹ for batch 3), an examination of L. monocytogenes was performed by adding Fraser supplement (Bio-Rad, Marnes la Coquette, France) to the BPW suspension. An isolation on Compass Listeria agar was performed after 24 h of enrichment at 30°C to confirm the presence of L. monocytogenes.

Growth predictions.

Two modeling approaches were used, and their ability to describe the distributions obtained with artificially contaminated cheese surfaces was compared. The first approach was an individual-based modeling approach of the bacterial behavior combined with the microscale characterization of cheese surface pH and water activity. The second scenario combined a population approach to bacterial growth and a macroscale description of cheese characteristics.

(i) IBM and microscale variability of cheese surface characteristics.

The IBM approach assumed that the behavior of each L. monocytogenes cell contaminating the cheese surface is independent and is characterized by a single-cell growth probability and a single-cell lag time dependent on the cell physiological state, as well as on the cheese characteristics and storage temperature.

The location of each cell was randomly selected on the cheese surface. The probability for a cell to be located at the radius r (measured in cm) was described by a distribution with a cumulative distribution function equal to (r/5.5)², and the probabilities for a cell to be located in hollows or on crests were both equal to 0.5. Knowing the location of cells, the microscale variability of physicochemical characteristics of cheese surfaces then was taken into account. Individual combinations of pH and a_w were generated for each cell, and the single-cell growth probabilities were calculated just as the single-cell lag times and growth rates for growing cells were (equations 6 and 7). Finally, these growth parameters were used in the growth model (equation 5) to predict the growth yield of each cell.

The following equations were used to describe the impact of growth conditions on the single-cell growth probability, p, of L. monocytogenes (14):

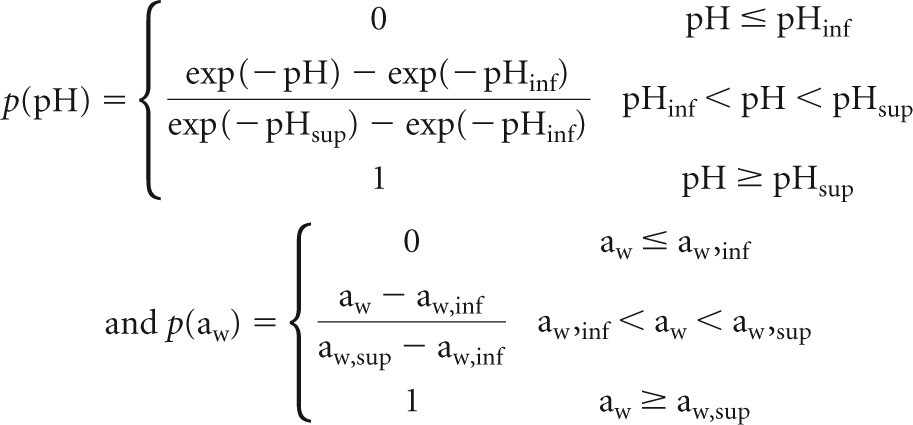
where c = 7.6, T_inf = −3.6°C, T_sup = 17.3°C, pH_inf = 4.34, pH_sup = 5.93, a_{w, inf} = 0.917, and a_{w, sup} = 0.988.

Individual cell lag times, lag_i, were derived from the individual physiological state, k, following an extreme value type II with parameters a and b (33):

$$a=E[k]-\frac{1.1642}{0.3658}\cdot S[k]\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}b=\frac{s[k]}{0.3658}$$ (10)

with S[k] = e^{1.004 · ln(E[k]) − 0.447} and ln(E[k]) = 0.0103 · ln(K)⁵ + 0.0065 · ln(K)⁴ − 0.039 · ln(K)³ + 0.0586 · ln(K)² + 1.1941 · ln(K) + 0.1549, where E[k] and S[k] are the expected value and the standard deviation of k, respectively. K is the population initial physiological state characteristic (equation 8).

(ii) Population behavior and macroscale variability of cheese surface characteristics.

In the population approach to bacterial growth, no variability is assumed between bacterial cells. The behavior of the bacterial population is described with the model described in equation 5.

Every cell located on the same cheese surface was assumed to face the same physicochemical characteristics. In this macroscale approach, random pH and a_w values were generated for each cheese surface. Growth parameters for L. monocytogenes cells located on these surfaces were calculated with equations 6 and 7, and the growth parameters were used with equation 5 to predict the bacterial growth.

(iii) Comparison of growth predictions to observed behavior of L. monocytogenes on irradiated cheese surface.

Monte Carlo simulations were performed with the Matlab R2012b software to predict the growth of L. monocytogenes on cheese surfaces.

The initial contamination of cheese surfaces was assumed to be log-normally distributed with an expected value equal to the log mean of three initial counts and a standard deviation of 0.2 log₁₀ CFU surface⁻¹. This standard deviation was estimated from preliminary experiments.

The micro- and macroscale variability of physicochemical characteristics was described with distributions estimated for the two batches used in this validation study (2 and 3).

In order to obtain stable predictions, 10,000 simulation runs were performed for each condition, and output-simulated distributions of L. monocytogenes concentrations on cheese surfaces were compared to distributions obtained from the 20 counts obtained on artificially contaminated surfaces after storage at 15°C.

(iv) Application of the models to the prediction of the growth of L. monocytogenes during the ripening of smear soft cheese.

Monte Carlo simulations were performed to predict the growth of L. monocytogenes on the cheese surface during ripening in dynamic pH conditions, unlike the static conditions used in the validation experiments, and at 13.5°C to simulate conditions encountered by L. monocytogenes cells during regular industrial ripening. The IBM and population approaches, coupled with the micro- and macroscale descriptions of the variability of cheese characteristics, were compared.

The simulations (10,000 runs) were performed by arbitrarily setting the initial contamination of the cheese surface to 10 cells and using the mean between-batch microscale pH characteristics (see Table 2), i.e., 4.78 and 4.70 for pH_i0 for hollows and crests, respectively; 7.46 for pH_fm; and 0.346 and 0.448 day⁻¹ for kpH₀ for hollows and crests, respectively. For macroscale pH (Table 2), the mean pH_i was 4.80, the mean pH_f was 6.79, and the mean kpH was equal to 0.421 day⁻¹.

Table 2.

Fitted parameters of the normal distributions describing the water activity variability of smear soft cheese surface

Scale and parameter	Estimate
Microscale
Expectation	0.969
σsurface	0.0041
σlocation	0.0025
Residual error	0.0009
Macroscale
Expectation	0.969
σsurface	0.0047
Residual error	0.0020

The differential form of the Baranyi and Roberts (30) model, coupled with the previously presented secondary model (equation 6), was used to estimate the growth of L. monocytogenes in dynamic pH conditions after 10, 15, and 20 days of ripening at 13.5°C:

$$\{\frac{dN}{dt}=(\frac{1}{1+\exp \hspace{0.17em}(-Q)})\cdot {\mu }_{\max \hspace{0.17em}}\cdot [1-\exp \hspace{0.17em}(N-N_{\max \hspace{0.17em}})]$$ (11)

$$\frac{dQ}{dt}={\mu }_{\max \hspace{0.17em}}$$

These equations were solved numerically by the Runge-Kutta method with the ode23 function of Matlab R2012b software.

RESULTS

Variability of smear soft cheese surface pH in space and time.

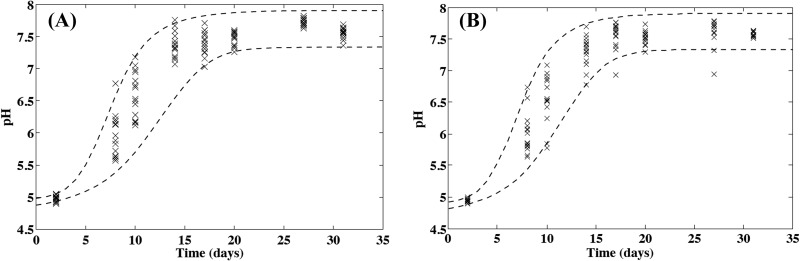
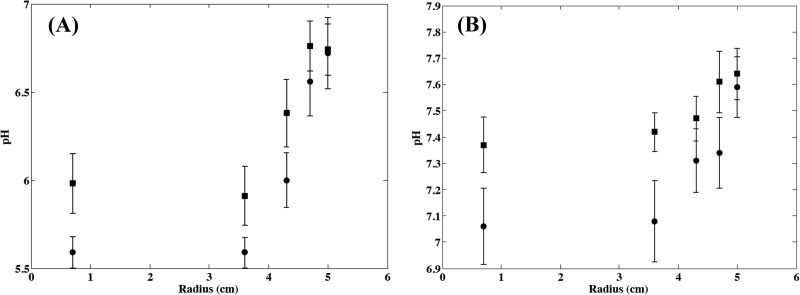
The increase in surface pH during cheese ripening is shown in Fig. 2. The pH increased from an initial value of approximately 5 for 2-day-old cheeses to values close to neutrality after approximately 10 days of ripening (15-day-old cheeses) at 13.5 ± 0.5°C. For microscale measurements, this increase in pH was also dependent on the microlocation on the cheese surface. A faster increase was observed with increasing radius (Fig. 3), and higher pH values were observed on crests than in hollows (Fig. 3). The model described in equation 1 was fitted to observed data by setting R to an average value of 4.1, as this constant did not seem affected by the location on the cheese surface and by the batch under consideration. The normal distributions describing the variability of microscale pH were then estimated, and parameters of equations describing the effect of the location on the expected values for the initial pH and the specific rate of pH increase (equations 2 and 3) are presented in Table 1. The standard deviations of the distributions describing the variability of pH_i0, pH_f, and kpH₀ were not affected by the location on the cheese surface or by the batch. Differences were noticed between pH evolution for the different studied batches, illustrating differences in the ripening control of this kind of cheese in natural conditions (Table 1). The variability simulated by using these models satisfactorily described the observed microscale pH variability according to the ripening stage and the location on the cheese surface (Fig. 2).

Fig 2.

Evolution of the microscale pH of smear soft cheese surface during ripening at 13.5°C on crests at a radius of 0.7 cm (A) and in hollows at a radius of 4.3 cm (B). Crosses are observed values (n = 15 for each date), and dashed lines show the 2.5th and 97.5th percentiles of the modeled variability region.

Fig 3.

Microscale pH observed at different radii in hollows (•) and on crests (▪) of smear soft cheese surface at 8 days (A) and 14 days (B) of aging. Points and error bars represent the means and standard deviations from observations for 15 replicated experiments.

Table 1.

Fitted parameters of the normal distributions describing the pH variability of smear soft cheese surfaces

Scale, parameter, and batch no.	Value for:
	pHi0		pHf (hollows/crests)	kpH0 (day−1)
	Hollows	Crests		Hollows	Crests
Microscale
Expectation
1	4.95	4.93	7.62	0.342	0.443
2	4.65	4.50	7.13	0.330	0.448
3	4.74	4.68	7.62	0.365	0.453
Standard deviation	0.027	0.027	0.143	0.0613	0.0613
Macroscale
Expectation
1	4.82		6.80	0.368
2	4.79		6.57	0.445
3	4.79		7.00	0.451

For macroscale pH, as only small between-cheese differences were observed, this variability was neglected and only the between-batch variability was taken into account (Table 1).

Variability of smear soft cheese surface water activity in space and time.

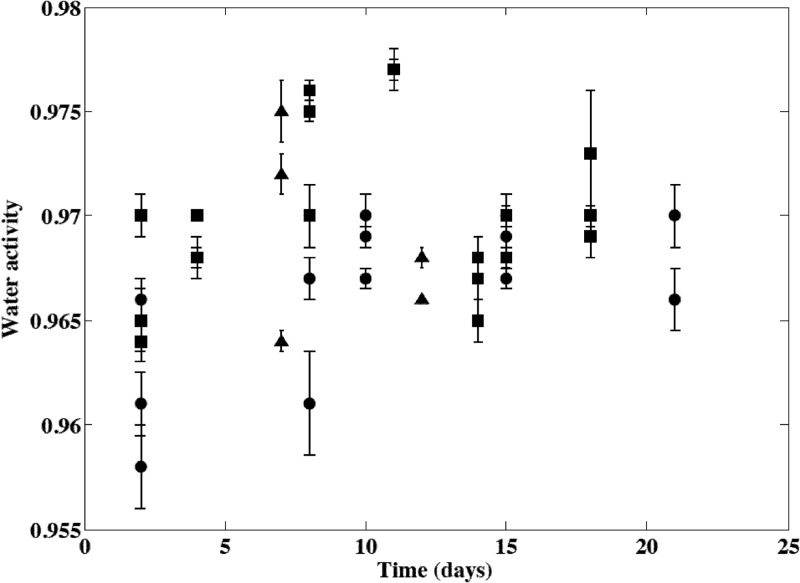
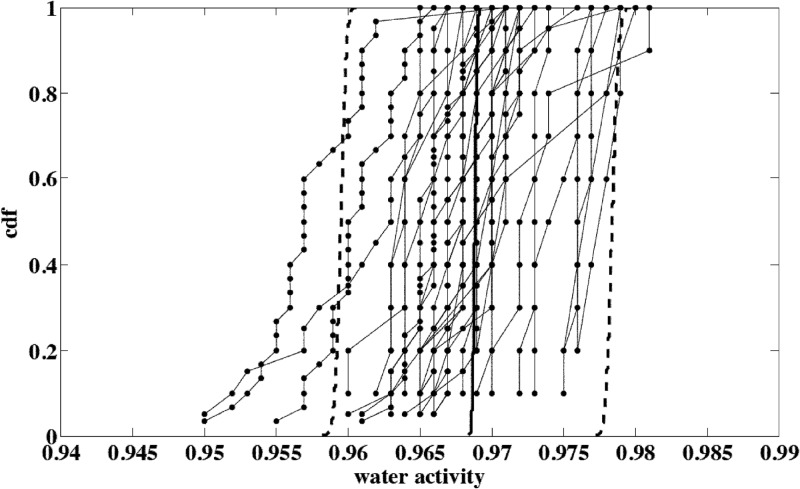
Neither deterministic evolution of the cheese a_w with time during ripening nor batch effect was observed, but great differences were observed according to the cheese surface under consideration (Fig. 4). Cheese washings performed during ripening after 9 to 10 and 13 to 14 days of storage did not have a noticeable impact on the cheese surface water activity. This potential effect was probably transcended by the between-cheese variability (Fig. 4). Estimated parameters of the distributions describing this variability for macro- or microscale levels are presented in Table 2. The variability simulated by using this model satisfactorily described the observed microscale a_w variability according to the cheese surface and the location on the cheese surface (Fig. 5).

Fig 4.

Evolution of the microscale water activity of smear soft cheese surfaces during ripening at 13.5°C. Values obtained for the three batches are represented by different symbols, and points and error bars represent the means and standard deviations from 15 or 30 observations obtained on the same cheese surfaces. Cheese washings were performed at days 9 or 10 and 13 or 14.

Fig 5.

Microscale water activity (a_w) variability observed for smear soft cheese surfaces according to the surface and the location. Joined points represent cumulative distribution functions (cdf) of values observed for one cheese surface and describe the within-surface location variability (σ_location). The dispersion of joined-point distributions illustrates the between-cheese or between-surface variability (σ_surface). The solid line is the median cdf of a_w for one surface, and the dashed lines show the 2.5th and 97.5th percentiles of the modeled between-surface variability region.

Growth of L. monocytogenes in irradiated smear soft cheese.

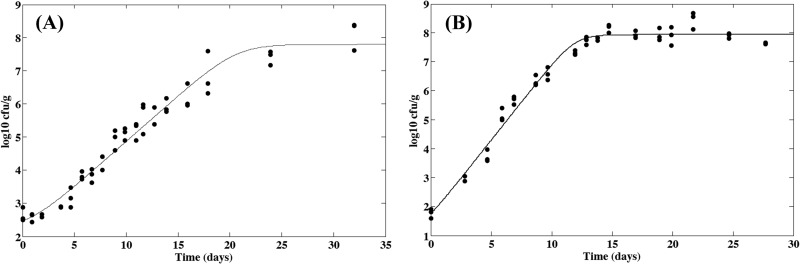
Figure 6 presents the L. monocytogenes growth curves obtained at 15°C in the cheese with pH/a_w characteristics of 5.81/0.962 and 6.56/0.986. Since no growth was observed in the cheese at pH 5.12 and a_w of 0.964, only the growth parameters obtained for the two other conditions were used to estimate μ_opt and K in Munster cheese. The growth model (equation 5) was fitted to these data, and the following values were obtained in the 5.81/0.962 and 6.56/0.986 cheeses, respectively: 31 and 4 h for lag and 0.026 and 0.050 h⁻¹ for μ_max. The deduced optimal growth rate (μ_opt) values (equation 7) were 0.23 and 0.22 h⁻¹, and the mean value of 0.23 h⁻¹ was retained for this matrix. The parameter K (equation 8) was equal to 0.8 and 0.2, respectively. Although the higher observed K value of 0.8 could have resulted from an abrupt shift in pH or a_w experienced by the bacterial cells (34) for the combination 5.81/0.962, this effect was neglected in the modeling approach. The parameter K was assumed to reflect the initial physiological state of the bacterial population and was assumed to be constant for the same preculturing conditions. The mean value of 0.5 was then used for future simulations. By using these estimates and the secondary growth models described in equation 6, values of 0.008 h⁻¹ and 2.6 days could be predicted for μ_max and lag, respectively, in cheese with 5.12/0.964 characteristics and stored at 15°C. Although growth was predicted, these growth parameters expressed a very slow bacterial multiplication, which was in agreement with the absence of observed growth for this cheese.

Fig 6.

Observed growth of L. monocytogenes in irradiated smear soft cheese at 15°C with pH 5.81 and a_w of 0.962 (A) or pH 6.56 and a_w of 0.986 (B). The solid line represents the fitted growth model.

Comparison of IBM combined with microscale approach and population growth combined with macroscale approach to describe the L. monocytogenes growth variability on irradiated smear soft cheese surfaces.

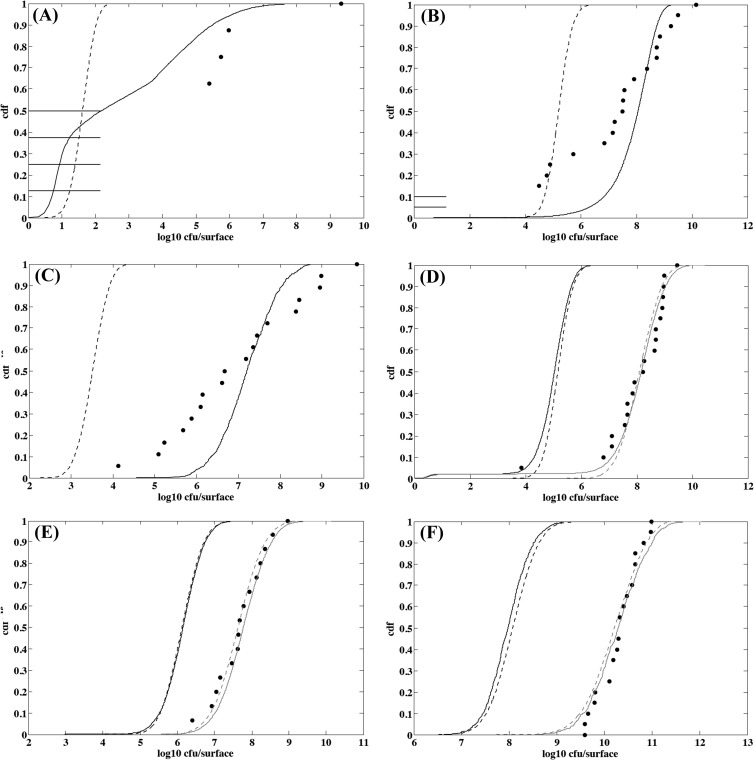
Observed and simulated distributions of L. monocytogenes concentrations on cheese surfaces are presented in Fig. 7. The IBM/microscale approach appeared more relevant than the population/macroscale approach to describe the observed variability of the counts of cheese surfaces. The difference between the two approaches was more pronounced when the initial number of cells was low and the intrinsic cheese characteristics were less favorable to growth (Fig. 7A and B). Under these conditions, the IBM approach was the only one that was able to predict no growth for L. monocytogenes on several cheese surfaces and a large variability in counts (Table 3). When conditions became more favorable to growth with increased pH, the difference between the two approaches was small (Fig. 7D, E, and F). For a high initial contamination and unfavorable growth conditions, the population/macroscale approach underestimated the actual growth yield (Fig. 7C) and variability (Table 3).

Fig 7.

Observed and simulated distributions of L. monocytogenes counts on irradiated smear soft cheese surface. (A) Five-day-old cheese from batch 2 contaminated with 8 cells and stored for 21 days at 15°C; (B) 7-day-old cheese from batch 3 contaminated with 21 cells and stored for 19 days at 15°C; (C) 5-day-old cheese from batch 2 contaminated with 630 cells and stored for 21 days at 15°C; (D) 12-day-old cheese from batch 3 contaminated with 7 cells and stored for 11 days at 15°C; (E) 19-day-old cheese from batch 2 contaminated with 24 cells and stored for 12 days at 15°C; and (F) 12-day-old cheese from batch 3 contaminated with 5,730 cells and stored for 11 days at 15°C. Points are observed counts, the solid line represents the distribution simulated with the IBM/microscale approach, and the dashed line represents the distribution simulated with the population/macroscale approach. Gray lines display distributions simulated by adjusting μ_opt to values ranging from 0.30 to 0.34 h⁻¹ instead of 0.23 h⁻¹.

Table 3.

Observed and simulated distributions of L. monocytogenes counts on soft smear cheese surfaces stored at 15°C

Batch no. and cheese age (days)	Mean initial contamination (CFU surface−1)	Storage duration (days)	Approacha	No-growth probability	Contaminationb (log10 CFU surface−1)
					Mean	SD
Batch 2
5	8	21	OBS	0.50	3.7	3.29
			IBM	0.29	2.8	1.93
			POP	0.003	1.6	0.32
5	630	21	OBS	0	7.0	1.54
			IBM	0	7.2	0.65
			POP	0	3.5	0.32
12	9	13	OBS	0	8.8	0.71
			IBM	0.01	5.9 (8.5)	0.79 (1.15)
			POP	0	5.6 (7.9)	0.45 (0.62)
12	1,040	13	OBS	0	10.5	0.38
			IBM	0	8.1 (10.5)	0.46 (0.46)
			POP	0	7.6 (9.8)	0.45 (0.47)
19	24	12	OBS	0	7.7	0.67
			IBM	0	6.1 (7.8)	0.49 (0.59)
			POP	0	6.1 (7.6)	0.46 (0.57)
19	700	12	OBS	0	9.5	0.68
			IBM	0	7.6 (9.3)	0.47 (0.54)
			POP	0	7.6 (9.1)	0.46 (0.56)
Batch 3
7	21	19	OBS	0.10	6.9	2.58
			IBM	0	7.9	0.83
			POP	0	5.2	0.41
7	4,510	19	OBS	0	9.6	1.08
			IBM	0	10.5	0.49
			POP	0	7.5	0.40
12	7	11	OBS	0	8.0	1.23
			IBM	0.02	4.9 (8.0)	0.79 (1.30)
			POP	0	5.2 (8.1)	0.43 (0.64)
12	5,730	11	OBS	0	10.3	0.41
			IBM	0	8.0 (10.3)	0.42 (0.55)
			POP	0	8.1 (10.2)	0.43 (0.54)

^aOBS are observed data, IBM are data simulated with the IBM/microscale approach, and POP are data simulated with the population/macroscale approach.

^bValues in parentheses were obtained by adjusting μ_opt to values ranging from 0.30 to 0.34 h⁻¹ instead of 0.23 h⁻¹.

Table 3 summarizes the characteristics of simulated and observed distributions. It must be specified here that for older cheeses (12 and 19 days of age), the optimal growth rate had to be increased from 0.23 h⁻¹ to values ranging from 0.30 to 0.34 h⁻¹ to predict mean bacterial increases in accordance with observed ones. In spite of a better description of observed data, the IBM/microscale approach still had a tendency to underestimate the actual variability for unfavorable growth conditions (Table 3).

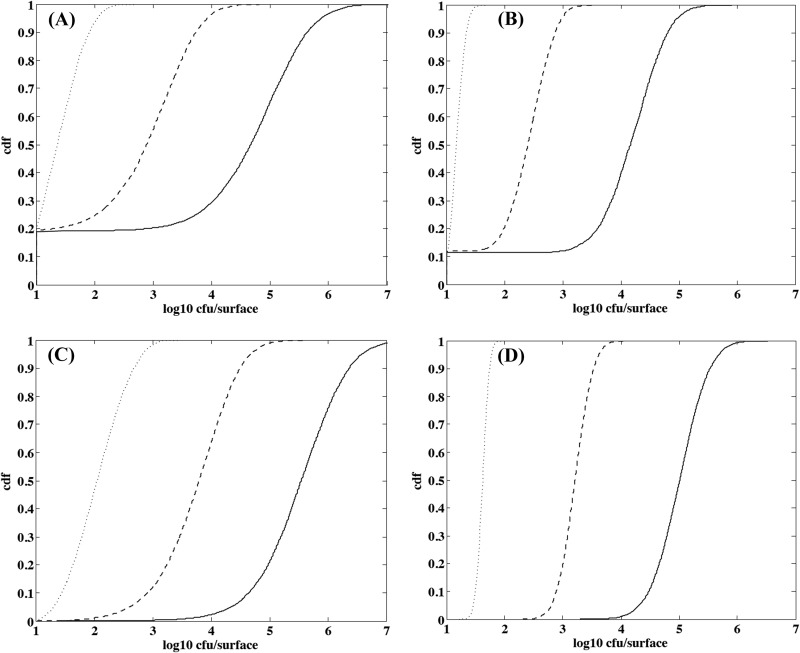
Figure 8 presents results obtained when simulating the growth of L. monocytogenes on cheese surfaces during ripening under dynamic pH conditions at 13.5°C to mimic the ripening of a batch of cheese in natural conditions. Nevertheless, the probable effect of washing steps on the bacterial dispersion was not taken into account in the simulation, because no information on the redistribution of bacterial cells on the cheese surface was available. The results are highly dependent on the approach under consideration regarding the bacterial behavior, i.e., IBM or population, and the scale used to describe the variability of physicochemical characteristics, i.e., micro- or macroscale. Only the IBM approach was able to predict no growth in a noticeable number of cases. With the microscale approach, the no-growth probability was approximately 0.2 (Fig. 8A), and it was a little more than 0.1 with the macroscale approach (Fig. 8B). With the IBM approach, bimodal distributions were observed when ripening increased, reflecting cheese surfaces where no growth occurred and cheeses where bacterial cells found favorable growth conditions. When growth occurred, the variability of contamination was larger with the microscale approach (Fig. 8A and C) than with the macroscale one (Fig. 8B and D), and the range of the contamination was approximately 1 log₁₀ larger at the microscale level than the macroscale.

Fig 8.

Simulated distributions of L. monocytogenes counts on smear soft cheese ripened at 13.5°C according to the IBM and microscale approaches to physicochemical variability (A), IBM and macroscale approaches to physicochemical variability (B), population bacterial growth and microscale approaches to physicochemical variability (C), and population bacterial growth and macroscale approaches to physicochemical variability (D). The dotted line represents the contamination after 10 days of ripening, the dashed line represents the contamination after 15 days of ripening, and the solid line represents the contamination after 20 days of ripening.

DISCUSSION

Physicochemical characteristics of smear soft cheese.

The increase in surface pH during cheese ripening is a typical phenomenon (35) linked to the activity of acid-tolerant yeasts, e.g., Debaryomyces hansenii, Geotrichum candidum, and Kluyveromyces species, metabolizing lactate at the beginning of the ripening process (36–38). This activity leads to the deacidification of the cheese surface, allowing the development of less acid-tolerant, aerobic or facultative anaerobic, halo-tolerant Gram-positive bacteria, e.g., Brevibacterium species, Staphylococcus species, Arthrobacter species, and Corynebacterium species. For instance, Irlinger et al. (39) observed an increase in surface pH of Livarot, another kind of smear soft cheese, from 5.2 to 5.4 up to 7.2 to 7.7 after 25 days of ripening.

The spatial variability of cheese pH was studied in Camembert cheese, the best known soft cheese (40, 41). Liu and Puri (41) investigated the pH distribution from the rind to the core, and for different radial distances, with a glass electrode. They also observed an increase in pH at the surface of Camembert cheese with increasing radius, denoting, as in our study, a more intense deacidification activity near the edge of the cheese compared to that at the center. The higher pH values obtained on crests than hollows in our study show a higher activity of yeasts on crests and outline the large variability of physicochemical characteristics at the microscale level. The relevance of investigating the heterogeneity of product characteristics with microelectrodes was already emphasized by Abraham et al. (40) with the study of pH and redox potential gradients of Camembert cheese. The observed pH gradient from the rind to the core (40, 41) could explain the difference between ultimate pH measured at the macro- and microscale levels in our study (Table 2) and a macroscale final pH lower than the microscale one. This can be related to the thickness of analytical portions used for the macroscale characterization, where curd below the cheese surface exhibiting a lower pH was inevitably sampled when preparing the test portions.

The measured water activity was relatively high, in the range of 0.95 to 0.98, and was consistent with the macroscale value of 0.97 observed in curds of similar smear soft cheese (19). Unlike Schvartzman et al. (25), who observed a continuous decrease of the a_w in the rind of smear semisoft cheese from 0.99 to values ranging from 0.75 to 0.80 during a 28-day ripening period, we did not observe any trend in the water activity on the cheese surface during ripening. This discrepancy is possibly related to the absence of washing during ripening for cheeses studied by Schvartzman et al. (25) and the difference in relative humidity of the atmosphere of the maturing cellars, i.e., 90 versus 98% in our study. The relative humidity plays an important role in the evolution of cheese ripening by influencing both the cheese weight loss and the water activity on the surface (42). Since no effect of the washing steps on the water activity was detected in our study, we can assume that the moisture equilibrium was quickly restored. We observed differences only between cheese surfaces, possibly reflecting the heterogeneity of ripening conditions according to the situation of cheeses in the manufacturer's maturing cellar. No spatial effect was observed for surface microscale a_w. Only a relatively small random variability was observed according to the location on the cheese surface. This variability is probably underestimated to accurately describe the environment surrounding bacterial cells, since relatively large 100-mg portions were used for the measurements. This can lead to an underestimation of the variability of bacterial behavior; however, to our knowledge, this is the first time that the microscale variability of this environmental factor is characterized in a food matrix, making the predicted bacterial behavior more reliable.

Growth of L. monocytogenes on irradiated smear soft cheese.

The observed optimal growth rate of L. monocytogenes in smear soft cheese, 0.23 h⁻¹ on average, is consistent with previously published values for this kind of matrix. A similar mean optimal value of 0.212 h⁻¹ was deduced from several studies of different cheeses (31), and Schvartzman et al. (25) reported optimal average growth rates of 0.18 and 0.16 h⁻¹ in the core and the rind of smear semisoft cheese, respectively.

Although the parameter K increased from 0.2 to 0.8 when the pH/a_w characteristics of cheese changed from 6.56/0.986 to 5.81/0.962, suggesting an effect of shifts in pH and a_w on this physiological parameter, we neglected this potential effect and used the mean value 0.5. The simulations could be refined by modeling the effect of the shifts in pH and a_w when L. monocytogenes cells are inoculated on the cheese surfaces (43). However, this simplification seemed acceptable, since simulated count distributions were close to the observed ones even for young cheeses with the lowest pH (Fig. 7A, B, and C).

The secondary model used in our study considered the effect of major environmental factors, i.e., temperature, pH, and a_w, and assumed that the other environmental factors were constant during cheese ripening. This is especially the case for the lactate concentration, of which the effect is implicitly encompassed in the optimal growth rate. Since the lactic acid concentration decreases during the ripening process, the optimal growth rate of L. monocytogenes is probably lower in early-stage curd, with high concentrations of lactate, than in ripened cheese, where lactate is metabolized. This phenomenon could explain why the optimal growth rate had to be increased to values of 0.30 to 0.34 h⁻¹ to appropriately describe the L. monocytogenes growth yield on the surface of older cheeses (12 and 19 days of age). The description of the microscale variability of lactate concentration in cheese and the insertion of this factor in the secondary model could increase the efficiency of the modeling exercise. However, whatever the μ_opt value used, the IBM approach always produced more variable count distributions than the population approach (Table 3).

Thus, the IBM approach, combined with the microlocal description of cheese characteristics, was more relevant than the population/macroscale approach to describe the observed variability of the growth of L. monocytogenes on the cheese surface. In particular, the IBM approach was the only one leading to a prediction of no growth when the number of cells contaminating the cheese surface was low. Recently, Koutsoumanis and Lianou (16) reported a highly heterogeneous behavior of individual cells of Salmonella enterica serovar Typhimurium and emphasized the importance of this single-cell variability to assess the behavior of microbial populations resulting from the contamination of foods with a low number of pathogenic cells (<100 cells). We also observed that the IBM/microscale approach was still not fully satisfactory to accurately describe the observed growth variability. The underestimation of the actual variability could be explained by the heterogeneous distribution of environmental factors not included in the modeling approach. We can assume, for instance, that the lactate concentration and the redox potential (40) are heterogeneously distributed on the cheese surface, leading to an additional variability of bacterial behavior. Other factors related to the colonial growth of L. monocytogenes on a solid matrix, such as oxygen availability, nutrient diffusion, and metabolite accumulation, could affect the growth of the pathogen and the behavior variability. Although the insertion of the lactate concentration into the model could improve the model performance, the conclusions regarding the IBM and population approaches would remain unchanged. The underestimation of the bacterial growth variability also may be due simply to an underestimation of the variability of pH and a_w of the microenvironment surrounding bacterial cells.

The underestimation of the growth yield observed with the population approach in unfavorable growth conditions (Fig. 7C) is probably related to a low macroscale pH, while at the microscale level the relatively high pH for some locations leads to an extensive growth of bacterial cells facing these conditions. For instance, the macroscale pH of 5-day-old cheeses coming from batch 2 was 5.0, whereas the microscale pH median was equal to 4.9 (pH values ranged from 4.7 to 5.6 [95% confidence interval]). To illustrate the impact of pH variability, we can predict that the log₁₀ increase in bacterial population after 21 days at 15°C and pH 5 is approximately 0.8, but this log₁₀ increase rises to 5.3 when the pH is equal to 5.6. This observation highlights the importance of performing challenge tests in homogeneous food to accurately estimate the growth rate of bacterial populations. Indeed, if challenge tests are performed in heterogeneous foods with high inocula, there will be a substantial probability of finding cells surrounded by a particularly favorable microenvironment leading to extensive growth. Under these conditions, the estimated growth rate will not be representative of the average macroscopic food characteristics.

Modeling approaches.

Since we observed large differences between IBM/microscale and population/macroscale approaches for low inocula and unfavorable environmental growth conditions but small differences when conditions became more favorable to growth, we investigated the consequences to simplify the complex IBM/microscale approach by shifting to population and/or macroscale approaches in the case of an initial contamination of the cheese surface with a few cells at the beginning of the ripening period.

IBM attempts to model a population or a community by describing the actions and properties of the individuals composing the population. In contrast to the population approach, IBM allows individual variability and regards organisms, i.e., bacterial cells, as the fundamental entities. This is an increasingly established approach to describe ecological communities in general (44), and its use is also becoming more widespread in microbiology (45–47). The drawback of this approach is the difficulty, on one hand, of studying the single-cell behavior, which requires specific devices (10, 16), and the characterization of the microenvironment surrounding bacterial cells, which requires micromethods (40), and, on the other hand, of computing complex models to simulate the behavior of bacterial populations issued from the individual cells. The preferred modeling approach should be translated into effective tools for real-world applications. Therefore, increasing complexity due to the IBM/microscale approach should be justified by a significant improvement in the assessment of the evolution of small populations on heterogeneous food matrices.

Contrary to predictions performed with cheese surfaces contaminated at different ripening ages (Fig. 7), the population approach led to higher counts than the IBM approach when simulating the growth of small initial populations of L. monocytogenes during cheese ripening (Fig. 8C and D). The mean contamination was approximately 1 log₁₀ higher with the population approach than with the IBM approach after 15 days of ripening at 13.5°C, and growth was systematically predicted with the population approach. The lower mean contamination obtained with the IBM approach in this case is caused by very unfavorable pH conditions at the beginning of the ripening process, corresponding to a single-cell growth probability of a little less than 0.2. The macroscale description of physicochemical characteristics led to lower counts for L. monocytogenes during cheese ripening compared to those for the microscale description (Fig. 8B and D). The contamination was less variable and was approximately 0.5 log₁₀ lower than the contamination observed with the microscale variability. Finally, the simplest usual approach, consisting of combining population behavior and macroscale physicochemical variability (Fig. 8D), led to a mean contamination of 0.8 log₁₀ above the mean concentration obtained with the IBM/microscale one (Fig. 8A). On the other hand, the variability of the contamination was greatly reduced, with 95% of the contamination ranging from 4.2 to 5.8 log₁₀ CFU surface⁻¹ against 1.0 (no growth) to 6.1 log₁₀ CFU surface⁻¹ for the IBM/microscale approach after 20 days of ripening. These results show that with this food model, the individual risk linked to highly contaminated cheeses would be underestimated by the classic population/macroscale approach, and that this approach overestimates contamination of cheese where no growth will occur.

The proposed modeling framework, combining IBM and description of the food microenvironment, seems highly suitable for this kind of heterogeneous product to accurately assess the behavior of bacteria that can contaminate foods with only a few cells and to predict high-risk situations, as well as no-growth or poor-growth situations corresponding asymptotically to bimodal distributions of the bacterial contamination for a given batch. At the batch level, this IBM approach improves the usual exposure assessment, considering only macroscale variability of foods (19). Future works could explore the relevance of this approach for other kind of foods and also when considering more or less large between-batch variability. In the next step, this stochastic approach could be improved by characterizing other microenvironmental factors, and especially the biotic environment, to include interactions with microorganisms present on the cheese surface (48, 49), which were deliberately excluded from this study.