How old is my gene?

Abstract

Gene functions, interactions, disease associations, and ecological distributions are all correlated with gene age. However, it is challenging to estimate the intricate series of evolutionary events leading to a modern day gene and then reduce this history to a single age estimate. Focusing on eukaryotic gene families, we introduce a framework in which to compare current strategies for quantifying gene age, discuss key differences between these methods, and highlight several common problems. We argue that genes with complex evolutionary histories do not have a single well-defined age. As a result, care must be taken to articulate the goals and assumptions of any analysis that uses gene age estimates. Recent algorithmic advances offer the promise of gene age estimates that are fast, accurate, and consistent across gene families. This will enable a shift to integrated genome-wide analyses of all events in gene evolutionary histories in the near future.

What is gene age?

The functions of a new gene are forged by the adaptive challenges facing the organism at the time the gene arose. For example, genes that encode functions associated with basic cellular processes, like transcription, are often as old as life itself, whereas many genes associated with cellular adhesion and communication arose at the dawn of multicellularity. Recent advances in computational biology and genome sequencing have made it possible to explore the connection between gene age and function across the tree of life. The resulting analyses are revolutionizing our understanding of embryonic development, molecular interactions, disease, and the interplay of environment and evolution on geological time scales.

Strictly speaking, however, a gene does not have a single age. Unlike fossils or specific evolutionary events, genes are dynamic entities with continuous histories that trace back to the origin of all life. So, how should “gene age” be defined? Many previous studies have simply used the most recent common ancestor (MRCA) of the species containing genes with similar sequences (e.g., with a significant BLAST score). While this relatively simple approach has produced compelling results, many genes have complex evolutionary histories that are not accurately summarized by the MRCA. Ideally, this entire history would be used in gene age analysis. In practice, gene age is frequently equated with the timing of a salient event, such as a gene duplication, horizontal transfer, or de novo creation of a gene [1]. However, many methodological and philosophical challenges arise when selecting the most appropriate event and estimating its age. To motivate our discussion of these problems, we first review a few striking findings that highlight the broad range of questions that can be addressed using gene age estimates.

A gene's evolutionary history is informative about its function

Gene age has been used productively in studies ranging from genome-scale statistical analyses to studies of specific gene families. The link between a gene's age and when it is expressed during embryonic development is a powerful example. Species in many phyla progress through a “phylotypic” stage, in which species with highly divergent adult morphologies display dramatic phenotypic similarities. This relationship between ontogeny and phylogeny has been known for decades, but its molecular basis is still not fully understood. A recent analysis of the phylogenetic age of the genes expressed across development in zebrafish, flies, and nematodes demonstrated that genes expressed in the phylotypic stage are significantly “older” than those expressed in earlier and later developmental stages that show species-specific characteristics [2].

Gene origin analysis has also demonstrated that many functional attributes of eukaryotic genes are associated with their time of origin. For example, younger genes in fungi, insects, and mammals have higher rates of evolution [3–5] and experience more variable selection patterns [6, 7] than older genes. In several yeast species, young genes have fewer physical interactions and are enriched for different functions than old genes [8–10]. Young genes are expressed in fewer tissues [11, 12] and are regulated by fewer genes [13] in humans.

The specific mechanism that gave rise to a new gene also influences its functional fate (reviewed in [1, 14]). It was long thought that duplicated genes are less likely to be essential than their singleton counterparts due to the potential for functional overlap and compensation. This pattern was observed among duplicate genes in yeast [15] but conflicting results were obtained in mouse [16–18]. By stratifying mouse genes by age, it was demonstrated that essentiality is in fact lower among duplicate genes compared to singletons of similar age [19]. This consistent pattern is masked among all genes because older mouse genes are more likely to be essential, and duplicates are often derived from older genes.

As suggested by the relationship between gene age and essentiality, a gene's evolutionary history is also connected to its disease associations. For example, Mendelian disease genes are on average older than non-disease genes, whereas genes associated with complex diseases are “middle-aged” [20]. Among genes associated with cancer there is strong enrichment for origins during two evolutionary periods: the origin of all cellular life and the emergence of multicellular animals [21]. More strikingly, this distinction based on age largely recapitulates a division of cancer genes based on the functional disruptions they produce. The older genes correspond to the “caretakers,” which support genome integrity and the fidelity of basic cellular processes, whereas many of the genes that arose around the origin of multi-cellular animals are the “gatekeepers,” in which mutations disrupt the regulation of cell signaling and growth.

Gene age analyses have also been used to relate the emergence of novel gene functions with ecological, geological, and evolutionary events. For example, an analysis showing that the metazoan ancestor likely possessed nearly all components of the post-synaptic scaffold was used to elucidate the origin of the animal nervous system [22]. Another study demonstrated that a gene duplication, which resulted in a novel fetal globin gene, coincided with the emergence of placental mammals [23]. This new gene plays a crucial role in mammalian development; fetal globin binds oxygen with a higher affinity, enabling efficient transfer of oxygen from the mother's bloodstream to the fetus. This links a novel gene to a novel developmental process.

Taken together, these studies highlight the diversity of questions that can be addressed by evolutionary analysis of gene age and the inferential power of gene age for understanding gene function. Gene age analysis helps to explain questions in comparative development, gene regulation, processes and rates of evolution, and disease genes. Consideration of gene age in the context of organismal evolution can shed light on the genetic forces driving morphological innovation. Analyses of gene age in the broader context of the history of the earth reveal connections between new metabolic capabilities and ecological change.

Estimating gene age in three steps

The above studies all analyze gene age, but closer scrutiny reveals that they vary substantially in how gene age is defined and the methods used to estimate this quantity. Although such differences are rarely acknowledged, they can drastically affect the conclusions of a study. To highlight these issues, we examine the process of estimating gene age step by step and propose guidelines for best practices.

Step 1: Time scales for gene age analyses

Several measures are used to quantify gene age. Here, we define the timing of an evolutionary event with respect to the lineage (i.e., the branch in the species tree) in which it occurred. For example, the duplication in Figure 1c occurred after the divergence of arabidopsis and gnathostomes and before the separation of shark and euteleostomes. Expressing gene age in terms of the species tree makes it easy to correlate new genes with functional innovations at the species level. Another common approach is to express gene age in terms of sequence divergence, which can be quantified in a variety of ways using sequence evolution models. Sequence divergence has been used, for example, to identify paralogs that originated from whole genome versus smaller scale duplications [24]. Both of these approaches can be extended to obtain age estimates in years if there is sufficient fossil evidence to date species divergence times or calibrate rates of sequence evolution (Box 1).

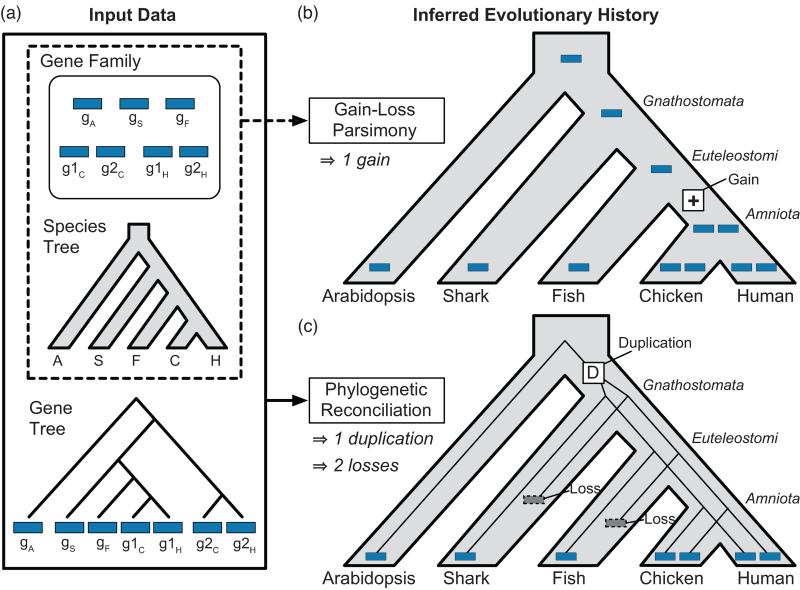
Figure 1. A typical error made by gain-loss methods is avoided with reconciliation.

A gene family with a history of parallel losses illustrates the increased accuracy associated with explicit use of a gene tree by phylogenetic reconciliation. (a) A hypothetical gene family, based on the real enzyme family in Figure 2, possesses one gene in arabidopsis, shark, amphibians, and fish, and two genes in each amniote species. (b) A gain-loss method, Wagner parsimony, incorrectly infers a single gene family member in the common ancestral species and a recent gain on the lineage leading to chicken and human. This scenario implies that all chicken and human genes are equally related to g_S and g_F, an inference that is not supported by the true tree. (c) Gene tree-species tree reconciliation correctly infers an earlier duplication, followed by parallel losses in the shark and fish lineages, and shows that g1_H and g1_C are more closely related to g_S in shark and g_F in fish, than to g2_H and g2_C.

Step 2: Inferring events in the evolutionary history of a gene

Identifying members of a homologous gene family is a prerequisite for most gene age inference methods (Box 2). Decisions made during homologous family identification, which is usually guided by sequence, structural, or contextual similarity, can affect gene age estimation, as described in Step 3. Once gene families have been defined, gene age inference methods are applied. These typically fall into two categories: gain-loss approaches and phylogenetic reconciliation (Figure 1).

The most basic and commonly used gain-loss algorithm, Dollo parsimony [25], considers only the presence or absence of a gene family in each leaf of the species tree; see, for example, the “phylostratigraphic” approach [2, 21, 26, 27]. Because Dollo parsimony allows multiple losses, but only one gain, it infers a gene family's origin to be the MRCA of all species that contain the family. More powerful gain-loss approaches, like Wagner parsimony [28], consider gene family size (i.e., the number of family members) in each species and allow different weights for gains and losses. The ancestral lineages in which gene family expansions and contractions occurred are inferred by minimizing the weighted sum of gains and losses.

Phylogenetic reconciliation also starts with a rooted species tree, a set of possible events, and a weight associated with each event. Gene family information is represented as a rooted gene tree reconstructed from gene sequences in a preprocessing step. Reconciliation uses the incongruence between the gene and species trees to infer the minimum weight set of events that best explains this incongruence and the correspondence between ancestral genes and ancestral species. Over the past two decades, a rich reconciliation methodology has emerged (reviewed in [29, 30]). A key distinguishing feature of different reconciliation algorithms is the set of allowable events used for inference. The most complete event model includes duplication, transfer, and loss, although many methods use only a subset of these events.

Gain-loss methods and phylogenetic reconciliation can yield very different evolutionary histories for the same family. At the heart of these differences is the way that each approach uses information from gene sequences and trees. Gain-loss methods only consider gene family size in each species, but do not take sequence variation or gene family history into account. Failing to consider these relationships can result in incorrect inference of gene duplications, gene transfers, and ancestral gene-to-species associations. In particular, gain-loss methods are unable to resolve families that sustained a transfer between distant species or parallel gains that occurred independently in two separate lineages. In both cases, gain-loss methods tend, incorrectly, to infer an early gain followed by later losses. Figure 1b shows another problem case in which parallel losses are erroneously interpreted as a single, recent gain. This error occurs in the HMG-CoA synthase (HMGCS) enzyme family (Figure 2). Amniotes have two copies of this enzyme: one that acts in the cytosol (HMGCS1) and one that acts in the mitochondria (HMGCS2). In contrast, fish, frogs, and sharks have a single HMGCS gene. Gain-loss parsimony implies that the second copy arose in the amniote ancestor, but reconciliation shows that it is much older. The more accurate, reconciliation-based estimate of HMGCS age is crucial for understanding the evolution of functional specialization in human deacetylation pathways: HMGCS1 and HMGCS2 are deacetylated by sirtuins, which are themselves ancient paralogs with distinct cytosolic and mitochondrial localization [31]. Gene age analysis makes it possible to assess the relative timing of the HMGCS and sirtuin duplications.

Figure 2. Phylogeny of the HMGCS gene family.

Human, mouse, rat, and chicken have two copies of this enzyme: one that acts in the cytosol (HMGCS1) and one that acts in the mitochondria (HMGCS2) [31]. In contrast, fish, frogs, and sharks have a single copy of the enzyme. Based on this phylogenetic distribution, gain-loss parsimony infers a recent gain on the branch leading to amniotes. The HMGCS gene tree tells a different story: the two HMGCS subfamilies arose via an early duplication at the base of the vertebrate lineage followed by three parallel losses in shark, fish and amphibians. The branching order of the gene tree, with branch support values > 0.9, strongly supports these conclusions and rejects the seemingly more parsimonious history with a single, more recent gain. Gene tree inferred using PhyML [52] from sequences aligned with MAFFT [53] and rooted using three invertebrate outgroup sequences. Branch support was assessed using aLRT scores [52]. Abbreviations: Human = Homo sapiens; Rat = Rattus norvegicus; Mouse = Mus musculus; Chicken = Gallus gallus; Frog = Xenopus tropicalis; Pufferfish = Takifugu rubripes; Zebrafish = Danio rerio; Shark = Callorhinchus milii; Fly = Drosophila melanogaster; Yeast=Saccharomyces cerevisiae; Arabidopsis = Arabidopsis thaliana.

Reconciliation, unlike gain-loss methods, can correctly diagnose distant transfers and handle independent expansions and contractions. This is because reconciliation methods explicitly account for gene family history by incorporating information from a gene tree. In general, reconciliation tends to be more accurate than gain-loss, provided that the gene tree is correct. If the gene family history is consistent with the assumptions of the gain-loss method, both gain-loss and reconciliation will infer the correct history. If the family violates those assumptions, gain-loss is likely to find an incorrect scenario that requires fewer events. Reconciliation is not sensitive to this type of error because it is constrained by the structure of the gene tree. Reconciliation assumes that any disagreement with the species tree is due to duplications, losses, or transfers. Errors can arise due to incomplete lineage sorting, which can result in a gene tree that disagrees with the species tree, but is not evidence of duplication or transfer. These errors can be avoided by using one of several recent methods that account for such incongruence [32–34]. Both gain-loss and reconciliation are also sensitive to family definition, species tree accuracy [35] sparse taxon sampling, gene conversion, and convergent evolution.

Most gain-loss and reconciliation methods infer ancestral gene content based on a parsimony criterion. Alternative probabilistic approaches have been proposed for both gain-loss (e.g., [36, 37]) and reconciliation models [34, 38, 39]. These methods are more suitable than parsimony when event rates are high, but they come at the cost of significantly increased computational time. They can also learn event weights from data if a large number of gene families are analyzed together.

Step 3: Assigning an age to a gene based on its evolutionary history

Each event in the evolutionary history of a gene has a uniquely defined age, even if it is difficult to estimate correctly in practice. By contrast, the age of a gene is not uniquely defined; there is often more than one ancestral gene that is a reasonable choice for the progenitor. Additional ambiguity results from the hierarchical structure of multigene families, which arises through repeated cycles of duplication followed by functional differentiation. This process creates functionally related, but distinct, subfamilies. To assign gene age in a multigene family, like the HMGCS enzymes or MaGuKs (see below), one must determine where to query the gene family hierarchy for a given analysis.

If the goal of the analysis is to consider how gene age is related to gene function, then the mode of functional differentiation following gene duplication also influences how age is best defined. Duplicates may continue to perform the ancestral function (e.g., for increased dosage), acquire new functions (neofunctionalization), or the ancestral functions may be partitioned between them (subfunctionalization). In the case of neofunctionalization, for example, it is reasonable to equate the age of the genes with the time of the duplication, but in cases where the ancestral function is retained, the appropriate age may be much earlier.

Defining gene age is even more complicated in multidomain gene families. These families encode proteins with multiple functional domains that have been integrated at different times and in different lineages. Again, the best solution depends on context. If the goal is to investigate how changes in domain content relate to protein function, then focusing on the age of the individual domains is a good approach. However, in a study concerned with overall protein function, rather than specific domains, gene age should be guided by the gene family organization and not by domain organization.

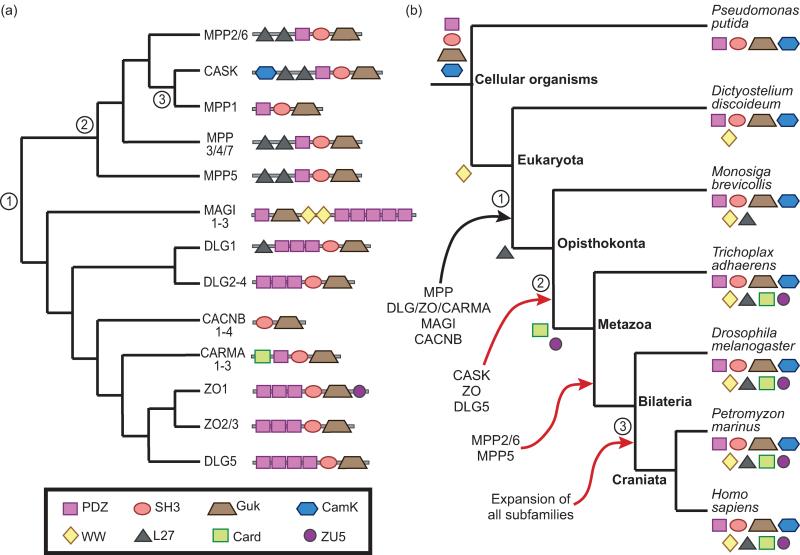
The problems of inferring gene age in hierarchical families and in families encoding multidomain proteins both arise in the Membrane-associated Guanylate Kinase (MaGuK) family (Figure 3). MaGuKs generally act as scaffolds that organize protein complexes required for cell-cell interactions (reviewed in [40]). This family evolved through multiple rounds of duplication and functional differentiation [41], resulting in subfamilies that perform more specific functions, such as synaptic signaling and plasticity (DLG1/2/3/4) [42] or organization of epithelial tight junctions (ZO) [40]. This hierarchical structure complicates gene age assignment (e.g., MPP1 has at least three possible ages). In addition, MaGuK genes are composed of complex combinations of domains with different histories. Domain architectures are not strictly conserved within subfamilies, and even orthologs sometimes differ in domain architecture (e.g., DLG3 has three PDZ domains in mouse and human, but only two in chicken (not shown)). Hence defining gene age in terms of the common ancestor of genes with exactly the same domain architecture is too restrictive. Defining the origin of the MaGuKs in terms of a single domain is also problematic, because most constituent domains predate, and none uniquely characterizes, this family. Thus, there are many reasonable definitions for the age of the MaGuK family—the best choice depends on the specific question that the analysis is intended to address.

Figure 3. Gene origin and age are not uniquely defined in the human MaGuK superfamily.

The membrane-associated guanylate kinase (MaGuK) superfamily is a multigene family with complex substructure and domain architecture. There are many potential choices for the MaGuK progenitor, which span a broad range of times. (a) MaGuK gene tree inferred from the guanylate kinase domain. Nodes 1–3 show three possible origins for MPP1: (1) the origin of the entire MaGuK family (pre-Opisthokonts), (2) the duplication that gave rise to separate CASK and MPP1 genes (pre-Metazoan), (3) the common ancestor of MPP1 and its orthologs (pre-Craniata). Domain architectures are shown on the leaves. Clades of genes with identical domain architectures are collapsed (e.g., MAGI1–3). (b) Species tree showing lineages when domains and specific MaGuKs first appeared. Leaves are decorated with the domains that are present in that species. Arrows indicate when the progenitor of a subfamily first arose, with the subfamily listed below that arrow. Red arrows indicate duplication events that either expanded a subfamily or gave rise to a new one. Branches 1, 2, and 3 represent three possible ages for MPP1, and correspond to nodes 1, 2, and 3, respectively, in the gene tree. Domain origins were inferred using Dollo parsimony with Count [36]. Gene origins are based on phylogenetic analysis [41] and Dollo parsimony.

Case Study: the complex evolutionary history of fungal wood decay enzymes sheds light on their role in forest ecology and coal deposition

A beautiful example of the power and the challenges of gene age analysis is provided by a series of studies of expansions and contractions in wood decay families during the evolution of white and brown rot fungi [43, 44]. Both rots can break down cellulose in wood, but only white rot can break down lignin. This difference has profound ecological and economic implications because lignin acts as a repository for non-atmospheric, organic carbon and is the primary precursor of coal.

To uncover the role of lignocellulose degradation genes in wood rot evolution, a recent study reconciled gene trees for 27 enzyme families with the associated tree of 31 fungal species using Notung [32] and DrML [39]. This analysis revealed ancestral gene family sizes and the gene duplications and losses on each branch of the species tree [44], showing that the MRCA of the white rots studied (starred node in Figure 4) possessed an enzymatic arsenal capable of lignin degradation and was likely a white rot. Subsequently, brown rots evolved independently, several times, through lineage-specific losses of lignin degradation enzymes. Simultaneously, white rot lineages experienced additional expansions of those families. These results, combined with a fossil-calibrated molecular clock analysis (Box 1), predict that the expansion in lignin degrading enzymes occurred at the beginning of the Permian era, suggesting a possible link between the emergence of white rot and the sudden drop in coal deposition at the end of the Permian [45]. Reliable methods for inferring gene age were essential to these studies, because their biological conclusions depend crucially on when lignocellulytic gene family expansions and contractions occurred.

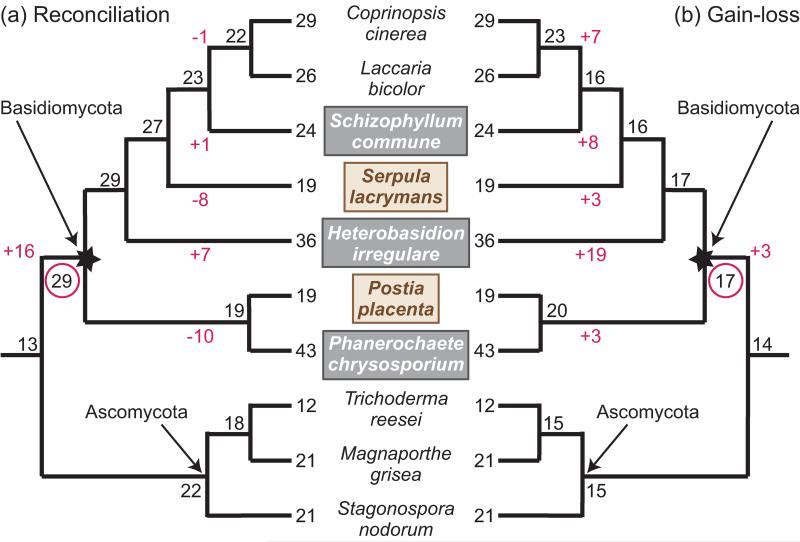
Figure 4. Reconciliation reveals the dynamic history of fungal oxidoreductase genes.

Analysis of fungal oxidoreductase gene families shows that a gain-loss approach can obscure the dynamics of gene family expansion and contraction, whereas reconciliation identifies a richer set of events. Internal nodes are labeled with the number of inferred ancestral oxidoreductase genes. Branch labels show inferred gains and losses that changed dramatically between the two analyses. Brown rot fungi are indicated by brown text in a tan box; white rot by white text in a gray box. (a) The original, reconciliation-based analysis of seven oxidoreductase gene families in 10 fungal species, adapted from Figure 1B in [43]. This analysis infers a moderate oxidoreductase complement in the white rot MRCA (starred node), with substantial independent expansions in the Ascomycota and the Basidiomycota. The oxidoreductase gene complement in the ancestral white rot species (red circle) has the most oxidoreductase genes among ancestral nodes. Independent, lineage-specific gene duplications and losses in white and brown rots, respectively, gave rise to present day oxidoreductase counts. (b) Our analysis of the same data set using a gain-loss analysis predicts smaller gene family sizes in the white rot ancestor and lineage-specific expansions, rather than contractions, in Serpula and the lineages leading to Coprinopsis and Laccaria and to Postia and Phanerochaete. The expansions in Heterobasidion and Schizophyllum are substantially over-estimated compared with (a). Ancestral gene family sizes were inferred using Wagner parsimony with equal weights implemented in Count [36].

To investigate how method choice influences gene age estimates, we compared the reconciliation-based analysis of seven families of wood degrading oxidoreductases [43] to our own gain-loss analysis of the same data (Figure 4b). The results show that the gain-loss method was not able to detect the pronounced increase in oxidoreductase gene content in the white rot ancestor (16 gains vs. 3 gains) and missed several of the independent expansions and contractions that the authors of the original paper identified by reconciliation.

These studies highlight important aspects of each of the three steps of gene age analysis. First, the species tree is used as the primary scale on which to express gene age, augmented by sequence divergence and fossil calibration to relate events in gene and species evolution to geological and ecological trends. Second, two different age estimation strategies predict dramatically different ages for the same gene, resulting in very different interpretations of wood rot evolution and carbon deposition. Third, this analysis sidesteps the problem of selecting a progenitor by considering gene duplications and losses throughout the species tree.

Perspectives

Gene age analysis has great power to highlight correlations between a gene's history and its functions in the context of organismal evolution, ecological dynamics, and global biogeochemical processes. At the same time, this field faces major challenges.

A fundamental problem is that a gene does not have a single, well-defined age. For genes in a complex, multigene family there are several events that could be considered the origin of the gene. Further, genes that encode multidomain proteins may contain sequence fragments with very different histories. The many potential ages for MaGuK genes illustrate both of these phenomena (Figure 3). An appealing solution is to consider all possible progenitors at all levels of the gene family hierarchy simultaneously by summarizing the collective events in a gene's history on a species tree. This comprehensive characterization solves the problem of selecting a single age for each gene and enables detection of subtle patterns in the family as a whole. New techniques enable testing of alternate hypotheses concerning when a novel function first arose, for example, by experimentally probing the function of an ancestral protein by resurrecting its inferred amino acid sequence via synthesis or mutagenesis of modern proteins [46–48].

The second major challenge is that current methods can predict very different ages for the same gene. Conceptual tractability and computational efficiency have made gain-loss methods popular, despite their biases [49]. However, reconciliation methods are more accurate, because they take advantage of the information encoded in the gene family tree and make less restrictive assumptions. The HMGCS and white rot studies provide concrete examples of how different gain-loss and reconciliation-based age estimates can be, to say nothing of the down-stream functional predictions. Fortunately, although reconciliation requires more complex calculations, algorithmic developments have made substantial headway in improving accuracy and reducing computational time [33, 50].

Unlike many other areas of genomics, inexpensive high-throughput sequencing is not a panacea for gene age analysis and introduces new problems. Accurate gene age analysis requires scalable algorithms for homology detection, multiple sequence alignment, phylogenetic inference and reconciliation that outpace sequencing projects and simultaneously improve accuracy. Further, increasing data not only changes the scale of the challenges we face, but their fundamental nature. In phylogenetic inference, for example, problems with taxon-sampling will likely decrease, but noise due to incomplete lineage sorting will increase as we sample more genomes.

Despite these challenges, gene age analysis on a multigenome scale offers exciting opportunities. With the ever-increasing rate of genome sequencing, reliable, automated gene annotation methods are essential. Because evolutionary patterns are now the main source of information about gene functions for the majority of genomes, the potential contribution of gene age analysis to functional annotation is significant. Genome-scale analyses of gene age in many gene families, considered simultaneously, can illuminate how genes work together in present day organisms and how systems of interacting components evolved. Statistical analyses of broad trends across a large number of gene families are revealing underlying principles, such as the complex association between age, mechanism of origin, and essentiality among mouse genes [19]. They can also link trends in gene family expansion and contraction to phenotypic and ecological changes.

More efficient algorithms and faster hardware are putting reconciliation-based age analysis of all gene families in a collection of genomes within reach, but fully exploiting this potential will require additional methodological advances. Genome scale phylogenetics requires better ways to assess how much noise there is in a large collection of trees. A related issue is that most nodes in the tree of life cannot be accurately dated (Figure 5, Box 1), making it challenging to link gene family origins and expansions to geologic events. Statistical methods for identifying significant trends in the resulting evolutionary data are also needed. Development of these methods would enable studies of the underlying principles of gene evolution and delineation of the extent to which events in a particular gene family (e.g., an expansion) are temporally associated with events in other families.

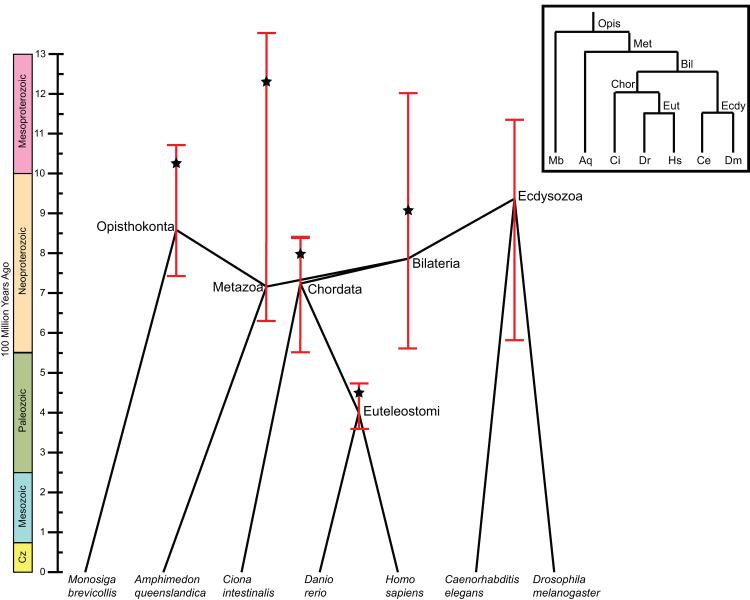
Figure 5. Estimates of species divergence times vary greatly.

Metazoan species tree annotated with estimates of ancestral divergence times, obtained from the TimeTree database (timetree.org) using the species tree obtained from the NCBI taxonomy [54]. Nodes are plotted at the mean age estimate across all surveyed literature that contained that divergence [55]. The relative timing of these mean estimates violates the branching order of the commonly accepted tree (inset box), as can be seen from the distorted layout in which several branches appear to be traveling backwards in time. In the accepted tree, the Opisthokonta, Metazoa, and Bilateria nodes all pre-date Ecdysozoa and its sister node Chordata. This uncertainty is further reflected in the fact that minimum and maximum age estimates for each node (red bars) differ by hundreds of millions of years. To attempt to resolve these issues, an “expert result” (starred) was selected for each node from a single article that was deemed to have the “best” estimate for that divergence [45]. Across the tree, this expert result is consistently much older than the mean age estimate for the same node, indicating that there may be systematic underestimation of node ages in the literature. The expert results are more consistent with the branching order of the accepted tree, although they do not correctly place Opisthokonta earlier than Metazoa.

With more genomes, the lines between phylogenetics and population genetics are increasingly blurred. In that context, gene age analysis can be extended to consider the age of alleles arising from recent mutations that are still polymorphic within a population. Allele age analyses typically use polymorphism frequencies to estimate when mutations arose and whether or not they were subject to selection during a particular time period [51].

As more researchers embrace a more accurate, phylogenetic approach to gene age analysis, we must develop analytical tools that are accessible to researchers with a range of quantitative skills. Developing user-friendly software that supports every step of the process from gene tree inference, to gene age inference and interpretation of gene age history results should be a priority. Tools that will have the greatest impact are those that automate processing of large-scale data sets, visualization tools for exploratory analysis, and statistical tools for correcting systematic error, assessing significance, and extracting trends (e.g., ProteinHistorian [49]). With the availability of methods that can analyze terabytes of gene sequence data at the push of a button, it will be more important than ever to clearly articulate the strengths and weaknesses of alternative gene age analysis methods and to evaluate these in the context of each study.

Box 1: Measuring gene age in years.

Methods for estimating gene age frequently define evolutionary events on a species tree. If nodes in these trees can be reliably dated, events in the history of a gene—from its origin to the most recent modification—can be interpreted in the context of geologic events and the evolution of molecular and organismal traits. For example, dating lignin-degrading enzyme duplications in the common ancestor of white rot fungi (Figure 4) to the same time as the origination of the boreal forest biome, demonstrated that diversification of fungal nutritional modes coincided with the diversification of forest plants [43]. Further, the expansion and subsequent contraction of white rot fungi correlated with variation in the rate of carbon deposition from the Carboniferous to the Permian, highlighting the importance of lignin-degrading enzyme origination in the earth's coal deposits [44].

When species and gene trees are built from sequence data, the length of a branch represents the expected number of substitutions per site. If the molecular clock hypothesis holds (i.e., if the rate of substitutions is the same in all lineages), then branch lengths can be translated into years using a single, accurately dated node. However, tests of the molecular clock hypothesis reveal that it is valid for relatively few data sets. In general, substitution rates vary over time, between species, and across different genes due to changes in mutation rates, selection pressures, generation times, population sizes, and many other forces. Underestimation of substitutions on long branches, taxon sampling, and extensive gene loss are additional sources of error. Finally, fossils sometimes provide good minimum ages for nodes in a species tree but provide less information about upper bounds [56] and about divergence times in gene trees. Thus, there is typically a great deal of variance in estimates of node ages in gene and species trees (Figure 5), which can confound gene age estimates and downstream analyses [57, 58].

Several recent approaches to gene age estimation have tackled the problems associated with calibrating phylogenetic trees in various ways. For instance, relaxed molecular clock methods (e.g., [59]) address these problems by jointly estimating substitution rates and node dates, although they rely upon modeling assumptions and often require substantial computation. Molecular clock calibration methods could also potentially leverage recent breakthroughs in sequencing ancient DNA from dated fossils [60]. Others have used simulations to suggest that evolutionary rate variation across genes does not dramatically affect gene age estimates [61].

Box 2: Finding homologous genes families.

Gene family identification is an essential prerequisite for most gene age analyses. This typically involves two steps: identifying pairs of homologous sequences and grouping those pairs into sets, each corresponding to a family that shares a common ancestor.

Several approaches to homology detection have been used in the context of gene age analysis. The most common strategy is the use of sequence comparison (e.g., BLAST [62]) to detect significant similarity between gene or protein sequences. However, as sequence similarity decreases, pairwise alignment approaches lose power to detect homology. Many additional sequence-comparison methods have been developed that are able to detect more remote homology by building statistical profiles from multiple alignments of sequences related to the query (e.g., [63–65]) or analyzing known and predicted structural similarities (e.g, SCOP [66, 67]). Homology detection methods that consider structural similarity between proteins have the ability to detect remote homology. Their use is rare in gene age analysis, but see [68] for an example. In all homology searches, parameter settings, e.g., the minimum sequence similarity or minimum coverage of the sequence required, can dramatically affect the resulting homology predictions.

Once homology has been established among pairs of genes, networks are constructed from the pairwise relationships, and dense sub-networks corresponding to gene families are identified, e.g., using OrthoMCL [69] or InParanoid [70]. In addition to grouping related sequences together, the clustering helps to correct false and missing homology predictions. Most clustering methods require setting one or more parameters that determine cluster sizes, and therefore, the degree of similarity among family members. A tight clustering will result in families that approximate orthologous groups, while more lenient parameters will yield homologous families containing paralogous subfamilies. These parameter choices influence the potential age estimates for a gene, for instance, by limiting the set of possible progenitors. Because a lenient clustering offers more flexibility in defining gene origins, it is often preferable, especially if reconciliation is used. However, large-scale resolution of orthologs and paralogs within a homologous family has proven to be a very difficult problem that requires further algorithm development [71–73].

HIGHLIGHTS

• Gene age is informative about gene function.

• Gene age analysis is complicated by the fact that a gene does not have a single well-defined age.

• Different methods for estimating gene age can yield dramatically different results.

• Computational advances enable analyses of full evolutionary histories of gene families.

Glossary Box

Character

any observable feature of an organism, e.g., a DNA sequence, a morphological phenotype, or a behavior.

Most recent common ancestor (MRCA)

the most recent ancestral organism from which all genes (or other characters) of interest are derived.

Homology

the relationship of DNA sequences (or other biological characters) related by vertical descent; that is, sequences derived from a common ancestor via speciation or gene duplication. Note that homology indicates only shared ancestry and does not imply conserved function.

Orthology

the relationship of homologous DNA sequences (or other biological characters) created by a speciation event at their most recent common ancestor. Sequences with this relationship are called orthologs and are said to be orthologous.

Paralogy

the relationship of homologous DNA sequences (or other biological characters) created by a duplication of their most recent common ancestor. Sequences with this relationship are called paralogs and are said to be paralogous.

Homologous family

a collection of genes with significant evidence of homology.

Subfunctionalization

when two genes created by gene duplication each take on a subset of their progenitor's functions.

Neofunctionalization

when one of the two genes created by gene duplication takes on a novel function not carried out by its progenitor.

Phylogenetic tree

a diagram that illustrates inferred evolutionary relationships between biological entities. For example, a species tree relates the history of speciation events that produced observed species. A gene tree gives the series of evolutionary events that relate genes observed across one or many species.

Gain-loss models

a class of methods for reconstructing the phylogenetic history of a biological character, i.e., its state at ancestral nodes in a species tree, that considers only gain and loss events along a species tree.

Parsimony

the principle that the simplest explanation should be preferred; e.g., when applied to phylogenetics, parsimony prioritizes the tree with the smallest number of evolutionary events that fits the observations.

Dollo parsimony

a common gain-loss phylogenetic analysis method based on parsimony and the assumption that a biological character can only be gained once, though it may experience multiple losses in different lineages.

Wagner parsimony

a gain-loss phylogenetic analysis method based on parsimony that allows multiple gain and loss events, potentially with different likelihoods.

Phylogenetic reconciliation

a method for reconstructing the phylogenetic history of a biological character that finds a correspondence between a character tree (usually a gene tree) and a species tree in terms of a set of allowable ancestral evolutionary events.

Incomplete lineage sorting

the presence of multiple gene genealogies across a genome, some of which may not match the species tree.