Bioactive Conformations of Two Seminal Delta Opioid Receptor Penta-peptides Inferred from Free-Energy Profiles

Abstract

Delta-opioid (DOP) receptors are members of the G protein-coupled receptor (GPCR) sub-family of opioid receptors, and are evolutionarily related, with homology exceeding 70%, to cognate mu-opioid (MOP), kappa-opioid (KOP), and nociceptin opioid (NOP) receptors. DOP receptors are considered attractive drug targets for pain management because agonists at these receptors are reported to exhibit strong antinociceptive activity with relatively few side effects. Among the most potent analgesics targeting the DOP receptor are the linear and cyclic enkephalin analogs known as DADLE (Tyr-D-Ala-GlyPhe-D-Leu) and DPDPE (Tyr-D-Pen-Gly-Phe-D-Pen), respectively. Several computational and experimental studies have been carried out over the years to characterize the conformational profile of these penta-peptides with the ultimate goal of designing potent peptidomimetic agonists for the DOP receptor. The computational studies published to date, however, have investigated only a limited range of timescales and used over-simplified representations of the solvent environment. We provide here a thorough exploration of the conformational space of DADLE and DPDPE in an explicit solvent, using microsecond-scale molecular dynamics and bias-exchange metadynamics simulations. Free-energy profiles derived from these simulations point to a small number of DADLE and DPDPE conformational minima in solution, which are separated by relatively small energy barriers. Candidate bioactive forms of these peptides are selected from identified common spatial arrangements of key pharmacophoric points within all sampled conformations.

INTRODUCTION

Opioid receptors continue to be prominent targets for pain relief and intravenous anesthesia. Analgesia mediated by the delta-opioid (DOP) receptor is usually not accompanied by unwanted effects (e.g., physical dependence), rendering selective agonists of this receptor more advantageous over agonists that preferentially bind mu- or kappa-opioid receptors (MOP and KOP receptors, respectively).¹

DOP receptor exhibits high affinity for two endogenous penta-peptides that are involved in regulating nociception in the body,² specifically: methionine-enkephalin (Tyr-Gly-Gly-Phe-Met) and leucine-enkephalin (Tyr-Gly-Gly-Phe-Leu). Several substitutions, deletions, or additions of artificial amino acids, as well as cyclization, have been introduced to reduce their natural flexibility and improve their selectivity for the DOP receptor^3–6. Among the several constrained enkephalin analogs that have been synthesized over the years are the linear peptide DADLE (Tyr1-D-Ala2-Gly3-Phe4-D-Leu5) and the cyclic peptide DPDPE (Tyr1-D-Pen2-Gly3-Phe4-D-Pen5), the latter featuring a disulfide bridge between the side-chains of the two non-natural D-Pen amino acids (i.e., D-penicillamine or D-β,β-dimethylcysteine) at positions 2 and 5.

While DADLE showed only moderate selectivity for the DOP receptor compared to the MOP receptor, DPDPE was found to be highly-selective for the DOP receptor.^7–9 Notably, the anti-nociceptive effect of DPDPE in vivo has recently been shown to be differentially modulated by KOP receptor antagonists, implying possible allosteric interactions between the DOP and KOP receptors.¹⁰

Both DADLE and DPDPE have been extensively studied by means of NMR and X-ray crystallography in different environments (e.g., see ^5,6,11–13). The crystal structure of DADLE revealed a single-bend folded conformation but instead of exhibiting the typical (type ′) β-bend characterized by the two intramolecular hydrogen bonds Nⁱ⁺³–H^{· · · ·}Oⁱ and Nⁱ–H^{· · · ·}Oⁱ⁺³, the latter was replaced by a hydrogen bonded bridge linking N1 and N5 through a Cl⁻ ion. Three independent molecules were present in the asymmetric unit of the DPDPE crystal structure.¹⁴ These molecules shared a similar conformation of the 14-membered ring and the Phe4 side chain, and differed exclusively in the orientation of the Tyr1 side chain.

Along with experimental efforts to elucidate the structural features of these penta-peptides, several computational approaches have been employed to explore their conformational space. However, these approaches have been mostly applied to the cyclic DPDPE,^15–20 using simplified solvent environments and relatively short timescales. Moreover, no study has yet provided free-energy profiles for these penta-peptides, or information about the relative stability of all sampled conformational minima. Here, we report estimates of the thermodynamic stability of both DPDPE and DADLE derived from microsecond-scale all-atom molecular dynamics (MD) simulations in an explicit water environment using either standard methods or an enhanced, bias exchange-metadynamics sampling algorithm. Putative bioactive conformations shared by these two potent DOP receptor agonists are inferred based on a comparison between spatial arrangements of key pharmacophoric points in all sampled conformations.

COMPUTATIONAL METHODS

System Setup and Standard MD Simulations

Initial conformations of both the linear (DADLE) and cyclic (DPDPE) penta-peptides were built using the Schrödinger molecular modeling environment Maestro, version 9.1.²¹ Natural amino acids were described using the Charmm27 force-field²² with the CMAP correction,²³ while D-penicillamine residues were parameterized based on similarity with the Leu and Cys residues in the same force-field. For the D-amino acids of DADLE, the backbone dihedral angles were inverted upon application of the CMAP correction, which is parameterized for L-amino acids.

DADLE and DPDPE were placed with periodic boundary conditions in cubic simulation boxes with diagonals of 86 Å or 64 Å, and containing ~4,000 and ~1,200 TIP3P water molecules, respectively. Van der Waals interactions farther than 10 Å were cut off using a switching function, while electrostatic interactions were described by the Particle Mesh Ewald algorithm. Non-bonded interactions were calculated based on a neighbor list updated every 10 fs. All bond lengths were maintained with the LINCS strategy, and a Verlet integrator was used with a timestep of 2 fs. Temperature and pressure of the system were kept at 300 K and 1 atm with V-rescale and Parrinello-Rahman algorithms, respectively. After solvation, the full systems were minimized for 1000 cycles using the steepest descent algorithm, and equilibrated for 5 ns of MD simulations prior to standard MD production runs of 1.0 μs for DADLE and 2.0 μs DPDPE. All calculations were carried out with the Gromacs 4.5.3 code,²⁴ enhanced with the Plumed routines.²⁵

Bias-Exchange Metadynamics Simulations

Bias-exchange metadynamics simulations were set up using a total of 5 replicas for each peptide. According to the strategy described in ²⁶, one replica (the neutral replica) evolved under the regular unbiased force-field, whereas each of the other four replicas were biased using two collective variables that represented the values of the backbone dihedrals (ϕ and ψ). Gaussian bias contributions with widths s_ϕ=s_ψ=0.2 radians were added within the framework of well-tempered metadynamics²⁷ with an initial rate of 0.83 kJ/(mol ps). Exchanges between replicas were attempted every 20 ps, and accepted using a modified Metropolis criterion. Each replica was simulated for 150 ns.

Free-Energy Reconstruction

Since the peptides’ 8 backbone dihedrals (ϕ and ψ) sampled during simulation naturally span a complex phase space, a meaningful interpretation of the conformational free-energy requires some form of dimensional reduction. To this end, we randomly extracted N_L=1000 conformations from the neutral replica trajectory in the bias-exchange simulations and used them as landmarks to produce a multidimensional scaling (MDS) embedding of the trajectories in two dimensions.²⁸ The MDS projection of the landmarks was calculated based on the heavy-atoms root mean square deviation (RMSD) pairwise dissimilarity matrix. To produce the embedding, the RMSD of each point in the standard MD from each landmark in the bias-exchange neutral replica trajectory were calculated and used to obtain low-dimensional projections. Two-dimensional free-energy profiles as a function of the two most representative components of the embedding, MDS₁ and MDS₂, were derived from the distribution probability p(MDS₁,MDS₂) and the Boltzmann relation G = −k_BT ln p(MDS₁,MDS₂), where k_B is the Boltzmann constant and T the temperature of the simulation.

Pharmacophore Choice and Analysis

According to classical DOP receptor pharmacophore models (e.g., see the Loew²⁹ and LMC³⁰ pharmacophores), recently supported by four different opioid receptor crystal structures,^31–34 at least three functional groups play a significant role in opioid ligand recognition. These have traditionally been described by three pharmacophoric points: a protonated nitrogen (N), the centroid of an aromatic ring (A), and the centroid of a hydrophobic region (B). In DADLE and DPDPE, these points correspond to: the backbone nitrogen of Tyr1, the centroid of the aromatic ring of Tyr1, and the centroid of the aromatic ring of Phe4. The relative positions of these 3 points in all sampled conformers can be defined by 3 distances (d_NA, d_NB, and d_AB) and 3 angles (α_ANB, α_NAB, and α_NBA), i.e., a total of 6 variables for each peptide. To identify the energy minima containing common arrangements of these pharmacophoric points among all sampled conformers of DADLE and DPDPE, we calculated the free-energy of the systems as a function of the full 6-dimensional variable ω=(d_NA, d_NB, d_AB, α_ANB, α_NAB, α_NBA). The trajectories of the neutral replicas were sub-sampled using one frame every 10 ps for a total of N=1.5×10³ frames for each trajectory, and the values of the 6 variables calculated for each point. The resulting data were binned into a common 6-dimensional grid spanning the whole region where any of the two free-energy functions is non-vanishing. A relatively coarse mesh of 60 bins of size δ_i for each dimension i=1, 2, …, 6 was used (for a total of 60⁶ ~10¹¹ 6-dimensional bins), and sparse matrix techniques were used to calculate the count of frames n(ω) falling in each bin and their respective probabilities p(ω)=n(ω)/(NΔ), N being the total number of points in the trajectory and Δ=δ₁×δ₂×…×δ₆ the volume of each bin. For each peptide, the regions with a probability above a given cutoff p_c, defined the region Ω_Q={ω: p_Q(ω)>p_c}, where Q is either DADLE or DPDPE. Thus, the common region Ω=Ω_DADLE∩Ω_DPDPE contains conformations of the peptides populated (with probability above p_c) by both peptides. Conformations from Ω were extracted and clustered using the full RMSD as a dissimilarity measure. To graphically illustrate the region Ω, and following the formulations reported in ²⁰, nine 2-dimensional projections were calculated for the free-energy F_Q(ω_α, ω_β) = −k_BT ∫Π_γ≠αβ dω_γ p_Q(ω) and for the region Ω_αβ={(ω_α, ω_β): ω∈Ω}, where ω_α is one of the three distances that define the pharmacophore and ω_β is one of the three angles.

RESULTS AND DISCUSSION

Conformational Free-Energy of DADLE

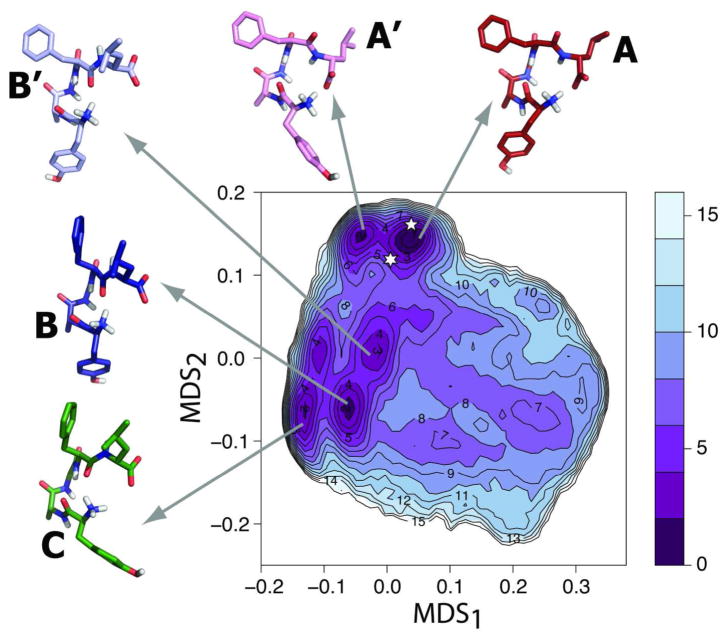
The free-energy profile of the linear peptide DADLE in solution, calculated with bias-exchange metadynamics (see Methods section for technical details), is reported in Figure 1. As shown in supplementary Figure S1, this free-energy profile is similar to that derived from an independent microsecond-long standard MD simulation. Three basins (A, B, and C), comprising five major minima (i.e., within 3 kJ/mol from the most stable minimum) can be identified on the free-energy surface of Figure 1. Representative structures of these conformational minima are shown as insets in this figure. Notably, the average RMSD for all heavy atoms of these representative structures is 0.5 Å from equivalent ones obtained by standard MD.

Figure 1. Free-energy surface of DADLE in solution.

Free-energy reconstructed from the bias-exchange metadynamics simulations of DADLE. Free-energy differences from the lowest energy minimum A are reported in kJ/mol. Representative structures (cluster medoids) for minima A, A′, B, B′, and C are reported in red, pink, dark blue, light blue, and green, respectively. The location on the map of representative, putative bioactive conformations is indicated with a six- or a five-point star for Clusters 1 and 2, respectively.

Basin A comprises minima A and A′, which are separated by a free-energy difference of ΔG~2 kJ/mol. This basin is separated by a barrier of ~7 kJ/mol from basin B, which contains minima B and B′ with free-energy differences from the most stable minimum A of ~2 and ~3 kJ/mol, respectively. Although basin C contains two minima, only one exhibits a free-energy difference within 3kJ/mol from the most stable minimum A. Values of the torsional angles of each of the representative structures of DADLE illustrated in Figure 1 are listed in Table 1. Minima A and A′ exhibit a very similar backbone conformation, which is characterized by a charge-charge interaction between the C-terminal carboxyl and the N-terminal amine groups, at variance with the other conformational minima in which the N-terminal amine group is interacting with the backbone carbonyl oxygen of Phe4 (see structures B, B′, and C in Figure 1). The only significant difference between minima A and A′ lies in the rotamer of the Tyr1 side chain (χ1 = −164° in A and χ1 = −58° in A′). While minima B and B′ exhibit a backbone conformation that is similar to those of A and A′ in the N-terminal region, their C-terminal region, including the Phe4 backbone dihedrals (ϕ₄ ~ −140°/−130° and ψ₄ ~ 160°/147° in B/B′ compared to ϕ₄ ~ −100°/−97° and ψ₄ ~ 2°/−3° in A/A′), adopt a different conformation. The representative conformation of basin C, which is within 3 kJ/mol from the most stable minimum A, exhibits a conformation similar to that of B with the exception of the side chain orientation of Tyr1. Based on these observations, it appears as if MDS₁ gives an indication of possible differences in the Tyr1 rotamer (χ1 is −164, −165, and 178 for A, B, and B′, respectively, whereas it is −58° and −73° for A′ and C, respectively), whereas MDS₂ can be interpreted as a descriptor of changes in the backbone conformation and interactions between peptide ends.

Table 1.

Dihedral angles of representative conformations of DADLE in water, along with corresponing values in its x-ray crystal structure. Side chains are defined as χ1= χ1¹ (N-C_α-C_β- C_γ), χ2= χ1^2,2.

Residue	Angle	A	A′	B	B′	C	X-ray
Tyr1	ψ	162.4	150.9	147.0	155.6	155.4	153
D-Ala2	ϕ	65.9	92.6	89.3	86.0	63.3	75
	ψ	21.9	13.7	37.3	37.0	46.9	8
Gly3	ϕ	87.2	91.0	83.4	80.0	80.2	98
	ψ	5.3	0.1	3.5	6.0	−0.6	−5
Phe4	ϕ	−100.0	−96.6	−139.5	−130.0	−138.8	−87
	ψ	2.4	−3.4	159.9	147.2	127.2	−15
D-Leu5	ϕ	118.7	107.9	63.6	87.5	99.1	111
Side chains
Tyr1	χ1	−163.6	−57.8	−164.8	178.4	−73.5	−166
	χ2	57.8	−66.0	−98.4	84.8	110.2	72
Phe4	χ1	−66.0	−62.6	−170.6	−61.7	−178.8	−71
	χ2	107.3	110.4	83.0	−77.2	68.1	−70
D-Leu5	χ1	87.7	59.3	56.3	65.0	44.0	68/159a
	χ2	68.0	68.2	86.1	54.0	66.5

^aThe side chain of residue D-Leu5 is described as disordered in the experimental paper; hence the different value for the same dihedral angle.

Notably, the conformation extracted from the lowest free-energy basin, i.e. minimum A, is the most similar one to the available X-ray crystal structure³⁵ of DADLE, with a heavy atoms RMSD of 1.2 Å. Comparison between the dihedrals of minimum A and the DADLE X-ray crystal structure³⁵ listed in Table 1 suggests that the only source of significant deviation between these two conformations stems from the different orientation of the side chains of Phe4 and D-Leu5.

Conformational Free-Energy of DPDPE

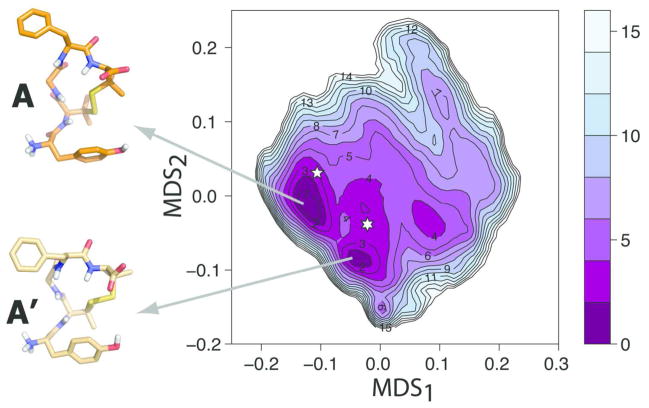
The free energy profile of DPDPE from bias-exchange metadynamics is reported in Figure 2. At variance with the case of the linear peptide, the region of the conformational space explored by the biased simulation was significantly broader than the region accessed by standard MD in 1 μs. Thus, we run standard MD for an additional 1 μs, and obtained the free-energy surface that we report in Figure S2 along with superimposed contour lines of the free energy obtained by bias exchange metadynamics. Although the two free-energy surfaces compare reasonably well in the lowest energy region, not surprisingly, regions of high free-energy (in particular the region with MDS₂ above ~0.1) are only explored by the enhanced bias-exchange metadynamics approach.

Figure 2. Free-energy surface of DPDPE solution.

Free-energy reconstructed from the bias-exchange metadynamics simulations of DPDPE in water. Free-energy differences from the lowest energy minimum A are reported in kJ/mol. Representative structures (cluster medoids) for minima A and A′ are reported in orange and light gold, respectively. The location on the map of representative, putative bioactive conformations is indicated with a six- or a five-point star for Clusters 1 and 2, respectively.

The bias-exchange free energy surface of Figure 2 reveals one large energy basin with two main minima (i.e., within ~ 2 kJ/mol from the lowest energy minimum), which are labeled A and A′ in Figure 2, and are separated by an energy barrier of ~ 4 kJ/mol. Representative conformations of these two minima are illustrated as insets in Figure 2. As evident from analysis of their dihedral angles listed in Table 2, these two conformational minima differ chiefly in the disulfide bridge dihedral angles. Specifically, the disulfide dihedral angle defined by atoms C_β-S-S-C_β of D-Pen2 and D-Pen5, as well as the dihedrals χ1 and χ2 of both D-Pen2 and D-Pen5 defined by atoms N-C_α-C_β-S and C_α-C_β-S-S, respectively, exhibit significantly different values in minima A and A′, with consequent variations in the conformation of the 14-membered ring of DPDPE.

Table 2.

Dihedral angles of representative conformations of DPDPE in water, along with corresponding values for the three molecules in the unit cell of the x-ray structure of DPDPE, and from the NMR structure. The χ1 and χ2 dihedral angles of the disulfide bridge between D-Pen2 and D-Pen5 are defined by atoms N-C_α-C_β-S and C_α-C_β-S-S, respectively.

Residue	Angle	A	A′	X-Ray 1	X-Ray 2	X-Ray 3	NMR
Tyr1	ψ	149.1	147.7	−157	9	−175	141
D-Pen2	ϕ	89.0	93.7	110	129	129	139
	ψ	42.8	36.9	−147	−152	−145	−151
Gly3	ϕ	−93.4	−115.6	98	107	99	70
	ψ	−124.2	−61.9	−141	−138	−138	88
Phe4	ϕ	−80.6	−78.3	−74	−76	−81	80
	ψ	−16.6	−41.0	−36	−30	−18	−70
D-Pen5	ϕ	116.3	112.7	126	116	106	144
Side chains
Tyr1	χ1	−173.3	−176.4	−68	−71	−61
	χ2	63.0	48.9	118	99	127
Phe4	χ1	−73.3	−58.0	−67	−67	−69
	χ2	−75.8	−67.6	−85	−80	−85
D-Pen2	χ1	−34.9	−59.0	−58	−59	−54	−51
	χ2	−71.2	−170.6	−73	−73	−74	−75
S-S bridge	S-S	−116.3	115.3	−105	−108	−104	−109
D-Pen5	χ2	−170.9	67.1	174	176	168	174
	χ1	−30.4	−72.5	−51	−46	−52	−47

The published X-ray crystal structure of DPDPE¹⁴ contains three molecules in the unit cell, and we report their dihedral angles in Table 2. Comparison of these experimental structures with the two minima shows that the majority of dihedrals in minimum A (the most stable according to our results) are in fair agreement with those of the experimental structures. One of the main differences is in the side chain orientation of Tyr1, which shows χ1 values that range from −173° to −176° in A and A′ compared to a −61° to −71° range in the three crystal molecules. This difference, however, may be due to crystal contacts in the unit cell. The experimental DPDPE structure obtained by NMR¹² is also close to minimum A. A structural overlap (data not shown) shows that small differences are focused on the backbone dihedral angles of D-Pen2 and Gly3 and on the orientation of the Phe4 side chain.

Putative Bioactive Conformations

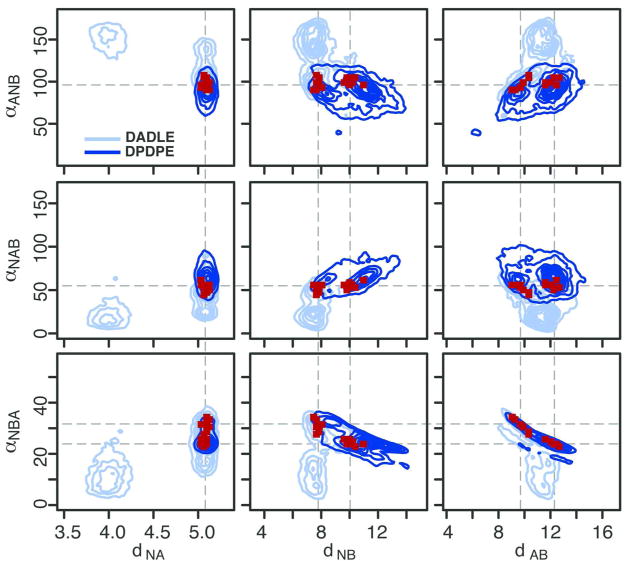
While there is no guarantee that the bioactive conformations of DADLE and DPDPE, i.e., the states acquired by the ligands in interaction with the receptor, correspond to the lowest free-energy minima in solution, it is reasonable to assume that they are present in solution with a non-negligible probability. Assuming that the two cognate peptide agonists follow a similar recognition pattern, we sought to identify the conformational states shared by the two penta-peptides in the search for possible bioactive conformations. To this end, we evoked classical DOP receptor pharmacophore models for recognition,²⁰ and described the sampled conformations of DADLE and DPDPE in terms of 3 distances (d_NA, d_NB, and d_AB) and 3 angles (α_ANB, α_NAB, and α_NBA) between three pharmacophoric points: the backbone nitrogen of Tyr1 (N), the centroid of the aromatic ring of Tyr1 (A), and the centroid of the aromatic ring of Phe4 (B). Thus, the free-energies reported in Figures 1 and 2 for DADLE and DPDPE, respectively, were recast using a 6-dimensional free-energy function epitomizing this pharmacophore. Selected projections of this function are reported in Figure 3 for both DADLE and DPDPE. While projections involving the d_NA distance and the αNBA angle are qualitatively similar for the two peptides, others exhibit hardly overlapping low-free-energy regions.

Figure 3. Overlap of the pharmacophoric parameters calculated for DADLE and DPDPE.

2D projections of the 6D free-energy functions (in light and dark blue, for DADLE and DPDPE, respectively) epitomizing the pharmacophoric model. Dark red points correspond to regions where free-energies are non negligible for both peptides.

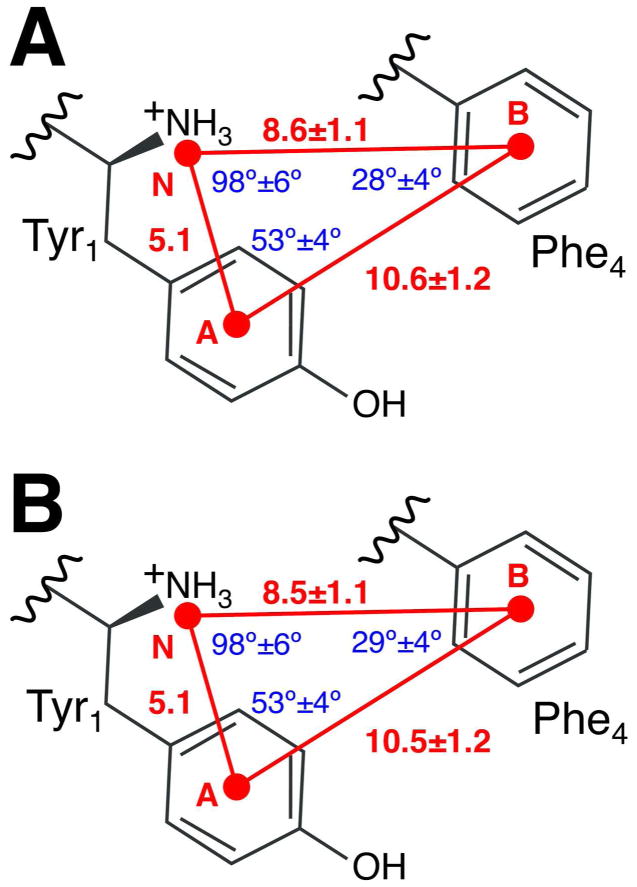
Regions sampled by both peptides are indicated in red on the 2-dimensional projections in Figure 3. We note that they do not correspond to minima of the bulk free-energy, indicating the possibility that the protein environment radically influences the conformational flexibility of the peptides upon their entrance in the binding pocket. Conformations in the two bias-exchange trajectories within these regions were extracted for both DADLE and DPDPE, and clustered. For each peptide, two clusters were obtained (see Table S1), visually corresponding to the two disconnected regions in the projections of Figure 3. The values of the most populated cluster for each peptide (respectively 83% and 68% of the total population), which represent putative binding conformations of the two peptides, are reported graphically in Figure 4. Values of the dihedral angles of representative conformations for each cluster are reported in Tables S2 and S3 for DADLE and DPDPE, respectively. Location of the representative structures of these peptides are indicated with stars on the free-energy maps of Figure 1 and Figure 2.

Figure 4. Graphical sketch of the pharmacophoric model.

Values of the pharmacophoric parameters of the most populated cluster (Cluster 1) for DADLE (in Panel A) and DPDPE (in Panel B).

CONCLUSIONS

We explored the conformational preferences of two DOP receptor peptides using both biased and unbiased MD approaches. As expected, the linear penta-peptide DADLE was found to be rather flexible in solution, as demonstrated by the large number of different metastable states identified in its free-energy surface. In contrast, the DPDPE 14-membered ring exhibits a more rigid structure, which required longer simulation times for a thorough conformational sampling.

While we did not attempt to derive the free-energy profile of the two penta-peptides in the receptor binding pocket, we inferred possible bioactive conformations of DADLE and DPDPE. Using the working hypothesis of a common binding mode for the two DOP-receptor agonists and a classical DOP receptor pharmacophore model for ligand recognition, we extracted common conformations in the DADLE and DPDPE trajectories that satisfied the pharmacophores requirements. Our analysis confirmed that the most stable structures of DADLE and DPDPE in the solvent are most likely not the ones that bind to the receptor. Yet, putative bioactive conformations of these two penta-peptides were inferred from their conformational free-energy profiles.