Interstitial Growth and Remodeling of Biological Tissues: Tissue Composition as State Variables

Abstract

Growth and remodeling of biological tissues involves mass exchanges between soluble building blocks in the tissue’s interstitial fluid and the various constituents of cells and the extracellular matrix. As the content of these various constituents evolves with growth, associated material properties, such as the elastic modulus of the extracellular matrix, may similarly evolve. Therefore, growth theories may be formulated by accounting for the evolution of tissue composition over time in response to various biological and mechanical triggers. This approach has been the foundation of classical bone remodeling theories that successfully describe Wolff’s law by establishing a dependence between Young’s modulus and bone apparent density and by formulating a constitutive relation between bone mass supply and the state of strain. The goal of this study is to demonstrate that adding tissue composition as state variables in the constitutive relations governing the stress-strain response and the mass supply represents a very general and straightforward method to model interstitial growth and remodeling in a wide variety of biological tissues. The foundation for this approach is rooted in the framework of mixture theory, which models the tissue as a mixture of multiple solid and fluid constituents. A further generalization is to allow each solid constituent in a constrained solid mixture to have its own reference (stress-free) configuration. Several illustrations are provided, ranging from bone remodeling to cartilage tissue engineering and cervical remodeling during pregnancy.

1. Introduction

Growth processes are fundamental in nature, whether they occur in biological or nonliving systems (Taber, 1995; Ambrosi et al., 2011). Theoretical frameworks for modeling growth can be used to gain insight into growth mechanics, by examining the theoretical feasibility of hypothesized growth mechanisms. Growth models may also be used to understand the evolution of tissue structure and function and to optimize growth conditions in tissue engineering studies. In the biomechanics literature, theoretical frameworks have addressed the challenge of modeling the adaptive response of tissues to loading (Cowin and Hegedus, 1976; Cowin, 1983; Huiskes et al., 1987; Weinans et al., 1992; Taber and Humphrey, 2001; Humphrey, 2009); describing morphogenesis using a kinematic description of growth (Skalak et al., 1982, 1997; Rodriguez et al, 1994; Menzel and Kuhl, 2012); accounting for distinct growth histories of the constituents of heterogeneous mixtures (Humphrey and Rajagopal, 2002; Garikipati et al., 2004; Ateshian, 2007; Wan et al., 2009; Ateshian and Humphrey, 2012; Cowin and Cardoso, 2012); describing the evolution of residual stresses due to growth (Skalak et al., 1996; Hoger, 1997; Taber and Humphrey, 2001; Guillou and Ogden, 2006; Ateshian and Ricken, 2010; Menzel and Kuhl, 2012); accounting for chemical reactions among fluid and solid constituents of a heterogeneous mixture (Garikipati et al., 2004; Ateshian, 2007; Narayanan et al., 2009; Ateshian, 2011); describing cell growth via osmotic mechanisms (Ateshian et al., 2009a, 2012); and other related phenomena.

Mixture theory (Truesdell and Toupin, 1960; Bowen, 1968, 1969) has been favored in many recent studies to describe growth mechanics (Humphrey and Rajagopal, 2002; Garikipati et al., 2004; Ateshian, 2007; Cowin and Cardoso, 2012). In this framework, interstitial growth represents the addition (or removal) of mass from the porous solid matrix of a mixture whose interstitial fluid provides the building blocks (or nutrients) for growth in the form of solutes mixed in a solvent. As such, the mass content, or composition, of the mixture represents a set of state variables in this growth framework (Ateshian, 2007; Ateshian and Ricken, 2010; Ateshian, 2011). Lengthy background reviews of the mixture theory framework have been presented elsewhere (Epstein and Maugin, 2000; Ateshian, 2007; Cowin and Cardoso, 2012). Given these extensive backgrounds, the objective of this review is to reformulate the salient aspects of mixture growth theory using a didactic approach that extends the framework of elasticity theory by simply adding mass content as a set of state variables. It is shown that this approach reiterates the pioneering work of Cowin and Hegedus (1976), who formulated a growth framework responsive to the loading environment without appealing explicitly to mixture theory, yet producing most of the salient findings from those subsequent derivations. This framework also serves as the foundation of the popular bone remodeling theory proposed by Huiskes and co-workers (Huiskes et al., 1987; Weinans et al., 1992; Mullender et al., 1994). Other examples of this growth framework are provided, which exhibit increasing levels of complexity with regard to dependence on composition, to illustrate the breadth and depth of this theoretical foundation for growth. Examples from cartilage tissue engineering provide illustrations of the interaction of proteoglycan growth and glucose supply, as well as the growth of collagen having different reference configurations at different times in the growth process. Another example proposes an approach for modeling the dramatic changes in the material behavior of the cervix over the normal period of gestation by considering the turnover of collagen from mature crosslinked fibers to immature loosely connected fibrils.

2. Growth Mechanics

2.1. Hyperelasticity

In classical hyperelasticity theory, the constitutive relation relating stress to strain in a solid is derived from an energy potential, usually described as the strain energy density, and more generally known as the Helmholtz free energy density. This energy potential is conventionally expressed as the free energy in the current configuration per volume of the solid in the reference configuration, where the reference configuration represents a stress-free state; it is denoted here as Ψ_r. Since all strain measures may be derived from the deformation gradient of the solid, F^s, the Helmholtz free energy density may be constitutively expressed as a function of this measure, Ψ_r (F^s). Following standard procedures involving entropy inequality, the Cauchy stress is then given by

$$\mathbf{\sigma }=\frac{1}{J^s}\frac{\partial {\mathrm{\Psi }}_r}{\partial {\mathbf{F}}^s}·{({\mathbf{F}}^s)}^T,$$ (2.1)

where J^s = det F^s. Any number of constitutive relations may be formulated for Ψ_r (F^s) and their associated material properties are necessarily constants. This constitutive formulation may be slightly generalized by letting the free energy also depend on absolute temperature, θ, but not its gradient, thus limiting analyses to isothermal problems. With Ψ_r (θ, F^s) the material properties associated with the stress-strain response may vary with temperature, and the entropy density (entropy per volume of the solid in the reference configuration) of the system is no longer zero,

$$H_r=-\frac{\partial {\mathrm{\Psi }}_r}{\partial \theta }.$$ (2.2)

When solving problems in hyperelasticity, it is necessary to also recognize that the mass density ρ^s of the solid is constrained by the relation

$${\rho }^s={\rho }_r^s/J^s,$$ (2.3)

where ${\rho }_r^s$ is the mass density in the reference configuration, which is invariant. This constraint is obtained from the balance of mass relation for the solid,

$$\frac{D^s{\rho }^s}{Dt}+{\rho }^s\text{div}{\mathbf{v}}^s=0,$$ (2.4)

where v^s is the velocity of the solid and D^s (·) /Dt is the material time derivative in the spatial frame, following the solid. Recognizing from kinematics that div v^s = (J^s)⁻¹ (D^sJ^s/Dt), the mass balance equation may also be written as D^s (ρ^sJ^s) /Dt = 0, which may be integrated to produce the result of eq.(2.3). Equations (2.1)–(2.4) provide a succinct summary of the classical framework for hyperelasticity in the absence of any growth processes.

2.2. Interstitial Growth of a Single Solid Constituent

Interstitial growth is the process that adds or removes solid mass at locations inside a solid material. For this process to occur, there must be interstitial space within this material to allow atoms or molecules to bind to the underlying substrate. For biological tissues, this is typically the pore space normally filled with the interstitial fluid that carries those molecules. Therefore, it is helpful to recognize the solid material as a porous matrix, whose pores fill with additional solid material during growth or conversely become more porous with negative growth (desorption of the solid). Growth may occur within cells as well as in the extracellular matrix (ECM) of a tissue. Both the cell and the ECM may be treated as mixtures with a porous matrix and an interstitial fluid consisting of a solvent and solutes. In a porous solid, the solid mass density ρ^s is called the apparent density, since it measures the mass of the solid per volume of an elemental region that contains porous solid and interstitial fluid (the mixture). Since mass is exchanged between the porous solid and the interstitial fluid, the mass balance relation for the solid must account for this exchange,

$$\frac{D^s{\rho }^s}{Dt}+{\rho }^s\text{div}{\mathbf{v}}^s={\mathrm{\rho ̂}}^s,$$ (2.5)

with ρ̂^s representing the mass supply to the solid from all solute species in the interstitial fluid. Using the kinematic relation relating the divergence of the solid velocity to the determinant of the deformation gradient, this balance relation may be rewritten as

$$\frac{D^s{\rho }_r^s}{Dt}={\mathrm{\rho ̂}}_r^s,$$ (2.6)

where ${\rho }_r^s={\rho }^s{J}^s$ and ${\mathrm{\rho ̂}}_r^s={\mathrm{\rho ̂}}^s{J}^s$. This relation shows that ${\rho }_r^s$ is no longer invariant when growth occurs, though its evolution over time may be obtained by integrating eq.(2.6) when given a suitable constitutive relation for ${\mathrm{\rho ̂}}_r^s$. This type of constitutive relation may be derived from chemistry (Prud’homme, 2010) to determine the rate of the chemical reaction for the exchange of mass with the solid, or from mechanics, as proposed by Cowin and Hegedus (1976) and further illustrated below.

Since ${\rho }_r^s$ is not constant in a growth process, it must enter the list of state variables on which ${\mathrm{\Psi }}_r^s$ and ${\mathrm{\rho ̂}}_r^s$ may depend. Similarly, since chemical reactions involve concentrations of all reactants and products, the apparent densities ρ^ι of the interstitial fluid species (solutes and solvent) must also be included as state variables, although the notation remains more consistent when using ${\rho }_r^{\iota }=J^s{\rho }^{\iota }$ instead. Thus,

$${\mathrm{\Psi }}_r={\mathrm{\Psi }}_r(\theta ,{\mathbf{F}}^s,{\rho }_r^s,{\rho }_r^{\iota }),$$ (2.7)

where it is implicit that there are multiple fluid species ι in this representation. Here, F^s is the overall deformation gradient of the porous solid matrix, representing a combination of the matrix skeleton deformation as well as the change in pore volume. With this list of state variables, the Cauchy stress and entropy are still given by eqs.(2.1) and (2.2), respectively. In addition, it may be noted that

$${\mu }^{\alpha }=\frac{\partial {\mathrm{\Psi }}_r}{\partial {\rho }_r^{\alpha }},\alpha =s,\iota$$ (2.8)

represents the chemical potential of mixture constituent α. These chemical potentials appear in the entropy inequality, where they help determine when chemical reactions involved in the growth process become thermodynamically favorable (Ateshian, 2007; Ateshian and Ricken, 2010). Equations (2.1)–(2.2) and (2.6)–(2.8) summarize the salient relations for growth mechanics.

Example 1. Adaptive Bone Remodeling

To illustrate the application of this growth mechanics framework, consider the ‘adaptive bone-remodeling’ theory of Huiskes and co-workers (Huiskes et al., 1987; Weinans et al., 1992; Mullender et al., 1994), which proposed a quantitative rule for Wolff’s law to describe how trabecular bone adapts its density in response to its loading environment. Though these authors did not use mixture theory to develop their model, it is straightforward to place their formulation within that framework. Accordingly, the state variables in their model reduce to (${\mathbf{F}}_r^s,{\rho }_r^s$), with nutrients ${\rho }_r^{\iota }$ needed for bone growth becoming implicit. Bone cells that deposit or remove bone matrix are also implicit in this model. The strain energy density they adopted was that of linear isotropic elasticity,

$${\mathrm{\Psi }}_r^s({\mathbf{F}}_r^s,{\rho }_r^s)=\frac{E_Y}{2(1+\nu )}[\frac{\nu }{1-2\nu }{(\mathrm{t}\mathrm{r}\mathit{\epsilon })}^2+\mathrm{t}\mathrm{r}{\mathit{\epsilon }}^2],$$ (2.9)

where ε is the infinitesimal strain tensor for the solid matrix, E_Y is Young’s modulus and ν is Poisson’s ratio. Based on prior findings by many investigators (Carter and Hayes, 1976, 1977; Currey, 1988; Rice et al., 1988), they proposed that E_Y depended on the apparent bone density ${\rho }_r^s$ according to a power law,

$$E_Y=c{({\rho }_r^s)}^{\gamma },$$ (2.10)

where c and γ are material constants. Thus, changes in bone density automatically produced changes in material properties. They also proposed that the mass supply to the solid was proportional to the difference between the specific strain energy (strain energy per mass of the solid) in the current state and a reference value k, representing homeostasis,

$${\mathrm{\rho ̂}}_r^s({\mathbf{F}}_r^s,{\rho }_r^s)=B(\frac{{\mathrm{\Psi }}_r}{{\rho }_r^s}-k),$$ (2.11)

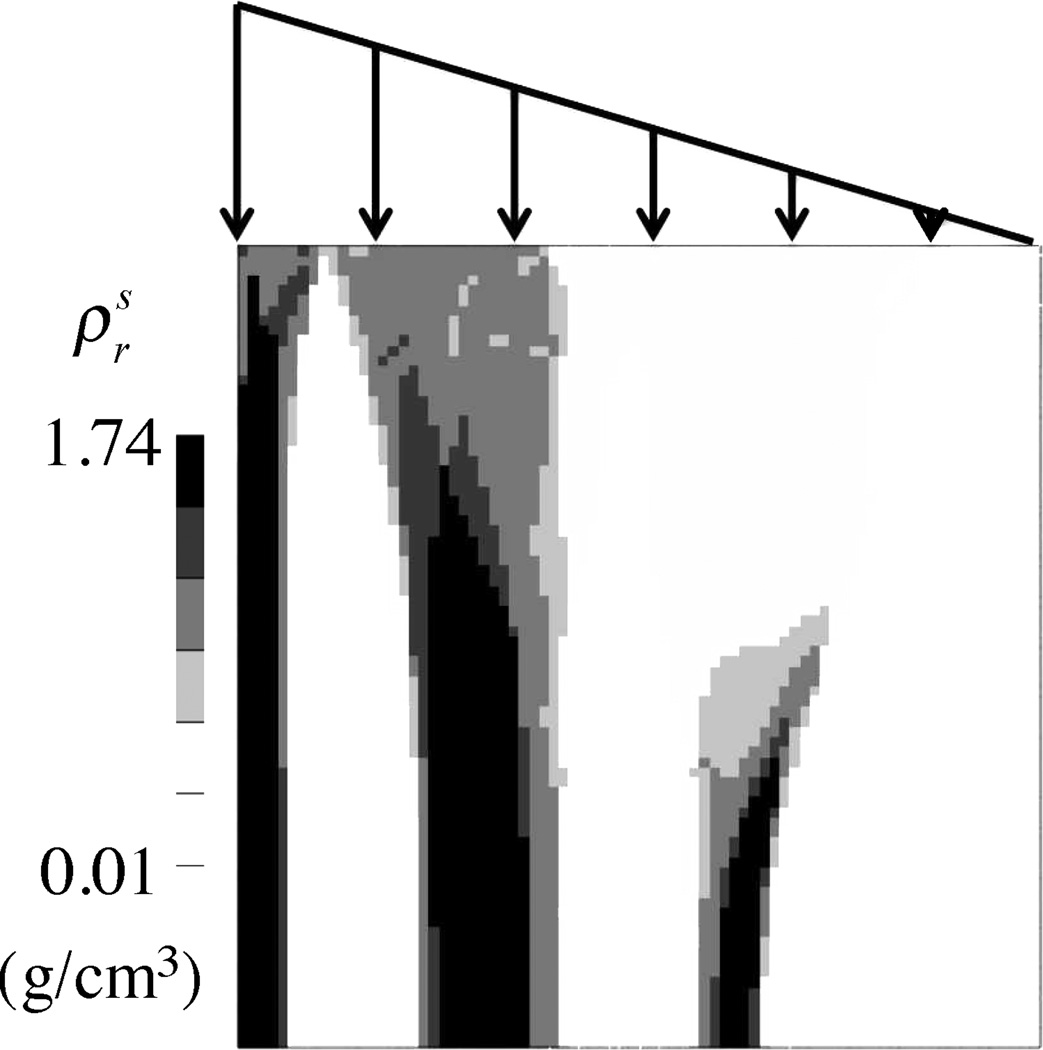
where B is a material constant. This constitutive model for the bone mass supply represented their proposed embodiment of Wolff’s law. This model could predict bone deposition (when ${\mathrm{\rho ̂}}_r^s>0$), bone resorption (when ${\mathrm{\rho ̂}}_r^s<0$), or homeostasis (when ${\mathrm{\rho ̂}}_r^s=0$). Substituting eq.(2.11) into eq.(2.6) produces an ordinary differential equation for ${\rho }_r^s$, whose solution provides the time evolution of the bone apparent density at every point in the material in response to the local loading environment. These authors also clarified that the apparent density is bounded on the lower end by zero (total bone resorption) and on the upper end by the true density ${\rho }_T^s$ of bone (e.g., the cortical bone density), when the pores have been completely filled, $0\le {\rho }_r^s\le {\rho }_T^s$. An illustration of this model is presented in Figure 4.1, which shows how a square sample of material which has an initially uniform density ${\rho }_r^s$ evolves intro a strut-like structure when subjected to a linearly varying load distribution. This model (Weinans et al., 1992) and its extensions (Mullender et al., 1994), which have proved to be quite successful at reproducing Wolff’s law (Van Rietbergen et al., 1993; Weinans et al., 1993), represent an excellent illustration of an interstitial growth framework. In this example the form of the constitutive stress-strain relation does not vary with growth, eq.(2.9), though its material properties evolve based on the bone content, eq.(2.10).

Figure 4.1.

Simulation of bone remodeling rule in a square region (10 cm × 10 cm) subjected to a linearly varying traction on the top face, using the approach of Weinans et al. Weinans et al. (1992) as reformulated in a mixture growth framework, Eqs.(2.6) & (2.9)–(2.11). The initial apparent density was uniform and equal to 0.8 g/cm³. Other properties: c = 10⁹ dyne/cm²/ (g/cm³)², γ = 2, k = 200 dyne · cm/g, B = 10⁻³ g²/(dyne · cm⁴ · s). This example was analyzed in the open-source, customizable finite element program FEBio (www.febio.org) Maas et al. (2012).

Huiskes and co-workers did not explicitly attribute their evolution equation for apparent bone density to the equation of mass balance, eq.(2.6), and the formulation of an explicit constitutive relation for the mass supply, eq.(2.11), even though their equations clearly fit within that framework. In a historical context, it is Cowin and Hegedus (1976) who derived a general framework that explicitly incorporated the mass balance relation of eq.(2.6), which they suitably converted to provide a relation for the trabecular bone volume fraction. Furthermore, their growth model (Hegedus and Cowin, 1976) provided an explicit constitutive relation for the mass supply as a function of the strain. In the current notation, they proposed a general form

$${\mathrm{\rho ̂}}_r^s({\mathbf{F}}_r^s,{\rho }_r^s)=a({\rho }_r^s)+\mathbf{A}({\rho }_r^s):\mathit{\epsilon }+\mathit{\epsilon }:\mathbf{ℬ}({\rho }_r^s):\mathit{\epsilon },$$ (2.12)

where a is a scalar function, A is a second-order tensor function, and ℬ is a fourth-order tensor function of the apparent bone density. This form encompassed in principle the subsequent approach by Huiskes and co-workers, with a = −B k, A = 0, and $\mathbf{ℬ}=\frac{B{E}_Y}{2{\rho }_r^s(1+\nu )}(\frac{\nu }{1-2\nu }\mathbf{I}\otimes \mathbf{I}+\mathbf{I}\overline{\underset{¯}{\otimes }}\mathbf{I})$, where, in a Cartesian frame, (I ⊗ I)_ijkl = δ_ijδ_kl and ${(\mathbf{I}\overline{\underset{¯}{\otimes }}\mathbf{I})}_{ijkl}=\frac{1}{2}({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk})$.

Example 2. Proteoglycan Growth in Cartilage Tissue Engineering

Cartilage tissue engineering represents a good illustration of growth mechanics of a solid constituent in response to nutrients in the interstitial fluid (Obradovic et al., 2000; Dimicco and Sah, 2003; Nikolaev et al., 2010). Unlike bone, cartilage does not appear to obey a clear adaptive rule for the dependence of growth on the state of loading.¹ Cartilage tissue engineering studies suggest a more prosaic growth process where deposition of extracellular matrix products depends primarily on the availability of the right set of nutrients for the cells (Obradovic et al., 1999; Heywood et al., 2006). For example, the synthesis rate for proteoglycans is critically dependent on the sufficient availability of glucose in the growth medium (Heywood et al., 2006; Cigan et al., 2013). Therefore, in this example, the state variables may be summarized as (F^s, ${\rho }_r^{\text{CS}},{\rho }_r^{\text{Glu}}$), where CS=chondroitin sulfate (the dominant glycosaminoglycan in cartilage proteoglycans), and Glu=glucose. In this analysis, CS belongs to the solid matrix (which also includes a scaffold) and Glu belongs to the interstitial fluid. The dependency of proteoglycan synthesis rate on glucose concentration is typically not a smoothly varying function: Above a certain threshold, the synthesis rate holds at a constant value; below that threshold, the synthesis rate drops dramatically to near-zero values (Heywood et al., 2006; Cigan et al., 2013). The transition between these two regimes appears to be relatively abrupt, therefore the formulation of a constitutive relation for the CS mass supply as a function of glucose concentration may be as simple as a step function,

$${\mathrm{\rho ̂}}_r^{\text{CS}}={\mathrm{\rho ̂}}_0^{\text{CS}}H({\rho }_r^{\text{Glu}}-{\rho }_0^{\text{Glu}}),$$ (2.13)

where ${\rho }_0^{\text{Glu}}$ is the threshold concentration of glucose in the growing tissue, H (·) is the Heaviside unit step function, and ${\mathrm{\rho ̂}}_0^{\text{CS}}$ is the synthesis rate when the glucose concentration ${\rho }_r^{\text{Glu}}$ exceeds this threshold value. Other nutrients and cytokines also play a role, such as the timed exposure of the tissue construct to certain growth factors (Lima et al., 2007; Byers et al., 2008), which may be similarly taken into account in the CS mass supply constitutive relation. Substituting eq.(2.13) into the mass balance relation in eq.(2.6) and integrating the resulting equation produces a linearly increasing value for the CS content with time t, ${\rho }_r^{\text{CS}}={\mathrm{\rho ̂}}_0^{\text{CS}}t$, as long as the glucose concentration exceeds the minimum threshold value for growth. Experimental observations confirm this simple relation in a well-controlled environment (Cigan et al., 2013).

Despite its apparent simplicity, the relation of eq.(2.13) can predict well-recognized phenomena in cartilage tissue engineering, such as the inhomogeneous growth of proteoglycans in tissue constructs. Experimental studies have shown that proteoglycan content tends to be greatest near the periphery of the construct and lowest at its center, producing correspondingly inhomogeneous compressive properties throughout the construct (Hung et al., 2003, 2004; Kelly et al., 2006). This type of inhomogeneous growth can be predicted by combining the relation of eq.(2.13) with equations that account for transport and consumption of glucose throughout the construct. In particular, using the current notation, the mass balance relation for glucose is

$$\frac{D^s{\rho }_r^{\text{Glu}}}{Dt}+J^s\text{div}{\mathbf{m}}^{\text{Glu}}={\mathrm{\rho ̂}}_r^{\text{Glu}},$$ (2.14)

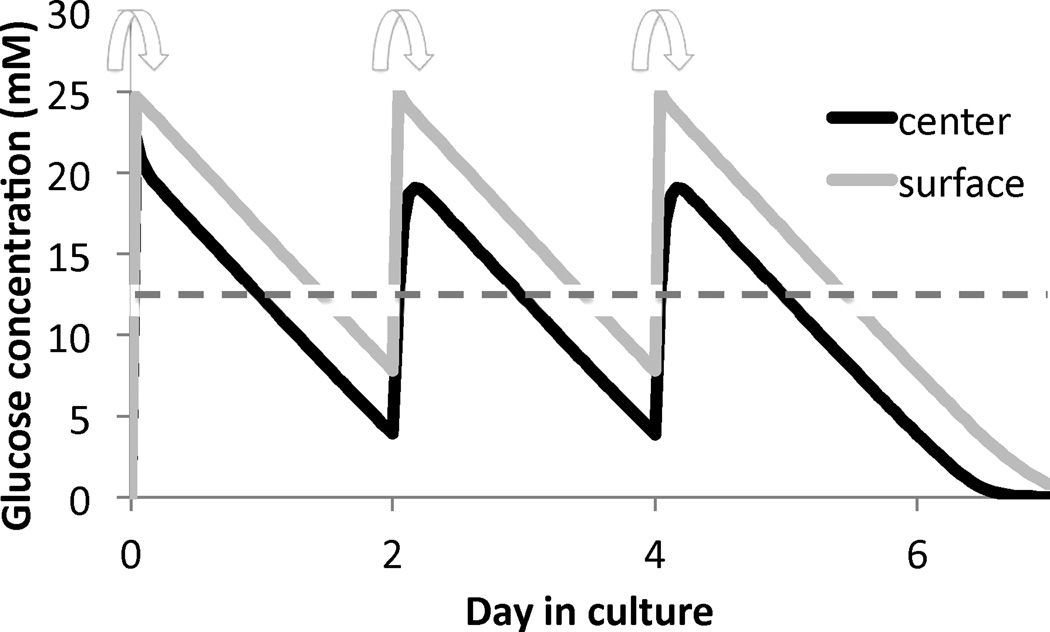
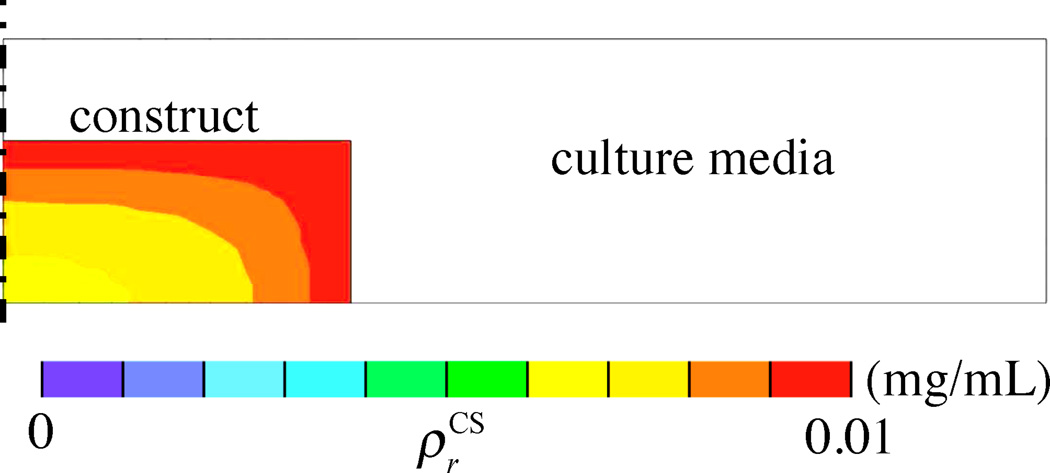
where m^Glu is the mass flux of glucose relative to the tissue solid matrix. A relation between m^Glu and ${\rho }_r^{\text{Glu}}$ may be given by Fick’s law. For example, assume that a cylindrical tissue construct, 10 mm in diameter and 2.3 mm thick, is cultured in a well-mixed bath containing 2.5 mL of culture media having an initial concentration of 25 mM of glucose (refreshed at days 0, 2, and 4 each week) (Figure 4.2). Consider that the glucose is consumed by cells at a rate governed by Michaelis-Menten kinetics, ${\mathrm{\rho ̂}}_r^{\text{Glu}}=-V_{\mathit{\text{max}}}{\rho }_r^{\text{Glu}}/(K_m+{\rho }_r^{\text{Glu}})$ (Sengers et al., 2005), using parameters V_max and K_m guided by experimental measurements (Cigan et al., 2013). The time evolution of the concentrations of glucose at the innermost center point and at the surface of the construct is shown in Figure 4.3 for a one-week culture period. These finite element predictions show that glucose concentrations reduce rapidly every day as a result of uptake by chondrocytes, and these concentrations are substantially lower at the center of the construct because chondrocytes that are closer to the surface consume the glucose first. Based on experimental measurements for chondrocyte seeding densities of 30 × 10⁶ cells/mL, proteoglycans are synthesized according to eq.(2.13) only when the minimum glucose threshold for growth, ${\rho }_0^{\text{Glu}}$, is equivalent to a concentration of 12.5 mM (Cigan et al., 2013). After one week in culture the proteoglycan growth (${\rho }_r^{\text{CS}}$) shows an inhomogeneous distribution as displayed in the prediction of Figure 4.4. This result is consistent with experimental observations of proteoglycan distribution in large cartilage tissue constructs (Hung et al., 2004; Bian et al., 2009a).

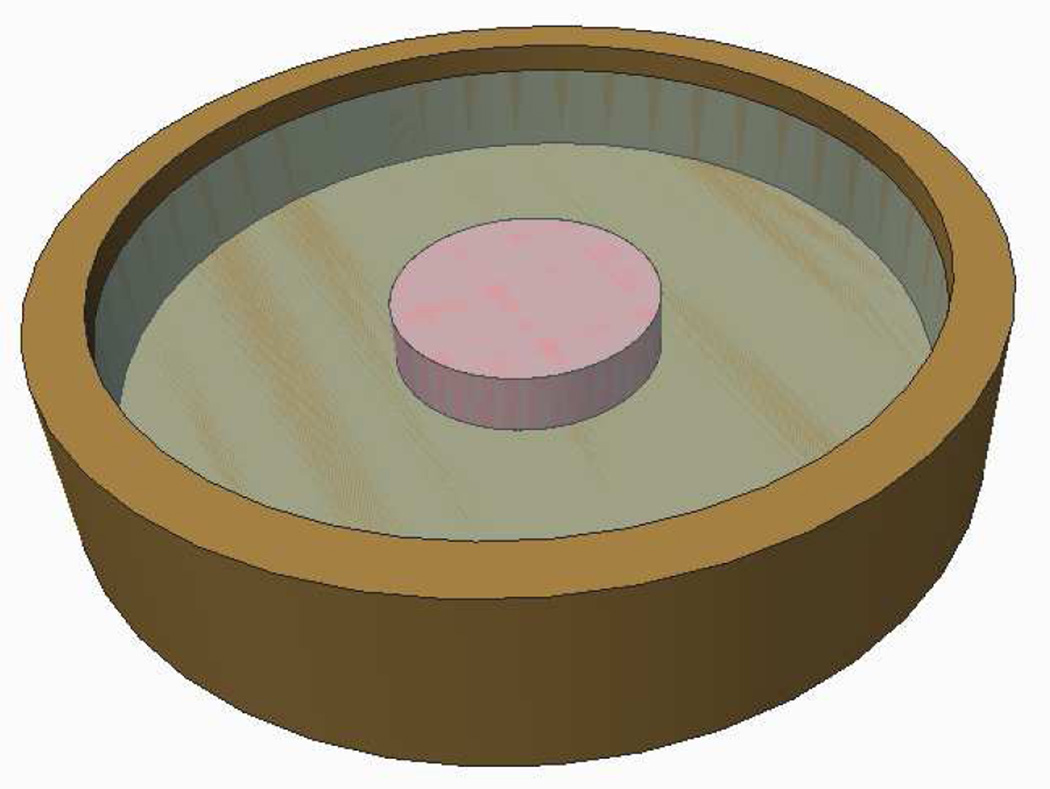
Figure 4.2.

An engineered cartilage construct (10 mm diameter × 2.3 mm thick) is cultured in a 30 mm diameter dish containing 2.5 mL of media. The initial concentration of glucose is 25 mM and media is refreshed thrice a week, on a 2-2-3 day schedule. The culture media is assumed to be well stirred. Glucose diffuses from the bath into the construct and is taken up by chondrocytes at a rate guided by Michaelis-Menten kinetics Sengers et al. (2005).

Figure 4.3.

Glucose concentration at the center and surface of the engineered cartilage construct, over time in culture. Arrows indicate times when culture media is refreshed. The dashed line represents the critical threshold in glucose concentration necessary for proteoglycan synthesis. Simulations were performed in the open-source, customizable finite element program FEBio (www.febio.org) Maas et al. (2012).

Figure 4.4.

Spatial distribution of chondroitin sulfate, ${\rho }_r^{\text{CS}}$, in the engineered cartilage construct at the end of one week. Predictions are based on the assumption that CS growth only occurs when glucose concentration exceeds the threshold value of 12.5 mM. Results only show a half-section of the construct and culture media bath, since axisymmetric conditions were assumed.

2.3. Effects of Interstitial Fluid Pressure on Residual Stresses

For biological tissues, it is often convenient to assume that the material forming the skeleton of the porous solid, as well as each of the interstitial fluid constituents, is intrinsically incompressible. The mixture as a whole remains compressible, since fluid may be exchanged with the pore space; thus J^s ≠ 1 under general deformations. However, the incompressibility of all the constituents requires the introduction of a fluid pressure p into the stress relation,

$$\mathit{\sigma }=-p\mathbf{I}+\frac{\partial {\mathrm{\Psi }}_r}{\partial {\mathbf{F}}^s}·{({\mathbf{F}}^s)}^T.$$ (2.15)

This fluid pressure arises from both mechanical and chemical (osmotic) effects. Mechanical effects typically represent pressurization in response to mechanical loading or deformation of the tissue, whereas osmotic effects arise from imbalances in the concentrations of solutes between the interstitial space and the surrounding environment. Imbalances in solute concentrations may arise from various factors, including electrostatic interactions of ions with charged macromolecules that are fixed to the solid matrix (such as proteoglycans), or selective partitioning of solutes by semi-permeable membranes (as occurs between intracellular and extracellular environments). When the solute partitioning is inhomogeneous throughout a tissue, residual stresses induced by the resulting osmotic pressure may manifest themselves in the form of tissue curling in response to cuts, as shown in articular cartilage (Setton et al., 1998), the aorta and the heart (Chuong and Fung, 1986; Lanir et al., 1996; Guo et al., 2007; Azeloglu et al., 2008; Takamizawa and Hayashi, 1987; Lanir, 2012).

Osmotic pressure arising from electrostatic effects may be described from Donnan equilibrium theory (Overbeek, 1956), which produces a closed-form expression for p when the interstitial fluid contains monovalent counter-ions, such as Na⁺ and Cl⁻. In this case,

$$p=R\theta (\sqrt{{(c^F)}^2+{(2c^{*})}^2}-2c^{*}),$$ (2.16)

where R is the universal gas constant, c^F is the fixed charge density arising from the charged molecules fixed to the solid matrix (charges per volume of interstitial fluid), and c* is the salt concentration in the external environment. For example, in the case of chondroitin sulfate, the charge number of the CS monomer is z^CS = −2, thus the fixed-charge density may be evaluated from

$$c^F=\frac{z^{\text{CS}}}{J^s-{\phi }_r^s}\frac{{\rho }_r^{\text{CS}}}{M^{\text{CS}}},$$ (2.17)

where M^CS is the molar mass of CS and ${\phi }_r^s$ is the volume fraction of the solid matrix relative to the reference configuration (volume of solid in current configuration per volume of mixture in the reference configuration). This expression shows that the fixed charge density depends on the amount of tissue swelling as represented by J^s; with increasing J^s, charges spread further apart, producing a reduction in the magnitude of c^F. Because of the dependence of c^F (and thus p) on J^s, the osmotic pressure in the tissue contributes to the tissue elasticity by a quantity called the osmotic modulus (Azeloglu et al., 2008), a fourth-order tensor whose representation in the spatial frame is

$$\mathbf{\Pi }=-J^s\frac{dp}{d{J}^s}\mathbf{I}\otimes \mathbf{I}+p(2\mathbf{I}\overline{\underset{¯}{\otimes }}\mathbf{I}-\mathbf{I}\otimes \mathbf{I}).$$ (2.18)

Example 3. Cartilage Curling Due to Inhomogeneous Proteoglycan Growth

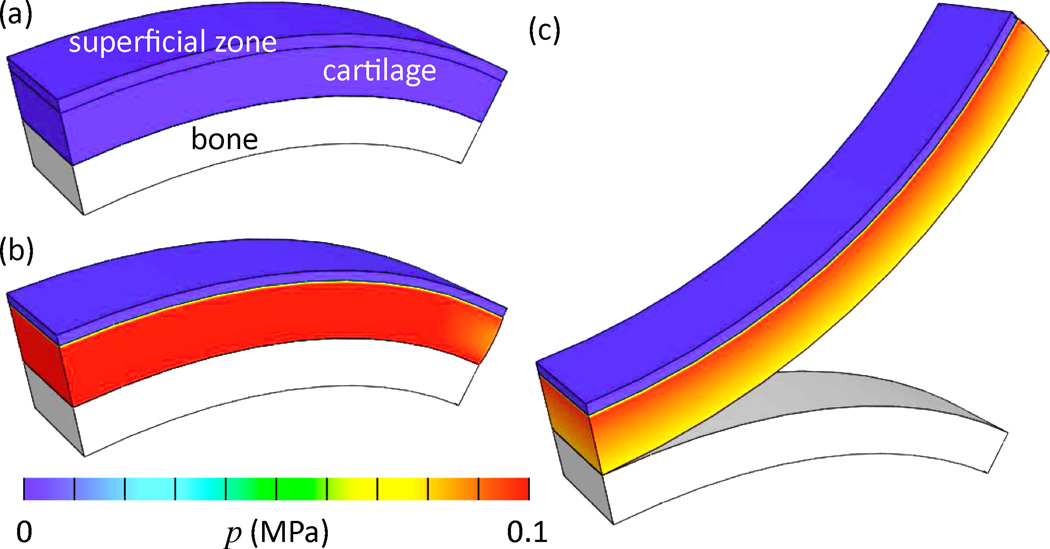
The proteoglycan content in articular cartilage is inhomogeneously distributed throughout the thickness of the articular layer, with the lowest amount found near the articular surface (the superficial zone) (Maroudas, 1979). Consider an articular cartilage layer bound to its subchondral bone, which exhibits this type of inhomogeneous distribution. The cartilage consists of a mixture of a solid matrix (collagen + proteoglycans) and an interstitial fluid (water + Na⁺ + Cl⁻), as described by the triphasic theory of Lai et al. (1991), with a continuous random fiber distribution assumed for the collagen (Ateshian et al., 2009b). The collagen in the superficial zone has a significantly higher tensile stiffness than in the middle and deep zones (material properties ξ = 3 MPa and β = 3 in superficial zone, ξ = 0.05 MPa, β = 3 in middle and deep zones, see below and (Ateshian et al., 2009b) for description of material model). Conversely, the fixed-charge density is significantly lower in the superficial zone ($c_r^F=-20\mathrm{m}\mathrm{E}\mathrm{q}/\mathrm{L}$ versus $c_r^F=-200\mathrm{m}\mathrm{E}\mathrm{q}/\mathrm{L}$, where $c_r^F$ is the value of c^F when J^s = 1). Assume that the stress-free, reference configuration of the collagen matrix corresponds to the configuration when the Donnan osmotic pressure is zero (a configuration that may be theoretically achieved when $c_r^F=0$ or c* → ∞), Figure 4.5a. This means that under in situ conditions (c* = 150 mM), the cartilage layer is in a swollen state, with the swelling pressure being resisted by tensile stresses in the collagen matrix (Figure 4.5b). If the cartilage layer is now cut from the underlying bone, as is commonly done when harvesting cartilage for explant studies, the inhomogeneous swelling pressure throughout the thickness causes the cartilage to curl up, as shown in the simulated results of Figure 4.5c. These predicted results are entirely consistent with experimental observations (Setton et al., 1998). A similar analysis of the opening angle of the aorta is reported by Azeloglu et al. (2008). These examples illustrate the fact that inhomogeneous growth of proteoglycans within a tissue may produce significant residual stresses whose effects may be readily observed experimentally.

Figure 4.5.

Finite element analysis of articular cartilage cut from its underlying subchondral bone. Proteoglycan content, and its associated fixed charge density, are significantly lower in the superficial zone, (a) Reference configuration when the osmotic pressure p is zero, (b) In situ configuration showing inhomoge-neous osmotic pressure distribution when the NaCl concentration in the external environment is physiological (c* = 150 mM). (c) Cartilage cut from bone, showing upward curling consistent with experimental observations (Setton et al., 1998). Simulation performed on FEBio (www.febio.org) (Maas et al., 2012).

2.4. Interstitial Growth of Multiple Solid Constituents

In most biological tissues, the composition of the solid matrix is heterogeneous. Humphrey and Rajagopal (2002) proposed to capture this heterogeneity by allowing the solid matrix to consist of a mixture of multiple solid constituents σ, all of which are constrained to move together (v^σ = V^s for all σ). They used this approach to describe the arterial wall as an intermingled solid mixture of elastin, collagen and smooth muscle cells (Humphrey and Rajagopal, 2002). Since the growth of each of these solid constituents may proceed at different rates, their associated content, ${\rho }_r^{\sigma }$, may evolve over time in response to associated mass supplies ${\mathrm{\rho ̂}}_r^{\sigma }$, following the same mass balance relation of eq.(2.6). Klisch and co-workers used a similar concept to describe the solid matrix of articular cartilage as an intermingled mixture of collagen and enmeshed proteoglycan macromolecules (Klisch et al., 2000, 2003).

Even though the constituents of a constrained solid mixture move together, they are not required to share the same reference (stress-free) configuration. Indeed, depending on the growth history of each constituent and the associated loading environment of the mixture, each solid constituent σ may have its own reference configuration and associated deformation gradient F^σ. Thus, the above formulation for growth may be extended by letting

$${\mathrm{\Psi }}_r={\mathrm{\Psi }}_r(\theta ,{\mathbf{F}}^{\sigma },{\rho }_r^{\sigma },{\rho }_r^{\iota }),$$ (2.19)

where it is implicit that there may be multiple solid constituents σ, just as there may be multiple fluid constituents ι. As shown by Ateshian and Ricken (2010), the stress may then be evaluated from

$$\mathbf{\sigma }=-p\mathbf{I}+\frac{1}{J^s}\sum _{\sigma }\frac{\partial {\mathrm{\Psi }}_r}{\partial {\mathbf{F}}^{\sigma }}·{({\mathbf{F}}^{\sigma })}^T,$$ (2.20)

where s denotes one of these solid constituents σ as the master reference configuration, which is also the reference configuration for the free energy density Ψ_r. According to this growth modeling approach, the reference configuration of solid σ is determined at the time when this material is deposited onto the underlying solid matrix. The specification of this configuration is based on a constitutive assumption. For example, it may be assumed that the reference configuration of σ is given by the current configuration of the solid matrix at the time t_σ when σ is being deposited (Ateshian and Ricken, 2010). In this framework, σ may either refer to different generations of the same solid species (e.g., collagen deposited at different times t_σ), or different solid species that may or may not share the same deposition time (e.g., collagen and elastin).

Example 4. Multigenerational Growth of Engineered Cartilage

Tissue engineering studies of articular cartilage have demonstrated that native levels of proteoglycan content may be achieved successfully when using primary immature bovine chondrocytes seeded in an agarose gel, with a temporary exposure to TGF-β3, cultured for several weeks (Lima et al., 2007; Byers et al., 2008). At high seeding densities, proteoglycan deposition becomes so elevated that the construct volume may swell more than sixfold by the end of the culture period, due to the associated Donnan osmotic pressure, eq.(2.16). Under these conditions, it is not realistic to assume that the collagen fibrils deposited at various time points in culture all share a common reference configuration. Thus, a multigenerational growth model seems to be well suited for describing this type of engineered tissue growth, to account for the rapidly evolving size of the growing construct.

In this example, consider that the engineered cartilage solid matrix is modeled as a mixture of constituents that include: (1) the agarose scaffold, whose reference configuration is the master configuration s; (2) a solid constituent representing the charged proteoglycans, whose evolving content is ${\rho }_r^{\text{CS}}$ (Figure 4.6, Control) and associated fixed charge density is evaluated from eq.(2.17), using the master reference configuration s; and (3) multiple generations of collagen matrix, with each generation σ assumed to represent collagen growth over one day in culture, for a total of 77 days. All daily generations of collagen are assumed to increment its content by the same amount. Each generation is assumed to have the same constitutive relation (a random fiber distribution with material coefficients ξ = 0.1 kPa and β = 2, similar to the model used for cartilage in Example 3), but its reference configuration is given by the current (swollen) configuration on the day that generation is deposited.

Figure 4.6.

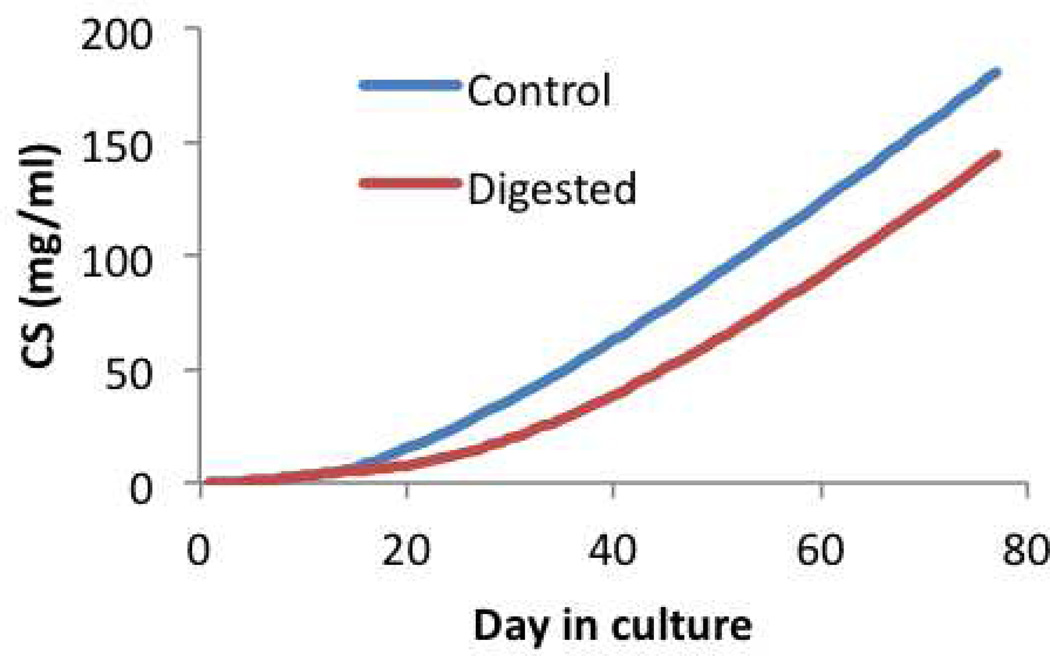
Chondroitin sulfate content in multigenerational growth of engineered cartilage, expressed as ${\rho }_r^{\text{CS}}$. The Digested group is subjected to chondroitinase-ABC digestion on day 14. At day 77, ${\rho }_r^{\text{CS}}=181\text{mg}/\text{mL}$ in the Control group, whereas ${\rho }_r^{\text{CS}}=144\text{mg}/\text{mL}$ in the Digested group.

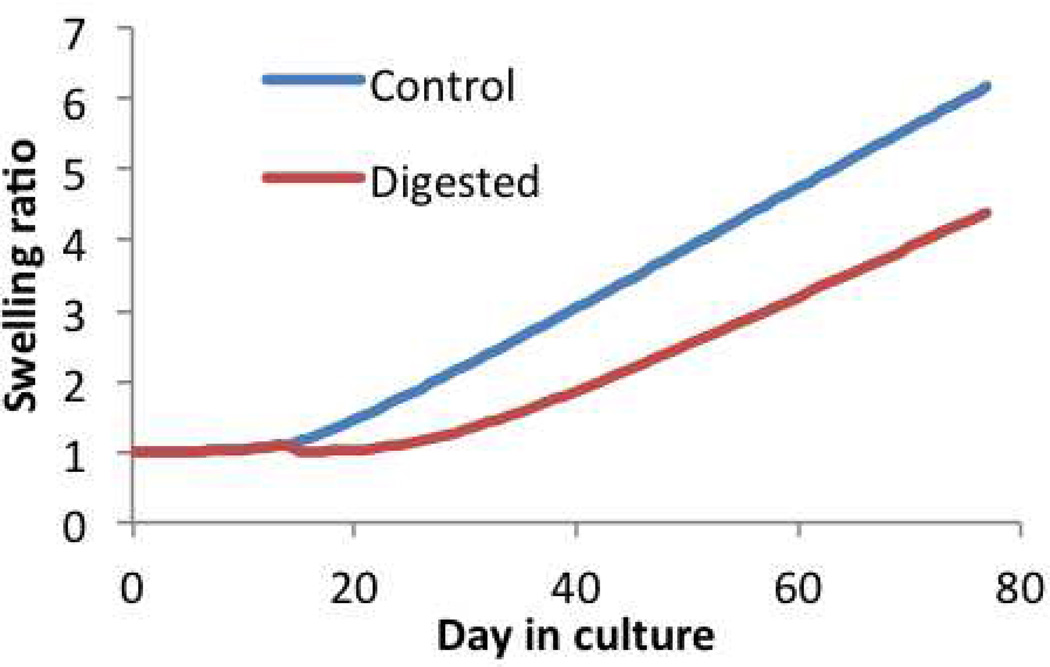
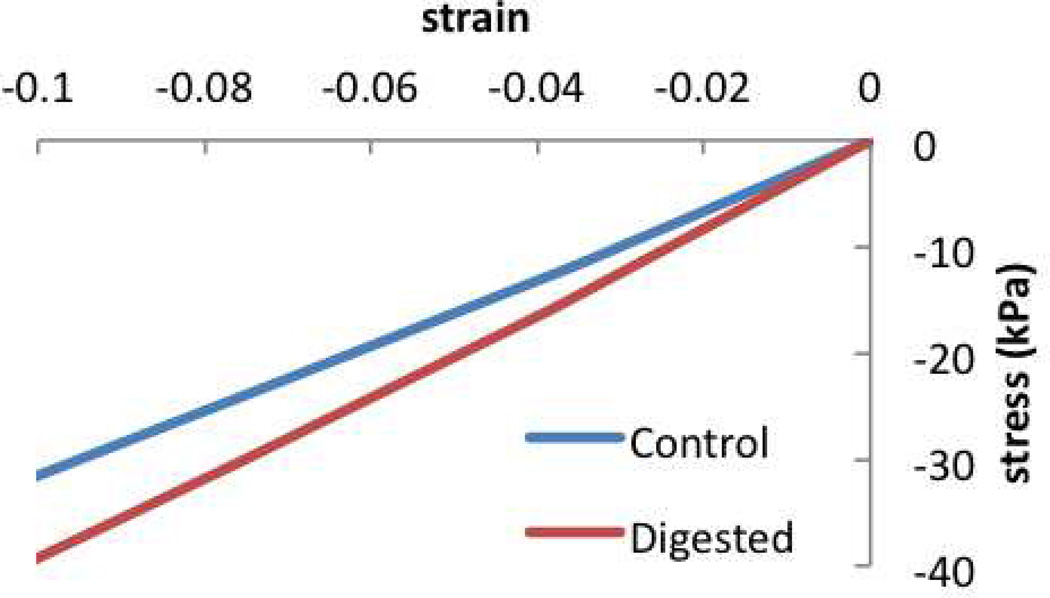
For this model, the predicted construct growth over time is given by J^s, Figure 4.7, showing more than sixfold increase in construct volume over 77 days. As a consequence of this swelling, the proteoglycan content normalized to the construct volume on day 77 is ${\rho }^{\text{CS}}={\rho }_r^{\text{CS}}/J^s=29.2\text{mg}/\text{mL}$. The stress-strain response of the construct on day 77, Figure 4.8, exhibits a compressive Young’s modulus of 0.31 MPa.

Figure 4.7.

Swelling ratio, J^s, of constructs in multigenerational growth of engineered cartilage. At day 77, J^s = 6.2 in the Control group and J^s = 4.4 in the Digested group.

Figure 4.8.

Stress-strain response of constructs in multigenerational growth of engineered cartilage, at day 77. Young’s modulus is evaluated from the slope of this response using linear regression.

Now consider that the tissue construct is treated with chondroitinase ABC (an enzyme which digests the chondroitin sulfate of proteoglycans) on day 14, in an effort to deplete the proteoglycan deposition in the early stages of tissue growth. This treatment does not prevent chondrocytes from depositing more proteoglycans and, eventually by day 77, the proteoglycan content rises again as shown in Figure 4.6. This strategy has been used successfully in past tissue engineering studies in an effort to enhance collagen deposition and improve the construct mechanical properties (Bian et al., 2009b). When simulated in this multigenerational growth model, the proteoglycan digestion predicts less swelling of the construct over time, Figure 4.7. In this digested group, the proteoglycan content normalized to the tissue volume on day 77 is ${\rho }^{\text{CS}}={\rho }_r^{\text{CS}}/J^s=32.7\text{mg}/\text{mL}$, which is slightly larger than the corresponding value in the undigested group, even though the total content in the construct is smaller (as deduced from ${\rho }_r^{\text{CS}}$, Figure 4.6). These predictions are consistent with experimental results (Bian et al., 2009b). Furthermore, the observed decrease in J^s implies that the various generations of collagen in the digested group have reference configurations that differ significantly from corresponding generations in the untreated group. Accordingly, the stress-strain response of digested constructs on day 77 (Figure 4.8) produces a Young’s modulus of 0.39 MPa, which is slightly larger than that of the untreated group.

This example illustrates that multigenerational growth can predict results that might otherwise seem counter-intuitive. Normally, since increased proteoglycan content increases the tissue modulus, according to eq.(2.18), it would appear at first that digesting proteoglycans should produce a smaller compressive modulus than the undigested control group. However, when combined with multigenerational growth, these simulations demonstrate a more subtle set of predictions that are consistent with experimental observations: The digested group shows less swelling than the control group; as a result, even though ${\rho }_r^{\text{CS}}$ is smaller in the digested group, ρ^CS is actually slightly larger. Similarly, Young’s modulus is larger in the digested group, partly because of the larger effective fixed charge density, and partly because of the multigenerational deposition of collagen. A similar analysis where all daily collagen depositions share the same reference configuration produces a slightly lower Young’s modulus for the digested constructs.

2.5. Evolving Constitutive Relations

Many biological tissues undergo significant remodeling as part of normal physiological processes as well as pathological conditions. A tissue that remodels may exhibit very significant changes in its material behavior, including changes in material properties, material symmetry, and even in the form of the stress-strain response. Remodeling occurs as a result of alterations in tissue composition, which may be triggered by biological and mechanical signals. For example, in a collagenous tissue, new fibers and crosslinks may form or existing ones may degrade away. Such changes in composition may also alter material symmetry. For instance, if new fibers form along preferred directions in a pre-existing matrix consisting of randomly oriented fibers, the material symmetry decreases as a result of this growth and remodeling process. Conversely, the material symmetry increases as a result of remodeling if preferentially aligned fibers are degraded and newly formed immature fibrils are deposited in a random orientation.

The set of state variables for such growth problems may thus be expanded to include the composition ${\rho }_r^{\sigma }$ of all solid constituents (e.g., collagen, collagen cross-links, proteoglycans, etc.) that get deposited or removed at various times during the remodeling process. To capture the evolving constitutive relations for such remodeling tissues, it may be convenient to blend constitutive relations characterized at various stages of the remodeling, using evolving values of the relevant ${\rho }_r^{\sigma }$ composition measures. Such an approach would make known information about evolving biochemistry straightforward to implement into a material constitutive framework.

For example, consider for simplicity a material whose behavior before remodeling is described by the free energy density ${\mathrm{\Psi }}_r^{(1)}$ (θ, F^s, ${\rho }_r^s$), where ${\rho }_r^s$ represents the composition of a solid constituent that evolves with remodeling; after remodeling, the material behavior is described by a free energy density ${\mathrm{\Psi }}_r^{(2)}$ (θ, F^s, ${\rho }_r^s$). During the remodeling process, assume that ${\rho }_r^s$ decreases. The constitutive relations for ${\mathrm{\Psi }}_r^{(1)}$ and ${\mathrm{\Psi }}_r^{(2)}$ may be constructed such that the contribution from ${\mathrm{\Psi }}_r^{(1)}$ becomes attenuated as ${\rho }_r^s$ decreases (akin to eq.(2.10)), while that of ${\mathrm{\Psi }}_r^{(2)}$ correspondingly increases. In that case, the complete description of the material over the entire remodeling process may be given by the blended constitutive relation

$${\mathrm{\Psi }}_r(\theta ,{\mathbf{F}}^s,{\rho }_r^s)={\mathrm{\Psi }}_r^{(1)}(\theta ,{\mathbf{F}}^s,{\rho }_r^s)+{\mathrm{\Psi }}_r^{(2)}(\theta ,{\mathbf{F}}^s,{\rho }_r^s).$$ (2.21)

Note that the blending functions are part of the constitutive formulations of ${\mathrm{\Psi }}_r^{(1)}$ and ${\mathrm{\Psi }}_r^{(2)}$; they need not be simple linear functions of ${\rho }_r^s$. This type of formulation is amenable to standard experimental characterization, by measuring the material response Ψ_r (θ, F^s, ${\rho }_r^s$) at various time points during a remodeling process, as well as measuring the composition ${\rho }_r^s$ at those same time points, then constructing blending functions of ${\rho }_r^s$ that can consistently reproduce the behavior at the various measured time points. The blending function may then be validated by testing the ability to predict the material response at a measured remodeling time point not used for characterizing the constitutive relation.

This approach for modeling tissue remodeling is a simple extension of the approaches of Cowin and Hegedus (Cowin and Hegedus, 1976; Hegedus and Cowin, 1976) and Huiskes et al. (Huiskes et al., 1987; Weinans et al., 1992; Mullender et al., 1994); it is also consistent with the approach of Baaijens et al. (2010) who examined reorientation of collagen fiber directions by allowing alterations in the fractional fiber distribution (a compositional measure) along various spatial directions in response to fiber stretch. By allowing multiple compositional measures ${\rho }_r^{\sigma }$ to evolve over time, this approach extends these earlier presentations and suggests that blending of constitutive relations for describing an evolving Ψ_r (θ, F^σ, ${\rho }_r^{\sigma }$) may be a practical general method for modeling tissue remodeling.

Example 5. Cervical Remodeling

The mechanical function of the uterine cervix becomes crucial during pregnancy when it is required to resist the compressive and tensile forces generated from the growing fetus. As the fetus grows, the mother’s body evolves to accommodate the increasing fetal volume through uterine growth, pelvic tissue softening, and progressive cervical remodeling. For a successful full-term pregnancy the cervix must remain closed during this time to retain the fetus within the uterus. Then nearing full-term, the cervix must accelerate its remodeling process in synchronization with increased uterine contractile activity to successfully dilate and deliver the fetus. The onset of accelerated cervical remodeling and reduced mechanical strength of the tissue has been hypothesized to cause preterm cervical dilation and preterm birth. Here we examine the cervical remodeling component of human parturition and propose a cervical material remodeling constitutive framework based on observed biochemical and mechanical changes of the tissue for normal pregnancy. An extension of this type of remodeling framework could then investigate the role of aberrant rates of change to the biochemical ultrastructure and composition on accelerated softening mechanisms in preterm birth.

Similiar to other load-bearing collagenous tissues, e.g. cartilage, the biochemical composition of the cervix consists of a solid ECM, which is surrounded by pressurized and viscous interstitial fluid. The ECM of the cervix consists of a cross-linked collagen andglycosaminoglycan network, which is maintained by a small fraction of cervical fibroblasts and smooth muscle cells (Granstrom et al., 1989). The cervical collagens are fibril-forming types I and III. In the nonpregnant state these collagen fibrils bundle together to form mature fibers that contain pyridinoline crosslinks, where an increase in crosslink density correlates to an increase in fiber maturity and mechanical modulus (Akins et al., 2011). Cervical glycosaminoglycans (GAGs) are present either in the form of proteoglycans, as in decorin, or they exist without a core protein as in hyaluronic acid (HA) (Shimizu et al., 1980; Uldbjerg et al., 1983; Osmers et al., 1993; Myers et al., 2009; Akgul et al., 2012). The mechanical role of these GAGs remain to be determined for cervical tissue. Studies from soft tissue with similar collagenous architectures have shown that the GAG sidechains organize collagen fiber structure by maintaining a uniform collagen fibril diameter and consistent collagen fibril distance within the fiber (Danielson et al., 1997). In addition, the negatively charged and hydrophilic GAGs also produce an osmotic swelling pressure that cause the tissue to imbibe fluid. This swelling tendency is counteracted by tensile forces of the collagen. If the collagen fibrils are loosely crosslinked and unable to resist swelling, the influx of interstitial fluid can break apart the solid matrix of the tissue during the remodeling process. On the other hand if the collagen fibrils are densely crosslinked, they can withstand swelling to maintain the fixed charge density (FCD) and provide added compressive strength (Basser et al., 1998).

Along with the amount and type of ECM components in the cervix, the organization and directionality of the collagen fibrils play a large role in cervical dilation resistance. The ultrastructure of the cervical stroma contains three seamless zones of preferentially-aligned collagen. The innermost and outermost zones contain collagen fibers that are preferentially aligned in the longitudinal direction (parallel to the inner canal) and the middle zone contains collagen fibers preferentially aligned in the circumferential direction (circling around the inner canal) (Aspden, 1988; Weiss et al., 2006). These collagen fibers provide the cervix resistance to circumferential dilation and provide a mechanical link to the contractile forces of the uterus. The size of these zones of preferential collagens, the amount of dispersion of the fiber families, and how these variables change for each woman remain to be determined. The rearrangement of this collagen ultrastructure along with the turnover of mature collagen fibers to less cross-linked immature fibers are postulated to cause cervical softening during remodeling.

The composition and ultrastructure of the ECM provide the cervix with its material characteristics and mechanical strength, and the evolution and remodeling of these constituents modulates cervical softening during pregnancy (Akgul et al., 2012; Akins et al., 2010, 2011; Holt et al., 2011; Mahendroo, 2012; Timmons et al., 2010; Word et al., 2007; Danforth, 1947; Danforth et al., 1960, 1974; Danforth, 1983; Leppert, 1992, 1995, 1998). The cervix is a biologically active material with the ability to adapt and remodel in response to hormonal, inflammatory, biochemical and mechanical triggers, with mass supply rates ${\mathrm{\rho ̂}}_r^{\sigma }$ being a function of these signaling mechanisms. The relative influence of each of these triggers on cervical remodeling continue to be investigated with much debate because of limited access and studies on human tissue samples. Therefore, casting constitutive relations for the mass supply rates remain elusive. A more practical approach to investigate cervical remodeling mechanisms is to quantify the biochemical composition and related mechanical property changes in gestation-timed cervical tissue samples taken from accessible small animal models. Cervical remodeling has been widely explored in mouse models of normal parturition and infection- and noninfection-based premature cervical remodeling (Akgul et al., 2012; Akins et al., 2010, 2011; Holt et al., 2011; Mahendroo, 2012). In normal pregnancy, the mouse cervix remodels in distinct phases during early and late gestation, which lead up to dramatic dilation at parturition. Gradual softening starts in the early stages of pregnancy, day 12 of a 19 day mouse gestation, and is characterized by collagen turnover, tissue growth, and increased vascularity. The collagen remodeling occurs via a turnover of mature cross-linked collagen fibrils to immature less cross-linked fibrils (Akins et al., 2011). During this early turnover of collagen fibrils, the sulfated GAG and HA content remain the same (Akgul et al., 2012) and there is evidence to suggest that the ultrastructure of preferentially aligned collagens preserve their directionality until day 12 of a mouse gestation (Akins et al., 2010). This preservation of the ultrastructure during these early remodeling phases most likely preserves dilation resistance as the cervical tissue gradually prepares for later stages of maturation. The next stage of cervical remodeling, termed ripening, happens late in gestation which may be initiated weeks or days before dilation in humans and hours before dilation in mice (Timmons et al., 2010). This phase of accelerated softening is characterized by a further decrease in collagen crosslink density, an increase in hydration, and a loss collagen directionality. The hydration increase is facilitated by an increase in the hydrophilic hyaluronic acid (Akgul et al., 2012), an increase in fixed charge density (FCD) (Xu et al., 2010), and a further collagen turnover (Akins et al., 2011). After ripening, cervical dilation occurs and is characterized by a decrease in collagen concentration, an increase in vascularity, and an increase in inflammatory processes. After delivery, the cervix enters the repair phase with the reversal of these processes (Timmons et al., 2010).

Based on these structure-function studies of nonpregnant and timed-pregnant tissue, the cervical stroma can be modeled as a hydrated porous material where the solid constituents are a composite of preferentially-aligned crosslinked collagen fibers and negatively charged GAGs. The density of collagen crosslinks, the morphology of the collagen ultrastructure, the swelling effect of the charged GAGs, and the pressurization of the interstitial fluid provide cervical compressive and dilation resistance. The evolution of these tissue variables facilitates cervical remodeling during pregnancy, where the cervix progressively softens in early pregnancy and then rapidly loses its dilation resistance in late pregnancy. Here we set-up a material modeling framework for different stages of cervical softening by incorporating a microstructurally-inspired mixture model, where evolving material parameters based on ECM content measured at specific gestational ages account for tissue remodeling.

Let the free energy density of a single fiber bundle (i.e. collection of crosslinked collagen fibrils) initially oriented along the direction n = cos θ sin ϕe₁ + sin θ sin ϕe₂ + cos ϕe₃, in a Cartesian basis {e₁, e₂, e₃}, be given by

$${\mathrm{\Psi }}_n=\{\begin{array}{cc}\frac{\xi }{2\beta }{(I_n-1)}^{\beta }\hfill & \hfill I_n>1\hfill \\ 0\hfill & \hfill I_n\le 1\hfill \end{array},$$ (2.22)

where I_n = n · C^s · n is the square of the fiber stretch, and C^s = (F^s)^T · F^s is the right Cauchy-Green tensor. Here, ξ and β represent material properties of the fiber bundle, with ξ having units of stress and β unitless. This formulation implies that fibers may only sustain tension. The Cauchy stress for this fiber bundle may be evaluated from

$${\mathbf{\sigma }}_n=\frac{2}{J^s}\frac{\partial {\mathrm{\Psi }}_n}{\partial I_n}{\mathbf{F}}^s·(\mathbf{n}\otimes \mathbf{n})·{({\mathbf{F}}^s)}^T.$$ (2.23)

To account for remodeling of this fiber bundle as a result of changes in collagen content, ${\rho }_r^{\text{COL}}$, and pyridinoline crosslinks, ${\rho }_r^{\text{PYR}}$, consider the hypothetical constitutive relation for the fiber bundle modulus ξ,

$$\xi ({\rho }_r^{\text{COL}},{\rho }_r^{\text{PYR}})=c{\left({\rho }_r^{\text{COL}}\right)}^{{\gamma }^{\text{COL}}}[1+\zeta {\left({\rho }_r^{\text{PYR}}\right)}^{{\gamma }^{\text{PYR}}}].$$ (2.24)

This relation accounts for the possibility that collagen fibers produce a tensile modulus even in the absence of pyridinoline crosslinks (${\rho }_r^{\text{PYR}}=0$), but ξ reduces to zero when collagen content is zero (${\rho }_r^{\text{COL}}=0$). Due to the complexity of signaling mechanisms and for simplicity, the values ${\rho }_r^{\text{COL}}$ and ${\rho }_r^{\text{PYR}}$ can be a function of gestation age measured from experimental timed pregnancy samples from animals models of normal and abnormal pregnancy. Note that the increase in amount of pyridinoline crosslinks relates to an increase in collagen fiber strength and maturity.

For a continuous, randomly oriented, distribution of fiber bundles, the free energy density may be obtained by integrating the fiber bundle energy density over the unit sphere,

$${\mathrm{\Psi }}_r({\mathbf{F}}^s,{\rho }_r^{\text{COL}},{\rho }_r^{\text{PYR}})={\int }_0^{2\pi }{\int }_0^{\pi }{\mathrm{\Psi }}_r^n(I_n,{\rho }_r^{\text{COL}},{\rho }_r^{\text{PYR}})\text{sin}\varphi d\varphi d\theta .$$ (2.25)

The net Cauchy stress in this continuous fiber distribution may be similarly obtained by integrating σ_n over the unit sphere. Now consider that each of the inner, middle and outer zones of the cervix is modeled as a mixture of a random collagen fiber distribution, eq.(2.25), a preferentially-aligned crosslinked fiber family (longitudinal for the innermost and outermost zones, circumferential for the middle zone), eq.(2.22), and negatively charged GAGs that produce a Donnan osmotic pressure p, eq.(2.16), based on an associated content ${\rho }_r^{\text{GAG}}$ and charge number z^GAG that produce a fixed charge density of the form given in eq.(2.17). Again these compositional values will be a function of gestation age. Furthermore, the preferentially aligned fibers may be distinguished from the randomly oriented fibers, ${\rho }_r^{\text{COL}(\mathrm{a})}$ versus ${\rho }_r^{\text{COL}(\mathrm{r})}$, with the corresponding free energy densities ${\mathrm{\Psi }}_r^{(\mathrm{a})}$ (I_n, ${\rho }_r^{\text{COL}(\mathrm{a})},{\rho }_r^{\text{PYR}(\mathrm{a})}$) and ${\mathrm{\Psi }}_n^{(\mathrm{r})}$ (F^s, ${\rho }_r^{\text{COL}(\mathrm{r})},{\rho }_r^{\text{PYR}(\mathrm{r})}$), respectively. Both of these relationships may also be indirectly dependent on the amount of GAG; when an increase in GAG occurs at the late stages of pregnancy, the resulting osmotic pressure p will induce swelling (an alteration in F^s) to break up the preferred directionality of the collagen turnover process. This relationship may be factored into the dependence of the collagen and pyridinoline mass supplies on the state of strain. Assuming for simplicity here that all these constituents share the same reference configuration, the mixture’s free energy density may then be given by

$${\mathrm{\Psi }}_r({\mathbf{F}}^s,{\rho }_r^{\text{COL}(\mathrm{r})},{\rho }_r^{\text{PYR}(\mathrm{r})},{\rho }_r^{\text{COL}(\mathrm{a})},{\rho }_r^{\text{PYR}(\mathrm{a})})={\mathrm{\Psi }}_r^{(\mathrm{r})}({\mathbf{F}}^s,{\rho }_r^{\text{COL}(\mathrm{r})},{\rho }_r^{\text{PYR}(\mathrm{r})})+{\mathrm{\Psi }}_n^{(\mathrm{a})}(I_n,{\rho }_r^{\text{COL}(\mathrm{a})},{\rho }_r^{\text{PYR}(\mathrm{a})})$$ (2.26)

where blending of the free energy densities occurs via the dependence of the collagen directionality on the evolving swelling strain. Here we can prescribe the energy densities such that ${\mathrm{\Psi }}_r^{(\mathrm{a})}$ attenuates with a decrease in ${\rho }_r^{\text{COL}(\mathrm{a})},$ and ${\rho }_r^{\text{PYR}(\mathrm{a})}$, according to (2.24).

This example for blending constitutive relations characterized at different stages of a remodeling process does not represent the most general approach for this type of problem. It may be argued that mature and immature crosslinked collagens, as well as GAGs, interact during the remodeling process, in which case all the free energy densities appearing in eq.(2.26) should depend on the complete set of compositional state variables, thus requiring more complex constitutive relations relating material constants to composition. The blending approach should be viewed as a suggested simpler method for formulating constitutive relations for remodeling tissues, which may be used as the starting point if more elaborate formulations are required.

3. Conclusion

The objective of this study was to present the mixture framework for growth mechanics using a didactic approach. Here growth is simply described by adding state variables ${\rho }_r^{\alpha }$ to account for the evolving composition of a growing tissue, in addition to the usual inclusion of solid matrix strain based on the deformation gradient F^s, eq.(2.7). The evolution of composition with growth is guided by a constitutive model for the mass supply ${\mathrm{\rho ̂}}_r^{\alpha }$, which enters into the equation of mass balance for solid constituents, eq.(2.6), and for solutes, eq.(2.14). The constitutive relation for the mass supply may depend on the state of strain, as in the case of the remodeling rules by Huiskes et al., eq.(2.11) (Figure 4.1), and Cowin and Hegedus, eq.(2.12).

The solid mass supply may also depend explicitly on composition, such as glucose concentration in the case of chondroitin sulfate synthesis in the cartilage tissue engineering analysis of Example 2, eq.(2.13) (Figure 4.4). The evolving composition may produce evolving material properties, with the relation between composition and properties described explicitly by constitutive models such as that of eq.(2.10) in Example 1, and the hypothesized model for cross-linked collagen remodeling of eq.(2.24) in cervical remodeling, Example 5, or implicitly by directly prescribing changes in material properties as in the cartilage tissue engineering analysis of Example 4.

Evolving tissue composition may also alter the interstitial fluid pressure of a hydrated tissue, as in the case of negatively charged proteoglycans, eq.(2.17), that produce a Donnan osmotic pressure, eq.(2.16). Heterogeneous distributions of osmotic pressure induce residual stresses, a common feature in growth mechanics, as illustrated in the curling of cut cartilage, Example 3 (Figure 4.5).

To account for multigenerational growth, where solid material deposited at some time t may have a different reference configuration than solid material deposited at an earlier time, the list of state variables may be expanded to include deformation gradients for each deposited generation, eq.(2.19). As long as all solid constituents of a mixture, and their various generations, are constrained to move together, the evaluation of the stress from the free energy density is given by eq.(2.20). Multigenerational growth may be used to describe matrix turnover, as illustrated in Example 4 for engineered cartilage growth, and may also result in residual stresses (Ateshian and Ricken, 2010).

These various features of growth mechanics may be combined to describe tissues that undergo drastic remodeling, producing significantly different stress-strain responses over time. Such drastic changes in the material behavior may be captured by blending various constitutive relations for the free energy density, Ψ_r, as illustrated in the remodeling of the cervix over the entire gestation and parturition process of Example 5.

The dependence of growth and remodeling on compositional state variables is not a novel concept, as it may be traced back to the studies of Cowin and Hegedus (1976). Mixture theory provides a continuum mechanics framework where the evolution of the composition is dictated by the axiom of mass balance and the formulation of constitutive relations for the mass supplies, describing mass exchanges among the various constituents of the mixture. While this concept has also been recognized for several decades (Bowen, 1968, 1969), the realization that these theoretical concepts may be broadly applied to biological tissue growth has evolved more slowly. Mixture theory also allows the formulation of mixtures of solids that are constrained to move together (Humphrey and Rajagopal, 2002) but are not required to share the same reference configuration (Ateshian and Ricken, 2010). These two features of mixture frameworks are essential for formulating growth theories. Despite the seeming complexity of establishing the mathematical foundations for such frameworks, the essential set of equations reduces to the mass balance formulation of eq.(2.6) and the multigenerational hyperelasticity relations of eqs.(2.19)–(2.20).