A new approach to structural integrity assessment based on axial and radial diffusivities

Summary

This study describes a method for performing diffusivity measures along and across a specific direction, derived from white matter in healthy controls. The diffusion tensor (DT) assigns a principal eigenvector (v₁) and eigenvalue (axial diffusivity, d_ax) to each voxel. The average of the second and third eigenvalues is the radial diffusivity, d_rad• v₁ may be affected by pathology, therefore when comparing d_ax and d_rad in patients one has to consider the direction of the measurement and underlying anatomy. Here we created a representative super-DT dataset, DT_ref, whose eigenvector, v_1,ref, was considered the most likely direction of diffusivity per voxel. We defined the projected axial diffusivity, d_p-ax, as the projection of individual DTs along v_1,ref and the projected radial diffusivity, d_p-rad, as the average of the projections along the second and third eigenvectors of DT_ref. The projected diffusivities are promising new parameters for studying white matter pathology.

Introduction

Magnetic resonance imaging (MRI) can be made sensitive to the displacement of water molecules in tissue in vivo and, under appropriate conditions, this displacement can be approximated with a Gaussian model, representing the overall effect as a diffusion tensor (DT).

This allows the definition of three unique vectors, the eigenvectors of the DT, v₁, v₂ and v₃, which represent the diffusivity along the principal direction and two orthogonal ones per each image voxel. Associated with these eigenvectors there are values corresponding to the apparent diffusion coefficient of the water molecules in each voxel along the direction of the eigenvectors. These diffusivities are known as the eigenvalues of the DT, λ₁, λ₂ and λ₃(1).

Axial and radial diffusivities, i.e. the water diffusion coefficient measured along and across axons, have been associated with the principal eigenvalue of the DT, λ₁, and the average of its orthogonal components, λ₂ and λ₃(2). This is an acceptable approximation if the voxel contains a healthy fibre bundle that determines the diffusion properties of the voxel, but can lead to misinterpretation of the results if the signal-to-noise ratio (SNR) is low, or if crossing fibres are present, or if pathology causes a decrease in anisotropy. The latter situation occurs within brain lesions, such as those affecting the brain of patients with multiple sclerosis (MS) (3). Thus, in all these conditions the uncertainty associated with the definition of the principal direction of diffusion increases, i.e., v₁ may be aligned with a direction other than that of the underlying “healthy” structure, as discussed in (4). In such voxels, comparing the eigenvalues of the DT between healthy controls and patients with lesions, such as those seen in MS, can be misleading because it corresponds effectively to comparing the diffusion coefficient along two different directions, hence representing different biological substrates.

This work proposes a new definition of the axial and radial diffusivities, which is consistent between subjects and independent of white matter focal pathology. This is achieved by calculating the diffusivity along directions that are defined in Montreal Neurological Institute (MNI) standard space, using a DT template generated from a control population.

Materials and methods

Subjects

Fifteen healthy controls (mean age 40±14 years, 6 females and 9 males) were scanned as the reference group (hcs). One additional healthy control (hc) (female, age 37 years) was included to be compared with the reference group, and two patients with a diagnosis of relapsing-remitting MS (5), p₁ (female, age 34 years, EDSS score = 2.5, disease duration = 1.5 years, total lesion load = 1,480.55 mm³) and p₂ (male, age 55 years, EDSS score = 5.5, disease duration = 7 years, total lesion load = 21,142.50 mm³), were also scanned with the same protocol. All the subjects gave their informed, written consent before the study, which was approved by the Joint Ethics Committee of the Institute of Neurology and the National Hospital for Neurology and Neuro-surgery (London, UK).

MRI protocol

Dual-Echo Fast Spin-Echo (DE-FSE)

Axial images, aligned to run parallel to a line that joins the most inferoanterior and inferoposterior parts of the corpus callosum (anterior commissure – posterior commissure: AC-PC line) were acquired with standard parameters (TE = 30/105 ms; TR = 2500 ms; number of slices = 28 contiguous; voxel size = 0.94 × 0.7 × 5 mm³).

Diffusion Tensor Imaging (DTI)

A single-shot cardiac-gated diffusion-weighted spin-echo echo-planar imaging (DW-SE-EPI) sequence was run with the following parameters: TE = 0.096 s, TR = 20RR (≈20 s), 2.3×2.3×2.3 10⁻⁹ m³ voxel size, 60 contiguous slices, aligned with the AC-PC line, 68 volumes of which 61 acquired with equally distributed (6) diffusion-weighted directions and b = 1200 10⁶ s m⁻² plus 7 volumes acquired with b = 0.

Processing pipeline

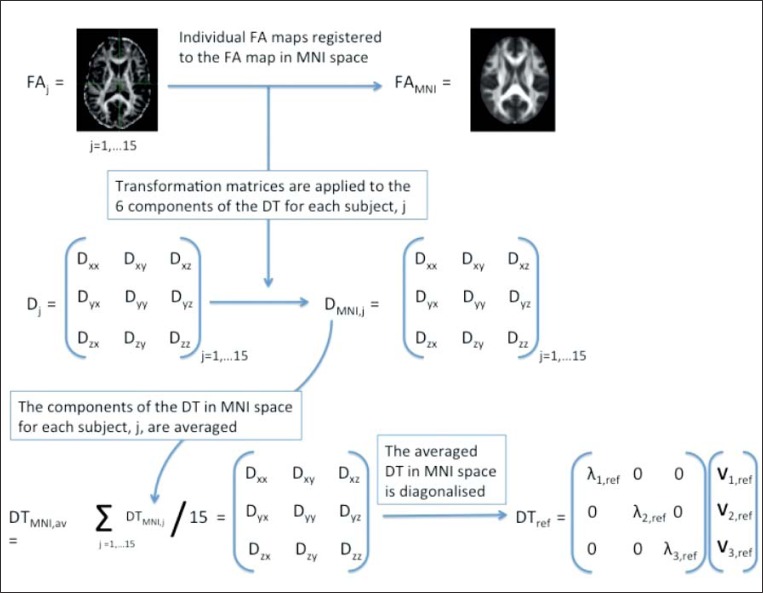
This section describes the steps taken to obtain a “super-DTI” control dataset in MNI space, which was used as a representative template for determining the main direction of diffusivity in each voxel for the healthy population. This super-DTI control dataset was used as the reference to define two new parameters, called “projected axial diffusivity”, d_p-ax, and “projected radial diffusivity”, d_p-rad. These new parameters were then compared on a voxel-by-voxel basis between i) the 15 hcs and the extra hc (whose scans were not used for the super-DTI dataset), and ii) the 15 hcs and the two MS patients, p₁ and p₂. The processing pipeline is also schematically represented in figure 1.

Figure 1.

Diagram of the pipeline used to obtain the super-DTI dataset and to calculate the projected axial and radial diffusivities, d_p-ax and d_p-rad, for an individual subject.

Definition of the reference axial and radial diffusivities

• DTI data from 15 healthy subjects were used to create a super-DTI dataset (7). For each subject, j, the DT was reconstructed voxelwise in native space using the Camino toolkit [http://www.camino.org.uk (8)] and diagonalised to produce traditional DTI metrics, including fractional anisotropy (FA_j), axial (d_ax,j) and radial (d_rad,j) diffusivities, where the axial diffusivity is assumed to coincide with the principal eigenvalue of the DT_j of subject j, λ_1,j, while the radial diffusivity is associated with the average of the second and third eigenvalues, λ_2,j and λ_3,j.

• For each subject j the FA_j map in native space was registered to the FA template from the Oxford Centre for Functional MRI of the Brain (FMRIB) library, FA_MNI, using first FLIRT, an affine registration step, followed by FNIRT, a non-linear registration algorithm, from the FSL toolkit (see FLIRT and FNIRT, http://www.fmrib.ox.ac.uk/fsl/fsl/list.html). The voxel resolution of the registered FA map matched the resolution of FA_MNI, i.e. 1×1×1 mm³. The transformation matrix was then applied to the non-diagonalised diffusion tensor components, DT_j, using the preservation of principal direction (PPD) algorithm to reorient the DTs (9), providing a DT in MNI space, DT_MNI,j, for each subject j.

• Before diagonalisation, the DT_MNI,j were averaged to produce a non-diagonalised super-DTI dataset, DT_MNI,av.

• DT_MNI,av was subsequently diagonalised to obtain the diagonalised reference dataset, DT_ref, which gave us the three reference eigenvectors, v_1,ref, v_2,ref, v_3,ref, and their corresponding eigenvalues, λ_1,ref, λ_2,ref, λ_3,ref for each 1×1×1 mm³ voxel.

• From the eigenvalues of DT_ref the FA map was calculated and used as the reference, FA_ref, for thresholding, assuming that voxels characterised by FA_ref>0.3 are most likely to be representative of white matter.

Definition of the projected axial and radial diffusivities

• For each subject we determined the component of the DT along each of the three eigenvectors of DT_ref, v_1,ref, v_2,ref, v_3,ref, and we called these values the “projected” diffusivities: d_p1,j, d_p2,j, d_p3,j where 1,2,3 indicates the projection along the first, second or third eigenvector of DT_ref, while j = 1…n indicates the subject investigated.

The projection of the DT of each subject j along v_1,ref is defined as the projected axial diffusivity for that subject, d_p-ax,j:

$${\text{d}}_{\text{p-ax},\text{j}}={\left({\mathbf{v}}_{1,\text{ref}}\right)}^{\text{T}}\cdot {\text{DT}}_{\text{MNI},\text{j}}\cdot \left({\mathbf{v}}_{1.\text{ref}}\right)$$ [eq 1]

The average of the projections of the DT of each subject j along v_2,ref and v_3,ref was also calculated and defined as the projected radial diffusivity for subject j, d_p-rad,j:

$${\text{d}}_{\text{p-radj}}=\left({\left({\mathbf{v}}_{2,\text{ref}}\right)}^{\text{T}}\cdot {\text{DT}}_{\text{MNI},\text{j}}\cdot \left({\mathbf{v}}_{2,\text{ref}}\right)+{\left({\mathbf{v}}_{3,\text{ref}}\right)}^{\text{T}}\cdot {\text{DT}}_{\text{MNI},\text{j}}\cdot \left({\mathbf{v}}_{3,\text{ref}}\right)\right)/2$$ [eq 2]

Voxel-based morphometry (VBM) analysis of d_p-ax and d_p-rad

• First, in the group of 15 hcs used for the super-DTI dataset we compared the axial diffusivity (d_ax) with the projected axial diffusivity (d_p-ax), and the radial diffusivity (d_rad) with the projected radial diffusivity (d_p-rad) using a paired-sample t-test in SPM5 (http://www.fil.ion.ucl.ac.uk/spm/software/spm5/).

• Second, we investigated differences in d_p-ax and d_p-rad between the 15 hcs and both i) the single healthy control (hc), and ii) the two patients with MS, p₁ and p₂, using a two sample t-test in SPM5. In particular, one group was set to be either hc, p₁ or p₂, while the other was set to be the hcs (i.e. the 15 healthy subjects used for the super-DTI dataset). Equality of variance for the two groups was assumed. We tested whether d_p-ax and d_p-rad of hc, p₁ and p₂ differed from the healthy population, and whether these differences overlapped with those obtained by comparing d_ax and d_rad, calculated from the DT, between subject groups.

MS lesions and axial and radial diffusivities

• Masks of the T₂-hyperintense MS lesions were drawn by an experienced neurologist (OC) on the proton-density-weighted scans of the DE-FSE dataset for both patients, p₁ and p₂;

• The T₂-weighted scans were then linearly registered to the b₀ scan of the super-DTI dataset via an affine transformation using FLIRT from the FSL library;

• The transformation coefficients from T₂ to b₀ space were subsequently combined with the non-linear transformation coefficients obtained from the non-linear registration of the individual FA maps to FA_MNI;

• The combined transformation was applied to the original lesion mask file in order to have the lesion masks co-registered with the DTI matrices in MNI space.

Results

By definition, d_p-ax is never greater than d_ax and d_p-rad is never smaller than d_rad. With this in mind, these are the main findings of our study:

Voxel-based analysis of d_p-ax and d_p-rad

Healthy controls

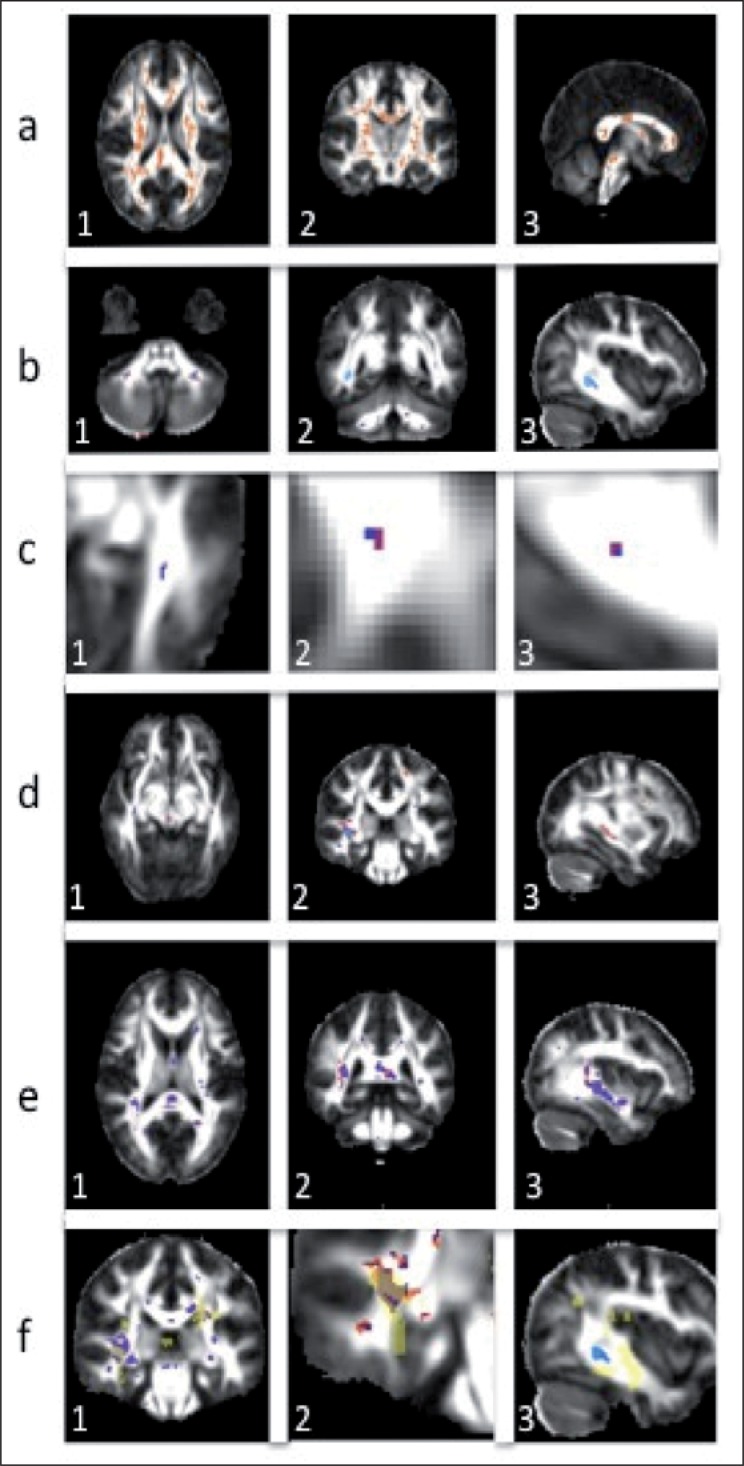
VBM comparisons of d_p-ax with d_ax and dp-rad with d_rad of the 15 healthy volunteers, used for creating the super-DTI dataset, show areas of decreased d_p-ax compared with d_ax; these areas overlap with regions showing an increased d_p-rad compared with the corresponding values of d_ax, (see Fig. 2a, over).

Figure 2.

a) Axial, coronal and sagittal views of fractional anisotropy with areas of increased projected radial, d_p-rad, compared with radial, d_rad, diffusivity and decreased projected axial, d_p-ax, compared with axial, d_ax, diffusivity in a population of 15 healthy controls; b) Areas of decreased projected axial diffusivity in p₂, d_p-ax,p2, shown in blue, overlaid on areas of decreased axial diffusivity, d_ax,p2, shown in red. c) The same as b) but for p₁; d) Areas of increased projected axial, d_p-ax,p2, (blue) and axial, d_ax,p2, (red) diffusivity in p₂; e) Areas of increased projected radial, d_p-rad,p2, (blue) and axial, d_rad,p2, (red) diffusivity in p₂; f) Overlay of areas of axial and radial diffusivity changes and lesion localisation (yellow) in p₂. 1 – areas of increased d_p-rad,p2 (blue) and d_rad-p2 (red); 2 – areas of increased d_p-ax,p2 (blue) and _dax-p2 (red); 3 – areas of decreased d_p-ax,p2 (blue) and d_ax-p2 (red). In all images, purple voxels are common voxels of changes in the projected and standard diffusivities.

Axial diffusivity in hc, p₁ and p₂

The most remarkable result of the analysis is that p₂ (the patient with the highest clinical disability and highest total lesion load) shows areas of decreased projected axial diffusivity, d_p-ax, compared with the hcs. These areas are not always highlighted when looking at the differences in d_ax between this patient and the hcs, and often appear to extend beyond these regions (Fig. 2b, over), indicating that projected axial diffusivity may be sensitive to pathology in a different way from the axial diffusivity parameter. On the other hand, p₁ shows only a few voxels characterised by a reduced d_p-ax, which mostly coincide with voxels of reduced d_ax and are typically of limited spatial extent (Fig. 2c, over). No voxels of decreased d_p-ax and d_ax are found in the hc when compared with the healthy population.

Areas of increased d_p-ax compared with the hcs are also found in both patients; these regions do not always overlap with regions of increased d_ax and, in some locations, extend beyond them, especially in p₂ (Fig. 2d, over).

Radial diffusivity in hc, p₁ and p₂

In contrast with the axial diffusivity results, the observed regions of increased d_p-rad mostly coincide with regions of increased d_rad. In particular, the areas of difference in d_p-rad between hc and p₁ and the healthy population (hcs) are almost identical to the regions obtained when comparing d_rad between these groups. Instead, p₂ shows regions of increased d_p-rad when compared with hcs that coincide with areas of increased d_rad, but are spatially more localised (Fig. 2e). No areas of significant decreased radial diffusivities, d_p-rad or d_rad, are found in any of the subjects, hc, p₁ and p₂, and hcs.

MS lesions and axial and radial diffusivities

The location of the white matter lesions of p₁ and p₂ was compared with the areas of increased radial diffusivity, increased axial diffusivity and decreased axial diffusivity, for both the traditionally defined parameters, d_ax and d_rad, and the projected parameters, d_p-ax and d_p-rad. Figure 2f shows the relative position of lesions and areas of changes for p₂.

Areas of increased d_p-rad and d_rad, observed in p₂ when compared with hcs, overlap with lesions identified on T₂-weighted scans and also extend beyond their boundaries (Fig. 2f-1). Areas of increased d_p-ax and d_ax observed in p₂ are localised within the lesion mask (Fig. 2f-2), while areas of decreased axial diffusivity in p₂ are not always related to the presence of focal lesions, but are also seen outside the focal lesions, in the normal-appearing white matter (Fig. 2f-3).

Discussion

We have defined two new parameters to be used for evaluating the diffusion coefficient of water molecule displacement along and across axons. We have called these parameters “projected axial” diffusivity, d_p-ax, and “projected radial” diffusivity, d_p-rad. They are obtained by calculating the component of the DT along a specific direction, defined as the direction of the principal eigenvector of a “super-DT” dataset, built from 15 hcs. In fact, it is well known that pathology can change the alignment of the eigenvectors of the DT with respect to the underlying tissue structure, and can also reflect actual changes in the tissue structures if invasive pathology is present, as in the case of tumours (10). If the first case, such as in MS in which white matter is affected by non-expansive lesions of a degenerative nature (11), the principal eigenvalue of the diseased brain may not reflect the same biophysical substrate as the principal eigenvalue of a healthy brain, as shown by Wheeler-Kingshott and Cercignani (4). The new parameters, d_p-ax and d_p-rad, therefore, aim to provide a means of evaluating possible changes along and across the most probable direction of healthy white matter fibres.

A reference DT dataset was built using data from 15 hcs and a non-linear registration algorithm to transform individual FA maps into MNI space. The registration of white matter structures was visually checked using reference landmarks. We applied the transformations to the individual components of each subject’s DT, applying the PPD algorithm to reorient the DTs. Peng et al. (12) adopted a similar approach: these authors used a large population of healthy subjects to create a high-resolution high-SNR DT dataset, using data acquired with Turboprop-DTI instead of the more commonly available and used DW-SE-EPI. The dependence of the resulting DT dataset on the population used for the averaged template remains to be tested. Also, it is known that there is an effect of age on the DT properties; for this reason, we, too, believe that building a specific template for each study will allow the use of an age- and gender-matched population for the super-DT control dataset.

Due to the low FA of grey matter structures and therefore the potential errors in inter-subject non-linear registration of grey matter voxels based on their FA maps, we decided to select only voxels characterised by FA greater than 0.3, on the assumption that they correspond mainly to white matter areas.

This paper presents a new method for analysing axial and radial diffusivities and also provides an example of its application to patients with MS, which causes the development of focal brain lesions, as well as widespread white matter damage. Voxel-based group mapping is typically used to compare two populations of subjects of similar size, with smoothing of the data ensuring that the model’s error terms are normally distributed. This assumption is violated when voxel-based analysis is used to investigate differences between a single subject and a control group, therefore results of this analysis need to be carefully interpreted as false positives may occur (13). A similar approach has been previously utilized elsewhere (14). With this consideration in mind this method can be used in future to assess, in vivo, the microstructural damage occurring in other neurological diseases that lead to neurodegeneration, such as amyotrophic lateral sclerosis, which is now regarded as a multisystem disorder in which the motor neurons are affected earliest and most severely (15). Other neurode-generative diseases that would benefit from the application of this method are those that fall into the category of the tauopathies, such as corticobasal degeneration and progressive supranuclear palsy; it would be interesting to test whether this method can help in the differential diagnosis between these diseases and Parkinson’s disease (16), on the basis of the differences in microstructural correlates detected with axial and radial diffusivity analysis.

In this study we first compared the projected diffusivities, d_p-ax and d_p-rad, with d_ax and d_rad, i.e. the axial and radial diffusivities defined from the eigenvalues of the DT, in the healthy population used for the super-DTI dataset. Because of individual normal variability even in core areas of white matter tracts, we found, not surprisingly, that several areas showed d_p-ax lower than d_ax and d_p-rad higher than d_rad (Fig. 2a). We then investigated changes in the new projected parameters between three further individual examples, i.e. hc, p₁ and p₂, and the 15 hcs, thus showing the potential clinical applications of d_p-ax and d_p-rad. These are the same subjects used in a previous publication (4), which demonstrated the weakness of the axial and radial diffusivities defined from the eigenvalues of the DT. By definition, d_p-ax is never higher than the corresponding d_ax measured in the same subject. When we report areas of increased d_p-ax these refer to individual subjects compared to the reference super-DT dataset. Equally, by definition d_p-rad is never smaller than the corresponding d_rad, measured in the individual subject.

When comparing d_p-ax and d_p-rad of the single hc, not included in the super-DT dataset, with the population of hcs, we did not find any area showing statistically significant differences, which indicates that the subject’s eigenvectors are aligned with the super-DTI template. When comparing the patient with the lowest disability and lowest lesion load (p₁) with the hcs, we observed only sparse and small areas showing differences in the new proposed parameters (Fig. 2c). Also, these areas were very similar to, and mostly coincided with, the regions obtained by the same analysis using the standard parameters, d_ax and d_rad, confirming that in healthy brain tissue and in the presence of mild tissue disruption the eigenvalues of the DT are suitable indicators of disease progression. This also means that in this case the eigenvectors of the DT are within the dispersion of the directions of the eigenvectors in the hcs used for the super-DTI template. The new parameters, though, give extra information when the pathology is more advanced, as in p₂, showing for example areas of normal-appearing white matter characterised by a reduced d_p-ax not shown by d_ax. This reduced projected axial diffusivity is likely to derive from a reduced precision of the principal direction in the affected areas, which causes a misalignment with the reference principal diffusivity and therefore a lower d_p-ax. The sensitivity of d_p-ax and d_p-rad to pathology needs to be confirmed, but our preliminary findings suggest that in the presence of a more severe pathology the comparisons show a more complex picture. In fact, we found in p₂ i) regions where a lesion overlapped almost perfectly with areas of both d_p-ax and d_p-rad changes; ii) areas where a lesion covered a subregion of d_p-ax and d_p-rad changes; iii) areas where there was a change of either d_p-ax or d_p-rad outside the lesion; iv) regions where lesions were not accompanied by changes in the diffusivities. The comparisons between the standard and newly proposed parameters showed that:

Radial diffusivity: i) areas of increased radial diffusivity overlap a portion of the lesions and extend beyond the lesions to normal-appearing white matter tissue (Fig. 2f-1); looking at the distribution of the affected voxels, it is apparent that in general d_p-rad is more spatially localised than d_rad in p₂, while in p₁ the two quantities extend over very similar voxels; ii) there are no areas of decreased radial diffusivities compared with hcs.

Axial diffusivity: i) the core of some lesions is accompanied by an increase of both d_ax and d_p-ax with only a slight difference in the extent of coverage of the area highlighted by the two diffusivity parameters (Fig. 2f-2); ii) most strikingly, d_p-ax shows areas of decreased diffusivity (Fig. 2f-3) highlighting areas of degeneration not shown by d_ax. This is particularly evident in p₂, but small areas of decreased d_p-ax are also present in p₁, while there are none in hc.

The pathological substrate of the projected axial and radial diffusivities needs to be confirmed with an appropriate post-mortem study. The design of such a study is not straightforward given the need to have a reference healthy template for the brain used for the registration, therefore whole-brain high-resolution acquisitions are recommended. Previous work on axial and radial diffusivities has used animal models to test the hypothesis that d_ax changes reflect axonal damage while d_rad changes are related to myelin breakdown and remyelination. In fact, Song et al., in an animal model of optic nerve retinal ischaemia (17), found that axial diffusivity, d_ax, was decreased and correlated with axonal degeneration in the absence of myelin breakdown. An increase in radial diffusivity, d_rad, was instead observed with the occurrence of myelin breakdown. A subsequent study of d_ax and d_rad in the corpus callosum of a mouse brain after cuprizone treatment (18) confirmed that d_rad is a marker of demyelination (increase) and subsequent remyelination (decrease). In this model Song et al. also observed a decrease in d_ax in conjunction with axonal damage, but the change did not reach statistical significance. In order to validate the biological substrate of d_p-ax and d_p-rad, in animal models, similarly to what has been done for d_ax and d_rad, one would need to acquire data on healthy animals first in order to be able to define a standard template to use as a healthy reference dataset. At present, on the basis of our current analysis of in vivo human data, we propose that the projected axial diffusivity, d_p-ax, may be more sensitive to axonal damage than d_ax because of the observation that there are areas of decreased d_p-ax where no d_ax changes occurred.

To assess their sensitivity to pathology, the new parameters can be studied in any patient population that is affected by white matter focal lesions. The projected axial and radial diffusivities cannot be used in cases where the pathology involves expansive lesions and disrupts white matter structures to the degree that registration to a template is not possible, as in the case of large and/or particularly invasive tumours, but in such cases it is strongly advisable not to analyse the eigenvalues of the DT either, because the direction of the eigenvectors becomes difficult to compare between time-points and between subjects, in relation to the underlying structures that they represent.

In conclusion, the projected axial and radial diffusivities not only have a more consistent interpretation than the axial and radial diffusivities calculated from the DT eigenvalues of the individual subject, but they also offer a new means of studying the evolution of degenerative pathologies such as MS.