Association between somatic cell count after first parturition and cumulative milk yield in dairy cows

Abstract

The aim was to assess the association between the somatic cell count of parity 1 cows between 5 and 30 days in milk (SCC1), and subsequent cumulative milk yield over approximately two years for cows in English and Welsh dairy herds. The dataset included records from 43,461 cows in 2111 herds, from 2004 to 2006. Cumulative milk yield was the model outcome, and a random effect was included to account for variation between herds. The model fitted the data well and was used to make predictions of cumulative milk yield, based on SCC1. A unit increase in the natural logarithm of SCC1/1000 was associated with a median decrease in cumulative milk yield of 482 kg, over a median study period of 868 days.

Introduction

Heifer mastitis has been recognised as a common problem of economic importance throughout the developed dairy industry worldwide (Piepers and others 2009, De Vliegher and others 2012). The negative effect of elevated somatic cell count (SCC) at 5–30 days in milk (DIM) during the first lactation on the milk yield of Irish dairy cows persisted for their entire lifetime, and the median decrease was 864 kg per unit increase in the natural logarithm of (ln) SCC/1000 (Archer and others 2013a). This result emphasised the importance of including milk production beyond the first lactation to fully understand the true extent of accrued losses. Considering impact on cumulative milk yield is therefore essential to evaluate the total cost of SCC early in the first lactation and aid decision making around mastitis control measures for prepartum and peripartum (ppp) heifers; this has not been evaluated for dairy herds in England and Wales.

The aim of this study was to assess the association between SCC of parity 1 cows between 5 and 30 DIM (SCC1) and cumulative milk yield over approximately two years for cows in English and Welsh dairy herds.

Materials and methods

Data selection

A cleaned, fully checked dataset was available for herds located in England and Wales, including recording dates from 2004 to 2006 (National Milk Records, Chippenham, UK); selection criteria for this dataset have been described in detail (Madouasse 2009). Briefly, herds with at least 10 test dates per year, and ≥20 cows per test day recording were included. Those with factored data (alternate morning and afternoon recording at subsequent herd test days) were removed. At least 80 per cent of cows within the herds in the dataset were of the Holstein or Friesian breed. To be eligible for inclusion, cows required a first calving in 2004, followed by a record of SCC between 5 and 30 DIM during parity 1; 43,461 cows in 2111 herds met these criteria, and were included in the study dataset (DATASET1).

Data analysis

Cumulative milk yield for each cow lactation in DATASET1 was calculated using the test interval method (ICAR 2011), and these were summed to give an estimate of cumulative milk yield for each cow from the date of first calving in 2004 until the end of the study period on December 31, 2006. For the selected cows, ‘survival time’ was estimated as the number of days between a first calving date in 2004, and their last recording date. Cows were censored, if present at the final available recording date for their respective herd; otherwise, it was assumed that disposal occurred at the last recording date for each cow. Kaplan-Meier survival curves were plotted using R (R-Development-Core-Team 2010), and summary statistics produced for cows stratified by SCC1 (SCC1_gp; 1; <55,000 cells/ml, 2; 55,000–149,000 cells/ml, 3; 150,000–400,000 cells/ml, 4; ≥400,000 cells/ml).

Model development

The outcome of interest was the cumulative milk yield (y_ij), for the ith cow, in the jth herd. The random effects model used for analysis took the form:

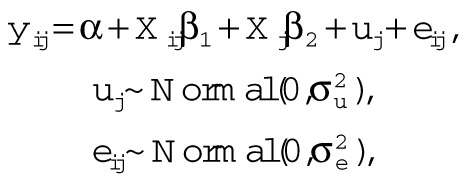where α=intercept value, X_ij=matrix of exposure variables for each cow, β₁=vector of coefficients for X_ij, X_j=matrix of exposure variables for each herd, β₂=vector of coefficients for X_j, u_j=a random effect to account for residual variation between herds (assumed to be normally distributed with mean=0, and variance=σ²_u)_, and e_ij=residual cow-level error (assumed to be normally distributed with mean=0, and variance=σ²_e). SCC1 was divided by 1000 and included on a (ln) linear scale. Potential confounding variables available by 30 DIM during parity 1 were investigated for inclusion; specifically to account for variables known at this time that influence the relationship between SCC1 and cumulative milk yield. Therefore, DIM at the first recording (polynomial terms), and month of first calving (categorical terms) were the only confounding variables investigated. Biologically plausible interactions, and herd-level random slopes (herd×fixed effect interactions) were assessed. Initial model exploration was conducted in MLwiN, with the iterative generalised least squares procedure (Goldstein 2003). To facilitate Bayesian posterior predictions from the model that incorporated all uncertainty in parameters, the model was further developed in WinBUGS 1.4.3 (Lunn and others 2000). Parameters were estimated from 10,000 Markov chain Monte Carlo simulations, following a burn in of 1000 simulations during which time chain convergence had occurred. This was assessed by inspection of three chains run in parallel to ensure a stationary distribution had been reached (Gilks and others 1996). Vague prior distributions were used for σ⁻²_u∼γ (0.001, 0.001), σ⁻²_e∼γ (0.001, 0.001), and β∼Normal (0, 10⁶), to give the major influence to the data in the estimation of parameters (Green and others 2004). Distributions of covariates and interaction terms were inspected, and these remained in the final model based on biological plausibility, and only if the 95% Bayesian credible interval (CI) excluded 0. Sensitivity of the results to prior distributions for the herd-level random effect variance (Spiegelhalter and others 2004) was evaluated by repeating simulations using the prior; σ²_u∼Uniform (10⁻⁷, 10⁷).

Model checking

The posterior distribution of the mean residual was inspected to determine if the 95% CI included 0, suggesting adequate model fit. Based on the methods proposed by Gelman and others (1996), model fit and usefulness were evaluated using fixed and random effects to predict the cumulative milk yield for each cow (y.pred_ij) as follows:

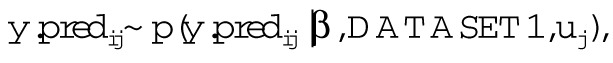where y.pred_ij are posterior predictions of cumulative milk yield for the ith cow in the jth herd in DATASET1, β is the vector of final model coefficient distributions, and u_j is the random effect for the jth herd. Mean cumulative milk yield was predicted for cows categorised by SCC1_gp; these categories were not used in the final model. Posterior predicted distributions of mean cumulative milk yield for cows in these groups were inspected to determine if the observed mean cumulative milk yields were within the 95% CI of the posterior predictions, indicating the extent of model usefulness for predictions based on SCC1 (Gelman and others 1996).

Results

Descriptive results

Summary statistics for variables in the dataset are shown in Table 1. Cumulative milk yield decreased from 16.9 tonnes (IQR; 12.2–20.4), to 15.8 tonnes (IQR; 8.9–19.8) for cows with SCC1 <55,000 cells/ml, and SCC1 >400,000 cells/ml, respectively. Overall, the median survival time was 791 days (IQR; 607–888). No cows were censored within 700 days of a first calving in 2004. Median survival time decreased from 796 days (IQR; 660–883), to 767 days (IQR; 432–882) for cows with SCC1 <55,000 cells/ml, and SCC1 >400,000 cells/ml, respectively (Table 1, Fig 1). The overall median time in the study was 874 days (IQR; 813–971). Median time in the study varied from 868 days (IQR; 812–959) for cows with SCC1 <55,000 cells/ml, to 881 days (IQR; 814–979) for cows with SCC1 150,000 cells/ml to 400,000 cells/ml (Table 1).

TABLE 1:

Descriptive results for 43,461 eligible cows* in 2111 English and Welsh dairy herds

Group	Variable	Median (IQR)
SCC1† <55,000 cells/ml	Cumulative milk yield‡ (tonne)	16.9 (12.2–20.4)
	Survival time§ (days)	796 (660-883)
	Time in study¶ (days)	868 (812–959)
	SCC1 (‘000 cells/ml)	31 (22–42)
	Number of cows	19,462
SCC1 55,000–149,000 cells/ml	Cumulative milk yield (tonne)	16.5 (11.5–20.3)
	Survival time (days)	796 (614–892)
	Time in study (days)	880 (815–974)
	SCC1 (‘000 cells/ml)	83 (67–109)
	Number of cows	13,878
SCC1 150,000–400,000 cells/ml	Cumulative milk yield (tonne)	16.3 (10.6–20.2)
	Survival time (days)	782 (534–887)
	Time in study (days)	881 (814–979)
	SCC1 (‘000 cells/ml)	221 (177–284)
	Number of cows	5889
SCC1 >400,000 cells/ml	Cumulative milk yield (tonne)	15.8 (8.9–19.8)
	Survival time (days)	767 (432–882)
	Time in study (days)	879 (805–997)
	SCC1 (‘000 cells/ml)	845 (553–1577)
	Number of cows	4232

*Cows with an SCC record between 5 and 30 days in milk during parity 1 during 2004

†SCC between 5 and 30 days in milk during parity 1

‡Estimated total milk yield from date of first calving to date of last recording up to December 31, 2006

§Number of days from date of first calving to date of last recording on or before December 31, 2006

¶Number of days from date of first calving to December 31, 2006

FIG 1:

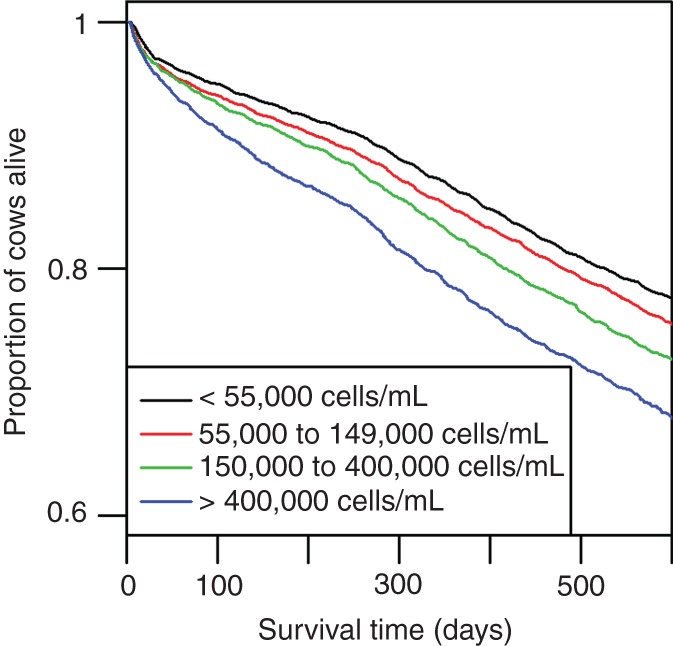
Kaplan-Meier survival curves (Cows were censored if present at the last available recording date for their respective herd) for cows in 2111 English and Welsh dairy herds grouped by somatic cell count between 5 and 30 days in milk during parity 1

Model results

The final model is presented in Table 2. Cows that calved in January 2004, with mean ln SCC1/1000 (4.33) were the baseline for comparison. Cows that calved from February to December 2004 had lower cumulative milk yields by the end of the study period. Having accounted for month of calving (which also adjusted for time in the study); a unit increase in ln SCC1/1000 (eg, from 55,000 to 150,000 cells/ml, or from 150,000 to 400,000 cells/ml) was associated with a median decrease in cumulative milk yield of 482 kg (95% CI 431 to 534) over a median of 868 days (IQR; 812–959) in the study.

TABLE 2:

Bayesian credible intervals from 10,000 simulations of the final model; outcome cow level cumulative milk yield (kg)

Exposure (baseline)	Lower 2.5%	Median	Upper 97.5%
Intercept	17,740	17,980	18,230
ln* SCC1† (4.33)	−534	−482	−431
Month of first calving (January) February	−813	−485	−175
March	−1367	−1020	−676
April	−1901	−1526	−1153
May	−1916	−1565	−1218
June	−2478	−2167	−1858
July	−2610	−2310	−2019
August	−3308	−3017	−2732
September	−3633	−3345	−3064
October	−4240	−3960	−3676
November	−4625	−4336	−4045
December	−5270	−4957	−4636
Random effects sd:
Cow level	6173	6215	6286
Herd level	2534	2641	2747

*Natural logarithm.

†First test day SCC record at 5–30 days in milk during parity 1 (‘000 cells/ml).

Model checking

The posterior distribution of the mean residual was normal and included 0 kg (95% CI −82 to 83), indicating the model fitted the data on which it was developed. Predictions of cumulative milk yield for cows in DATASET1, aggregated by SCC1 group also indicated good fit and, hence, that the model was suitable for predictions in these herds (Fig 2). There was <0.5% difference in the median, and 95% CI limits of the ln SCC1/1000 coefficient distribution when a uniform prior distribution for the herd level random effect variance was used, and this had no substantive impact on model interpretation.

FIG 2:

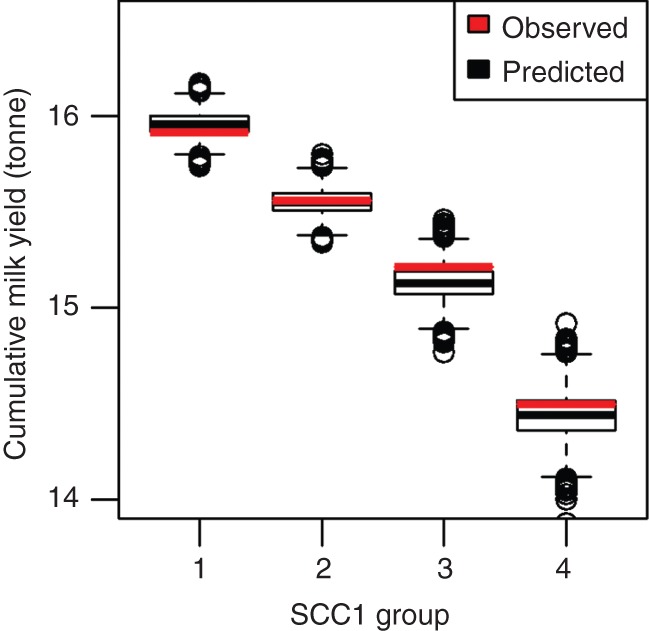
Model predictions of cumulative milk yield (From date of first calving in 2004 to date of last recording up to December 31, 2006) from 10,000 simulations, and observed values in 2111 English and Welsh dairy herds, for cows grouped by somatic cell count (Group 1; <55,000/ml, group 2; 55,000–149,000/ml, group 3; 150,000–400,000/ml, group 4; ≥400,000/ml.) at 5–30 days in milk during parity 1 (SCC1)

Discussion

A previous study identified important losses in lifetime milk yield associated with SCC between 5 and 30 DIM for cows in Irish dairy herds (Archer and others 2013a). The current study is the first to demonstrate differences in the milk yield of cows in English and Welsh dairy herds associated with changes in SCC early in the first lactation, and is in agreement with the study on Irish dairy herds. Measures of cumulative milk yield were different between these studies, however, the magnitude of losses are comparable. Unit increase in ln SCC /1000 at 5–30 DIM during parity 1 in both studies was associated with a 3 per cent decrease in cumulative milk yield over approximately two years, assuming proportional losses over time. The estimated impact of SCC between 5 and 30 DIM during parity 1 on cumulative milk yield for cows in English, and Welsh herds over one year (482 kg per two years) was five times larger than an estimate of milk loss in Belgian cows of around 47 kg over 365 day/unit increase in ln SCC /1000 shortly after the first calving (De Vliegher and others 2005b). The analysis of De Vliegher and others (2005b) only included cows that survived the first lactation, and excluded cows that were culled. Therefore, the estimated milk loss is likely to be an underestimate of the true effect. Cumulative milk yield is a composite of both decreased milk yield while alive, and decreased longevity to give a realistic estimate of milk loss at cow level. Decreased milk yield attributable to high SCC between 5 and 30 DIM during parity 1 extended into subsequent lactations and was associated with a decrease in survival time as has been observed previously (De Vliegher and others 2005a, Archer and others 2013a, b).

In order to focus attention on the potential impact of mastitis control measures for ppp heifers, only parameters available by 30 DIM during parity 1 were used to model the cumulative milk yield of cows, and this could be predicted by including SCC1. Risk factors for heifer mastitis have been identified and include those related to increased challenge such as poor environmental hygiene during the ppp period, and those related to host resistance such as udder oedema (De Vliegher and others 2012). However the relative cost and efficacy at herd level of specific management interventions for control remain unknown. This information would be important to offset against potential savings, including increase in cumulative milk yield, to assess the cost-effectiveness of interventions. Investment in control measures for heifer mastitis depends on many factors, such as the decision makers' financial situation, willingness to pay and attitude to risk. Further research is needed into the cost-effectiveness of possible interventions in different herd scenarios, and knowledge of differences in the management, and environment of herds with varying prevalence of cows with high SCC early in the first lactation would be of use in formulating advice. In addition to cumulative milk yield, further savings may be accrued through reduced incidence of clinical mastitis and replacement costs that have not been considered, however, the economic impact of the latter is expected to be small (Archer and others 2013b). There may have been further losses in milk production beyond the time period considered in this research (Archer and others 2013a), and this could make control of heifer mastitis even more economically favourable.

Conclusion

This study demonstrated that for cows in English and Welsh dairy herds, SCC between 5 and 30 DIM during parity 1 (SCC1) was negatively associated with cumulative milk yield over approximately two years. This result highlights a need for further research into the cost-effective control of mastitis in ppp heifers.

Funding Simon Archer was funded by a Teagasc Walsh Fellowship.

Open Access This is an Open Access article distributed in accordance with the Creative Commons Attribution Non Commercial (CC BY-NC 3.0) license, which permits others to distribute, remix, adapt, build upon this work non-commercially, and license their derivative works on different terms, provided the original work is properly cited and the use is non-commercial. See: http://creativecommons.org/licenses/by-nc/3.0/