Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Oct 31;3:3116. doi: 10.1038/srep03116

Wideband THz Time Domain Spectroscopy based on Optical Rectification and Electro-Optic Sampling

A Tomasino 1,a, A Parisi 1, S Stivala 1, P Livreri 1, A C Cino 1, A C Busacca 1, M Peccianti 2, R Morandotti 3
PMCID: PMC3813929  PMID: 24173583

Abstract

We present an analytical model describing the full electromagnetic propagation in a THz time-domain spectroscopy (THz-TDS) system, from the THz pulses via Optical Rectification to the detection via Electro Optic-Sampling. While several investigations deal singularly with the many elements that constitute a THz-TDS, in our work we pay particular attention to the modelling of the time-frequency behaviour of all the stages which compose the experimental set-up. Therefore, our model considers the following main aspects: (i) pump beam focusing into the generation crystal; (ii) phase-matching inside both the generation and detection crystals; (iii) chromatic dispersion and absorption inside the crystals; (iv) Fabry-Perot effect; (v) diffraction outside, i.e. along the propagation, (vi) focalization and overlapping between THz and probe beams, (vii) electro-optic sampling. In order to validate our model, we report on the comparison between the simulations and the experimental data obtained from the same set-up, showing their good agreement.

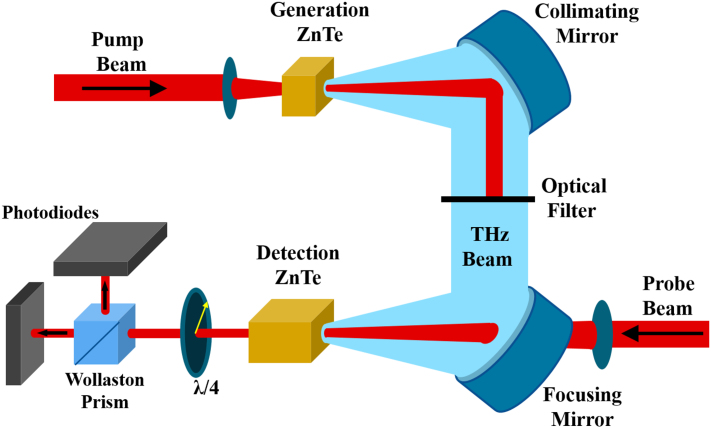
Generation and detection of THz electromagnetic waves (0.1–10 × 1012 Hz) is not a novel topic1,2,3, but it has been arousing an ever-increasing interest only in the last decade. Recent studies demonstrated that many substances and particularly bio-polymers like proteins, amino and DNA possess specific global and sub-global modes in the THz band. Hence, particular consideration has been recently devoted to THz spectroscopy since it reveals information on the conformational stage of molecules and potentially enables their discrimination in various compounds. Indeed, THz pulses have been broadly used, ranging from spectroscopy and time-resolved pump-probe experiments to imaging applications4,5. Moreover, the negligible ionization power of the THz radiations compared to optical and X-rays technologies make them perfectly suitable for biological applications6. For the above-mentioned reasons, THz technology are penetrating in lots of areas, beyond fundamental Physics investigation, spanning from medical care and homeland security to cultural heritage conservation7,8,9,10,11,12,13. The most challenging technology development remains in the area of THz sources and detectors, since, in general, both wide band and high power are required at the same time. Thanks to the improvement of the pulsed laser technology, different types of stable THz sources have been developed so far, with peak power values ranging from kW to MW14,15. In particular, Optical Rectification (OR)16 combined with Electro-Optic Sampling (EOS) detection is still the configuration of choice in the few standard high energy pulsed THz system. For this reason, in this paper we present an analytical model able to simulate the full electromagnetic propagation which takes place in the THz-TDS set-up17, sketched in Fig. 1 (refer to Methods), based on OR and EOS and employing <110> ZnTe crystals. We will explain and justify the approach and the approximations which underlie the modelling of each stage and that allowed us to build a complete transfer function in the frequency domain, in order to predict the set-up behaviour.

Figure 1. Sketch of a typical THz Time Domain Spectroscopy (THz-TDS) set-up.

Figure 1

Open in a new tab

Results

Optical rectification

In noncentrosymmetric crystals the second-order nonlinear optical susceptibility χ(2) is nonzero18 and, for this reason, parametric processes (such as second-harmonic generation, sum- and difference-frequency generation, parametric solitons, optical rectification, etc.) can take place19,20,21,22,23,24. As regards Optical Rectification, when a CW laser impinges on such a material, the latter responds generating a DC -i.e. rectified- electric field proportional to the pump intensity. On the other hand, when an ultrashort (i.e., broadband) laser pulse (≈100 fs) passes through a non-centrosymmetric crystal, optical rectification performs a mixing of the frequencies within each pulse -i.e., difference-frequency generation (DFG) between pairs of frequencies within the pulse bandwidth- generating a low-frequency radiation, that is the THz wave. The time dependent equation describing this phenomenon is25,26,27:

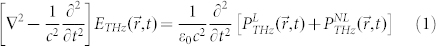graphic file with name srep03116-m1.jpg

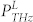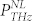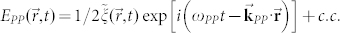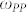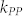where ETHz is the instantaneous THz field, Inline graphic is the linear polarization induced by the THz electric field and Inline graphic is the nonlinear polarization induced by the electric field of the laser pump Inline graphic, where Inline graphic and Inline graphic are the carrier frequency and the wave vector respectively, and 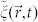Inline graphic is the slowly-varying envelope both in 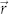Inline graphic and t, for each pulse. We will neglect the contribution of other nonlinear processes, such as, second harmonic generation, two photon absorption, free carrier absorption and self-phase modulation. In addition, the pump depletion is always negligible in most practical cases, since the conversion efficiency for the OR case (≈10−6–10−4) is far below the upper limit of the quantum efficiency, given by the ratio of the central THz frequency and the optical carrier. By assuming a near-infrared pumping and pulses of transform-limited duration of 100 fs or longer, we neglect the second time-derivative of 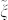Inline graphic (slowly varying envelope approximation, SVEA). Furthermore, we consider both pump and THz beams as plane waves, neglecting the dependence on the transverse coordinates (x, y), being the diffraction length in those cases always much larger than the crystal thickness in all the generated spectrum. By taking the Fourier transform of eq. (1), with 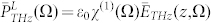Inline graphic, we obtain28:

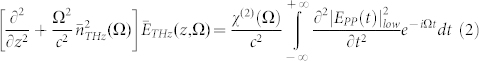graphic file with name srep03116-m2.jpg

where the over-lines stand for the Fourier operator and 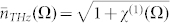Inline graphic is the refractive index at the THz frequency (Ω). It is worth highlighting the presence of the second spatial derivative in eq. (2), since the generated THz wave has a bandwidth comparable to its central frequency, i.e. SVEA does not hold for THz radiation. According to the laser features commonly employed in the THz collinear generation, we approximate the pump pulse envelope with a Gaussian profile 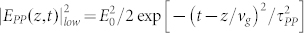Inline graphic, where by definition 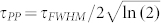Inline graphic, τFWHM being the full-width at half maximum pulse duration of the pump intensity, νg = c/ng and E0 the group velocity and the magnitude of the electric field, respectively. Here, we assume that τPP is not varying along the propagation because of dispersion, since the thickness of the crystal (~1 mm) is much smaller than the dispersion length of both fields. Thus, by considering the boundary conditions 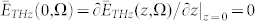Inline graphic, one obtains the exact solution for the THz electric field in the frequency domain, from eq. (2):

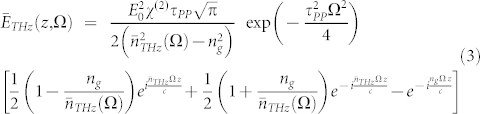graphic file with name srep03116-m3.jpg

THz wave properties

In eq. (3), we wrote the THz frequency-dependent electric field as the product of three main terms in order to point out the properties of the THz wave. The third factor shows that the THz waveform is actually the result of the interference among three waves: the first two travel with the same phase velocity 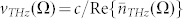Inline graphic (precisely, one is backward29,30 and the other one is forward with respect to the z axis), whereas the third one is a forward wave with phase velocity matching the group velocity of the pump beam. However, the amplitudes of the three contributions are quite different: it results that although the backward wave vanishes at the frequency satisfying the phase-matching condition, as explained below, it has always negligible magnitude in the whole THz range. The relative term will be therefore neglected. Conversely, the forward wave reaches its maximum at the phase-matching. It is generally comparable with the third wave in the whole THz range and they together contribute to the generated THz beam. The second factor in eq. (3) is a Gaussian term centred at Ω = 0, which acts as a low-pass filter: the shorter the transform-limited pulse duration τpp the wider the bandwidth. Indeed, there is an upper limit for the THz band ΔνTHz obtainable via ultrashort laser pulses, according to Heisenberg's principle25, i.e., the time-bandwidth product, 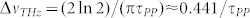Inline graphic. However, in most practical cases of femtosecond-pulse driven generation, the achievable bandwidth is never as wide as it is determined by the latter expression, since it mostly depends on the chosen crystal, as we will show later. Finally, the first factor in eq. (3) is comprehensive of the nonlinear parameter and the difference between the refractive index of the crystal in the THz range and the infrared group index. Both χ(2)(Ω) and 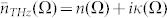Inline graphic are complex frequency-dependent functions, accounting for dispersion and absorption, whose effects are not negligible because of the ultrashort nature of the pulse pump. Hence, we model the refractive index of the crystal, in the THz range, using Maxwell-Helmholtz-Drude's semi-quantic model31 of the transversal phonon resonance modes which establishes that the dielectric permittivity can be expressed by:

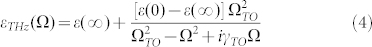graphic file with name srep03116-m4.jpg

where ε(∞) is the dielectric constant at frequencies much higher than 1 THz, ε(0) is the DC dielectric constant, ΩTO is the transversal optical (TO) resonance frequency, γTO is the full-width of the mode. Noteworthy, this model is the best choice for our purposes, since ZnTe is featured by a very weak coupling between the transversal and longitudinal modes. Hence, for frequencies close to ΩTO, the resonant absorption becomes so strong that the material appears completely opaque. As ΩTO/2π = 5.32 THz32, ZnTe sources exhibit a contiguous generation window between hundreds of GHz up to 3 THz. Note that other materials guarantee larger bandwidths33,34,35,36. ZnTe is still the material of choice in many set-up due to a nicely shaped THz generation spectrum and the significant power-spectral density within the lower THz band. For the nonlinear susceptibility, we have used Miller's rule18.

Phase-matching and coherence length

The phase matching condition is fulfilled when the optical group velocity matches the THz phase velocity:

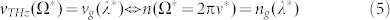graphic file with name srep03116-m5.jpg

For ZnTe it turns out that 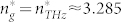Inline graphic, ν* ≈ 2.55 THz, λ* ≈ 788 nm37. The THz frequency Ω* is generated with the maximum possible conversion efficiency. This could be further ascertained by manipulating eq. (3), as it follows:

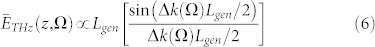graphic file with name srep03116-m6.jpg

where Δk(Ω) = Ω(n − ng)/c is the mismatch term and Lgen is the generation crystal thickness. Close to the PM condition, i.e. Δk(Ω) ≈ 0, the THz field magnitude scales almost proportionally to the crystal length. Anyway, for each frequency within the bandwidth and for a fixed laser wavelength, there is an upper theoretical limit for Lgen, related to the so-called coherence length:

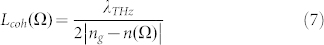graphic file with name srep03116-m7.jpg

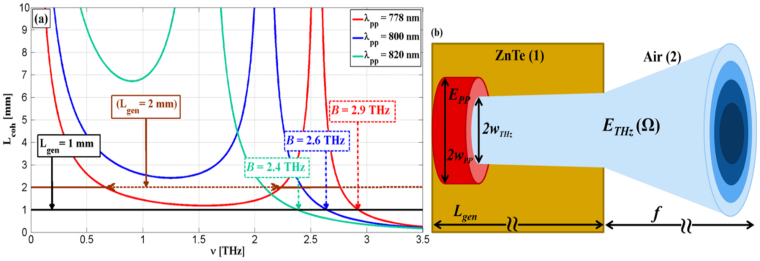
The physical meaning of (7) is that, when the propagation length approaches Lcoh, the generation process equates the back-conversion process that reconverts the THz photons into pump power until the THz field vanishes for z = 2Lcoh. This means that it is necessary to achieve a trade-off between power and bandwidth when the thickness of the generation crystal has to be chosen according to the proper application. To this end, Fig. 2a shows how the coherence length is related to the frequency for three different pump wavelengths. We note that employing a 1-mm thick ZnTe crystal, the bandwidth is maximum (about 2.9 THz) for a 778 nm pump (red line), but it shrinks when the laser wavelength moves away from λ*, even if the generation efficiency (related to Lcoh) becomes higher for all the frequencies within the band (blue and green lines).

Figure 2.

Figure 2

Open in a new tab

(a) Coherence Length vs. frequency for the case of three different pump wavelengths in ZnTe. The black line indicates the generation crystal thickness. (b) Sketch of the emitting cone for the THz beam both inside and outside the ZnTe crystal.

The Lgen = 2 mm case is also plotted showing that the generation process is not efficient for a relatively large THz window when λ* is employed as pump source. Indeed, in this case, as pointed out by the double brown dashed-arrow, the most of the bandwidth achievable with ZnTe in the rage Ω < ΩTO, is not practically generated, resulting in a narrow-band spectrum centred at the frequency Ω*.

Crystal interface

The effect of the crystal-air interface can be formalized considering the dispersion of the Fresnel reflection and transmission coefficients within the THz band within the hypothesis of non-diffracting (collimated) beam. These considerations are sketched on Fig. 2b. We can then introduce frequency-dependent Fresnel coefficients for transmission (T) and reflection (R), as:

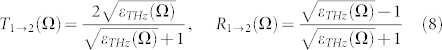graphic file with name srep03116-m8.jpg

where “1” and “2” in the subscripts stand for ZnTe and air, respectively. As the dielectric constant diverges for Ω → ΩTO, eq. (8) has a resonant complex nature that emphasizes reflection in the high THz band. From the previous consideration, it immediately follows that an important phenomenon which takes place inside the crystal is the Fabry-Perot (FP) effect, which acts as a selective filter, according to:

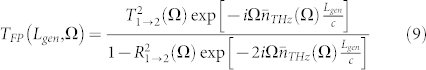graphic file with name srep03116-m9.jpg

From eq. (9) we note that if the crystal is thin enough, the longitudinal resonances are established for those frequencies which do not fall into the achievable THz bandwidth, thus resulting in no THz pulse-repetitions outside the material. In addition, eq. (9) somewhat modifies the THz bandwidth, because it mostly transmits those frequencies which fulfil the nonlinear condition, 2Ωn(Ω)Lgen/c + ϕ(Ω) = 2 πm, where ϕ(Ω) is the phase of R2(Ω)and m is the order of the longitudinal mode.

Diffraction

Outside the crystal, the broadband THz beam propagates toward the mirror that lies in the far field region, but it diffracts out much quickly than a Gaussian beam. Therefore, we cannot use Rayleigh's law to quantify its aperture along the propagation, since the latter only holds in the paraxial approximation. Instead, we can apply Bethe's theory of diffraction by small holes38. If fact, since the THz field is proportional to the pump intensity, we can assume that the THz wave is generated by a spot size whose waist satisfies the following relation: 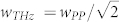Inline graphic. This means that the THz source size could be smaller than most of the emitted wavelengths, as Bethe's theory assumes. Avoiding the exact treatment of the diffraction, the main result of the theory is that we can introduce a different confocal parameter similar to the Rayleigh length, defined as 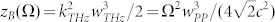Inline graphic, which shows how the lower frequencies diffract quicker than what is predicted by Rayleigh's law, since in this case zB depends on the square of frequency. However, we note how for larger waist size wPP, Bethe's diffraction is practically negligible for the whole bandwidth, as we will show in the following. Then, in order to compute the field rate gathered by the first mirror, we would follow the procedure proposed in Ref. 28, calculating the transfer function for the diffraction stage:

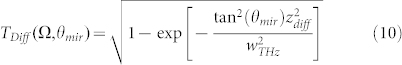graphic file with name srep03116-m10.jpg

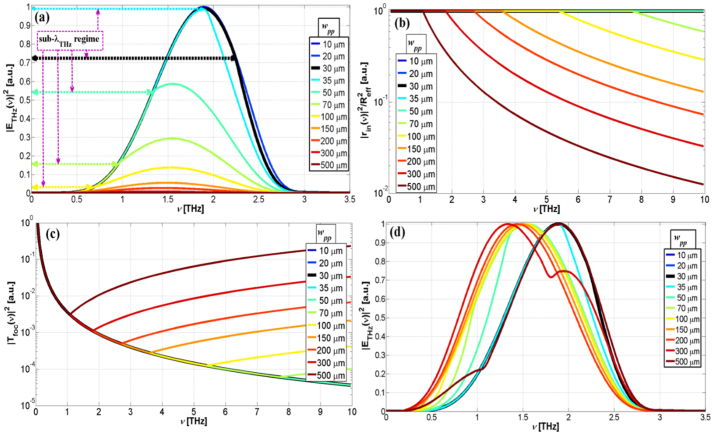
here θmir = arctan[1/(2f#)] and f# = f/D are the semi-aperture and the f-number of the mirror, respectively, whose diameter and focal length are D and f, respectively (see Figs. 3b and 3c). For more accuracy, we distinguished two cases, defining the confocal parameter zdiff(Ω) = zB if kTHzwTHz ≤ 1 whereas zdiff(Ω) = zR if kTHzwTHz > 1, with 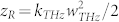Inline graphic the usual Rayleigh length, which anyway describes quite well the behaviour of the higher frequencies. In order to show the effect of Bethe's diffraction, we report on a plot of eq. (10) in Fig. 3a, under our working conditions, i.e. f# ≈ 1.4, wpp ≈ 30 μm, which shows the different behaviour of the two laws. As we can see, the frequencies lower than 2 THz -which fall in the so-called sub-wavelength regime- are very weakly collected by the mirror since its numerical aperture is not wide enough. The black circles in Fig. 3a indicates the trend switch of the curve, i.e. those frequency whose propagation follow again Rayleigh's law. Since we are mainly interested in as diffraction is related to the pump beam waist and how the former affects the THz pulse bandwidth, we simulated several cases, as reported in Fig. 4, where the generation parameters are fixed, except for the pump waist size. In particular, in Fig. 4a, the comparison among the bandwidths collected through the first parabolic mirror -varying the parameter wpp- is shown. Again, it is possible to recognize how the mirror cannot efficiently collect the lowest side of the THz bandwidth - which includes the sub-wavelength regime, highlighted by the dashed lines- and that smaller wPP, wider such region, as it is stressed by the trend of the curves. The black thicker curve indicates our generation condition, meaning that most of the bandwidth we generated falls into Bethe's regime, so its inclusion in the model is a crucial aspect in order to achieve agreement with the experiments. Simulations reasonably show that the generation process -for a fixed pump power- is more efficient when the pump beam is tightly focused (in fact, the THz intensity for wPP ≥ 200 μm is at least one order-of-magnitude lower than the other cases). However, it should be kept in mind that waist sizes too small (wPP ≤ 200 μm) fail to satisfy the hypothesis we imposed when we solved eq. (2), and which could probably give rise to other nonlinear phenomena due to the extreme pump beam focusing, phenomena which are not included in the model and which we are not interested to. On the other hand, pump waists too large (wPP ≥ 500 μm) are not suitable -in addition to the too low efficiency conversion- because, for this case, it has been shown that the THz radiation generated at peripheral transversal positions along the pump beam destructively interfere with the one generated on the axis39. It is also worth noting that the THz pulse gathered by the off-axis is featured by a central frequency (given by the intensity-weighted average frequency, i.e. the first-order moment with respect to intensity) that moves towards higher frequencies as the waist size decreases.

Figure 3.

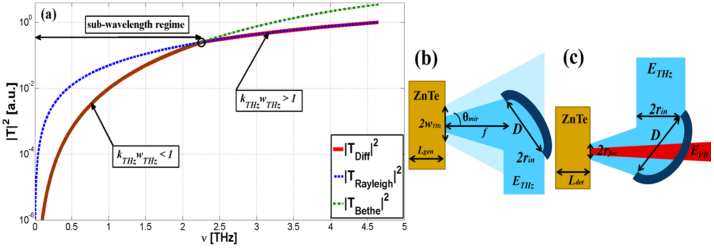
Figure 3

Open in a new tab

(a) |TDiff|2 transfer function (eq. 9) compared with Rayleigh's and Bethe's diffraction (plotted for a pump beam waist fixed at wPP ≈ 30 μm). Sketch of the (b) collimating stage and (c) focusing stage.

Figure 4.

Figure 4

Open in a new tab

(a) Comparison among the bandwidths collected through the first off-axis for different values of the pump beam waist wpp (normalized with respect to the maximum of the curve at wpp = 10 μm). It is also shown Bethe's regime extension (dashed arrows). (b) Frequency-dependent transversal size of the THz beam collected through the first off-axis (normalized with respect to the effective mirror radius 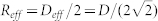Inline graphic). Curves corresponding to a waist smaller than 50 μm are constantly equal to 1 for the whole investigated THz range. (c) Transfer function |Tfoc|2 of the focusing stage through the second off-axis. Curves corresponding to a waist smaller than 50 μm are entirely overlapped. (d) Comparison among the bandwidths focused through the second off-axis for different values of the pump beam waist wpp. Each curve is normalized with respect to its own maximum. In all the figures, the thicker black curves highlight our working conditions.

Focusing

THz beam focusing is hampered by the same issues of the collecting stage. Because of the broadband nature of the THz beam, each frequency-component is being focused not only to different spot sizes, but also to different focal planes. This is a serious problem because the strength of the THz electric field is distributed on a volume of the detection crystal, making the detection process more difficult, being based on the optical index modulation caused by the THz field, as we will see later. However, we have to stress that the bandwidth of the beam arriving at the second mirror has not significant low-frequency terms, so their contribution is marginal. This consideration allows us to simply apply the geometrical optics rules. The beam size arriving at the second mirror is:

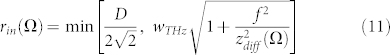graphic file with name srep03116-m11.jpg

where we have supposed, for sake of generality, that the THz beam could diffract more than the dimension of the mirror. Actually, eq. (11), plotted in Fig. 4b, shows how in the sub-wavelength regime, the THz beam diffraction is so strong that the beam radius - ideally measured in front of the mirror - is larger than the cross section of the mirror. This means that the collected THz beam waist is essentially fixed by the mirror dimension for most of the band of interest, for several suitable values of wPP. Now, if we use Gauss' formula, it is found out that the mirror focuses the THz beam to a waist as wide as rfoc(Ω) = 2cf/Ωrin(Ω), from which the focusing effect could be modelled as40:

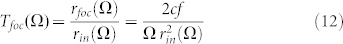graphic file with name srep03116-m12.jpg

A plot of this transfer function is reported in Fig. 4c, revealing some interesting aspects. Certainly, the most important effect of this stage is the low-frequency enhancement of the generated bandwidth, as it can be also seen in Fig. 4d, in the case of rin practically constant within the entire band. This because the focusing effect is stronger for wide rather than thin beams impinging on the mirror. However, we want to highlight that, for larger pump waist (wPP ≥ 200 μm), rin is no longer constant within the whole band but tends to decrease starting from that frequency whose beam component does not diffract out more than the mirror size. Considering eq. (12), this entails that the higher frequencies are now emphasized as well (see, for example, the wPP = 500 μm case in Fig. 4d). Consequently, this stage actually performs a reshape of the spectrum such that, for example, the normalized bandwidth for the wPP = 500 μm case is almost overlapped with those for the wPP ≤ 30 μm case (even if the spectra amplitudes are obviously more than one order-of-magnitude different). Anyway, we note how the most interesting aspect is that if it is possible to reach a trade-off for the pump waist size (as the wPP = 300 μm case), the reshape-effect of this stage could be helpful to achieve wider bandwidths for fixed nonlinear generation crystal.

Electro-optic sampling

Free-space electro-optic sampling is a coherent pulse detection technique, which has been extensively experimented for several years41,42,43. The working principle is sketched in Fig. 5a (refer to Methods). The advantage of EOS is that one can determine not only the amplitude of the pulses but also their phases with high accuracy (< 10−2 rad). Although the simplicity of the above-described mechanism, EOS is afflicted by the same issues of the OR, such as44,45: (i) dispersion and absorption inside the crystal and at the air-crystal interface; (ii) Fabry-Perot effect inside the detection crystal; (iii) finite pulse duration of the probe beam; (iv) phase-mismatch between probe and THz pulses. Furthermore, a critical problem is (v) the geometrical overlapping between the probe and THz beams. While the modelling of (i–ii) is the same as the previous stages, for (iii–iv) we write the following frequency response for the detection stage:

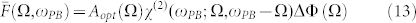graphic file with name srep03116-m13.jpg

where Aopt(Ω)is the autocorrelation of the Gaussian probe pulse, which accounts for the loss of resolution due to the finite pulse duration, χ(2)(ωPB; Ω, ωPB − Ω) is the second-order susceptibility for the DFG case (the same as the OR case, according to Kleinman's symmetry) and ΔΦ(Ω) is the frequency-dependent mismatch factor. With simple manipulations, it is found out:

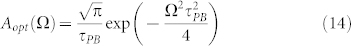graphic file with name srep03116-m14.jpg
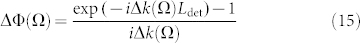graphic file with name srep03116-m15.jpg

where τPB is the probe pulse duration, Δk(Ω) = kP(ωPB) + k(Ω) − kP(ωPB − Ω) is the mismatch term between the probe field, the THz field and the frequency-difference field wave vectors, respectively, and Ldet is the thickness of the detection crystal.

Figure 5.

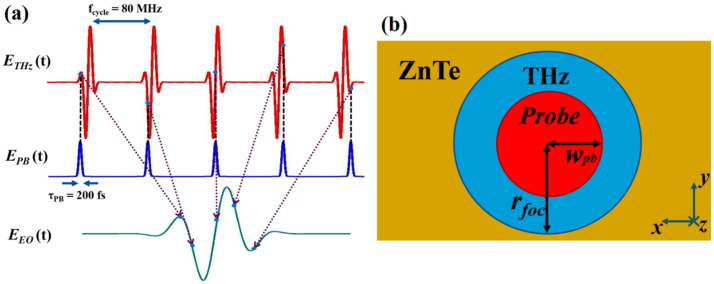
Figure 5

Open in a new tab

(a) EOS working principle for a train of pulses. (b) Sketch of the overlapping between probe and THz beams inside the detection crystal.

Beams overlapping

The issue mentioned in (v) is due to the fact that THz focusing is frequency-dependent as well. The THz beam could be ideally considered as the overlap among lots of single-frequency beams, whose waist is frequency-dependent. So, those frequencies whose spot size is more spatially overlapped with the probe one are being detected with higher efficiency, as shown in Fig. 5b. To compute this effect, we have to consider the transversal beam profiles and solve the overlap integral:

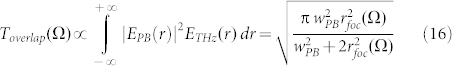graphic file with name srep03116-m16.jpg

where we have assumed a Gaussian shape for both beams, whereas rfoc(Ω)is the THz waist and wPB is the probe one. It should be noted that eq. (16) is only valid when the two beams are exactly concentric. This effect can be quite important, since the probe beam size is generally smaller than the THz one, due to its focusing into the detection crystal, in order to obtain an enhancement of the EOS efficiency.

Discussion

As we mentioned in the beginning, we can then multiply together all the previous terms in order to obtain an overall transfer function Tset-up in the frequency domain, which models the entire set-up behaviour providing the detected THz electric field:

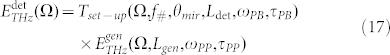graphic file with name srep03116-m17.jpg

where 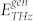Inline graphic is the THz electric field emerging from the generation crystal. Obviously, taking the Fourier transform of eq. (17), one can analyse the instantaneous THz electric field in the temporal domain. However, it should be kept in mind that this can be only performed with a numerical approach, since generally 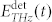Inline graphic cannot be expressed with elementary functions. In order to test the effectiveness of the model, we report on the comparison with the experimental results. As we have mentioned through the text, we built an ad-hoc model for our set-up, so we have already given many experimental parameters, which we list again in the following for simplicity. The generation and detection crystals are both <110> ZnTe: the first one length is Lgen = 1 mm, whereas for the second one Ldet = 2 mm. The optical source is a Ti:Sapphire pulsed laser (Mai Tai, Spectra-Physics) whose centre emission line is λPP = 800 nm. The intensity pulse duration is τPP = τPB = 200 fs, whereas the waist sizes focused to the crystals are equal to wPP = wPB = 30 μm, for both beams. The f-number of both collimating and focusing optics is f# ≈ 1.4. By using these parameters for the simulations, we obtained the results plotted in Figs. 6a and 6b, which represent the comparison between the experimental (circles) and the simulated (red solid-line) spectra and waveforms, respectively. The experimental data were obtained in a temporal window of about 50 ps and are indicated as green circles in both the figures. In order to make a convenient comparison with the model, we had to perform a post-processing of these data. In fact, we note how the corresponding spectrum in Fig. 6a (green circles) is corrupted by some unwanted phenomena, mainly related to the choice of the observation window and to the laboratory atmosphere. As regarding to the first point, the observation window at the detection stage has to be wide enough in order to achieve a good frequency resolution. However, in this way, the instrumentation also reveals the spurious THz pulse repetitions, because of the FP effect inside the crystals. From theory, we know that the Fourier transform of a periodically repeated signal in time domain, appears as the sampled spectrum of the fundamental waveform (which, instead, we are interested to). With regards to the standard laboratory atmosphere, it results quite opaque to THz41, because of the presence of many resonance lines in such a range of the spectrum, due to the water vapour. As a consequence, the bandwidth lacks the contribution of such frequency components, because of the efficient resonant absorptions. In particular, we stress that the notch around 1.7 THz in Fig. 6a is so strong that the waveform is featured by a residual quasi-sinusoidal ripple at that frequency for positive times. Obviously, the latter is not predictable with an analytical approach. These considerations help us to explain the form of the curve (indicated by the green circles). Nevertheless, to test our model, we needed to manipulate a quasi-ideal waveform and its related spectrum. Thus, we isolated the fundamental THz pulse in time domain - corresponding to the blue circles in Fig. 6b - and calculated the corresponding spectrum plotted via the blue circles, as shown in Fig. 6a. The two curves can now be compared with our simulations. As we can see, the agreement between the model (red line) and the experimental curves is very good, meaning that our model is able to describe quite well the various phenomena that take place in the set-up. In particular, the spectra demonstrate the hypothesis of sub-wavelength generation for almost all the bandwidth, exactly as described by Bethe's diffraction, which is a crucial aspect of the THz propagation modelling. Moreover, it can be noticed that the central frequency is about fmean = 1 THz, whereas the bandwidth measures about B1/e = 1.2 THz, as provided by the PM conditions (5) and (7) with Lgen = 1 mm. Conversely, in time domain, the matching between the simulated and experimental waveforms is very good, and both show that the obtained THz profile significantly deviates from the single-cycle case -as usual for ZnTe crystal- since the bandwidth generated is not wide enough.

Figure 6.

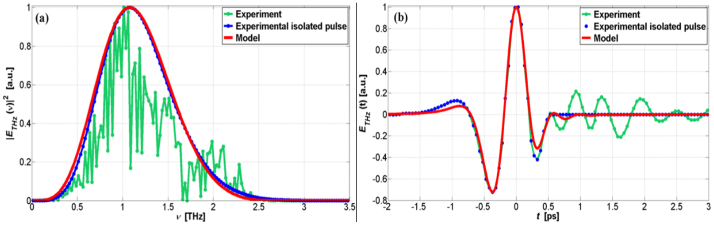
Figure 6

Open in a new tab

(a) Comparison between theoretical and experimental spectra. (b) Comparison between theoretical and experimental waveforms.

In this work we built an analytical 1-D model able to simulate a typical generation and detection THz pulses set-up based on OR and EOS. We studied the phenomena that occur along the THz beam propagation, in order to obtain an analytical approach that allowed us to predict the behaviour of each stage by means of a proper frequency-dependent transfer function. We compared the results of the simulations with the experimental data, obtaining a good agreement. This means that our study of the theoretical phenomena was careful enough to take into account the main frequency properties of the stages. The peculiarity of the simulated waveforms consists in assuming them as reference signal, when employed for the study of particular properties of materials such as their frequency-response (for example in the TDS technique), whenever it is not possible to obtain their profile without external and unwanted phenomena.

Methods

Experimental set-up

The experimental set-up is sketched in Fig. 1. A train of ultrashort laser pulses at 800 nm, emitted by a Ti:Sapphire laser (Mai Tai, Spectra-Physics) is focused through a lens into a <110> ZnTe sample, which acts as the nonlinear generation crystal, giving rise to the OR. It is worth to highlight the possibility of tailoring the size of the pump waist focused into the generation crystal, by moving the position of the lens along the propagation axis. The resulting THz broadband beam and the optical beam emerge from the crystal and are handled by a f-2f-f coherent system consisting of two 90° off-axis parabolic metal mirrors with focal f = 50 mm and diameter D = 50.8 mm (see Figs. 2b and 2c), for both the collecting and the focusing stages, which are free from spherical aberrations. The latter is an essential property, since THz beam spreads very strongly and spherical mirrors are thus not suitable. After the collecting mirror, the pump beam is filtered by means of an IR-opaque material, whereas the THz beam is focused into the detection crystal -a <110> ZnTe sample- together with the optical (IR) probe pulse, thus providing the coherent nature of the set-up. Also the focusing lens allows to adjust the waist size of the focused THz beam. Finally, the EOS technique (see the following subsection) permits to detect the train of THz pulses, by means of the downstream electronic instrumentation.

EOS working-principle

The Electro-Optic Sampling is based on the Pockels effect inside electro-optic (EO) crystals, the dual phenomenon of the OR, thus it can be described with similar equations. Physically, a linearly polarized optical probe pulse EPB(ωPB) -generally obtained by splitting the pump beam- is launched into the detection crystal together with the THz wave under the PM condition. However, compared to the optical field, THz field is almost constant for several tens of optical periods. This means that THz field -which we assume linearly polarized as well- provides a change of the refractive index along one axis of the EO crystal, making it slightly birefringent. Therefore, while EPB is being propagated through the material, its polarization becomes slightly elliptical depending on the THz strength. By separating the two optical orthogonal components and sending them to a balanced photodetector, THz field time-varying amplitude is recovered by their difference. As indicated in Fig. 5a, this process is said “sampling”, since the electronics on the detection side captures a sample of the instantaneous THz pulse at each laser probe pulse so the pulse is simply obtained by bringing together this value sequence.

Author Contributions

A.T. studied the theoretical background, built the model and carried out the simulations. A.T. and A.P. performed data analysis and wrote the main manuscript text with contributions of all the authors. S.S. and M.P. performed set-up preparation, conducted the experiments and contributed to discussions. P.L., A.C., A.C.B. and R.M. conceived and supervised the work. All authors reviewed the manuscript.

References

  1. Zernike F. & Berman P. R. Generation of Far Infrared as a Difference Frequency. Phys. Rev. Lett. 15, 999–1001 (1965). [Google Scholar]
  2. Yang K. H., Richards P. L. & Shen Y. R. Generation of Far-Infrared Radiation by Picosecond Light Pulses in LiNbO3. Appl. Phys. Lett. 19, 320 (1971). [Google Scholar]
  3. Auston D. H. & Cheung K. P. Picosecond photoconducting Hertzian dipoles. Appl. Phys. Lett. 45, 284 (1984). [Google Scholar]
  4. Hu B. B. & Nuss C. M. Imaging with terahertz waves. Opt. Lett. 20, 1716 (1995). [DOI] [PubMed] [Google Scholar]
  5. Nuss C. M. & Orenstein J. Terahertz dime-domain spectroscopy (THz-TDS). Top. Curr. Chem. 74, 7–50 (1998). [Google Scholar]
  6. Berry E. et al. Do in vivo terahertz imaging systems comply with safety guidelines? J. Laser. Appl. 15, 192 (2003). [Google Scholar]
  7. Horiuchi N. Terahertz technology: Endless applications. Nat. Photonics 4, 140 (2010). [Google Scholar]
  8. Fukunaga K. et al. Investigating the use of terahertz pulsed time domain reflection imaging for the study of fabric layers of an Egyptian mummy. J. Eur. Opt. Soc. Rapid Commun. 6, 11040 (2011). [Google Scholar]
  9. Clerici M. et al. Counterpropagating frequency mixing with terahertz waves in diamond. Opt. Lett. 38 (2013). [DOI] [PubMed] [Google Scholar]
  10. Mounaix P. et al. Spectroscopy and terahertz imaging for sigillography applications. J. Eur. Opt. Soc. Rapid Commun. 6, 11002 (2011). [Google Scholar]
  11. Chen Q., Jiang Z. & Zhang X. C. All-optical THz imaging. In Proc. SPIE 3617, 98 (1999). [Google Scholar]
  12. Tinkiel D., White D. & Trappe N. A. Efficient design of THz security systems. In Proc. IEEE Int. Carnahan Conf. on Security Technology (2011). [Google Scholar]
  13. Fukunaga K. et al. Terahertz imaging systems: a non-invasive technique for the analysis of paintings. In Proc. SPIE 73910D (2009). [Google Scholar]
  14. Clerici M. et al. Wavelength Scaling of Terahertz Generation by Gas Ionization. Phys. Rev. Lett. 110, 253901 (2913). [DOI] [PubMed] [Google Scholar]
  15. Siegel P. H. et al. Terahertz Technology. IEEE Trans. Microw. Theory Techn. 50, 910 (2002). [Google Scholar]
  16. Bass M., Franken P. A., Ward J. F. & Weinreich G. Optical rectification. Phys. Rev. Lett. 9, 446 (1962). [Google Scholar]
  17. Peccianti M. et al. Exact Reconstruction of THz Sub-λ Source Features in Knife-Edge Measurements. IEEE J. Sel. Topics Quantum Electron 19, 8401211 (2013). [Google Scholar]
  18. Boyd R. W. (ed.) Nonlinear Optics, Third Edition (Academic Press, Boston, 2008). [Google Scholar]
  19. Franken P. A., Hill A. E., Peters C. W. & Weinreich G. Generation of Optical Harmonics. Phys. Rev. Lett. 7, 118–119 (1961). [Google Scholar]
  20. Fejer M. M., Magel G. A., Jundt D. H. & Byer R. L. Quasi-phase-matched second harmonic generation: tuning and tolerances. IEEE J. Quantum Electron. 28, 2631–2654 (1992). [Google Scholar]
  21. Busacca A. C., Sones C. L., Eason R. W. & Mailis S. First-order quasi-phase-matched blue light generation in surface-poled Ti:indiffused lithium niobate waveguides. Appl. Phys. Lett. 84, 4430–4432 (2004). [Google Scholar]
  22. Cherchi M. et al. Exploiting the optical quadratic nonlinearity of zinc-blende semiconductors for guided-wave terahertz generation: a material comparison. IEEE Journal of Quantum Electronics 46, 368–376 (2010). [Google Scholar]
  23. Torruellas W. E. et al. Observation of two-dimensional spatial solitary waves in a quadratic medium. Phys. Rev. Lett. 74, 5036 (1995). [DOI] [PubMed] [Google Scholar]
  24. Gallo K., Pasquazi A., Stivala S. & Assanto G. Parametric Solitons in Two-Dimensional Lattices of Purely Nonlinear Origin. Phys. Rev. Lett. 100, 053901 (2008). [DOI] [PubMed] [Google Scholar]
  25. Diels J. C. & Rudolph W. (ed.) Ultrashort Laser Pulse Phenomena (Academic Press, 2006). [Google Scholar]
  26. Ding Y. J. Quasi-Single-Cycle Terahertz Pulses Based on Broadband-Phase-Matched Difference-Frequency Generation in Second-Order Nonlinear Medium: High Output Powers and Conversion Efficiencies. IEEE J. Sel. Topics Quantum Electron. 10, 1171 (2004). [Google Scholar]
  27. Ding Y. J. Efficient generation of high-power quasi-single-cycle terahertz pulses from a single infrared beam in a second-order nonlinear medium. Opt. Lett. 29, 2650–2652 (2004). [DOI] [PubMed] [Google Scholar]
  28. Faure J., Van Tilborg J., Kaindl R. A. & Leemans W. P. Modelling laser-based table-top THz sources: Optical rectification, propagation and electro-optic sampling. Opt. Quant. Electron. 36, 681 (2004). [Google Scholar]
  29. Ding Y. J. & Khurgin J. B. A new scheme for efficient generation of coherent and incoherent submillimeter to THz waves in periodically-poled lithium niobate. Opt. Commun. 148, 105–109 (1998). [Google Scholar]
  30. Xu G., Mu X., Ding Y. J. & Zotova I. B. Efficient generation of backward terahertz pulses from multiperiod periodically poled lithium niobate. Opt. Lett. 34, 995–997 (2009). [DOI] [PubMed] [Google Scholar]
  31. Palik E. D. (ed.) Handbook of Optical Properties of Solids II (Academic Press, San Diego, 1998). [Google Scholar]
  32. Schall M., Walther M. & Uhd Jepsen P. Fundamental and second-order phonon processes in CdTe and ZnTe. Phys Rev B 64, 094301 (2001). [Google Scholar]
  33. Carey J. J. et al. Terahertz pulse generation in an organic crystal by optical rectification and resonant excitation of molecular charge transfer. Appl. Phys. Lett. 81, 4335 (2002). [Google Scholar]
  34. Schneider A. et al. Generation of terahertz pulses through optical rectification in organic DAST crystals: theory and experiment. J. Opt. Soc. Am. 23, 1822 (2006). [Google Scholar]
  35. Mutter L., Brunner F. D. J., Yang Z., Jazbinsek M. & Gunter P. Linear and nonlinear optical properties of the organic crystal DSTMS. J. Opt. Soc. Am. B 24, 2556 (2007). [Google Scholar]
  36. Zheng X., McLaughlin C. V., Leahy-Hoppa M. R., Sinyukov A. M. & Hayden L. M. Modeling a broadband terahertz system based on an electro-optic polymer emitter-sensor pair. J. Opt. Soc Am. B 23, 1338 (2006). [Google Scholar]
  37. Ahn J., Efimov A. V., Averitt R. D. & Taylor A. J. Terahertz waveform synthesis via optical rectification of shaped ultrafast laser pulses. Opt. Express 11, 2486 (2003). [DOI] [PubMed] [Google Scholar]
  38. Bethe H. A. Theory of Diffraction by small holes. Phys Rev 66, 163 (1944). [Google Scholar]
  39. Kleinman D. A. & Auston D. H. Theory of Electrooptic Shock Radiation in Nonlinear Optical Media. IEEE J. Quantum Electron. 20, 964 (1984). [Google Scholar]
  40. Löffler T., Hahn T., Thomson M., Jacob F. & Roskos H. G. Large-area electro-optic ZnTe terahertz emitters. Opt. Express. 13, 5353 (2005). [DOI] [PubMed] [Google Scholar]
  41. Lee Y. S. (ed.) Principles of Terahertz Science and Technology (Springer, New York, 2009). [Google Scholar]
  42. Sharma G. et al. Self-referenced spectral domain interferometry for improved signal-to-noise measurement of terahertz radiation. Opt Express 38, 2705 (2013). [DOI] [PubMed] [Google Scholar]
  43. Sharma G., Singh K., Al-Naib I., Morandotti R. & Ozaki T. Terahertz detection using spectral domain interferometry. Opt Express 37, 178 (2012). [DOI] [PubMed] [Google Scholar]
  44. Gallot G. & Grischkowsky D. Electro-optic detection of terahertz radiation. J. Opt. Soc. Am. B 16, 1204 (1999). [Google Scholar]
  45. Bakker H. J., Cho G. C., Kurz H., Wu Q. & Zhang X. C. Distortion of terahertz pulses in electro-optic sampling. J. Opt. Soc. Am. B 15, 1795 (1998). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES