Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Oct 31;3:3102. doi: 10.1038/srep03102

Hierarchical chirality transfer in the growth of Towel Gourd tendrils

Jian-Shan Wang 1,2,a, Gang Wang 3, Xi-Qiao Feng 4,b, Takayuki Kitamura 2, Yi-Lan Kang 1, Shou-Wen Yu 4, Qing-Hua Qin 5
PMCID: PMC3813933  PMID: 24173107

Abstract

Chirality plays a significant role in the physical properties and biological functions of many biological materials, e.g., climbing tendrils and twisted leaves, which exhibit chiral growth. However, the mechanisms underlying the chiral growth of biological materials remain unclear. In this paper, we investigate how the Towel Gourd tendrils achieve their chiral growth. Our experiments reveal that the tendrils have a hierarchy of chirality, which transfers from the lower levels to the higher. The change in the helical angle of cellulose fibrils at the subcellular level induces an intrinsic torsion of tendrils, leading to the formation of the helical morphology of tendril filaments. A chirality transfer model is presented to elucidate the chiral growth of tendrils. This present study may help understand various chiral phenomena observed in biological materials. It also suggests that chirality transfer can be utilized in the development of hierarchically chiral materials having unique properties.

Many biological materials, such as climbing plant tendrils1,2, flower petals of Paphiopedilum dianthum3, and snail shells4, exhibit chiral growth. In these natural materials, there are a number of distributed chiral elements, e.g., biomacromolecules, which lead to the formation of various chiral morphologies and surface patterns at the macroscopic scale. For example, helices and twisted belts are often observed to form in growing biological materials. These chiral morphologies generally tend to a specific handedness, either right or left5. A well-known example is climbing tendrils, which help some climbing plants attach to trees or other objects and to provide supporting forces2. The investigation of the mechanisms underlying the chiral growth of biological materials is a fundamental and important issue in not only developmental biology but also materials science and technology.

The chiral shapes of some biological and artificial materials may origin from the asymmetry of growth, deswelling6,7, surface stresses8,9 and other physical quantities associated with anisotropic atomic or molecular structures10. For example, the formation of twisting belts of Bauhinia seed pods6 and chiral polymer lamellae3 has been attributed to the anisotropy of material properties and surface stresses, respectively. From the view point of chirality transfer, the chiral morphologies of many biological materials originate from the chirality of their microscopic constituent building blocks. Typical examples include the flagellar filaments of bacteria11,12,13, the flower petals of Paphiopedilumdilum dianthum3, and the stork's bill awns14,15. Their chiral growth is caused by the helical arrangements of protein lattices, cortical microtubules, and tilted celluloses at the micro scale, respectively. The helical tendrils of climbing plants have attracted the interest of many scientists since the pioneering work of Charles Darwin2. A recent study suggested that Cucumber tendril coiling might be induced by the asymmetric contraction of g-fibers16. However, this mechanism does not appear to explain the predominance of left-handed or right-handed helical growth in climbing plants. Analysis of the global twining direction of climbing plants shows that the predominance of a specific chirality in the helical growth of climbing plants should be attributed to the microstructures at the subcellular level rather than the Coriolis effect17. In addition, previous studies revealed that the intrinsic torsion of tendril filaments drives them to form helices with a specific handedness or opposite handednesses1,18,19. However, the physical mechanisms underlying the intrinsic torsion of tendril filaments have rarely been discussed. Furthermore, it is still unclear how the chiralities at the molecular, microscopic, and macroscopic scales in tendrils are correlated with each other.

According to Neumann's principle of symmetry, the absence of the mirror symmetry of molecules, the arrangements of atoms and protein lattices, microstructures and even morphologies of biological materials has remarkable effects on their physical and chemical properties and functions. In the present study, we investigate, both experimentally and theoretically, how the chirality is transferred from molecules to the macroscopic morphology of tendrils. To clarify their chiral growth, a theoretical model of chirality transfer in tendril filaments is developed to correlate the chirality at the subcellular level with that at the macro scale.

Results

In the experiments, we collected mature and dry tendril helices of Towel Gourd as samples. Swelling and deswelling experiments of the tendril helices were first performed, and then the microstructures of their tendril filaments were observed to investigate the mechanisms of chiral growth. These experiments revealed that the shape of the tendril helices can distinctly change during swelling/deswelling. Based on these results, we use the chirality transfer mechanism to explain the shape formation and evolution of tendril filaments during their growing and swelling/deswelling processes.

When the growing tip of a tendril filament is free, the tendril normally forms a helix with a specific handedness. Most free Towel Gourd tendril helices we observed are left-handed. However, when a tendril filament catches a supporting object, as shown in Fig. 1, the tendril will gradually evolve into a helical shape with opposite handedness, providing an elastic spring-like support that enables the plant to climb to a sufficient height. The chiral perversion process of a tendril can be interpreted by the topological conservation law18,19. In both cases, tendrils assume an initial curvature induced by differential growth. The formation of a helical tendril with either a specific chirality or two opposite handednesses in two segments will be elucidated using a chirality transfer model in the sequel.

Figure 1. Towel Gourd tendrils: (a) growing tendril helices without hooking and (b) tendril helices with hooking attached to a supporting object.

Figure 1

Open in a new tab

“LH” and “RH” denote left and right handednesses, respectively.

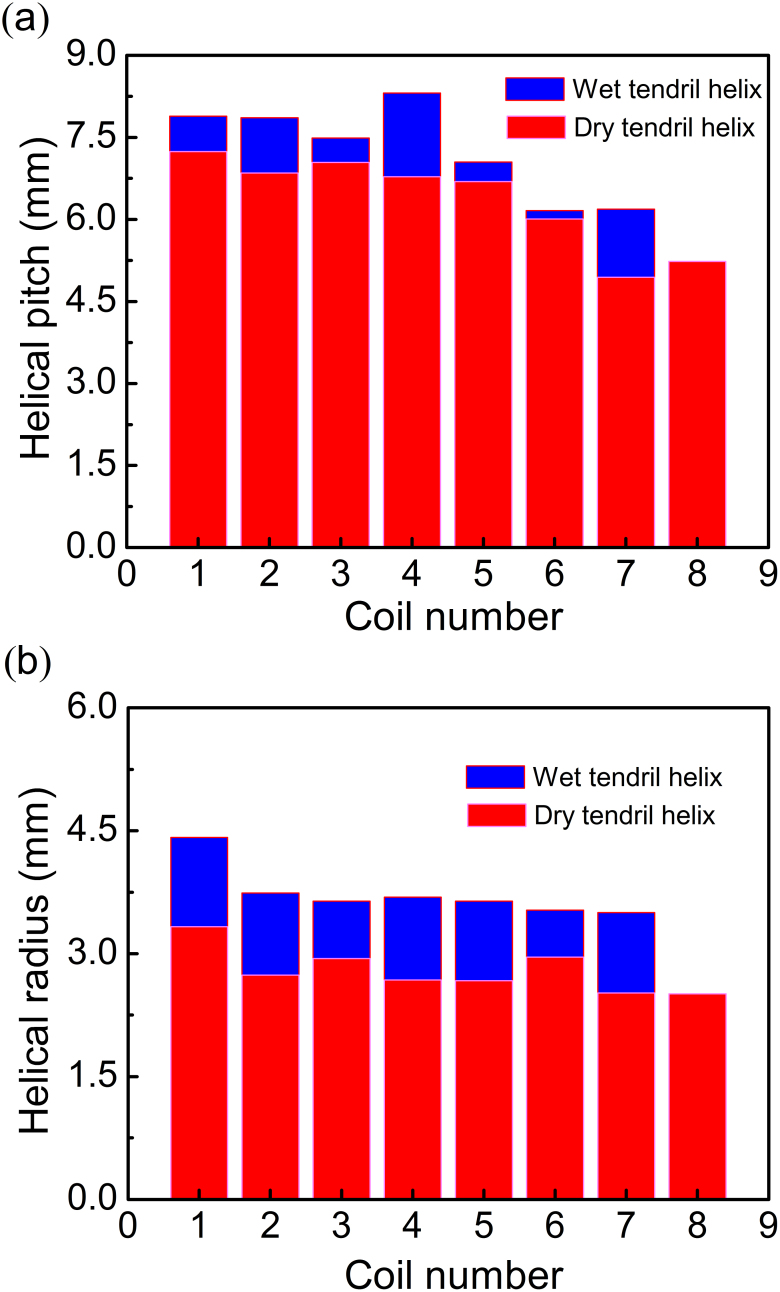
We experimentally investigated the physical origin of intrinsic torsion and the mechanisms underlying the chiral growth of tendril filaments. The samples of dry and mature Towel Gourd tendril helices were immersed in water for 24 hours to allow the tendril helices to fully swell. The shape parameters of the left-handed part of the swelled and deswelled tendril helix were measured for four samples, and the average results of helical radii and pitch are plotted in Figs. 2(a) and (b). Compared to the dry tendrils, the number of coils of the left-handed helical part of the fully swelled tendril samples decreased from eight to seven. The helical radii of each coil had an average increase of approximately 31.6%, and the helical pitch of each coil increased by approximately 12.1%. Moreover, the cross-sectional areas of the swelled sample increased by about 6.1% compared to those of the dry tendrils. The straight part connecting the left- and right-handed helices also exhibited a distinct increase in length (approximately 11.7%). These experiments revealed that the intrinsic chirality of the building elements, rather than simple water-induced expansion/shrinkage, causes the morphological evolution of tendril helices.

Figure 2. Changes in (a) the helical pitches and (b) radii of tendril helices before and after swelling.

Figure 2

Open in a new tab

The swelled tendril helices were then placed in air for 72 hours so that they became fully deswelled. Their helical shapes returned to their initial states before swelling. Such shape changes of tendrils in the swelling/deswelling process are consistent with those of tendrils during growth. Thus they provide an ideal system to investigate the mystery of the widely observed chiral growth of natural materials.

The shape evolution of tendril helices is attributed to the changes in their microscopic structures during the swelling and deswelling processes. We observed the microstructures of tendril filaments using a scanning electron microscope (SEM). At the macro scale, a tendril filament has an approximately circular cross section with a characteristic size of 0.6–1.5 mm, containing primarily a surface layer (L1), an inner layer (L2) and a core (L3), as shown in Figure 3(a). L1 is composed of connected epidermis cells, L2 consists primarily of parallelized cells, which are tightly glued together, and L3 contains relatively large sized cells. To further study the microstructures of tendril, we cut a tendril filament into slices and observed the slices under SEM. The cells in L2 contain cellulose fibril helices as shown in Figure 3 (b) and (c), whereas the cells in L3 are soft and hollow tubes, with a characteristic size of 40–50 μm (Figure 3(d)). Each cell in L2 takes a tubular shape with a circular cross section of approximately 10 μm in diameter, and the circular cross section of each cellulose fibril is approximately 1–2 μm in diameter (Figure 3(e)–(f)). As shown in Figure 3(c), the helical angle of the cellulose fibril helices in the segment linking the left- and right-handed parts is significantly smaller than that in the left-handed part shown in Figure 3(f).

Figure 3. Hierarchical structures of tendril filaments.

Figure 3

Open in a new tab

(a) Cross section of a tendril filament, (b) inner layer of a tendril filament dissected longitudinally, (c) cells in the straight part of a tendril filament connecting the left- and right-handed parts, (d) core layer of a tendril filament (e) two cellulose fibril helices separated from the cell wall, (f) a single cellulose helix, and (g) cross section of a cellulose fibril.

Discussion

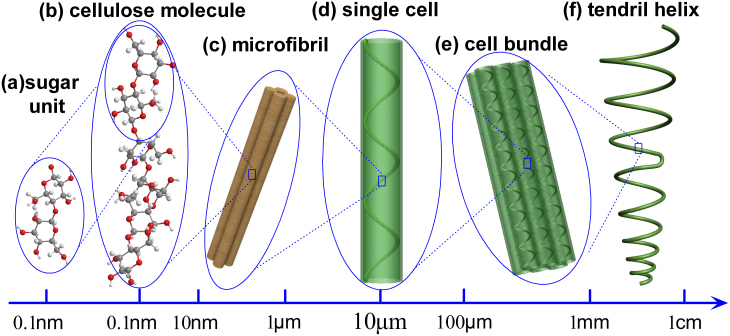
Our observations indicate that helical tendrils have a hierarchy of chirality, consisting of at least six length scales from molecules, microfibrils, cellulose fibrils, cells, tendril filaments to the macroscopic tendril helix. At the molecular level, sugar units and cellulose molecules take the form of asymmetric and chiral configurations. Cellulose molecules assemble into single microfibrils at the nanoscale, which further assemble into a cellulose fibril as shown in Figure 4. At the subcellular level, the chirality occurs in the cellulose fibril helix. At the cell level, each long cell can be regarded as a chiral rod in which cellulose fibril helices exist as helical inclusions embedded in the matrix. At the tendril filament level, chirality exists in the cell bundles, i.e., chiral rod bundles. Finally, these bundles further assemble into macroscopic tendril helices with either left- or right-handedness. Therefore, the tendrils have a typical hierarchy of chirality from the molecular scale to the macroscopic scale, providing a good example for the study of chirality transfer in biological materials. The hierarchical structures of tendrils are different from those of non-chiral hierarchical materials and artificial chiral materials such as chiral polymer lamellae20,21,22.

Figure 4. Hierarchy of chirality in a tendril helix: (a) sugar unit, (b) cellulose molecule, (c) microfibril consisting of cellulose molecules, (d) single cell containing a cellulose helix, (e) cell bundle, and (f) tendril helix.

Figure 4

Open in a new tab

The chiral growth, as well as the swelling and deswelling processes in the experiments, involves complicated physical mechanisms of chirality transfer. The macroscopic deformation of a tendril during swelling and deswelling depends upon the features of chirality, deformation and interaction of its constituent elements at lower levels, e.g. cell bundles, cell walls, and cellulose fibril helices.

In each cell bundle, the tight cellular connections constrain the free movement and deformation of the cells. Thus the deformation of a helical tendril should be derived from the geometric and mechanical properties of the cells. As a bundle of large sized hollow cell tube, the core of tendril filament is soft. The outer layer only plays a role of protecting the inner layer and the core. In some coils of tendril helix, the outer layer can be peeled off and the tendril helix still has the similar shape changes during the swelling and deswelling processes. This fact excludes the possibility that the out layer controls the shape changes of tendril helix. Microscopic observations in Figures 3(b) and 3(f) show that for a cell in the inner layer, the cell wall is a thin, flexible membrane assembled by polysaccharides and proteins. Thus helical cellulose fibrils should be the primary structural components of the cell. Due to the close packing of cellulose fibril helices, the cell wall can be regarded as a fiber-reinforced polymer composite, and the helical feature of ordered texture endows the cell wall with strongly orientation-dependent properties. In addition to enhancing the mechanical stiffness of the cell wall under tension, which is significant for the supporting function of tendrils, the helical structure of cellulose fibrils can also make the tendril soft and flexible upon bending, allowing the tendrils to more easily wrap around supporting objects. Thus, the cellulose fibril helices significantly affect the mechanical properties of tendrils. This structural characteristic of the inner layer cells indicates that the shape changes induced by twisting and bending deformations should be attributed to the cellulose fibril helices. Our observations of the different helical arrangements of cellulose fibrils in both the left-handed and the straight parts of a tendril also support this conclusion.

In order to further understand the microscopic mechanisms in a tendril helix, it would be of interest to compare the tendril helix with a chiral paper sheet. The twisting of paper sheets during swelling/deswelling provides another typical example of chirality transfer23. A twisted paper sheet is made up primarily of woody plant fibers that are glued together, and twisted paper sheets also have a hierarchy of chirality. A flat and straight swelling paper sheet can become a twisting belt because of the helical angle changes of the cellulose chain winding in the cell wall. As pointed out by Dionner et al.23, the twisting of paper sheets also results from the helical shape changes of cellulose chains. This inspires us how the chiral structures at a lower level can induce the twisting deformation at its higher neighbor level. Unlike most woody plant cells, in which cellulose chains wind right-handed helically outside the cell wall, the inner layer cell wall of tendrils is thin, and the cellulose fibril forms a helix with left-handedness and is contained in the tendril cell wall. Moreover, the cross-sectional size of a cellulose fibril is 1–2 μm, which is much larger than the cross-sectional size of the fibrils in woody pant cells, which is only approximately 3–4 nm. Comparison of cell microstructures in tendrils and papers indicates that cellulose fibril helices play an important role during the chirality transfer process at the subcellular level.

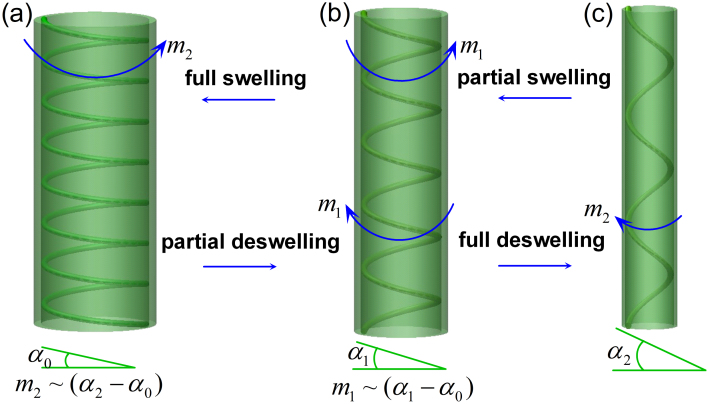
Based on the above observations and discussions, the physical mechanisms underlying the shape changes of tendril helices during swelling and deswelling processes can be better understood. As shown in Figure 5, the typical structure of a cell in tendrils consists of a cell wall tube containing an array of cellulose fibril helices. At the fully swelled state, the cell wall tube would have a larger cross section and a relatively smaller helical angle. As the tendril gradually deswells, the radius of the cell wall cross section will decrease, corresponding to an increase in the helical angle. Thus, the cell wall would have a minimal cross-sectional radius and the cellulose fibril helix would have a maximal helical angle when the tendril is fully deswelled. The mechanical stiffness and the relatively large size of the cross section of cellulose fibril provide the cellulose fibril helix with a finite structural stiffness. During deswelling, the helical angle of cellulose fibril helices increases, leading to twisting in their morphology. Equivalently, a change in the helical angle produces a torque acting on its cross section, making the cell wall twist with either left- or right-handedness. The value of the torque depends primarily on the helical angle change at a specific swelling or deswelling state. Thus, the tendril filament will be subjected to an internal torque and undergo an intrinsic torsion, which can change the helical pitch and radius of a tendril helix during swelling or deswelling.

Figure 5. Physical mechanisms of the intrinsic torsion of tendrils.

Figure 5

Open in a new tab

(a) A fully swelled cell containing a cellulose fibril helix with the lowest value of helical angle α = α0, (b) a partially swelled cell with α = α1 > α0, and (c) a fully deswelled cell with the largest helical angle α = α2 > α1.

To rationalize the physical mechanisms underlying the formation of the helical morphology and the shape change of tendril helices, we here develop a theoretical model of tendril filaments with a spatial configuration. In this model, the effects of cellulose fibril helices at the subcellular level are taken into account. Due to the close packing of cellulose fibril helices, the cell wall is regarded as a helical and orthotropic layer. Through coordinate transformation, the constitutive relation of a tendril filament in the Frenet coordinate system of spatial curve can be written as

graphic file with name srep03102-m1.jpg

where {σ′} and {ε}FCS are the stress and the strain, respectively, and [Q′] is the material stiffness matrix of the tendril filament. A detailed derivation of equation (1) is given in the Supplementary Information. We assume the length and cross-sectional size of the tendril filament during swelling and deswelling keep unchanged. The helical angle of the cellulose fibril helix, α, is used to quantify the degree of swelling or deswelling of a tendril filament. The minimal and maximal values of α correspond to the fully swelled and deswelled states, respectively.

The potential energy of the tendril filament can be written as

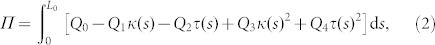graphic file with name srep03102-m2.jpg

where s is the arc length, κ(s) and τ(s) denote the curvature and twist of the tendril filament, respectively. The coefficients Q0–4 are functions of the helical angle α of the cellulose fibril helix and are presented in the Supplement Materials. Using the variational principle of energy9,24,25, we can derive the following shape equation for a tendril filament with an arbitrary spatial configuration:

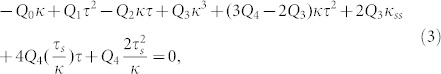graphic file with name srep03102-m3.jpg

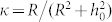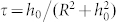with κs = dκ/ds, τs = dτ/ds, and κss = d2κ/ds2. For the helical shape of a tendril filament, we have Inline graphic and Inline graphic, where R denotes the helical radius and h0 = P/2π, with P being the helical pitch of the tendril helix. For simplicity, assume that the helical radius and pitch of the tendril helix are constant. Then, based on equation (3), the shape equation governing the shape change of a tendril helix is rewritten as

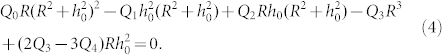graphic file with name srep03102-m4.jpg

For a helical tendril during swelling and deswelling, the helical radius R and pitch P must satisfy equation (4).

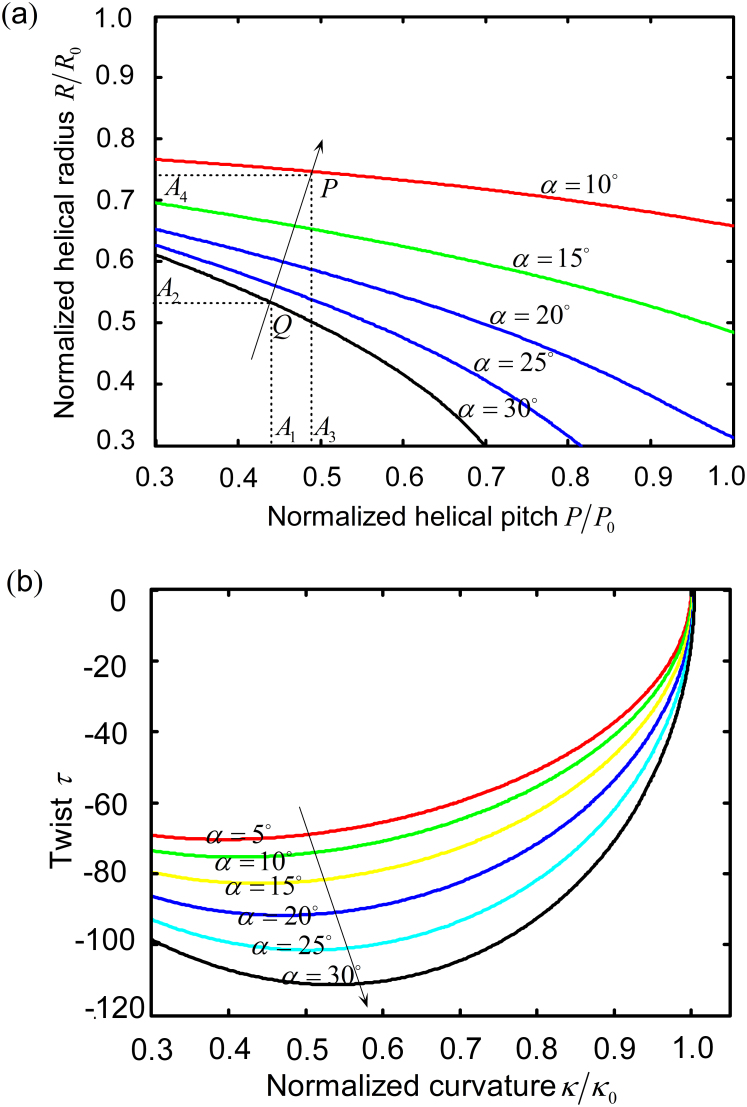
The above model allows us to predict the shape change of helical tendrils induced by swelling or deswelling. For tendril helices with different helical angles α, the helical radii and pitches calculated from equation (4) are plotted in Figure 6(a). Both the normalized helical radius and pitch decrease with the increase in α. Thus for a tendril helix during deswelling, the coil number will increase as the helical angle of the cellulose fibril helix increases because the total length of a tendril filament is approximately constant. In the case of swelling, which induces a decrease in the helical angle α of cellulose fibril helices, the shape change of tendrils can be determined easily. Figure 6(a) shows that during swelling, both the helical radius and pitch of the tendril helix increase and, therefore, its coil number decreases. In Figure 6(a), a curve PQ perpendicular to the helical angle contours is drawn to illustrate the changing tendency of the helical pitch and radius, where points P and Q are located at the curves of α = 10° and α = 30°, respectively. Here, the curve PQ can be approximately treated as a line. Let A1A3 and A2A4 denote the projections of PQ on the two axes, respectively. It can be seen that with the decrease of the helical angle α during swelling, the helical radius increases more significantly than the helical pitch. As α changes from 30° to 10°, the helical radius and pitch increase about 16.7% and 37.7%, respectively. These results predicated by the present theoretical model have a good agreement with the experimental measurements shown in Figure 2, verifying the proposed physical mechanism of chirality transfer.

Figure 6. (a) Helical shape variations of tendrils with respect to the helical angle α, and (b) formation and evolution of a growing tendril helix.

Figure 6

Open in a new tab

Here, we take the cross-sectional radius of cellulose fibrils as r0 = 1.2 × 10−6 m, the tendril cell radius as r1 = 7.0 × 10−6 m, and the tendril radius as r2 = 5.0 × 10−4 m. For the fully swelled cellulose fibril helices, the helical angle is set as α0 = 1° and the helical radius 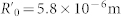Inline graphic. The elastic modulus of cellulose fibrils E = 0.45 GPa, and the shear modulus G = 0.173 GPa.

The above model reveals how the chirality at the micro scale determines the chiral shape changes at larger scales and also helps to clarify the chirality transfer of other materials with hierarchical chiral structures. It is worthy mentioning that in the proposed model, the shape change of a tendril helix results mainly from the deformation induced by the changes of chiral microstructures at the subcellular level, but the effects of chiral structural elements at lower levels (e.g., cellulose molecules) have not been considered in detail. Although cellulose molecules and their interactions have no direct influence on the mechanical properties of helical tendrils at the macroscopic scale, they do affect the mechanical behavior of cellulose fibrils and even control the handedness of cellulose fibril helices at the subcellular level. Figure 5 demonstrates that the change of the helical radius and pitch of a tendril helix during swelling/deswelling can be determined primarily by the handedness of cellulose fibril helices. Thus the chiral elements and their interactions at the molecular level may indirectly contribute to the chiral shape changes at the macro scale.

Tendril helices provide us an ideal system not only to investigate the correlation of chiralities at different length scales but also to understand the formation of helical morphologies of tendril filaments. Our experiments reveal that the deformation of tendril helices during the swelling/deswelling processes derives from the shape changes of cellulose fibril helices at the subcellular level. Similar reorientation of cellulose fibrils is also observable in growing tendrils. During the growth of tendril filaments, the growth-strain and turgor pressure may induce an elongation of cells, rendering an increase of helical angles of cellulose fibril helices and an intrinsic torsion of tendril filaments. Furthermore, intermolecular interactions also contribute to the reorientation of cellulose fibrils. For example, hemicellulose molecules in the cell walls can self-assemble in cholesteric liquid crystals, which, in turn, mediate the assembly of cellulose microfibrils into helical patterns through hydrogen bonds between hemicelluloses and cellulose chains26,27. During the swelling/deswelling and growth processes, some intermolecular hydrogen bonds may be broken with the appearance of water molecules28, which may also induce the reorientation of cellulose fibrils. Thus a tendril will assume a helical shape due to the intrinsic torsion. The reorientation of cellulose fibrils drives the transfer of chirality from the molecular level to the morphological scale, as shown in Figure 4. Therefore, the shape changes of tendril helices during swelling/deswelling shed new lights on the chiral growth of tendril filaments.

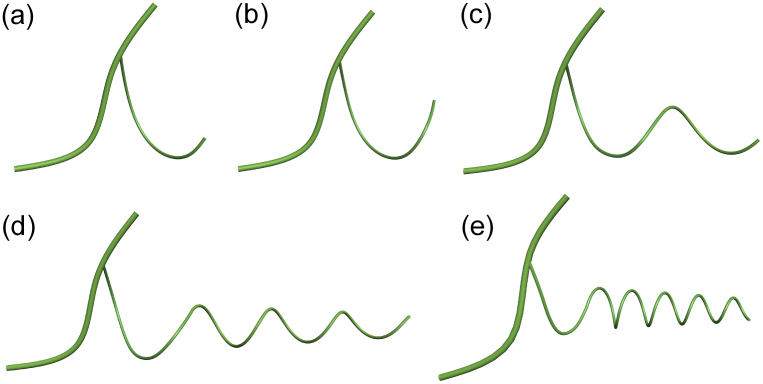
A growing tendril filament usually has a small initial curvature induced by differential growth. During the growth process, the helical angle of cellulose fibril helices gradually increases due to the increase in the turgor pressure and the growth strain, leading to an intrinsic torsion of tendril filaments, as shown in Figure 7(a). If the initially bended tendril filament has caught a support, chiral perversion may occur as a result of the intrinsic torsion. However, if no supporting object can be found, the tendril filament will twist into a helix. With the further increase of the helical angle of cellulose fibril helices, the helical pitch and radius of the tendril helix will decrease, just as in the deswelling process. According to equation (4), the variation of the helical shape of a growing tendril is plotted in Figure 6(b). In the calculation, we assume that the tendril filament has an initial curvature and a zero twist, i.e. 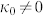Inline graphic and τ0 = 0. To illustrate the efficacy of our theoretical model, Figure 7 shows the helical shape formation and evolution of a growing tendril with different helical shapes at the subcellular level. Here, our primary concern is the physical origin of the intrinsic torsion and the chirality transfer underlying the chiral growth of tendrils.

Figure 7. Schematic diagram of the morphological evolution of a growing tendril helix.

Figure 7

Open in a new tab

(a) The growing tendril filament with an initial curvature and zero twist, (b) the twist of the bent tendril filament induced by intrinsic torsion, (c) the formation of a tendril helix with definite curvature and twist, (c) a tendril helix with a relatively large helical radius and pitch, (d) and (e) the variations of the helical radius and the helical pitch with respect to the helical angle α.

For helical tendrils and other biological materials with a hierarchy of chirality as well, growth is not only a complex process involving biochemical and physical components and structural evolutions at many different length and time scales, but also a chirality transfer process from the molecular level to the macroscopic level, as shown in Figure 4. In other words, the chirality at a lower structural level often begets a higher level chirality29. During the morphogenesis and remodeling process, the chirality undergoes a series of transfers from the molecular level, the cellulose fibril level, the cell level, and eventually to the macroscopic morphology of tendrils. In the theory of chirality transfer, the formation of hierarchical chiral structures at the macroscopic scale can be regarded as a consequence of multiscale chirality transfers. Here, we are primarily concerned with two issues: (i) why are the helical shapes of tendrils formed during growth, and (ii) how do they change during swelling and deswelling? In fact, both the problems involve multiscale chirality transfers.

As aforementioned, cellulose molecules have an indirect but significant influence on the chiral growth of tendrils by affecting the mechanical properties and handedness of cellulose fibrils. Although not essentially necessary for chiral growth, the chirality of cellulose molecules helps these molecules to self-assemble into cellulose fibril helices. In addition, the interactions among chiral elements at lower levels (e.g., intermolecular forces) and some other factors (e.g., growth induced residual stresses) can influence, to different extents, the chirality transfers among different length levels. Therefore, the macroscopic morphological chirality of tendrils is closely but not univocally correlated with those of cellulose fibril helices and cellulose molecules. For a tendril helix with chiral perversion, for example, the right-handed morphology is induced by an intrinsic torsion in order to compensate for the twist of its left-handed part, although the cellulose fibril helices are intrinsically left-handed. Some other climbing plants also have both right- and left-handed chiral morphologies, whereas their constituted molecules have an identical chirality.

In addition to the tendrils of climbing plants, many other biological materials, e.g., twisted tree trunks, flagellar filaments of bacteria, flower petals of Paphiopedilum dianthum and the stork's bill awns, have a hierarchy of chirality. Most of their chiral morphologies or patterns at the macro scale also derive from the chirality at the molecular, nano and micro scales, and their chiral growth usually involves a complicated process of chirality transfer. The theory of chirality transfer can help understand many interesting phenomena associated with chiral growth and establish the correlation between macroscopic morphologies and molecular structures.

In summary, we have investigated the intrinsic torsion of tendril filaments from the viewpoint of chirality transfer. Both swelling/deswelling experiments and theoretical analysis have been performed to reveal the multiscale chirality transfer mechanism underlying the chiral growth of tendrils. Based on microscopic observations of the hierarchical chiral structures of tendrils, we have developed a model to correlate the macroscopic chiral morphology and the cellulose fibril helices. Our findings may deepen our understanding of the widely observed chiral growth in biological and artificial materials. The proposed chirality transfer mechanism can also be applied to facilitate three-dimensional self-assembly and fabrication of hierarchical chiral structured materials with unique properties and functions.

Methods

(1) Swelling and deswelling experiments

Mature and dry tendril helices of left-handedness and tendril helices of opposite handednesses of Towel Gourd (Tianjin, China) were used as samples. In order to make the tendril filaments fully swelled, the samples were immersed in water for 24 hours. Then they were placed in air for 72 hours for deswelling. All tendril helices exhibited similar shape changes during swelling and deswelling, regardless of their handedness. The swelling-deswelling process was repeated four times. We measured the filament diameter, helical pitch, and radius of tendril helices at the fully swelled and deswelled states using vemier caliper with a precision of 0.01 mm.

(2) Microscopic observations

Microstructure observation of tendrils was carried out using a SEM (Hitachi SU-1500) and a field emission high-resolution SEM (JSM 6700F). The acceleration voltages of the two microscopes were set to be 30 kV and 15 kV, and their maximum resolutions were 3 nm and 1 nm, respectively. The tendril samples were coated with gold in order to enhance their conductivity.

(3) Measurement of the mechanical properties of tendrils

We determined the mechanical parameters of tendril filaments required in the theoretical analysis by tensile experiments. An electronic universal testing machine (Instron 3343) with a loading rate of 1.0 mm/min was used for this purpose. Straightened helical tendril filaments were taken as samples, and their force-displacement curves were recorded automatically. Based on the theory of composites, the mechanical properties of the tendrils were calculated from the experimental curves as Q11 = 0.408 GPa, Q22 = 0.082 GPa, Q12 = 0.094 GPa, and Q66 = 0.067 GPa.

Author Contributions

J.S.W. and X.Q.F. designed and directed this study. J.S.W. carried out the experiments and theoretical simulations. G.W. carried out the microscopic observations. T.K., Y.L.K., S.W.Y. and Q.H.Q. contributed to the analysis of experimental and simulation results. All authors contributed to writing and revising the manuscript.

Supplementary Material

Supplementary Information

Supplementary Info

srep03102-s1.pdf (208.4KB, pdf)

Acknowledgments

This work was supported by the National Basic Research Program of China (Nos. 2012CB937500 and 2012CB934101), Grants-in-Aid for Scientific Research (No.21226005) from Japan Society for the Promotion of Science (JSPS) and National Natural Science Foundation of China (Nos. 11272230). J.S. thanks the supports from the JSPS research fellowship (No. P12359) and the Elite Scholar Program of Tianjin University. G.W. thanks the supports from Shanghai Pujiang Program (Nr. 11PJ1403900) and the Eastern Scholar Program at Shanghai Institutions of Higher Learning. We thank X. L. Bian and W. L. Deng for their help in the experiments.

References

  1. Darwin C. On the movement and habits of climbing plants. (John Murray, London, 1865).
  2. Isnard S. & Silk W. K. Moving with climbing plants from Charles Darwin's time into the 21st century. Am. J. Bot. 96, 1205–1221 (2009). [DOI] [PubMed] [Google Scholar]
  3. Ye H. M. et al. Surface stress effects on the bending direction and twisting chirality of lamellar crystals of chiral polymer. Macromolecules 43, 5762–5770 (2010). [Google Scholar]
  4. Grande C. & Patel N. H. Nodal signaling is involved in left-right asymmetry in snails. Nature 457, 1007–1011 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Lough W. J. & Wainer I. W. Chirality in nature and applied science. (Blackwell Science, Oxford, 2002).
  6. Armon S., Efrati E., Kupferman R. & Sharon E. Geometry and mechanics in the opening of chiral seed pods. Science 333, 1726–1730 (2011). [DOI] [PubMed] [Google Scholar]
  7. Forterre Y. & Dumasis J. Generating helices in nature. Science 333, 1715–1716 (2011). [DOI] [PubMed] [Google Scholar]
  8. Wang J. S., Feng X. Q., Wang G. F. & Yu S. W. Twisting of nanowires induced by anisotropic surface stresses. Appl. Phys. Lett. 92, 191901 (2008). [Google Scholar]
  9. Wang J. S., Ye H. M., Qin Q. H., Xu J. & Feng X. Q. Anisotropic surface effects on the formation of chiral morphologies of nanomaterials. Proc. R. Soc. A 468, 609–633 (2012). [Google Scholar]
  10. Chen Z., Majidi C., SroIovitz D. J. & Haataja J. Tunable helical ribbons. Appl. Phys. Lett. 98, 011906 (2011). [Google Scholar]
  11. Berg H. C. & Anderson R. A. Bacteria swim by rotating their flagellar filament. Nature 245, 380–382 (1973). [DOI] [PubMed] [Google Scholar]
  12. Silverman M. & Simon M. I. Bacterial flagella. Annu. Reve. Microbiol. 31, 397–419 (1977). [DOI] [PubMed] [Google Scholar]
  13. Calladine C. R. Construction of bacterial flagella. Nature 225, 121–124 (1975). [DOI] [PubMed] [Google Scholar]
  14. Aharoni H., Abraham Y., Eibaum R., Sharon E. & Kupferman R. Emergence of spontaneous twist and curvature in non-Euclidean rods: application to Erodium plant cells. Phys. Rev. Lett. 108, 238106 (2012). [DOI] [PubMed] [Google Scholar]
  15. Abraham Y. et al. Titled cellulose arrangement as a novel mechanism for hygroscopic coiling in the stork's bill awn. J. R. Soc. Interface 9, 640–647 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gerbode S. J., Puzey J. R., McCormick A. G. & Mahadevan L. How the cucumber tendril coils and overwinds. Science 337, 1087–1091 (2012). [DOI] [PubMed] [Google Scholar]
  17. Edwards W., Moles A. T. & Franks P. The global trend in plant twining direction. Global Ecol. Biogeogr. 16, 795–800 (2007). [Google Scholar]
  18. Goriely A. & Tabor M. Spontaneous helix hand reversal and tendril perversion in climbing plants. Phys. Rev. Lett. 80, 1564–1567 (1998). [Google Scholar]
  19. Pieranski P., Baranska J. & Skjeltorp A. Tendril perversion – a physical implication of the topological conservation law. Eur. J. Phys. 25, 613–121 (2004). [Google Scholar]
  20. Maillard D. & Prud'sHomme R. E. Crystallization of ultrathin films polylactides: from chain chirality to lamella curvature and twisting. Macromolecules 41, 1705–1712 (2008). [Google Scholar]
  21. Schulgasser K. & Witztum A. The hierarchy of chirality. J. Theor. Biol. 230, 281–288 (2004). [DOI] [PubMed] [Google Scholar]
  22. Fratzl P. & Weinkamer R. Nature's hierarchical materials. Prog. Mater. Sci. 52, 1263–1334 (2007). [Google Scholar]
  23. Dionner I., Werbowyj R. S. & Gray D. G. Chiral twisting curl in newsprint sheets. J. Pulp. Pap. Sci. 15, J123–J126 (1991). [Google Scholar]
  24. Tu Z. C., Li Q. X. & Hu X. Theoretical determination of the necessary conditions for the formation of ZnO nanorings and nanohelices. Phys. Rev. B 73, 115402 (2006). [Google Scholar]
  25. Gao L. T., Feng X. Q., Yin Y. J. & Gao H. J. An electromechanical liquid crystal model of vesicles. J. Mech. Phys. Solids 59, 2844–2862 (2008). [Google Scholar]
  26. Neville A. C. Molecular and mechanical aspects of helicoid development in plant cell walls. BioEssays 3, 4–8 (1985). [Google Scholar]
  27. Neville A. C. Biology of fibrous composites. (Cambridge University Press, New York, 1993).
  28. Khazraji A. C. & Robert S. Self-assembly and intermolecular forces when cellulose and water interact using molecular modeling. J. Nanomater. 2013, 1–12 (2013). [Google Scholar]
  29. Wang J. S., Feng X. Q., Xu J., Qin Q. H. & Yu S. W. Chirality transfer from molecular to morphological scales in quasi-one-dimensional nanomaterials: A continuum model. J. Comput. Theor. Nanos. 8, 1278–1287 (2011). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Info

srep03102-s1.pdf (208.4KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES