White Ethnic Residential Segregation in Historical Perspective: U.S. Cities in 1880

Abstract

Investigating immigrant residential patterns in 1880 offers a baseline for understanding residential assimilation trajectories in subsequent eras. This study uses 100% count information from the 1880 Census to estimate a multilevel model of ethnic isolation and exposure to native whites in 67 cities for individual Irish, German and British residents. At the individual level, the key predictors are drawn from assimilation theory: nativity, occupation, and marital status. The multilevel model makes it possible to control for these predictors and to study independent sources of variation in segregation across cities. There is considerable variation at the city level, especially due to differences in the relative sizes of groups. Other significant city-level predictors of people’s neighborhood composition include the share of group members who are foreign-born, the disparity in occupational standing between group members and native whites, and the degree of occupational segregation between them.

Immigrant groups in the United States have typically experienced a high degree of residential segregation, though from the perspective of spatial assimilation theory this separation is expected to be transitory (Massey 1985). Individual members of these groups, as they move into the second and third generation, learn English, and improve their educational and occupational status, should be less likely to live in ethnic enclaves and more likely to find homes in mainstream neighborhoods. Some of the clearest evidence for this view comes from trends from the early to mid-20^th Century (Lieberson 1980), showing that segregation for white ethnics declined substantially in this period. But most emphasis in this historical account has been on what we might call “second wave” white ethnics, the Italians and East European Jews who arrived in very large numbers, predominantly to cities, during 1890–1920. These groups were highly segregated at that time. Lieberson (1959, pp. 209, 215) found segregation of immigrant Russians and Italians from U.S. born whites at the ward level in 1910 (Index of Dissimilarity) to be .48 and .66, respectively, in Boston and .58 and .61, respectively, in Philadelphia. Much less is known about the earlier 19^th Century arrivals, mainly Irish, Germans, and British. There is scattered evidence that these groups experienced only modest residential segregation in the 19^th Century. Kantrowitz (1979, p. 45) reports that in Boston at the ward level the magnitude of segregation between immigrant Germans and immigrant Irish as early as 1850 was only .36. Tract-level segregation in Philadelphia between native whites (third and later generation) and immigrant Irish or Germans was in the range of .30–.33 in 1850 (Hershberg et al 1981) and .35–.37 in 1880 (Greenberg 1981). If these early arriving groups were never highly segregated, how do theories of residential assimilation apply to them?

This study adds substantially to the evidence regarding segregation of Germans, Irish, and British in 1880, fully three decades earlier than the most comprehensive previously published data for white ethnic groups (Lieberson 1959). We document the extent of segregation for these groups at the enumeration district level for all cities with population over 25,000 in 1880. Further, we analyze the predictors of their residential location in a multilevel framework that allows us to estimate relationships at the individual level that are key to assimilation theory and also to identify independent effects of the cities that people lived in. For the first time in this period it is possible to determine how residential patterns were affected by the size of the group, the share that were foreign-born, their socioeconomic standing relative to native whites, and their occupational segregation from native whites.

Working with publicly available aggregate census data, researchers interested in contemporary situations have searched for ways to decompose segregation into a component that can be attributed to group differences in income (or education, or any other single variable for which the necessary tables are available) and a component that is net of such differences. A significant development in research on minority residential patterns has been examination of the determinants of locational outcomes for individual group members. A series of studies (Alba and Logan 1992, 1993; Logan et al 1996; Alba, Logan and Stults 2000) established the utility of locational attainment models for the study of segregation. Recent research has exploited multilevel datasets to understand the individual-level processes that result in group differences in neighborhood characteristics such as value of housing (Woldoff and Ovadia 2009) and environmental hazards (Crowder and Downey 2010) and has taken advantage of longitudinal surveys to examine inter-neighborhood mobility (South, Crowder and Pais 2008; Sampson and Sharkey 2008). One aim of our use of multi-level modeling is to determine how variations in people’s socioeconomic status, attributes associated with immigration, and other personal characteristics feed into the creation of separate racial and ethnic communities. Another is to assess whether and why outcomes differ across cities.

Historical and theoretical background

A key theoretical perspective in this field is spatial assimilation, the hypothesis that over time minority racial and ethnic groups will tend to become integrated into the social mainstream and that this integration will be reflected in where they live. Typical hypotheses from this perspective, mostly confirmed through locational attainment models, show that minority persons with higher income and education, born in the U.S. and who speak English well, are likely to live in higher status neighborhoods and with greater exposure to the non-Hispanic white majority. Another viewpoint emphasizes place stratification (Logan 1978), positing that there is a hierarchy of neighborhoods in most cities whose racial/ethnic composition mirrors a durable hierarchy of groups. Past work with locational attainment models has addressed this perspective by evaluating whether members of some groups do not attain locational outcomes equivalent to comparable majority group members even after controlling for background characteristics, or whether the locational payoff to income, education or home ownership is lower for minorities than for non-Hispanic whites.

We contribute to this research tradition on sources of residential segregation in two ways. First, we apply the logic of locational attainment modeling at a national level, including not just one or several cities, but all identifiable urban areas. This breadth allows us to extend individual-level models to a multi-level framework, where we examine the relationship of characteristics of the city where people live to the extent of their ethnic isolation or exposure to the majority group. Introducing contextual variables in this way extends the reach of locational attainment models, allowing a more direct assessment of conditions that are important from the place stratification perspective, such as the strength of group boundaries in the labor market. Second, we shift attention from the contemporary period to a much earlier point in the history of immigration and intergroup relations in the United States, the late 19^th Century just prior to the wave of immigration from Southern and Eastern Europe, when the principal white ethnic groups in U.S. cities were German, Irish, and British. We are studying intergroup relations for groups who are the earliest illustration of spatial assimilation and the model against which the experience of subsequent groups has been assessed (Foner 2000, Perlman 2007).

In 1880, the date of this study, the main newcomer groups in the United States were Irish, Germans, and British. These were the Northern Europeans whom the Dillingham Commission (1911, p. 13) would later describe as “quickly assimilated … while the racial identity of their children was almost entirely lost and forgotten.” Some historians have argued that though these groups established ethnic enclaves in some cities, the 19^th Century walking city limited ethnic segregation. People needed to live close to work, and except for cases where a particular industry was geographically concentrated and effectively restricted to members of a single group, this meant that segregation would be based more on occupation than on ethnicity. As noted above, demographic studies have documented that these white ethnic groups experienced only modest residential segregation in late 19^th Century cities and even less in the second generation (Kantrowitz 1979, Greenberg 1981), and that their segregation declined further in the 20^th Century (Guest and Weed 1976, Alba et al 1997). Their experience appears to contrast with later arriving groups from Europe (Italians and Jews), from the American hinterland itself (blacks and Puerto Ricans), and more recent waves of immigrants from Latin America and Asia for whom separation into distinct ethnic neighborhoods was initially more pronounced and proved to be more persistent. We examine the earlier experience of Northern Europeans in order to evaluate how the models of spatial assimilation and place stratification apply in their case. How did the relatively early arriving immigrants from Britain, Ireland, and Germany fit into the neighborhoods of urban America in 1880, a moment when there had already been several decades of large scale movement from these countries to the U.S.? If they were not fully assimilated and if the “racial identity of their children” was not “entirely lost and forgotten,” what can we learn about their relationship with native whites (that is, whites born in the U.S. whose parents were also U.S.-born) from their residential pattern?

Prior historical research on segregation of white ethnic immigrant groups

Urban historians have given much attention to the ethnic character of neighborhoods. Studying 19^th Century New York, Binder and Reimers (1995) note that immigrant neighborhoods of the Lower East Side were not ethnically homogeneous, but there nevertheless existed clear ethnic concentrations. In 1855 the Irish constituted more than 40% of the First, Fourth, and Sixth wards, while Germans were above 25% of the population in the Tenth, Eleventh and Seventeenth Wards. Nadel (1990) calls particular attention to the area on the Lower East Side that came to be called Kleindeutschland. This neighborhood was newly built in the 1840s, but became distinctly German by 1855, and was 64% German by 1875. Nadel’s ward data (1990, p. 28) for the period 1855–1875 (combining first and second generation group members) revealed values of segregation (D) from native whites of around 35 for Germans. This is close to the contemporary value for white-Asian segregation but much lower than the value of around 75 found for Italians and Jews in 1920 (Logan 1998). Irish-native white segregation was even lower, below 20.

Similar findings have been reported for Philadelphia. Greenberg (1981) analyzed 1880 census data for Philadelphia that had been mapped to tract boundaries from 1930. She reports that the segregation (D) between native (3+ generation) whites and immigrant Irish was 35, and 37 between native whites and immigrant Germans. Segregation of second-generation Irish and Germans was somewhat lower (29 and 31). Her conclusion (p. 215) is that “segregation from the native population is not a basic feature of the immigrant residential experience,” a forceful rejection of the relevance of residential assimilation for these groups.

Apart from the issue of the degree of segregation, there are theoretically significant questions about processes: how segregation is linked to characteristics of group members and the cities where they lived. Historical studies of segregation have paid most attention to sources of variation at the individual level, emphasizing especially generational differences and effects of occupation. As noted above, Greenberg found only a small difference in segregation between first and second generation group members in Philadelphia. Hershberg et al (1981) replicated this finding with longitudinal data. Foreign-born Irish even in 1850 had a value of D from native whites of only 30 (33 for foreign-born Germans), scarcely different from the magnitude of segregation of foreign stock persons (including both first and second generation) in 1880. The most careful study in this general time frame was conducted for New York City in 1910 by White et al (1994). Using data on people’s next-door neighbors, White found that there was a negative effect of being an immigrant on the likelihood of living next to a native white for member of all ethnic groups. However this effect was small for the Irish, and only moderately negative for Germans and British. That is, generational differences were in the hypothesized direction, but highly attenuated for the early arriving ethnic groups.

Researchers have also asked how occupational status affected residential patterns. Referring to New York, McCaffery (1996) pointed out that post-1870 Irish immigrants still were relatively unskilled, and had to compete with other groups even for unskilled jobs as dockworkers, laborers, hod carriers on construction sites, service workers in restaurants and bars, garment workers, and domestic servants. This, he believed, accounted for their clustering in the lower class neighborhoods of Five Points, Chelsea, Hell’s Kitchen, and the Gas House district. Further, one source of ethnic segregation is segregation in the workplace, and as Greenberg (1981) points out, workers in a particular industry in 1880 tended to live within a mile around the main job locations for that industry. Yet in Detroit Zunz (1982) argues that segregation in 1880 was primarily based on ethnicity. He reports significant ethnic clustering (overrepresentation of a particular group) in 30% of the blocks that he sampled in 1880, but at that time it was common for ethnic blocks to include a wide range of occupations, from laborers to professionals and shopkeepers.

Others have suggested that occupation effects may be group-specific. Moore (1994, p. 145) argued that Germans in New York settled near industries established by German entrepreneurs. They “constructed a fairly complete ethnic economy that included workers as well as a range of mercantile establishments … thus German ethnicity permeated the urban class culture of the neighborhood” in places like Bushwick and Williamsburg. The Irish, in contrast, “rarely concentrated in such numbers throughout a neighborhood that they created a complete local ethnic economy. Instead they fashioned an ethnic network through politics and the church which did not require significant residential concentration.” Following this reasoning one would hypothesize that occupation mattered more for Germans than for Irish. Again the analysis by White et al (1994) for New York in 1910 has suggestive results. Although occupational standing had strong effects on the likelihood of a native white neighbor for new immigrant groups (e.g., Italians, Russians), the effects were only moderate for Germans and British, and very modest for Irish. Occupation was a part of the sorting process in 1880, based on this partial evidence, but not a large part.

Based on these findings, we anticipate that individual-level differences had significant but small effects on residential outcomes for these groups. We turn to another theoretical tradition to identify other sources of segregation, and specifically sources at the level of cities. The stratification perspective (Logan and Molotch 1987, Alba, Logan and Bellair 1994) begins from the premise that racial and ethnic groups compete for advantaged locations in urban space and that there is a hierarchy of groups that affects where people can live, above and beyond their individual resources. Based on their relative occupational standing, native whites were the most advantaged group in 1880, followed closely by the British, with Germans at a lower rank and Irish further behind. One might expect, therefore, that measures of residential segregation would align similarly.

In this study there are two potential indicators of the strength of intergroup stratification, both of which can be used to ask if the degree of residential segregation of members of any group depends on the relative standing of that group in a given city. Whatever the overall national ethnic hierarchy, in other words, there might well be differences from city to city in the strength of segregating processes experienced by a given group. One such measure is the relative occupational standing of group members at the local level. Another is the degree of occupational segregation (the degree to which group members and native whites are employed in different occupations and industries) in the city.

The question of contextual effects has received little attention in historical studies, most of which have been restricted to single cities. It is a standard question in contemporary research, however. For example recent studies (Farley and Frey 1994; Logan, Stults and Farley 2004) suggest that residential segregation of blacks, Hispanics, and Asians across cities and metropolitan regions is often greater in areas where the class disparities between them and non-Hispanic whites are largest. Among our primary goals is to evaluate similar differences across cities in the late 19^th Century.

Research design

These considerations lead us to define our research problem as analyzing sources of residential outcomes at both the individual level (examining factors associated with individual spatial assimilation) and the city level (probing differences in the context of segregation that may affect all group members). This approach has high data requirements – information on individual location for a large sample of persons across a large number of urban areas. Some contemporary survey data sets with appended locational information meet this requirement, although samples are usually sufficient only to study large groups (e.g., blacks or Hispanics but not national origin categories within them, and often not Asians) in larger cities or metropolitan regions. Historical research at the individual level has mostly been based on samples that had to be drawn painstakingly from census manuscripts and therefore were limited to a single city or some neighborhoods of that city (for Boston: Thernstrom 1973; for New York: Kessner 1977 and Model 1985; for Detroit: Zunz 1982; for Philadelphia: Hershberg 1981; and for Providence: Perlmann 1988). Comparisons across cities (e.g., Lieberson 1963) have been based on aggregate population statistics for areas like city wards, with no information about variations among individual residents with different backgrounds.

Our study is made possible by the newly available national full-count data of the 1880 U.S. Census prepared by Minnesota Population Center. The 100% sample for the 1880 Census of Population covers the entire U.S. population and contains approximately 50 million records. Key population characteristics, such as family size and composition, race, gender, age, marital status, occupation, and state or country of birth of the person and the person’s mother and father, are included. IPUMS codes occupation and industry into categories that are comparable to those used in the mid-20^th Century, including occupational SEI scores. A unique advantage of the 1880 dataset is that it makes it possible to estimate causal models that incorporate characteristics of cities as predictors of group members’ residential patterns. For this particular analysis, we extract records of individual aged 18 and above for 67 cities, each of which had more than 25,000 residents in 1880 (see Appendix Table 1).

Appendix Table 1.

Segregation measures for 67 cities in 1880

	Group Population in the City				Dissimilarity - Native Whites			Isolation				Exposure to Native Whites
	Native White	Irish	German	British	Irish	German	British	Native White	Irish	German	British	Irish	German	British
Albany	16,698	21,672	9,600	4,301	0.339	0.496	0.121	0.373	0.474	0.346	0.089	0.262	0.225	0.344
Allegheny	12,409	9,624	14,158	4,167	0.146	0.523	0.183	0.351	0.268	0.479	0.127	0.322	0.179	0.308
Baltimore	76,543	24,599	55,279	6,402	0.316	0.349	0.203	0.432	0.187	0.366	0.038	0.355	0.319	0.392
Boston	86,412	92,450	9,576	14,796	0.473	0.494	0.286	0.477	0.503	0.087	0.069	0.248	0.298	0.358
Bridgeport	7,925	6,323	1,814	1,776	0.372	0.242	0.194	0.480	0.420	0.112	0.100	0.338	0.393	0.425
Brooklyn	90,451	116,932	72,408	39,339	0.434	0.516	0.199	0.365	0.450	0.422	0.133	0.215	0.178	0.303
Buffalo	15,074	16,922	36,002	8,016	0.453	0.630	0.248	0.296	0.376	0.603	0.128	0.166	0.093	0.230
Cambridge	12,788	11,873	776	2,398	0.368	0.469	0.236	0.456	0.430	0.043	0.081	0.307	0.302	0.385
Camden	14,790	2,530	2,065	2,107	0.181	0.260	0.158	0.627	0.111	0.098	0.088	0.563	0.555	0.581
Chicago	61,113	64,661	83,514	22,825	0.523	0.608	0.275	0.376	0.307	0.431	0.105	0.168	0.124	0.278
Cincinnati	29,197	24,678	75,152	7,752	0.342	0.446	0.191	0.275	0.272	0.609	0.069	0.201	0.144	0.240
Cleveland	18,581	16,584	27,460	12,247	0.408	0.405	0.234	0.272	0.286	0.386	0.161	0.178	0.168	0.216
Columbus	12,959	4,293	7,690	2,577	0.313	0.511	0.159	0.467	0.218	0.463	0.101	0.421	0.279	0.454
Covington	4,901	2,599	6,246	1,229	0.217	0.385	0.219	0.329	0.191	0.459	0.089	0.293	0.237	0.304
Dayton	9,240	2,395	8,242	1,077	0.254	0.310	0.095	0.428	0.135	0.426	0.051	0.390	0.343	0.421
Detroit	12,496	10,761	19,890	8,101	0.275	0.563	0.154	0.256	0.232	0.468	0.147	0.205	0.110	0.228
Elizabeth	5,375	5,245	3,221	1,364	0.390	0.523	0.235	0.426	0.398	0.295	0.088	0.261	0.241	0.341
Erie	3,838	2,878	5,534	1,026	0.293	0.323	0.135	0.289	0.256	0.422	0.070	0.235	0.214	0.261
Evansville	4,034	897	7,595	1,199	0.190	0.288	0.121	0.262	0.062	0.497	0.081	0.248	0.214	0.255
Fall River	6,328	10,186	73	7,479	0.411	0.442	0.407	0.367	0.414	0.006	0.292	0.174	0.273	0.178
Grand Rapids	7,730	1,922	2,603	1,368	0.262	0.346	0.157	0.434	0.112	0.180	0.072	0.361	0.358	0.391
Harrisburg	12,517	1,279	2,025	544	0.266	0.203	0.157	0.703	0.091	0.130	0.037	0.623	0.667	0.685
Hartford	12,157	9,625	1,815	1,815	0.251	0.356	0.175	0.476	0.378	0.095	0.073	0.394	0.362	0.440
Hoboken	2,263	5,091	7,740	1,194	0.387	0.171	0.134	0.154	0.331	0.440	0.071	0.105	0.130	0.138
Indianapolis	20,509	5,863	9,582	2,228	0.323	0.297	0.120	0.470	0.184	0.273	0.051	0.401	0.402	0.451
Jersey City	17,676	27,288	12,959	7,972	0.368	0.444	0.159	0.330	0.467	0.282	0.128	0.210	0.204	0.285
Kansas City	14,283	5,423	3,201	1,928	0.318	0.198	0.124	0.440	0.193	0.117	0.058	0.368	0.421	0.410
Lancaster	9,540	929	4,303	290	0.195	0.315	0.155	0.635	0.072	0.348	0.021	0.610	0.518	0.614
Lawrence	6,890	10,172	941	4,368	0.345	0.652	0.272	0.322	0.495	0.150	0.251	0.230	0.218	0.281
Lowell	14,809	14,118	118	3,464	0.429	0.340	0.282	0.455	0.463	0.006	0.111	0.283	0.443	0.369
Lynn	16,748	5,397	69	1,040	0.333	0.396	0.131	0.653	0.271	0.005	0.041	0.556	0.584	0.623
Manchester	10,135	4,651	355	1,010	0.541	0.534	0.308	0.609	0.396	0.074	0.062	0.272	0.485	0.468
Memphis	5,049	2,504	1,766	647	0.272	0.239	0.164	0.280	0.148	0.112	0.034	0.218	0.244	0.244
Milwakee	6,385	6,935	37,891	3,589	0.359	0.575	0.165	0.193	0.295	0.673	0.092	0.145	0.064	0.165
Minneapolis	11,010	3,571	3,281	1,689	0.346	0.440	0.182	0.451	0.140	0.169	0.061	0.312	0.291	0.388
Mobile	4,025	2,596	1,104	785	0.244	0.314	0.168	0.268	0.165	0.094	0.051	0.226	0.236	0.251
Nashville	10,356	2,330	1,164	790	0.274	0.422	0.153	0.434	0.116	0.122	0.033	0.356	0.377	0.405
New Bedford	10,497	2,973	177	1,465	0.245	0.312	0.390	0.626	0.187	0.016	0.131	0.518	0.586	0.451
New Haven	17,714	13,448	3,584	2,580	0.435	0.346	0.184	0.523	0.474	0.120	0.071	0.314	0.413	0.460
New Orleans	22,400	21,045	23,974	4,357	0.359	0.340	0.247	0.219	0.240	0.236	0.047	0.160	0.159	0.195
New York	127,972	276,197	208,187	52,006	0.420	0.523	0.244	0.280	0.458	0.411	0.084	0.152	0.119	0.209
Newark	23,084	19,075	23,106	7,747	0.414	0.548	0.214	0.400	0.351	0.479	0.118	0.251	0.176	0.336
Oakland	7,753	4,051	2,289	2,341	0.290	0.250	0.173	0.381	0.210	0.112	0.107	0.306	0.325	0.342
Omaha	6,750	2,609	2,917	1,705	0.235	0.280	0.165	0.385	0.160	0.178	0.101	0.329	0.322	0.363
Paterson	7,858	8,277	2,627	7,210	0.492	0.400	0.314	0.350	0.400	0.125	0.265	0.177	0.244	0.240
Peoria	6,091	3,359	4,811	1,112	0.287	0.337	0.164	0.388	0.230	0.322	0.074	0.312	0.300	0.369
Philadelphia	200,521	160,376	86,783	49,617	0.369	0.376	0.284	0.436	0.393	0.267	0.127	0.310	0.343	0.360
Pittsburgh	19,941	26,493	24,282	10,048	0.290	0.332	0.233	0.271	0.360	0.353	0.131	0.211	0.203	0.221
Portland	12,691	4,951	126	946	0.424	0.317	0.217	0.616	0.323	0.008	0.046	0.455	0.555	0.540
Providence	29,224	24,373	1,390	7,518	0.423	0.288	0.352	0.510	0.452	0.027	0.141	0.319	0.425	0.367
Reading	18,814	1,047	3,930	597	0.362	0.251	0.189	0.757	0.071	0.198	0.029	0.729	0.708	0.756
Richmond	15,416	1,770	2,195	914	0.307	0.280	0.164	0.435	0.069	0.081	0.033	0.382	0.405	0.453
Rochester	13,854	11,205	15,859	5,476	0.276	0.540	0.162	0.331	0.259	0.444	0.114	0.265	0.167	0.290
Saint Louis	43,712	42,847	80,613	11,834	0.369	0.488	0.258	0.316	0.298	0.504	0.078	0.203	0.147	0.242
Salem	9,117	5,915	70	812	0.346	0.436	0.252	0.557	0.386	0.010	0.066	0.432	0.465	0.483
San Francisco	26,727	42,031	24,200	13,548	0.340	0.270	0.204	0.244	0.365	0.195	0.104	0.170	0.186	0.200
Scranton	5,588	9,055	4,039	5,343	0.471	0.541	0.398	0.334	0.498	0.348	0.352	0.171	0.179	0.228
Springfield	11,757	5,831	546	1,059	0.272	0.347	0.121	0.566	0.320	0.040	0.050	0.486	0.542	0.541
Syracuse	11,521	7,610	7,177	2,532	0.319	0.586	0.150	0.443	0.318	0.521	0.094	0.354	0.192	0.403
Terre Haute	8,787	2,034	3,095	838	0.209	0.181	0.155	0.558	0.150	0.208	0.057	0.517	0.518	0.532
Toledo	7,964	4,666	8,730	1,736	0.286	0.313	0.099	0.312	0.225	0.373	0.068	0.272	0.239	0.301
Trenton	9,019	3,813	2,127	2,058	0.316	0.329	0.286	0.528	0.247	0.143	0.132	0.409	0.434	0.458
Troy	10,355	16,831	2,091	3,181	0.393	0.242	0.273	0.375	0.545	0.084	0.116	0.231	0.339	0.304
Utica	5,702	5,328	4,361	4,272	0.277	0.482	0.127	0.316	0.302	0.327	0.222	0.254	0.191	0.291
Washington	39,436	11,979	7,614	4,593	0.300	0.266	0.129	0.442	0.163	0.106	0.052	0.364	0.397	0.423
Wilmington	13,321	5,939	1,294	1,720	0.205	0.239	0.103	0.512	0.257	0.065	0.068	0.487	0.511	0.504
Worcester	16,899	12,684	537	1,869	0.504	0.386	0.258	0.578	0.477	0.019	0.059	0.304	0.384	0.445

We study only three groups, because other groups had substantial populations in only a few cities. In the identified cities (8.5 million inhabitants), 27.6% were native white, 24.7% Irish, 23.6% German, and 7.1% British. The next largest group is Canadians, whom we do not study because they have ambiguous ethnicity (a mix of British, French, and other groups who entered the U.S. through Canada). The next largest European group, the French, is only 1.4% of the total urban population. Further, only the three largest European groups are well represented in most of the 67 cities. The Irish have more than 1000 residents in every city, Germans in 58 cities, and British in 63 cities. The French have over 1000 residents in only 12 cities.

Multilevel models are increasingly used in situations where the units of study are clustered into nested partitions (e.g., students and schools, cities and countries). In this case we are interested in two levels: individual factors such as age and nativity at level one and variations across cities at level two. Because cases are nested in many different cities, other methods (such as OLS regression) would not produce correct standard errors to test the significance of individual and city effects on residential outcomes. The multi-level model adjusts for correlated errors and provides more realistic and conservative statistical testing. We apply a random intercept model. This model assumes that the variation between cities (level 2) can be represented by a single additive parameter (the u_j in the equation below). This implies that unexplained variations in the citywide aggregate amount of segregation depend only on average differences between cities themselves. The mathematical form for the model is shown in the following equation:

$$Y_{ij}=b_0+b_1{X}_{ij}+u_j+e_{ij}$$

J refers to the jth city in this application. The level-2 residual u_j is usually not estimated as a parameter in the random intercept model. But in the final part of our analysis, we will calculate this city-specific intercept and use it to illustrate the variations in the outcome variables for group members in each city.

The rationale for estimating multilevel models is that some portion of the segregation experienced by members of a given ethnic group is expected to be a function of their own individual traits (such as their occupational standing). The distribution of these traits among group members in a given city should affect the citywide aggregate amount of segregation. That is, for example, if many Irish in a city were unskilled workers and if unskilled workers tend to live in ethnic enclaves, segregation of the Irish in that city would be high as a direct consequence of this individual-level process. All prior studies of variation across cities or metropolitan regions (carried out at the aggregate level) have implicitly incorporated individual-level theories into their interpretation of segregation. When a researcher included the group’s average socioeconomic standing in a city as a predictor of its segregation, the resulting coefficient was interpreted mainly in terms of whether higher-status minorities were more easily integrated into white neighborhoods. Our approach here is to make this individual-level interpretation explicit and to model it directly. Having done so, we can also introduce predictors that reflect processes that are believed to affect all group members in a city, i.e., true contextual effects.

Multilevel models are used in a similar way by Tolnay, Crowder and Adelman (2002) to analyze neighborhood outcomes for black and white migrants to Northern and Western cities in 1920. Their city-level predictors included percent black and percent foreign-born white, manufacturing employment share, population and population growth.

Dependent Variables

The dependent variables in our analysis are two measures of racial/ethnic composition of neighborhood residents, the percentage of coethnic residents (isolation) and the percentage of native white residents (exposure). Here we define native white as native born whites with native born parents and the neighborhood is taken to be an enumeration district (ED). Previous historical studies have relied on census tracts (1930 and subsequent years, and also recreated for 19^th Century Philadelphia based on 1930 tract definitions) and wards (most studies prior to 1930). Kantrowitz (1979) calculated dissimilarity scores for several cities in 1930 using both wards and tracts, and found a consistent difference of approximately 10 points between the two (see also Lieberson 1959). There is consensus that either unit can be used, while recognizing that tract-level measures will yield higher values. ED’s are typically subdivisions within wards, comparable in population size to a contemporary census tract. In this study the average population of ED’s was 3597, and 80% were in the range of 1738 to 5832. ED composition is calculated by aggregating data for all residents of the ED in our 100% sample. This dependent variable is parallel to isolation and exposure measures of segregation (p_ii* and p_ij*) at the group level, which are equivalent to the average isolation or exposure experienced by group members in a particular locale (Lieberson 1976).

As individual factors, in addition to age and gender that are used as control variables, we construct measures for ancestry and generation, individual socioeconomic standing, domestic service, and intermarriage.

Ancestry and Generation

Like previous researchers, we rely on the person’s and parents’ race and place of birth to create categories of race, ethnicity, and generation. Among whites the categories are based on country of birth or parents’ country of birth, classifying people as 1st or 2nd generation members of a particular ethnicity or as native (3+ generation) whites. Those in the 1st generation were born abroad, and their country of birth determines their ethnicity. Those in the 2nd generation were born in the United States, but at least one parent was born abroad. If the mother was foreign-born, the person is classified according to her country of birth. If only the father was foreign-born (or if the mother was foreign-born but her birthplace was not reported, as is true in some cases in 1970), the father’s country of birth is applied.

Socioeconomic Standing

The 1880 census did not gather information on income or education, the most conventional indicators of socioeconomic standing. But it provides detailed information on occupations. We use the Socio-Economic Index of occupational standing (SEI), provided by IPUMS and based on the average education and earnings of persons in each occupation as measured in 1950 (and validated by a 1947 survey of the “general standing” of a sample of occupations). For persons with no reported occupation, SEI was coded at the mean, and an additional dummy variable is included in the model to adjust for these missing values.

Domestic Service

We also use the information on occupation and household relationships to discover whether the person was a servant and lived in the employer’s house at the time when the census was conducted. Many immigrants, especially young and single women, were domestic servants in 1880. We identified over 200,000 persons in the 67 cities as live-in domestic servants, more than 40% of whom were Irish. Among the total Irish population, 7.3% were servants, compared to 2.9% of Germans and 2.4% of British. In each ethnic group more than 90% of servants were women, more than 75% were unmarried (and the majority of others were divorced or widowed), and a majority were 1^st generation immigrants. Hence this variable is an essential control as our model also includes gender, generation, and marital status.

Inter-group Marriage

An important correlate of residential choice is a central family behavior, marital choice. Endogamy and exogamy have been operationalized in many different ways, depending on how group boundaries are defined (Alba and Golden 1986; McCaa 1993). We combine country of birth with marital status for the person and (if married) the person’s spouse to create the following categories of marital status: unmarried, married to a co-ethnic, married to a native white, married to people of other ethnic groups, and divorced/widowed (with a residual “not reported” category).

Contextual factors

In addition to these individual-level measures, we construct five group-specific contextual variables by aggregating individual data to the city level: total city population, percent native white population, percent foreign-born in the ethnic group, average group SEI as a ratio to native whites’ SEI, and group industrial segregation from the native white population.

The latter two measures require further explanation. The SEI ratio is calculated as the mean SEI of group members in the city divided by the mean SEI of native whites. It is intended to reflect the relative socioeconomic standing of the group, which is an indicator of its position in the ethnic hierarchy. The segregation index draws upon an industry-based approach established by Logan, Alba and McNulty (1994). First, we recode the original industry categories of the 1880 U.S. Census into 66 categories based on two-digit codes of the 1950 industrial classification system. As the next step, we calculate the dissimilarity indices of segregation across these categories between native whites and the Irish, Germans, and British based on all employed persons in each city. Although our measure is based on industries, the industry categorization in our data is based on a person’s occupational responses in the original census manuscripts as coded by the Minnesota Population Center.

Ethnic segregation across cities

As an introductory step, we compute segregation indices for cities and examine their variation. The most common measure of segregation in the historical literature is the Index of Dissimilarity (D), and we have computed D from aggregated data at the level of enumeration districts. (These and other segregation indices are listed in Appendix Table 1 for all 67 cities in 1880.) As pointed out by Massey and Denton (1988) D measures the degree of unevenness in the distribution across neighborhoods of two groups. It has the advantage for many purposes that it is not affected by the relative size of groups. The (unweighted) mean values of segregation from native whites are moderate: .38 for Germans, .34 for the Irish and only .20 for British. The values also vary widely across cities: from .15 to .66 for Germans, from .15 to .55 for Irish, and from .10 to .40 for British.

In this study we give more attention to p* measures of intergroup exposure and isolation. Apart from the evenness of distribution as measured by D, it can be important to know what the ethnic composition of typical group members’ neighborhoods is, and this is a strength of p* measures. As Lieberson and Carter (1982), among others, have pointed out, it is relevant to take into account the relative sizes of groups if researchers want to assess the extent of diversity actually experienced by people in their neighborhoods. The exposure and isolation measures also have the advantage in this study that they are the city-level counterparts of the dependent variable in this study: individuals’ neighborhood composition. Table 1 summarizes the degree of exposure and isolation in 1880. The table provides information on the distribution of values (the mean value; at the low end, the minimum and value at the 10^th percentile; and at the high end, the maximum and 90^th percentile). The table also provides the values for the six largest cities, each of which had more than 300,000 residents in 1880. Because the relative size of groups is a core component of exposure and isolation indices, the table also lists values for the share of each group in the city population.

Table 1.

Group size, Exposure Index, and Isolation Index between Native White, Irish, Germans and British in 1880: Distribution for 67 Cities and Individual Cities with Population Over 300,000

	Group % of Total Population				Exposure Index			Isolation Index
	Native White	Irish	German	British	Irish	German	British	Native White	Irish	German	British
Minimum	9.5	4.2	0.2	1.8	0.105	0.064	0.138	0.154	0.062	0.005	0.021
10th percentile	17.5	9.6	1.4	3.1	0.170	0.133	0.209	0.262	0.112	0.019	0.038
Mean	34.8	21.9	17.4	7.9	0.314	0.314	0.364	0.416	0.291	0.248	0.097
90th percentile	56.4	36.3	36.5	11.7	0.517	0.542	0.540	0.616	0.474	0.479	0.147
Maximum	74.7	47.0	56.2	25.4	0.729	0.708	0.756	0.757	0.545	0.673	0.352
New York	16.8	36.3	27.3	6.8	0.152	0.119	0.209	0.280	0.458	0.411	0.084
Brooklyn	25.9	33.5	20.7	11.3	0.215	0.178	0.303	0.365	0.450	0.422	0.133
Philadelphia	36.8	29.4	15.9	9.1	0.310	0.343	0.360	0.436	0.393	0.267	0.127
Chicago	20.3	21.5	27.8	7.6	0.168	0.124	0.278	0.376	0.307	0.431	0.105
Boston	35.5	38.0	3.9	6.1	0.248	0.298	0.358	0.477	0.503	0.087	0.069
St. Louis	17.2	19.5	39.1	5.4	0.179	0.133	0.204	0.253	0.276	0.499	0.069
Baltimore	37.1	11.9	26.8	3.1	0.355	0.319	0.392	0.432	0.187	0.366	0.038

On average native whites comprise the largest group in these cities, about a third of the population. However their size is quite variable even among the six largest cities, only about 17% in New York and St. Louis, but over 35% in Philadelphia, Boston, and Baltimore. In a few smaller cities native whites are a majority population, but their size ranges as low as 9.5%. The Irish and Germans are generally a smaller population group, averaging around 20% of the population, but again there is a substantial range. Among the major cities, the Irish are the larger group in New York, Brooklyn, Philadelphia, and (by a wide margin of 34 percentage points) in Boston, but the Germans are a larger share of residents in Chicago, Baltimore, and especially St. Louis (39.2%). Finally, the British are typically a much smaller minority, rarely over 10% of the population though reaching 25.5% in one city.

Exposure and isolation indices vary over a wide range. Depending on what city a white ethnic person lived in, he/she might expect on average to live in a neighborhood that is as little as 10% or 15% native white, or as high as 70% to 75%. The mean values across cities show that exposure to native whites tended to be somewhat higher for the British than for Irish or Germans, while isolation was highest for the Irish and lowest for the British.

As is well known, these indices hinge in part on the overall population composition of cities. For this reason Bell (1954) proposed a “revised index of isolation” (I₁) that normalizes the isolation index to values in the range from 0 to 1 by introducing information about the group’s share of the total population and a “revised group segregation ratio” (I₂) that normalizes the exposure index between two groups in a similar way. ¹ We present these standardized values in Table 2. The table reinforces our impression that there is much variation across cities. For both indices and for every group the interdecile range is quite large (exposure to native whites is about twice as high at the 90^th percentile than at the 10^th, and variation in isolation is much greater). Standardizing leads to somewhat different conclusions about this variation. Table 2 suggests that the British were indeed much less isolated than other groups (even after taking into account their small share of the population), but the Irish on average were about equally isolated as native whites and Germans. Exposure to native whites is shown to be highest for Irish in the average city, though German had higher exposure to native whites than did the Irish in St. Louis and Baltimore.

Table 2.

Standardized Segregation Indices for Native Whites, Irish, Germans and British in 1880: Distribution for 67 Cities and Individual Cities with Population Over 300,000

	Standardized Exposure to Native Whites			Standardized Isolation Index
	Irish	German	British	Native White	Irish	German	British
Minimum	0.302	0.248	0.211	0.015	0.010	0.002	0.002
10th percentile	0.345	0.312	0.300	0.053	0.026	0.006	0.003
Mean	0.506	0.456	0.448	0.103	0.097	0.100	0.020
90th percentile	0.687	0.616	0.582	0.157	0.199	0.254	0.040
Maximum	0.770	0.855	0.780	0.273	0.235	0.385	0.175
New York	0.479	0.313	0.294	0.135	0.150	0.189	0.017
Brooklyn	0.492	0.320	0.435	0.143	0.173	0.271	0.023
Philadelphia	0.557	0.492	0.450	0.108	0.139	0.128	0.040
Chicago	0.345	0.294	0.382	0.217	0.117	0.213	0.031
Boston	0.514	0.331	0.419	0.189	0.199	0.050	0.009
St. Louis	0.381	0.434	0.268	0.097	0.100	0.177	0.016
Baltimore	0.469	0.550	0.425	0.097	0.077	0.134	0.007

The variation among cities invites consideration of what city-level factors affected segregation, and the difference between unadjusted and standardized exposure measures emphasizes the importance of controlling for group size.

Multivariate estimates

We turn now to the multilevel models predicting % native white and % co-ethnic separately for each of the three immigrant groups. Analysis of the variance components in these models is summarized in Table 3, and Table 4 presents results of the full multilevel models for each group.

Table 3.

Variance Components of multi-level model models

	% Native White			% Co-ethnic
	Irish	German	British	Irish	German	British
Unconditional intra-class Correlation (null model)	0.450	0.598	0.447	0.355	0.433	0.554
Model 1: Only group % in the model
R2 within cities	-	-	-	-	-	-
R2 between cities	0.909	0.923	0.959	0.916	0.902	0.936
R2 overall	0.229	0.375	0.247	0.213	0.242	0.461
Model 2: Group % + individual variables
R2 within cities	0.089	0.054	0.061	0.059	0.044	0.017
R2 between cities	0.923	0.929	0.970	0.918	0.917	0.940
R2 overall	0.281	0.445	0.311	0.283	0.373	0.481
Model 3: All individual and city variables
R2 within cities	0.089	0.054	0.061	0.059	0.044	0.017
R2 between cities	0.975	0.971	0.979	0.956	0.966	0.953
R2 overall	0.305	0.462	0.317	0.289	0.398	0.487

Table 4.

Multilevel model estimates of the effects of individual and city predictors on neighborhood composition (EDs in 67 Cities)

	Exposure (% Native White)						Isolation (% Co-ethnic)
	Irish		German		British		Irish		German		British
	b	SE	b	SE	b	SE	b	SE	b	SE	b	SE
Intercept	13.647	5.493*	−15.389	6.062*	5.872	5.743	−7.182	6.940	14.102	8.453	1.136	3.014
Age (centered on the mean)	0.037	0.001***	0.034	0.001***	0.084	0.002***	−0.041	0.002***	−0.041	0.002***	−0.010	0.001***
Female	−0.256	0.046***	−1.044	0.049***	−0.366	0.084***	0.373	0.055***	1.615	0.077***	0.030	0.036
Nativity
2nd Generation, both parents foreign (reference)
1st Generation	−0.311	0.040***	−0.988	0.037***	−2.534	0.070***	0.424	0.047***	0.844	0.058***	0.032	0.030
2nd Generation, one parent native white	3.894	0.076***	3.360	0.079***	1.999	0.089***	−4.218	0.090***	−4.456	0.123***	−0.438	0.038***
2nd Generation, one parent “other” nativity	1.766	0.112***	1.141	0.117***	−1.545	0.148***	−4.109	0.133***	−4.155	0.183***	−0.800	0.064***
Occupational SEI (centered on overall mean)	0.071	0.001***	0.087	0.001***	0.110	0.002***	−0.074	0.001***	−0.104	0.001***	−0.012	0.001***
SEI missing (0=measured SEI; 1=missing SEI)	1.310	0.049***	2.294	0.051***	3.047	0.090***	−1.386	0.058***	−2.753	0.080***	−0.236	0.039***
Domestic servant	16.150	0.073***	12.326	0.094***	11.031	0.188***	−14.244	0.087***	−15.252	0.147***	−1.327	0.081***
Marital status
Unmarried (reference)
Married within group	−2.605	0.042***	−2.323	0.040***	−2.060	0.079***	2.756	0.050***	3.997	0.063***	1.192	0.034***
Married to native white	4.320	0.083***	4.026	0.079***	2.045	0.088***	−4.995	0.099***	−4.621	0.124***	−0.312	0.038***
Married to another group	−0.280	0.070***	−0.431	0.063***	−3.800	0.087***	−2.847	0.084***	−2.885	0.098***	−0.886	0.038***
Divorced or widowed	−2.251	0.064***	−1.825	0.067***	−1.179	0.115***	2.023	0.077***	2.681	0.106***	0.016	0.049
Not reported	−0.769	0.080***	0.176	0.081*	−1.257	0.130***	−0.032	0.096	−1.353	0.126***	0.084	0.056
Percent native white	0.853	0.021***	0.906	0.027***	0.895	0.020***	---	---	---	---	---	---
Percent co-ethnics	---	---	---	---	---	---	1.037	0.046***	1.064	0.043***	1.133	0.033***
Group occupational segregation from native whites	−0.261	0.038***	−0.168	0.030***	−0.158	0.038***	0.260	0.051***	0.305	0.042***	0.043	0.012***
Ratio of group SEI to native white SEI	−0.014	0.030	0.121	0.022***	0.013	0.037	−0.027	0.039	−0.093	0.038*	−0.041	0.018*
City population (logged)	0.443	0.360	0.148	0.414	−0.086	0.323	1.246	0.438**	0.385	0.561	0.046	0.155
Percent foreign-born co-ethnics	−0.098	0.048*	0.160	0.042***	0.047	0.042	−0.121	0.069	−0.260	0.061***	0.020	0.017

^*p < .05,

^**p < .01,

^***p < .001

The null multi-level model predicts % native white and % co-ethnic in the neighborhood with no covariates. A useful parameter of that model shown in Table 3 is the intra-class correlation (ICC, also referred to as the unconditional intra-class correlation), which is the share of variation for individuals that is across cities. For the outcomes studied here the ICC is substantial, ranging from .36 to .60. This result is an indication that a search for city-level effects will be fruitful.

Other statistics shown in Table 3 provide an assessment of which predictors contribute to the model fit. The coefficient of determination for two-level models, suggested by Snijders and Bosker (1994, 1999), is the proportional reduction in the estimated total residual variance comparing the null model without covariates with the model of interest,

$$R^2=\frac{{\widehat{\psi }}_0+{\widehat{\theta }}_0-({\widehat{\psi }}_1+{\widehat{\theta }}_1)}{{\widehat{\psi }}_0+{\widehat{\theta }}_0}$$ (1)

where ψ̑₀ and θ̂₀ are the estimates for the null model and ψ̑₁ and θ̂₁ are the estimates for the model of interest. Equation (1) is the basis of the overall explained variance (R²) for each model in Table 3. Raudenbush and Bryk (2002) suggest considering the proportional reduction in each of the variance components separately. In our case, the proportion of level-1 variance explained by the covariates is

$$R_1^2=\frac{{\widehat{\theta }}_0-{\widehat{\theta }}_1}{{\widehat{\theta }}_0}$$ (2)

The proportion of level-2 variance explained is

$$R_2^2=\frac{{\widehat{\psi }}_0-{\widehat{\psi }}_1}{{\widehat{\psi }}_0}$$ (3)

Equations (2) and (3) are the basis for our estimates of R² within cities and between cities.

Table 3 summarizes the performance for three versions of the multi-level model.² Model 1 includes only group % and a constant term. The city’s % native white is included in the model predicting the native white share in each group member’s neighborhood; the city’s % co-ethnic is included in the model predicting the co-ethnic share. Hence all the explained variance is explained between cities, and no within-city variance is explained. Model 2 adds the individual-level predictors. Model 3 adds the remaining city-level predictors.

Model 1 results demonstrate that the relative size of groups is responsible for around 90% of the variation in intergroup exposure and group isolation across cities. Differences across cities, however, account for less than half (generally between a quarter and half) of the total variation in individuals’ experience of segregation. Model 2 shows that controlling for individual-level predictors hardly affects the explained between-city variation. These predictors are significant, however, for within-city variance. They are most potent in the Irish model for exposure to native whites, where they explain nearly 10% of the variance within cities, and including them in the model raises the total explained variance from .237 to .310. They are least effective in the British model for co-ethnic isolation, where they add little to the total explained variance, which increases from .473 to .481.

Results for Model 3 show the importance of other city-level predictors. Because groups have such heterogeneous residential experiences within any city, the increment to overall explained variance is modest, an increase of R² of at most .025. However they are quite substantial predictors if evaluated in terms of how much of the remaining between-city variance they account for. For example, in the Irish model for exposure to native whites, the between-city R² in Model 2 was .923. That leaves .077 to be explained, of which .052 is accounted for by the added variables in Model 3.

What are the predictors that contribute to these results? In order to evaluate the importance of each separate variable, Table 4 presents the full set of multi-level model coefficients for Model 3. Note that most coefficients are significant at the .001 level.

Individual-level effects: evidence of spatial assimilation

Although many coefficients are reported in Table 4, the individual-level relationships form a fairly consistent pattern. For convenience let us refer to living in a more native white and less co-ethnic neighborhood as being “more spatially assimilated.” In general, for Irish, Germans, and British, spatial assimilation is positively associated with being older and being a man. We included these characteristics as control variables without clear theoretical expectations. Possibly the age coefficients suggests a life cycle process, but we might have expected the opposite – that younger people might be more likely to learn to speak English well and to feel comfortable in unfamiliar (mixed ethnicity) settings. We might have expected a gender difference due to intermarriage by women who live in their husbands’ neighborhoods or to domestic servants who live with their employers, especially if they are young and unmarried, but the models control for these situations. We note that these are also very weak relationships. For example, being a German female is associated with living in a neighborhood that is 1.6% more German, but the difference in % native white is only 1%, and coefficients for other groups are even smaller.

Other individual-level variables have clearer connections with assimilation theory. Compared to second generation persons whose parents were both born in the same foreign country (the reference category), those who have at least one native white parent and even those whose parents were born in different countries are more spatially assimilated. (An exception is in the British model, where 2^nd generation persons with a parent who was neither British nor native white are shown to be significant less exposed to native whites). These “mixed second generation ancestries” are associated with living in an ED that is 3–4% more native white and 4% less coethnic for Irish and Germans. But 1^st generation immigrants are least spatially assimilated, though the difference between their neighborhoods and that of the second generation is typically less than a percentage point. (Again there is a British exception: the coefficient for immigrants in the isolation model is not significant.)

Occupational SEI also exerts a significant but small influence. Compared to a person whose SEI is at the mean value for the group, a person with a ten-point higher SEI (equivalent to the difference between a laborer and a machinist) is predicted to live in a neighborhood that is about 1% more native white and 1% less co-ethnic. (Again there is a British exception: the effect on co-ethnic residence is much smaller for the British, though still significant at.001.) A more striking occupational effect is from being a domestic servant (which we have defined to include only people who live in their employer’s household) – an 11–16% difference in most models, though much smaller for British isolation. It was common for more affluent households to employ a live-in servant of their same ethnicity, but apparently native whites were more likely than other groups to employ a servant of a different ethnicity. Many white ethnics were brought into native white neighborhoods in this way. Not having a reported occupation (the SEI dummy variable) is also associated with greater spatial assimilation. In the majority of cases this reflects women identified as housewives, so it may reflect the situation of households where the spouse of the household head does not need to be employed outside the home.

Finally, marital status also counts heavily. The key comparisons are between unmarried persons and those who are in-married, on the one hand, or intermarried with native whites, on the other. In-married persons are predicted to live in neighborhoods that are 2–3% less native white and 1–4% more co-ethnic. Persons intermarried with a native white, by contrast, are more spatially assimilated by a similar margin.

To summarize these results, we contrast the predicted values for exposure and isolation for men with two opposite sets of individual characteristics (holding city-level variables constant at the group average). Bundle 1 represents characteristics associated with less spatial assimilation: young (age 22), 1^st generation immigrant, low SEI score (12, which lies at the 25^th percentile for all employed persons in the 67 cities), and married to a coethnic woman. Bundle 2 represents characteristics associated with more spatial assimilation: older (age 50), 2^nd generation with one native white parent, relatively high SEI (44, which is at the 75^th percentile), and married to a native white woman. The difference in predicted values for these two bundles in predicted exposure to native whites is about 10%. For Germans and Irish the difference in predicted values of ethnic isolation are about 12%, but for the British this difference is only 2%. Our three ethnic groups vary greatly in their composition on these individual attributes, which to some extent accounts for their differences in spatial assimilation.

On the whole these findings suggest individual-level patterns of residential location that are consistent with spatial assimilation theory. To the extent that results for the British are weaker or in a different direction, one might argue that this is because the British are the smallest and least segregated group, the most culturally similar to native whites, and therefore the least affected by assimilation processes.

City-level differences

As already seen in Table 1, there is a strong relationship between a city’s ethnic composition and the composition of group members’ neighborhoods. Table 4 shows that exposure to native whites increases by close to 1% for every 1% increase in the city’s native white share – hence in a city with 10% more native whites, the average Irish, German or British resident would live in a neighborhood that is about 9% more native white. A similar relationship is found for co-ethnic population share, where a 10% higher share of the group’s city population is associated with an average 10–11% increase in group isolation.

Among other city-level predictors, coefficients for the group’s average SEI in relation to native whites, population size, and group percent foreign-born are mixed and inconsistently significant. However one other predictor is consistent in both direction and statistical significance. Cities where group members are more industrially segregated from native whites also offer less residential exposure to native whites and greater co-ethnic isolation. Irish can be taken as an example. Living in a city where the industrial segregation is 10 points higher (measured by the Index of Dissimilarity) would predict living in a neighborhood with close to 3% fewer native whites, and an equal increase in percent Irish.

Interpreting the effects of industrial segregation

Aside from relative group population sizes, industrial segregation is the contextual variable with the most consistent effect in this analysis. Even controlling for the individual-level effect of a person’s own occupational standing (SEI), an Irish, German, or British person living in a city where their ethnic group experiences a high degree of industrial segregation from native whites is also likely to live in a neighborhood with less exposure to native whites and a larger share of co-ethnics. We hypothesized such an effect based on stratification theory, anticipating that higher industrial segregation could be interpreted as a measure of the strength of group boundaries in a city. However there is another possible interpretation. If Germans and native whites, for example, tended to work in different industries and occupations, then they might be residentially segregated simply by virtue of having different workplace locations. This explanation is strengthened by the fact that most working class people walked to their jobs in 1880, so there may have been a tight connection between place of work and place of residence.

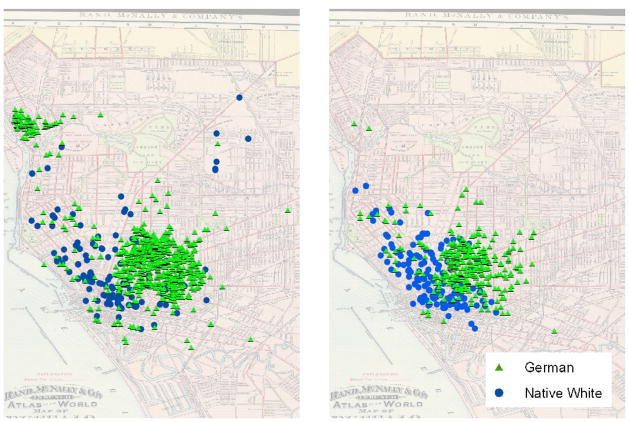
A full evaluation of this question would require extensive additional research. Here we report the results of an investigation for one group (Germans) in one city (Buffalo, NY), made possible by the fact that we have geocoded the residential locations of all residents of Buffalo in 1880. This is a city in which Germans were a large share of the population (40.9%), and they were highly segregated from native whites by both neighborhood (D = .537) and industry sector (D = .397). Our first step was to identify industries in which Germans were highly over-represented compared to non-Germans, but in which there were nevertheless a substantial number of native white workers. We present here the results for two manufacturing categories. One of these, “sawmills, word products, and furniture and fixtures,” was disproportionately German, employing 891 Germans and 143 native whites. The other, “paper, publishing, and printing” had more similar representation of both Germans (359) and native whites (161). Our questions are whether Germans and native whites who worked in the same kind of job tended to live closer to one another, and whether the same pattern would be found in a more segregated and less segregated sector.

One way to answer the question is to calculate Dissimilarity Indices at the level of enumeration districts, comparing the location of people across combinations of ethnicity and occupation. Relevant counts at the ED level were aggregated from the 100% microdata for Buffalo. We found that indeed there is moderate residential segregation between people employed in a given sector and people in other sectors (D = .332 for “sawmills” and D = .279 for “paper”). However there was much higher segregation between Germans and native whites who worked in the same sector (D = .779 and D = .708, respectively). (These values are both even higher than the overall magnitude of segregation of Germans from native whites in Buffalo, D = .630 for persons over 18).

We present these data graphically in Figure 5, on which we have plotted the residential location of all Germans and native whites in these two sectors. Regardless of the sector it is evident that Germans were highly concentrated and east of the city center, while native whites lived mainly closer to the waterfront. In addition there was a second concentration of Germans in the “logging, etc.” sector in the far north of the city. Hence we find little support for the view that working in different sectors resulted in residential segregation at the individual level. Rather, regardless of sector, these groups were highly residentially segregated. Our tentative conclusion is that the effect of industrial segregation at the city level represents a true contextual effect, and that industrial segregation can be understood as an indicator of the strength of group boundaries.

Discussion and conclusion

This study provides new systematic evidence about the extent and sources of residential segregation in U.S. cities near the end of the 19^th Century. Results are consistent with prior research that suggested that segregation between the main immigrant minorities of the period – Irish, Germans, and British – was moderate, much lower than would be found within a few years for the growing Italian, East European, and black populations in urban areas.

Though urban historians have often been drawn into discussions of how individual-level differences showed up in lower or higher segregation for these Northern European groups, up to now there has only been suggestive evidence on this question. Some aggregate segregation indices showed somewhat similar segregation for immigrants and the second generation, and the most relevant research (for 1910) showed only modest effects of occupation for these groups. Analyses presented here show that in fact processes of spatial assimilation linked with nativity, occupational standing, and marital choice had consistent and strong associations with group isolation and intergroup exposure. Working with cross-sectional data limits our ability to interpret these relationships. The standard interpretation of the greater ethnic isolation of first generation immigrants is that it is due to their limited exposure to American culture, poor English language ability, and reliance on ethnic institutions available in ethnic neighborhoods. It is, however, independent of occupation. The effect of occupational SEI itself may be due to market resources that determine one’s ability to buy into a more affluent neighborhood; we do not know whether it also represents intergenerational mobility or career mobility, because we have no information prior to 1880. The lack of prior year information also limits interpretation of the effects of the greater exposure to native whites of second-generation persons with a native parent and persons with a native spouse. In both cases the associations could reflect greater ethnic assimilation, or it could be that those who lived with a native parent were raised in a less ethnic neighborhood and people who were young adults in a less ethnic neighborhood were more likely to intermarry.

This study breaks new ground in the multilevel study of residential outcomes. Because it draws on non-confidential information about all individuals in the population, it is well positioned for this approach. Not only does this methodology provide solid evidence of individual-level effects, but it also allows examination of differences across cities. The findings in this regard make a strong case that the “context of reception” (a concept originated by Portes and Rumbaut 1996) has important effects over and above a person’s own characteristics. Even a second-generation Irishman is likely to have less residential exposure to native whites and live in a more ethnically isolated neighborhood if he lives in a city where a higher share of Irish is immigrant. Even a German with a lower-status occupation is likely to be more spatially assimilated if she lives in a city where Germans on average have better occupations. And regardless of one’s own occupational standing, an Irish, German or British person is likely to live in a less native white neighborhood in a city where his or her group’s industrial segregation from native whites is higher. With regard to the latter finding, we provide suggestive evidence from one city that the effect of occupational segregation does not result simply from the fact that people in different industries live in different parts of the city. Even Germans and native whites working in the same industry were very highly residentially segregated from one another. Rather, our interpretation is that industrial segregation is an indicator of ethnic boundaries in the local society that are manifested also in residential patterns.

These city effects are not inconsistent with assimilation theory, but they call more attention to the character of intergroup relations in a city. From an assimilation perspective, there is a tendency to see groups as progressing toward greater integration mainly through an accumulation of individual-level advancements. While this study certainly finds evidence of that process, it also suggests that there are macro-level conditions that can independently facilitate or retard mobility. We have incorporated here the indicators of the context of reception that can be readily gleaned from the rich demographic data that we are working with.

This research takes advantage of full access to information about people and where they lived from a historical census. The same procedures can be used with contemporary data in a Census Data Research Center. And for both historical and contemporary studies, the way is open for research that incorporates other non-census measures of city-level or metropolitan-level political, economic, or social relations. Although studies of aggregate segregation measures continue to be a mainstay of urban research, many questions can be more directly addressed in a multilevel framework. A much discussed characteristic of all segregation measures is that one would like to know how much segregation is due to the distinctive income or age or nativity profile of group members, rather than due to residential processes that are better understood as a global attribute of a given locality. Working with publicly available aggregate census data, researchers interested in contemporary situations have sought to decompose segregation into a component that can be attributed to group differences in income (or education, or any other single variable for which the necessary tables are available) and a component that is net of such differences (as in Winsborough 1973). A multilevel model using data on individuals offers a means of handling these questions explicitly, controlling simultaneously for multiple factors, and also examining contextual effects.

This study is consistent with a tradition of thinking of the city or metropolis as the key aggregate unit and asking how people are segregated within this unit by neighborhoods. The city neighborhood is not, of course, the only scale at which people are separated, and it would be valuable to explore other levels of aggregation. Our approach could be usefully extended to studying segregation at other geographic scales, as is possible with some aggregate indices (Wong 2003; Feitosa et al 2007). For example, the entropy index (Theil’s H) has the desirable property that it can be decomposed geographically to determine what share of segregation between two (or more) groups occurs at various scales, such as the census tract, city, and state. Fischer et al (2004) exploited this property to show that the segregation of blacks decreased considerably after 1960 largely because neighborhoods became more integrated, but the foreign born became more segregated largely because they concentrated in particular metropolitan areas. No analysis of aggregate data can accomplish the objective of partialing out processes that occur at the individual level. But identifying the geographic scale of segregation processes using such measures can serve as a guide to estimating more complex multilevel models that take into account areal differentiation within cities that occurs at a larger scale than the local neighborhood (such as inner core and newer periphery) or variations between states or geographic regions.

Figure 1.

Residential location of Germans and native whites employed in the same manufacturing industry in Buffalo, NY, in 1880. The left panel is for a German-dominated sector: sawmills, wood products, and furniture and fixtures. The right panel is for a sector in which Germans were slightly-under-represented: paper, printing and publishing.