The Influence of Annuloplasty Ring Geometry on Mitral Leaflet Curvature

Abstract

Background

The effect of mitral leaflet curvature on stress reduction is an important mechanism in optimizing valve function. We hypothesize that annuloplasty ring shape could directly influence leaflet curvature and, potentially, repair durability. We describe an echocardiographically based methodology for quantifying mitral valve geometry and its application to the characterization of ovine mitral valve geometry before and after implantation of an annuloplasty ring.

Methods

Multiple mitral annular and leaflet geometric variables were calculated for 8 naïve adult male sheep using real-time three-dimensional echocardiographic images. These indexes were recalculated after annuloplasty using a 30-mm Carpentier-Edward Physio ring (n = 4; Edwards Lifesciences, Irvine, CA) or a 30-mm saddle ring (n = 4).

Results

After implantation of the Physio ring, the annular height to commissural width ratio (AHCWR) decreased from 19.4% ± 2.3% to 11.1% ± 2.5% (p = 0.06). After implantation of the saddle ring, AHCWR increased from 19.6% ± 1.3% to 24.3% ± 1.3% (p < 0.05). Statistically significant increases in three-dimensional Gaussian curvature occurred after implantation within six defined leaflet regions (A1 to A3, P1 to P3) of the saddle ring but only within the P1 and P3 leaflet regions with the Physio ring.

Conclusions

Annuloplasty ring shape affects leaflet curvature. Implantation of a saddle ring reflecting normal human annular geometry augmented ovine annular non-planarity and increased three-dimensional leaflet curvature across the entire mitral valve surface. The Physio ring decreased annular nonplanarity and increased leaflet curvature only across limited regions of the posterior leaflet. These findings confirm the hypothesis that ring design influences leaflet curvature.

During the past three decades, mitral annuloplasty has become an important component of most mitral valve repair techniques [1]. As collective experience has increased, many surgeons have come to view mitral valve repair as the treatment of choice in patients with severe mitral regurgitation (MR). However, longer-term follow-up has revealed that between 10% and 16% of patients undergoing mitral repair for myxomatous disease will require reoperation for severe MR within 10 years [2–5]. Even more concerning are the recent reports of an unexpectedly high incidence of recurrent moderate MR after mitral valve repair. Four recent studies from experienced centers indicate that the recurrence of 2+ or greater MR is between 2% and 4% per year [6–9]. Considering that patients with even mild residual or recurrent MR after valve repair have decreased exercise tolerance and longevity compared with patients with competent repairs [10], a need exists to develop improved repair techniques. This is particularly true because more asymptomatic patients are being referred for valve repair [11–13].

A significant number of repair failures result from chordal, leaflet, and suture line disruption, which suggest that mechanical leaflet stress plays a significant role [14]. Leaflet curvature is an important determinant of valve stress [15]. As such, repair devices and techniques that optimize leaflet curvature will reduce valvular stress and may increase repair durability.

In a previous work, we presented a finite element model describing the synergistic contributions of annular nonplanarity [16, 17] and leaflet billowing to leaflet curvature and the relative effect of each on leaflet stress [18]. These results led us to hypothesize that annuloplasty ring shape could directly affect leaflet curvature and potentially repair durability.

To evaluate this hypothesis, we describe a novel method using real-time three-dimensional (rt-3D) echocardiography for quantifying mitral valve geometry and apply this technique to the characterization of ovine mitral valve geometry before and after implantation of either the Carpentier-Edwards Physio ring (Edwards Lifesciences, Irvine, CA) or a custom-built rigid saddle annuloplasty ring that conforms to normal human annular geometry.

Material and Methods

Saddle Annuloplasty Ring Specifications

During the past 15 years, we have worked to quantitatively describe the saddle shape of the mitral annulus using sonomicrometry, 3D echocardiography, computed tomography (CT) imaging, and magnetic resonance imaging (MRI) [unpublished data] in humans and several mammalian species [17, 18]. From this imaging data we developed the following parametric expression, which can be used to describe a range of mitral annuloplasty ring geometries:

$$X=\mathit{aCos}(\theta )$$ (1)

$$Y=b(\theta )\mathit{Sin}(\theta )$$ (2)

$$Z=\left(\frac{h}{2}\right)\mathit{Cos}(2\theta )$$ (3)

Where θ varies from 0 to 2π, a is a nominal scaling constant (2a is defined as the intercommissural width), b(θ) is an empiric function derived from our imaging data, and h is the vertical height of the annulus where the annular height to commisural width ratio (AHCWR) = h/2a.

For the ring used in this study, b(θ) and AHCWR were defined by normal human data obtained using rt-3D echocardiography. The parameter a was chosen to make the ring similar in area to a 30-mm Carpentier-Edwards Physio ring. Using these specifications, prototype rings were generously created by Medtronic (Medtronic Inc, Minneapolis, MN).

Surgical Protocol

The animals used in this study were cared for in compliance with Guide for the Care and Use of Laboratory Animals (National Institutes of Health Publication No. 85-23, revised 1996). The 8 adult male sheep were pretreated with buprenorphine (2 μg/kg) and then induced with intravenous (IV) sodium thiopental (10 to 15 mg/kg), intubated, and anesthetized with isoflurane (1.5% to 2.0%) and oxygen. All animals received glycopyrrolate (0.02 mg/kg IV) and cefazolin (1.0 g IV). After left thoracotomy and pericardiotomy, epicardial echocardiography was performed in all sheep.

The 8 animals were randomized to undergo placement of a 30-mm Physio ring (n = 4) or a 30-mm saddle ring (n = 4). Annuloplasty was performed on cardiopulmonary bypass (CPB) through a left atriotomy using standard techniques. After separation from CPB, epicardial echocardiography was repeated.

Image Acquisition

An epicardial rt-3D echocardiogram was performed at baseline and was then repeated 1 hour post-CPB separation after annuloplasty. In each case, electrocardiogram-gated, full-volume data sets were acquired by a single operator using a Sonos 7500 (Philips Medical Systems, Andover, MA) platform equipped with a 2- to 4-MHz X4 handheld transducer. Each full-volume data set was exported to a dedicated Cardio-View (Tomtec Imaging Systems, Munich, Germany) software workstation for image manipulation and analysis.

Image Analysis

Image analysis was performed in Cardio-View by visual inspection. Cardio-View allows the interactive manipulation—including rotation, translation, surface rendering, and measurement—of fully 3D ultrasound data sets. All analysis was performed at end-systole, which was defined as the first frame demonstrating closure of the aortic valve. In Cardio-View, the plane of the mitral valve orifice was rotated into a short-axis view. The geometric center of the mitral valve was then translated to the intersection of the two corresponding long-axis planes, which then corresponded to the intercommissural and septolateral axes of the mitral valve orifice. A rotational template consisting of 18 long-axis cross-sectional planes separated by 10° increments was superimposed on the 3D echocardiogram. The two annular points intersecting each of the 18 long-axis rotational planes were identified by orthogonal visualization of each plane; the two points were marked interactively in Cardio-View (Fig 1A and B).

Fig. 1.

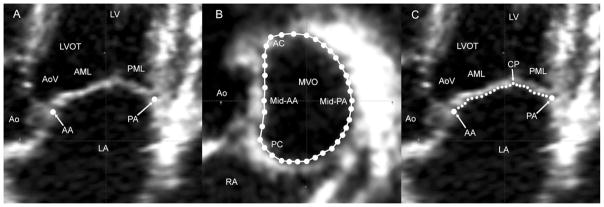
(A) A single long-axis view of the heart shows labeling for the left ventricle (LV), left ventricular outflow tract (LVOT), anterior (AML) and posterior (PML) mitral leaflets, left atrium (LA), aortic valve (AoV) and the aorta (Ao). Anterior (AA) and posterior (PA) annular points have been marked. Note that in this orientation, the negative z-axis (for purposes or annular height calculations) extends towards the apex, and the positive z-axis extends towards the left atrium. (B) All mitral annular data points are shown. The anterior commissure (AC), posterior commissure (PC), aorta (Ao), and right atrium (RA) are labeled in this view. (MVO = mitral valve orifice.) (C) As illustrated in this view, in each of the septolateral measurement planes, between 5 and 40 individual points (depending on the septolateral diameter of the MV at the position of a given measurement plane) on the atrial surface of the MV are manually marked. The position of each point is recorded as anterior mitral leaflet (AML), coaptation point (CP), or posterior mitral leaflet (PML).

Measurement planes were then marked at fixed 1-mm intervals along the entire length of the intercommissural axis, from the anterior commissure to the posterior commissure.

Continuous free-hand curves, each consisting of between 5 and 40 data points, connecting the juxtaposed anterior and posterior annulus across the surfaces of the anterior and posterior leaflet, were constructed in each long-axis cross section (Fig 1C), resulting in a 600- to 1200-point data set for each mitral valve (Fig 2). Each data point fit within a given measurement plane was then assigned to the anterior mitral leaflet (AML), the posterior mitral leaflet (PML), or the coaptation point (CP).

Fig. 2.

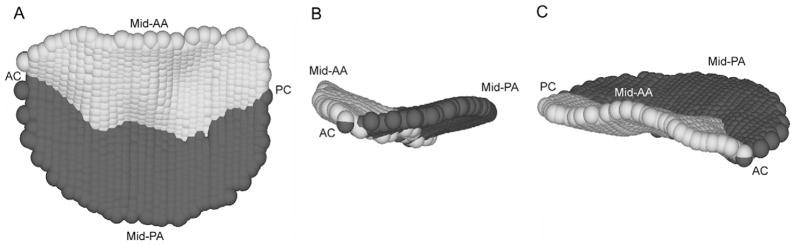
A typical 1200-point three-dimensional data set for a normal ovine mitral valve is shown in three views: (A) transvalvular, (B) intercommissural, (C) and oblique. Data points on the anterior leaflet are shaded light grey, and those on the posterior leaflet are shaded dark gray. The midanterior annulus (mid-AA), midposterior annulus (mid-PA), anterior commissure (AC), and posterior commissure (PC, if visible) are indicated for purposes of orientation.

Calculation of Annular Geometry

Geometric modeling and analysis of each data set, consisting of 36 annular points, was performed using a series of Matlab (The Mathworks Inc, Natick, MA) algorithms. The center of gravity of the data set was translated to the origin. The least squares plane of the 3D data set was then calculated by means of orthogonal distance regression and the annular model rotated such that this MV orifice plane was aligned with the x-y plane. The data set was then rotated around the z-axis such that the x-axis bisected the midanterior and midposterior annulus. Under these geometric conditions, the z-coordinate (z_n) of each annular point was therefore equal to its distance to the best-fit plane of the MV. The annular height of a given data set was defined as z_max – z_min. The septolateral diameter (SL) for a given data set was defined as the distance, in 3D space, separating the two data points located along the x-axis. The intercommissural width (CW) for a given data set was defined as the distance, in 3D space, separating the two data points with the lowest values of z_n. The annular height to commissural width ratio (AHCWR) for a given annular data set was defined as [(CW/AH) × 100%. T]. Mitral annular area (MAA) was defined as the area enclosed by the 2D projection of a given annular data set onto its corresponding least squares plane.

Calculation of Leaflet Surface Area and Curvature

Subsequently, each point along the anterior mitral annulus (as determined by visual inspection) was merged with the anterior mitral leaflet data set for a given subject, and each point along the posterior mitral annulus was merged with the corresponding posterior mitral leaflet data set. All coaptation points were subsequently added to both data sets. Separate meshed grids with boundary conditions determined by the given data set extremes were then created for the anterior leaflet and posterior leaflet data sets.

Smoothing splines were constructed separately for anterior and posterior leaflet data sets using the Matlab TPAPS function. The smoothing parameter (P), which varies between 0 for a least squares approximation and 1 for a thin-plate spline interpolant, was assigned automatically for each data set using the Matlab default. The z-coordinates of the spline surface at each point of the rectangular mesh grid were calculated separately over each leaflet. An iterative Delaunay triangulation was used to exclude mesh points that fell outside of the borders described by annular data points.

The area of each triangle described by three adjacent mesh points was then calculated continuously across both anterior and posterior leaflets. The anterior leaflet surface area (SA_AL) was then defined the as the sum of triangular areas across the anterior leaflet. The posterior leaflet surface area (SA_PL) was calculated analogously. The total mitral valve surface area (SA_Total) was then defined as the sum of SA_AL and SA_PL. The ratio of total leaflet surface area to annular area, which reflects relative leaflet redundancy, was subsequently defined as SA_Total:MAA.

The coapting regions of the leaflets are not measured using this technique. As a result, SA_AL, SA_PL, and SA_Total are underestimates and represent the leaflet area of the closed valve as viewed from the left atrium.

The 3D leaflet Gaussian curvature (K)

$$K_{\mathit{XYZ}}=\frac{det(x_{uu}{x}_u{x}_v)det(x_{vv}{x}_u{x}_v)-{[det(x_{uv}{x}_u{x}_v)]}^2}{{[{\left|x_u\right|}^2{\left|x_v\right|}^2-{(x_u{x}_v)}^2]}^2}$$

of the spline fits was then calculated for every mesh point on both grids.

Septolateral and intercommissural 2D leaflet curvatures (K_SL, K_IC) were then calculated as follows. Let a, b, and c be the distances between each of three sequential mesh points along either the x (septolateral) or y (intercommissural) axis. Then the 2D curvature along the selected axis at a given mesh point is defined as:

$$K_{SL}or{K}_{IC}=\frac{\sqrt{(a+b+c)·(b+c-a)·(c+a-b)·(a+b-c)}}{a·b·c}$$

Both K_SL and K_IC were calculated for every mesh point on both anterior and posterior leaflet grids.

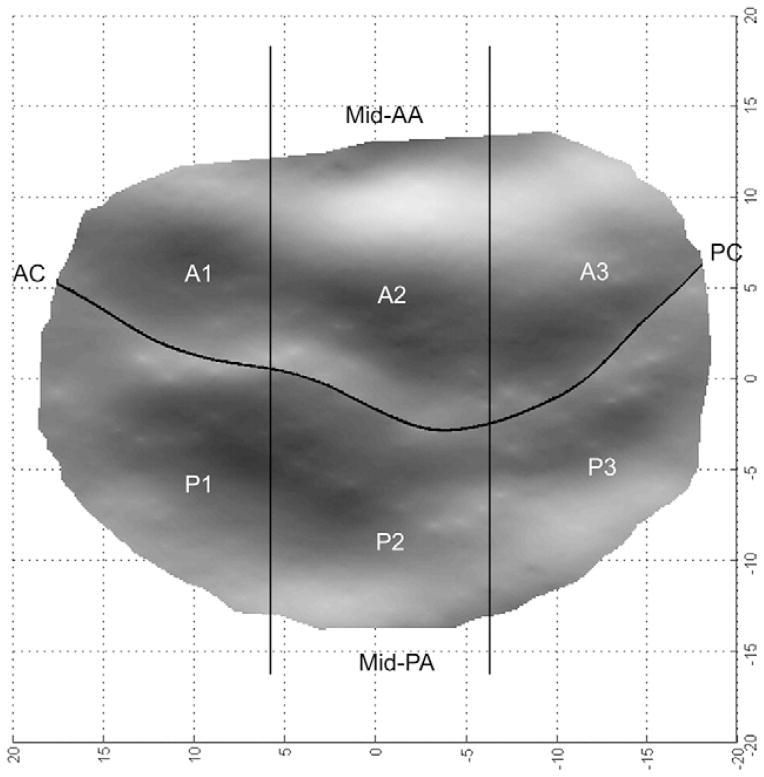
For purposes of subsequent data analyses, the intercommissural axis of each mitral valve data set was then subdivided into equal thirds. Each mesh point in a given data set was subsequently assigned to one of six leaflet zones—A1, A2, A3, P1, P2, P3—as illustrated in Figure 3. Values of K_XYZ, K_SL and K_IC were subsequently grouped on the basis of their assigned position on the mitral valve. In order to negate the influence of curvature directionality, the absolute values of K_XYZ, K_SL and K_IC were used for the calculation of regional mean values.

Fig. 3.

A transvalvular view shows a single subject three-dimensional rendering. The geometric relationships between anterior and posterior leaflet zones (A1 to A3 and P1 to P3) are illustrated. The midanterior annulus (mid-AA), midposterior annulus (mid-PA), anterior commissure (AC) and posterior commissure (PC) are indicated for purposes of orientation.

Construction of Hybrid 3D Renderings

To facilitate the presentation of quantitative geometric data, a 3D hybrid rendering was constructed for all subjects at baseline and then separately for each of the cohorts after annuloplasty.

The hybrid anterior and posterior leaflets were modelled independently. The individual geometric centers of each anterior and posterior leaflet mesh within a given cohort were translated to their averaged geometric centers, scaled to their averaged area in 2D (xy) space, and then overlapped. Those areas of the overlapped individual leaflet meshes in which all data sets—or all data sets except one—coincided were included in the hybrid mesh. All other points were excluded. The z-coordinate at each point along the hybrid anterior and posterior leaflet meshes was determined by the arithmetic mean of the compiled z-coordinates of the individual overlapped models. Finally, the point in 2D (xz) space at which anterior and posterior leaflet meshes intersected was defined for each mesh interval along the intercommissural (y) axis. The resultant series of coaptation points was then defined as the line of leaflet coaptation for the 3D rendering.

Visualization and Statistics

Three distinct shading techniques, in which interpolated color contouring was determined by K_XYZ, K_SL, and K_IC at a given mesh point, were then applied to each hybrid rendering to facilitate visualization of each of these geometric indexes in 3D space. All graphics were produced using Matlab.

Comparisons between values at baseline and after annuloplasty were made using the Student paired t test. All statistical analysis was performed using SPSS software (SPSS Inc, Chicago, IL). The level of significance selected for all variables was p < 0.05. Numerical results are presented as mean ± standard error of the mean (SEM).

Results

Hemodynamics

To ensure that mitral leaflet loading conditions, which influence both annular and leaflet geometry [19, 20], were similar at both data acquisition time points, statistical comparisons were performed for all hemodynamic parameters at each data acquisition point. These comparisons are summarized in Table 1. Although the observed changes in heart rate and diastolic pulmonary arterial pressure after annuloplasty in the saddle ring cohort did reach significance, the absolute changes were relatively small in both cases. Furthermore, neither of these variables would be expected to influence valvular geometry. There were no additional statistically significant differences between time points; therefore, leaflet-loading conditions were similar at both data acquisition points for both animal cohorts. None of the animals had significant MR either at baseline or after annuloplasty.

Table 1.

Hemodynamic Data^a

Variable	Baseline	After Annuloplasty
30-mm CE Physio
Heart rate, beats/min	115 ± 10	124 ± 21
ABP, mm Hg
Systolic	127 ± 11	122 ± 15
Diastolic	98 ± 8	88 ± 16
PAP, mm Hg
Systolic	18 ± 2	24 ± 1
Diastolic	13 ± 2	15 ± 1
PCWP, mm Hg	10 ± 2	12 ± 1
CVP, mm Hg	6 ± 1	9 ± 2
Cardiac output, L/min	3.9 ± 0.3	3.7 ± 0.4
30-mm saddle
Heart rate, beats/min	112 ± 8	95 ± 11b
ABP, mm Hg
Systolic	113 ± 7	119 ± 11
Diastolic	83 ± 9	83 ± 11
PAP, mm Hg
Systolic	17 ± 1	26 ± 2
Diastolic	11 ± 1	17 ± 1a
PCWP, mm Hg	9 ± 1	15 ± 2
CVP, mm Hg	6 ± 2	9 ± 1
Cardiac output, L/min	5.6 ± 0.4	4.6 ± 0.6

^aHemodynamic variables, as measured at the time of echocardiographic data acquisition are summarized, are presented as mean ± standard error of the mean.

^bp < 0.05 compared with baseline value.

ABP = arterial blood pressure; CVP = central venous pressure; PAP = pulmonary arterial pressure; PCWP = pulmonary capillary wedge pressure.

Mitral Annular Geometry

Annular geometric measurements are presented for both animal cohorts in Table 2. After implantation of the Physio ring, AH decreased by 49.0%, from 6.0 ± 0.6 to 3.1 ± 0.6 mm (p < 0.05), and CW decreased by 15.8%, from 32.8 ± 1.2 to 27.6 ± 1.5 mm (p < 0.05), thus producing a 43.0% decrease in AHCWR from 19.4% ± 2.3% to 11.1% ± 2.5% (p = 0.06). SL decreased by 24.2%, from 26.3 ± 2.2 to 19.9 ± 1.0 mm (p < 0.05), and MAA decreased by 38.3%, from 869 ± 37 to 537 ± 26 mm² (p < 0.05). After implantation of the saddle ring, AH increased by 18.9%, from 5.7 ± 0.3 to 6.8 ± 0.3 mm (p = 0.08), and CW decreased by 4.4%, from 29.5 ± 1.8 to 28.2 ± 1.2 mm (p = 0.14), thus producing a 23.8% increase in AHCWR from 19.6% ± 1.3% to 24.3% ± 1.3% (p < 0.05). SL decreased by 24.5%, from 24.8 ± 1.6 to 18.7 ± 1.1 mm (p < 0.05), and MAA decreased by 42.2%, from 841 ± 46 to 486 ± 31 mm² (p < 0.05).

Table 2.

Mitral Annular Geometry^a

Variable	Baseline	After Annuloplasty	% Change
30-mm CE Physio
AH, mm	6.0 ± 0.6	3.1 ± 0.6b	−49.0
CW, mm	32.8 ± 1.2	27.6 ± 1.5b	−15.8
SL, mm	26.3 ± 2.2	19.9 ± 1.0b	−24.2
AHCWR, %	19.4 ± 2.3	11.1 ± 2.5	−43.0
MAA, mm2	869 ± 37	537 ± 26b	−38.3
30-mm saddle
AH, mm	5.7 ± 0.3	6.8 ± 0.3	18.9
CW, mm	29.5 ± 1.8	28.2 ± 1.2	−4.4
SL, mm	24.8 ± 1.6	18.7 ± 1.1b	−24.5
AHCWR, %	19.6 ± 1.3	24.3 ± 1.3b	23.8
MAA, mm2	841 ± 46	486 ± 30.9b	−42.2

^aAnnular geometric parameters are summarized. Data are presented as mean ± standard error of the mean for the cohort.

^bp < 0.05 compared with baseline value.

AH = annular height; AHCWR = global annular height to commissural width ratio; CW = intercommissural width; MAA = mitral annular area; SL = septolateral diameter.

Mitral Leaflet Surface Area

Leaflet surface areas are presented for both animal cohorts in Table 3. Implantation of both types of rings reduced total leaflet surface area. The saddle ring decreased SA_Total by 35.7%, from 930 ± 50 to 598 ± 44 mm² (p < 0.05), and the Physio ring decreased it by 33.5%, from 966 ± 33 to 643 ± 44 mm² (p < 0.05). Most of this reduction occurred in the posterior leaflet in both ring cohorts. The saddle ring reduced SA_PL by 50.3%, from 433 ± 90 to 215 ± 19 mm² (p < 0.05), and the Physio ring decreased it by 47.6%, from 481 ± 18 to 252 ± 36 mm² (p < 0.05). Both rings diminished SA_AL, but the changes did not reach significance in either group (Table 3).

Table 3.

Mitral Leaflet Surface Area^a

Surface Area	Baseline	After Annuloplasty	% Change
30-mm CE Physio
SAAL, mm2	484 ± 38	390 ± 38	−19.5
SAPL, mm2	481 ± 18	252 ± 36b	−47.6
SATotal, mm2	966 ± 33	643 ± 44b	−33.5
SATotal:MAA	1.11 ± 0.03	1.19 ± 0.04	7.2
30-mm saddle
SAAL, mm2	497 ± 41	382 ± 26	−22.9
SAPL, mm2	433 ± 90	215 ± 19b	−50.3
SATotal, mm2	930 ± 50	598 ± 44b	−35.7
SATotal:MAA	1.11 ± 0.01	1.23 ± 0.04b	11.1

^aMitral leaflet surface areas are summarized. Data are presented as mean ± standard error of the mean for the cohort.

^bp < 0.05 compared to baseline value.

SA_AL/PL/Total = anterior/posterior/total leaflet surface area; SA_Total:MAA = leaflet surface area to mitral annular area ratio.

The saddle ring increased the SA_Total:MAA ratio by 11.1%, from 1.11 ± 0.01 to 1.23 ± 0.04 (p < 0.05), and the Physio ring increased this ratio by 7.2%, from 1.11 ± 0.03 to 1.19 ± 0.04 (p = 0.90).

Mitral Leaflet Geometry

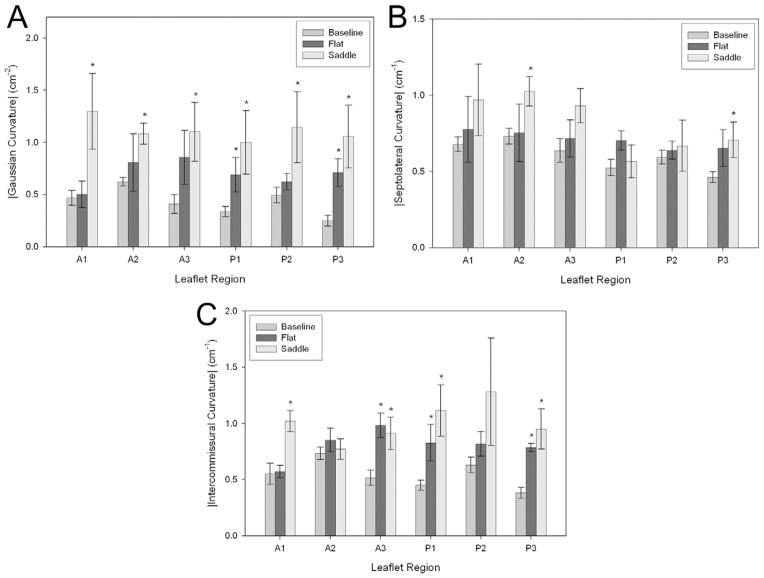
Regional mean values ± SEM are presented for |K|, |K_SL| and |K_IC| in Figure 4 for both animal cohorts. Baseline values were derived collectively from all 8 animals. However, the statistical significance of changes in regional curvature was determined with respect to the baseline values for the 4 animals comprising each cohort (using the paired Student t test).

Fig. 4.

(A) Values of the three-dimensional leaflet Gaussian curvature, (B) intercommissural, and (C) and septolateral two-dimensional leaflet curvatures are presented by leaflet region (A1 to A3; P1 to P3) at baseline (medium grey bars) and after implantation of a flat 30-mm Physio ring (black bar) or a 30-mm saddle ring (light gray bar) on a common axis. To clarify the graphic representation of the results, data are presented here as mean ± standard error of the mean for the cohort. (*p < 0.05 compared with baseline value.)

After implantation of the Physio ring, statistically significant increases in |K_IC| were observed in the A3, P1 and P3 leaflet regions, whereas the observed changes in |K_SL| did not reach statistical significance for any leaflet region. Statistically significant increases in |K| occurred in both the P1 and P3 leaflet regions.

After implantation of the saddle ring, statistically significant increases in |K_IC| were observed in the A1, A3, P1 and P3 leaflet regions, whereas statistically significant increases in |K_SL| occurred in both the A2 and P3 leaflet regions. Statistically significant increases in |K| occurred in all six of the defined leaflet regions.

Figure 5 illustrates the changes in global valvular geometry as well as the changes in both the magnitude and spatial distribution of 3D Gaussian curvature that accompanied placement of both the saddle ring (Fig 5B) and the Physio ring (Fig 5C) when compared with baseline (Fig 5A). A marked reduction in mitral annular area is apparent in both cases, but the observed patterns of geometric change are otherwise dissimilar.

Fig. 5.

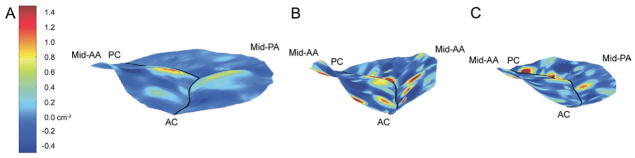
Hybrid three-dimensional renderings of all sheep at (A) baseline and (B) after implantation of the (B) saddle ring or the (C) Physio ring. In all cases color contouring is determined by three-dimensional leaflet Gaussian curvature (K), with K_min equal to −0.5 cm⁻² and K_max equal to 1.5 cm⁻² as illustrated in panel A. Negative K indicates saddle-shaped– or hyperbolic–local surface curvature. Positive K indicates elliptic local surface curvature– but may be concave towards the left ventricle or the left atrium. The midanterior annulus (mid-AA), midposterior annulus (mid-PA), anterior commissure (AC), and posterior commissure (PC) have been labeled in each view.

Augmentation of annular nonplanarity is evident after implantation of the saddle ring, whereas annular flattening is apparent after implantation of the CE ring. Increased magnitude of Gaussian curvature within the hyperbolic (K ≪ 0) and elliptical (K ≫ 0) surfaces in the A2 region is evident after implantation of the saddle ring. Likewise, there is increased magnitude of negative Gaussian curvature in regions A1 and A3 adjacent to the anterior annulus near the anterior and posterior commissures. In contrast, Gaussian curvature is markedly diminished at each of these sites after implantation of the Physio ring. Increased magnitude of posterior leaflet Gaussian curvature—with preservation of the pattern of alternating elliptic (positive K) and hyperbolic (negative K) curvature present at baseline—is apparent after implantation of both ring types, although the magnitude of this increase is greater in the case of the saddle ring.

Figures 6 and 7 illustrate the relationship between 3D valvular geometry and orthogonal 2D curvature (K_SL and K_IC). Note that in both cases, positive curvature indicates atrially oriented surface concavity, whereas negative curvature indicates apically oriented surface concavity.

Fig. 6.

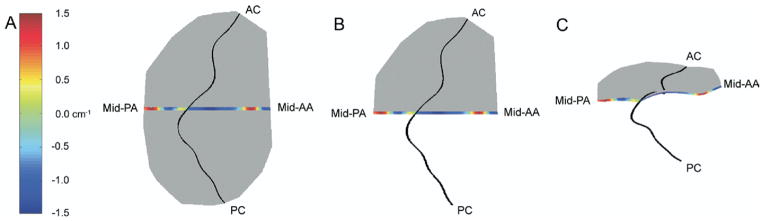
Multiple hybrid three-dimensional renderings of the 8-animal cohort at baseline. In each case, color contouring, which is determined by septolateral two-dimensional leaflet curvatures, has been superimposed across a 1.0-mm wide-septolaterally oriented segment of the mitral valve (anterior and posterior leaflets). (A) This is a transvalvular (xy) view of the rendering. (B) The same view is illustrated where the medial hemi-valve is transparent. (C) This is an oblique view of the rendering where the medial hemi-valve is transparent; in this case, the relationship between curvature sign and surface concavity/convexity is readily apparent. The midanterior annulus (mid-AA), midposterior annulus (mid-PA), anterior commissure (AC), and posterior commissure (PC) have been labeled in each view.

Fig. 7.

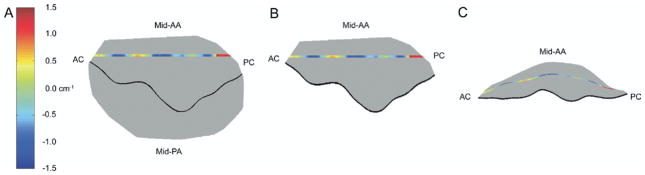
Multiple hybrid three-dimensional renderings of the 8-animal cohort at baseline. In each case, color contouring, which is determined by intercommissural two-dimensional leaflet curvatures, has been superimposed across a 1.0-mm-wide, intercommissurally oriented segment of the anterior leaflet. (A) This is a transvalvular (xy) view of the rendering. (B) The same view is illustrated where the posterior leaflet is transparent. (C) This panel illustrates an oblique view of the isolated anterior leaflet; in this case, the relationship between the curvature sign and surface concavity/convexity is readily apparent. The midanterior annulus (mid-AA), midposterior annulus (mid-PA) anterior commissure (AC), and posterior commissure (PC) have been labeled as appropriate.

Figure 8 illustrates the changes in 2D septolateral curvature that accompanied implantation of both ring types. A marked increase in the magnitude of anterior leaflet curvature is apparent after implantation of the saddle ring. Although increased positive septolateral curvature within the anterior leaflet belly is apparent after implantation of the Physio ring, the negative septolateral curvature adjacent to the anterior annulus and to the coaptation line has decreased in magnitude, indicating disruption of normal compound anterior leaflet curvature. Increased posterior leaflet septolateral curvature—with preservation of the complex geometric pattern present at baseline—is apparent after implantation of both ring types, although the magnitude of this increase is greater in the case of the Physio ring.

Fig. 8.

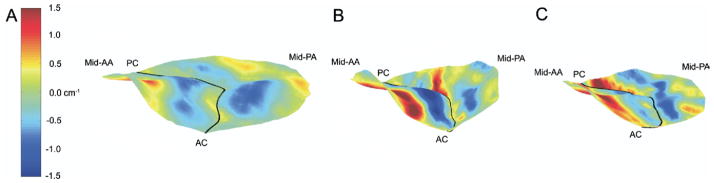
Hybrid three-dimensional renderings of all subjects at (A) baseline and after implantation of either the (B) saddle ring or the (C) Physio ring. In all cases color contouring is determined by septolateral two-dimensional leaflet curvatures (K_SL), with K_SLmin equal to −1.5 cm⁻¹ and K_SLmax equal to 1.5 cm⁻¹ as illustrated in panel A. Negative K represents local surface curvature concave towards the left ventricle; positive K represents local surface curvature concave towards the left atrium. The midanterior annulus (mid-AA), midposterior annulus (mid-PA), anterior commissure (AC), and posterior commissure (PC) have been labeled in each view.

Figure 9 illustrates the changes in 2D intercommissural curvature that accompanied implantation of both ring types. Marked increase in the magnitude of anterior leaflet curvature is apparent after implantation of the saddle ring. This increase is particularly prominent adjacent to the commissures. The negative intercommissural curvature within the A2 leaflet belly is preserved after implantation of the Physio ring, but the negative intercommissural curvature adjacent to the midanterior annulus has been substantially reduced in magnitude. The positive intercommissural curvature adjacent to the commissures is preserved after implantation of the Physio ring, but not increased in magnitude, as in the case of the saddle ring. The posterior leaflet intercommissural curvature—characterized by a complex geometric pattern at baseline—is increased in magnitude after implantation of both ring types, but this increase is greater in the case of the saddle-shaped ring.

Fig. 9.

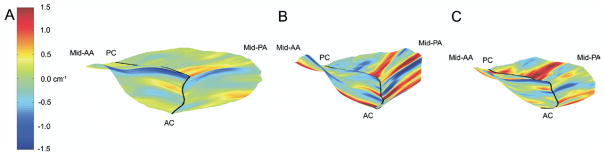
Hybrid three-dimensional renderings of all subjects at (A) baseline and after implantation of either the (B) saddle ring or the (C) Physio ring. In all cases color contouring is determined by intercommissural two-dimensional leaflet curvatures (K_IC), with K_ICmin equal to −1.5 cm⁻¹ and K_ICmax equal to 1.5 cm⁻¹ as illustrated in panel A. Negative K represents local surface curvature concave towards the left ventricle; positive K represents local surface curvature concave towards the left atrium. The midanterior annulus (mid-AA), midposterior annulus (mid-PA), anterior commissure (AC), and posterior commissure (PC) have been labeled in each view.

Comment

The growing appreciation that mitral valve repair is not as durable as once thought [2–9], combined with the fact that many repair failures are stress related, has stimulated an interest in the development of repair techniques and devices that diminish valve stress. Because of the well-described relationship between leaflet curvature and valve stress [15], our work in particular has centered on methods for maintaining more normal leaflet geometry during repair procedures.

Levine and colleagues [16, 21] first described the non-planar saddle shape of the mitral annulus nearly two decades ago. Subsequently, our group used a combination of sonomicrometry and early stage rotational 3D echocardiography to quantify the maximal nonplanarity of the mitral annulus by describing the AHCWR [17, 18].

Using a quantitative knowledge of annular geometry, numeric simulation, and simplified leaflet models, we have previously demonstrated that alterations in annular saddle shape are capable of affecting both leaflet geometry and stress distribution. In that theoretic analysis, we also demonstrated that leaflet stress reaches a minimum at AHCWR values between 15% and 30% (normal anatomic range) and increases exponentially as ACHWR approaches zero or as the annulus approaches planarity. This work has led us to the general hypothesis that annuloplasty ring shape may influence leaflet curvature and, more specifically, to postulate that a saddle ring designed to approximate normal annular shape may maintain leaflet curvature whereas standard flat rings would diminish it. Although theoretic work supports these hypotheses, experimental conformation has been absent due to a relative inability to describe mitral valve geometry precisely and in reproducible terms.

To provide such experimental confirmation, we have developed an imaging methodology utilizing rt-3D echocardiography in conjunction with commercially available image-processing software and a series of custom mathematic algorithms to examine the impact of annuloplasty ring shape on leaflet geometry. Geometric modeling and graphic rendering techniques have been used to characterize the direction, orientation, and magnitude of both 2D and 3D curvature across the entire ovine mitral valve.

We have previously derived a series of parametric equations based on imaging data obtained using both sonomicrometry and rt-3D echocardiography [17, 18, 22] that can be used to describe the 3D shape of the normal mitral annulus where the only independent variable is intercommissural width. The geometry of the saddle ring used in the current study was derived from these equations.

The current study used these tools to corroborate several previous studies and demonstrates the effect of annuloplasty ring shape on the entire mitral valve, including all surfaces of the mitral leaflets.

Miller and colleagues [23, 24] have previously described substantial reduction in both annular height and AHCWR after implantation of a Physio ring in naïve sheep. The current study confirms their findings. Implantation of a 30-mm Physio ring into naïve sheep decreased AH by 49.0% and reduced CW by 15.8%, thus effecting a 43.0% decrease in AHCWR. Conversely, implantation of a 30- mm saddle ring into naïve sheep increased AH by 18.9% and reduced CW by 4.4, thus effecting a 23.8% increase in AHCWR. Both ring types reduced SL and MAA by similar degrees.

It is interesting to note that the saddle ring augmented normal ovine mitral annular nonplanarity at end systole. This is because the saddle ring geometry was derived from measurements of the normal human mitral annulus, which is markedly more nonplanar than its ovine counterpart [18]. Although the effect of ring geometry on annular and mitral leaflet geometry was not studied in pathologic states in the current study, this finding supports the conclusion that a saddle shaped ring will not only maintain normal annular geometry but may also be efficacious in restoring annular geometry when used in the context of ischemic mitral regurgitation, a disease process known to flatten the mitral annular shape [25–27]. In fact, the AHCWR of 24.3% observed after implantation of the saddle ring was nearly identical to that of the ring itself (25%). The relative geometries of the Physio and saddle rings can be appreciated in Figure 10.

Fig. 10.

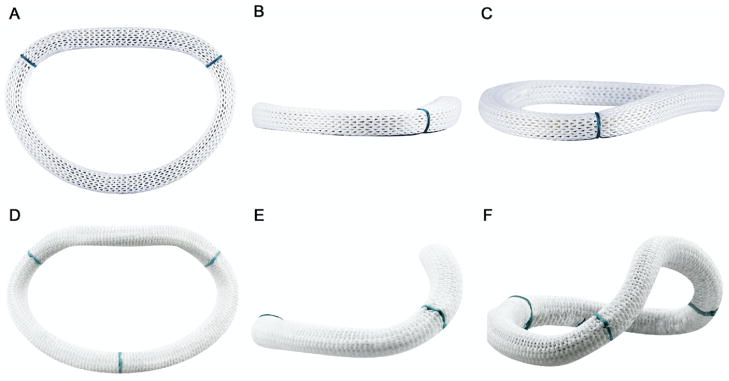
Images of the (A–C) Physio and (D–F) saddle ring as viewed from several orientations are provided. Subtle differences in the shape of the flow orifice (although the mitral annular areas are quite similar) can be appreciated in the short-axis views (A and D), whereas dramatic differences in annular height and nonplanarity are evident in the intercommissural (B and E) and oblique (C and F) views.

Implantation of either ring produced statistically significant decreases in both SA_PL and SA_Total at end systole. Interestingly, SA_AL was not significantly reduced in either case. Although the SA_Total:MAA did not increase to a statistically significant degree after implantation of the Physio ring, it did increase after implantation of the saddle ring, indicating greater relative leaflet redundancy [28] in the latter case, which would tend to promote leaflet billowing and additional stress reduction.

Multiple previous studies involving invasive imaging techniques have also documented compound curvature along the septolateral meridian of the anterior leaflet as well as hyperbolic surface geometry within the belly of the midanterior (A2) leaflet due to the presence of directionally opposed, orthogonally oriented intercommissural curvature in this region [29–31]. The current results both confirm the presence of compound meridional curvature and indicate that compound septolateral curvature is in fact present along nearly the entire surface of the anterior leaflet.

Our findings indicate that posterior leaflet septolateral curvature is also compound rather than simple and is far more spatially heterogeneous than previously believed [29].

The most compelling finding of this study is that annular geometry influences leaflet curvature to a substantial degree. Implantation of a 30-mm saddle ring in naïve sheep affected increases in both annular nonplanarity and 3D Gaussian curvature in all leaflet zones as well as marked augmentation of both septolateral and intercommissural curvature in multiple leaflet zones. It follows from the law of Laplace that these observed increases in leaflet (membrane) curvature would tend to reduce leaflet stress. Furthermore, the preservation of normal spatial patterns of leaflet curvature (Figs 5, 6, and 7) indicates that optimal valvular loading patterns are maintained in this geometric configuration.

Conversely, implantation of 30-mm Physio ring markedly reduced annular nonplanarity. Although substantial foreshortening of the septolateral axis of the mitral annulus was achieved, no appreciable increase in septolateral curvature occurred in any leaflet zone, although intercommissural curvature and 3D Gaussian curvature increased within multiple leaflet zones. Normal patterns of 2D and 3D curvature were obliterated in several leaflet regions with implantation of the Physio ring (Fig 5, Fig 6, and Fig 7), indicating that optimal valvular loading patterns are disrupted in this configuration.

The current study establishes the relationship between annular nonplanarity and mitral leaflet geometry and also provides a series of quantitative indexes with which to describe this relationship. The imaging and analytic techniques we describe can be used to study and describe detailed geometric features in patients with various valvular and subvalvular pathologies. Furthermore, as this technique is applied to patients with MR, preoperative and postoperative geometric predictors of surgical outcomes may begin to emerge. This work represents an initial foray into the realm of rational mitral prosthesis design. The imaging, visualization, modeling, and simulation techniques described here will in the near future constitute the basis for both cardiac valvular prosthetic design and patient-specific customized valvular repair and prostheses.