Platelet size and density affect shear-induced thrombus formation in tortuous arterioles

Abstract

Thrombosis accounts for 80% of deaths in patients with diabetes mellitus. Diabetic patients demonstrate tortuous microvessels and larger than normal platelets. Large platelets are associated with increased platelet activation and thrombosis, but the physical effects of large platelets in the microscale processes of thrombus formation are not clear. Therefore, the objective of this study was to determine the physical effects of mean platelet volume (MPV), mean platelet density (MPD), and vessel tortuosity on platelet activation and thrombus formation in tortuous arterioles. A computational model of the transport, shear-induced activation, collision, adhesion, and aggregation of individual platelets was used to simulate platelet interactions and thrombus formation in tortuous arterioles. Our results showed that an increase in MPV resulted in a larger number of activated platelets, though MPD and level of tortuosity made little difference on platelet activation. Platelets with normal MPD yielded the lowest amount of mural thrombus. With platelets of normal MPD, the amount of mural thrombus decreased with increasing level of tortuosity but did not have a simple monotonic relationship with MPV. The physical mechanisms associated with MPV, MPD, and arteriole tortuosity play important roles in platelet activation and thrombus formation.

1. Introduction

Patients with diabetes mellitus (DM) demonstrate a much higher incidence of thrombosis. In type2 DM, 80% of deaths result from thrombotic causes [1]. This percentage is much higher than in the general population for which 33% of deaths are due to cardiovascular disease overall [2]. Although platelet count (number of platelets per unit volume) is normal in type 1 and type 2 DM [1, 3, 4], mean platelet volume (MPV) is larger in type 2 DM [5, 6], and mean platelet density (MPD) is lower in poorly-controlled type 1 DM [7]. Higher MPV has also been found in DM patients who experienced microvascular diseases [6] or acute myocardial infarction [3], compared with DM patients who did not. Larger platelets in DM likely produce more thrombotic factors, stimulate thrombopoiesis, are more sensitive to platelet agonists, and are associated with vascular damage [5, 6, 8]. A state of hypercoagulability has also been observed in type 1 and type 2 DM along with altered MPV and MPD [1,4,5]. However, the physical effects of increased MPV and altered MPD remain unclear.

In addition, changes in MPV and MPD are associated with changes in platelet function under physiological conditions. For example, increased MPV has been shown to increase platelet aggregation in platelet rich plasma of normal healthy human subjects [9]. Platelets of low density from healthy human subjects showed increases in reactivity, α-granules, and intracellular P-selectin, and a decrease in dense bodies, compared with higher density platelets from the same subjects [10]. Furthermore, altered MPV and MPD are also observed in various pathologies. Specifically, MPV is elevated in hypertrophic cardiomyopathy [11], acute myocardial infarction [12], restenosis following coronary angioplasty [12], pulmonary hypertension [13], and giant platelet disorders [14]. Additionally, both MPV and MPD are increased in myocardial infarction [15], and MPD is decreased in Wiskott-Aldrich syndrome [16]. Changes in MPV and MPD in these pathological conditions are associated with either thrombotic or bleeding complications. Hence, it is of clinical importance to fully understand the effects of platelet volume and density.

On the other hand, patients with DM often demonstrate microvessel tortuosity [17], as commonly seen in the retinal [18], conjunctival [19, 20], and coronary [21] microcirculations. Microvessel tortuosity has been associated clinically with thrombosis [22, 23]. In vivo experiments and in silico simulations in microvessels have demonstrated that high fluid shear stress due to tortuosity promoted platelet activation and thrombus formation [24, 25]. Therefore, it is of clinical importance to understand the mechanisms of thrombus formation in tortuous microvessels and to determine the possible physical interactions of increased MPV, altered MPD, and microvessel tortuosity during thrombus formation in DM.

In recent years, computational models have been developed as powerful tools to study the process of thrombus formation in blood flow by simulation of large numbers of individual platelets (e.g., see the reviews [26] and [27]). Computational simulations have been performed in straight vessels and channels, with some studies focused on effects of factors such as patient-specific platelet phenotypes, red blood cells, binding proteins, activation delay time, and flow and fluid properties [28–37]. A few other studies have also included geometric features in vessels to investigate the effects of fluid shear stress on thrombus formation in stenoses [38, 39] or on platelet aggregation in channels containing baffles that characterized stenotic or valvular flow [40]. In these studies, platelets became activated during the simulations by chemical agonists due to an injured segment of a vessel wall or due to other activated platelets. On the other hand, platelets are not activated under normal conditions but can be activated by high shear stress. The shear-induced activation of individual platelets in thrombus formation has not been incorporated into these models. Accordingly, the objective of the current work was to determine the physical effects of vessel tortuosity, MPV, and MPD on platelet activation and thrombus formation in tortuous arterioles by computational simulation of the microscale physical processes of platelet interactions.

2. Methods

We numerically simulated the transport, shear-induced activation, collision, adhesion, and aggregation processes of hundreds of individual platelets of different MPV and MPD in tortuous arterioles, using a discrete element computational model and a platelet activation model as described below.

2.1. Computational simulation conditions

Tortuous segments of arterioles of a diameter D = 25 μm were computationally modeled as two-dimensional (2D) channels in the shape of cosine curves with two periods (figure 1). We defined the arteriole tortuosity index T as the ratio of amplitude A to wavelength λ of the cosine curve (T = A/λ). Amplitude and wavelength were varied to obtain arterioles with different tortuosity indices (0 ≤ T≤ 0.21), as listed in Table 1. All arterioles had the same vessel arc length for comparison between different tortuosity indices. Walls near the bends (locations with highest curvature) were designated as either inner or outer walls (figure 1). The selected arteriole diameter falls in the range of diameters of tortuous microvessels observed in the bulbar conjunctiva and retina of DM patients, which were between 25 to more than 80 μm [19, 41]. Most recent studies that quantify arteriole tortuosity in DM utilized automated or semi-automated computer algorithms to calculate tortuosity, for example, as the integral of the squared curvature along the path of the vessel divided by arc length [18, 19, 41]. Although it is possible to calculate the tortuosity of our simulated tortuous arteriole segments in this manner, it is difficult to compare with values of tortuosity calculated in these previous studies. Note that the path along a vessel in these previous studies might have included segments that were straight, in addition to tortuous. Hence, the calculated value of tortuosity of the entire vessel would have been smaller than for the most tortuous segment of the vessel, as was considered in our simulated tortuous arteriole segments. Instead, we estimated tortuosity indices (T = A/λ) of these previous studies to be between 0.06 and 0.36 based on figures of tortuous retinal arterioles [18, 41]. Our selected tortuosity indices fall within this range. We expect tortuous arterioles at other locations within the body may have similar tortuosity indices, and so the current study did not focus on a particular location.

Figure 1.

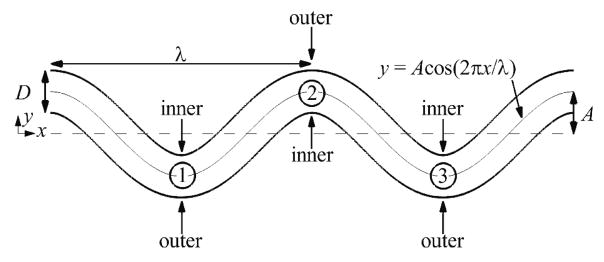
Schematic of a representative arteriole with tortuosity index T = 0.16, showing the locations of inner walls, outer walls, and bends, which are labeled numerically.

Table 1.

Parameters for shapes of arterioles.

Tortuosity Index (T = A/λ)	Normalized Amplitude (A/D)	Normalized Wavelength (λ/2πD)
0.00	0.00	-
0.09	0.64	1.13
0.12	0.81	1.08
0.16	1.00	1.00
0.21	1.20	0.90

Platelets were modeled as three-dimensional (3D) spheres, which is similar to previous computational studies of thrombus formation that utilized spherical or circular platelets [28, 31, 40]. Spheres were utilized in the current work because activated platelets are more spheroidal, even though unactivated platelets are disk shaped [42–44]. As the focus of this study was on thrombus formation by activated platelets that were physiologically spheroidal, we expected the assumption of spherical shape to have a small effect on the results. In a given simulation, all platelets had uniform volume and density equal to the MPV and MPD, respectively. Simulations used the normal MPV and MPD in humans, which are 7.1 fl and 1063 kg m⁻³, respectively [6, 15]. A high MPV (15.8 fl) was also used that is about double the normal MPV as occurs in diabetes mellitus [6]. A low MPV (3.8 fl) was also used that is about half the normal MPV as seen in Wiskott-Aldrich syndrome [16]. MPD was varied from normal as 1009, 1040, 1080, and 1117 kg m⁻³. The lower MPD (1040 kg m⁻³) and higher MPD (1080 kg m⁻³) correspond to the lower and upper values, respectively, of the distribution of platelet density in humans [10]. As well, the higher MPD (1080 kg m⁻³) is relevant to myocardial infarction because this MPD is close to the mean modal platelet density 1071 kg m⁻³ that has been observed in patients after myocardial infarction [15]. The lowest (1009 kg m⁻³) and highest (1117 kg m⁻³) MPDs were set to be about ±5% of the normal MPD to amplify the effect of MPD on thrombus formation. Values of MPV and MPD used in simulations, as well as tortuosity index, are listed in Table 2. Also listed in Table 2 are the types of interactions that platelets were subjected to, which are defined later in this section along with rationales for selection of simulation cases.

Table 2.

Parameter values of tortuosity index, MPV, and MPD, and type of interactions to which platelets were subjected for each case.

Case	T	MPV (fl)	MPD (kg m−3)	Interaction Type
1	0.00	7.1	1063	All interactions
2	0.09	7.1	1063	All interactions
3	0.12	7.1	1063	All interactions
4	0.16	7.1	1063	All interactions
5	0.21	7.1	1063	All interactions
6	0.00	7.1	1063	No interactions
7	0.09	7.1	1063	No interactions
8	0.12	7.1	1063	No interactions
9	0.16	7.1	1063	No interactions
10	0.21	7.1	1063	No interactions
11	0.00	7.1	1063	Collisions only
12	0.09	7.1	1063	Collisions only
13	0.12	7.1	1063	Collisions only
14	0.16	7.1	1063	Collisions only
15	0.21	7.1	1063	Collisions only
16	0.00	3.8	1063	All interactions
17	0.09	3.8	1063	All interactions
18	0.12	3.8	1063	All interactions
19	0.16	3.8	1063	All interactions
20	0.21	3.8	1063	All interactions
21	0.00	15.8	1063	All interactions
22	0.09	15.8	1063	All interactions
23	0.12	15.8	1063	All interactions
24	0.16	15.8	1063	All interactions
25	0.21	15.8	1063	All interactions
26	0.00	3.8	1063	Collisions only
27	0.21	3.8	1063	Collisions only
28	0.00	15.8	1063	Collisions only
29	0.21	15.8	1063	Collisions only
30	0.00	7.1	1009	All interactions
31	0.21	7.1	1009	All interactions
32	0.00	7.1	1040	All interactions
33	0.21	7.1	1040	All interactions
34	0.00	7.1	1080	All interactions
35	0.21	7.1	1080	All interactions
36	0.00	7.1	1117	All interactions
37	0.21	7.1	1117	All interactions
38	0.00	7.1	1009	Collisions only
39	0.21	7.1	1009	Collisions only
40	0.00	7.1	1040	Collisions only
41	0.21	7.1	1040	Collisions only
42	0.00	7.1	1080	Collisions only
43	0.21	7.1	1080	Collisions only
44	0.00	7.1	1117	Collisions only
45	0.21	7.1	1117	Collisions only

Computations were performed for incompressible, steady, fully developed, 2D channel flow in the x-y plane. Steady flow was assumed because flow pulsatility is minimal in the microvasculature. The physiological volume fraction of platelets (ratio of total volume of platelets to lumen volume) was sufficiently low (0.2%) such that the effects of platelets and thrombi on the fluid flow were neglected. Centroids of 3D spherical platelets remained in the x-y plane in the 2D flow. Red blood cells and white blood cells were neglected in simulations. A Poiseuille velocity profile with typical mean arteriole velocity U = 6 ×10⁻³ m s⁻¹ was imposed on the fluid at the inlet of the arteriole. For a straight arteriole, this velocity profile yielded a wall shear rate |γ̇₀| = 1440 s⁻¹ that was in the range of typical values in arterioles [45]. Properties of the Newtonian fluid were chosen to be those of plasma with fluid density ρ_f = 1030 kg m⁻³ and dynamic viscosity μ = 1.2 ×10⁻³ kg m⁻¹ s⁻¹ (1.2 cP). The parameter values utilized gave Reynolds number (Re = ρ_fUD/μ) ~0.1 and particle Stokes numbers (St = ρ_pd²U/18μD) on the order of 10⁻⁵, where ρ_p is density of a platelet, and d is diameter of a platelet.

Unactivated platelets entered the arteriole at the inlet with an initial velocity equal to the local fluid velocity at the location of the platelet centroid. The number of platelets that entered the arteriole per unit time was set such that a physiological time-averaged platelet count (300,000 mm⁻³) would be achieved in the absence of platelet adhesion to the walls. Initial positions of platelet centroids at the inlet followed a pseudorandom probability distribution that excluded the region about one radius from the wall such that platelets entered anywhere along the inlet boundary without touching the wall. The inlet platelet distributions were kept the same in simulations for a given MPV. Although in straight vessels the concentration of platelets is known to be much higher at the walls than in the center of the vessel due to the presence of red blood cells, we expected that use of a pseudorandom distribution of platelets at the inlet might delay the onset of thrombosis and reduce the proportion of activated platelets, but would not change the relative effects of MPV, MPD, and tortuosity. Further discussion of the possible effects of platelet concentrations, as well as red blood cells, is given in the Discussion section. Simulations were deterministic, which was in consensus with previous computational studies that employed a single simulation for each situation of interest (e.g., [28, 31, 33, 36, 39]). Simulations were run to a final time (t_f = 1.7 s) at which the rate of platelet collisions with the walls reached a state of statistical equilibrium. Measurements were made at the final time and at an initial time t_i = 0.4 s, by which time emboli had begun to detach from mural thrombi for each tortuous arteriole with normal MPV and MPD.

For all simulations, platelets were subjected to shear-induced activation. Unless otherwise noted, platelets were subjected to all interactions, namely platelet-platelet collisions, platelet-wall collisions, platelet-platelet aggregation, and platelet-wall adhesion. In some simulations, platelets were not subjected to aggregation or adhesion but were subjected to platelet-platelet and platelet-wall collisions. This case was called “collisions only.” In other simulations, platelets were subjected only to platelet-wall collisions, but not subjected to platelet-platelet collisions, aggregation, or adhesion. This case was called “no interactions” as platelets did not interact with each other or adhere to the wall. These cases were used to determine the individual contributions of specific interactions.

Simulation cases, as listed in Table 2, were selected to determine the effects of specific factors on thrombus formation and platelet activation. To determine the effect of tortuosity, vessel tortuosity was increased from straight to tortuous in Cases 1–5, which included normal platelets subjected to all interactions. To determine the effect of platelet-platelet collisions, aggregation, and adhesion of normal platelets at each tortuosity index, Cases 1–5 were repeated with either “no interactions” (Cases 6–10) or “collisions only” (Cases 11–15). To determine the effect of MPV with platelets of normal MPD subjected to all interactions at each tortuosity index, Cases 1–5 were repeated with either low MPV (Cases 16–20) or high MPV (Cases 21–25). The remaining cases (Cases 26–45) utilized either the straight arteriole or the arteriole with the highest tortuosity index (T = 0.21), rather than the other three tortuous arterioles also. This strategy reduced the number of simulations while it still included an effect of tortuosity. To determine the effect of aggregation and adhesion with platelets with abnormal MPV and normal MPD in a straight arteriole and a tortuous arteriole, Cases 16, 20, 21, and 25 were repeated with “collisions only” (Cases 26–29). To determine the effect of MPD with platelets of normal MPV subjected to all interactions in a straight arteriole and a tortuous arteriole, Cases 1 and 5 were repeated with each of the four different values of MPD (Cases 30–37). To determine the effect of aggregation and adhesion with platelets with abnormal MPD and normal MPV in a straight arteriole and a tortuous arteriole, Cases 30–37 were repeated with “collisions only” (Cases 38–45).

Three measures of thrombosis based on platelet activation, aggregation, and adhesion were determined throughout the simulation time. An aggregate was defined as a group of two or more platelets in contact with each other. A platelet was considered to be part of a mural thrombus if the platelet was in contact with the wall or if it was part of an aggregate that was in contact with the wall. One measure of thrombosis was the number of platelets in mural thrombi at a given time (mural thrombus size), which represented platelets that were in the vessel at the specified time. Another measure was the cumulative number of activation events (activation count). This measure was a count of the number of platelets that had become activated since the start of the simulation. A third measure was the number of platelets in contact with the wall averaged over time from the start of the simulation (wall contact).

2.2. Discrete element computational model

The transport, collision, shear-induced activation, receptor-ligand adhesion, and receptor-ligand aggregation of hundreds of platelets involved in thrombus formation was simulated in tortuous arterioles by a mesoscale, discrete element method for blood cells [25, 46, 47]. The method has been demonstrated on a single computer processor to be capable of simulating 3D flows with tens of thousands of aggregating ellipsoidal red blood cells [48] and 2D flows with hundreds of aggregating and adhering spherical platelets [25]. In the current work, the computational model followed the motion of each spherical platelet due to interactions with the fluid, vessel walls, and other platelets. Platelets were modeled as 3D spheres, rather than 2D circles, so that they possessed mass and could be subjected to the dominant 3D forces and torques as defined below, and so that the original 3D computational method could be utilized, which can be reduced to 2D flow. Fluid flow was modeled in 2D to increase computational efficiency. Platelet centroids were initiated on the 2D flow plane, which was the x-y plane. As the fluid velocity component in the z-direction was zero, and the only non-zero fluid vorticity component was in the z-direction, centroids of 3D platelets remained in the x-y plane. Thus, the 3D angular and linear momentum equations reduced to 2D and were solved for each 3D platelet in 2D flow, given by

$$m\frac{d\mathbf{v}}{dt}={\mathbf{F}}_F+{\mathbf{F}}_A,I_z\frac{d{\mathrm{\Omega }}_z}{dt}=M_{F,z}+M_{A,z},$$ (1)

where m is platelet mass, v is platelet velocity, I_z = (1/10)md² is moment of inertia, Ω_z is platelet rotation rate, F_F and M_F,z are respectively fluid-induced force and torque on the platelet, F_A and M_A,z are respectively force and torque on the platelet due to adhesion and collision, and t is time. Fluid-induced force F_F was composed of the dominant fluid-induced forces, which were drag force F_d and added mass force F_a given by

$${\mathbf{F}}_d=-3\pi \mu d(\mathbf{v}-\mathbf{u}){(1-c)}^{-3.7},{\mathbf{F}}_a=-\frac{1}{2}\frac{{\rho }_f}{{\rho }_p}\left(\frac{d\mathbf{v}}{dt}-\frac{d\mathbf{u}}{dt}\right),$$ (2)

respectively, where u is fluid velocity at the location of the platelet centroid, and c is local platelet volumetric concentration. Fluid-induced torque was calculated as

$$M_{F,z}=\pi \mu d^3\left({\omega }_{xy}-{\mathrm{\Omega }}_z\right),$$ (3)

where ω_xy is fluid vorticity. Adhesion and collision forces acting on two colliding platelets consisted of a force due to elastic deformation of platelets F_ne, a force due to energy dissipation from collision F_nd, and a resistance force F_s due to sliding of one platelet over another. Adhesion and collision torques acting on two colliding platelets consisted of a torque generated by the sliding resistance force F_s and a torque due to resistance of rolling of one platelet over another M_r. Adhesion and collision forces and torques were given by

$${\mathbf{F}}_A=F_{ne}\mathbf{n}+F_{nd}\mathbf{n}+F_s{\mathbf{t}}_s,M_{A,z}=\frac{d}{2}{F}_s(\mathbf{n}\times {\mathbf{t}}_s)+M_r({\mathbf{t}}_r\times \mathbf{n}),$$ (4)

where n is a unit vector tangent to the line connecting the centroid of the platelet to the centroid of the other platelet, t_s is a unit vector in the direction of relative motion of the platelet surfaces projected onto the plane orthogonal to n, and t_s is a unit vector in the direction of rolling velocity of the platelet. Forces F_nd, F_s and torque M_r were determined using equations given in the literature. Elastic deformation force F_ne was determined, as described below, based on the theory of Johnson et al [49].

To facilitate computations with large numbers of cells, the computational model used various approximations. Specifically, platelets were modeled as spherical particles that were constrained to be rigid except during collision with each other and the walls. Upon collision, platelets retained their shape except within a flattened circular region of contact, for which the platelet surfaces were separated by a constant gap distance (figure 2(left)), similar to the idealized geometry of cell-cell contact as modeled by Bell et al [50]. Platelet adhesion and aggregation was assumed to take place through receptor-ligand binding, which occurred only within the contact region. Receptor-ligand bonds were modeled as springs following Bell et al [50]. Under these assumptions, receptor-ligand binding took a form that was mathematically analogous to van der Waals adhesion with a time-dependent adhesive surface energy density α(t) given by

Figure 2.

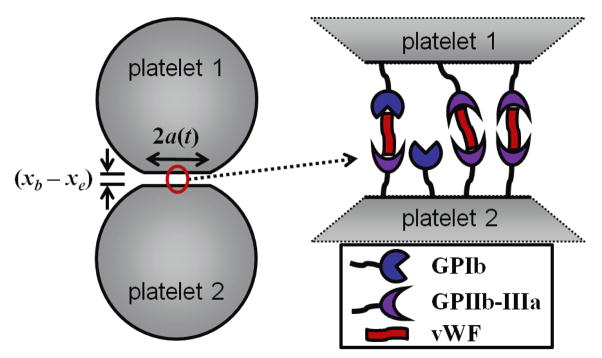
Schematic showing the flattened circular region of contact of radius a(t) between two colliding spherical platelets. The gap distance (x_b − x_e) between platelet surfaces is larger than normal to show detail (left). Schematic of adhesive interactions of vWF, GPIb, and GPIIb-IIIa in the region of contact (right).

$$\alpha (t)=-\frac{\sigma }{2}{(x_b-x_e)}^2{\int }_0^1{N}_b(t-t_0(s))\mathit{sds},$$ (5)

where σ is spring constant, x_b is length of the bond, which is also the gap distance between platelet surfaces, x_e is equilibrium length of the bond, N_b is number density of bonds, and s is radial position with the contact region divided by the radius of the contact region. The variation of N_b with time was given by a kinetics equation of Bell [51] that accounted for forward and reverse reactions of bond formation given by

$$\frac{{dN}_b}{dt}=k_f(N_{L0}-N_b)(N_{R0}-N_b)-k_r{N}_b,$$ (6)

where k_f and k_r are respectively forward and reverse reaction rate coefficients, and N_L0 and N_R0 are respectively initial ligand and receptor densities. The reaction rate coefficients vary with the gap distance in accordance to Dembo et al [52]

$$k_f=k_{f0}exp\left[-\frac{{\sigma }_{ts}{(x_b-x_e)}^2}{2k\overline{T}}\right],k_r=k_{r0}exp\left[\frac{(\sigma -{\sigma }_{ts}){(x_b-x_e)}^2}{2k\overline{T}}\right],$$ (7)

where k_f0 and k_r0 are respectively initial forward and reverse equilibrium reaction rates, σ_ts is transition state spring constant, k is the Boltzmann constant, and T̄ is absolute temperature. Number density of bonds in equation (6) was obtained using the solution given by Chesnutt and Marshall [46]. Number density of bonds represented the bonds formed in either platelet adhesion to the wall or platelet-platelet aggregation. Mechanisms of platelet aggregation and adhesion differ depending on shear rate. At low to intermediate wall shear rates below 1000 s⁻¹, platelet aggregation is predominantly mediated by platelet glycoprotein GPIIb-IIIa and fibrinogen [45, 53–55]. At high wall shear rates between 1000 to 10,000 s⁻¹, platelet aggregation is mediated by von Willebrand factor (vWF), and by platelet glycoproteins GPIIb-IIIa and GPIb, which promote the initial formation of adhered platelet aggregates [45, 54, 55]. At exceedingly high wall shear rates above 10,000 s⁻¹, platelet aggregation is mediated solely by vWF and GPIb and does not require platelet activation [54]. As maximum wall shear rates in the current work ranged from about 1400 to 3200 s⁻¹, platelets were assumed to adhere to vWF immobilized on the subendothelium through GPIb or GPIIb-IIIa [45, 56–58]. Aggregation between platelets was assumed to occur through bridging of GPIb or GPIIb-IIIa by plasma vWF [45, 57, 58] (figure 2(right)). Typical ranges of values obtained from the literature for parameters in equations (6) and (7), which vary widely for different cell adhesion problems, are given in table 3, along with values used in simulations. Few values of parameters in table 3 are known specifically for platelet adhesion or aggregation. We selected the density of platelet receptors and other parameters to achieve an effective spring constant for adhesion and aggregation of a platelet that was of the same order of magnitude as that determined in a previous study [32] (see Results).

Table 3.

Values of parameters related to receptor-ligand binding used in simulations and ranges of experimental values

Parameter (units)	Value Used in Simulations	Range of Experimental Values	References
kf0 (cm2 s−1)	10−7	10−12 to 10−7	[80]
kr0 (s−1)	10−5	10−5 to 10	[51, 81]
NL0, NR0 (cm−2)	1.115 × 1012	109 to 1012	[35, 43, 52, 73, 82]
xe (nm)	20	5 to 50	[50, 52, 83]
xb (nm)	29	0 to length at which bond breaks	-
σ (dyn cm−1)	1.98	0.01 to 10	[52, 84]
σts (dyn cm−1)	−5	−5 to 5	[52]

For simulations in the current work, the time scale for bond formation was much less than the time scale for elastic response of two colliding platelets. Thus, number density of bonds was approximated by its equilibrium value N_b(∞), such that adhesive surface energy density simplified to a constant value, given by

$$\alpha (t)=-\frac{\sigma }{4}{(x_b-x_e)}^2{N}_b(\infty ),$$ (8)

where calculations yielded α(t) = −0.4 dyn cm⁻¹.

Because of the analogy with van der Waals adhesion, we used the theory of Johnson et al [49] for adhesive elastic particles to approximate elastic deformation forces acting between two colliding platelets, given by

$$\frac{F_{ne}}{F_c}=4{\left(\frac{a}{a_0}\right)}^3-4{\left(\frac{a}{a_0}\right)}^{3/2},\frac{{\delta }_n}{{\delta }_c}=6^{1/3}\left[2{\left(\frac{a}{a_0}\right)}^2-\frac{4}{3}{\left(\frac{a}{a_0}\right)}^{1/2}\right],$$ (9)

where a(t) is contact region radius, and δ_n is normal overlap distance (or gap distance) of platelet surfaces. Critical force F_c and critical overlap δ_c can be written in terms of contact region radius at equilibrium a₀ as

$$F_c=3\pi \alpha R,{\delta }_c=\frac{a_0^2}{2(6^{1/3})R},a_0={\left(\frac{9\pi \alpha R^2}{E}\right)}^{1/3},$$ (10)

where R and E are respectively effective radius and effective elastic modulus of the two particles, with adhesive surface energy density α given by equation (5). For full details of this discrete element model, the reader is referred to Chesnutt and Marshall [46].

2.3. Shear-induced platelet activation model

We used our model of shear-induced platelet activation as in [25]. This activation model ensured the assumption that a platelet cannot become activated by a physiological shear rate or shear stress, irrespective of the amount of time a platelet is subjected to physiological shear stress. As well, this activation model clearly indicated the point at which an individual platelet became activated. These two attributes of our activation model are not necessarily apparent in other existing models that also account for exposure time to shear stress. Our model assumed that a platelet became activated if it experienced a shear rate above a critical shear rate (γ̇_crit) defined as

$${\stackrel{.}{\gamma }}_{\mathit{crit}}=f\mid {\stackrel{.}{\gamma }}_0\mid ,$$ (11)

where f is a scaling factor greater than unity, and (γ̇₀ is the wall shear rate in a corresponding straight arteriole that has the same mean fluid velocity and vessel diameter as the tortuous arteriole. To calculate critical shear rate, a critical shear stress was chosen as 6 N m⁻² (60 dyn cm⁻²). Justification of the choice of this critical shear stress is presented in the Discussion, which highlights examples of shear-induced platelet activation and aggregation that has occurred due to this and smaller shear stresses. With |γ̇₀| = 1440 s⁻¹ in the current simulations and with approximate apparent viscosity of whole blood μ_b = 4 × 10⁻³ kg m⁻¹ s⁻¹ (4 cP), a shear stress τ = 6 N m⁻² corresponds to shear rate γ̇ = τ/μ_b = 1500 s⁻¹. Hence, the scaling factor was chosen to be f = 1.042 to yield a critical shear rate γ̇_crit = 1500 s⁻¹. This shear-induced platelet activation model was termed the critical-shear model.

Both the magnitude of shear stress and exposure time to shear stress have been shown to affect shear-induced platelet activation in vitro [59–63]. Other existing models of shear-induced platelet activation utilized an activation index as a measure of shear stress history that accounted for magnitude and exposure time [61, 62, 64, 65]. With some of these models, depending on selection of adjustable parameters and amount of time examined, the activation index could continually increase under physiological conditions and could even become larger under physiological conditions compared with pathological conditions, rather than being smaller as expected. To compare our critical-shear model with one of these previous models, we implemented the model of Alemu and Bluestein [65] into our computational model. We termed this activation model as the shear-history model, which is given by

$$P(t)=P(t_0)+\underset{t0}{\overset{t}{\int }}{\left(\frac{\tau (t)}{{\tau }_0}\right)}^{\beta }\frac{dt}{{[1-P(t)]}^{\kappa }},$$ (12)

where P(t) is activation index at time t, P(t₀) is activation index at the initial time t₀, τ₀ is a characteristic shear stress, and β and κ are characteristic model parameters. P is a value between 0 (no activation) and 1 (full activation). In the current study, we set κ = −1 as in [65], which ensured that activation index did not decrease under shear stress or with exposure time. We examined β = 40 and 60. We did not use β = 5 as in [65] because platelets became quickly activated in our simulations at physiological shear rates in a straight arteriole. Characteristic shear stress was set as the wall shear stress in a straight arteriole, τ₀ = μ_b γ̇₀ 5.76 N m⁻² (57.6 dyn cm⁻²), and initial activation index was set as P(t₀) = 0. With these parameter values and simulation conditions, P could not reach 1 (full activation) but could only asymptote to 1. Hence, a platelet was considered to be activated once P was sufficiently close to 1 (i.e., P ≥ 1–10⁻¹²). The shear-history model with these parameter choices was applied to Case 5, which included normal platelets subjected to all interactions in the most tortuous arteriole with T = 0.21.

In both the critical-shear model and shear-history model, to account for the presence of chemical agonists released by activated platelets, we assumed a platelet became activated if it contacted another activated platelet, similar to Kamada et al [31]. In our simulations, only activated platelets were subjected to adhesion and aggregation, and activation was considered irreversible. Unless otherwise stated, the critical-shear model was employed in simulations.

3. Results

Each simulation was accomplished as a serial (non-parallel) program on a 3.0 GHz node having either 4 or 8 processing cores, with 2 GB of RAM per core. Simulations were run simultaneously on these processing cores. CPU times ranged from 7 to 17 days per simulation.

3.1. Model validation

We previously qualitatively validated the computational model [25] with in vivo experiments of Liu et al [24]. Our computational simulations of platelet interactions in tortuous venules under similar conditions to the experiments showed thrombus initiation at inner walls of tortuous venules due to high shear rates, in agreement with the experiments. This result was shown to be independent of the scaling factor and adhesive surface energy density.

In the current work, platelet adhesion initially occurred in regions of high shear rates (e.g., figure 4(a)), which agreed with ex vivo experiments of Wootton et al [66] at similar shear rates in stenoses for which platelet adhesion occurred more quickly in regions of high shear rates. Furthermore, our results showed that shear-induced platelet activation, adhesion, and aggregation occurred within milliseconds, in accordance with in vivo and in vitro observations [55, 67]. In addition, our effective spring constant for platelet adhesion and aggregation was calculated as the same order of magnitude as that determined by Filipovic et al [32] who compared their simulations with experiments. Specifically, the spring constant for a platelet with normal volume (7.1 fl), calculated as $\sigma \pi a_0^2{N}_b(\infty )$ was approximately 34 N m⁻¹. This value compared well with the platelet effective spring constant 50 N m⁻¹, which was determined by Filipovic et al [32] from computational simulations by comparison with experiments. The qualitative agreement of our simulations with experiments further validates our model.

Figure 4.

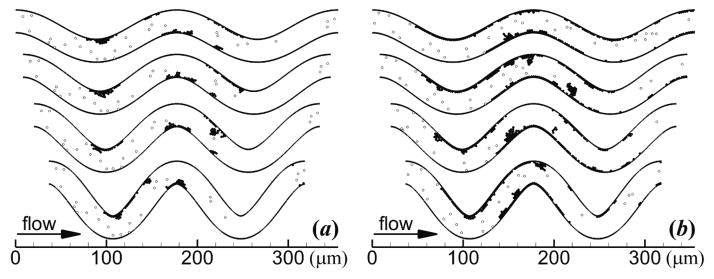
Thrombus formation showing activated platelets (solid circles) and unactivated platelets (open circles) at (a) t_i = 0.4 s and (b) t_f = 1.7 s. Tortuosity index increases from the top vessel to the bottom vessel as follows: T = 0.09, 0.12, 0.16, 0.21. Platelets had normal MPV and MPD, and were subjected to collision, aggregation, and adhesion.

3.2. Effect of tortuosity with platelets of normal MPV and normal MPD

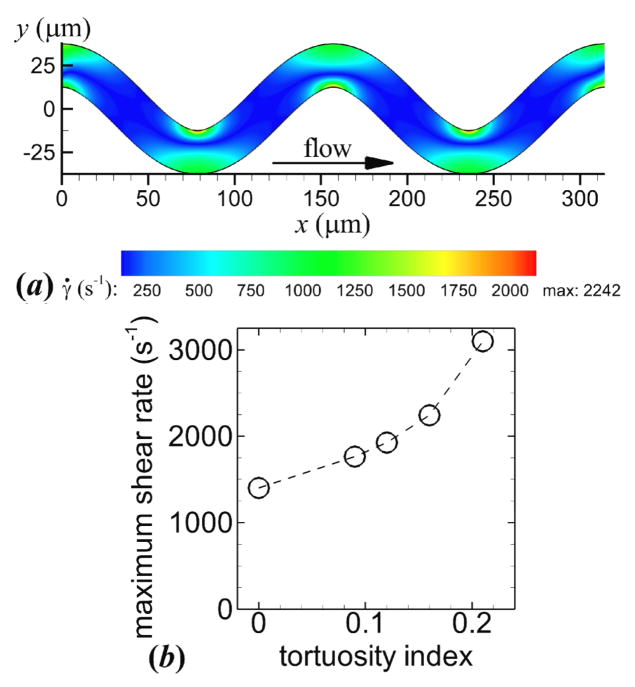
To examine thrombus formation, the flow and dynamic platelet interactions, including collision, activation, aggregation, and adhesion of normal platelets (MPV = 7.1 fl and MPD = 1063 kg m⁻³), were simulated in straight and tortuous arterioles. In the straight arteriole (T = 0), the maximum shear rate |γ̇₀| = 1440 s⁻¹, which was constant along the wall, was less than the critical shear rate such that platelet activation did not occur. In tortuous arterioles (T > 0), the maximum shear rate occurred at inner walls (figure 3(a)) and was greater than the critical shear rate, which activated platelets. The maximum shear rate ranged from 1764 to 3099 s⁻¹ for the lowest to highest level of tortuosity (figure 3(b)), which was 23 to 115% higher than the straight arteriole, respectively.

Figure 3.

Shear rate contours of a representative arteriole with tortuosity index T = 0.16 (a). Maximum shear rate versus tortuosity index (b).

Mural thrombus was initiated at inner walls of the two most upstream bends (figure 4(a)). Throughout the simulations, mural thrombi detached from the walls and either exited the arteriole or deposited at other locations, while a monolayer of platelets remained adhered to the wall at the site of the detached thrombi. For each level of tortuosity, the first occurrence of the disassociation of a mural thrombus was at the first bend. The thrombus size at the first bend continually increased until part of the thrombus detached from platelets that were adhered to the wall. The amount of time that elapsed between adhesion of the first platelet at the first bend and the first thrombus disassociation was smallest for the highest level of tortuosity. These values were 0.12, 0.15, 0.20, and 0.10 s for T = 0.09, 0.12, 0.16, and 0.21, respectively. At the end of the simulation, mural thrombi were present at both inner and outer walls for each level of tortuosity (figure 4(b)). Activation count at the initial time t_i and final time t_f generally increased slightly with level of tortuosity, except with T = 0.21 at t_f (figure 5(a)). Mural thrombus size at a given time was largest with T = 0.12 (figure 5(b)). Of the tortuous arterioles, the most tortuous vessel (T = 0.21) had the smallest mural thrombus size. Wall contact increased slightly with level of tortuosity initially, but by the final time decreased with increasing level of tortuosity (figure 5(c)). Of the 1111 platelets that entered each tortuous arteriole, 56 to 60% became activated and 16 to 21% were present in mural thrombi at the final time.

Figure 5.

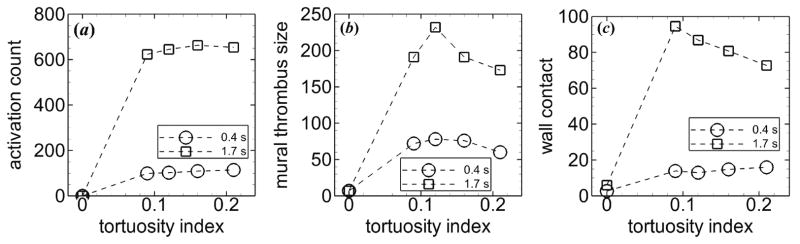
Measures of thrombosis versus tortuosity index at t_i = 0.4 s (circles) and t_f = 1.7 s (squares), including (a) activation count, (b) mural thrombus size, and (c) wall contact. Platelets had normal MPV and MPD, and were subjected to collision, aggregation, and adhesion.

To further determine the relative contributions of specific interactions, we virtually excluded these interactions in some simulations. With platelets subjected to “no interactions,” activation count was much lower with only 30 to 36% of the 1111 platelets that entered the arteriole becoming activated by the final time t_f of the simulation. Activation count and wall contact generally increased with increasing tortuosity index (figure 6(a–b)). These results indicated that platelet activation and platelet-wall collisions in tortuous arterioles did not require platelet-platelet collisions, aggregation, or adhesion. No platelets contacted the walls for the straight arteriole (T = 0) because there were no collisions to push platelets toward the walls. With platelets subjected to “collisions only,” activation count remained about the same compared with platelets subjected to “no interactions.” Hence, the higher activation count with platelets subjected to all interactions was not due to platelet-platelet collisions, but was due to either or both aggregation and adhesion. The presence of activated platelets in mural thrombi, for the case with all interactions, could activate additional platelets. In contrast, mural thrombi were not possible for the cases without aggregation and adhesion (“no interactions” and “no collisions”). Wall contact significantly increased with “collisions only”, compared with the case without interactions. Wall contact was largest for the straight arteriole due to platelets rolling along the walls for a long distance, which occurred less frequently in tortuous arterioles. Among the tortuous arterioles, wall contact was largest for an intermediate tortuosity index T = 0.16, though all values were less than half that in the straight arteriole (figure 6(c)).

Figure 6.

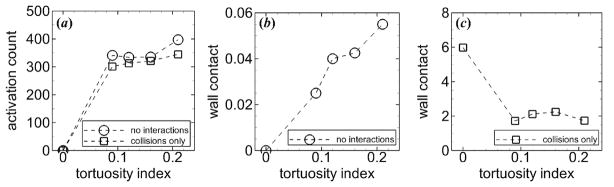
Measures of thrombosis versus tortuosity index, including (a) activation count, and (b-c) wall contact, in two hypothetical cases at t_f = 1.7 s. Platelets were subjected to either “no interactions” (circles) or “collisions only” (squares). In both cases, platelets had normal MPV and MPD.

Comparing these simulations that included and excluded certain interactions indicated that platelet-platelet collisions hardly affected activation count but greatly increased wall contact, especially in the straight arteriole. In addition, for normal platelets with all interactions considered (i.e., platelet-platelet collisions, aggregation, and adhesion), at t_f activation count increased 5% from the low tortuosity index (T = 0.09) to the highest tortuosity index (T = 0.21) (figure 5). However this increase was greater at 15% for the case with “collisions only”, and was 16% for the case with “no interactions” (figure 6). This comparison indicated that aggregation and adhesion lessened the effect of level of tortuosity on activation count.

3.3. Effect of shear stress exposure time with platelets of normal MPV and normal MPD

With the shear-history model, platelets did not become activated in the straight arteriole, in agreement with the critical-shear model. With β = 40 in the most tortuous arteriole (T = 0.21), platelets only became activated after passing near the inner wall of the third bend (figure 7(a)). With β = 60 in the tortuous arteriole, platelets became activated at the inner walls of each bend, similar to the critical-shear model (figure 7(a)). Activation count and mural thrombus size at t_f were comparable for the shear-history model with β = 60 and the critical-shear model (figure 7(b)). These values were lower for the shear-history model with β = 40 due to platelet activation occurring farther downstream. Along the convex wall (as viewed within the lumen) that contained the bend at which platelet activation first occurred in a given simulation, values of mural thrombus size normalized by the arc length of the specific wall (mural thrombus density) were very close for the critical-shear model simulation and the two shear-history simulations at t_f (figure 7(c)). To evaluate the effect of tortuosity on activation index, we examined the first 50 platelets that exited the arteriole. Average activation indices upon exit were 0.018 and 0.020 with β = 40 (or 0.0015 and 0.020 with β = 60) for the straight and tortuous arterioles, respectively. One of the 50 platelets, which was traveling close to the wall, became activated in the tortuous arteriole with both β = 40 and 60. In the straight arteriole, this same platelet that was traveling close to the wall gained a larger than average activation index in the straight arteriole, with P = 0.75 for β = 40 and P = 0.075 for β = 60.

Figure 7.

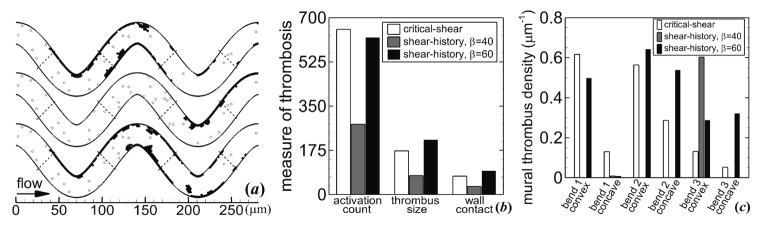
Measures of thrombosis for different models of shear-induced platelet activation including critical-shear model (top vessel, white bars), shear-history model with β = 40 (middle vessel, gray bars), and shear-history model with β = 60 (bottom vessel, black bars). (a) Thrombus formation showing activated platelets (solid circles), unactivated platelets (open circles), and boundaries that separate convex and concave walls (dashed lines). (b) Measures of thrombosis, including activation count, mural thrombus size, and wall contact. (c) Mural thrombus density on specified walls, for which wall boundaries are marked in (a). Platelets had normal MPV and MPD, and were subjected to collision, aggregation, and adhesion. Tortuosity index is T = 0.21, and time is t_f = 1.7 s.

The critical-shear model gave results that were either in quantitative agreement or qualitative agreement with the shear-history model with β = 60. Hence, in this case, the omission of exposure time to shear stress in the critical-shear model would not have a large effect on thrombus formation and platelet activation. On the other hand, the critical-shear model quantitatively and qualitatively agreed with the shear-history model with β = 40 in the region in which platelets first became activated. If the arteriole continued downstream of the simulated outlet with the same tortuosity index, then the results of the critical-shear model would be similar to results of the shear-history mode with β = 40, except that thrombi locations would be shifted downstream by one wavelength. These results indicate that the critical-shear model is justified in the current work because results are similar to a shear-history model, depending on choice of shear-history model parameters and location at which measurements are observed.

3.4. Effect of MPV with platelets of abnormal MPV and normal MPD

With platelets of various MPVs and normal MPD that were subjected to collisions, activation, aggregation, and adhesion, all tortuosity indices were examined. For most MPVs and levels of tortuosity, platelets that adhered to the wall remained on the wall, except for the two cases with high MPV at intermediate tortuosity indices T = 0.12 and 0.16. For these two cases, some mural thrombi rolled along the wall and exited the arteriole. For all cases, mural thrombi detached from the walls and exited the arteriole, while a layer of platelets remained adhered to the wall at the site of the detached thrombi.

Activation count increased with MPV for a given tortuosity index, and values were similar for each tortuosity index for a given MPV. For example, in the most tortuous arteriole (T = 0.21), activation count increased 37% from the low to high MPV (figure 8(a)). Mural thrombus size decreased with increasing MPV for a given level of tortuosity at t_f, except for the highest tortuosity index (T = 0.21) for which the highest MPV yielded the largest mural thrombus size (figure 8(b)). The relationship between wall contact and MPV depended on tortuosity index at t_f, with wall contact increasing with MPV for some tortuosity indices (e.g., figure 8(c)) and decreasing for other tortuosity indices (not shown).

Figure 8.

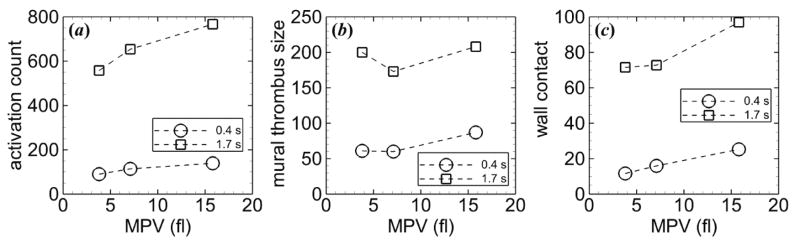
Measures of thrombosis versus MPV at t_i = 0.4 s (circles) and t_f = 1.7 s (squares), including (a) activation count, (b) mural thrombus size, and (c) wall contact. Tortuosity index is T = 0.21. Platelets had normal MPD and were subjected to collision, aggregation, and adhesion.

With platelets of various MPVs and normal MPD that were subjected to “collisions only” in the straight and most tortuous arterioles, the activation count and wall count reduced compared with cases with all interactions, similar to the cases with normal MPV at various levels of tortuosity. Activation count increased with MPV for the tortuous arteriole, with a 58% increase from the low to high MPV (figure 9). Wall contact generally increased slightly with MPV in both the straight and tortuous arterioles. For a given MPV, wall contact was lower for the tortuous arteriole compared with the straight arteriole.

Figure 9.

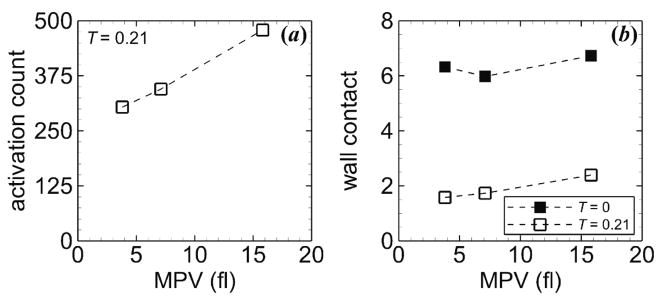
Measures of thrombosis versus MPV for the straight arteriole (T = 0, solid squares) and a tortuous arteriole (T = 0.21, open squares) at t_f = 1.7 s, including (a) activation count and (b) wall contact. Platelets had normal MPD and were subjected to “collisions only”.

3.5. Effect of MPD with platelets of abnormal MPD and normal MPV

With normal MPV in the most tortuous arteriole, platelets of all MPDs formed thrombi and emboli similarly to platelets of normal MPD. Rather than initiated by high shear, thrombi at the third bend were initiated by activated platelets and emboli that originated from the first bend.

Activation count did not depend greatly on MPD for a given time (figure 10(a)). Mural thrombus size was initially largest for the highest MPD, but nearly the same for the other MPDs (figure 10(b)). At the final time, the normal MPD had the smallest mural thrombus size, and low MPDs had higher values than high MPDs. Wall contact at t_f had a similar trend as mural thrombus size (figure 10(c)). At t_i, wall contact was nearly the same for each MPD, while at t_f, the normal MPD had the lowest value and low MPDs had the highest values.

Figure 10.

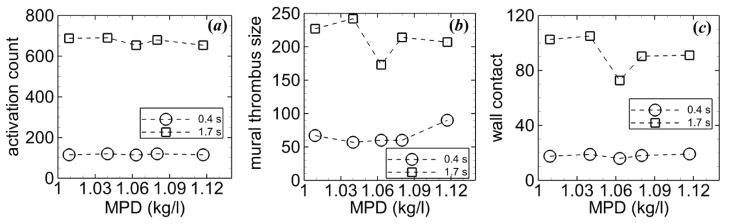
Measures of thrombosis versus MPD at t_i = 0.4 s (circles) and t_f = 1.7 s (squares), including (a) activation count, (b) mural thrombus size, and (c) wall contact. Tortuosity index is T = 0.21. Platelets had normal MPV and were subjected to collision, aggregation, and adhesion.

With platelets of various MPDs and normal MPV that were subjected to “collisions only,” both activation count and wall contact dramatically decreased by ~50% and ~98%, respectively, compared with cases with all interactions in the most tortuous arteriole (figure 11). In a given arteriole (straight or most tortuous), activation count was similar for each MPD, but slightly higher for normal MPD, and wall contact generally did not depend on MPD. For a given MPD, wall contact was lower for the tortuous arteriole compared with the straight arteriole.

Figure 11.

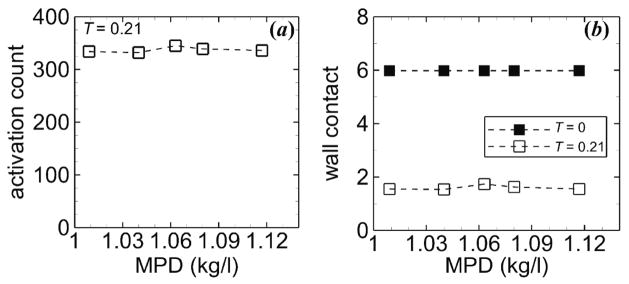
Measures of thrombosis versus MPD for the straight arteriole (T = 0, solid squares) and a tortuous arteriole (T = 0.21, open squares) at t_f = 1.7 s, including (a) activation count and (b) wall contact. Platelets had normal MPV and were subjected to “collisions only.”

4. Discussion

In this work, we investigated the transport, collision, shear-induced activation, receptor-ligand adhesion, and receptor-ligand aggregation of hundreds of platelets using a computational model. Our results showed that for normal platelets, increased level of tortuosity generally decreased mural thrombus size and wall contact, though level of tortuosity had only a slight effect on activation count. A higher MPV yielded a higher activation count in tortuous arterioles; however, the relationships of MPV to other thrombosis measures depended on level of tortuosity. The normal MPD showed the smallest mural thrombus size and wall contact compared with abnormal MPD, though MPD had little effect on activation count.

4.1. Effect of arteriole tortuosity

Tortuosity promoted platelet activation, which did not occur in the straight arteriole, though the level of tortuosity had a small effect on activation count. With platelets subjected to “no interactions,” wall contact increased with increasing level of tortuosity. This result was due to platelets closely following fluid streamlines, which occurred due to the low normalized stopping distances of particles, or Stokes numbers, which were on the order of 10⁻⁵ in these simulations. An increase in tortuosity index lead to an increased shift of fluid streamlines toward inner walls, which carried platelets closer to walls to increase wall contact. In comparison, with platelets subjected to “collisions only,” wall contact was increased by at least 10-fold for all arterioles. This considerable increase indicated that, in the absence of aggregation and adhesion, alterations to the fluid flow by tortuosity had a small effect on wall contact compared to the effect of platelet-platelet collisions. With all platelet interactions included, wall contact was greatly increased in the tortuous arterioles compared to the case with “collisions only” at t_f, as expected. However, an increase in level of tortuosity produced a decrease in wall contact at t_f, and a somewhat similar relationship was found for mural thrombus size. The decrease in mural thrombus size at the highest level of tortuosity (see figure 5(b)) may be partly due to higher shear rates, which could reduce mural thrombi due to quicker disassociation of thrombi. As activation count was nearly the same for each tortuous arteriole, this result indicated that in general more activated platelets exited the arteriole as tortuosity index increased. Furthermore, comparison of activation count and wall contact with and without platelet interactions suggests that platelet-platelet collisions, adhesion, and aggregation are all very important for thrombus formation.

If we were to consider that platelets were already activated upon entering the arteriole (pre-activated) and were subjected to all interactions, then thrombus formation would occur not only in tortuous arterioles, but also in straight arterioles. In tortuous arterioles, mural thrombi would be expected to occur at more locations along the walls, and hence mural thrombus size would be larger than with shear-activated platelets, for a given level of tortuosity. Mural thrombi would also be expected to be more prevalent at inner walls due to platelets following fluid streamlines, which were shifted towards inner walls. Additionally for this reason, mural thrombus size would be expected to be larger in tortuous arterioles compared with a straight arteriole that would exhibit fewer platelet-wall collisions. In fact, we observed each of these phenomena in previous simulations we performed with pre-activated platelets in tortuous venules, which had a lower mean fluid velocity than arterioles [68]. Additionally, these previous simulations with pre-activated platelets showed that mural thrombus was initiated upstream of the first bend along both walls. This result was in contrast to cases with shear-activated platelets both in our previous simulations of venules and in our current simulations of arterioles, for which mural thrombus was initiated at inner walls.

4.2. Effect of MPV

Larger MPV increased platelet activation count in the most tortuous arteriole. One reason for this increase was that Stokes number more than doubled from the low to high MPV (St = 4.4 × 10⁻⁵ to 11.4 × 10⁻⁵), which shows that the stopping distance was larger for larger platelets. Hence larger platelets were more likely to drift from fluid streamlines, especially near inner walls where platelets could become activated by passing through critical shear regions (where shear rate was higher than the critical shear rate) or by colliding with mural thrombi. Another reason for the increase in activation count with MPV was that collisions between larger platelets resulted in larger collision forces that could increase the possibility of driving platelets toward critical shear regions and mural thrombi. Wall contact with or without aggregation and adhesion generally increased with MPV for the straight and highest tortuosity index arterioles. Because higher MPV resulted in larger stopping distances and larger platelet-platelet collision forces, an increase in platelet-wall collisions could occur to lead to increased wall contact.

For the case with aggregation and adhesion, the increase in wall contact with MPV may also be due to increased adhesion force due to an increase in number of receptor-ligand bonds for platelet-wall adhesion, which results from increased contact area of a platelet. Considering the case with a platelet that is adhered to the wall with a contact region radius at equilibrium (a₀), a₀ increases with increasing MPV due to increasing platelet radius (e.g., equation (10)). The contact region radius at equilibrium for the large MPV (15.8 fl) platelet is 19% larger than that of the normal platelet, while this contact radius is 13% smaller for the small MPV (3.8 fl) platelet.

If we were to consider disk shaped, rather than spherical, platelets, then platelets would undergo flipping motions in the flow and possibly along the walls. An increase in MPV would increase the frontal area exposed to fluid flow, which could increase the occurrence of flipping. This increase in flipping may result in more platelet-platelet collisions and platelet-wall collisions with platelets of large MPV, compared with smaller platelets. As a result, an increase in MPV with disk shaped platelets could provide more opportunities for platelets to encounter critical shear regions and existing mural thrombi to increase activation count. Hence, in addition to hypercoagulability and altered platelet function, the risk of thrombosis in DM may also be due to the physical effects of increased MPV, for the several reasons listed above.

4.3. Effect of MPD

With normal MPV and all platelet interactions, abnormal MPD caused larger mural thrombus size and more wall contact in the most tortuous arteriole compared with normal MPD. However, MPD had a small effect on activation count, whether or not aggregation and adhesion occurred. Because activation count was nearly the same for each MPD, the decreases in mural thrombus size and wall contact for normal MPD showed that more emboli exited the arteriole. With platelets subjected to “collisions only” in the most tortuous arteriole, MPD had nearly no effect on wall contact, which suggests that the effect of MPD is only important in platelet-platelet and platelet-wall interactions and not platelet-fluid interactions. Although the low Stokes numbers (on the order of 10⁻⁵) may have predicted the negligible effect of MPD on platelet-fluid interactions, the low Stokes numbers could not have predicted the larger effects of MPD on platelet-platelet and platelet-wall interactions.

4.4. Relative importance of tortuosity, MPV, and MPD

Arteriole tortuosity yielded an increase in maximum shear rate compared with the straight arteriole, which was above the critical shear rate that could activate platelets. However, in tortuous arterioles with all platelet interactions, activation count did not greatly depend on level of tortuosity for a given MPV. Meanwhile, MPV had a large effect on activation count at a given level of tortuosity. The effect of MPV, however, varied with tortuosity index for wall contact and mural thrombus size at the final time, which demonstrated that level of tortuosity had a greater effect on wall contact and mural thrombus size than MPV.

In the most tortuous arteriole (T = 0.21), MPV had a greater effect on activation count than MPD. One reason for this result was the higher range of MPV values (−46% to +122% of normal) compared with the lower range of MPD values (±5% of normal), which are based on clinically observed values. Another reason was that Stokes number (St = ρ_pd²U/18μD) depends more on MPV than MPD, because St depends on the square of platelet diameter d, while it only depends linearly on platelet density ρ_p. The range of Stokes numbers was larger with different MPVs (St = 4.4 ×10⁻⁵ to 11.4 ×10⁻⁵) compared with the range with different MPDs (St = 6.3 ×10⁻⁵ to 7.1 ×10⁻⁵). Thus, MPV had a larger effect than MPD on the stopping distance of platelets and the drift of platelets from fluid streamlines near inner walls where they could become activated by high shear rates or mural thrombi.

4.5. Model limitations

Our model of shear-induced platelet activation did not account for the amount of time a platelet was exposed to different levels of shear rate. Instead, platelet activation was assumed to be instantaneous above a critical shear rate. Our model was in agreement with in vivo and in vitro observations of shear-induced platelet activation and aggregation that occurred within milliseconds [55, 67]. To our knowledge, no studies reported in the literature simulate shear-induced activation of individually tracked platelets in thrombus formation. Our activation model based on a critical shear rate clearly indicated the event of activation and did not allow for activation due to physiological shear rates. These two points are not necessarily clear in activation models in the literature that include the effect of exposure time (e.g., [62, 64, 65]). Some previous models of shear-induced platelet activation utilize an activation index that is a measure of shear stress and exposure time. However, in some of these activation models, the parameter value at which an individual platelet becomes activated is either not defined or cannot be reached (e.g., equation (12)). Hence, we employed our activation model to avoid these types of uncertainties.

The critical shear stress (6 N m⁻²) used in simulations was similar to the lower end of threshold values of shear-induced activation and aggregation of platelets found in previous in vitro studies, including 7.5 N m⁻² in platelet rich plasma, [57] and 8.3 N m⁻² [57] and 14.0 N m⁻² [69] in whole blood. In each of these cases, platelet activation and/or aggregation occurred below the threshold and were significantly higher above the threshold. Shear-induced platelet activation and aggregation have been shown to occur at our critical shear stress of 6 N m⁻² in vitro and to increase with increasing shear stress. For example, Konstantopoulos et al [69] showed that in vitro shear-induced aggregation of platelets in whole blood occurred for tested shear stresses from approximately 2.3 to 32.0 N m⁻², with a trend of increased activation with increased shear stress. Similarly, Konstantopoulos et al [56] showed that shear-induced activation of platelets in platelet rich plasma occurred for tested shear stresses from 1.5 to 12 N m⁻², with a trend of increased activation with increased shear stress. Additionally, Chow et al [70] demonstrated elevated platelet calcium and platelet aggregation for tested shear stresses from 3 to 12 N m⁻², with an increase in calcium and aggregation with shear stress. Although our critical shear stress was smaller than shear stresses (7.5 to 14 N m⁻²) in in vitro studies that yielded large increases in platelet activation or aggregation compared with lower shear stresses [57, 69], low shear stresses (1.5 to 3 N m⁻²) have caused platelet activation or aggregation in vitro [56, 69, 70]. As well, shear stresses estimated to be about 0.8 N m⁻² produced thrombosis due to curvature in rat venules in vivo [24]. Hence, the critical shear stress for shear-induced platelet activation and aggregation varies based on experimental conditions. Our critical shear stress was chosen to be close to experimental values to illustrate trends in the early stage of thrombus formation in response to shear stress induced by changes in MPV, MPD, and tortuosity.

The mean fluid velocity at the arteriole inlet in each simulation was assumed to be that in a physiological, straight arteriole. However, increased fluid velocity could result from hypertension, which is associated with DM [71, 72]. Hypertension is 1.5 to three times more common in DM and increases the risk of microvascular complications [71]. An increase in blood pressure due to hypertension would increase the mean fluid velocity and shear rates present in vessels. To include the effect of hypertension in DM in the current simulations, the mean fluid velocity at the arteriole inlet could be increased in “diabetic” simulation cases that had platelets of large MPV. As a result, shear rates would be increased in both straight and tortuous arterioles in diabetic simulations, compared with “non-diabetic” simulations that had normal mean fluid velocity at the inlet and platelets of normal or small MPV. As a result, the increases that were observed in measures of thrombosis (i.e., activation count, mural thrombus size, wall contact) in the original simulations with normal velocity and large MPV would be more evident in simulations with higher velocity. As well, the maximum shear rate in the straight arteriole in the diabetic simulations could exceed the critical shear value to activate platelets of large MPV, unlike the non-diabetic simulations.

The density of receptors and ligands in our model (1.115 ×10¹² cm⁻²) was high compared with the estimation of Reininger et al [73] for platelet GPIb (1.5 ×10¹¹ cm⁻²). Our value was chosen to amplify platelet adhesion and aggregation in order to more easily observe the effects of MPV, MPD, and tortuosity on thrombosis. Nonetheless, our value of receptor and ligand densities gave an effective spring constant for adhesion and aggregation of a platelet that was of the same order of magnitude as that determined by Filipovic et al [32] by experimental data.

To focus on individual effects of abnormal MPV and abnormal MPD, and to reduce the number of simulations, either MPV or MPD was varied from the normal value, but not both. However, low MPD in poorly-controlled type 1 DM [7] is likely accompanied by elevated MPV, and increases in both MPV and MPD have been observed with myocardial infarction [15]. Our simulations with abnormal MPD and normal MPV in a tortuous arteriole gave nearly no change in activation count and gave an in increase in mural thrombus size. Hence if we had included abnormal MPD with say, elevated MPV, we would expect the same result for activation count but a possible increase in mural thrombus size, compared with normal MPD and elevated MPV.

Because of the low physiological volume fraction of platelets (0.2%), the effect of platelet motion on fluid flow was neglected. Individual platelets, small emboli, and small non-occlusive mural thrombi that were present in simulations were expected to have small effects on fluid flow. As well, due to the low Reynolds number (~0.1), any change in fluid flow due to mural thrombi was not expected to produce recirculation zones in which platelets could become trapped. Hence, the computational model did not measure platelet residence times. Note that an activated platelet that was adhered to the wall necessarily would have a large near-wall residence time. Platelets could be adhered at locations where shear stress may not be high and could have large near-wall residence times. Thus, the effect of increased near-wall residence time, in addition to elevated shear stress, would be to increase activation count due to unactivated platelets contacting these adhered activated platelets, and to possibly increase mural thrombus size.

Another assumption was to neglect red blood cells because they are not major components of microvascular thrombi [74]. Nevertheless, red blood cells are known to force platelets toward vessel walls in straight vessels such that the concentration of platelets is high at the walls and low in the center [75]. For example in straight arterioles, in vivo animal studies have shown that the wall excess concentration of platelets was about three times higher than in the center [76]. On the other hand, the wall excess concentration of platelets in tortuous vessels is not well known. Our simulations assumed that platelets entered at random locations at the vessel inlet, rather than being concentrated at the walls. Under the assumption that the concentration profile of platelets before entering the simulated tortuous arteriole was that in a straight in vivo arteriole, then we would expect that the upstream wall excess concentration of platelets would be close to three times that in the center. Hence, we expected that platelet activation might have occurred sooner than in our simulations that used random distributions of platelets at the inlet. This result would be due to either platelets already being near arteriole walls or red blood cells forcing platelets toward arteriole walls, where they could become activated by high shear rates or by already activated platelets in mural thrombi. However, the relative effects of MPV, MPD, and tortuosity on thrombus formation would be similar to our results. The effects of red blood cells and the resultant platelet concentration profile on thrombus formation and platelet activation in tortuous vessels need to be investigated. In future studies, we will enhance the model to include red blood cells.

For computational efficiency, we modeled all platelets, both activated and unactivated, as 3D spherical particles. The assumption of 3D spherical or 2D circular platelets has been used in several previous computational studies of thrombus formation with large numbers of individual platelets (e.g., [28–31, 40]). Although unactivated platelets are disk shaped, activated platelets are more spheroidal [42–44]. The motion and collision of unactivated platelets modeled as disks would differ from those modeled as spheres. As observed in vitro, platelets that were purified from citrated whole blood were ellipsoidal and flipped along vWF coated surfaces, without rolling on their edges [77]. In contrast, platelets modeled as spheres would not be able to flip and can possibly roll along a surface. Because the current study focused on thrombus formation by activated platelets that were physiologically spheroidal, we expected the assumption of spherical shape to have a small effect on the results. As well for computational efficiency, we utilized 2D flow in a curved channel. The assumption of 2D flow was similar to that of most previous computational studies of thrombus formation with large numbers of individual platelets. In most previous studies, straight channels with either 2D [28–30, 40] or 3D [31] flow were utilized. Because similar characteristics in aggregate size distributions of red blood cell aggregates in both 2D and 3D simulations have been observed [46], we expected that platelet aggregates in our 2D simulations would be similar to 3D. Hence, results of 2D simulations were expected to be qualitatively similar to 3D results. Our computational model can be extended from 2D to 3D. Because the forces and torques on platelets, as well as equations of motion of platelets, were derived from those of 3D spherical particles, the model of platelet interactions and motions can be extended into 3D with little modification to accommodate an extension from 2D to 3D flow. In future work, we will develop efficient algorithms to simulate large numbers of ellipsoidal platelets in 3D tubular vessels.

4.6. Clinical relevance

Our results regarding MPV and tortuosity are clinically relevant. The results indicate that the changes in physical interactions due to larger MPV have a significant effect on thrombus formation, in addition to the biochemical changes. For example, our results showed that regardless of level of tortuosity, or whether platelet aggregation and adhesion were allowed, the number of platelets that became activated during the simulation increased with increasing MPV. Hence, a treatment to reduce MPV toward normal may reduce the possibility of platelet activation due to high shear stress induced by tortuosity. Metformin, which is the most commonly used drug for type 2 DM, has been shown to reduce MPV in newly diagnosed type 2 DM patients [78]. Thus, in addition to the benefits of reduced glucose and thromboxane B₂ (an index of in vivo platelet activation) [78, 79], metformin may reduce the possibility of a platelet to encounter critical shear regions in tortuous vessels and become activated in DM.

5. Conclusion and outlook

The current work elucidated the physical effects of various factors, including arteriole tortuosity, MPV, MPD, and platelet interactions (i.e., collision, aggregation, and adhesion) on platelet activation and thrombus formation. Our results suggest that the physical mechanisms associated with platelet interactions, MPV, MPD and tortuosity, play important roles in platelet activation and thrombus formation.

An advantage of our computational model is the ability to predict both outcomes and processes of thrombus formation under various conditions. Our model can serve as a tool for future studies to help determine the risk of thrombosis in patients due to vessel tortuosity and/or due to altered platelet morphology and to help predict the effects of new treatments that may change vessel tortuosity or platelet morphology toward normal conditions.