Sensitivity of Rabbit Ventricular Action Potential and Ca²⁺ Dynamics to Small Variations in Membrane Currents and Ion Diffusion Coefficients

Abstract

Little is known about how small variations in ionic currents and Ca²⁺ and Na⁺ diffusion coefficients impact action potential and Ca²⁺ dynamics in rabbit ventricular myocytes. We applied sensitivity analysis to quantify the sensitivity of Shannon et al. model (Biophys. J., 2004) to 5%–10% changes in currents conductance, channels distribution, and ion diffusion in rabbit ventricular cells. We found that action potential duration and Ca²⁺ peaks are highly sensitive to 10% increase in L-type Ca²⁺ current; moderately influenced by 10% increase in Na⁺-Ca²⁺ exchanger, Na⁺-K⁺ pump, rapid delayed and slow transient outward K⁺ currents, and Cl⁻ background current; insensitive to 10% increases in all other ionic currents and sarcoplasmic reticulum Ca²⁺ fluxes. Cell electrical activity is strongly affected by 5% shift of L-type Ca²⁺ channels and Na⁺-Ca²⁺ exchanger in between junctional and submembrane spaces while Ca²⁺-activated Cl⁻-channel redistribution has the modest effect. Small changes in submembrane and cytosolic diffusion coefficients for Ca²⁺, but not in Na⁺ transfer, may alter notably myocyte contraction. Our studies highlight the need for more precise measurements and further extending and testing of the Shannon et al. model. Our results demonstrate usefulness of sensitivity analysis to identify specific knowledge gaps and controversies related to ventricular cell electrophysiology and Ca²⁺ signaling.

1. Introduction

Several ionic models have been developed to investigate the subcellular mechanisms regulating excitation-contraction coupling (ECC) in rabbit ventricular cardiomyocytes [1–7]. In 2004, Shannon and colleagues published a detailed model for Ca²⁺ handling and ionic current that accurately represents sarcoplasmic reticulum (SR) Ca²⁺-dependent release and simulates basic ECC phenomena. This model was the first to include (1) the subsarcolemmal Ca²⁺ compartment to the other two commonly formulated cytosolic Ca²⁺ compartments (junctional and bulk, [8]), (2) the variations in the locations of ion transporters throughout the cell surface membrane, (3) Ca²⁺ and Na⁺ transport between the subcellular compartments, and (4) Na⁺ buffering inside. Latest studies extended further the Shannon et al. ionic model in rabbit ventricular cells. Mahajan and colleagues modified L-type Ca²⁺ current and Ca²⁺ cycling formulations, based on new experimental patch-clamp data, and used the updated model to investigate the mechanisms regulating ventricular tachycardia and fibrillation [4, 5]. Morotti et al. improved Mahajan's et al. model of rabbit ventricular I _Ca and examined the relative contributions of voltage- and Ca²⁺-dependent inactivation to total current inactivation [7]. Aslanidi et al. determined the functional role of each ionic channel current in modulating the action potential (AP) shape from different locations in rabbit ventricular wall [6]. Recently, using parameter sensitive analysis, Romero et al. [9] identified also key subcellular factors involved in the electrical signal generation and Ca²⁺ signal regulation in two rabbit cell models [1, 4]. Systematically characterizing AP properties, Ca²⁺ and Na⁺ dynamics, and their rate dependence on ±15%, ±30, and ±45% variations in the main transmembrane currents' conductance they found that APD is significantly modified by most repolarization currents and that steady-state Ca²⁺ levels are strongly dependent on I _Ca, I _NCX, and I _NaK currents. Important limitation of these “common pool models”, however, is that the subcellular compartment geometries (junctional cleft, submembrane space, cytosol, and SR) were simplified to allow prediction of total Ca²⁺ concentration ([Ca](t)) in the compartment of interest only.

A few reaction-diffusion models that seek to incorporate the effects of idealistic or more realistic subcellular and whole-cell geometries and to compute the spatial distributions of [Ca] in cardiac, skeletal or smooth muscle cells have been published also [10–19]. Recently, the contributions of structural heterogeneities to local and global Ca²⁺ signals in rabbit ventricular myocytes with realistic t-tubule microanatomy have been investigated [20]. Limitations of these spatial models, due to complexities, are that the cell electrophysiology was simplified, the AP dynamics was not reproduced, and the effects of intracellular Na²⁺ diffusion and buffering on ECC were not investigated.

Taken together the published computational models have provided important insights into the underlying mechanisms regulating intracellular Ca²⁺ dynamics and electrophysiological behavior in rabbit ventricular cells under control and certain pathological conditions. It remains, however, poorly understood how small variations in ion currents conductance and distribution and small changes in Ca²⁺ and Na⁺ transport between cellular subdomains affect important cellular biomarkers (i.e., AP shape, [Ca]_i, [Ca]_SL, and [Ca]_jct). In this study, we applied sensitivity analysis and used parameter estimation tools to investigate these questions. The sensitivity of each biomarker to 5%–10% changes in ionic currents properties and Ca²⁺ and Na⁺ diffusion coefficients were quantified using the Shannon et al. model. Validation of simulation results was performed by a comparison to experimental data in rabbit ventricular myocytes. This study identifies new experimental data required for better understanding of rabbit's electrophysiology and demonstrates the importance of sensitivity analysis as a powerful method for systematic and in-depth validation of AP models.

2. Methods

2.1. Electrophysiological Model in Rabbit Ventricular Myocytes

A diagram describing the arrangement of subcellular compartments, ionic currents and pumps, and intracellular Ca²⁺ fluxes included in the Shannon et al. electrophysiological model is shown in Figure 1.

Figure 1.

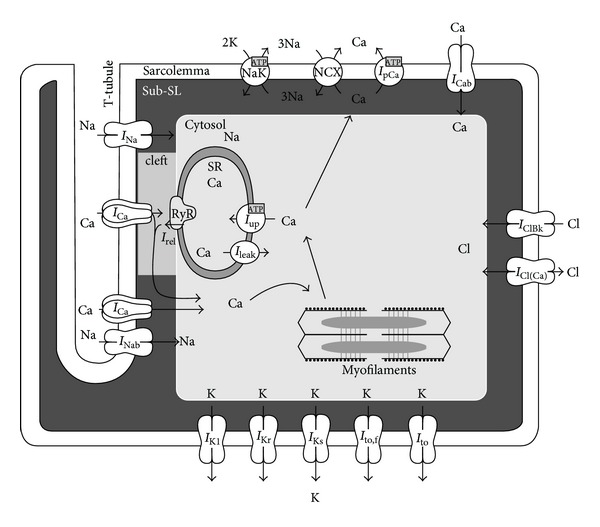
Schematic diagram illustrating the four subcellular compartments, electrophysiology, and Ca²⁺ dynamics in the Shannon et al. model in rabbit ventricular myocytes [1]. See Glossary and Tables 1–3 for the notations of the parameters used throughout the study.

The Shannon et al. model was adopted without changes and recent MatLab version of the code has been uploaded (http://somapp.ucdavis.edu/Pharmacology/bers/). The model behavior at 1 Hz pacing frequency is consistent with experimental measurements for AP-shape and global cytosolic Ca²⁺ concentrations ([Ca]_i) changes under control conditions [1].

2.2. Sensitivity Analysis Tools

Recently, several sensitivity analysis and parameter estimation tools and methodologies have been developed with a specific aim to assess the robustness of the cardiac cell models' parameters, including (1) the parameter variability analysis which examine the effects of varying one parameter in time [21], (2) techniques which assess the significance of parameters using multivariable regression over randomized set of input parameters values [22], and (3) global sensitivity analysis tool which implements the Morris screening algorithm [23] within the Nimrod platform [24]. In this study, we explored two methodologies [22, 23] and compared each method potential in evaluating parameter-output correlations in the Shannon et al. electrophysiological model.

2.2.1. Partial Least Squares (PLS) Regression

PLS is a statistical method that creates a linear regression model to predict a set of dependent variables (i.e., model outputs) from a set of independent variables (i.e., model inputs) [22, 25]. PLS is particularly useful when inputs are highly correlated (i.e., multicollinear) and when there are more inputs than outputs. In regression analysis, if two highly correlated effects are measured, the more dominant effect will falsely enhance the weaker effect, leading to inaccurate sensitivity information, and misinform truly significant parameter effects [25]. Since PLS retains good predictive power when working with multicollinear data, myocyte models containing multiple correlated variables can be analyzed using PLS.

2.2.2. Nimrod Tool Family

Nimrod uses a simple declarative modeling language to define parametric experiments, and it automates the tasks of formulating, running, monitoring, and collecting results from multiple individual experiments. Nimrod is not a single tool. It incorporates Nimrod/G, component that distributes computations to the recourses [24, 26]; Nimrod/O, a component that searches for “good” solutions using nonlinear optimization algorithms [27]; Nimrod/E, component that helps evaluating which parameter settings are important using the experimental design [28]. Nimrod/G is designed to assist scientists in performing studies, using concurrent execution on a cluster of processors or the resources of a computational grid. The user prepares a “plan file” which specifies the experiment [24]. A plan file is expanded into a “run file” which lists the appropriate parameter combinations required for execution. The Nimrod/G core runs on a processor called the “root node” whereas individual jobs are executed on “remote nodes.” Nimrod/G handles the file transfers required for the remote nodes, execution of computational tasks, and transfer of results back to the root node. The number of concurrent jobs is limited only by the number of processors available. Thus the user may achieve high concurrency without modifying the executables and without concern for grid specific details. Nimrod/O optimizes the numerical outputs of computational models. It provides a range of optimization algorithms and leverages Nimrod/G to perform batches of concurrent evaluations. The user prepares a “schedule file,” which, like the Nimrod/G plan file, specifies the parameters, their ranges, and the tasks required for execution of the model. But it also specifies the optimization algorithms to be used and the settings for the algorithms. Nimrod/O performs multiple searches for an algorithm and multiple algorithms, all in parallel.

2.2.3. Nimrod/E and Fractional-Factorial Design (FFD)

It is often of interest for researchers to identify variable interactions because they may provide physiological insights into cell dynamics. While colinearity in multiple linear regressions is problematic and can lead to inaccurate predictions, Nimrod/E is able to circumvent this problem and successfully identify both main effects and multifactor interactions [28]. Similar to PLSR, FFD attempts to create a linear model to explain the data generated from the model; it measures and ranks main effects and two-level interactions of input variables with outputs via experimental design. However, the method chooses only those jobs that generate the most significant results by ignoring high-level interactions with little influence, thereby saving a lot of computation time. From the resulting linear model effect coefficients can also be extracted that tells the correlation between parameters and model outputs. For more complete view of successes and failures in modeling pursuits of Nimrod toolsets, refer to Abramson and colleagues papers [24, 26–28].

2.3. Parameter Sensitivity Analysis

To perform sensitivity analysis, the Shannon et al. MatLab code was modified to extract the desired model outputs. Under basal conditions or by varying one parameter at a time AP and Ca²⁺ transients appeared stable (after 6–8 s until 8 min) at stimulus frequency of 1 Hz. For this reason we recorded and analyzed AP and Ca²⁺ signals ([Ca]_i, [Ca]_SL, [Ca]_jct) at 9-10 s of every simulation. In all numerical experiments (0 ≤ t ≤ 8 min) [K]_i remained unchanged while the variations in [Na]_i were small (ranging from 20 μM to 100 μM) with insignificant effects on calculated AP and Ca²⁺ traces at 6–8 s. The APD₆₀ and delta [Ca]_j (Δ[Ca]_j, j = i, SL,  jct) quantities were used to analyze the model sensitivity. Δ[Ca]_j is defined as the difference between peak Ca²⁺ concentration in the particular compartment and the diastolic Ca²⁺ concentration of 0.1 μM. The modified code was uploaded onto Nimrod/E toolset and was executed repeatedly using permutations of parameter sets that were ±10% or ±5% of default values (see the appendix, Tables 1–3). Then Nimrod/E fractional-factorial analysis and PLS were used to analyze the effects of single parameter changes. In addition, Nimrod/E allowed examining the two-level parameter interactions on model outputs. In the Results section the sensitivities of selected biomarkers to variations of parameters are displayed graphically as either “Lenth plots” in Nimrod/E, or as “bar plots” in PLS. Before performing PLS regression analysis to obtain sensitivity values, z-scores of input and output matrices were calculated using MatLab's z-score function; that is, z = (x − mean(x))/std(x). Each z-score value was computed using the mean and standard deviations along each column of the matrices. The columns of matrices have mean zero and standard deviation one. The PLS regression coefficients, or sensitivity values (see Figures 2, 4, and 6), indicate how changes in input parameters lead to changes in outputs. Examining these numbers allows for an assessment of the relative contributions of the various parameters. The sensitivity values in the “bar plots” could be interpreted quantitatively as follows. Because input and output matrices are mean-centered and normalized to standard deviations computed column by column, each sensitivity value is defined relatively to the relevant deviations. For instance, if the regression coefficient for the input P _CaL and the output APD₆₀ is 0.5, then when P _CaL is one standard deviation greater than the mean, APD₆₀ will increase by half a standard deviation. Conversely, if the value is −0.5, then when P _CaL is one standard deviation greater than the mean, APD₆₀ will decrease by half a standard deviation, and vice versa. The estimate values in the “Lenth plots” (y-axis) provide a qualitative overview of the inputs' relative effects on outputs and offer a comparison to the PLS-bar graphs. Changing the number of parameters studied slightly varied the magnitude of “regression coefficients” of bar plot and “estimate” of Lenth plot, but the relative effects and overall parameter-to-output relationships remained constant. The effects of sample sizes on model predictive efficacy by randomly picking subsets from sample pool, ranging from 15, 20, 50, 100, 200, and 500 to 1000 trials was examined. The adjusted R ² values (coefficient of determination, quantifying the explanatory capacity of the regression analysis) were calculated and averaged. At the low end of 15 samples, the regression model explained 90.8 ± 2.4% of the variance. At the high end of 1000 samples, the model explained 96.4 ± 0.3% of the variance. This relatively low decrease in prediction efficacy suggests that sample sizes do not significantly change the qualitative information obtained from the experiments. Considering this statistical analysis, the results were not included.

Table 1.

Maximal conductance varied in the model.

Definition		Symbol	Baseline value
1	Maximal Na+ conductance	G Na	16 mS/μF
2	Background Na+ conductance	G Nab (G NaBk)	0.297 10−3 mS/µF
3	Maximal rapid delayed rectifier K+ conductance	G Kr (G IKr)	0.07 mS/µF
4	Maximal slow delayed rectifier K+ conductance	G Ks	0.013 mS/µF
5	Maximal fast transient outward K+ conductance	G to,f	0.06 mS/µF
6	Maximal slow transient outward K+ conductance	G to (G to, s)	0.02 mS/µF
7	Maximal inward rectifier K+ conductance	G K1	0.9 mS/µF
8	Maximal Ca-activated Cl− conductance	G Cl(Ca)	0.109625 mS/µF
9	Background Cl− conductance	G ClBk	0.009 mS/µF
10	Maximal permeability of L-type Ca2+ channel for Ca2+	P CaL (P Ca)	5.4 10−4 cm/s
11	Maximal permeability of L-type Ca2+ channel for Na+	P CaNa (P Na)	1.5 10−8 cm/s
12	Maximal permeability of L-type Ca2+ channel for K+	P CaK (P K)	2.7 10−7 cm/s
13	Background Ca2+ conductance	G Cab (G CaBk)	0.0002513 ms/µF
14	Maximal Na+-Ca2+ exchange current	K NCX (${\overline{I}}_{\text{NCX}}$)	9 A/F
15	Maximal sarcolemmal Ca2+ pump current	K pCa (${\overline{I}}_{\text{SLCaP}}$)	0.0673 A/F
16	Maximal Na+-K+ pump current	K NaK (${\overline{I}}_{\text{NaK}}$)	1.91 A/F
17	SR Ca2+ release scaling factor	K rel⁡ (k s)	25 ms−1
18	Maximal rate of SR Ca2+ uptake (SERCA)	K up (${\overline{I}}_{\text{SRCaP}}$)	5.3 10−3 mM/ms
19	Passive SR Ca2+ leak scaling factor	K leak (K SRleak)	5.348 10−6 ms−1

Note: notations in brackets, for example, (…), show corresponding notations of some parameters used in Shannon et al. article [1]. The baseline conductance values used in this study are the same as in [1].

Table 3.

Diffusion coefficients varied in the model.

Definition		Symbol	Baseline value
1	Diffusion coefficient for Ca2+ from junctional cleft to SL compartment	D Ca(jct-SL)	1.64 10−6 cm2/s
2	Diffusion coefficient for Ca2+ from SL compartment to bulk cytosol	D Ca(SL-i)	1.22 10−6 cm2/s
3	Diffusion coefficient for Na+ from junctional cleft to SL compartment	D Na(jct-SL)	1.09 10−5 cm2/s
4	Diffusion coefficient for Na+ from SL compartment to bulk cytosol	D Na(SL-i)	1.79 10−6 cm2/s

Notes: in the Shannon et al. article [1] D _{Ca(junction-SL)} corresponds to   D _Ca(jct-SL),   D _{Ca(SL-cytosol)}  to  D _Ca(SL-i),  D _{Na(junction-SL)}  to D _Na(jct-SL), and D _{Na(SL-cytosol)} to D _Na(SL-i). The baseline diffusion coefficients values used in this study are the same as in [1].

Figure 2.

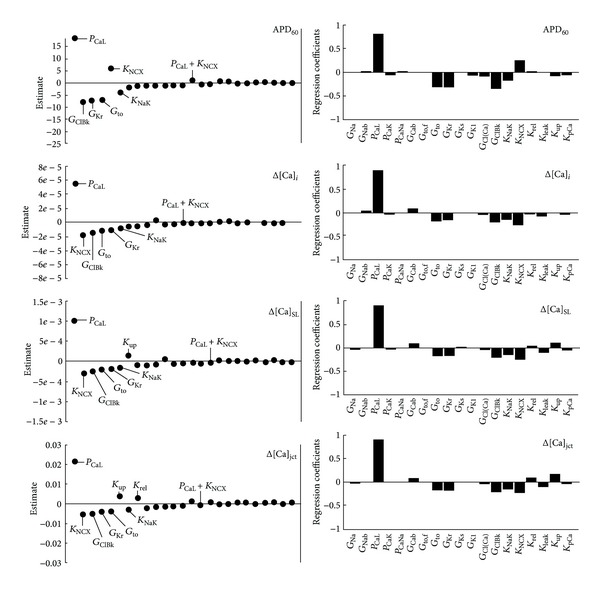
Parameter sensitivity analysis of APD₆₀, Δ[Ca]_i, Δ[Ca]_SL, and Δ[Ca]_jct sensitivities toward 10% increases in maximal transporters' conductance and permeability. Positive value indicates direct relationship between parameter and output (e.g., enhanced L-type Ca²⁺ permeability prolongs APD₆₀), and negative value indicates indirect relationship between parameter and output. Nimrod/E-Lenth plots (left column), PLS-bar plots (right column). Nimrod/E analysis produced similar qualitative results as PLS analysis.

Figure 4.

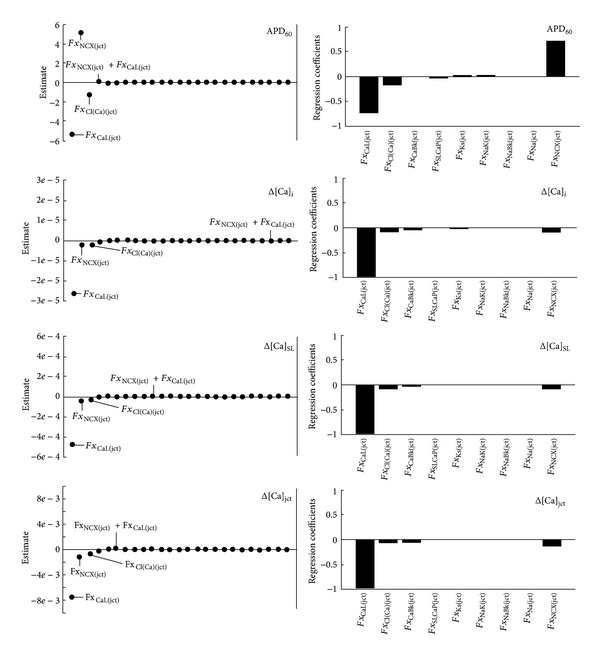
Parameter sensitivity analysis of APD₆₀, Δ[Ca]_i, Δ[Ca]_SL, and Δ[Ca]_jct sensitivities toward 5% increases in ion transporter distributions in the junctional cleft. Transporters' distribution between sarcolemma and junctional cleft summed up to 100%. Increasing fraction of total j-current in the junction by 5% is analogous to decreasing fraction of total j-current in the subsarcolemma by 45% for I _Ca and by 40-41% for all other currents. Positive value indicates direct relationship between distribution and output (e.g., increased density of I _Ca in the junctional cleft shortens APD₆₀) and negative value indicates indirect relationship between parameter and output. Nimrod/E-Lenth plots (left column), PLS-bar plots (right column). Nimrod/E analysis produced similar qualitative results as PLS analysis.

Figure 6.

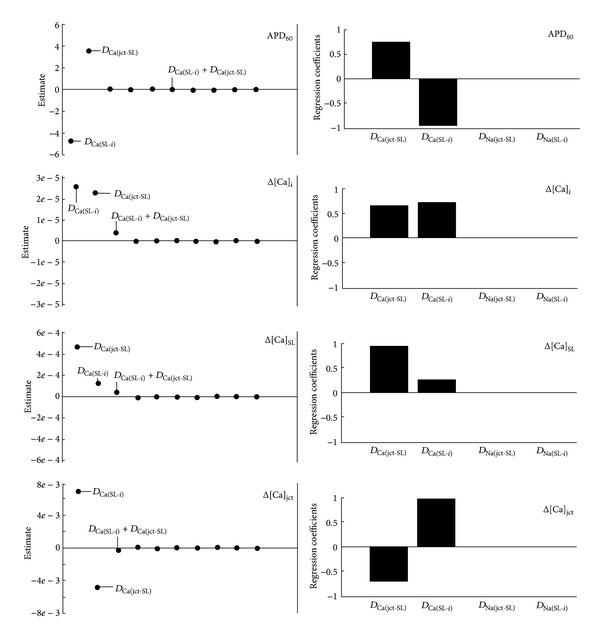
Parameter sensitivity analysis of APD₆₀, Δ[Ca]_i, Δ[Ca]_SL, and Δ[Ca]_jct sensitivities toward 10% increases in Ca²⁺ and Na⁺ diffusion coefficients between subcellular compartments. Positive value indicates direct relationship between diffusion coefficient and output (e.g., increased diffusion coefficient between junctional cleft and sarcolemma prolongs APD₆₀) and negative sensitivity value indicates indirect relationship between parameter and output. Nimrod/E-Lenth plots (left column), PLS-bar plots (right column). Nimrod/E analysis produced similar qualitative results as PLS analysis.

3. Results

3.1. Effects of 10% Changes in Channels Conductances on AP Morphology and Intracellular Ca²⁺ Dynamics

Figure 2 shows the effects of 10% changes in 19 default ion channel conductances and permeabilities (see the appendix, Table 1). Both PLS and Nimrod/E methods yielded consistent results with respect to single parameter's changes on the model outputs (APD₆₀, Δ[Ca]_i, Δ[Ca]_SL, Δ[Ca]_jct).

The increase in L-type Ca²⁺ channel permeability (P _CaL) had the most pronounced effects on APD₆₀ and Ca²⁺ signals, by increasing action potential duration and enhancing maximum Ca²⁺ peaks. The effects of G _Kr, G _to, and K _NCX, while less pronounced than P _CaL, were still significant. Figure 2 also shows that 10% increases in G _Kr and G _to decreased APD₆₀ and Ca²⁺ peaks while 10% increase in K _NCX decreased Ca²⁺ peaks but increased APD₆₀. The increase in maximal NaK pump rate (K _NaK) had still detectable but minor effect, by decreasing both APD₆₀ and Ca²⁺ peaks. The changes in SR parameters (K _rel⁡, K _up, and K _leak) by 10% had negligible effects on APD₆₀ and Δ[Ca]_i whereas the submembrane and junctional Ca²⁺ peaks (e.g., Δ[Ca]_SL and Δ[Ca]_jct) were most affected. Figure 2 shows that 10% increases in K _rel⁡ and K _up increased Δ[Ca]_SL and Δ[Ca]_jct while K _leak had the opposite effect. Interestingly, 10% increase in background Cl⁻ conductance (G _ClBk) showed similar magnitude as G _Kr and G _to and demonstrated the same effects in decreasing APD₆₀ and Ca²⁺ peaks. Furthermore, Nimrod/E had the advantage in predicting how 10% increases in two-parameter group can affect the model outputs. Nimrod/E predicts here that P _CaL and K_NCX combined, as well all other two-parameter group combinations (not shown in Figure 2), had slight or no effect on the selected cellular biomarkers (APD₆₀, Δ[Ca]_i, Δ[Ca]_SL, and Δ[Ca]_jct). The plots in Figure 3 confirm further the specific, quantitative predictions made by PLS and Nimrod/E for the effects of 10% increases in P _CaL, K _NCX, G _Kr, G _to, K _NaK, and G _ClBk on AP morphology and Ca²⁺ transients.

Figure 3.

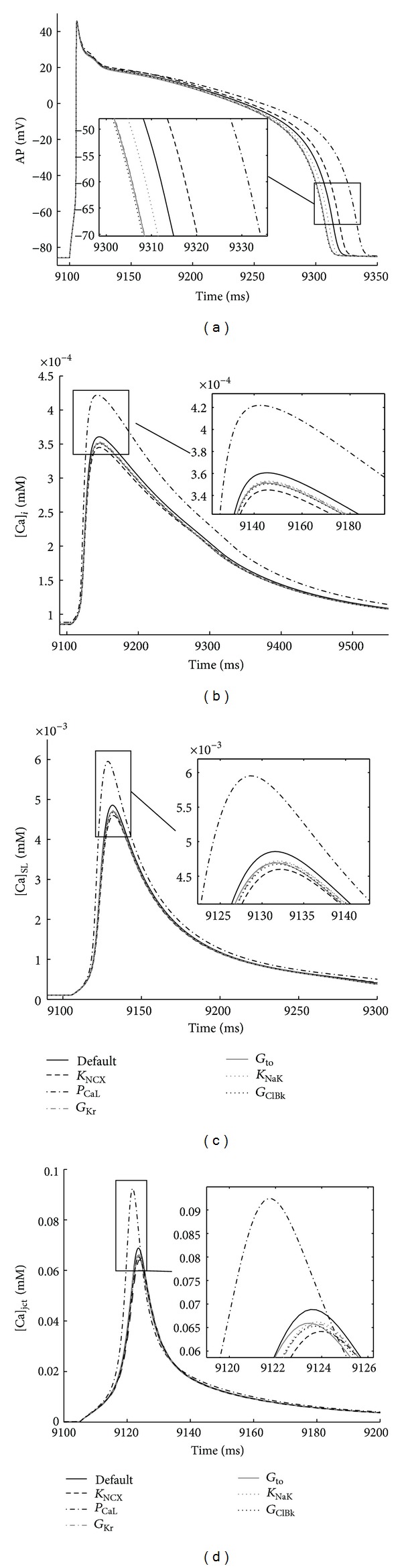
Verification of ion conductance sensitivity predictions. Steady-state AP and Ca²⁺ transients (recorded 9-10 s) in each of the three non-SR compartments in response to 1 Hz stimulus. The predicted changes in APD₆₀ and Ca²⁺ peaks (see Insets also) are consistent with the generated by Nimrod/E and PLS outputs with respect to 10% increases in transporters' conductance. Control conductance values (black solid line) and 10% increases in K _NCX (black dashed line), P _CaL (black dash-dot line), G _Kr (gray dash-dot line), G _to (gray solid line), K _NaK(gray dotted line), and G _ClBk (black dotted line).

3.2. Effects of Changes in Membrane Transporter Distributions on AP Morphology and Intracellular Ca²⁺ Dynamics

In Shannon et al. model, cell was separated into four lumped compartments (see Figure 1): the junction junctional cleft (0.077% of total cell volume assuming 11% of the surface membrane junctional), the subsarcolemmal space (2% of total cell volume assuming 89% of the membrane nonjunctional) the bulk cytosol space (65% of total cell volume with remainder of the volume accounted for by mitochondria) and the SR (3.5% of total cell volume). The L-type Ca²⁺ channels were assumed concentrated within the junctional membrane such that 90% of total number were located there while all other membrane transporters (Na⁺ channels, Na⁺ leak, Na⁺/K⁺ pump, slow delayed rectified K⁺ channel, Ca²⁺ activated Cl⁻ channel, Ca²⁺ leak, Na⁺/Ca²⁺ exchanger, and sarcolemmal Ca²⁺ pump) were considered evenly distributed across the sarcolemma with 11% in the junctional cleft and 89% in the subsarcolemmal compartment [1].

To examine how the changes in ion transporter distributions affect the selected cellular biomarkers (APD₆₀, Δ[Ca]_i, Δ[Ca]_SL, and Δ[Ca]_jct), we performed systematic analysis, increasing by 5% the basic Fx _j(jct) while decreasing Fx _j(SL) to keep total number of transporter protein complexes within the sarcolemma unchanged; that is, Fx _j(jct) + Fx _j(SL) = 1 (the appendix, Table 2). Figure 4 shows that PLS and Nimrod/E analysis again showed consistent results. The 5% increase in L-type Ca²⁺ channels fraction in the junctional cleft (Fx _CaL(jct) = 0.945) had the most pronounced effect on the model outputs, decreasing APD₆₀ and Ca²⁺ peaks. The results also suggest that 5% increase in the junctional Na⁺-Ca²⁺ current (Fx _NCX(jct) = 0.1155) prolonged APD₆₀ while slightly affected Ca²⁺ peaks in the junctional cleft and subsarcolemmal and bulk cytosol compartments. The 5% increase in the junctional I _Cl(Ca) (Fx _Cl(Ca)(jct) = 0.1155) had similar effect on all model outputs as the increase in Fx _CaL(jct) but with much smaller magnitude. Results in Lenth plot (Figure 4) for the four model outputs reveal that “Fx _NCX(jct) Fx _CaL(jct) combination” as well all other two-parameter combinations had insignificant impact (not shown in Figure 4). Additional analysis of the data has been done by increasing each Fx _j(jct) by 5% and decreasing Fx _j(SL) (j = CaL, NCX, Cl(Ca)) while keeping all other model parameters constant. The results in Figure 5 confirm the predictions made by both PLS and Nimrod/E methods.

Table 2.

Fractions of total “j” flux varied in the model.

Definition		Symbol	Baseline value
1	Fraction of total Na+ current in junctional cleft	Fx Na(jct)	0.11
2	Fraction of total background Na+ current in junctional cleft	Fx NaBk(jct)	0.11
3	Fraction of total Na+-K+ current in junctional cleft	Fx NaK(jct)	0.11
4	Fraction of total slow delayed rectifier K+ current in junctional cleft	Fx Ks(jct)	0.11
5	Fraction of total Ca-activated Cl− current in junctional cleft	Fx Cl(Ca)(jct)	0.11
6	Fraction of total Ca-dependent L-type Ca2+ current in junctional cleft	Fx CaL(jct)	0.9
7	Fraction of total background Ca2+ current in junctional cleft	Fx CaBk(jct)	0.11
8	Fraction of total Na+-Ca2+ current in junctional cleft	Fx NCX(jct)	0.11
9	Fraction of total sarcolemmal Ca2+ pump current in junctional cleft	Fx SLCaP(jct)	0.11

Notes: fraction of total j flux in SL (Fx _j(SL) = 1 − Fx _j(jct)). In the Shannon et al. article [1]  Fx _Cl(jct)  corresponds to  Fx _Cl(Ca)(jct). The baseline total “j” flux fraction values used in this study are the same as in [1].

Figure 5.

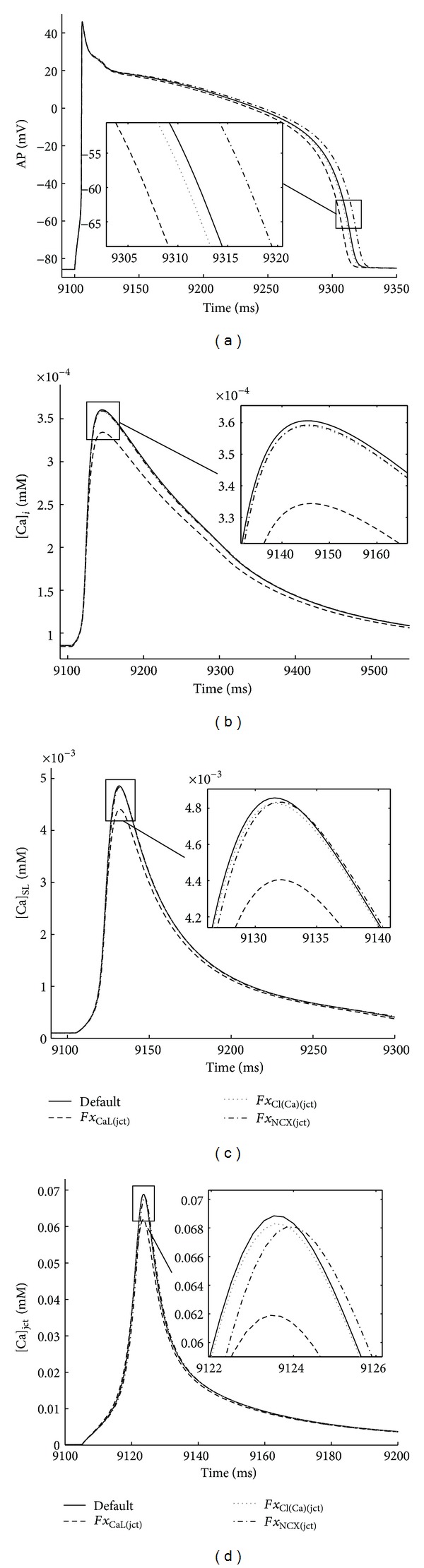
Verification of transporter distribution sensitivity predictions. Steady-state model outputs (recorded 9-10 s) in response to 1 Hz periodic pulse. The predicted alterations in APD₆₀ and Ca²⁺ peaks (see Insets also) are consistent with the generated by Nimrod/E and PLS results with respect to 5% increases in transporters' fraction in the junctional cleft. Default j-currents' fractions in junctional cleft (black solid line) and 5% increases in Fx _CaL(jct) (black dashed line), Fx _Cl(Ca)(jct) (grey dotted line), Fx _NCX(jct) (black dash-dot line).

3.3. Effects of 10% Changes in Diffusion Constants on AP Morphology and Intracellular Ca²⁺ Dynamics

The effects of changes in default parameters describing Ca²⁺ and Na⁺ diffusion between junctional and subsarcolemmal compartments and between subsarcolemmal and bulk compartments were also analyzed in this study (the appendix, Table 3). Figure 6 shows that 10% increases in basal D _Ca(jct-SL) altered all model outputs, prolonging APD₆₀ and increasing Δ[Ca]_i and Δ[Ca]_SL but decreasing Δ[Ca]_jct. Moreover 10% increases in basal D _Ca(SL-i) value shortened APD₆₀ and increased Δ[Ca]_i, Δ[Ca]_jct, and Δ[Ca]_SL. Interestingly, 10% increases in basal D _Na(jct-SL) and D _Na(SL-i) values in all three compartments had no effect on APD₆₀ and Ca²⁺ peaks. Nimrod/E analysis also suggests that two-level interaction between D _Ca(jct-SL) and D _Ca(SL-i) had a minor effect on increasing Δ[Ca]_i while APD₆₀, Δ[Ca]_SL, and Δ[Ca]_jct were unaffected. Figure 7 additionally confirms the PLS and Nimrod/E predictions for the effects of 10% increases in D _Ca(jct-SL) and D _Ca(SL-i) on AP morphology and Ca²⁺ transients.

Figure 7.

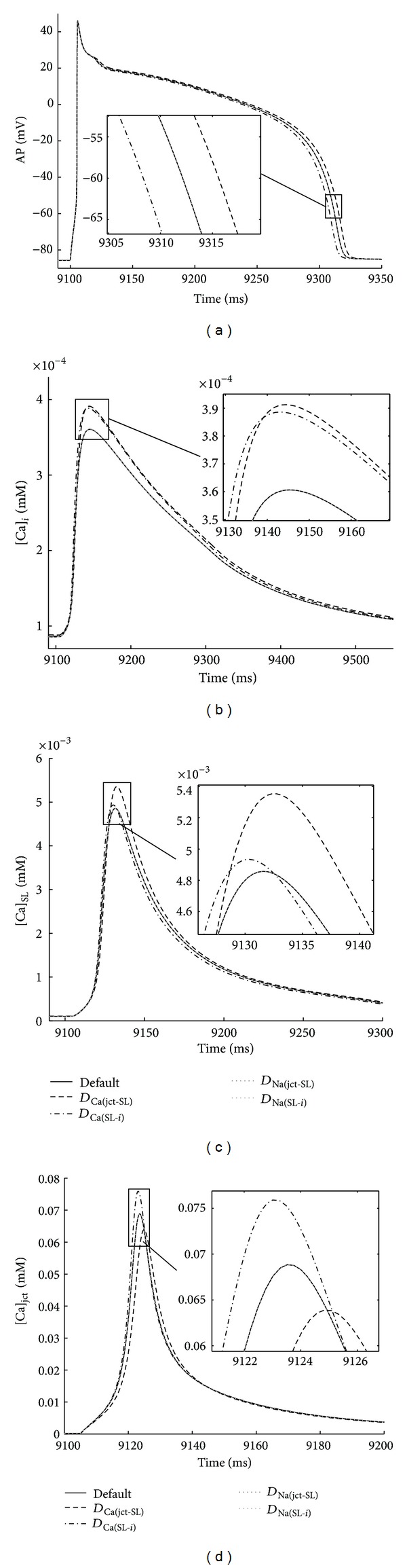
Verification of Ca²⁺ and Na⁺ diffusion sensitivity predictions. Steady-state AP and Ca²⁺ transients (recorded 9-10 s) in three non-SR compartments in response to 1 Hz stimulus. The relative changes in APD₆₀ and Ca²⁺ peaks (see Insets also) are consistent with predictions generated by Nimrod/E and PLS with respect to 10% increases in Ca²⁺ and Na⁺ diffusion constants. Control diffusion coefficients (black solid line) and 10% increases in D _Ca(jct-SL) (black dashed line), D _Ca(SL-i) (black dash-dot line), D _Na(jct-SL) (gray dotted lines), D _Na(SL-i) (light gray dotted lines).

4. Discussion

The main goal of this study was to perform a systematic investigation on how small variations in ionic currents and Ca²⁺ and Na⁺ diffusion coefficients modulate ventricular myocyte electrophysiology and Ca²⁺ dynamics in rabbit ventricular myocytes. To determine the most influential parameters controlling underlying subcellular mechanisms, we applied and compared the outcomes from two sensitivity analysis toolkits (PLS and Nimrod). The sensitivity of selected biomarkers (APD₆₀, Δ[Ca]_i, Δ[Ca]_SL, and Δ[Ca]_jct) to the alterations in ionic currents' properties and intracellular ionic transport was quantified using the Shannon et al. ionic model in rabbit ventricular cells, the predictive power of which has been demonstrated previously [1, 2].

4.1. Effects of Small Variations in Ionic Currents on AP Duration and Ca²⁺ Transients

Using parameter sensitive analysis, Romero et al. quantified the sensitivity of AP properties, Ca²⁺ and Na⁺ dynamics, and their rate dependence with respect to ±15%, ±30%, ±45%, and ±100% variations in the main transmembrane currents' conductance [9]. It remains, however, poorly understood how small variations (±5, ±10%) in ion currents conductance affect cellular biomarkers. Our next studies contribute to filling up this knowledge gap further. Analysis suggests that the selected biomarkers were strongly dependent on I _Ca current properties. Results indicate that 10% increase in maximal permeability of L-type Ca²⁺ channel (P _CaL), with respect to other currents' conductance changes, most notably affected APD₆₀ and Ca²⁺ transients' peaks at 1 Hz. Our predictions for the effects of P _CaL on APD and cytosolic Ca²⁺ peak are also consistent with reported data in rabbit ventricular myocytes after applications of I _Ca blockers [5, 9, 29] or in cells with high L-type Ca²⁺ channel density [30]. The effects of 10% increase in G _Kr, G _to, K _NCX, or K _NaK on cellular biomarkers, while less pronounced than P _CaL, were still detectible. Our predictions for K _NCX increase at 1 Hz are in qualitative agreement with data in ferret myocytes [31] and data supporting APD prolongation following I _NCX block reported in some experiments in rabbit cardiomyocytes [32, 33]. Several studies in rabbit ventricular cells report also a strong effect of I _NCX in modulating systolic [Ca]_i transient [31–34] while others report only a moderate effect [35], similar to our predictions for Δ[Ca]_i. Results demonstrate also that 10% increase in K _NCX slightly decreased [Ca]_jct and [Ca]_SL peaks. Increase in G _Kr and G _to at 1 Hz resulted in APD shortening, which is consistent with experiments in rabbit ventricular myocytes [36, 37]. Important role of I _to in modulating Ca²⁺ transients through its effects on I _Ca and I _NCX during AP repolarization period has been suggested [38, 39]. Slight effects, however, due to 10% increase in G _to at 1 Hz on Ca²⁺ peaks are predicted here. Furthermore, at stimulus frequency of 2.5 Hz, Romero et al. report I _NaK (±30% changes or severe I _NaK block; 0–8 min) as important influent current in most simulated cellular biomarkers, including APD₆₀ [9]. Our studies quantitatively confirmed Romero et al. findings at 2.5 Hz (data not shown). At 1 Hz, however, the effect of ±30% changes in K _NaK (increment 5%, 0–8 min) on APD₆₀ was less pronounced. The main reason for this observation was that the predicted changes in [Na]_i were smaller at 1 Hz (20–100 μM) versus 1–1.5 mM at 2.5 Hz, in this way affecting differently I _NaK and I _NCX activities. These results indicate that the stimulus frequency is important factor regulating the electrophysiological biomarkers. Accordingly, because the Shannon et al. model mimics rabbit electrophysiology more accurately at normal pacing rates of 1 Hz [9], the model predictions for the effects of changes of ion current conductivities at faster rates should be considered with caution. Interestingly, 10% increase in Cl⁻ background current (I _ClBk), which is a new feature of the Shannon et al. model, showed a negative relationships with four outputs (APD₆₀, Δ[Ca]_i, Δ[Ca]_SL, and Δ[Ca]_jct) of approximately similar magnitude as for G _to or G _Kr. Experimental data reporting the effects of I _ClBk on rabbit ECC are missing in the literature however. Another interesting finding is the relatively small sensitivity of the biomarkers to 10% increases in G _Na, G _Na,b, P _CaK, P _CaNa, G _Ca,b, G _to,f, G _Ks, G _K1, G _Cl(Ca), K _rel⁡, K _leak, K _up, and K _pCa factors at 1 Hz. Thus, to further test the predictive power of the Shannon et al. model we examined the effects of severe currents' and SR-fluxes' block (up to 100%) (data not shown). In qualitative agreement with experiment [9] our studies show that (1) APD₆₀ was highly sensitive to 100% I _Na, I _K1, K _rel⁡, and K _up and block and less sensitive to I _CaK, I _Cl(Ca), I _to,f, and I _pCa inhibition while 100% block of I _Na,b, I _CaNa, I _Ca,b, and I _Ks currents and SR Ca²⁺ leak (K _leak) had small or no effect; (2) steady-state Ca²⁺ peaks were strongly affected when I _Na, I _Ca,b, and SR Ca²⁺ fluxes (K _rel⁡, K _leak, and K _up) were inhibited whereas 100% block I _pCa, I _Cl(Ca), I _CaK, I _K1, and I _to,f had less pronounced effects. New measurements in rabbit ventricular myocytes are needed to define the relative importance of G _Na, G _Na,b, P _CaK, P _CaNa, G _Ca,b, G _to,f, G _Ks, G _K1, G _Cl(Ca), K _rel⁡, K _leak, K _up, and K _pCa in determining physiological responses due to the small changes in these factors at 1 Hz and to test further the capabilities and limitations of the Shannon et al. model. Using Nimrod/E, we also examined how simultaneous changes in two transmembrane currents affect APD and Ca²⁺ dynamics. Our analysis suggests that 10% increase in both P _CaL and K _NCX had minor effect at 1 Hz. Additionally, Nimrod/E showed that simultaneous increases in control I _Ca and K⁺ related currents had slight or no effect (data not shown). Furthermore, the predicted effects of ±5% changes in channels conductance were identical to those with ±10% variations (data not shown). Such insights, coming from mathematical models, might be useful in searching new avenues for development of methodologies to predict drug action effects on behavior of cardiac cells. For example, most I _Ca inhibitors suppress partially K⁺-related currents also; therefore the balance of these currents is critical for predicting I _Ca-related drug action.

4.2. Effects of Variations in Membrane Transporters Distribution on AP Duration and Ca²⁺ Transients

Experimental studies have demonstrated that in rabbit ventricular myocytes marked variations in the distribution of ion transports along the surface membrane probably exist [1, 40–42]. Using reaction-diffusion models, recently we demonstrated that the subcellular Ca²⁺ signals are highly sensitive to I _Ca and I _NCX fluxes distributions via the sarcolemma [13, 16, 19, 20]. In these spatial models, however, the cell electrophysiology was simplified; equations describing I _Ca, I _NCX, I _pCa, and I _Ca,b properties were only included; and AP dynamics were not reproduced. Additionally, small variations in L-type Ca²⁺ channels density in junctional cleft have been suggested to lead to large changes in control SR Ca²⁺ release, subcellular Ca²⁺ transients, and AP waveform [4, 5]. Thus, we used PLS and Nimrod/E to gain further insights into how ±5% changes in L-type and other ion transporters' distributions influence control AP and Ca²⁺ transients. We evaluated the biomarkers' sensitivity to 5% increases in the fraction of total ionic current in the junctional cleft (Fx _j(jct)) assuming total number of transporters within the sarcolemma unchanged; that is, Fx _j(jct) + Fx _j(SL) = 1. Our results yielded three channel distributions (Fx _CaL(jct), x _NCX(jct), and Fx _Cl(Ca)(jct)) that significantly affect the model outcomes of interest (i.e., APD₆₀, Δ[Ca]_i, Δ[Ca]_SL, and Δ[Ca]_jct). Increasing by 5% the density of L-type Ca²⁺ channels in the junctional cleft (while decreasing by 45% I _Ca density in SL compartment to keep Fx _CaL(jct) + Fx _CaL(SL) = 1) had the strongest effect on both APD₆₀ and Ca²⁺peaks, decreasing APD₆₀ and [Ca]_i, [Ca]_SL, and [Ca]_jct peaks. The reason for the predicted decrease in [Ca]_jct was the strongly increased rate of Ca²⁺ transfer from the junctional cleft to the submembrane space evoked by the 5% increase of Fx _CaL(jct) and reduced I _Ca (~45%) into the SL compartment. The predicted decreases into [Ca]_SL peak and APD₆₀ were also consequence of Fx _CaL(SL) reduction to 45% though Ca²⁺ flux from the cleft was increased. The drop in [Ca]_SL evoked decrease in the rate of Ca²⁺ transfer from the SL to cytosolic compartment thus causing drop in [Ca]_i peak as well. Our studies also showed that the effects of I _NCX redistribution were quite different. The 5% increase in Fx _NCX(jct) (while decreasing by 40-41% I _NCX density in SL compartment to keep Fx _NCX(jct) + Fx _NCX(SL) = 1) prolonged APD₆₀to approximately the same magnitude as for I _Ca and slightly decreased the control Ca²⁺ peaks. Significant effects due to I _Ca redistribution and negligible effects due to I _NCX redistribution on the local and global Ca²⁺ transients' peaks were also found using our reaction-diffusion model in rabbit ventricular cells [20]. Calcium activated chloride current (I _Cl(Ca)) has been extensively studied [43–45]. Experimental data in rabbit ventricular myocytes suggest that I _Cl(Ca) is strongly temperature dependent (very small at room temperature but substantial at 35°C–37°C); I _Cl(Ca) can be eliminated by blocking I _Ca; and I _Cl(Ca) may normally facilitate rapid repolarization when SR Ca²⁺ load and release are high. To bring further insights into the effects of I _Cl(Ca) properties on ECC, we examined how 5% increase in I _Cl(Ca) density in the junctional cleft (assuming Fx _Cl(Ca)(jct) + Fx _Cl(Ca)(SL) = 1) may affect the cell electrical activity and Ca²⁺ signaling. Interestingly, although much less pronounced than Fx _CaL(jct) variations, changes in Fx _Cl(Ca)(jct) were able also to shorten APD₆₀  and provide negative feedback on cell Ca²⁺ load. Negligible effects due to 5% increases in I _Na, I _Na,b, I _NaK, I _Ks, I _Ca,b, and I _pCa currents' fractions in the junctional cleft were found. Finally, Nimrod/E predicted slight or no effect on model outputs when Fx _CaL(jct) and Fx _NCX(jct), or any other two-parameter Fx _j(jct) groups, were combined. These model studies imply that more accurate experimental knowledge of I _Ca, I _Cl(Ca) and I _NCX, fluxes distributions is needed to better understand the physiological role of I _Cl(Ca) current, the local Ca²⁺ signaling, and the electrical cell activity. Furthermore, the estimates of % total flux in junctional cleft versus submembrane space under control conditions are still under debate. Additional quantification of the model sensitivity to ±10% changes in Fx _CaL(jct) or ±10% and ±15% variations in other transporters' densities in the cleft (not done in this study) may provide a more convincing conclusions.

4.3. Effects of Small Variations in Intracellular Ion Transport on AP Duration and Ca²⁺ Transients

In the Shannon et al. model the diffusion of Ca²⁺ and Na⁺ ions was considered where (1) the junctional compartment communicates only with the SL compartment, (2) the SL compartment with the junctional and the bulk cytosolic compartments, and (3) the bulk cytosolic compartment only with the SL compartment. The values of the effective diffusion coefficients for Ca²⁺ and Na²⁺ were average values measured in different cardiac tissues and species under control conditions. In the literature, however, these estimates are contradictable [1, 8, 10–20]. In this study, we tested how small changes (±5, ±10%) in suggested diffusion coefficients may influence the model outputs. We used PLS and Nimrod toolkits to determine the most influential ion diffusion parameter(s) governing the properties of the electrical signal (such as APD₆₀) and of the Ca²⁺ signal (such as peak level of Ca²⁺ transient in the junctional cleft, subsarcolemmal space, and bulk cytosol). While 10% increases in basal Ca²⁺ diffusion coefficients (D _Ca(jct-SL) and D _Ca(SL-i)) had pronounced effects on the model outputs, no visible changes in all selected biomarkers were detected due to 10% increases in Na⁺ diffusion coefficients (D _Na(jct-SL) and D _Na(SL-i)). Interestingly marked effects on both APD₆₀ and Ca²⁺ peaks were predicted when Na⁺ diffusion was blocked, assuming D _Na(jct-SL)and D _Na(SL-i) zeros shorten APD₆₀ and decreased [Ca]_i, [Ca]_SL, and [Ca]_jct peaks (data not shown). Our results also demonstrate that accelerating Ca²⁺ transfer from junctional to submembrane space (e.g., increasing D _Ca(jct-SL)), (1) sensitively decreased Ca²⁺ peak in the junctional cleft and prolonged [Ca]_jct time to peak, (2) enhanced [Ca]_SL and [Ca]_i peaks, and (3) prolonged APD₆₀. The effects of D _Ca(SL-i) increase were quite different. Accelerating Ca²⁺ transfer from the SL compartment to the bulk cytosol (e.g., increasing D _Ca(SL-i)) shortened APD₆₀ and enhanced all Ca²⁺ transients' peaks. In addition, D _Ca(SL-i) increase most significantly enhanced [Ca]_jct peak while the control [Ca]_SL peak was less affected. Possible reason for the predicted increase in [Ca]_jct peak, due to D _Ca(SL-i) increase, was enhanced [Ca]_i which promoted increase in the SR load (i.e., [Ca]_SR) in this way causing additional Ca²⁺ release from the SR and consequent elevations in [Ca]_jct and [Ca]_SL, respectively. The enhanced [Ca]_SL transient produced faster Ca²⁺-dependent inactivation of I _Ca, thus leading to APD shortening. Nimrod/E showed also that simultaneous increases in control D _Ca(jct-SL) and D _Ca(SL-i) slightly increased Δ[Ca]_i while all other biomarkers remained insensitive to the changes in any other two-level parameter combinations. Also predicted relative effects of ±5% changes in intracellular ion transport were identical to those of ±10% variations (data not shown). In summary, our results reveal that small variations in diffusion coefficients for Ca²⁺ may impact sensitively the cell electrical activity and Ca²⁺ homeostasis. New and more precise estimates of the effective Ca²⁺ and Na⁺ diffusion constants are needed to better understand ECC in rabbit ventricular myocytes under control and certain pathologies.

We need to acknowledge that although we demonstrated good correlation with experiment, the results of sensitivity analysis strongly depend on the model details and simplifications. For example, in the lumped Shannon et al. model the ionic diffusion from junctional cleft to cytosolic compartment goes solely through subsarcolemmal space which is questionable with regard to the contact areas between these compartments [19]. In addition, in all studied cases the variations of intracellular potassium concentration were disabled (i.e., d[K]_i/dt = 0 in Shannon's MatLab code) and whether or not this drawback was eliminated in the Romero's code or in recent modifications of the Shannon's code is unclear [4–7, 9]. This limitation leaded to the following: (1) fast stabilisation of the model for [Ca]_i and AP (after 6–8 s until 8 min); (2) [Na]_i appeared stable after ~200 s; (3) diastolic [K]_i remained unchanged in the interval 0 ≤ t ≤ 8 min. Thus, models neglecting slow intracellular concentration changes in [K]_i produced mainly by Na/K pump need to be revised further. Finally, the t-tubule compartment, the ion diffusion between the t-tubule lumen and bulk extracellular space, and the mitochondrial Ca²⁺ fluxes were omitted [46–50]. These are likely to have important impact on predicted AP and Ca²⁺ profiles as well.

5. Conclusions

Our studies demonstrate that parameter sensitivity approaches can be used to obtain new insights into relationships between model parameters, model outputs, and experimental data. More specifically, the simulation results provided information on how small variations in the ionic currents and intracellular Ca²⁺ and Na⁺ diffusion modulate ventricular myocyte electrophysiology and Ca²⁺ dynamics in rabbit ventricular myocytes at 1 Hz. We found that APD₆₀ and Ca²⁺ peaks are (1) highly sensitive to 10% increase in I _Ca, while the effects of I _NCX, I _NaK, I _Kr, I _to, and I _ClBk were moderate, and (2) insensitive to 10% increases in all other Ca²⁺, Na⁺, and K⁺ transmembrane currents and SR Ca²⁺ fluxes. The myocyte electrical activity is highly sensitive to 5% variations in I _Ca and I _NCX and less sensitive to I _Cl(Ca) redistribution between junctional cleft and submembrane space. Small changes in submembrane and cytosolic diffusion coefficients for Ca²⁺, but not in Na⁺ diffusion coefficients, may impact notably the myocyte contraction. This study highlights the need for additional and more precise experimental data and further updating and testing of the Shannon et al. model and its recent modifications to fill specific knowledge gaps related to rabbit ventricular electrophysiology and intracellular Ca²⁺ signaling.

Glossary

Abbreviations

ECC:

Excitation-contraction coupling

AP:

Action potential

APD₆₀:

Action potential duration at 60% repolarization

SL:

Sarcolemmal membrane

SR:

Sarcoplasmic reticulum

RyR:

Ryanodine receptor

SERCA2:

SR Ca²⁺ ATPase pump

TnC:

Troponin C

NIMROD:

Parameter modeling toolkit for sensitivity analysis

PLS:

Partial least square tool.

Membrane Currents

I_Na:

Na⁺ current

I_Na,b (I_NaBk):

Na⁺ background current

I_Ca (I_CaL):

L-type Ca²⁺ channel current

I_Ca,b (I_CaBk):

Ca²⁺ background current

I_to,f:

Fast transient outward K⁺ current

I_to (I_to,s):

Slow transient outward K⁺current

I_Kr:

Rapid delayed rectifier K⁺ current

I_Ks:

Slow delayed rectifier K⁺ current

I_K1:

Inward rectifier K⁺ current

I_Cl(Ca):

Ca²⁺ activated Cl⁻ current

I_ClBk:

Cl⁻ background current

I_NaK:

Na⁺-K⁺ pump current

I_NCX:

Na⁺-Ca²⁺ exchanger current

I_pCa (I_SLCaP):

Sarcolemmal Ca²⁺ pump current.

Concentrations

[Ca]_i:

Cytosolic Ca²⁺ concentration

[Ca]_SL:

Subsarcolemmal Ca²⁺ concentration

[Ca]_jct:

Junctional cleft Ca²⁺ concentration

[Ca]_SR:

SR Ca²⁺ concentration

[Na]_i:

Cytosolic Na⁺ concentration

[K]_i:

Cytosolic K⁺ concentration.

Appendix

See Tables 1, 2, and 3.