On the Need for Mechanistic Models in Computational Genomics and Metagenomics

Abstract

Computational genomics is now generating very large volumes of data that have the potential to be used to address important questions in both basic biology and biomedicine. Addressing these important biological questions becomes possible when mechanistic models rooted in biochemistry and evolutionary/population genetic processes are developed, instead of fitting data to off-the-shelf statistical distributions that do not enable mechanistic inference. Three examples are presented, the first involving ecological processes inferred from metagenomic data, the second involving mechanisms of gene regulation rooted in protein–DNA interactions with consideration of DNA structure, and the third involving existing models for the retention of duplicate genes that enables prediction of evolutionary mechanisms. This description of mechanistic models is generalized toward future developments in computational genomics and the need for biological mechanisms and processes in biological models.

Introduction

A recent opinion piece in the journal Science (Brunham and Hayden 2012) described perhaps the biggest hurdle in the move to personalized genomics as the bioinformatics of analyzing personal genomic data. Although this may be true, the hurdles are even bigger than commonly appreciated. Biological models that actually incorporate biology are an important component of the future success of personalized genomics. Disease risk is typically assessed using purely statistical association measures (not rooted in biological processes), as is the reverse problem of associating single nucleotide polymorphisms (SNPs) with a disease (see, e.g., Stephens and Balding [2009] for a discussion of the underlying statistics). Given the recent exponential expansion of the human population (Keinan and Clark 2012), the number of rare variants that are uncharacterized medically is expected to be large. Further, given the context-dependent nature of the functional effects of mutations, especially in an expanding outbred population, nonsynonymous SNPs (nsSNPs) may cause disease in some genetic backgrounds and not in others. Using statistical methods that ignore known biological processes to analyze such data does not appear to be the best strategy.

Moving from biomedicine to basic molecular biology and especially to comparative genomics, we are presented with a wealth of sequence and functional data. Reductionism in molecular biology and biochemistry has missed the context-dependence of changes as well as the larger picture of cell and organismal functions. As molecular biology moves from data collection to theory development, a theoretical foundation that enables mechanistic analysis will be necessary. While motivated by questions in basic molecular biology, it will have clear applications in human health as well as in evolutionary biology.

What Differentiates a Mechanistic Model from a Phenomenological Model?

A major theme of this work will be to call for mechanistic models as differentiated from off-the-shelf distributions and phenomenological models. Rodrigue and Philippe (2010) have presented a nice discussion of this topic; although for reasons outlined in this article, we would go further than they do in questioning the utility and reliability of parameterization of phenomenological models. In reality, there is a continuum between these extremes, and the mechanistic nature of the model also depends on the hypothesis being addressed. First, we will now define what we mean with a mechanistic and phenomenological model.

Two key features characterize mechanistic models. The model to fit the data bears some relationship to the process that generated the data and the parameters of the model are interpretable with respect to the underlying process. In many cases, it is the parameterization of the model that enables mechanistic inference. Models can be mechanistic for some hypotheses but not for others. All models necessarily have some level of coarse graining (approximation of processes to make models simpler and more tractable), but it is important that the coarse graining does not affect estimation of parameters used for mechanistic interpretation.

One important concern is that the parameterization of the model is such that the relationship between the model and what is being fit is well understood. The model space consists of a continuum of mechanistic models ranging from the simplest to the most complicated models. The parameters in the mechanistic models should be clearly biologically interpretable, and the importance of including model parameters is testable using likelihood ratio tests or standard model selection criteria such as Akaike information criteria (AIC), Bayesian information criteria, and goodness-of-fit tests. Validating the robustness of mechanistic inference is another concern, and this discussion is extended in the section below on validating mechanistic models.

By contrast, the nonmechanistic models utilize off-the-shelf probability distributions that are fit to the data. As the parameters in the assumed probability distribution do not have biological interpretations, the inference based on the off-the-shelf distribution may not be able to address the biological questions of interest.

Examples of Mechanistic Models in Evolution and Ecology

Detailed examples of mechanistic and phenomenological models for various hypotheses are given below. We start with an example from evolutionary biology. In the field of evolutionary biology, mechanistic models have roots dating back 150 years. In the mid-19th century, realizing that similar species are likely due to shared ancestry, Darwin introduced a mechanistic model describing the emergence and disappearance of species, combining micro-evolutionary processes with macro-evolutionary processes, which we call natural selection. More recently, a mathematical backbone to the evolution of species has begun to be developed with scientists fitting distributions to species abundance curves. However, identifying that, for example, a lognormal curve fits the empirical data well or not well tells us little about the underlying mechanistic speciation and extinction process. Thus, mechanisms producing these abundance curves have been proposed, which are based on modeling population dynamics, niche partitioning, and spatial distribution (for a review, see McGill et al. 2007) and relating ecological and evolutionary processes to observed data. Although these evolutionary and ecological models are controversial, the mechanistic approaches provide a tool to test evolutionary and ecological hypotheses which was not possible by simply fitting off-the-shelf distributions (McGill et al. 2007). Combining theory in evolutionary ecology and metagenomic data will be discussed later in this article.

In further steps in evolutionary biology, one wishes to reconstruct the ancestry of the species and individuals of a species in a population. This is typically done using molecular sequence data, where macroevolutionary processes are linked to changes in, for example, protein-coding genes. Sequence data have signal from multiple sources, including ancestry, selection and function (with the possibility of convergence), and shifting population genetic parameters. In systematics, it is commonly assumed that a tree is reflective of ancestry, even if the model used to generate the tree is phenomenological at the level of inference. The problems with this and the need for more mechanistic amino acid models (which complement nucleotide models) are discussed in more detail in Liberles et al. (2012). Ideally, these models (at both the nucleotide and the amino acid levels) should differentiate between signals from ancestry and signals from other sources if the goal is to obtain a tree reflective of ancestry.

More generally, in phylogenetic analyses, each column of an alignment of n nucleotide sequences may have 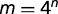possible patterns. Let x_i be the count (or frequency) of pattern i along the alignments. Assuming that each site evolves independently, the probability distribution of the alignments is a multinomial distribution with parameters P = {p₁, p₂, … p_m}. The parameters in this model are simply the probabilities of observing particular patterns. As parameters P are not connected to the underlying substitution process along the lineages of a phylogenetic tree, it is impossible to use this model to estimate phylogenies or substitution rates, which are the primary goals of most phylogenetic studies. Although this nonmechanistic model can perfectly describe the observed patterns using a multinomial distribution, it is practically useless as it is incapable of making inference on the phylogeny-related parameters, even though the DNA sequence data contain phylogenetic information. On the other hand, a simple mechanistic phylogenetic model further describes parameters P as functions of a phylogenetic tree and rate parameters in the substitution model. With reparameterization of P, a mechanistic model builds a bridge between data and biological parameters. As the probability of a particular pattern observed in the sequence data varies upon the change in the topology of the phylogenetic tree and the substitution rates in the phylogenetic model, certain site patterns can be used to infer phylogenetic trees and substitution rates. In the nonmechanistic model, parameters P are the ultimate outputs of the substitution process running along the lineages of the phylogenetic tree, which makes it difficult to scrutinize the effects of individual parameters involved in the substitution process.

Of course, mechanistic models can also be mis-specified. The simple mechanistic model described above ignores the context-dependence of mutation, the population genetic process of fixation, linkage of sites, and specific types of selection. If the mis-specifications affect the type of inference being made or the interpretability of parameters for the question being asked, that is another potential concern. This would occur when, for example, parameters do not fit what they are intended to fit because the process is not sufficiently well captured by the structure of the model.

Linking Evolution to Molecular Biology with Mechanistic Models

In parallel to ecology and evolution, in thinking about building up a theory for molecular biology, where does one start? The human genome contains about 20,000 genes. These genes need to be expressed. Once expressed, they need to function. Functions typically include processes such as intermolecular binding, catalysis, and transport. These are all processes that are well described by physical chemistry and biochemistry. A growing field has developed methodologies to understand pathway functions in a cell based on the underlying physical rate constants of binding and catalysis (see Hoops et al. [2006] for an example of software that enables this).

Understanding the relationship between gene content, gene sequence, and biological function is also dependent on population genetic and evolutionary processes. The number of mutations segregating in a population will depend on the population size. The optimality of proteins for the selective constraints applied by evolution for proper function will depend on the effective population size (N_e). The amount of mutation available for selection to act upon and the strength of selection are considered forward and backward looking N_e (Nei 1987). They are not always the same and likewise, it is not clear how they ultimately relate to the number of individuals in a population. Ultimately, although the concept of effective population size is important, one needs a measure that relates to the expected biological mechanism controlling the process (e.g., the strength of selection).

Another important consideration is the difference between a mutation and a substitution, as their selective coefficients are known to show a different profile (Tamuri et al. 2012). For biomedical problems involving nsSNPs, mutations may have emerged recently and are likely to be deleterious. Substitutions have reached fixation in a population and show a distribution of selective coefficients that includes an enrichment for neutral and advantageous mutations over the background distribution observed for mutations.

We have previously reviewed models for amino acid substitution (Liberles et al. 2012; Teufel et al. 2012) and selection in the context of protein structure (Siltberg-Liberles et al. 2011). In this review, mechanistic insights into biological processes such as gene expression, bacterial species distributions, and finally gene content will be described. These processes call for new mechanistic models to use in computational genomics and metagenomics, whether for biomedical purposes, molecular biological purposes, or comparative/evolutionary purposes.

Gene Expression Analysis

Gene expression has been recognized as an important contributor to the genotype–phenotype mapping (Wray 2007; Gordon and Ruvinsky 2012). This is because there is a lot of mutational opportunity to affect phenotype through the mutational process acting on the genotype that affects gene expression. Although some studies on the evolutionary rates of promoter regions averaged over all DNA sites regardless of whether they were transcription factor binding sites or not, most recent studies have focused on transcription factor binding sites, including examination of binding site specificity of individual transcription factors (Wray 2007; Tsoy et al. 2012). The common goal is to describe the mechanistic link between transcription factor binding and gene expression. Current methods sometimes fail to identify common transcription factor binding sites linked to gene expression changes. One potential reason is the lack of context dependence of the mechanisms of transcription factor binding site functions. Current models still neglect the role of DNA in transcriptional regulation. For example, a recent study showed allosteric regulation of gene expression mediated by DNA itself (Kim et al. 2013). Although properties like intrinsic DNA curvature are also known to affect transcription levels (Gimenes et al. 2008), more fundamental are the helical properties of DNA. B-form DNA has a periodicity of 10.4 bp per turn (Saenger 1984). That means that transcription factors with binding sites separated by multiples of 10.4 will be more likely to interact (both directly and indirectly) than those separated by odd multiples of 5.2.

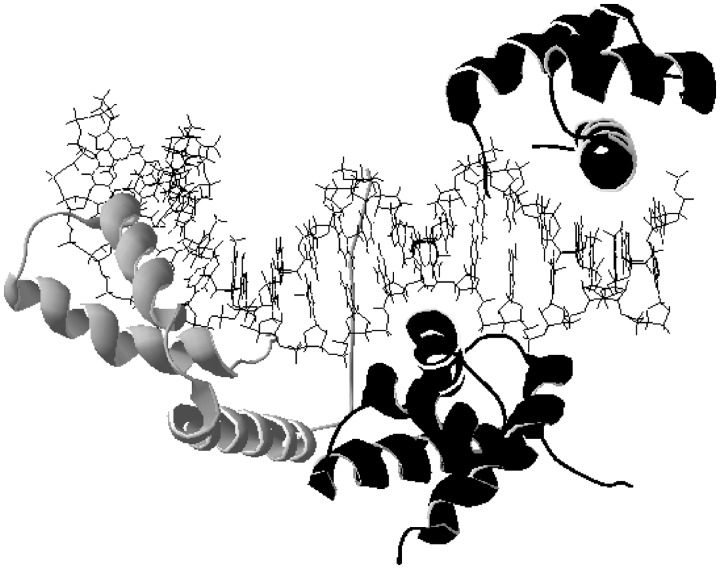
In figure 1, the structure of two transcription factors that bind adjacent sites in a promoter cooperatively to recruit a third transcription factor is shown (Williams et al. 2004). For this mechanism to operate, the interacting transcription factors need to be on the same face of DNA and over short distances, and this can be accomplished with bent structures when the phasing of the binding sites is maintained. This process can apply both to transcription factor interactions that are necessary to recruit additional transcription factors to the promoter (including the basal apparatus) and to proteins that dimerize on DNA (see Funnell and Crossley 2012 for a review). Both the insertion and deletion processes as well as the mutational process of binding sites fading in and out can lead to changes in spacing between transcription factor binding sites that can affect transcription. This larger level organization of promoter regions has not been described in computational approaches examining the evolution of gene expression from homologous promoter regions. Considering the physical structure of DNA as well as proteins in the evolution of gene expression may be important.

Fig. 1.—

The two domains of Oct1 (POU_S [bottom right] and POU_HD [top right]) and the SOX2 (left) transcription factors bind adjacently to the Hoxb1 element on DNA. Sox2 and POU_S interact by binding cooperatively to adjacent sites to facilitate the binding of co-activator OBF-1 (Williams et al. 2004). The image is generated from PDB file 1O4X.

To develop a model along these lines, not only the binding site sequence and its affinity for a transcription factor but also the spacing of the sites should be considered. At a first approximation that ignores the sequence context of the spacer regions and any local structure, the distance between sites (in base pairs) over a phylogeny describing the evolution of the promoters would be registered and considered with the helical structure to generate a modulator of effective local concentration for co-interaction as a component of the transcriptional regulation model.

Metagenomic Data Analysis

Metagenomics has emerged as a powerful approach for assessing microbial diversity in medical and environmental samples. Current data analysis in metagenomics has ignored biologically motivated bacterial species concepts and arbitrarily defined species as those with sequences showing less than 3% divergence. Several species concepts that are relevant to bacteria have been described (de Queiroz 2007; Hausdorf 2011). One such concept is a phylogenetic species concept that defines species as those separated by discrete breaks in the distribution of branch lengths of the phylogeny of individual sequences (to define clades), suggesting for various mechanistic reasons, that individuals form natural groups that can be defined as species when assayed phylogenetically. Another such concept is the ecological species concept that defines species by a combination of genetic similarity and ecological role. A third species concept for bacteria that has been recently introduced is more fluid across layers of biological organization, combining selfish gene thinking with population genetics to produce a continuous species concept called the goods hypothesis (McInerney et al. 2011).

In evaluating the 3% divergence level that is commonly used, it is well known that individuals with less than 3% divergence can be members of different species and more importantly, that important ecological niche differentiation can occur between individuals with less sequence divergence.

Two challenges are presented here. The first challenge is to use a more appropriate measure of species. In metagenomic analysis, all that is known about species is the sequence of sometimes only a single gene. As has been shown for Pseudomonas (Özen and Ussery 2012), the phylogenetic species concepts which would be the obvious choice do not obviously work, as there do not appear to be discrete breaks in branch length separating individuals. There may be large continua of sequences that play divergent ecological roles. But how could one discover ecological roles without defining species?

This now intertwines the first challenge with the second. Are there patterns of sequence co-occurrence in metagenomic data that one can look for, even if the species are not predefined a priori? To the extent that ecological interactions are not purely context-dependent, the answer is perhaps. There are patterns of ecological relationships between organisms that have well-defined mathematical relationships. This can then be examined by looking at co-occurrence data of different species, where the model is more complex in iteratively evaluating species clusters as part of the model-fit process. In this case, given the fluidity of species definitions in bacteria, the relationships between groups of individuals can be evaluated at different levels of sequence divergence, and natural ecological roles of individuals can be identified without a fixed a priori sequence-based species definition.

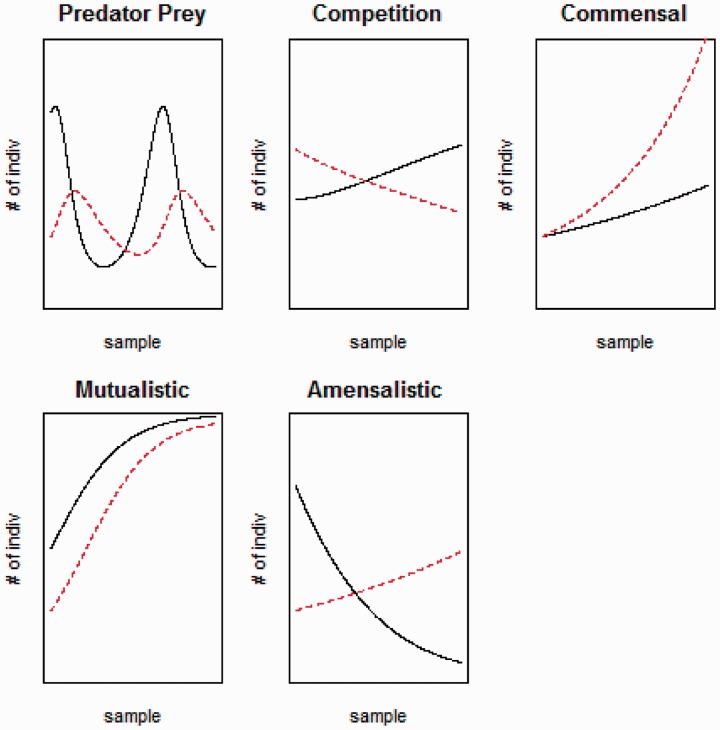
For example, the most famous set of ecological relationships are predator–prey dynamics, where the predator population changes with a time delay in response to the prey population changing, in the same direction. This then causes the prey population to change in the opposite direction with a time delay (although the nature of this delay is controversial and may be very small in some cases). Other relationships include competitive (anticorrelated), amensalistic (one is asymmetrically anticorrelated with another), mutualistic (correlated), and comensalistic (one is asymmetrically correlated with another) relationships. These relationships are shown in figure 2. Some of these relationships are well known in bacterial species. For example, a predator–prey relationship and the associated gene content underlying antibiotic production as prey species-specific chemical warfare between Myxococcus xanthus as predator and Escherichia coli or Micrococcus luteus as prey has been described by Xiao et al. (2011). The analysis suggested here represents a coarse-grained attempt to suggest an evolutionary-ecological basis for the analysis of metagenomic data.

Fig. 2.—

A set of ecological relationships with different nonindependence of species is shown. This includes the classic predator–prey cycles, competition leading to anticorrelation, commensalism where the presence of one species is beneficial to the other, mutualism where two species are positively correlated as mutually beneficial, and amensalism, where the presence of one species is deleterious to the other. The statistical signatures of these relationships can be identified in metagenomic data, where samples vary either across time or geographically.

One complicating factor with this type of correlative analysis is that relationships may be indirect rather than direct. This has led to controversy in the ecology community in the past, and as discussed later, even more mechanistic models may be necessary that also include proper null models with evolutionary and ecological process information (Connor and Simberloff 1979). The analysis ultimately becomes similar to the construction of genetic interaction networks in molecular biology, where with enough experiments, network architecture and direct interactions can be inferred. A framework of this nature for analyzing metagenomic data has not yet been developed.

It should be noted that this framework, although a step beyond the type of analysis that is currently applied to metagenomic data, is probably insufficiently mechanistic for a theoretical ecologist. Alternatively, more detailed frameworks exist that rather than modeling abundances directly model species interactions using parameters such as species interaction coefficients or even more detailed descriptions of interactions (see, e.g., Holt 1977; Morin 2011). Ultimately, more sophisticated models may be possible to envision applying to metagenomic data as this type of ecological inference is performed.

Analysis of Gene Content

Gene content, in combination with gene expression and the exact amino acid sequence of underlying genes, can be used to define an individual and the species that it belongs to. Changes in gene content can be important to understanding changing phenotypes of organisms. Evolution of gene content along a species tree requires a model.

Several processes lead to gene trees that are different from species trees. Incomplete lineage sorting is a process where shared ancestral alleles partition differently from other genes in the genome across two or more speciation events (Degnan and Rosenberg 2009). Horizontal gene transfer involves the transfer of DNA between two contemporaneously living organisms (or genomes). The organisms presumably must have some ecological or spatial relationship to each other (Jain et al. 2003). Transfer of DNA from organellar genomes to nuclear genomes is an increasingly well-characterized process (Maruyama et al. 2011). Organisms that have speciated can hybridize with each other, generating various signals in gene trees (McDonald et al. 2008).

Now if we build a phylogenetic tree based on a gene or a concatenation of genes, we may assume that this reflects the history of the gene (ignoring any uncertainty in the construction of gene trees), but due to any of the processes described earlier, the species tree may be different. Ideally, all of the processes discussed earlier should be simultaneously modeled to fully characterize the evolution of gene content and the consequent evolution of species (Roth et al. 2007; Liberles et al. 2010). Although much of the discussion will assume that the species tree is known topologically, a mechanistic framework has been proposed to infer species trees from multiple genes in the context of incomplete lineage sorting (Liu and Pearl 2007; Heled and Drummond 2010). The Bayesian inference method is available within the BEST (Liu 2008) and *BEAST (Heled and Drummond 2010) software packages. In essence, a model for speciation and extinction with the growth of the species tree has to be assumed. Such a model may be the coalescent or a birth–death model. Second, population dynamics within the lineages of the species tree are assumed, where the individuals of a species replicate and die according to some model; typically, the dynamics are assumed to follow the coalescent assumptions. Thus, a mechanistic model for the species tree and the gene lineages coalescing within the species tree is assumed, and the species tree together with its gene trees is inferred. Ideally, the model would not only consider incomplete species sampling when performing species tree inference but also other processes influencing gene content which have not been included in species tree inference to date.

However, these other processes have been studied independently of the species tree reconstruction problem and thus in the future might be combined with species tree reconstruction. The remainder of this section will focus on a model for one particular process of gene content evolution, gene duplication, and loss. The modeling discussion will be used to frame the trade-offs between biological considerations and statistical considerations in making biological inference.

Many models assume that gene duplication is an independent process acting on one gene at a time at a constant rate. Of course, models that enable rate variation and the simultaneous duplication of multiple genes (either that functionally interact or that do not) are needed to deal with the violation of the independence assumption at the level of the gene. Once a gene is born, there is a complex process that describes if it is retained. The probability of loss of a gene becomes reduced as redundancy with other genes decreases. Modeling that process will be described in the next section and in more detail in a companion article (Zhao J, Teufel AI, Liu L, Liberles DA, manuscript submitted). These models treat each gene independently while acknowledging that the process is interdependent, analogous to the common treatment of amino acid substitution in a protein in Markov models.

Gene Loss

Genes are retained in genomes by several processes that prevent gene loss. All of these retention processes play out against a neutral backdrop leading to nonfunctionalization. Neofunctionalization describes a process where one gene obtains a new function whereas the other copy retains the ancestral function (Ohno 1970). Subfunctionalization describes the neutral partition of functions from a multifunctional ancestral state through degenerate changes that are neutral in the context of redundancy (Lynch et al. 2001). Dosage balance describes the co-retention of duplicate genes that are in stoichiometric balance and deleterious when out of stoichiometric balance (Freeling and Thomas 2006). There are other processes and many variations on these themes (Innan and Kondrashov [2010] provide a useful review).

Many early characterizations of gene loss relied on an exponential distribution of retention (where the retention probability is 1 − loss probability), implying a constant rate of loss until all duplicates are lost (Lynch and Conery 2000; Lynch and Conery, 2003; Arvestad et al. 2009). In the survival function in equation (1), t is time measured in dS units and d reflects the loss rate.

(1)

Of course, gene duplication is a biologically meaningful process because duplicates diverge in function generating unequal rates of loss and genes that have never been observed as lost from genomes (e.g., ribosomal RNA subunit genes and other genes involved in translation). Several such mechanisms have been described above. Many ancient duplicates, such as those involved in translation that have never been lost, have a hazard rate (the instantaneous rate of loss) that must be extremely close to zero, although probably not initially after the duplication event. A first step toward changing this modeling framework to enable rate variation used a Weibull distribution with a concavely decaying loss rate (Hughes and Liberles 2007). In this context, the Weibull distribution mathematically describes the loss process associated with a specific mechanism but is not fully mechanistic (as in the DNA substitution models described earlier) in that it does not consider other biological processes (see both the following discussion and the companion article [Zhao J, Teufel AI, Liu L, Liberles DA, manuscript submitted]). In the expansion of equation (1) described in equation (2), d₂ enables a time-dependency to the loss rate.

(2)

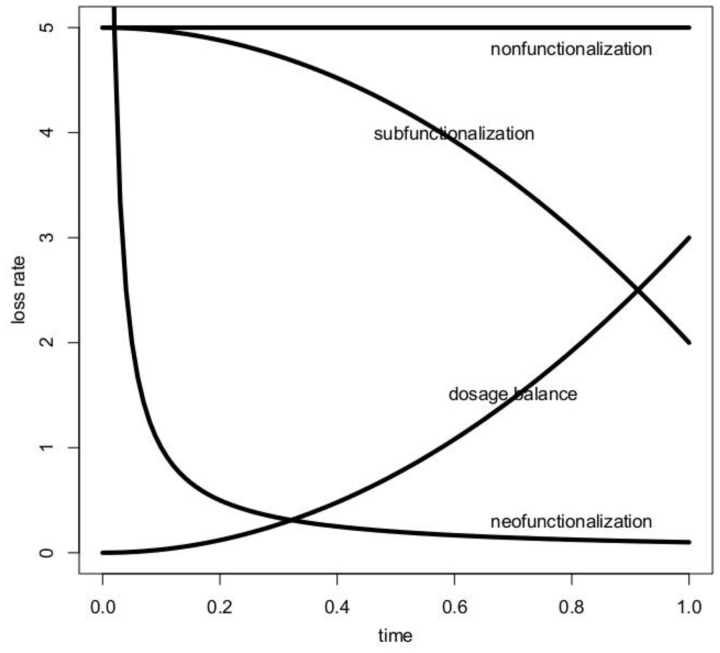
The Weibull model was designed to characterize the retention of duplicate genes on average according to a neofunctionalization process against a backdrop of nonfunctionalization. Concave decay was consistent with a waiting time for a single event, such as a neofunctionalizing event. This is in contrast to a convexly decaying loss rate that is not parameterizable with a standard Weibull and that would be consistent with a waiting time for multiple events, such as subfunctionalizing events. It was proposed that the dosage balance mechanism would be consistent with a concavely increasing loss rate based on the expectation of stochastic loss of one partner leading to cooperative loss of the remaining duplicates (Hughes et al. 2007). Konrad et al. (2011) then derived a more complex distribution that could accommodate all the curve shapes consistent with the four mechanisms described earlier (nonfunctionalization [constant loss rate], neofunctionalization, dosage balance, and subfunctionalization).

The Konrad Model and Its Implementation

The Konrad et al. (2011) model presented a set of hypotheses derived from theory for the expected hazard functions associated with different processes and derived survival functions from the hazard function using the following formulae in equations (3) and (4). The b and c parameters control the loss rate and its time dependency, whereas the f and d parameters control the instantaneous and asymptotic loss rates.

(3)

(4)

In this case, the hazard function reflects the instantaneous rate of loss of a duplicate gene in a genome, dependent on the time it has survived in the genome. This modeling framework reflects a first step toward the development of mechanistic models for duplicate gene retention (see fig. 3). The models will need to be expanded to accommodate hybrid processes, like initial dosage balance followed by either subfunctionalization or neofunctionalization. In extending the model to a phylogenetic framework, the retention/loss model will need to be coupled to models that examine variability and complexity in the gene birth process. Further, the robustness of population genetic assumptions about the fixation process will need to be tested with more realistic simulations. Duplicate gene loss models represent an example where mechanistic model development in computational genomics is progressing but still at an early stage. As indicated, a more detailed technical discussion of these models and their development appears in a companion article (Zhao J, Teufel AI, Liu L, Liberles DA, manuscript submitted).

Fig. 3.—

The hazard functions associated with the nonfunctionalization, neofunctionalization (plus nonfunctionalization), subfunctionalization (plus nonfunctionalization), and dosage balance (plus nonfunctionalization) processes as described by sample parameterization from equation (5) are shown. Equation (3) generates a similar set of curve shapes.

How to Validate Mechanistic Models

With this call for mechanistic models, the question arises of how to validate models for biological data. The question one might address is how well a particular model fits the data. For mechanistic models, it is at least as important to ask whether the biological inference made by the model is both robust and correct. The latter analysis to evaluate the biological interpretability of the model can be completely orthogonal to goodness of fit of the model.

Standard statistical approaches for model selection and validation include comparison of the likelihood score with the number of parameters to justify the model and prevent overfitting, the identifiability of parameters, data simulation under the model to evaluate how well the data are explained, P–P plots, Q–Q plots, and other measures of goodness of fit that have been reviewed elsewhere (see Jermiin et al. [2008] for a discussion in a phylogenetic context). Under certain conditions, these model selection criteria perform appropriately in selecting models that explain the biological processes in the data well, corresponding to a good fit. There are cases, however, in which these conditions are not met, and the use of these criteria can lead to selecting inappropriate models. For instance, when selecting a model using AIC, it should be noted that AIC and its variants were developed to approximate the expected Kullback–Leibler divergence, which measures in the context of model selection the difference between the target model and the true model. AIC works well under certain conditions, but these conditions may not hold for complex, say phylogenetic, models with complex parameters including tree topology. Although AIC is not known to fail in model selection in these contexts, it is of great interest theoretically and practically to further investigate the performance of AIC in selecting phylogenetic models. These topics have been discussed elsewhere as well (see, e.g., Hurvich and Tsai 1991; Posada and Buckley 2004).

It has been suggested that summary statistics, like those from the previously discussed multinomial distribution describing sequence character distributions, can be used to evaluate model fit (Goldman 1993), but it is important to also ask how the summary statistics relate to the hypotheses being tested with the model. This can be complex, as biological assumptions like the independence of evolution of sites in a protein can generate patterns that are not well characterized by amino acid frequencies and tree topologies that are inferred from changes at individual sites. Goldman (1993) was aware of these concerns but constrained by the state of modeling in 1993.

Beyond these considerations, with mechanistic models used for mechanistic inference (inference about the biological process based on parameter values), there is the added importance that the model does not just fit the data well but that it enables robust mechanistic inference from the parameterization. Simulations of data using a plausible mechanistic approach that does not embed the simple inference model may be a powerful approach for evaluating correctness of mechanistic inference. In Konrad et al. (2011), both statistical identifiability of parameter values and mechanistic identifiability using simulations under a different model were the approaches applied to validate the inferential model, although further mechanistic validation is clearly required. The simulations involved a network of genes in a population, where mutations affected the function of the genes and thereby the fitness of the cells in the population. These simulations involve a much more complex biological process that encapsulates as much of the underlying biology as realistically as possible, but that would be difficult to describe mathematically in an inference framework. In these simulations, the parameters (e.g., effective population size) and the selective regimes are known and can be validated with the simpler mechanistic statistical model. This would be impossible on real data, where the underlying biology (including population size, selective regime, and the precise biochemical function of a gene under selection) is typically not known.

The use of mechanistic simulations in this way that could be turned into receiver operating characteristic curves rather than fitting real data is controversial in statistics but worthy of exploration. The use of such simulations is, of course, dependent on the closeness of the simulated processes to the actual processes generating real data. In Konrad et al. (2011), there was the added case that the models fit only a portion of the curve where the model was mis-specified in cases where multiple processes acted, but the mechanistic model forced the fit to a single process. This was then validated by a priori knowledge of the processes that acted, whereas it would have been rejected by a P–P or Q–Q plot test. With the addition of two additional parameterization ranges (for the simultaneous action of neofunctionalization and dosage balance as well as the simultaneous action of subfunctionalization and dosage balance), goodness-of-fit tests can also be applied with tests for proper mechanistic inference.

There is a question that does emerge. Does the existence of a model that explains the data better with fewer parameters but that is mechanistically uninterpretable, invalidate a mechanistic model that needs more parameters to explain the data? There are many explanations for the nonmechanistic simple model fitting the data better, from the mechanistic model being mis-specified to the mechanistic parameters not behaving fully independently. The worse fit of the mechanistic model does not necessarily invalidate mechanistic conclusions from that model, but controls involving simulations under different conditions to evaluate the relationship between mechanism, parameters, and data are always a good idea. The constraint on mechanistic model parameterization to mechanistically interpretable ranges may in fact doom mechanistic models to poorer fit for the number of parameters compared with freely parameterized phenomenological models. Model comparison between mechanistic and phenomenological models in standard model comparison frameworks may therefore not be appropriate. Ultimately, there are famous quotes from George Box and others that touch on this including, “… all models are wrong, but some are useful” (Box and Draper 1987).

There is something to worry about though, as it may be that all parameters are needed to explain the process fully, but different parameter combinations give rise to the same likelihood, as the considered data are only a snapshot of the full process. For example, this happens when looking at species phylogenies. Clearly, we need independent speciation, extinction, and sampling parameters. However, if our data consist of only extant species data, where fossils are ignored, the three parameters are nonindependent and therefore non-identifiable (Stadler 2009).

Model Complexity versus Priors

The phenomenological modeling has drawbacks in fitting and interpreting complex biological data. One suggestion is to use mechanistic information in generating informative priors rather than generating complex models with mechanisms embedded in the likelihood calculation. However, even if mixture models (as an example of a strategy for using simpler off-the-shelf distributions) are used to fit the data, mechanistic information may not fit obviously into prior probabilities on parameter values in phenomenological models. It is conceivable that a priori inequality of mixture components through the prior probabilities could be used to capture such mechanistic information, but this would likely lead to more complex models than simply building a mechanistic or theoretical model where the parameters have clear scientific interpretation. It would be the equivalent of using a mixture of Jukes–Cantor components in modeling codon evolution rather than the Goldman–Yang model (Goldman and Yang 1994). In this case, the differences in rates between synonymous and non-synonymous sites and their relative frequencies in the data might be used to inform priors about the rate and mixture parameters. This is a clearer case of relationship between model parameters in the different models than would occur in purely phenomenological models, as the rate parameter in a Jukes–Cantor model has some relationship to biological processes being studied. The statistical argument might be to let the data drive the model fit in preferring the mixture of Jukes–Cantor models, but that only goes so far if the biological hypothesis involves dS or omega values that are parameters in the model. On the other hand, there is a potential advantage to a mixture of simpler models that does enable discovery if the process is not well understood and the mechanistic model is mis-specified.

Problems with Hybrid Models for Mechanistic Inference

In using simpler models that include a combination of phenomenological parameters and mechanistic parameters (hybrid models), the question emerges whether the parameterization of the two components can remain accurate if there is not a clear separation between what is being fit by different parameters. To examine this, a birth–death model was described with a dampening periodic birth function (eq. 5) and a Weibull death function (eq. 6).

(5)

(6)

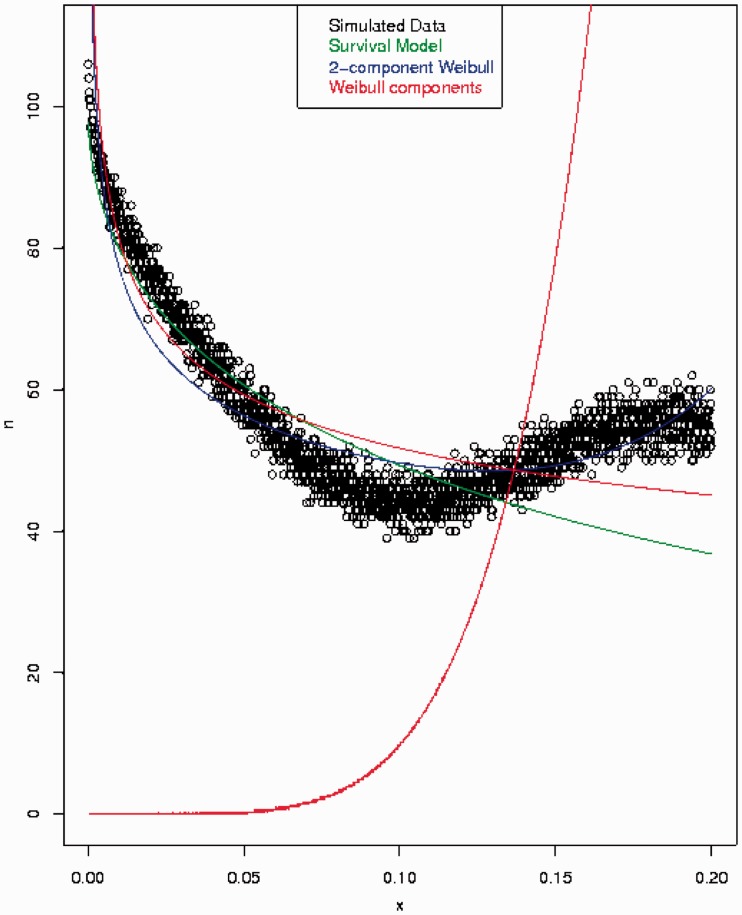
This model was then fit with a mixture of Weibull distribution probability density functions (the simulated data and the R code used to fit the data are included as supplementary materials, Supplementary Material online). Two Weibull components were found to be statistically justified. Neither the mixture Weibull nor either of the individual Weibull components showed parameters consistent with those used in equation (6), which is a Weibull distribution (fig. 4). Identifying such a case required little effort and generating a reasonable fit was much more difficult, even with mixtures of these flexible distributions.

Fig. 4.—

Using the birth process in equation (5) and the death process in equation (6) (green curve), a survival function is simulated (black curve). This is fit statistically with a mixture of two Weibull distributions (blue curve), where the individual components are shown in red. Neither recovers the Weibull loss process of the green curve, with the decaying Weibull function following the data (black) more closely than the green generative process.

Although it is possible that a better fitting model can be identified, it still suggests that care should be taken in interpreting the parameterization of models that are either mechanistically mis-specified or are hybrid models containing mechanistic and nonmechanistic parameters (part of the data comes from a Weibull distribution and one Weibull component can be considered mechanistic). In interpreting such parameterizations, it is important to examine what is being fit by which parameter in addition to standard goodness-of-fit evaluations.

Conclusions

Phenomonological models, including those based on statistical associations, work well when the signal is clear and the mechanistic interpretation of the signal is unambiguous. In many cases of biology, spanning from biomedicine to ecology, there are complex mechanistic processes that underpin the generation of biological data. Analyzing and interpreting these data in the absence of mechanistic insight is fraught with complications. Ultimately, as in physics, biology will need to push down the path of becoming a theoretical science instead of a purely data-driven one.

Supplementary Material

Supplementary materials are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).