Relationship Between Wealth and Age Trajectories of Walking Speed Among Older Adults: Evidence From the English Longitudinal Study of Ageing

Abstract

Background.

Slow walking speed is associated with higher risk of accidents, disability, and mortality in older adults, with people in more disadvantaged socioeconomic positions being at higher risk. We explore the relationship between wealth and age trajectories of walking speed among older adults.

Methods.

Data come from three waves (2002–2003 to 2006–2007) of the English Longitudinal Study of Ageing. We use latent growth curve models and aging-vector graphs to explore individual changes and average population age trajectories of walking speed by wealth among 7,225 individuals aged 60 and older.

Results.

For someone aged 71 in the poorest wealth quintile, the baseline mean walking speed was 0.75 m/s, which decreased to 0.71 m/s 4 years later, whereas that of a person in the richest wealth quintile was 0.91 m/s, which decreased to 0.82 m/s. Although the decline in walking speed was faster among people in the richest wealth (net of covariates), the gaps in walking speed between richest and poorest did not close. Even after accounting for covariates, people in the richest wealth only reached critical values (0.60 m/s) of walking speed at the age of 90, whereas people in the poorest wealth reached that level 6 years earlier.

Conclusions.

Our findings showed continuing gaps in physical functioning by wealth, even among people with the same health, psychosocial, and demographic conditions. As wealth reflects both past and current socioeconomic status, the implications of our findings are that reducing socioeconomic inequalities at all stages of the life course may have a positive impact on functioning in old age.

Previous research has shown that socioeconomic position is related to functional decline and mobility disability in later life (1–8). Among the indicators used to measure socioeconomic position in relation to health, it has been suggested that for older adults wealth is particularly important (9,10). Wealth refers to an individual’s or a household’s total financial assets and net worth (assets − debts) accumulated over their lifetime (10). Hence, wealth may be a better marker for cumulative advantage over the life course (11) and in particular a better measure of the permanent economic status of older people than income (9,10). Among older adults, there is evidence that wealth is a key determinant of health outcomes (10–13) and mortality (14).

In recent years, studies have focused on the relationships between socioeconomic position and health driven by two contrasting hypotheses, the cumulative advantage or disadvantage hypothesis and the age-as-leveler hypothesis (15,16). The cumulative disadvantage hypothesis states that the effect of socioeconomic position on health increases over the life course, whereas the age-as-leveler hypothesis states that health inequalities decrease at older ages. Results from these studies are mixed: some support the cumulative advantage hypothesis finding a consistent diverging gap by socioeconomic position with age (15,17–20), whereas others support the age-as-leveler hypothesis indicating that disparities widen over most of the life course until early old age followed by convergence in later life (11,21–23).

Despite evidence of the importance of using wealth as an indicator of socioeconomic position of older individuals (10–13), the studies mentioned previously did not use wealth to test the cumulative advantage or disadvantage hypothesis and/or the age-as-leveler hypothesis (15,17–23), with the exception of one (11); also none of the studies used an objective measure of health, such as walking speed. Waking speed is a commonly used performance-based measure, and it is a simple and accessible indicator of older individuals’ health status (1). Slow walking speed is considered an early marker of disability and frailty (1), as well as a predictor of dementia (24) institutionalization and mortality (2). Therefore, in this study, we examine the relationship between wealth and age trajectories of walking speed in order to contribute to the debate about the cumulative disadvantage hypothesis and age-as-leveler hypothesis in older ages using recent data from a national-based longitudinal study (2002–2003 to 2006–2007) on older people living in England (25). The study is the first in England to collect very detailed information on respondents’ wealth, including their financial, physical, and housing wealth, as well as debts. Therefore, the measure of wealth we use encompasses assets and net worth, carrying with it information on individuals’ past circumstances.

Methods

Data

The data are from three waves of the English Longitudinal Study of Ageing, where the same individuals aged 50 and older and living in private households in England, were followed and reinterviewed every 2 years (25). For the purpose of this study, we used people aged 60 or older, consisting of 7,225 individuals at wave 1, 5,371 at wave 2, and 4,576 at wave 3. Data collection consists of a face-to-face interview and a self-completion questionnaire.

Participants gave their informed consent to take part in the study. Ethical approval for the three waves of English Longitudinal Study of Ageing was given by the London multicentre research ethics committee.

Measures

Respondents aged 60 and older were eligible for a walking speed test, which involved timing, how long it took to walk a distance of 8 ft (2.4 m) and back to the start. Walking aids were permitted for the walking speed test and were used by approximately 4% of the respondents who successfully completed the task. We used mean walking speed based on the two timings (range = 0.09 – 2.2 m/s).

Information regarding sociodemographic characteristics, health, and health behaviors was collected during the face-to-face interview. Total wealth (excluding regular pension payments, but including lump sums from private pension that have already been received but not yet consumed) was defined as financial wealth, physical wealth (such as business wealth, land, or jewels), and housing wealth (primary and secondary residential housing wealth), minus debts (9). We used quintile of total wealth, with the top quintile indicating the richest group. We grouped the second, third, and fourth quintiles into one category labeled “middle” because there was little variation in walking speed among these quintiles. We used a continuous variable for age (ranging from 60 to 100 at baseline). Dichotomous variables were used for sex (0 = male; 1 = female); ethnicity (0 = white; 1 = non-White); cohabitation status (currently living with a partner or not); smoking status (0 = never and exsmoker; 1 = current smoker); physical activity (0 = physically active; 1 = inactive); and for the presence of coronary heart disease, diabetes, chronic respiratory illness (bronchitis, emphysema, pulmonary disease, or asthma), and arthritis. Symptoms of depression (ranging from 0 to 8) were measured using the eight-item version of the Centre for Epidemiologic Study Depression scale (26).

In a self-completion questionnaire, respondents were asked to indicate the number of family members and friends with whom they had a close relationship. A continuous variable was derived from the reported number of close friends and/or family in the respondent’s social network.

Statistical Analyses

To examine trajectories of change over time in walking speed, we used latent growth curve methodology (27–29). Latent factors representing intercept (baseline status) and slope (rate of change) components are extracted from the three observations of walking speed across time, here identified as wave 1 (baseline), wave 2, and wave 3. Factor loadings of the intercept component to all three observations were fixed to 1, and the linear slope component was defined by fixing the parameters to 0 (baseline, wave 1), 1 (wave 2), and 2 (wave 3). In order to test the age-as-leveler hypothesis, we fitted a model (results not shown) where baseline levels in walking speed and the rate of change (slope) in walking speed were predicted by age, wealth, and an interaction term between age and wealth. The effect of age–wealth interaction was not significant, neither on the baseline level of walking speed nor on the rate of change. Additionally, we tested a gender-specific model and found no evidence for an age–wealth interaction in either men or women. Based on these preliminary results and on the likelihood ratio test for nested models, we found that the best model for this study data was a model with wealth adjusted for time-invariant factors, such as age at baseline, ethnicity and sex, and time-varying factors’ cohabiting status, number of close friends and/or family, symptoms of depression, coronary heart disease, diabetes, chronic respiratory illness, arthritis, physical inactivity, and smoking status.

The model is expressed as follows:

(1)

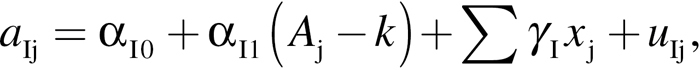(2)

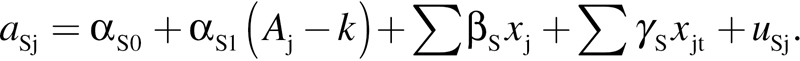(3)

where y _jt is the walking speed score for individual j at time t, a _Ij is the intercept for individual j, a _Sj are individual slopes, and t _jt is the time score for individual j at time t. Time is expressed by wave (0, 1, or 2), the gap between each wave is 2 years. Equations 2 and 3 are extensions of the basic Equation 1. The intercept a _Ij for individual j is a function of age at baseline (A _j) centered at its mean of 71 years (k), time-invariant factors x _j, and individual random deviation u _Ij; the slope a _Sj for individual j is a function of age at baseline (A _j) centered at its mean (k = 71), time-invariant factors x _j, time-varying factors x _jt, and individual random deviation u _Sj. Time-invariant factors, x _j, and time-varying factors, x _jt, were mean centered (with the exception of wealth and sex); centering involves subtracting the mean from each score.

To determine the fit of the models, we employed Chi-square test, the Tucker–Lewis index, the Comparative Fit Index, and the root-mean-square error of approximation, which represents closeness of fit (30). To handle missing data, we used full information maximum likelihood estimation, which computes parameter estimates on the basis of all available data under the assumption that data are missing at random (31,32). However, attrition due to mortality or dropout can violate this assumption. In addition to the models described earlier, we jointly modeled loss to follow-up with the latent growth curve. Logistic regression was used to estimate the probability of loss to follow-up at wave t based on the individual’s age, ethnicity, and wealth at baseline and walking speed score at t – 1; results are presented in Supplementary Table 1. Estimates from this model showed that loss to follow-up does not affect estimates of mean levels (intercept and slope) of walking speed. Models were fitted using the Mplus v6 software package.

We present aging-vector graphs of predicted walking speed in order to show graphically the level of walking speed at baseline, direction, and amount of change throughout the age range of our sample. The aging graph reveals both trends by age of the sample at baseline and cohort-specific within-person changes over time in walking speed by wealth (33) and were fitted using Stata 11.

Results

Table 1 reports sample characteristics at baseline (2002–2003). The mean walking speed was 0.8 m/s, and the mean age of respondents was 71. About 22% of participants were in the poorest wealth quintile. A large proportion of the population was cohabiting with a partner, and only 3% was of non-White ethnic origin. Around 16% of participants had diagnosed coronary heart disease and chronic respiratory illness, about 8% had diagnosed diabetes, and 33% reported arthritis. More than 70% of participants reported not being engaged in any physical activity, and about 14% were current smokers. A large proportion of the population experienced one or more symptoms of depression during the past month; on average, participants had eight close friends or family friends.

Table 1.

Baseline Characteristics of Participants, England 2002–2003

	M (SD)	n
Walking speed, m/s	0.82 (0.3)	5,578
Age	71.2 (7.9)	7,225
	%	n
Men	44.6	7,225
Cohabiting with a partner	62.9	7,225
Non-White	2.5	7,169
Total wealth		7,184
Richest	19.1
Poorest	22.2
Coronary heart disease	15.7	7,218
Diabetes	8.4	7,225
Respiratory illness	16.4	7,218
Arthritis	33.3	6,923
Physically inactive	71.4	7,090
Current smoker	14.3	7,088
Psychosocial
≥1 symptoms of depression	61.3	6,954
	M (SD)	n
Number of close friends/family	8.1 (5.4)	5,246

Note: Mean and percentages are weighted for nonresponse.

Table 2 shows the estimates of baseline walking speed and change over time after accounting for age and wealth. The intercept value 0.72 (SE = 0.01) refers to mean walking speed (m/s) of respondents who were aged 71 at baseline (2002–2003) and were in the poorest wealth quintile, this decreased at an average rate of 0.02 m/s (SE = 0.01) for each additional wave of the study (2-year interval). People in the richest wealth quintile had mean walking speed 0.22 m/s higher than those in the poorest wealth quintile at baseline, which decreased by 0.03 m/s over each additional wave of the study, meaning that they had a faster decline in walking speed than those in the poorest quintile (slope = −0.03). The fit indices suggest that the proposed model fit the data well.

Table 2.

Latent Growth Model of Walking Speed With Age and Wealth, England 2002–2003 to 2006–2007

Growth Parameters	Estimate	95% CI
Intercept	0.715	0.701, 0.729
Intercept variance	0.032	0.028, 0.036
Slope	−0.020	−0.030, −0.010
Slope variance	0.008	0.006, 0.010
Intercept regressed on
Baseline age, 71 y	−0.012	−0.012, −0.012
Wealth—middle	0.112	0.096, 0.128
Wealth—richest	0.220	0.200, 0.240
Slope regressed on
Baseline age, 71 y	−0.003	−0.003, −0.003
Wealth—middle	−0.015	−0.027, −0.003
Wealth—richest	−0.027	−0.041, −0.013
Model Fit	Estimate	Df
Chi-square test	6314.9	12
CFI	0.995
TLI	0.985
RMSEA	0.033
N	7,225

Note: CFI = Comparative Fit Index; RMSEA = root-mean-square error of approximation; TLI = Tucker–Lewis index (TLI).

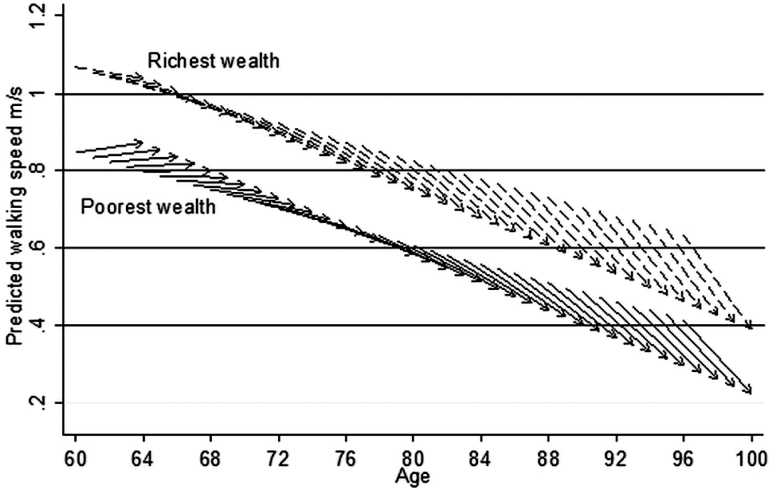
The aging-vector graph (Figure 1) provides a summary of the model presented in Table 2. The vectors in the top part of the figure show the walking speed trajectories of people in the richest wealth quintile and the vectors in the lower portion show those of people in the poorest wealth quintile. Each arrow (vector) represents the predicted score at baseline and change in walking speed during 6 years for a 1-year cohort. The horizontal axis indicates the respondent’s age. The vertical axis indicates the respondent’s predicted walking speed. The figure shows that for people up to the age of 64 in the poorest wealth quintile, walking speed was almost constant over time, but for older respondents, it declined over time. Among people in the richest wealth quintile, walking speed declined more steeply from the age of 60. However, these people only reached critical values (less than 0.6 m/s) of walking speed at the age of 89, whereas people in the poorest wealth quintile reached that level 9 years earlier. The gaps in walking speed trajectories between the richest and poorest never close.

Figure 1.

Vector graph showing the predicted 4-year aging vectors of walking speed by socioeconomic status for the model with age only, England 2002–2003 to 2006–2007.

Table 3 shows parameter estimates adjusted for sociodemographic, behavioral, and health factors (mean centered) that may be confound or mediate the association of wealth with walking speed. The value 0.77 m/s (SE = 0.01) represents the estimated baseline mean walking speed for men, aged 71 in the poorest wealth quintile with average conditions, which declined 4 years later to 0.74 m/s. For the corresponding person in the richest quintile of wealth, the mean walking speed at baseline was 0.93 m/s, which declined 4 years later to 0.84 m/s. The fit indices suggest that the proposed model fit the data well. The values of the residual variance of both the slope and intercept were smaller than that in the model with age only, indicating that the factors added to the model explain some of the variability in baseline levels and changes in walking speed. Significant differences between richest and poorest wealth quintiles in both baseline walking speed and average decline in walking speed remained after adjustment for these factors.

Table 3.

Adjusted Latent Growth Model of Walking Speed and Wealth, England 2002–2003 to 2006–2007

Growth Parameters	Estimate	95% CI
Intercept	0.765	0.749, 0.780
Intercept variance	0.025	0.021, 0.029
Slope	−0.014	−0.024, −0.004
Slope variance	0.007	0.005, 0.009
Intercept regressed on
Baseline age, 71 y	−0.010	−0.010, −0.010
Wealth—middle	0.078	0.062, 0.094
Wealth—richest	0.162	0.142, 0.182
Slope regressed on
Baseline age, 71 y	−0.003	−0.003, −0.003
Wealth—middle	−0.015	−0.027, −0.003
Wealth—richest	−0.029	−0.043, −0.015
Model Fit	Estimate	Df
Chi-square test	4901.53	99
CFI	1.00
TLI	1.02
RMSEA	0.00
N	7,225

Notes: CFI = Comparative Fit Index; RMSEA = root-mean-square error of approximation; TLI = Tucker–Lewis index.

Results adjusted for sex, ethnicity, cohabitation status, number of close friends and/or family, depressive symptoms, coronary heart disease, diabetes, respiratory illness, arthritis, smoking status, physical activity. The variables have been mean centered, so that the reference category of each indicates the average conditions (except for sex and wealth).

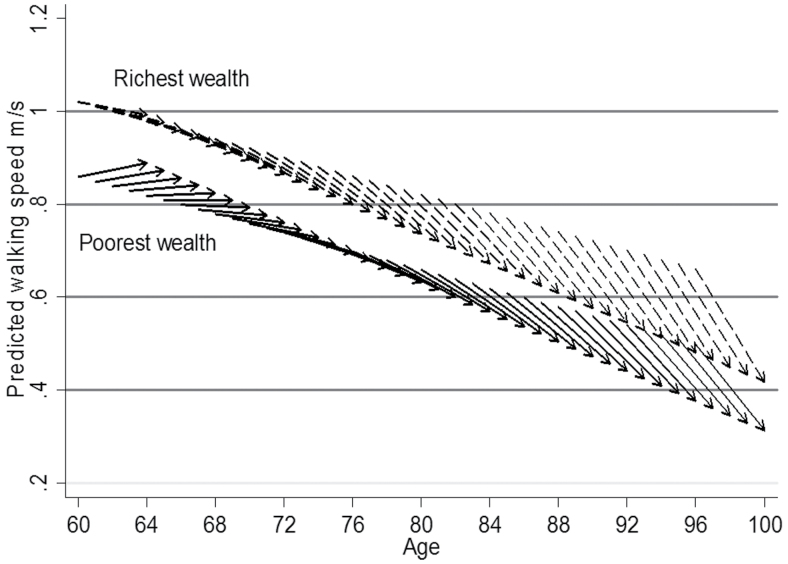
Figure 2 provides summaries of the model presented in Table 3, comparing people in the richest and poorest wealth quintiles. All variables including sex have been centered on their overall mean; therefore, the mean walking speed at baseline is now 0.75 m/s and the change per each additional wave of the study (slope) is −0.018. Centering allows describing the predicted walking speed trajectories of people with average conditions (gender, health, etc.). For people up to the age of 64 in the poorest wealth quintile, walking speed increased slightly over time; between the ages of 65 and 66, walking speed was constant and then from the age of 67 it started declining. A person aged 71 in the poorest wealth quintile had mean walking speed of 0.75 m/s, which decreased to 0.71 m/s 4 years later, whereas that of a person in the richest wealth quintile was 0.91 m/s at baseline, which decreased to 0.82 m/s after 4 years. For a person aged 80 in the poorest wealth quintile, walking speed was 0.66 m/s at baseline and 4 years later further decreased to 0.57 m/s, the corresponding walking speed of an individual of the same age but in the richest wealth quintile was 0.82 m/s at baseline, which decreased to 0.67 m/s 4 years later.

Figure 2.

Vector graph showing the predicted 4-year aging vectors of walking speed for the fully adjusted model by socioeconomic status, England 2002–2003 to 2006–2007.

Even after adjustment, people in the richest wealth quintile only reached critical values (0.60 m/s) of walking speed at the age of 90, whereas people in the poorest wealth quintile reached that level 6 years earlier.

Discussion

In this study, we examined age-specific 6-year trajectories of physical functioning (walking speed) among older adults by wealth in order to contribute to the debate about the cumulative disadvantage hypothesis and age-as-leveler hypothesis in older ages. Our results support the cumulative disadvantage hypothesis of physical functioning by wealth in older ages. The results showed that wealth disparities in walking speed persist across all age cohorts over the 6 years of the study, even after accounting for sociodemographic, health behaviors, and health factors that predicted wealth. We found that the difference in walking speed between the richest and the poorest quintiles at baseline was 0.16 m/s (equivalent to 1.2 times the effect of having arthritis). Between baseline and 4-year follow-up, walking speed of people in the poorest wealth quintile declined by 0.05 m/s less than the walking speed of people in the richest wealth quintile (at average age of 71). Although the decline in walking speed was faster among people in the richest wealth quintile (net of covariates) at older ages, the gaps in walking speed between richest and poorest did not close, discarding the age-as-leveler hypothesis. This finding was also supported by a nonsignificant age–wealth interaction term (results not shown). The aging-vector graphs allowed us to explore both the trends by age of sample at baseline and cohort-specific within-person changes over time in walking speed by wealth. The aging-vector graphs revealed that people in the richest quintile of wealth only reach critical values (0.60 m/s) of walking speed at the age of 90, whereas people in the poorest wealth quintile reach that level 6 years earlier.

To date, this is the first longitudinal study to contribute to the debate about the cumulative disadvantage hypothesis and age-as-leveler hypothesis in older ages using an objective measure of health, walking speed, and using wealth to measure socioeconomic status. Our results of persisting gaps in physical functioning by socioeconomic status are consistent with previous studies (7,8,18) that used a nonwealth measure of socioeconomic status. Nevertheless, our results supporting the cumulative disadvantage hypothesis disagree with a previous study by Robert and colleagues (11) exploring health disparities by wealth. Although the findings from the Robert and colleagues (11) study were more consistent with the age-as-leveler hypothesis, the analysis was cross-sectional and therefore the hypothesis could not be rigorously tested. Also in the Robert and colleagues (11) study, an objective measure of health, such as walking speed, was not used.

Strengths and Limitations

Strengths of this study include the use of a large longitudinal data set from a national sample of older people, with an objective physical functioning measure. Walking speed is a performance-based measure of physical functioning that provides important information not available in self-report items (34). Impaired function on performance tests has been shown to be strongly predictive of future disability, nursing home entry, and mortality (35).

A limitation of this study is that, due to the study design, the cumulative advantage/disadvantage and the age-as-leveler hypotheses could not be tested in younger participants. It is possible that a leveling-off process could have happened before the age of 60.

Another limitation of our study is the proportion of missing data. In order to minimize the potential bias derived from missing data, in addition to nonresponse weighting, we used full information maximum likelihood estimation. It is unlikely that attrition substantially influenced our results about wealth disparities in physical functioning. We used joint modeling to provide estimates of decline in walking speed that allow for correlation between walking speed at previous waves and attrition. The results from the joint models (Supplementary Table 1) were similar, which suggests that the missing data at random assumption may be reasonable.

We did not attempt to ascertain the extent to which wealth was acting as a proxy for the effects of early life education or occupational status. However, previous studies suggest that education may be more important earlier in life (35). The measure of wealth we used could be considered more appropriate than education because it encompasses assets and net worth, carrying with it information on individuals’ past circumstances.

Finally, we did not explore whether other factors such as time-varying income, poverty, and economic hardship mediate the relationship between wealth and walking speed. This may represent an important direction for future research.

Conclusions

Our findings reinforce the hypothesis of continuing gaps in physical functioning by socioeconomic status, even among people with the same health, psychosocial, and demographic conditions. As wealth reflects both past and current socioeconomic status, the implications of our findings are that reducing socioeconomic inequalities at all stages of the life course may have a positive impact on functioning in old age.

Supplementary Material

Supplementary material can be found at: http://biomedgerontology.oxfordjournals.org/

Funding

This study was supported by National Institutes of Health/National Institute of Aging (5R01AG017644-08); and the Office for National Statistics for UK Government departments (NT-4779A/01). A.S. was supported by the Economic and Social Research Council (RES-596-28-0001). J.H was partially supported by the National Institute on Aging (NIH; R01AG013196), and the Economic and Social Research Council (ES/K01336X/1).

Conflicts of Interest

None declared.