Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2013 Nov;23(11):1829–1838. doi: 10.1101/gr.157008.113

High-throughput chromatin motion tracking in living yeast reveals the flexibility of the fiber throughout the genome

Houssam Hajjoul 1,2,6, Julien Mathon 1,2,6, Hubert Ranchon 1,2, Isabelle Goiffon 2,3, Julien Mozziconacci 4,5, Benjamin Albert 2,3, Pascal Carrivain 4,5, Jean-Marc Victor 4,5, Olivier Gadal 2,3, Kerstin Bystricky 2,3, Aurélien Bancaud 1,2,7
PMCID: PMC3814883  PMID: 24077391

Abstract

Chromosome dynamics are recognized to be intimately linked to genomic transactions, yet the physical principles governing spatial fluctuations of chromatin are still a matter of debate. Using high-throughput single-particle tracking, we recorded the movements of nine fluorescently labeled chromosome loci located on chromosomes III, IV, XII, and XIV of Saccharomyces cerevisiae over an extended temporal range spanning more than four orders of magnitude (10−2–103 sec). Spatial fluctuations appear to be characterized by an anomalous diffusive behavior, which is homogeneous in the time domain, for all sites analyzed. We show that this response is consistent with the Rouse polymer model, and we confirm the relevance of the model with Brownian dynamics simulations and the analysis of the statistical properties of the trajectories. Moreover, the analysis of the amplitude of fluctuations by the Rouse model shows that yeast chromatin is highly flexible, its persistence length being qualitatively estimated to <30 nm. Finally, we show that the Rouse model is also relevant to analyze chromosome motion in mutant cells depleted of proteins that bind to or assemble chromatin, and suggest that it provides a consistent framework to study chromatin dynamics. We discuss the implications of our findings for yeast genome architecture and for target search mechanisms in the nucleus.

Chromosome higher-order architecture has been increasingly studied over the last decade thanks to technological breakthroughs in imaging and in molecular biology ranging from painting single chromosomes in fixed cells (Cremer and Cremer 2001) to mapping physical interactions between genomic elements at the genome-wide level (Hi-C) (Dekker 2008). It is now established that chromosome large-scale organization plays important roles in all aspects of genomic transactions, allowing contact between distant chromatin loci (Göndör and Ohlsson 2009) that trigger concomitant genomic processes in cis and in trans. Although several models have been proposed to describe the folding of chromosomes (Lieberman-Aiden et al. 2009; Bohn and Heermann 2010; Bancaud et al. 2012), the physical principles governing this organization are still largely debated.

Despite its small size, budding yeast has become a unique model that recapitulates some of the main features of higher eukaryotes, including heterochromatin-like regions, and an organization mediated by the nuclear envelope (NE), the nucleolus, and the spindle pole body (SPB). Structural data obtained by statistical positioning of a gene in a yeast cell population led to a surprisingly simple model to define yeast nuclear architecture (Zimmer and Fabre 2011): Chromosome position can be predicted by a few parameters such as genomic arm length, telomeres (TEL), and centromeres (CEN) tethered to the NE via nuclear-envelope-tethered proteins and to the SPB via microtubules, respectively (Bystricky et al. 2005; Therizols et al. 2010; Zimmer and Fabre 2011). This description was recently complemented by the first Hi-C comprehensive maps (Rodley et al. 2009; Duan et al. 2010), which confirmed an organization guided by nuclear landmarks, including TEL that congregate in foci (Gotta et al. 1996; Schober et al. 2008). Recent Brownian dynamics (BD) simulations confirmed this structural model by recapitulating Hi-C and imaging data, assuming that physical tethering at TEL and CEN and volume exclusion were driving chromosome conformations (Tjong et al. 2012; Wong et al. 2012).

The large spatial fluctuations of chromosome loci inferred from particle tracking in living yeast suggested a highly dynamic character of chromosome architecture at the molecular level (Marshall et al. 1997; Heun et al. 2001; Hihara et al. 2012). Chromatin dynamics appeared to be determined by nuclear constraints, in particular, the NE (Heun et al. 2001; Bystricky et al. 2004), and by the position along the chromosome, e.g., TEL (Bystricky et al. 2005). Furthermore, a large body of data provides information on spatio-temporal dynamics in wild-type versus mutant cells (see, e.g., Bystricky et al. 2009) and elucidates how chromatin properties are regulated by structural proteins. However, the quantitative analysis of these movements remains controversial, and essentially two models have been used: (1) Chromatin segments were suggested to undergo normal Brownian fluctuations at small time scales and to be confined in regions of ∼0.3 μm2 at time scales longer than ∼100 sec (Marshall et al. 1997); or (2) the movement of GAL1-10 genes on chromosome II appeared to follow an anomalous behavior characterized by a diffusion coefficient of ∼0.4 (Cabal et al. 2006). This anomalous behavior was also detected in bacteria (Weber et al. 2010) and thoroughly studied using polymer models. In yeast, the narrow temporal range of measurements within less than two decades was insufficient for a truly quantitative analysis of chromatin dynamics.

Here we develop high-speed live cell imaging and high-throughput image analysis techniques to monitor the spatio-temporal fluctuations over an extended temporal range spanning more than four decades (10−2–103 sec) of nine chromosome loci on chromosomes III, IV, XII, and XIV of the yeast Saccharomyces cerevisiae. We show that chromatin segments move subdiffusively and that the characteristics of the anomalous response are largely conserved for every locus distant by more than ∼50 kb from TEL and CEN. Similar dynamic behavior was also observed for two telomeric loci whenever they adopt a central localization in the nucleus, thus leading to a consistent picture for chromosome movement within the entire nuclear volume. We then demonstrate that these dynamics are consistent with the Rouse model using BD simulations and statistical analysis of the trajectories and suggest that chromatin is a flexible polymer in yeast, characterized by a persistence length of <30 nm. Finally, we show that the Rouse model is also relevant in mutants for proteins involved in chromatin structure, and propose that this model defines a consistent framework to study chromosome motion. Our findings significantly advance the quantitative understanding of chromosome dynamics and their implications for yeast genome architecture.

Results and Discussion

The dynamics of chromosome loci are uniform throughout the nucleus and anomalous over a broad temporal range

We assayed the dynamics of chromatin in a collection of yeast strains each bearing a single fluorescently labeled chromatin locus (see Methods for details). The labels were inserted on chromosomes III, IV, XII, and XIV at loci distant from TEL and CEN (Figs. 1, 2A). The chromosomes tested ranged in size from 300 kb to 1500 kb, which is well suited to assess whether the dynamics are affected by chromosome length. Motion was analyzed over a temporal range spanning more than four decades (15 msec to 400 sec) (Fig. 2B). This broad temporal analysis is more than two orders of magnitude larger than in previous studies performed in living yeast (Heun et al. 2001; Bystricky et al. 2004; Cabal et al. 2006) or in bacteria (Weber et al. 2010), and investigations on similar time domains were only conducted in mammalian cells for telomere dynamics (Bronstein et al. 2009). The motion of chromosome loci was recorded using a bright-field microscope and analyzed using a customized high-throughput tracking software based on the Multiple-Target Tracing algorithm (Supplemental Fig. S1; Sergé et al. 2008; Albert et al. 2013). Because physical tethering of chromosomes may occur at the nuclear periphery (Heun et al. 2001; Hediger et al. 2002), the nucleus was divided into two regions of equal surfaces, and every tracked locus was automatically assigned to a central or peripheral localization based on the segmentation of the first image of the acquisitions (see image in Fig. 1).

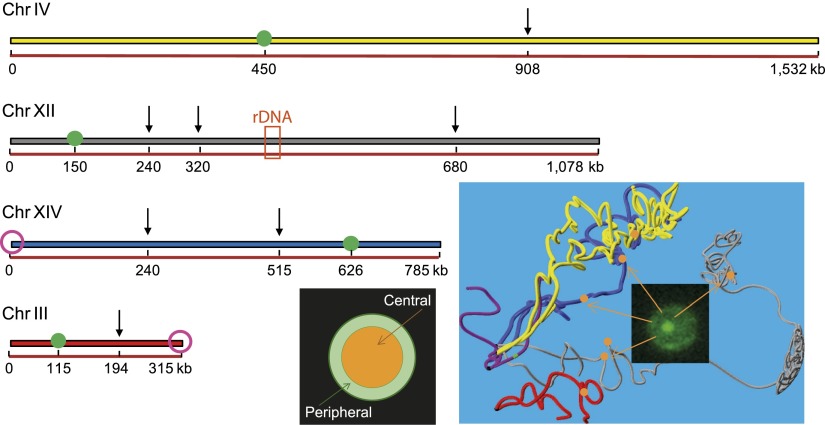
Figure 1.

Figure 1.

Open in a new tab

Collection of loci used to monitor chromosome spatio-temporal dynamics. Arrows indicate the genomic positions at which TetO or LacO repeats were inserted in four chromosomes. These loci are also represented by orange spheres on the yeast nuclear map obtained by Hi-C (Duan et al. 2010). The two purple circles represent the telomeres that were tracked with the same labeling technique, and the green circles correspond to the centromere. The orange box corresponds to the rDNA locus, which represents ∼1 Mb of ribosomal DNA. The preferred localization of these loci was scored using a subdivision of the nucleus into two regions of equal surface (orange and green for central and peripheral localizations, respectively).

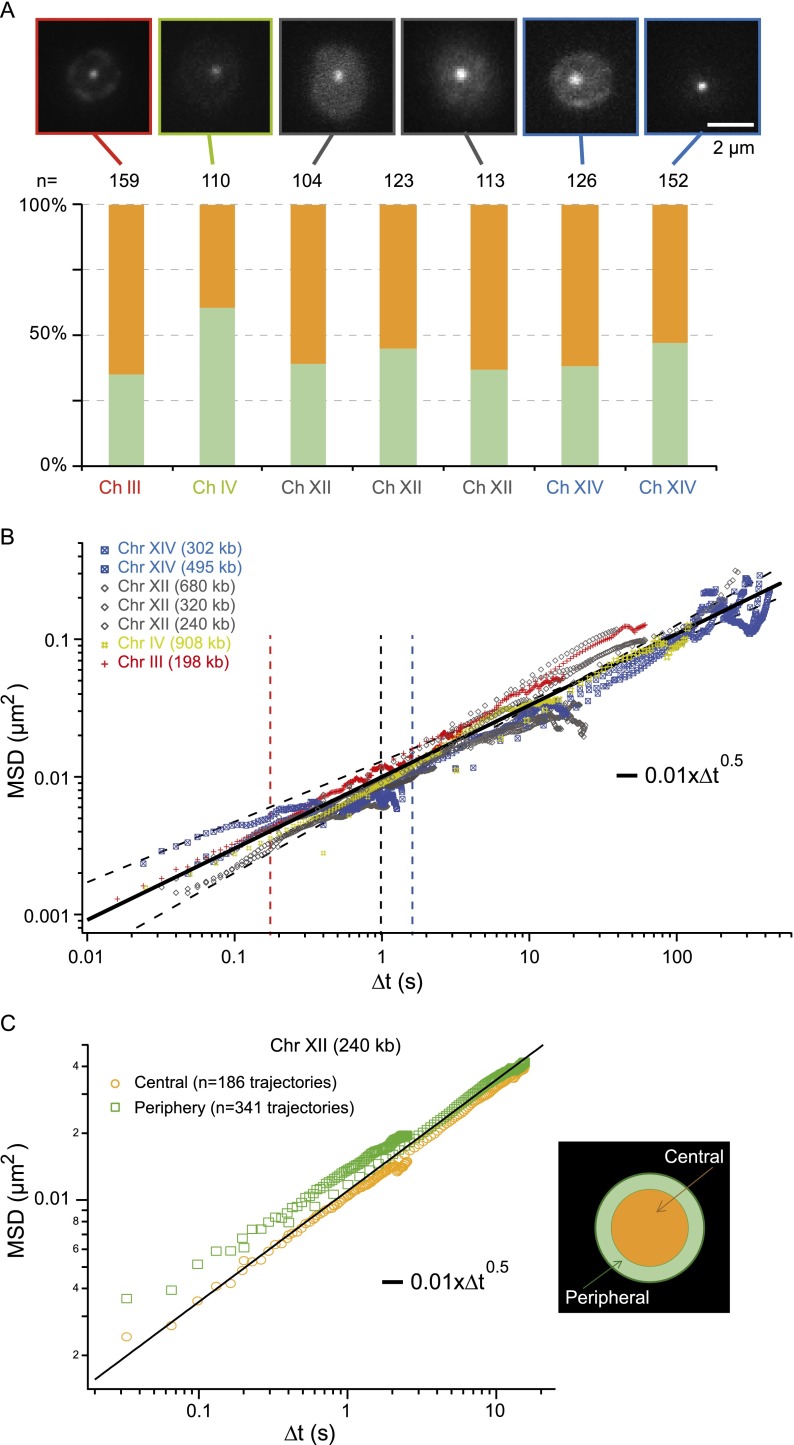
Figure 2.

Figure 2.

Open in a new tab

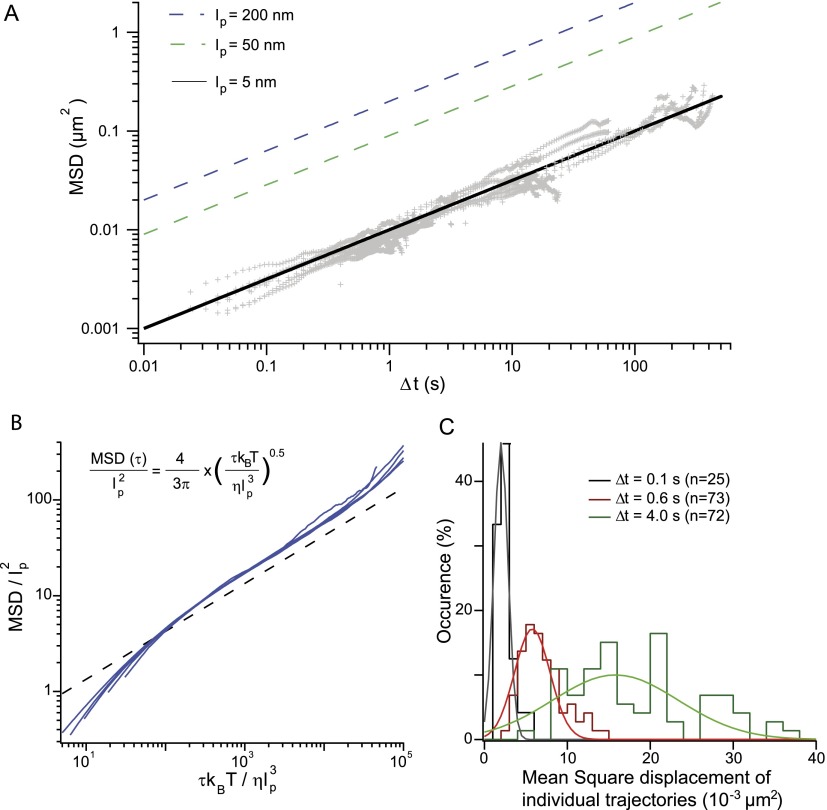
Chromatin dynamics in living budding yeast. (A, upper panel) Fluorescence micrographs of different yeast strains for interframe intervals of 200 msec (for interframe intervals of 16–50 msec and mutants, see Supplemental Fig. S2); (lower plot) the spatial distribution of these loci in the nuclear volume. (B) The temporal evolution of the MSD for seven different chromatin loci with central localization is plotted over a broad temporal range covering more than four orders of magnitude. These data show a universal behavior characterized by an anomalous diffusive response associated to power low scaling comprised between t0.44 and t0.6 (thin dashed lines). (Black solid line) The Rouse regime, which is associated with an exponent of 0.5 (see details in Fig. 4). Note that each data set is the average over 30–200 trajectories and that we selected tracks with signal-to-noise ratios (SNR) >30 dB. (C) The MSD response for loci with central or peripheral localization is compared (yellow and green data sets, respectively), showing similar dynamics. (Black solid line) The behavior measured in B. The departure of the two curves in the short time regime is associated with the lower SNR of peripheral loci (data not shown).

We first focused on loci located in the nuclear center, far from constraints imposed by the nuclear membrane, and representing ∼60% of the observed positions (Fig. 2A). We then characterized their motion by plotting the temporal evolution of the mean square displacement (MSD), which describes the average displacement after a given time lag τ:

graphic file with name 1829equ1.jpg

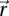with Inline graphic the position vector, and 〈–〉 denoting the temporal average. We observed similar responses for every locus (data points in Fig. 2B), which appeared to fold onto a single master curve (solid line). This curve follows an anomalous diffusive behavior over a broad temporal range characterized by a power-law scaling response in tα with α = 0.52 ± 0.08 (α = 1 for normal diffusion). This result is consistent with an earlier study describing the motion of GAL1-10 genes, which exhibited a nonlinear MSD response characterized by an exponent of ∼0.4 in the temporal range of 4–80 sec (Cabal et al. 2006), but it departs from other contributions showing normal diffusion and a plateau in the long time limit (see, e.g., Heun et al. 2001). The anomalous subdiffusion response is associated with a slow increase in MSD over time. Its persistence over an extended period indicates that chromatin loci explore a broad region of the nucleus of 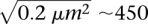Inline graphic nm in ∼400 sec. This estimate is consistent with the extent of “gene territories” of ∼500 nm, which are obtained by statistical mapping of the position of loci in cell populations of ∼2000 individuals (Berger et al. 2008).

Next we studied the motion of chromosome loci located at the periphery and observed that they frequently oscillated between the nuclear center and periphery during the time course of the acquisition (Supplemental Fig. S1), suggesting that the localization classification based on a single image is somewhat artificial. We did not detect significant differences in the MSD response for peripheral or central localization for the three loci on chromosome XII (see, e.g., position 240 kp in Fig. 2C) and on chromosomes IV and XIV (data not shown), so the anomalous diffusive response appears to be largely conserved and appropriate to describe chromosome segmental dynamics for loci distant by more than ∼50 kb from TEL and CEN.

The dynamics of telomeres are anomalous in a central localization

In yeast, the 32 TEL tend to cluster near the NE, and the motion of tagged chromosome sites in the vicinity of a TEL is constrained (Heun et al. 2001; Sage et al. 2005). Using our reference behavior for chromosome loci located halfway along chromosome arms, we set out to perform an MSD analysis on TEL 3R and 14L (Fig. 1; hereafter denoted Tel3R and Tel14L). Although TEL predominantly accumulate near the periphery (Fig. 3A, right panel), their positioning in the nuclear center can be detected with an occurrence of ∼30%, and we analyzed their dynamics in this central region. The amplitude of spatial fluctuations in the short time regime appeared to be relatively similar compared with the reference response (Fig. 3A), although Tel3R appeared to be slightly less mobile after ∼10 sec than Tel14L, presumably because telomeric interactions between the two ends of chromosome XIV are much less frequent than that of chromosome III (Bystricky et al. 2005; Duan et al. 2010).

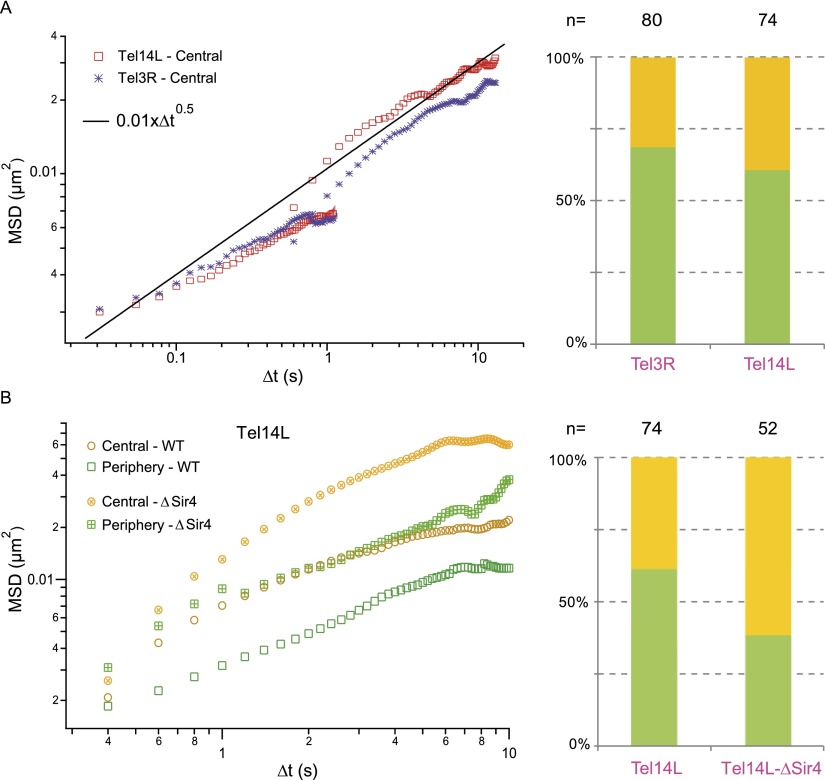
Figure 3.

Figure 3.

Open in a new tab

Telomere dynamics in living budding yeasts. (A, left plot) The MSD temporal evolution for telomere XIV-L and III-R with central localization (red and blue data sets). (Black solid line) The average response obtained in Figure 2B. (Right plot) Telomeres preferentially accumulate at the periphery (green and orange bars, respectively). (B, left plot) The comparison of the MSD response for telomere XIV-L at a central or peripheral localization in wild-type cells (open yellow and green symbols, respectively) or in sir4 mutant strains (crossed symbols) favoring a central localization of telomere XIV-L.

In contrast to the bulk of chromosomes, telomere dynamics appeared to be reduced at the nuclear periphery (Fig. 3B), in agreement with the idea that telomere peripheral localization is mediated by protein interactions involving, among others, Sir4 and Yku70/Yku80 (Hediger et al. 2002; Taddei et al. 2004; Bupp et al. 2007; Schober et al. 2009). It has been shown that deletion of either YKU70 or SIR4 leads to delocalization of some TEL to the nuclear center (Laroche et al. 1998; Hediger et al. 2002), but it remains unclear whether this deletion affects TEL dynamics aside from chromosome III (Bystricky et al. 2009). We thus investigated the movements of Tel14L in wild-type and in SIR4 mutant strains. Deletion of SIR4 leads to a predominant localization of Tel14L in the center (62%), likely due to loss of anchoring to the nuclear membrane. Moreover, telomere mobility is increased in SIR4 mutant strains when the tagged locus resides at the periphery and even more drastically at the nuclear center (Fig. 3B), confirming that physical interactions of the extremities of chromosomes are an essential player of their spatio-temporal dynamics. Overall, this study tends to support the proposition of uniform fluctuations throughout the nucleus for chromatin loci provided that they are sufficiently distant from anchoring regions.

Chromosome segmental dynamics are consistent with the Rouse model

To interpret our results with a polymer model, we make the assumptions that chromosome conformation and dynamics are mainly determined by (1) the permanent tethering of CEN to the SPB and the more transient attachment of TEL to NE (Zimmer and Fabre 2011), and (2) the level of crowding mediated by chromosomes and nuclear proteins. Crowding is expected to screen out hydrodynamic effects, which otherwise induce long-range interactions in between chromosome segments (Doi and Edwards 1988), so that nearest-neighbor elastic interactions between consecutive chromosome segments dominate their local dynamics. This approximation, which leads to the “Rouse” regime (Rouse 1953), has been extensively documented for concentrated solutions of synthetic polymers (see, e.g., Ewen and Richter 1997) and was recently validated in vivo for the bacterial chromosome (Weber et al. 2010).

Chromosomes are modeled by a Rouse chain, which is composed of a series of N elastic segments of length b. The motion of each bond is determined by its elasticity defined by the stiffness 3kBT/b2 with kBT the thermal energy, and its viscous drag ζ. Assuming that chromosomes are tethered at CEN and TEL, the MSD of monomers can be solved analytically in the short time regime (see Model section):

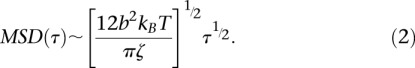graphic file with name 1829equ2.jpg

The Rouse segmental dynamics are characterized by an anomalous diffusive response uniform along the chain, in good agreement with our data. We wished to test the predictions of the Rouse model further by extracting the histogram of the displacement after a time lag of 0.18, 1.0, and 1.6 sec from the trajectories of locus 240 on chromosome XII (Fig. 4A). The histograms were first fitted with a normal diffusion model (Fig. 4A, left panel and equation in inset), which relies on one fitting parameter, the diffusion coefficient D. The diffusion coefficient of 4.8, 2.2, 1.8 × 10−3 μm2/sec was very different for τ = 0.18, 1.0, and 1.6 sec, respectively, showing the inconsistency of this model. We then used the formalism described in Guérin et al. (2012) to compute the histogram of the displacement for a Rouse chain tethered at its extremities (see expression in Model section). One single parameter was sufficient to reproduce the three distributions (Fig. 4A, right panel), and the quality of the fitting was significantly improved (note the departure of the red fit from the conventional model), hence strongly supporting the relevance of the Rouse model to describe the segmental dynamics of yeast chromosomes.

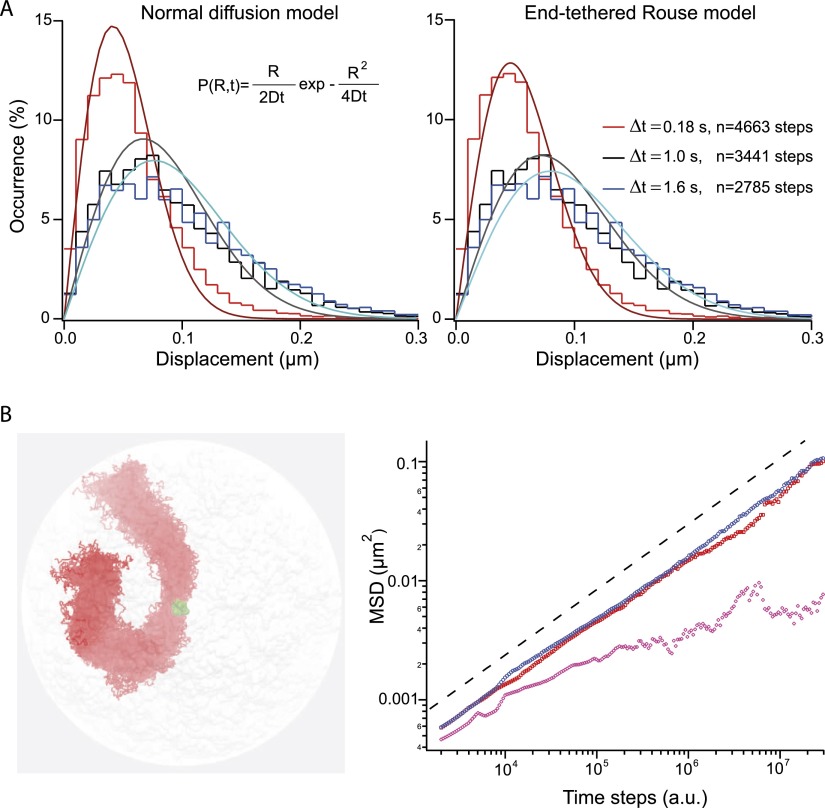
Figure 4.

Figure 4.

Open in a new tab

Rouse model for chromosome segmental dynamics. (A) The two graphs represent the step distribution functions measured for three different time intervals, which are represented by dashed lines in Figure 2A. The genomic position of the locus on chromosome XII is 240 kb, and the interframe interval of the acquisition is 59 msec. Note the deviation of the distributions toward longer displacements for increasing time lags, which is consistent with the progressive exploration of the nuclear volume. The three curves are fitted to a normal diffusion model (equation in the inset) or an end-tethered Rouse model (Eqs. 4, 5) (left and right panels, respectively). (B) Brownian dynamics simulation was implemented with polymer chains and in a realistic yeast nucleus using the nuclear conformation obtained by Hi-C as initial state (Duan et al. 2010). Chromosomes are tethered at their centromeres (green spheres) and free at their telomeres. The figure in the left panel represents the orthographic projection of 100 conformations of chromosome III in the course of one simulation of 106 time points. The polymer is elongated, and its diameter is ∼300 ± 50 nm. The MSD is computed for loci localized near the SPB, or at 200–400 nm and more than 400 nm from this anchor (purple, red, and blue data sets, respectively), showing that the response follows Rouse dynamics (black dashed line) provided that the locus is sufficiently distant from CEN.

We then performed BD simulations of yeast chromosome dynamics in a volume the geometry of which is consistent with yeast nuclear size, and using the structure derived from Hi-C experiments as the initial state (Duan et al. 2010). We assumed that chromosomes were attached to the SPB at their CEN (i.e., neglecting the contribution of microtubules connecting SPB to kinetochores), and freely diffusing at their TEL (chromosome III is represented in the left panel of Fig. 4B). The computed MSD for loci distant from CEN (>400 nm; blue data set in the right panel of Fig. 4B) reproduced the anomalous diffusive response associated with a power-law scaling of ∼0.54 over a temporal domain of four orders of magnitude that we observed experimentally (dashed line in Fig. 4B, right panel). The motion is more restricted for segments located at 10–100 nm from the CEN (pink data set) versus at a distance comprised between 200 and 400 nm (red data set). In addition, superposing the conformations of chromosome III during 106 time steps shows an elongated state of diameter ∼300 nm. This conformation is associated with volume exclusion between chromosomes (see also Supplemental Fig. S4B), an effect that was recently shown to be a key parameter of yeast nuclear architecture (Tjong et al. 2012). We thus conclude that the dynamics of chromosome loci in living yeast are accurately described by the Rouse model.

The Rouse dynamics imply that chromosome segments search for target sites by compact exploration (de Gennes 1982), meaning that they systematically visit neighboring sites as they look for targets during repair or transcription activation (Condamin et al. 2007). Because the probability that chromosome loci find a nearby target is increased (Guigas and Weiss 2008), the Rouse dynamics are likely efficient to create specific chromosome contacts in cis or in trans over distances of less than ∼400 nm, which are explored in a few minutes (Fig. 2B). The notion of territoriality remains controversial, whether it is absent based on the observation that broken ends of chromosomes are free to search the entire genome for appropriate partners (Haber and Leung 1996), or partial as telomere colocalization and coordinated movement would indicate (Bystricky et al. 2005). Future BD simulation studies should therefore evaluate whether and how compact exploration is related to chromosome territoriality in the yeast genome.

MSD fluctuations suggest that chromatin is highly flexible

The level of flexibility of a chromatin fiber is a matter of debate. In vitro single-molecule experiments have shown that the persistence length lp of nucleosome arrays is 20–30 nm (Cui and Bustamante 2000; Bancaud et al. 2006; Celedon et al. 2009; Kruithof et al. 2009). Conversely, analyses based on polymer models of in vivo distance measurements or Hi-C experiments (Bystricky et al. 2004; Dekker 2008; Tjong et al. 2012) provided estimates of ∼200 nm and 66–134 nm, respectively. Physical modeling of the mechanical properties of nucleosome arrays predicts a persistence length smaller than 30 nm for chromatin (Ben-Haïm et al. 2001; Schiessel et al. 2001), except in the case of highly ordered arrays with strong nucleosome–nucleosome interactions (Wedemann and Langowski 2002), in which case lp increases to ∼250 nm.

The amplitude of spatial fluctuations can be qualitatively linked to the flexibility of chromatin using the Rouse model, given that the bond length b and the viscous drag coefficient ζ are equal to 2lp and 6πηlp with η the viscosity, respectively (de Gennes 1979). Injecting this term in Equation 2 implies that the amplitude of the MSD increases with the square root of the polymer persistence length. The extent of spatio-temporal fluctuations therefore increases as the rigidity of the fiber increases, in qualitative opposition to free diffusion of an isolated tracer that increases as the diameter of the particle decreases. The MSD response can then be predicted for a persistence length comprised between 50 and 200 nm, given that the nuclear viscosity is η ∼ 7 ± 3 × 10−3 Pa.s based on GFP diffusion coefficient measurements (Kawai-Noma et al. 2006; Slaughter et al. 2007). This conjecture exceeds our measurements by a factor of 10–20 (dashed lines in Fig. 5A). In contrast, fitting of our data with the Rouse model leads to an amplitude of the MSD of 1.0 ± 0.2 × 10−2 μm2/sec−1/2 (solid line in Fig. 5A), suggesting that the persistence length of chromatin in living yeast is ∼5 nm. This length scale is coherent with the dimensions of a single nucleosome, which is a ∼5-nm by ∼10-nm disk-like structure. Hence, the analysis of chromosome motion suggests that chromatin is a flexible polymer in vivo.

Figure 5.

Figure 5.

Open in a new tab

Assaying chromatin flexibility from MSD analysis. (A, gray) The MSD response plotted in Figure 2B is analyzed with the Rouse model for different values of the persistence length of 200, 50, and 5 nm, as specified in the inset. The dynamics of chromosome loci are consistent with highly flexible chromatin. (B) Brownian dynamics simulations of an isolated chain containing 100 segments have been performed to confirm the relevance of the Rouse model. Dimensionless variables are defined using lp and 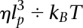Inline graphic as characteristic length and time scales; the MSD of a central monomer is plotted with different persistence lengths of 15, 30, 60, or 90 nm and for two different viscosities of 10−3 and 10−2 P (blue data sets). These data sets fall on a master curve, which follows the power law scaling of the analytical Rouse model: The black dashed line is derived from Equation 2 using the dimensionless variables (see exact expression in inset). (C) The histogram of the average square displacement after 0.1, 0.6, and 4.0 sec is represented for ∼70 trajectories of a locus at position 680 on chromosome XII, with a broad cell-to-cell variability within a single clone. The lines are Gaussian fits and serve as guides to the eye.

Because the Rouse model is a simplified model that does not take volume exclusion between monomers into account, we wished to strengthen our conclusions by running BD of a single chain composed of self-avoiding segments (see Model section). The extracted MSD shows an anomalous diffusive response, as well as the dependence on the persistence length and the viscous drag (Eq. 2) expected from the Rouse model (Fig. 5B). This analysis showed that the numerical prefactor of Equation 2 is underestimated by 1.4, suggesting that volume exclusion enhances the rate of spatial exploration. This difference implies that the persistence length of ∼5 nm is overestimated, and a correct estimate may be as small as ∼3 nm. This length scale, which is comparable to the DNA diameter, is unrealistic and points to an additional parameter related to the chromosomal environment.

Each MSD curve represented in Figure 2B is the average response over a population of ∼100 cells. The clonal variability of the spatio-temporal dynamics is not shown in this graph, although this variability is large, as inferred from the distribution of average displacements after a time lag of 0.1, 0.6, and 4.0 sec for ∼70 trajectories of a locus on chromosome XII (position 680, Fig. 5C). Because the difference between the average and the maximal or minimal MSD is about threefold, this variability is unlikely related to changes in persistence length, which should vary over two orders of magnitude from 0.3 to 30 nm. We rather suggest that this variability is associated with the existence of dynamic chromosomal contacts, as previously indicated in, e.g., the dynamic random loop model derived to interpret distance measurements in human cells (Mateos-Langerak et al. 2009). Dynamic and random contacts should transiently restrict spatial exploration (Supplemental Fig. S5), reduce the effective diffusion of a genomic site over a population average, and hence lead to an apparent persistence length smaller than chromatin intrinsic properties. We propose that chromosome loci with maximal mean square displacements in the short time regime represent the “interaction-free” limit, because their motion is not hindered by distant contacts. Given that the difference between the average and the maximal MSD is less than threefold (Fig. 5C), we can evaluate an upper limit for the persistence length of 32 × 3 nm <30 nm. Consequently, chromatin appears as a flexible polymer, and its persistence length can be qualitatively estimated to be less than ∼30 nm.

Chromatin structural proteins alter chromosome mobility

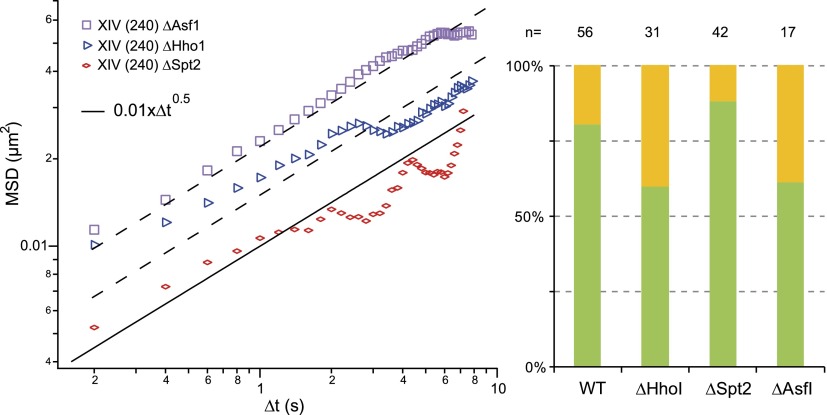
Finally, we investigated whether the dynamics of chromosomes was altered in the absence of chromatin structural proteins or chromatin assembly proteins. We first considered the HMG-like protein Spt2 in S. cerevisiae, which interacts with the histones H3 and H4 (Horn et al. 2002). The statics and the dynamics of one locus on chromosome XIV were assayed in wild-type (WT) and mutant spt2 cells, showing an accumulation at the periphery for the mutant and similar MSD responses in the short time regime (Fig. 6, right and left panels, respectively). We then performed the same analysis with Hho1p (Levy et al. 2008), which is considered as the linker histone analog in S. cerevisiae, although its structure differs from the linker histone in other organisms because it bears two globular domains. So far it remains unclear whether and how this protein participates in chromatin condensation. The deletion of HHO1 increases the proportion of spots detected in the nuclear center compared with wild type, and increases ∼1.5-fold the amplitude of chromatin loci displacements (Fig. 6). Given that the ratio Hho1p versus nucleosome remains poorly estimated (comprised between 1:37 and 1:4) (Freidkin and Katcoff 2001; Downs et al. 2003), these enhanced dynamics may be associated with the reduced frequency of chromosome interactions mediated by the two domains of Hho1p and/or with an onset in flexibility due to conformational changes at the nucleosome level. Finally, we probed the role of the nucleosome assembly chaperone Asf1p, which is involved in replication-dependent and replication-independent chromatin assembly (Loyola and Almouzni 2004). As for hho1 deletion mutant, the labeled locus appeared to be more frequently central than in wild-type nuclei, and its mobility was 2.2-fold increased. The Rouse model therefore seems to account for the dynamics of chromosome loci in WT cells, as well as in hho1, asf1, and spt2 mutants, suggesting that this approach is sufficiently generic to perform systematic motion analyses.

Figure 6.

Figure 6.

Open in a new tab

Chromatin structural/modifying proteins and chromosome dynamics. (Left plot) The MSD temporal evolution for a locus on chromosome XIV, genomic position 240 kb. (Black solid line) The wild-type situation was identical to the Rouse response described in Figure 3A. The dynamic response obtained in hho1 (red symbols), asf1 (blue symbols), and spt2 (purple symbols) mutant yeast. The two dashed lines represent fits to the data with the Rouse model. (Right plot) Asf1p and Hho1p participate in the nuclear localization of the tagged locus (the yellow and green bars correspond to central and peripheral localizations, respectively).

Conclusion

We demonstrate that the motion of chromosome loci in living yeast is characterized by anomalous subdiffusion with an exponent of 0.52 over a temporal domain spanning more than four orders of magnitude. We then show that this response, which appears to be relevant for the analysis of WT and mutant cells, is consistent with the Rouse dynamics. Because the Rouse regime is characteristic of polymers in crowded environments, our result strengthens the relevance of polymer models for the description of the yeast genome (Gehlen et al. 2012; Tjong et al. 2012; Wong et al. 2012). In addition, the Rouse dynamics is associated with compact exploration, implying that chromosome loci efficiently search for nearby targets. We speculate that this property guides chromosome interactions in cis and trans, and envision that this hypothesis can be tested using BD simulations in combination with Hi-C experiments aiming to evaluate the number of chromosome contacts as a function of the genomic distance. Furthermore, the amplitude of chromatin spatio-temporal fluctuations shows that this polymer is flexible. Yet the cell-to-cell variability of the amplitude of chromosome movements only allows for a qualitative determination of the persistence length of <30 nm. We propose that this variability is associated with dynamic interactions between chromosomes, and future BD simulations may confirm or invalidate this conjecture, in turn, providing new insights on the statics and the dynamics of the yeast genome.

The folding of interphase chromosomes in metazoans involves loops of variable sizes defining topological domains of 0.2–5 Mb (Nora et al. 2012; Sexton et al. 2012). Because the dimension of these domains, which can be described as end-tethered chromosome fragments, is consistent with the length of yeast chromosome arms, we speculate that the Rouse model is relevant to higher-order eukaryotes. This model has recently been implemented in numerical simulations (Bohn and Heermann 2010), showing that the dynamics of loop formation may interfere with the segmental motion of human chromosomes, a hypothesis that remains to be tested quantitatively in vivo.

Model

Dynamics

The motion of an end-tethered Rouse chain can be studied analytically using normal mode decomposition (Vandoolaeghe and Terentjev 2007), and the MSD of the nth segment (MSDn) reads:

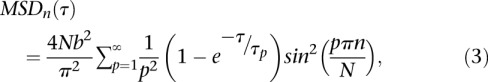graphic file with name 1829equ3.jpg

with τp the relaxation time of each mode τp = τR/p2 and τR = L2ζ/3π2kBT the Rouse time identified as the longest relaxation time of the chain. Note that this equation is valid in three dimensions (3D), and its two-dimensional (2D) version is readily obtained with a multiplication by 2/3, assuming that the motion is isotropic. The temporal evolution of the MSD is plotted in Supplemental Figure S4As. In the short time limit (τ ≪ τR), Equation 3 is dominated by the terms with large p, and it can be simplified to obtain Equation 2. In addition, the formalism described in Guérin et al. (2012) (see details in the Supplemental Material) enables us to extract the distribution of the displacement R for the nth segment after a time lag τ:

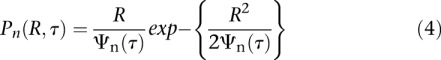graphic file with name 1829equ4.jpg
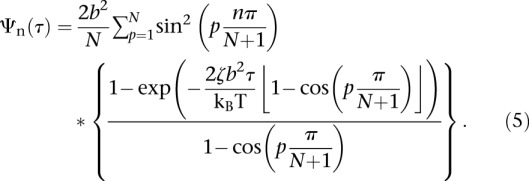graphic file with name 1829equ5.jpg

The movements of chromosomes, which were modeled by a series of bead linked by springs or ball-in-socket joints, was also analyzed by BD. The size of each bead was set to 15 nm in diameter, and it was assumed to contain approximately three nucleosomes, so that the full genome consists of 27,000 beads. Chromosomes were constrained in a sphere of 2 μm in diameter, and the CEN were fixed to the SPB using harmonic constraints. We used the Langevin dynamics algorithm implemented in the NAMD software (Phillips et al. 2005) with an appropriate in-house force field. The Langevin equation for the nth monomer has the form:

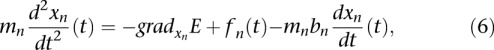graphic file with name 1829equ6.jpg

where the random force fn(t) is derived from a Gaussian distribution with the properties:

graphic file with name 1829equ7.jpg
graphic file with name 1829equ8.jpg

with ζ the friction coefficient. The energy E of each bead is the sum of three contributions associated with the confinement in the nucleus, the elasticity of the chain, and the repulsive interactions between monomers, which are expressed as:

graphic file with name 1829equ9.jpg
graphic file with name 1829equ10.jpg

with r the distance of the bead to the center of the nucleus, and r1 the radius of the nucleus.

graphic file with name 1829equ11.jpg
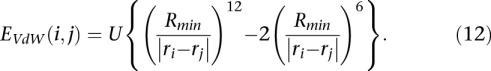graphic file with name 1829equ12.jpg

The parameters of this model can be found in Table 1. BD were run during 3 × 107 time steps, starting from the conformation obtained by Hi-C (Duan et al. 2010) equilibrated during 106 time steps. We also performed BD to investigate whether spatio-temporal fluctuations were different for 1, 4, or 10 segments, or for one segment of large diameter along the chain. We did not detect differences on the MSD response (data not shown), in agreement with our observation of similar dynamics with Lac or Tet labeling, which measure ∼10 and 7 kb in length, respectively.

Table 1.

Set of parameters to run Brownian dynamics simulations

graphic file with name 1829tbl1.jpg

Open in a new tab

Methods

Plasmids and strains

All the strains we used are described in Supplemental Table 1.

Cell culture

Cells were grown in YPD or YNB at 30°C starting from a fresh overnight culture. They were diluted at 106 cells/mL, and harvested when OD600 reached 4 × 106 cells/mL and rinsed twice with the corresponding SC media. Cells were then spread on a SC media patch containing a 2% agarose and 2% glucose coated slide. A coverslip was deposited over the cells, and the construction was finally sealed with “VaLaP” (one-third vaseline, one-third lanoline, one-third paraffin). Live microscopy was limited to 20 min after mounting the coverslip. Extreme care was taken to ensure that cells are at approximately equal stages of growth based on their shapes, as inferred from a single image of transmission light microscopy, and based on the nucleus shape using the roundness parameter R, which was defined as:

graphic file with name 1829equ13.jpg

with Surface the number of pixels after segmentation of the nucleus, and Perimeter the outline in pixels (see Supplemental Fig. S2). We considered nuclei with R > 0.8 to avoid mitotic phenotypes.

Live cell imaging

Yeast cells were imaged at room temperature with a BX-51 upright microscope equipped with a laser diode (Lumencor), a 100× oil immersion objective (NA = 1.4), and an EMCCD camera (Andor DU-897), as described in Hajjoul et al. (2009) (see Supplemental Video 1). The excitation emission at 470 ± 10 nm was set to 7.53 W/μm2, about 100 times less than the value that is necessary for normal cell growth (Carlton et al. 2010), and we observed consecutive rounds of divisions during ∼2 h (data not shown). For slow acquisitions of interframe intervals of 2 sec or more, we used a 100× oil immersion objective with a variable NA set to ∼1.1–1.2. The acquisition was performed with a shutter synchronized with the camera to minimize photobleaching, and we checked for drifts by monitoring the position of the center of the nucleus in the first and last image of the recording. Optimal interframe intervals of ∼20 msec were reached by cropping regions of interest and using a 2 * 2 binning with the Andor iQ imaging software. The loss in pixel size resolution was compensated with a 2× lens placed in the microscope light path.

We focused on 2D single-particle tracking and checked that similar information was retrieved with 3D tracking using micro-mirrors (Supplemental Fig. S3; Hajjoul et al. 2009, 2011). We note that 2D acquisitions may bias MSD responses for loci preferentially localized at the periphery, because in some cases central loci in the projected view may be peripheral in the 3D nucleus.

Data analysis

Video sequences consisted of 300 consecutive images, and we displayed MSD traces on 150 time intervals at most in order to ensure the statistical relevance of mean displacements. The movements of chromosome loci were systematically analyzed using a custom software that was developed in Matlab (Mathworks) (Sergé et al. 2008; Albert et al. 2013 [source code at http://jcb.rupress.org/content/202/2/201/suppl/DC1, and the executable file at ftp://intermtt:MTTinterface@ftp.laas.fr/]). This software enabled us to extract (x, y) coordinates by Gaussian fitting, to reconstruct the trajectories, and to compute the MSD and the step distribution function (see Supplemental Video 1). Note that the MSD in fixed cells was 20- to 30-fold lower than in living cells (Supplemental Fig. S3B).

Acknowledgments

We thank the University Paul Sabatier for Ph.D. fellowship funding (to J.M.). This work was partly supported by the ANR program JC08_341867, by the CNRS program PIR, and by the LAAS-CNRS technology platform, a member of the French Basic Technology Research Network. We are grateful to Nathalie Daigle for critical reading of the manuscript. We are grateful to Charlotte Galimow for strain construction and initial characterization of gene position.

Author contributions: H.H. and J.M. designed the study and performed data analysis. H.R. developed analytical models. I.G. generated new strains. J.M. and P.C. performed Brownian dynamics simulations. B.A. provided new strains. P.C. and J.M.V. designed models. O.G. and K.B. developed the manuscript. A.B. designed the study, developed models, and wrote the paper.

Footnotes

[Supplemental material is available for this article.]

Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.157008.113.

References

  1. Albert B, Mathon J, Shukla A, Saad H, Léger-Silvestre I, Normand C, Villa D, Kamgoue A, Mozziconacci J, Wong H, Zimmer C, Bhargava P, Bancaud A, Gadal O 2013. Systematic characterization of the conformation and dynamics of budding yeast chromosome XII. J Cell Biol 202: 201–210 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bancaud A, Conde e Silva N, Barbi M, Wagner G, Allemand JF, Mozziconacci J, Lavelle C, Croquette V, Victor JM, Prunell A, et al. 2006. Structural plasticity of single chromatin fibers revealed by torsional manipulation. Nat Struct Mol Biol 13: 444–450 [DOI] [PubMed] [Google Scholar]
  3. Bancaud A, Lavelle C, Huet S, Ellenberg J 2012. A fractal model for nuclear organization: Current evidence and biological implications. Nucleic Acids Res 40: 8783–8792 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Ben-Haïm E, Lesne A, Victor JM 2001. Chromatin: A tunable spring at work inside chromosomes. Phys Rev E Stat Nonlin Soft Matter Phys 64: 051921. [DOI] [PubMed] [Google Scholar]
  5. Berger A, Cabal G, Fabre E, Duong T, Buc H, Nehrbass U, Olivo-Marin J, Gadal O, Zimmer C 2008. High-resolution statistical mapping reveals gene territories in live yeast. Nat Methods 5: 1031–1037 [DOI] [PubMed] [Google Scholar]
  6. Bohn M, Heermann DW 2010. Diffusion-driven looping provides a consistent framework for chromatin organization. PLoS ONE 5: e12218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bronstein I, Israel Y, Kepten E, Mai S, Shav-Tal Y, Barkai E, Garini Y 2009. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys Rev Lett 103: 18102. [DOI] [PubMed] [Google Scholar]
  8. Bupp JM, Martin AE, Stensrud ES, Jaspersen SL 2007. Telomere anchoring at the nuclear periphery requires the budding yeast Sad1-UNC-84 domain protein Mps3. J Cell Biol 179: 845–854 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bystricky K, Heun P, Gehlen L, Langowski J, Gasser SM 2004. Long range compaction and flexibility of interphase chromatin in budding yeast analysed by high-resolution imaging techniques. Proc Natl Acad Sci 101: 16495–16500 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bystricky K, Laroche T, Van Houwe G, Blaszczyk M, Gasser S 2005. Chromosome looping in yeast. J Cell Biol 168: 375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bystricky K, Van Attikum H, Montiel M, Dion V, Gehlen L, Gasser S 2009. Regulation of nuclear positioning and dynamics of the silent mating type loci by the yeast Ku70/Ku80 complex. Mol Cell Biol 29: 835. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cabal G, Genovesio A, Rodriguez-Navarro S, Zimmer C, Gadal O, Lesne A, Buc H, Feuerbach-Fournier F, Olivo-Marin J, Hurt E 2006. SAGA interacting factors confine sub-diffusion of transcribed genes to the nuclear envelope. Nature 441: 770–773 [DOI] [PubMed] [Google Scholar]
  13. Carlton P, Boulanger J, Kervrann C, Sibarita J, Salamero J, Gordon-Messer S, Bressan D, Haber J, Haase S, Shao L 2010. Fast live simultaneous multiwavelength four-dimensional optical microscopy. Proc Natl Acad Sci 107: 16016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Celedon A, Nodelman IM, Wildt B, Dewan R, Searson P, Wirtz D, Bowman GD, Sun SX 2009. Magnetic tweezers measurement of single molecule torque. Nano Lett 9: 1720–1725 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Condamin S, Bénichou O, Tejedor V, Voituriez R, Klafter J 2007. First-passage times in complex scale-invariant media. Nature 450: 77–80 [DOI] [PubMed] [Google Scholar]
  16. Cremer T, Cremer C 2001. Chromosome territories, nuclear architecture and gene regulation in mammalian cells. Nat Rev Genet 2: 292–301 [DOI] [PubMed] [Google Scholar]
  17. Cui Y, Bustamante C 2000. Pulling a single chromatin fiber reveals the forces that maintain its higher-order structure. Proc Natl Acad Sci 97: 127–132 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. de Gennes P-G. 1979. Scaling concepts in polymer physics. Cornell University Press, Ithaca, NY. [Google Scholar]
  19. de Gennes PG 1982. Kinetics of diffusion-controlled processes in dense polymer systems. I. Nonentangled regimes. J Chem Phys 76: 3316–3321 [Google Scholar]
  20. Dekker J 2008. Mapping in vivo chromatin interactions in yeast suggests an extended chromatin fiber with regional variation in compaction. J Biol Chem 283: 34532. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Doi M, Edwards S 1988. The theory of polymer dynamics. Oxford University Press, New York [Google Scholar]
  22. Downs JA, Kosmidou E, Morgan A, Jackson SP 2003. Suppression of homologous recombination by the Saccharomyces cerevisiae linker histone. Mol Cell 11: 1685–1692 [DOI] [PubMed] [Google Scholar]
  23. Duan Z, Andronescu M, Schutz K, McIlwain S, Kim YJ, Lee C, Shendure J, Fields S, Blau CA, Noble WS 2010. A three-dimensional model of the yeast genome. Nature 465: 363–367 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Ewen B, Richter D 1997. Neutron spin echo investigations on the segmental dynamics of polymers in melts, networks and solutions. Adv Polym Sci 134: 1–129 [Google Scholar]
  25. Freidkin I, Katcoff DJ 2001. Specific distribution of the Saccharomyces cerevisiae linker histone homolog HHO1p in the chromatin. Nucleic Acids Res 29: 4043–4051 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Gehlen LR, Gruenert GM, Jones B, Rodley CD, Langowski J, O'Sullivan JM 2012. Chromosome positioning and the clustering of functionally related loci in yeast is driven by chromosomal interactions. Nucleus 3: 370–383 [DOI] [PubMed] [Google Scholar]
  27. Göndör A, Ohlsson R 2009. Chromosome crosstalk in three dimensions. Nature 461: 212–217 [DOI] [PubMed] [Google Scholar]
  28. Gotta M, Laroche T, Formenton A, Maillet L, Scherthan H, Gasser S 1996. The clustering of telomeres and colocalization with Rap1, Sir3, and Sir4 proteins in wild-type Saccharomyces cerevisiae. J Cell Biol 134: 1349–1363 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Guérin T, Bénichou O, Voituriez R 2012. Non-Markovian polymer reaction kinetics. Nat Chem 4: 568–573 [DOI] [PubMed] [Google Scholar]
  30. Guigas G, Weiss M 2008. Sampling the cell with anomalous diffusion—the discovery of slowness. Biophys J 94: 90–94 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Haber JE, Leung W-Y 1996. Lack of chromosome territoriality in yeast: Promiscuous rejoining of broken chromosome ends. Proc Natl Acad Sci 93: 13949–13954 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Hajjoul H, Kocanova S, Lassadi I, Bystricky K, Bancaud A 2009. Lab-on-Chip for fast 3D particle tracking in living cells. Lab Chip 9: 3054–3058 [DOI] [PubMed] [Google Scholar]
  33. Hajjoul H, Mathon J, Viero Y, Bancaud A 2011. Optimized micromirrors for three-dimensional single-particle tracking in living cells. Appl Phys Lett 98: 243701 [Google Scholar]
  34. Hediger F, Neumann F, Van Houwe G, Dubrana K, Gasser S 2002. Live imaging of telomeres: yKu and Sir proteins define redundant telomere-anchoring pathways in yeast. Curr Biol 12: 2076–2089 [DOI] [PubMed] [Google Scholar]
  35. Heun P, Laroche T, Shimada K, Furrer P, Gasser S 2001. Chromosome dynamics in the yeast interphase nucleus. Science 294: 2181. [DOI] [PubMed] [Google Scholar]
  36. Hihara S, Pack C-G, Kaizu K, Tani T, Hanafusa T, Nozaki T, Takemoto S, Yoshimi T, Yokota H, Imamoto N, et al. 2012. Local nucleosome dynamics facilitate chromatin accessibility in living mammalian cells. Cell Reports 2: 1645–1656 [DOI] [PubMed] [Google Scholar]
  37. Horn PJ, Crowley KA, Carruthers LM, Hansen JC, Peterson CL 2002. The SIN domain of the histone octamer is essential for intramolecular folding of nucleosomal arrays. Nat Struct Biol 9: 167–171 [DOI] [PubMed] [Google Scholar]
  38. Kawai-Noma S, Ayano S, Pack C-G, Kinjo M, Yoshida M, Yasuda K, Taguchi H 2006. Dynamics of yeast prion aggregates in single living cells. Genes Cells 11: 1085–1096 [DOI] [PubMed] [Google Scholar]
  39. Kruithof M, Chien F-T, Routh A, Logie C, Rhodes D, van Noort J 2009. Single-molecule force spectroscopy reveals a highly compliant helical folding for the 30 nm chromatin fiber. Nat Struct Mol Biol 16: 534–540 [DOI] [PubMed] [Google Scholar]
  40. Laroche T, Martin SG, Gotta M, Gorham HC, Pryde FE, Louis EJ, Gasser SM 1998. Mutation of yeast Ku genes disrupts the subnuclear organization of telomeres. Curr Biol 8: 653–657 [DOI] [PubMed] [Google Scholar]
  41. Levy A, Eyal M, Hershkovits G, Salmon-Divon M, Klutstein M, Katcoff DJ 2008. Yeast linker histone Hho1p is required for efficient RNA polymerase 1 processivity and transcriptional silencing at the ribosomal DNA. Proc Natl Acad Sci 105: 11703–11708 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. 2009. Comprehensive mapping of long-range interactions reveals folding principles of the human chromosome. Science 326: 289–293 [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Loyola A, Almouzni G 2004. Histone chaperones, a supporting role in the limelight. Biochim Biophys Acta 1977: 3–11 [DOI] [PubMed] [Google Scholar]
  44. Marshall W, Straight A, Marko J, Swedlow J, Dernburg A, Belmont A, Murray A, Agard D, Sedat J 1997. Interphase chromosomes undergo constrained diffusional motion in living cells. Curr Biol 7: 930–939 [DOI] [PubMed] [Google Scholar]
  45. Mateos-Langerak J, Bohn M, de Leeuw W, Giromus O, Manders EM, Verschure PJ, Indemans MH, Gierman HJ, Heermann DW, van Driel R, et al. 2009. Spatially confined folding of chromatin in the interphase nucleus. Proc Natl Acad Sci 106: 3812–3817 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Nora EP, Lajoie BR, Schulz EG, Giorgetti L, Okamoto I, Servant N, Piolot T, van Berkum NL, Meisig J, Sedat J, et al. 2012. Spatial partitioning of the regulatory landscape of the X-inactivation centre. Nature 485: 381–385 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalé L, Schulten K 2005. Scalable molecular dynamics with NAMD. J Comput Chem 26: 1781–1802 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Rodley CDM, Bertels F, Jones B, O'Sullivan JM 2009. Global identification of yeast chromosome interactions using genome conformation capture. Fungal Genet Biol 46: 879–886 [DOI] [PubMed] [Google Scholar]
  49. Rouse PE 1953. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J Chem Phys 21: 1272–1280 [Google Scholar]
  50. Sage D, Neumann F, Hediger F, Gasser S, Unser M 2005. Automatic tracking of individual fluorescence particles: Application to the study of chromosome dynamics. IEEE Trans Image Process 14: 1372–1383 [DOI] [PubMed] [Google Scholar]
  51. Schiessel H, Gelbart WM, Bruinsma R 2001. DNA folding: Structural and mechanical properties of the two-angle model for chromatin. Biophys J 80: 1940–1956 [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Schober H, Kalck V, Vega-Palas M, Van Houwe G, Sage D, Unser M, Gartenberg M, Gasser S 2008. Controlled exchange of chromosomal arms reveals principles driving telomere interactions in yeast. Genome Res 18: 261. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Schober H, Ferreira H, Kalck V, Gehlen LR, Gasser SM 2009. Yeast telomerase and the SUN domain protein Mps3 anchor telomeres and repress subtelomeric recombination. Genes Dev 23: 928–938 [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Sergé A, Bertaux N, Rigneault H, Marguet D 2008. Dynamic multiple-target tracing to probe spatiotemporal cartography of cell membranes. Nat Methods 5: 687–694 [DOI] [PubMed] [Google Scholar]
  55. Sexton T, Yaffe E, Kenigsberg E, Bantignies F, Leblanc B, Hoichman M, Parrinello H, Tanay A, Cavalli G 2012. Three-dimensional folding and functional organization principles of the Drosophila genome. Cell 148: 458–472 [DOI] [PubMed] [Google Scholar]
  56. Slaughter BD, Schwartz JW, Rong L 2007. Mapping dynamic protein interactions in MAP kinase signaling using live-cell fluorescence fluctuation spectroscopy and imaging. Proc Natl Acad Sci 104: 20320–20325 [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Taddei A, Hediger F, Neumann FR, Bauer C, Gasser SM 2004. Separation of silencing from perinuclear anchoring functions in yeast Ku80, Sir4 and Esc1 proteins. EMBO J 23: 1301–1312 [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Therizols P, Duong T, Dujon B, Zimmer C, Fabre E 2010. Chromosome arm length and nuclear constraint determine the dynamic relationship of yeast subtelomeres. Proc Natl Acad Sci 107: 2025–2030 [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Tjong H, Gong K, Chen L, Alber F 2012. Physical tethering and volume exclusion determine higher-order genome organization in budding yeast. Genome Res 22: 1295–1305 [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Vandoolaeghe WL, Terentjev EM 2007. A Rouse-tube model of dynamic rubber viscoelasticity J Phys A Math Theor 40: 14725 [Google Scholar]
  61. Weber S, Spakowitz A, Theriot J 2010. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm. Phys Rev Lett 104: 238102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Wedemann G, Langowski J 2002. Computer simulation of the 30-nanometer chromatin fiber. Biophys J 82: 2847–2859 [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Wong H, Marie-Nelly H, Herbert S, Carrivain P, Blanc H, Koszul R, Fabre E, Zimmer C 2012. A predictive computational model of the dynamic 3D interphase nucleus. Curr Biol 22: 1881–1890 [DOI] [PubMed] [Google Scholar]
  64. Zimmer C, Fabre E 2011. Principles of chromosomal organization: Lessons from yeast. J Cell Biol 192: 723–733 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES