Demonstration of a software design and statistical analysis methodology with application to patient outcomes data sets

Abstract

Purpose: With emergence of clinical outcomes databases as tools utilized routinely within institutions, comes need for software tools to support automated statistical analysis of these large data sets and intrainstitutional exchange from independent federated databases to support data pooling. In this paper, the authors present a design approach and analysis methodology that addresses both issues.

Methods: A software application was constructed to automate analysis of patient outcomes data using a wide range of statistical metrics, by combining use of C#.Net and R code. The accuracy and speed of the code was evaluated using benchmark data sets.

Results: The approach provides data needed to evaluate combinations of statistical measurements for ability to identify patterns of interest in the data. Through application of the tools to a benchmark data set for dose-response threshold and to SBRT lung data sets, an algorithm was developed that uses receiver operator characteristic curves to identify a threshold value and combines use of contingency tables, Fisher exact tests, Welch t-tests, and Kolmogorov-Smirnov tests to filter the large data set to identify values demonstrating dose-response. Kullback-Leibler divergences were used to provide additional confirmation.

Conclusions: The work demonstrates the viability of the design approach and the software tool for analysis of large data sets.

INTRODUCTION

Construction of databases to prospectively collect data for all patients that would enable examination of the relevance of treatment parameters on patient outcomes is an area of active interest.^{1, 2, 3, 4, 5, 6, 7, 8, 9} Several groups have heralded the rise in interest in this area for radiation oncology. Quantitative Analysis of Normal Tissue Effects in the Clinic, a joint venture between The American Association of Physicists in Medicine and The American Society for Radiation Oncology (ASTRO), highlighted the need for more data to detail the relationships between various dose volume histogram (DVH) metrics and the response of normal tissues. This group called for the development of a culture of data pooling in order to construct the large data sets needed.¹ A survey by the Radiation Oncology Institute (ROI) of the membership of ASTRO highlighted that the development of a radiation oncology registry was a key priority.³ ASTRO is now supporting the construction of a national registry.⁵ Underpinning efforts to pool multi-institutional data with minimal additional overhead is the routine use of databases to collect and analyze outcomes data at individual institutions. Such efforts can minimize the extra effort, particularly manual effort, needed to participate in collaborations.

The department of Radiation Oncology at Mayo Clinic is constructing a comprehensive outcomes database based upon the experience gained from constructing pilot databases⁶ that contained subgroups of data needed for the comprehensive database. Two factors that have emerged from that pilot experience as being necessary for the overall success of the final project are (1) a need for tools to assist in the analysis of large data sets produced from the outcomes database and (2) a need to develop standards to enable automated exchanges among federated databases developed independently by other specialty groups (e.g., surgery). There is an advantage in addressing these two factors concurrently and in concert with collaborators from other institutions (M.D. Anderson Cancer Center and University of Alabama for this work). Software algorithms analyzing these data sets will require at least minimal standardization of data element types and formats for saving, retrieving, and analyzing the data. Similarly, the development of automated tools for exchanging data with collaborators also requires standardization. The ability to use the same standard for both would simplify software development.

Datasets from outcomes databases are large and contain several data types (e.g., toxicity, survival, DVH metrics, treatment plan information, and demographic data). Manually searching through the data sets to carry out statistical examination of the interrelationships among the data elements is impractical. Software tools are needed that can automate, or semiautomate, statistical analysis and reports of large data sets pulled from the outcomes databases to generate a hypothesis about interactions among the data elements.

We took a two-stage approach to this problem. We would first develop software tools that could automate the application of a wide range of statistical tests to a flexible input data standardization format. The analysis algorithms act independently of a priori assumptions of the interactions of particular data types, using just the data values. We would then develop algorithms that couple results of the analysis with understanding of the data type characteristics to highlight hypothesis-generating patterns.

We report here on our work on the first stage, which has produced a software application named DataMole. Design considerations for the application and the data exchange/input formats included an approach that is affordable, extensible to accommodate the addition of statistical methods, and able to be implemented by research staff to produce applications that may be generalized to use in production-level software supported by IT professionals. We benchmarked the formats and applications to demonstrate calculation time and accuracy. Utility in the second stage was demonstrated by applying the software to simulated and clinical data sets and by developing an analysis algorithm that would highlight dose-response thresholds by combining a subset of results from the statistical tests.

METHODS AND MATERIALS

Databases for analyzing patient outcomes are developed independently among institutions and among specialty groups within institutions. This decentralized, federated approach to database development offers several advantages. Groups retain control and ownership over their data, security and confidentiality for the institutions are maintained, and the development of database schemas that reflect quantization of data elements and relationships can mature at a pace set by the groups. When data, other than the Digital Imaging and Communications in Medicine (DICOM) standard, are exchanged among investigators, spreadsheets are typically used for researcher-to-researcher (RtoR) exchanges. Automated server-to-server (StoS) exchanges are typically enabled by setting up web services that allow virtual queries to the database, with the results returned in an eXtensible markup language (XML) file. The focus of a federated data exchange model is the definition of standards for exchange rather than construction of a centralized database.

For both RtoR and StoS formats, it is desirable to achieve a balance in the ability to convey sufficient information without the formats becoming overly prescriptive so that they become cumbersome to use. Since StoS XML exchanges will typically construct data sets electronically from populated databases, they may encapsulate fairly detailed information about the data sets and values without requiring extensive manual effort. RtoR spreadsheet exchanges, however, require a very simple format requiring minimal information in addition to the data. Since both spreadsheet and XML files are commonly used, and reformatting the data received from collaborators is undesirable, the development of standard input file formats (e.g., XML, Excel) for our statistical analysis software necessitates the co-development of a data class that may also be used for generalized federated data exchanges.

Coordination of these objectives can be efficiently accomplished with object-oriented programming methods by defining a class and taking advantage of built-in functionality to read and write (serialize) the class data in XML. Methods were added to the class to serialize the data into Excel (Microsoft, Redmond, WA) spreadsheets. For this project, we used C#.Net (Microsoft) in compliance with our institutional standards. The Express version is freely available and sufficient. Within that environment, we also used language-integrated query (LINQ) classes, which facilitate sorting and extracting data from large data arrays with heterogeneous data types. While we applied the tools to practical examples using the DVH data in radiation oncology, the methods are agnostic for the underlying data type. In practice, our DVH metrics and other plan and outcomes parameters are stored within SQL databases. We additionally investigated options for extracting plan parameter data values (e.g., beam angles, MUs, etc.) from DICOM RT files from within the C# program, using an application programming interface (API) (MyDicom.Net). Other options such as dicompyler (Python) used in conjunction with IronPython.Net, or Evil Dicom (evildicom.rexcardan.com) would have been viable alternatives. The DataMole software application was created to use both Excel and XML GFDE formats for both input and output, allowing recursion on the results. The XML-based Predictive Modeling Markup Language (PMML) developed by the Data Mining Group¹⁰ to capture all the details of statistical models or data-mining tools used, was considered for this initial phase of the project. Extensive use of R as a statistical package and ready ability to use C#.Net to integrate the application into a wide range applications that could be supported at an enterprise level were compelling. In addition, the DataMole output files were designed to allow recursion of the results for additional analysis, but this was not straightforward for PMML output files.

A wide range of statistical analysis metrics are frequently employed in data sets that may potentially be returned from an outcomes database.^{10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20} For our initial development, we targeted the automation of calculations for several. For correlations among data columns, the Pearson correlation (PC) coefficient can have statistical power advantages (even with slightly non-normal data), but it comes with the assumption of a linear relationship. The nonparametric measures Kendall tau (KC) and Spearman (SC) rank correlation coefficients avoid assumptions of linearity and normality in the data, and they are not strongly affected by outliers. However, with small sizes, it can be mathematically impossible to measure a statistically significant difference between samples with the nonparametric measures, whereas a Pearson correlation can still capture strong differences. The data set may contain columns with continuous values that are systematically related in a pairwise fashion (e.g., lung V13Gy [%] and lung V20Gy [%] for any given treatment plan). We used the parametric paired Student's t-test (ST) and the nonparametric Wilcox signed rank sum (WRS) tests to define p-values for the mean difference in the paired values.

A data set may contain columns with stratified values (e.g., National Cancer Institute Common Terminology Criteria for Adverse Events [CTCAE] toxicity scores for pneumonitis 1,2,3,4,5) along with columns of continuous numeric values (e.g., DVH metrics, lung V20Gy [%]) for which thresholds in response are of interest. Binary renderings were automatically generated if the number of unique data values in the column was fewer than the square root of the number of data values and less than a user defined limit (e.g., 12). Receiver operator characteristic (ROC) curves for binary renderings of the stratified columns (e.g., CTCAE toxicity < 1, 2, 3, 4 or 5 vs ≥ 1, 2, 3, 4 or 5, respectively) were calculated and used to determine for each combination a cut-point (i.e., threshold) value corresponding to the maximum of the Youden Index.^{10, 11, 12, 13} The area under the ROC curve is a relative indicator of the ability of the values of the continuous variable to predict for the binary rendering of the stratified column. Data were subgrouped according to the cut point value for each of the binary renderings of the stratified column to form 2 × 2 contingency tables, and the sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV) were calculated for each. For each of the contingency tables, Fisher's exact test (FET) was used to calculate the p-value for the association of the group defined by the binary rendering to the group defined by the cut point value.

The distributions of values in each of the continuous columns were subgrouped according to the binary renderings (e.g., V20Gy [%] for CTCAE toxicity < 2 vs ≥ 2) of the stratified columns. The significance of differences in the means was compared using the two sample Welch t-test (WT), which is a variation on the Student's t-test that does not require the underlying assumption that the variances of the two distributions are equal.^{14, 15} When the number of values in each of the groups is large, the difference in the means of two distributions may be significant even when the distributions have substantial overlap. Additional information may be needed when looking for thresholds in response, to address not just differences in the means, but differences in the distributions. We used one-sided Kolmogorov-Smirnov (KS) tests to calculate the p-value that the underlying probability distribution function (pdf) for values in one group is not stochastically ordered as greater/less than the pdf of the other group.^{16, 17} In addition, we gauged the “distance” between the two distributions by calculating the Kullback-Leibler divergence (KLD).^{18, 19} KLD is calculated from a probability-weighted log odds ratio, with 0 indicating that the distributions are identical and larger values indicating a diminishing likelihood that one distribution (A or B) is a subset of the other (B or A) where these are notated as KLD(A∥B) or KLD (B∥A).

Writing the code to execute and benchmark all of these tests implies a substantial investment in time for software development. Moreover, it is highly likely that the set of statistical tests determined to be optimal at one point in time will evolve with experience. To facilitate this evolution, it is important to be able to add or remove tests to pursue refinements with minimal investment in coding effort. The cost of vended statistical packages can be prohibitive; other resources may prove more cost-efficient. An open-source tool for statistical analysis and graphing with an extensive user base is R (www.r-project.org).^{21, 22} The application was developed by John Chambers and colleagues at Bell Laboratories. While R is extremely versatile for statistical analysis, it does not lend itself well to the range of functionality of an object-oriented programming language such as C#.Net for serialization, queries of SQL databases or DICOM RT files, algorithm development, and the use of advanced visualization tools (e.g., DirectX).

For the development of DataMole, we combined the use of C#.Net with R. Code for the R scripts was stored in an XML library to facilitate the future development of additional tests that could be executed from within the C# program without the need to recompile the application. This approach enables one researcher with skills in R to design a statistical test that could then be plugged into the DataMole program; it also allows the results to be used by institutional programmers more familiar with the C# environment. The capabilities and libraries of R were accessed through the statconn DCOM interface (www.statconn.com) as a COM object in the Windows .NET framework. The statconn API is an open-source suite of modules published by Thomas Baier and Erich Neuwirth. An XML schema was developed to store libraries of R commands, symbols, etc., for use in the DataMole program.

The statistical calculations carried out with the R-based code were benchmarked. A standard data set was defined and used with programs written in MATLAB (MathWorks, Natick, MA) to calculate the statistical metrics calculated by DataMole using R to compare agreement.

When considering the application of a wide array of statistical tests described to a large data set, the ability to project the time for calculations and serialization is relevant. Measurements were carried out with large sample data sets to examine factors affecting calculation time, such as number of records, number of data values, and read time for XML vs Excel formats. A data processing benchmarking data set was used that contained 1416 records (rows) and 184 fields (columns). The data set contained one stratified field. Subsets of the data were used, varying the number of records and columns, to examine the effect on processing time.

A data set (Fig. 1) simulating clinical data was constructed to test the DataMole tool using a data set of values with/without a dose-response threshold. The set contains three groups (A, B, C) of toxicity (ten with/ten without) vs dose data. Group A dose values were derived from gamma distributions with mean and standard deviations of 30 and 7.7 vs 16 and 5.6, respectively, for points with and without toxicity. Group B dose values were obtained by scaling A values by factors derived from a normal distribution with a mean and standard deviation of 0.8 and 0.08. Group C dose values were derived from a normal distribution with a mean of 20 and a standard deviation of 2. Groups A and B demonstrate a dose-response threshold; group C does not. Groups A and B are correlated; group C is not.

Figure 1.

Illustration of benchmark data sets used to examine illustrated results from a range of statistical measures applied to data sets with and without dose response characteristics.

The program was applied to the simulation data set as well as to a clinical data set to demonstrate its ability to highlight clinically relevant interdependencies of data elements. Characteristics of statistical analysis metrics, applied to these sets, were considered to explore ability to formulate an algorithm using a combination of metrics to highlight values demonstrating threshold in dose-response.

RESULTS

We developed Generalized Federated Data Exchange (GFDE) classes and serialization formats for Excel and XML for our application. The classes allow specification of detail about the contents of the data set and data value items, but only require a minimal subset of that information in order to be used for the statistical analysis application. We adopted a standard approach to presenting the data for exchange or use within the analysis that could be used with all data element types. We were able to classify the data for particular purposes by defining standard class members that categorize the data and then allowing standardized values for those members to reflect that definition. Table 1 defines the class members used for this categorization and the current standardized values used. The table indicates that only three data elements were required for input into the statistical analysis software. The GFDE XML file format was used to transmit all of the class information specified. Since the GFDE Excel format was designed to be readily used for manual, RtoR construction of tables to be input into the analysis program, only a small subset of the data was required. Figures 23 illustrate XML and Excel files used in GFDE format.

Table 1.

Standard class members and standardized values for categorization of data.

Class	Members	Purpose
GFDE		Header for the data set. Data set may hold multiple DataSetRecords.
	Facility	Name of facility generating data set
	Creation Date	Date
	DataSetType	Used to create hash table that can be used for mapping and setting expectations for contents: e.g., unspecified, outcomes-DVH, RTOG
	DataSetDescription	Additional information on data set
	DataSetName	Name used in reference to DataSetRecord
	DataSetDescriptions	Collection of information about DataValueItems
	DataSetRecords	A collection of DataSetRecord items
DataSetItem		A record (row) in the data set
	PrimaryKeyHeader	Header of DataValueItem that is the primary key for the record
	IsAllowedForResearch	Provide ability to identify restricted data elements
	RecordOfDataSetName	Identify parent-child relationship among data groups
	DataValues	Collection of DataValueItems (the fields in the record)
DataValueItem		A field in the record
	IsPrimaryKey	True or false
	IsMultiDateData	True or false. Enables grouping longitudinal DataValueItems that have the same DataHeader but different DataValueDates
	DataHeader	Name of data item (e.g., Lung_R V20Gy [%])
	DataType	Standardized values. Current list: ID, DVH, Toxicity, PatientInfo, CourseInfo, PlanInfo, Lab, FieldInfo, unspecified
	DataValueType	Standardized values. Current list: Text, Numeric, Boolean, DateTime
	DataValueDate	Date associated with DataValue
	DataValue	Text field for DataValue

Figure 2.

A GFDE XML file. The file format is suitable for server to server web based exchange and short serialization time into the analysis program.

Figure 3.

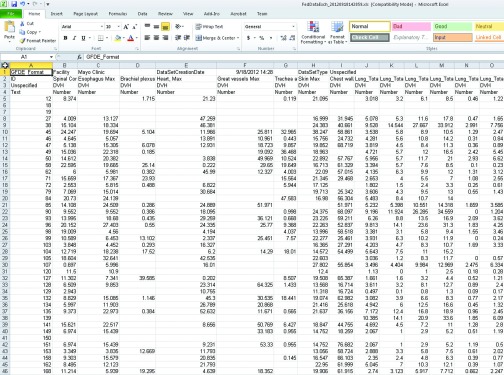
A GFDE Excel file. The file format is best suited for manual data processing, exchange and analysis of results. It may be serialized into the analysis program.

Table 2 defines the current analysis test sets in the XML library and the calculation results saved in the corresponding files. Calculation benchmarks demonstrated agreement between R calculations using DataMole and MATLAB was better than 0.001%, except for p-values, which differed by less than 0.04%.

Table 2.

Current analysis test sets in XML library and saved calculation results.

Analysis set	Test type	Values returned
Columns	A	For each data column: maximum, minimum, median, mean, standard deviation, upper quartile, and lower quartile
Kendall	B	Correlation coefficient, p-value
Pearson	B	Correlation coefficient, p-value, Fisher-Z statistic, upper and lower 95% confidence intervals for correlation coefficient using Fisher-Z statistic
Spearman	B	Correlation coefficient, p-value
ROC	C	Using pROC package in R: area under ROC curve (AUC), maximum value for Youden Index, cut-point value corresponding to maximum in Youden Index, 2 × 2 contingency table cells formed using cut-point value: True Positive (TP), True Negatives (TN), False Positives (FP), False Negatives (FN), Sensitivity (SE), Specificity (SP), NPV, PPV, and Fisher's exact test for the p-value of the 2 × 2 contingency table, number of samples.
Stratified response	D	Welch t-test p-value, for each of the two groups: number of samples, mean, and standard deviation, Kolmogorov-Smirnov tests, Kullback-Leibler divergences
t-test	E	Paired Student's t-test z-value, p-value, for each of the two groups: number of samples, mean, and standard deviation
Wilcox	E	Wilcox rank sum u-value, p-value, number of samples

Notes: A: For each column, calculate basic statistics on values. B: For each pair of columns in the data set, calculate correlations between values. C: For pairs of stratified and nonstratified columns, calculate the ability of a threshold in a nonstratified column values to serve as a predictor for binary rendering of stratified values in the stratified column, D: For single nonstratified columns, segregate values into two groups according to corresponding binary rendering of a paired, stratified column. Determine significance of difference in means E: For pairs of nonstratified columns, calculate the significance in the difference of the means of the two columns.

Benchmarking performance measures were carried out on a laptop with 3 GB RAM and a dual-core 64-bit processor running Windows 7. Results of the performance benchmarking measures are summarized in Table 3. Median read times were 320 times shorter for XML than for Excel files, whereas write times were half as long. Generally, calculation times for particular statistics increased with the number of cells. For variable-comparison measures, such as correlation, additional variables (columns) carried a higher time cost than additional observations (rows). Comparing the average execution times per cell, the overall average was 3 ms. Spearman (0.7 ms) and Pearson (0.9 ms) were faster than Kendall tau (1.1 ms). ROC calculations (21 ms) required more time than Wilcox Rank Sum (0.7 ms), Welch t (1.7 ms), or Kolmogorov-Smirnov (0.3 ms) tests.

Table 3.

Benchmark performance measures.

Characteristics of files (1–7)	#1	#2	#3	#4	#5	#6	#7
No. of rows	118	118	118	118	236	236	472
No. of columns	10	46	92	184	92	184	92
No. of cells	1180	5428	10 856	21 712	21 712	43 424	43 424
File size (kB)	44	104	181	337	334	639	640
File input/output times (s)
Read Excel	11.32	21.3	35.55	75.02	69.55	142.95	135.97
Write Excel	1.56	0.06	0.18	0.43	0.85	1.08	1.16
Read XML	0.05	0.12	0.13	0.44	0.42	0.76	0.51
Write XML	1.27	0.58	0.55	0.84	1.07	1.13	1.01
Analysis set calculation times (s)
Columns	3.54	0.12	0.21	0.57	0.42	0.82	0.51
Kendall	0.5	5.21	22.31	89.53	33.57	139.42	54.51
Pearson	0.94	4.49	21.07	88.91	24.85	103.32	32.59
Spearman	0.39	2.87	15.94	66.32	19.85	82.78	27.02
ROC	0.05	91.54	409.61	1724.56	619.55	2457.05	588.86
Kendall	0.5	5.21	22.31	89.53	33.57	139.42	54.51
Stratified response	0.01	8.21	12.52	52.55	21.7	87.74	27.49
t-test	1.46	5.72	23.78	118.85	32.4	141.12	37.12
Wilcox	0.36	3.56	15.25	62.26	21.95	89.05	31.92

Note: Performance measures for input, output, and analysis times of seven benchmark data files.

Simulated data set illustration

A subset of the results obtained for the simulated dose-response data set (Fig. 1) are presented in Table 4. The difference in the probability of toxicity with respect to the cut-off point [PPV−(1−NPV)] was larger for groups A (0.7) and B (0.8) than for group C (0.4). However, the differences were only significant (Fisher exact test p-value < 0.025) for groups A and B. Differences in the mean dose values of groups with and without toxicity were significant (Welch t-test p-value < 0.025) for A and B, but not for C. The pdf of dose values of the group with toxicity was significantly larger than the pdf of the group without toxicity (Kolmogorov-Smirnov p-value < 0.025) for A and B, which supports the more frequent occurrence of toxicity with increasing dose. The difference was not significant for C. The “distance” between the distributions of dose values was larger (Kullback-Leibler divergence > 1) for A and B than for C (< 0.3).

Table 4.

Subset of results obtained for simulated dose-response data set.

	ROC	Cut	No toxicity	With toxicity					FET	WT	KS (T > NT)	KS (NT > T)	KLD	KLD
	AUC	point	(NT) mean ± SD	(T) mean ± SD	SE	SP	PPV	NPV	p-value	p-value	p-value	p-value	(T∥NT)	(NT∥T)
A	0.89	19.2	16.64 ± 7.44	27.23 ± 6.39	0.9	0.8	0.818	0.889	0.0055	0.0032	0.007	1.0	1.48	1.33
B	0.91	15.3	13.22 ± 5.96	22.60 ± 5.49	1.0	0.8	0.833	1.000	0.0007	0.0018	0.002	1.0	1.38	1.13
C	0.52	19.0	19.94 ± 2.38	20.22 ± 1.29	0.9	0.4	0.600	0.800	0.3034	0.7493	0.407	0.67	0.27	0.13

Note: Table of statistical measures for benchmark groups, illustrating combinations of metrics useful for highlighting dose response.

Correlation coefficients for A vs B dose values were 0.98 (Pearson), 0.96 (Spearman), and 0.87 (Kendall tau). A or B vs C for all coefficients ranged from −0.042 (Kendall tau) to 0.08 (Pearson). This supported the hypothesis of a scaled relationship of A to B. Correlation of toxicity vs dose for A and B ranged from 0.56 (Kendall tau) to 0.71 (Pearson). C values ranged from 0.029 (Kendall tau) to 0.071 (Pearson). This supported the hypothesis of a response with increasing doses for A and B.

Clinical data set illustration

The tool was applied to a lung stereotactic body radiation therapy data set of 221 patients, containing 26 DVH metrics for 11 structures (PTV lung, cord, skin, esophagus, trachea, bronchus, heart, great vessels, and chest wall). DVH metrics included the percentage of volume receiving at least x Gy (VxGy [%]) and the minimum dose delivered to the “hottest” y cubic centimeters (Dycc [Gy]) of a structure. The primary data set contained 32 CTCAE toxicities graded for these structures. For this analysis, we limited our examination to pneumonitis only; 95 instances of pneumonitis toxicity were scored for grades 1(58), 2(25), 3(10), 4(0), and 5(2). Calculation time was 151 s and the analysis produced 7758 metrics.

DVH metrics that might indicate dose thresholds were highlighted with an algorithm that combined statistical measures from the ROC analysis, [PPV−(1−NPV) ≥ 0.25, Fisher exact test p-value ≤0.025] and stratified response (Kolmogorov-Smirnov p-value ≤ 0.025, Welch t-test p-value ≤ 0.025) analysis sets. A low p-value for FET indicated that differences between groups in the 2 × 2 contingency table formed using the threshold value, was statistically significant. The requirement that the contrast in probabilities for toxicity on either side of the threshold value [PPV−(1−NPV)] exceeded some minimum value (e.g., 25%), was used to aid in filtering out DVH correlations with toxicity that might be statistically, but not clinically significant. Additionally requiring that not only the differences in the means (WT), but also the distributions (KS) demonstrate significant differences with increasing dose was used to further filter the results.

In this clinical data set, only seven measures (Table 5) met these criteria. All corresponded to pneumonitis grade ≥ 2, and none were met for other grade thresholds. Kendall tau coefficients ranged from 0.37 to 0.51 for PTV volume vs the total lung volume metrics. Total lung mean dose was correlated with V10Gy [%] (0.83), V13Gy [%] (0.82), and V20Gy [%] (0.77) but not with D1000cc [Gy] (0.33) or D1500cc [Gy] (0.27). D1000cc [Gy] was correlated with D1500cc [Gy] (0.844). Kullback-Leibler divergence for groups with vs without pneumonitis for all seven measures ranged from 0.38 for D1000cc [Gy] to 0.6 for D1500cc [Gy], with an average value of 0.51.

Table 5.

DVH metrics indicating dose thresholds.

Pneumonitis	ROC		No toxicity	With toxicity					FET	WT	KS
grade ≥ 2	AUC	Cut-point	(NT) mean ± SD	(T) mean ± SD	SE	SP	PPV	NPV	p-value	p-value	(T > NT) p-value
PTV volume [cc]	0.73	35.2	40 ± 40	84 ± 68	0.73	0.66	0.57	0.79	0.0003	0.0006	0.0012
Total lung V10Gy [%]	0.67	9.6	10.7 ± 5.0	15.5 ± 8.5	0.81	0.49	0.5	0.8	0.0045	0.0035	0.021
V13Gy [%]	0.67	7.8	8.2 ± 4.1	12.2 ± 6.7	0.77	0.53	0.51	0.79	0.0048	0.0022	0.017
V20Gy [%]	0.67	4.3	4.7 ± 2.8	7.3 ± 4.4	0.83	0.53	0.53	0.83	0.0005	0.0033	0.0033
Mean [Gy]	0.67	2.9	3.6 ± 1.6	5.2 ± 2.5	0.92	0.39	0.48	0.88	0.0015	0.0022	0.017
D1000cc [Gy]	0.68	2.6	1.8 ± 1.8	3.6 ± 3.4	0.54	0.8	0.63	0.73	0.0013	0.008	0.0075
D1500cc [Gy]	0.69	1.2	0.75 ± 0.79	1.6 ± 1.5	0.57	0.82	0.67	0.75	0.0002	0.0035	0.0017

Note: Results of application of the dose-response algorithm to a SBRT lung data set examining relevance of 26 DVH measures to incidence of pneumonitis. Seven measures meet the algorithm requirements for one toxicity grade condition.

Heart Maximum dose and Chest Wall and Ribs D30cc [Gy] had PPV−(1−NPV) and Fisher exact test p-values of 0.4, 0.002 and 0.44, 0.023, respectively. However, the Welch t-test and Kolmogorov-Smirnov p-value tests for Heart Max (0.12, 0.027) and Chest Wall and Ribs D30cc [Gy] (0.07, 0.27) did not pass, indicating that the underlying dose distributions were too close to distinguish. There were two grade 5 toxicities; however, none of these met the criteria of the algorithm. The lung and PTV metrics PPV−(1−NPV) ranged from 0.04 to 0.15 [Fisher exact test p-values, 0.06–0.23, Welch t-test p-value > 0.23–0.71, and Kolmogorov-Smirnov p-value (0.1–0.47)].

The hypothesis that the DVH metrics identified by the algorithm from the data set correspond to a reproducible dose response is supported by a recent publication by Barriger et al.²³ In their multi-institutional analysis of 251 patients, with 23 having pneumonitis grade ≥ 2, they identified total lung mean dose ≥ 4 Gy, V20Gy [%] ≤ 4% as significant. Also of interest were the results of V10Gy [%] ≤ 12% (p = 0.1) and PTV volume ≤ 48 cc (p = 0.18).

DISCUSSION

We have described a design methodology for constructing software algorithms to sort through outcomes data sets to generate hypotheses for underlying patterns in the data with minimal assumptions on the underlying characteristics of the data types. The situation is analogous to examining cell cultures under a microscope. From among the wide range of visual features, the most relevant details are highlighted with a range of staining methods. Protocols are developed that aggregate results from the staining methods to characterize particular features of interest in the cell cultures. The approach described here constructs statistical staining methods that may be applied to data sets from outcomes databases to identify patterns of interest.

The benchmarking dataset and clinical example are representative of what is currently encountered in practice as a “large” data set. Calculation times of a couple of minutes for several thousand statistical metrics, coupled with ability to modify the metrics calculated or explore other metrics is a substantial gain. As the field of radiation oncology matures in aggregation of outcomes data, data sets that are 2–3 orders of magnitude larger may be encountered. In general, calculation times increase more rapidly with increase in the number of metrics (columns) than in the number of patient records (rows). When the field matures to routine exploration of tens or hundreds of thousands of metrics, hard coding the statistical test rather than using the R libraries and using narrower groupings of tests will be advantageous for final calculations. However, for exploration of suitable statistical approaches to reveal particular behaviors, ability of the present methodology to explore other metrics will still be valuable.

Software tools were selected to couple robust, open-source statistical tools in common use with development environments used by institutional programmers. Our approach may be adopted into use in clinical environments and facilitate adding other statistical methods with minimal need to recompile code. This makes application of a broad range of statistical measures with minimal a priori assumptions about the data, practical as a means to carry out “statistical staining” of an arbitrary data set. These tools can then serve as the foundation for exploration of algorithms, using combinations of statistical measures to highlight patterns of clinical interest in the data set, such as dose response. We believe that the general approach may be implemented using other software languages or environments, e.g., Python or MATLAB. Our selection of the combination of C#.Net with R merged an enterprise level programming language used to develop applications by our institutions’ IT professionals, with a widely adopted statistical computation language recommended as a standard by research groups at our institutions. We believe that selection reduces technical barriers to use of the approach by broad range of groups. Other emergent data mining technologies, such as PMML or Cube Analysis Services (Microsoft Corporation) are promising in their development and likely to become as accessible in future as the technologies selected for the current effort.

The generalized federated data exchange classes described here as a means to standardize serializing data in Excel and XML formats is envisioned as a starting point for collaborative development of tools and standards that meet the requirements of multiple institutions. Our use here highlights the importance of developing these standards with the dual purpose of facilitating data exchange and as a standard input for analysis programs. Where possible, finding common cause with parallel efforts to build databases, web services, and other tools for promoting routine aggregation and analysis of outcomes data promotes efficiency of the overall effort.

The analysis methods described and standardizations for data exchange are data agnostic. We have applied them here to dose response data for radiation oncology, but they are equally viable for a wide range of data sets, since no assumptions are made about the underlying relationships of the data elements. Since detection of stratifications in data values, which form the basis of carrying out ROC analysis and construction of contingency tables, is carried out automatically, there is no need for a priori specification columns suitable for this analysis. Relaxing the stratification detection condition from a limited number of unique values to clusters of data separated by carefully defined intervals^{24, 25, 26} could expand on the range of significant dependencies detected without substantial increase in calculation time.

Development of tools like DataMole that facilitate calculation of a broad range of statistical methods, may promote more accurate use of these metrics. We have highlighted some of the distinctions among underlying assumptions of various tests, but appreciation for the implications of those details in a given data set may not be common. It is likely that the amount of manual effort required to carry out a single test using traditional tools has the effect of making it less likely that authors would revise their analysis using more appropriate tests. The approach that we present has the effect of eliminating that extra effort by automatically carrying out analysis for a range of tests. Then if a user, after considering the analysis results in the context of their own data, comes to appreciate that a different test or a combination of tests would have been more appropriate, they are much more likely to use it if it is already calculated.

Our efforts to detect and predict patterns of adverse events mirror efforts outside of medicine to determine the best uses for mass data analysis.²⁷ Large scale data mining typically resides in the domain of informatics. However, few Radiation Oncology clinics have an inhouse informatician, whereas most have an inhouse medical physicist. The American Association of Physicists in Medicine Scope of Practice of Clinical Medical Physics (policy number PP 17-B) lists involvement in informatics development and direction as a component of the practice of therapeutic Medical Physics. As the role of information technology in medicine has expanded, within Radiation Oncology it is the medical physicist who is responsible for the implementation of and the safe and efficient use of information technology.²⁸ Medical Physicists have made significant contributions to many areas of medical informatics, including computer aided diagnosis, picture archival and communications systems (PACS), record and verify systems, and electronic health records (EHRs). Medical physicists typically have oversight of the sources for dosimetry data, and frequently are involved with the sources for outcomes data. The role of the medical physicist in data mining is not only a practical issue of access, but also a professional issue. The training of medical physicists and the role they play in a modern radiation oncology position places them in a unique position to create the bridge between technical and clinical needs. The importance of physicists having overlap skills and knowledge to interact with physicians, dosimetrists, therapists, etc., is well understood. With more routine use of informatics and analysis on the horizon, overlap skills with statisticians and IT professionals is increasingly important to bridging those uses into the clinic. We believe that development of statistical methods to facilitate routine and automated detection of patterns in a wide range of outcomes and other data in radiation oncology will emerge as an active area of research in our field just as it has in others as large sets of accessible data become more routine in clinical practice.