Abstract
We compare the efficiency of multicanonical and replica exchange molecular dynamics for the sampling of folding/unfolding events in simulations of proteins with end-to-end β-sheet. In Go-model simulations of the 75-residue MNK6, we observe improvement factors of 30 in the number of folding/unfolding events of multicanonical molecular dynamics over replica exchange molecular dynamics. As an application, we use this enhanced sampling to study the folding landscape of the 36-residue DS119 with an all-atom physical force field and implicit solvent. Here, we find that the rate-limiting step is the formation of the central helix that then provides a scaffold for the parallel β-sheet formed by the two chain ends.
Introduction
Molecular dynamics and Monte Carlo simulations have become often used tools for exploring the molecular machinery of cells. However, their accuracy of predicting experimental observables is still limited as the computational costs increase at least exponentially with the size of system (either a single protein or a complex of interacting biomolecules). Even with the recent advances in hardware, the problem remains that biomolecular motions often cover time scales which exceed the ones achievable in atomistic simulations. The problem can be alleviated by using enhanced sampling techniques such as replica exchange sampling,1,2 also known as parallel tempering3 and first introduced to protein simulations in Ref.4 In this method, replicas of the protein system evolve in parallel by standard Monte Carlo or molecular dynamics at different values of a control parameter, most often temperature. At certain times, conformations Ci of replicas at neighboring temperatures Ti and Tj=i+1 are exchanged with a probability
| (1) |
where βi = 1/kBTi, and kB is the Boltzmann constant. For a given replica the swap moves induce a random walk from low temperatures, where relaxation times are long, to high temperatures, where barriers can be crossed, and back. This results in a faster convergence at low temperatures. However, the application of replica exchange techniques is inherently limited for systems with first-order-like transitions, where folding/unfolding transitions become rare events and thermodynamic quantities need long times to converge.
In such cases, it may be more appropriate to utilise other techniques that are designed to maximize sampling of transition states. One example is multicanonical sampling5,6 where weights w(E) lead to a distribution
| (2) |
with n(E) the density of states. From such a multicanonical simulation one can calculate the thermodynamic average of any physical quantity
 at a temperature T by re-weighting:7
at a temperature T by re-weighting:7
| (3) |
where x labels the configurations and R is the gas constant.
While implementation of the method is straightforward for Monte Carlo sampling, it is less so for the in protein studies more commonly used molecular dynamics.7,8 Hence, most applications of multicanonical sampling in protein science rely on Monte Carlo updates,9–14 and only a few applications of multicanonical molecular dynamics exist (see15 and references therein). Besides the technical difficulties of implementing multicanonical sampling in molecular dynamics, application to proteins6,9 has been limited by the need to determine estimators of the not a priori known weights w(E) by an iterative procedure.5,6 However, the additional workload may well be worthwhile for proteins with strong cooperative transitions. The purpose of the present paper is to investigate systematically the relative efficiency of multicanonical molecular dynamics and replica exchange molecular dynamics for this class of systems.
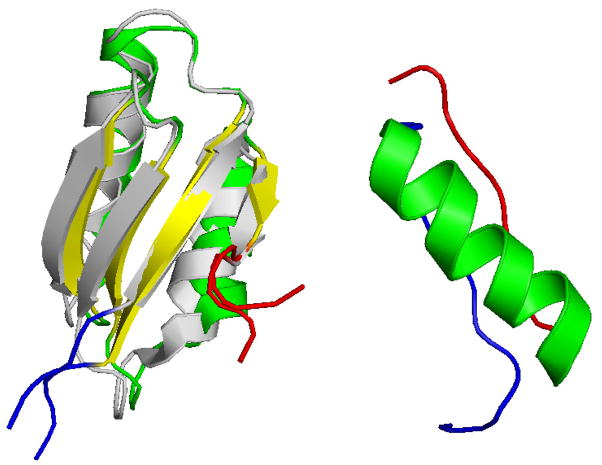
As our test system we use an all-atom Go-model16 of wild type and mutant of the 75-residue Menkes protein MNK6 (PDB-code: 1YJV and 1YJT), displayed in Figure 1(left), with that we are familiar from previous work.17 We demonstrate that multicanonical molecular dynamics enhances indeed the efficiency of sampling transition states over replica exchange molecular dynamics, allowing for a more detailed insight into the folding mechanism of this protein. In the second part, we present as an interesting application of multicanonical molecular dynamics a study of the folding mechanism of the 36-residue protein DS119 (PDB-code: 2KI0), displayed in Figure 1(right). Unlike MNK6, this protein is studied by implicit solvent simulations with a physical force field. The enhanced sampling of folding events allows us to observe that the rate-limiting step in the folding process is the formation of the central helix which serves as a scaffold for the parallel β-sheet formed by the terminal residues of the βαβ protein.
Figure 1.
(Left: Overlay of the wild type (online color yellow/green) and mutant (online color grey) NMR structure of 75-residue MNK6 (PDB-identifier 1YJV and 1YJT) ; right:) NMR structure of the 36-residue protein DS119 (PDB-identifier 2KI0). The online color of the N-terminals is blue, and that of the C-terminals red.
Methods
Multicanonical molecular dynamics
In order to enhance the sampling of otherwise exponentially suppressed transition states, the weights are chosen in multicanonical simulations such that the resulting distribution is either flat over a range of energies (see Eq. 2),5,6 or peaked around the energies of transition states.18 The flat distribution of Eq. 2 is obtained in Monte Carlo simulations by replacing Boltzmann-weights with multicanonical weights exp(−E/RT) → exp(−S(E)). The microcanonical entropy S(E) = ln n(E) is estimated by an iterative procedure:
| (4) |
Here, P(n)(E) is the histogram of energy in the n–th iteration, and S0 = E/RT.
In the context of molecular dynamics it is convenient to rewrite the multicanonical weights as
| (5) |
where T̂ is a pre-chosen thermostat temperature. The “effective” energy Emuca is defined by Emuca = RT̂S(E) and calculated iteratively by
| (6) |
with , the “physical” potential energy of a given configuration. With this definition, the forces in multicanonical molecular dynamics follow as
| (7) |
| (8) |
| (9) |
where ∇ is the gradient operator and r⃗ marks the positions of all atoms in the system. Hence, in multicanonical molecular dynamics simulations the regular forces F⃗can(r⃗) (that one would integrate in constant temperature simulations) are scaled by an energy-dependent factor Λ(E) which needs to be calculated iteratively through
| (10) |
In order to get an intuitive picture of how the energy dependent scaling of forces alters the dynamics we note that (because of Newton’s Law) scaling the forces by an energy-dependent factor Λ(E) is equivalent to scaling all masses in the system by . Hence, in a multicanonical molecular dynamics simulation the viscosity (which is proportional to mass) changes energy-dependent as
| (11) |
Hence, the effective viscosity of the system is lowered by a factor when at a low energy E, and raised by that factor when in the high-energy region allowing the system to escape local minima and sample energy space in a diffusive process. With Λ(E) = RT̂∂S(E)/∂E = T̂/T(E) and assuming that in first approximation the viscosity , the effective viscosity ηmuca(E) becomes constant in multicanonical molecular dynamics, leading to a flat distribution in potential energy E.
Because of bottlenecks and hidden barriers, a simulation that leads to a flat distribution in energy may still not be the one that maximizes the number of folding/unfolding transitions. In order to optimize that number, we further improve on our weights by using the approach of Trebst et al.18 Its underlying idea is that the number of round trips between the low-energy region (in which folded structures are expected) and high-energy regions (corresponding to unfolded configurations) is a lower bound for the number of independent folding/unfolding events. Hence, in order to maximize the number of folding transitions one needs to maximizing the current j of configurations evolving from a low-energy El to high-energy Eh, and back. For this purpose, a tag t is attached to a configuration. This tag is set to one when the energy of the configuration become equal or larger than Eh, and is set to zero when the energy becomes equal or less than El. For energies between El and Eh, the tag is not changed. Defining now
| (12) |
where H(E) is the number of times that the system has taken energy E, one can calculate the current as
| (13) |
with the energy-dependent diffusion coefficient D(E). Maximizing the current j, leads to the following iterative scheme for optimized multicanonical weights:
| (14) |
or in terms of the effective “multicanonical energies” Emuca employed in multicanonical molecular dynamics:
| (15) |
Hence, assuming N iterations to generate a flat distribution and M further iterations to maximize the number of folding/unfolding events, we choose as final effective “multicanonical energies” in our multicanonical simulation:
| (16) |
From a multicanonical molecular dynamics simulation with forces scaled by the resulting energy-dependent factors
, one can calculate now the average of a physical quantity
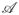 at a temperature T by re-weighting:
at a temperature T by re-weighting:
| (17) |
where x labels the configurations and T̂ is again the thermostat temperature.
Systems and simulation protocol
In order to evaluate the efficiency of multicanonical molecular dynamics, we have studied the following proteins with mixed αβ-topology: wild type and mutants of the sixth domain MNK6 of Menkes protein (PDB: 1YJV and 1YJT), and the de novo designed peptide DS119 (PDB: 2KI0).19 These proteins were chosen because they allow us a comparison with previous work by us or other groups,17,20 but are at the same time of a complexity that makes the simulations non-trivial.
In case of wild type and mutant of MNK6, we use the Go-model developed by the Onuchic group,16 modified in such a way that takes into account protein flexibility in the construction of the energy function by utilizing all structures of an NMR ensemble17 instead of only a single structure. In the case of MNK6, this modification is important as the first models of wild type and mutant differ by only ≈ 2 Å, comparable to the differences within the respective NMR ensembles. Using this modified Go-model, we have described recently the differences in the folding pathways of wild type and mutant, and we have presented evidence for a possible mechanism in the pathology of Menkes disease.17 However, our analysis suffers from low statistics, as the number of folding/unfolding transitions was small in our replica exchange molecular dynamics simulations of wild type and mutant. Comparing our previous results with such from multicanonical molecular dynamics simulations of the same system therefore allows us to quantify the gain in efficiency by the later approach.
The shorter peptide DS119 is build from 36 amino acids and adopts in solution a βαβ structure,19 making it a simple model for proteins with end-to-end β-sheet. Previous work using canonical molecular dynamics suggests that DS119 is a downhill folder with only moderate cooperativity.20 However, this study relies only in part on all-atom simulations with a “physical” force field (Amber ff03 and a GB/SA implicit solvent model), while the folding cooperativity is studied by Go-model simulations. In contrast, our investigation relies solely on simulations with a “physical” all-atom force field. This is because we expect that multicanonical molecular dynamics will enable us to sample a number of folding/unfolding events that is sufficiently large to probe the folding mechanism of this peptide. Note that we use the same energy function as Ref.20 to allow for a comparison with previous work.
All simulations are performed in double precision GROMACS 4.5.5.21 The subroutine do_force is modified to implement the energy dependent scaling of forces in multicanonical simulations. A lookup table of force-scale factors (λE) is included in the source file sim_util.c and has to be updated for each iteration. The time step in the molecular dynamics runs is 2 fs. Hydrogen atoms are constrained to their bonded heavy atoms by LINCS algorithm.22 Van der Waals and Coulomb energy are calculated with twin range cut-offs. Temperature is kept constant by a Nose-Hoover thermostat.23
Each of the three systems is studied with the same simulation protocol. The starting point is an initial (short) replica exchange molecular dynamics run covering the temperature range of interest. In the case of MNK6, 14 replicas are spread between 107 u to 115 u for the wild type, and 109 u to 114 u for the mutant. Here, temperatures are given in arbitrary units “u” instead of Kelvin as the Go-model is not a physical force field. On the other hand, simulations of DS119 rely on a physical force field, and the thirteen replicas cover a temperature range from 280 K to 600 K. From these simulations we can extract over a large range of energies an initial estimate of the microcanonical entropy S(E). In a second step, we run several short multicanonical molecular dynamics runs to iterate the weights (i.e. the factors Λ(E) by that the forces are scaled) using Eq. 16, choosing as the temperature of the thermostat T̂ = 120.3 u for MNK6 (leading in our units to β = 1), and T̂ = 300K for DS119. Such combination of a short replica exchange run with succeeding multicanonical iterations results in faster convergence to the target distribution than starting from a single high temperature canonical simulation. Note that in the case of MNK6, we start the multicanonical iterations the data from the 100 ns replica exchange molecular dynamic run of Ref.17 Likely, a shorter run would have been sufficient for priming the iteration of multicanonical weights: we have needed only 25 ns in the case of DS119.
During each iteration, five independent simulations are performed in parallel, starting from either folded, unfolded, or partially unfolded states. This distribution of start configurations, with energies distributed over the whole energy range considered by us, accounts for the problem that in the first iteration folding/unfolding events are rare events. As the iterations progress, the energy histogram becomes approximately flat, and folding/unfolding transitions occur more often. In the final iteration, we used the optimization procedure of Eq. 14 to maximize the transition rate. While this step can be repeated as often as needed, we found one iteration sufficient.
The multicanonical weights obtained by the above described iterations are used in long simulations from which physical quantities at the desired temperatures are calculated by re-weighting (Eq. 17). Note that for each system we perform multiple data-production run to ensure multiple independent data sets. Table 1 summarizes the utilized simulation resources.
Table 1.
Breakdown of computational resources required in multicanonical simulations of wild type (WT) and mutant (MT) of MNK6, and of DS119. The resources for the initial replica exchange molecular dynamics run are listed under REMD.
| System | REMD | Pre-production | Production | Total |
|---|---|---|---|---|
| MNK6(WT) | 1400 ns (100 ns×14)1 | 300 ns (20 ns×5×3)2 | 250 ns (50 ns×5)3 | 900 ns |
| MNK6(MT) | 1400 ns (100 ns×14)1 | 300 ns (20 ns×5×3) | 250 ns (50 ns×5) | 900 ns |
| DS119 | 325 ns (25 ns×13) | 750 ns (50 ns×5×3) | 720 ns (120 ns×6) | 1795 ns |
The replica exchange run of Ref. 17 was used to prime the multicanonical simulation, hence, this is an overestimation of required resources.
simulation length of one multicanonical simulation × number of parallel runs × number of pre-production iterations
simulation length of one multicanonical simulation × number of production runs
Results and discussions
Efficiency of multicanonical and replica exchange molecular dynamics
The first purpose of the present paper is to compare the efficiency of replica exchange and multicanonical molecular dynamics in simulations of proteins with strong folding transitions. While such transitions are observed experimentally for many fast folding proteins, they are also a hallmark of Go-models which by construction exhibit strong cooperativity. For this reason, we chose to compare the two methods in a Go-model simulations of the sixth domain of Menkes protein (MNK6) with that we are familiar from previous work. This polypeptide is at the cytosolic N-terminus of a copper-transporting transmembrane ATPase encoded by the ATP7A gene on the X chromosome.24 Various mutations in this gene are associated with Menkes disease, a copper deficiency disease which in most cases leads to death in early childhood. One example is the single mutation A69P on the 75-residue MNK6 domain. Both wild type and mutant MNK6 adopt a ferredoxin-like fold (βαβ βαβ) with a root-mean-square deviation between wild type and mutant of around 2 Å, comparable to the deviations within the respective NMR ensembles, see Figure 1(left).
Our simulations of MNK6 rely on the structure-based model SMOG (Structure-based MOdels in Gromacs), developed by the Onuchic group.16,25,26 Using the SMOG@ctbp server we have prepared topology and coordinate files of the wild type and mutants as described in the method section, and employed these in molecular dynamics simulations with the GROMACS 4.5.5 software package.21 Utilizing our data from a previous replica exchange molecular dynamics run of 100 ns, we obtained an initial estimate of multicanonical parameters which we improve iteratively with the procedure described above.
The resulting probability distributions P(E) of each iteration are shown in 2. Already after the second iteration (online color red), the energy histogram is reasonably flat in both low and high energies, but transition states at intermediate energies are still suppressed. This gap is filled in the third iteration (online color green). This more flat distribution results from a diffusive walk in energy that enhances also the number of observed folding/unfolding transitions by a factor 5 over the number observed in the previous replica exchange molecular dynamics simulation which itself already relied on an optimized temperature distribution.27 In order to maximize the number of folding/unfolding events, we utilize in the fourth iteration the approach of Trebst el al.18 to obtain a final distribution P(E) (online color blue) where transition states are now no longer suppressed but instead enhanced. This last iteration increases further the rate of transitions, raising improvement to a factor of 30. Computational resources (which include time spent for iterating the weights) and transition rates are summarized in Table 2 demonstrating for all our studied systems that multicanonical simulations lead to higher rates of transitions while requiring less resources. This is exemplified for MNK6 in Figure 3.
Table 2.
Summary of computational resources and transition rates (TS) in multicanonical (MuCa) and replica exchange molecular dynamics (REMD) simulations.
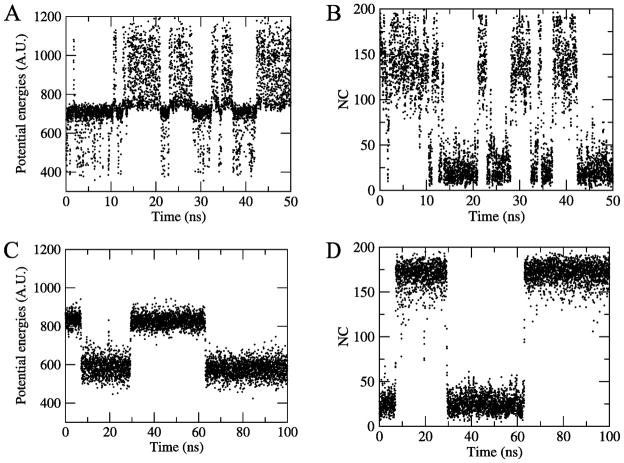
Figure 3.
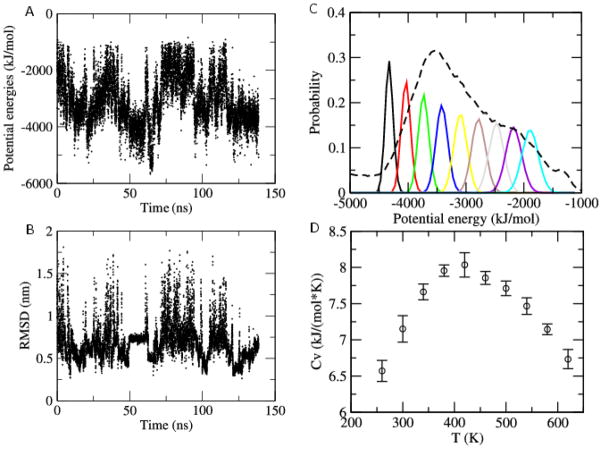
Time evolution of potential energies and number of native contacts (NC) in multicanonical molecular dynamics (top) and replica exchange molecular dynamics (bottom). The multicanonical trajectory of 50 ns length is randomly chosen, while the 100 ns trajectory of the replica exchange simulation is for the replica with most transitions.
At the top of that figure we show the time evolution of the potential energy (A) and the number of native contacts NC (B) as observed during 50 ns of a randomly chosen multicanonical trajectory, while the bottom panels display the corresponding time series of potential energy (C) and number of native contacts (D) for the replica with most transitions (i.e. the best case) in the replica exchange molecular dynamics simulation of Ref.17 Because of the small number of transitions we had to choose a interval of double length, i.e. 100 ns. Note that the walk in energy space in the multicanonical simulation does indeed correspond to a walk in configurational space, moving between folded structures (the number NC of native contacts being a large number) and unfolded structure (NC being a small number).
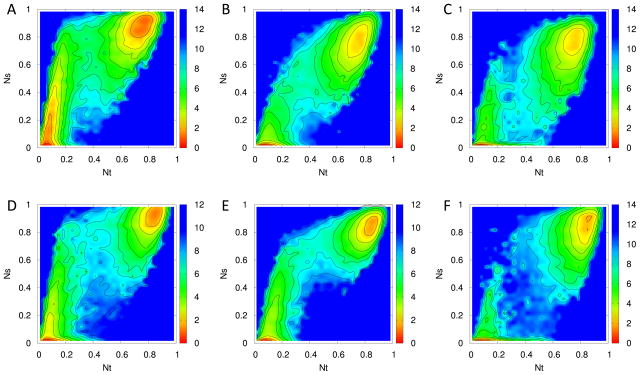
The high transition rate in the multicanonical run guarantees that the relative frequencies of folded and unfolded states are correct, i.e. allows one to calculate reliable estimators of their free energy difference. This made us revisit the folding mechanism of MNK6 that we have studied earlier by replica exchange molecular dynamics. In the previous investigation17 we have projected the free-energy landscape of the protein on the normalized number Nt of native contacts as primary reaction coordinate, and the normalized number Ns of native contacts in a given secondary structure element as secondary reaction coordinate. Because of insufficient sampling of transition states we had to approximate the main folding path by a smoothened curve. The increased statistics of the multicanonical simulation allows us now to draw this landscape in a much higher resolution, see Figure 4 which displays the folding landscape of the three β-ladders β23, β13, and β14. The higher statistics of the multicanonical molecular dynamics runs allows us a more detailed analysis of these landscapes, especially in the transition state region defined by us as the range where Nt = 0.2 – 0.56 for the wild type, and Nt = 0.2 – 0.68 for the mutants. These ranges correspond to regions where the frequency of configurations P(Nt) is smaller than 2% after re-weighting, and that clearly exclude folded and completely unfolded configurations.
Figure 4.
Folding landscapes of three β-ladders. Two reaction coordinates of folding used to construct the folding landscape are Nt, the normalized number of native contacts of the whole protein, and Ns, the number of native contacts of each β-ladder, β23 (A and D), β13 (B and E), and β14 (C and F). Sub-figures A–C are for wild type and D–F are for mutant.
For the wild type, the only elements that grow strongly within this transition region are the β-ladders-β13 and β14 (Figure 4B and C). The β23 ladder emerges before the formation of transition states (i.e. for Nt > 0.2). The growth of β13 and β14 dominates the transition from unfolded to folded states. States with the two well-formed β ladders (Nt > 0.56) have low free energy, indicating that the formation of the two elements β13 and β14 are the rate-limiting steps in the folding of the wild type of MNK6. On the other hand, the order by that the ladders β23 and β13 are formed is switched in the mutant. In our previous work,17 we have conjectured that competition for the shared β-strand in the four-strand β-sheet is responsible for the difference in folding pathway. In Figure 5, where we focus on the part of the free energy landscapes that corresponds to the transition region, we can now verify this conjecture. As the multicanonical simulation leads to an enhanced sampling of transition states, we find by comparing the formation of each β-ladder in mutant and wild type that only a small part of mutant configurations have β14 contacts when Nt is between 0.2 to 0.3. As a result, the loosely connected strand β1 is able to form steady contacts with strand β3, leaving β23 less contacts to form.
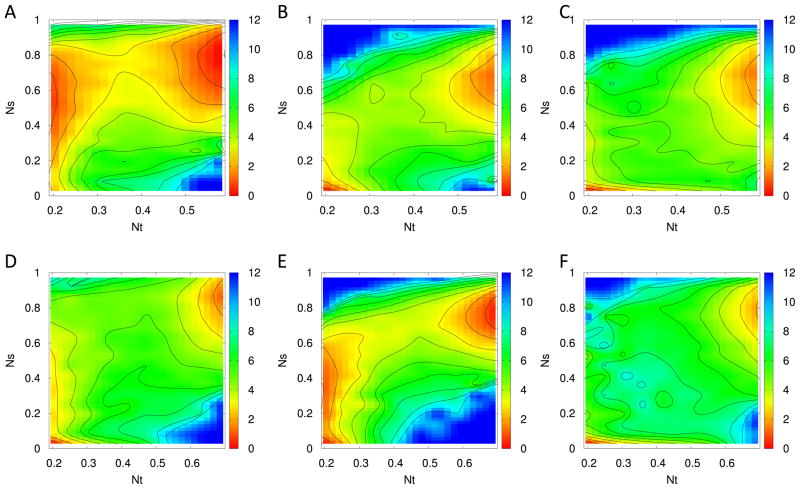
Figure 5.
Folding landscapes of three β-ladders in the transition state ensemble. See 4 for notations.
Folding of the βαβ protein DS119
Our above comparison of the efficiency of multicanonical and replica exchange molecular dynamics did rely on Go-model simulations. However, Go-models can lead to wrong conclusions on the folding dynamics of proteins if folding involves intermediates with non-native contacts29. More accurate are energy functions that describe the physical interactions between the atoms in a protein, and between the protein and its surrounding. As such simulations are computationally more costly than Go-model simulations, we have chosen as our second system the 36-residue DS119 which also has an end-to-end-β-sheet topology forming a βαβ motif. While this protein is smaller than the 75 residue MNK6, the computational cost for simulation of both proteins is similar as DS119 is simulated with a physical all-atom force field and implicit solvent instead of a Go-model. Our aim here is not to compare sampling techniques but to utilize multicanonical molecular dynamics for exploring the folding mechanism of DS119.
The de novo designed DS119 is characterized by a central helix of 12 residue length and N-terminal and C-terminal strands that together form a parallel β-sheet19 stabilized by a contact between residues 9TRP and 34TRP. Previous Go-model simulation led to the claim that the protein is more cooperative than downhill folder, but less cooperative than two-state folder.20 Canonical molecular dynamics simulations of the peptide seem to indicate that folding starts with a collapse into amorphous state, followed by formation of an N-terminal helix which afterwards elongates to C-terminus. The last step is the reorganization of the terminal residues and their folding into a β-sheet.
Our simulations rely on the same physical force field and implicit solvent as the above canonical simulations, but multicanonical molecular dynamics allows for an enhanced sampling of folding events and therefore can lead to deeper insight into the folding mechanism of this protein. Using the protocol described in the method section we have generated multicanonical weights that we then employe for data generation in six independent multicanonical molecular dynamics runs. As a consequence, our analysis relies on an accumulated simulation time of 720 ns. The resulting energy distribution is shown Figure 6C (dashed curve). Note that the curve is centered around energies of ≈ −3500 kJ/mol which we identified as the transition region, corresponding to a transition temperature of T ≈ 420 K (see 6D). The small standard deviation in the specific heat values of (6D) indicates the convergence of all six multicanonical production runs. The total accumulated simulation time, including the time needed to generate the multicanonical weights, is 1.9 μs (see 2). On the other hand, the accumulated simulation time of the four constant temperature simulations of Ref.20 is 5 μs. In only one of these four canonical molecular dynamics runs was a single folding event observed. The oscillations in energy and root-mean-square-deviation to the native structure (PDB-Identifier: 2KI0) in 6A and B demonstrate the much higher rate of folding transitions in multicanonical molecular dynamics. The best configuration differs by only 2.4 Å from the first model of the NMR ensemble, and is overlaid on this structure in Figure 7. At T = 300 K about 70% of the configurations are native-like, compared with 86% in the NMR experiments of Ref.19 A direct comparison with the constant temperature molecular dynamics runs of Ref.20 is difficult as only one out of four runs led to a folded structure. In this specific run, about 60% of configurations are native-like. These results show again that, unlike simple constant temperature simulations, the enhanced sampling of folding events of multicanonical molecular dynamics leads to a correct representation of the ensemble of configurations in which a protein exist at biologically relevant temperatures.
Figure 6.
Potential energy (A) and root-mean-square deviation (RMSD) to the native structure (B) as function of time for a randomly selected trajectory. Distribution of potential energy without re-weighting (dashed line) and after re-weighting to nine different temperatures between 280 K and 600 K (solid lines) (C). Specific heat capacity as a function of temperature (D).
Figure 7.
Free energy landscape at 300 K projected on the helicity of the central helix and the distance between residues 7THR - 30ARG as reaction coordinates. Ten minima are identified and the lowest energy structure corresponding to each minimum shown together with the corresponding value of the free energy. The structure (online color blue) enclosed by the square is the one with the lowest RMSD (2.4 Å) and shown overlaid on the first model of the NMR ensemble (online color green).
The βαβ fold of DS119 suggests as order parameters for the folding of the peptide, the degree by that the central helix is formed, and the degree by that the terminal segments form a β-sheet. The later is characterized by two quantities, the distance between residues 9TRP and 34TRP, and the distance between residues 7THR and 30ARG. Both contacts have to be formed for the β-sheet. However, from circular dichroism measurements it is known that the 9TRP-34TRP contact is very stable and observed for temperature up to 360 K, i.e. is also observed in the ensemble of unfolded configurations.19 Hence, we project in Figure 7 the folding landscape of the protein on the helicity and the 7THR - 30ARG distance as reaction coordinates. Ten minima are identified, and the lowest energy structure corresponding to each minimum is shown together with its free energy. The global free energy minimum (set to zero) is given the index one. Note that the strong correlation between the degree by that the central helix is formed, and the formation of the 7THR - 30ARG contact. The distance between the two residues diverges once the helix length becomes less than ten residues. Hence, a fully formed helix build out of the central 12–13 residues seems to precede and to be necessary for formation of the β -sheet build out of the terminal segments. A cluster consisting of minima 3–7 are separated from the native minimum (index 1) and each other by only small barriers. Minima 3 and 4 have a longer helix (ten residues long) than the minima 5–7 (a total of eight residues). In addition, the helix in minima 5–7 is split into two short segments. We do not observe any preference for either N or C-terminus for the helical segments to form earlier. Hence, we conclude that the central helix growth together from segments forming independently at the terminals rather than nucleating in the middle of the peptide and growing towards the ends.
In order to investigate these transition states in more detail, we compare the folding landscape at the transition temperature 420 K (Figure 8B with the landscapes either 40 K lower in temperature or 40 K higher in temperature (Figure 8A and C). Comparing these three landscapes, one finds that decreasing the temperature from 460 K to 380 K does not significantly change the distance between residues 7THR - 30ARG, as the free energy minima do not move in this coordinate. More dramatic are the changes along the second coordinate, the length of helical segments. Configurations with a short helix (length = 4 residues) become less frequent, while configurations with two short helices of total length 10 emerge. The maximum frequency of such configurations is observed at the transition temperature 420 K. Below that, at 380 K, their frequency has decreased, and configurations with a single long extended helix of length of at least ten residues do now dominate. Such long helices are not observed at 460 K. We conclude that transition states are characterized by partially folded short helical segments at the terminals. These are often stabilized by salt bridges of 6ARG and/or 30ARG with lysine side chains, see 9, as such salt bridges hinder the two helices to merge. Both residues can form such non-native salt bridges with a probability of 60%, while the other arginines in the peptide have a much smaller probability (20%) of forming non-native salt bridges (Figure 9B and C).
Figure 8.
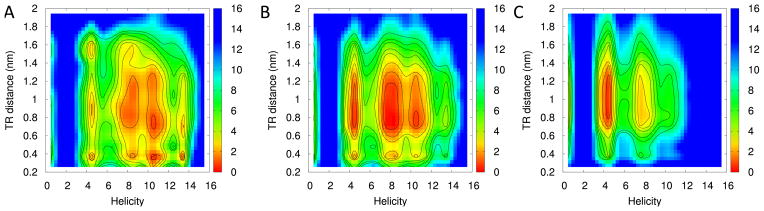
Free energy landscapes using the same coordinates as in 7. The temperatures are 380 K (A), 420 K (B), and 460 K (C), with 420 K the folding temperature. The evolution of three plots from high to low temperature indicates what are the predominating events that are occurring doing the transition.
Figure 9.
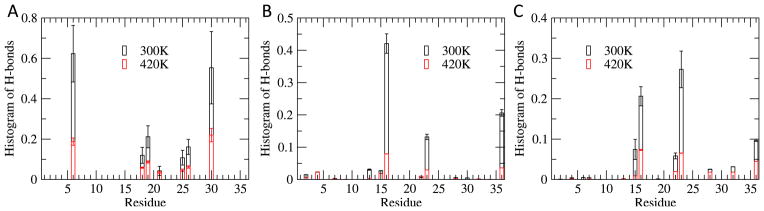
(A) Probability of forming salt bridges or hydrogen bonds for all Arg residues. (B) The probability of forming polar contacts with residue 6ARG. (C) The probability of forming polar contacts with residue 30ARG.
One could argue that the occurrence of these non-native salt bridges, formed by 6ARG and 30ARG with lysine side chains, is due to the implicit solvent model used in our simulations.28 In turn, this assumption would imply that the observed folding mechanism is an artifact of the implicit solvent model. In order to exclude this possibility, we have taken the ten representative configurations of Figure 8 and immersed them in explicit solvent (TIP3), minimized the resulting system, and allowed it to thermalize at 300 K during a 40 ns of constant temperature molecular dynamics. Analyzing these auxiliary simulations we find that the residues 6ARG and 30ARG do not form well-defined and stable salt bridges, but take part in a network of 2–11 salt bridges that are transiently formed and dissolved while the network itself persists throughout the simulation. Hence, we believe that the occurrence of such salt bridges, which slow down the formation of the central helix, are not an artifact of the implicit solvent model. While in the design of DS119, 6ARG was chosen to reduce self-aggregation, and design experiments switching 5VAL and 6ARG were unsuccessful, our results suggest to mutate the two residues 6ARG and 30ARG into ones that inhibit such non-native salt bridges as a way to enhance folding of DS119. Note that the crucial role of such non-native salt bridges in defining the rate-determining transition states could not be detected in the earlier Go-model simulations as by construction Go-models bias against the formation of non-native contacts.
Conclusions
Simulating proteins with end-to-end β-sheet we have demonstrated the efficiency of multicanonical molecular dynamics in sampling folding/unfolding events. In the case of the 75-residue MNK6, simulated by us with an all-atom Go-model, we find improvements of factors 30 over replica exchange. This demonstrates that despite the additional efforts needed to generate the weights multicanonical molecular dynamics is a suitable alternative to the more common replica exchange molecular dynamics, especially in cases where there is a strong cooperative transition between folded and unfolded states. The method may also be advantageous in cases where the transition is less strong. For instance, using our protocol for generating multicanonical weights, we have studied the folding landscape of the 36-residue DS119 with a physical all-atom force field and an implicit solvent. Here, our focus was not on a comparison of sampling techniques, but on probing the folding mechanism of this protein. We find that the rate-limiting step in the folding of this protein is the formation of the central helix which serves as a scaffold for the parallel β-sheet formed by the terminal residues. Identifying this bottleneck is again only possible because multicanonical protein simulations are designed to sample a large number of folding/unfolding events. While the overhead in generating multicanonical weights is considerably (about 60% of the computational resources went into this step), the gain in sampling efficiency outweighs the costs. Including the time needed to generate the multicanonical weights, the multicanonical simulation of DS119 required less than half of the accumulated times of previous constant temperature simulations resulting in a single folding event, but let with 432 folding/unfolding transitions to orders of magnitude better statistics.
Figure 2.
Probability of potential energies P(E) calculated after each of the four multicanonical iterations. From the first to the fourth iteration, the online colors are black, red, green, and blue.
Acknowledgments
We acknowledge support from the National Institutes of Health (grant number GM62838). The simulations were done on the BOOMER cluster of the University of Oklahoma. F.Y. thanks the Department of Chemistry and Biochemistry for kind hospitality during his sabbatical stay at University of Oklahoma.
Contributor Information
Ping Jiang, Email: pingj@ou.edu.
Fatih Yaşar, Email: fatih@hacettepe.edu.tr.
Ulrich H. E. Hansmann, Email: uhansmann@ou.edu.
References
- 1.Hukushima K, Nemoto K. Exchange Monte Carlo Method Applications to Spin Glass Simulations. J Phys Soc (Japan) 1996;65:1604–1608. [Google Scholar]
- 2.Geyer GJ, Thompson EA. Annealing Markov Chain Monte Carlo with Applications to Ancestral Inference. J Am Stat Assn. 1995;90(431):909–920. [Google Scholar]
- 3.Swendsen R, Wang J. Replica Monte Carlo Simulation of Spin-Glasses. Phys Rev Lett. 1986;57:2607–2609. doi: 10.1103/PhysRevLett.57.2607. [DOI] [PubMed] [Google Scholar]
- 4.Hansmann UHE. Parallel Tempering Algorithm for Conformational Studies of Biological Molecules. Chem Phys Lett. 1997;281:140–150. [Google Scholar]
- 5.Berg B, Neuhaus T. Multicanonical Algorithms for First Order Phase Transitions. Phys Lett B. 1991;267:249–253. doi: 10.1103/PhysRevLett.68.9. [DOI] [PubMed] [Google Scholar]
- 6.Hansmann UHE, Okamoto Y. Prediction of Peptide Conformation by Multicanonical Algorithm: A New Approach to the Multiple-Minima Problem. J Comput Chem. 1993;14:1333–1338. [Google Scholar]
- 7.Hansmann UHE, Okamoto Y, Eisenmenger F. Molecular Dynamics, Langevin and Hydrid Monte Carlo Simulations in a Multicanonical Ensemble. Chem Phys Lett. 1996;259:321–330. [Google Scholar]
- 8.Nakajima N, Nakamura H, Kidera A. Multicanonical Ensemble Generated by Molecular Dynamics Simulation for Enhanced Conformational Sampling of Peptides. J Phys Chem. 1997;101:817–824. [Google Scholar]
- 9.Hansmann UHE. Folding Simulations of the Parathyroid Hormon Fragment (1–34) J Chem Phys. 2004;120:417–422. doi: 10.1063/1.1630563. [DOI] [PubMed] [Google Scholar]
- 10.Yaşar F, Çelik S, Köksel H. The Investigation of the Secondary Structure of Various Peptide Sequences of Beta-Casein by Molecular Modeling. Physica A. 2006;363:348–358. [Google Scholar]
- 11.Mitsutake A, Okamoto Y. Helix-Coil Transitions of Amino-acid Homo-oligomers in Aqueous Solution Studied by Multicanonical Simulations. J Chem Phys. 2000;112:10638–10647. [Google Scholar]
- 12.Junghans C, Bachmann M, Janke WW. Thermodynamics of Peptide Aggregation Processes. An Analysis from Perspectives of Three Statistical Ensembles. J Chem Phys. 2008;128:085103. doi: 10.1063/1.2830233. [DOI] [PubMed] [Google Scholar]
- 13.Chen T, Lin XS, Liu Y, Lu T, Liang HJ. Microcanonical Analyses of Homopolymer Aggregation Processes. Phys Rev E. 2008;78:056101. doi: 10.1103/PhysRevE.78.056101. [DOI] [PubMed] [Google Scholar]
- 14.Bachmann M. Multicanonical Simulation of Biomolecules and Microcanonical Statistical Analysis of Conformational Transitions. Phys Scr. 2013;87:058504. [Google Scholar]
- 15.Higo J, Ikebe J, Kamiya N, Nakamura H. Enhanced and Effective Conformational Sampling of Protein Molecular Systems for Their Free Energy Landscapes. Biophys Rev. 2012;4:27–44. doi: 10.1007/s12551-011-0063-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Whitford P, Noel J, Gosavi S, Schug A, Sanbonmatsu K, Onuchic J. An All-Atom Structure-Based Potential for Proteins: Bridging Minimal Models with All-Atom Empirical Forcefields. Proteins. 2009;75:430–441. doi: 10.1002/prot.22253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Jiang P, Hansmann UHE. Modeling Atructural Flexibility of Proteins with Go-Models. J Chem Theory Comput. 2012;8:2127–2133. doi: 10.1021/ct3000469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Trebst S, Huse D, Troyer M. Optimizing the Ensemble for Equilibration in Broad-Histogram Monte Carlo Simulations. Phys Rev E. 2004;70:046701–046705. doi: 10.1103/PhysRevE.70.046701. [DOI] [PubMed] [Google Scholar]
- 19.Liang H, Chen H, Fan K, Wei P, Guo X, Jin C, Zeng C, Tang C, Lai L. De Novo Design of a βαβ Motif. Angew Chem-Int Edit. 2009;48:3301–3303. doi: 10.1002/anie.200805476. [DOI] [PubMed] [Google Scholar]
- 20.Qi Y, Huang Y, Liang H, Liu Z, Lai L. Folding Simulations of a De Novo Designed Protein with a βαβ Fold. Biophys J. 2010;98:321–329. doi: 10.1016/j.bpj.2009.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hess B, Kutzner C, van der Spoel D, Lindahl E. Gromacs 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J Chem Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 22.Hess B. P-Lincs: A Parallel Linear Constraint Solver for Molecular Simulation. J Chem Theory Comput. 2008;4:116–122. doi: 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
- 23.Nose S. A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J Chem Phys. 1984;81:511–519. [Google Scholar]
- 24.Vulpe C, Levinson B, Whitney S, Packman S, Gitschier J. Isolation of a Candidate Gene for Menkes Disease and Evidence that It Encodes a Copper-Transporting Atpase. Nat Genet. 1993;3:7–13. doi: 10.1038/ng0193-7. [DOI] [PubMed] [Google Scholar]
- 25.Lammert H, Schug A, Onuchic J. Robustness and Generalization of Structure-Based Models for Protein Folding and Function. Proteins. 2009;77:881–891. doi: 10.1002/prot.22511. [DOI] [PubMed] [Google Scholar]
- 26.Noel J, Whitford P, Sanbonmatsu K, Onuchic J. Smog@ctbp: Simplified Deployment of Structure-Based Models in Gromacs. Nuc Acids Res. 2010;38:657–661. doi: 10.1093/nar/gkq498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Trebst S, Troyer M, Hansmann UHE. Optimized parallel tempring simulations of Proteins. J Chem Phys. 2006;124:174903. doi: 10.1063/1.2186639. [DOI] [PubMed] [Google Scholar]
- 28.Geney R, Layten M, Gomperts R, Hornak V, Simmerling C. Investigation of Salt Bridge Stability in a Generalized Born Solvent Model. J Chem Theory Comput. 2006;2:115–127. doi: 10.1021/ct050183l. [DOI] [PubMed] [Google Scholar]
- 29.Gaye ML, Harwick C, Kouza M, Hansmann UHE. Chamelonicity and Folding of the C-Fragment of TOP7. Eur Phys Let. 2012;97:68003. [Google Scholar]