Origin and Impact of Phototransduction Noise in Primate Cone Photoreceptors

Abstract

Noise in the responses of cone photoreceptors sets a fundamental limit to visual sensitivity, yet the origin of noise in mammalian cones and its relation to behavioral sensitivity are poorly understood. Our work here on primate cones improves understanding of these issues in three ways. First, we find that cone noise is not dominated by spontaneous photopigment activation or by quantal fluctuations in photon absorption but instead by other sources, namely channel noise and fluctuations in cGMP. Second, we find that adaptation in cones, unlike that in rods, affects signals and noise differently. This difference helps explain why thresholds for rod- and cone-mediated signals have different dependencies on background light level. Third, past estimates of noise in mammalian cones are too high to explain behavioral sensitivity. Our measurements indicate a lower level of cone noise, and thus help reconcile physiological and behavioral estimates of cone noise and sensitivity.

INTRODUCTION

Daylight vision relies on high sensitivity to subtle changes in the spatial pattern, contrast and chromaticity of light inputs. Noise in the responses of cone photoreceptors sets a fundamental limit to such sensitivity. Our goal here was to improve understanding of the magnitude, origin and properties of noise in the responses of primate cones, particularly with regard to the implications of cone noise for visual function.

Rods and rod vision provide a useful point of comparison. In darkness, noise in rods consists of occasional photon-like events originating from the spontaneous activation of the photopigment rhodopsin and continuous fluctuations originating from spontaneous activity of other components of the phototransduction cascade^1–3. The low level of rod noise permits detection of single absorbed photons⁴. Dark-adapted behavioral sensitivity approaches limits set by rod noise and statistical fluctuations associated with the division of light into discrete quanta^5–6. The similarity of rod and behavioral noise requires that the retinal readout of rod responses operate efficiently, a constraint that has guided investigation of the underlying circuitry⁶. In the presence of dim backgrounds, quantal fluctuations dominate rod noise. As a consequence, the detection sensitivity of rod responses scales with the square root of the background light level⁷; this scaling is in close agreement with the classic Rose-DeVries region of behavioral threshold-versus-intensity curves⁸.

The situation is much less clear for cones and cone-mediated vision. While the rate of spontaneous activation of cone photopigments is much higher than that of rhodopsin^9–10, the kinetics of noise in primate cones suggests that most noise originates downstream of the photopigment¹¹. However, measured noise in primate cones is too high to account for behavioral sensitivity, suggesting that one or both estimates are in error⁵. Thus the impact of cone noise remains unclear. Further, over a wide range of backgrounds, behavioral thresholds for cone-mediated vision increase linearly with background (the classic Weber region), a property important for coding contrast independently of background light level¹². It is unclear, however, how the Weber region relates to the background dependence of cone signal and noise.

Here we characterize signal and noise in primate cone photoreceptors and their dependence on background light level. Our measures of cone noise and detection thresholds are considerably lower than past estimates, helping reconcile cone physiology with behavioral measures of the sensitivity of cone vision. Further, we find that adaptation affects cone signal and noise very differently, providing a natural explanation for the Weber region of behavioral threshold-versus-intensity curves.

RESULTS

The results below are divided into four parts. First, we describe empirical properties of noise in primate cone photoreceptors. Second, we manipulate the cone phototransduction cascade to identify where noise originates. Third, we determine how light-adaptation affects the signal and noise of primate rod and cone responses. Fourth, we explore how detection thresholds for rod and cone responses depend on background light level.

Cone noise exhibits several distinct temporal components

We started by characterizing the amplitude and kinetics of noise in the responses of primate cones. Past work indicates that cones are noisy, with most noise originating downstream of the photopigment in the transduction cascade¹¹. We felt it was important to begin with similar experiments given that past measures of cone noise exceed the noise inferred from behavior⁵ and the properties of cone noise are a foundation for the remainder of the work here.

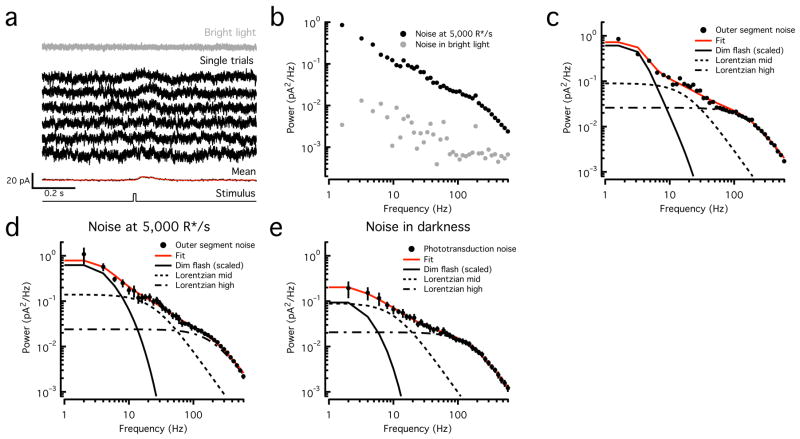
We recorded the current responses of voltage clamped long (L) or middle (M) wavelength sensitive cones to brief 100% contrast flashes (producing ~50 opsin isomerizations or R*) in the presence of a moderate background (Fig. 1a). Individual responses to such flashes are difficult to distinguish from baseline noise, but the response can be uncovered by averaging multiple trials (Fig. 1a). The recorded current fluctuations include noise arising in the outer segment, noise arising from conductances in the inner segment, and noise produced by the recording itself (instrumental noise). Exposing cones to a near-saturating light step closed most of the cGMP-gated channels in the cone outer segment, decreasing the recorded current and markedly decreasing the current fluctuations (Fig. 1a,b). Instrumental noise and noise from (voltage-clamped) inner segment conductances should not be light dependent; these sources account for the most of the noise remaining in bright light.

Figure 1. Temporal components of cone outer segment noise.

a. Cone current responses to 10 ms flashes producing ~50 opsin activations (R*) delivered on a 5000 R*/s background (black traces). The mean of ~50 responses is at the bottom, fitted (red) with Equation 6 with the following parameters: α = 0.1993, τ_rise = 20.2 ms, τ_decay = 75.6 ms, τ_osc = 397.1 ms and ϕ = −79.5 degrees. Current recorded in bright light is at the top (gray trace).

b. Power spectra of noise in constant and bright light from cone in (a).

c. Power spectrum of the outer segment cone noise (black circles, noise in background minus that in saturating light from b) and fit (red trace) obtained by summing a scaled version of the power spectrum of the fitted average dim flash response and two Lorentzian functions (Equation 5) with distinct corner frequencies (18 Hz and 170 Hz) (black lines).

d. Average outer segment cone noise measured at 5000 R*/s (n=6, black circles, mean ± SEM) and fit as in (c) (red trace). Corner frequencies of Lorentzian functions are 24 Hz and 200 Hz.

e. Average outer segment cone noise measured in darkness from foveal cones (n = 7, black circles, mean ± SEM) and fit as in (c) (red trace). Corner frequencies of Lorentzian functions are 10 Hz and 150 Hz.

We characterized noise by calculating average power spectra from stretches of data without flashes (see Methods). Assuming that outer segment and inner segment/instrumental noise are independent, we isolated outer segment noise by subtracting the spectrum in bright light from that in moderate light (Fig. 1c). This process underestimates the total outer segment noise since bright light did not fully suppress the current; such errors were small, however, as the subtracted noise was 20–100-fold smaller than that measured in darkness or in the presence of moderate steady light (Fig. 1b). In the remainder of the paper, outer segment cone noise has been isolated similarly.

Both noise generated within the cone phototransduction cascade (intrinsic noise) and noise generated by quantal fluctuations in photon absorption (extrinsic noise) contribute to outer segment noise; extrinsic noise follows Poisson statistics and is absent in complete darkness (see below). Assuming linearity of the cone response, both extrinsic noise and noise from spontaneous pigment activation should have a power spectrum similar to that of the cell’s dim flash response (Fig. 1c). As has been described previously¹¹, cone noise instead extended to much higher frequencies, indicating a substantial contribution from events with faster kinetics than the single photon response. By recording noise in voltage clamp, we characterized outer segment noise up to high temporal frequencies (600 Hz); noise spectra had three clear components and were fit empirically as the sum of a low frequency component with the shape of the dim flash response, and two Lorentzian functions with distinct corner frequencies (Equation 5). Adequate fits were obtained on a single cell basis (Fig. 1c), or by averaging over a population of L and M cones recorded with the same background illumination (5000 R*/s; Fig. 1d). Based on these fits, the lowest frequency component accounted for ~30% of the total variance, which corresponds to the maximal fraction of noise that could be attributed to both spontaneous and background opsin activation.

To separate phototransduction noise from extrinsic noise, we repeated these experiments in complete darkness, targeting foveal cones to eliminate possible contributions from rod photoreceptors coupled to cones via gap junctions¹³. The average noise showed less power at low frequencies (Fig. 1e), such that at most ~10% of the total current variance could be attributed to spontaneous opsin activation. L and M cones exhibited similar noise, and in particular did not show the ~50-fold difference that would be expected from the scaling of spontaneous opsin activation rates with wavelength¹⁴.

Although most low-frequency noise is not associated with spontaneous pigment activation, we can still define a rate of pigment activation that would produce an equivalent level of noise. Experiments described below indicate that this equivalent dark noise is ~600 R*/s, substantially lower than previous estimates¹¹. First, however, we describe experiments identifying the sources of noise within the transduction cascade.

Two dominant sources of noise: pharmacology

Rod and cone photoreceptors share the same basic phototransduction scheme, yet their light responses differ considerably in sensitivity and kinetics. Does noise in rods and cones also differ in origin? Rod noise is dominated by early events in phototransduction - namely spontaneous activation of rhodopsin and phosphodiesterase (PDE)^1–3. As shown below, cone noise is instead dominated by open/close transitions in the cyclic-GMP-gated channels and fluctuations in the cyclic-GMP (cGMP) concentration.

Because the low- and mid-frequency noise components we identified overlap spectrally (Fig. 1), we focused on a frequency range (up to 20Hz) that includes contributions mainly from both low- and mid-frequency components, and a range (100–600 Hz) that is dominated by the high-frequency component. To maximize sensitivity to pharmacological manipulations that produced modest changes in the phototransduction cascade, we used two approaches to compare noise before and after drug application in single cells: (1) We delivered membrane-impermeable drugs (specifically 8′Bromo-cyclic-GMP or 8′Br-cGMP) using a two electrode recording technique in which both a recording electrode and a drug-delivery electrode were sealed onto a single cone cell body. After attaining whole-cell mode with the recording electrode and getting baseline measurements of noise and light response (in under 30s), we achieved access with the drug-delivery electrode and monitored noise and signal as the drug was introduced into the cytoplasm. (2) We delivered membrane-permeable drugs (specifically 3′-isobutyl-1′-methylxanthine or IBMX) using a puffer pipette located near the cone outer segment after recording baseline noise and light response.

Control experiments for two-electrode recordings

Because the two-electrode technique has not been used previously in cones, we started by checking for artifactual changes in noise. We first used a normal internal solution in both electrodes, keeping the phototransduction cascade as intact as possible (Fig. 2a). Rupturing the membrane occluding the tip of the second electrode did not significantly change the holding current (Fig. 2b) or the kinetics or amplitude of the light response (Fig. 2c); some alterations in noise were apparent (Fig. 2c,d). We summarized the results across cells by computing the ratio, at each temporal frequency, of the noise spectra before and after rupturing the membrane at the tip of the second electrode (Fig. 2e); only pharmacological manipulations that produced changes in this ratio larger than the control case were deemed significant.

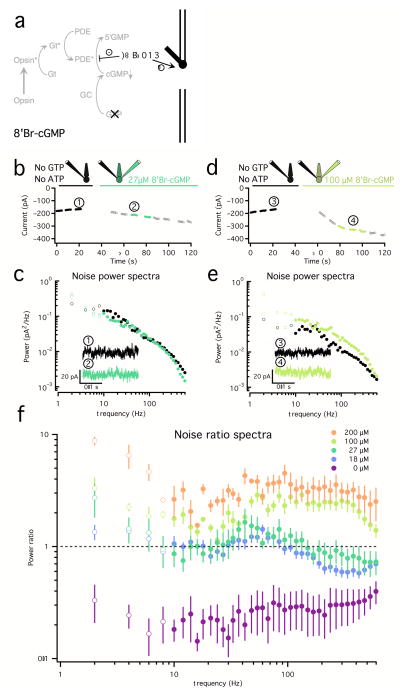
Figure 2. Two-electrode recordings allow pharmacological manipulation of cone phototransduction.

a. Phototransduction cascade. Light-activated Opsin activates transducin (Gt), which then activates phosphodiesterase (PDE). Active PDE reduces the cyclic-GMP (cGMP) concentration, closing membrane channels. Cyclic-GMP is restored by guanylate cyclase (GC).

b. Changes in holding current before (black) and after (gray) introduction of a second electrode; both electrodes contained control internal solution. Filled black and gray circles represent 500 ms stretches of noise used to calculate the spectra in (d).

c. Light responses and noise before (black) and after (gray) introduction of the second electrode (time points noted in (b)). Upper left shows expanded examples of noise used to calculate the power spectra in (d).

d. Power spectra before (black circles) and after (gray circles) the introduction of the second electrode.

e. Average (± SEM, n=16) ratio between power spectra calculated before and after introduction of the second electrode.

f. Omission of both ATP and GTP from the internal solution shuts down the phototransduction cascade, causing cGMP-gated channels to close.

g. Changes in holding current during a two-electrode recording in which both electrodes contained a solution lacking ATP and GTP. Filled black and purple circles represent 500 ms stretches of noise used to calculate the spectra in (i).

h. Examples of light responses and noise recorded before (black) and after (purple) the introduction of a second electrode (time points noted in (g)).

i. Power spectra before (black) and after (purple) the introduction of the second electrode.

j. Average (± SEM, n=6) ratio of power spectra before and after the introduction of the second electrode. Conditions as in (g).

Next, we tried to eliminate all outer segment noise pharmacologically. Since all phototransduction noise sources ultimately cause fluctuations in the current flowing through the cGMP-gated channels, one way to eliminate noise is to promote depletion of the internal cGMP, which will in turn cause the cGMP-gated channels to close (Fig. 2f). Cyclic-GMP is produced from GTP by the guanylate cyclase (GC); thus we omitted GTP from the electrode solution. We also omitted ATP since transfer of its high-energy phosphate can produce GTP¹⁵. Hydrolysis of cGMP by phosphodiesterase (PDE) via transducin (Gt) activation requires considerably lower concentrations of GTP than synthesis^3,16, and hence will contribute to reducing the cGMP concentration. As expected, currents steadily decreased (i.e. cGMP-gated channels closed) in two-electrode recordings using internal solutions lacking both ATP and GTP (Fig. 2g); this was accompanied by a loss in the light response and a marked attenuation of the current fluctuations (Fig. 2h). The decrease in noise spanned all relevant frequencies (Fig. 2i,j) and had the same spectral characteristics as the decrease in noise seen during exposure to near-saturating light steps, which also close the cGMP-gated channels (compare to Fig. 1a,b). We obtained similar results in recordings with single electrodes filled with a solution lacking ATP and GTP (n=3, data not shown).

This pharmacological manipulation served several purposes: (1) it confirms that most of the noise in our recordings originates in the cone outer segment; (2) it shows that manipulation of the electrode solutions can affect the phototransduction cascade; and, (3) the current changes provide a basis for evaluating experiments in the next section, where a synthetic agonist will be used to open the cGMP-gated channels.

Channel noise

The two-electrode experiments described in this section, isolated noise produced by cGMP-gated channels. Changes in cGMP were again suppressed by omitting ATP and GTP from the internal solution, and cGMP channels were activated with 8′Br-cGMP, a potent agonist of the cGMP-gated channels (Fig. 3a). Because 8′Br-cGMP is also poorly hydrolyzed by PDE, it suppresses activity within the PDE arm of the phototransduction cascade. Introduction of 8′Br-cGMP through the second electrode would ideally occur only after the internal cGMP has been depleted, but this process can take up to 5 min (Fig. 2g), and long recordings with two electrodes are technically difficult. Instead, we relied on shorter experiments in which we compared different concentrations of 8′Br-cGMP with the case where 8′Br-cGMP is absent (Fig. 2j).

Figure 3. High frequency noise arises from open/close transitions in the cGMP-gated channels.

a. Channel noise was separated from sources causing fluctuations in [cGMP] by suppressing cGMP synthesis by omitting ATP and GTP from the internal solutions in a two-electrode recording. Different concentrations of the cGMP-channel agonist 8′Bromo-cyclic-GMP (8′Br-cGMP) were added to the second electrode.

b. Changes in holding current before (black) and after (green) the introduction of a second electrode containing 27 μM 8′Br-cGMP. The filled black and green circles represent 500ms stretches of noise used to calculate the spectra in (c).

c. Average noise power spectra for the cone in (B) before (black) and after (green) the introduction of a second electrode containing 27 μM 8′Br-cGMP. Insets show example noise traces in each condition corresponding to (1) and (2) in (b).

d and e. Same as in (b) and (c) for an 8′Br-cGMP concentration of 100 μM.

f. Average (± SEM) ratio of power spectra before and after introduction of 8′Br-cGMP. The color scale corresponds to the concentration of 8′Br-cGMP (18 μM: n = 10; 27 μM: n = 4; 100 μM: n = 3; 200 μM: n = 2). Changes in noise below 10Hz are unreliable due to slow drift in the measured current and are displayed as open circles. The increase at high frequencies (100 Hz–600Hz) is significant across all concentrations.

We empirically determined appropriate concentrations of 8′Br-cGMP and found that modest concentrations (27 μM) ‘rescued’ (and even overshot) the loss in holding current (Fig. 3b) and noise (Fig. 3c) produced by the omission of GTP and ATP alone (compare to Fig. 2g–i). Under these conditions, measured currents and noise were dominated by channels opened by the added 8′Br’cGMP. Higher concentrations produced a further increase in holding current (Fig. 3d) and noise (Fig. 3e) compared to baseline.

The concentration of 8′Br-cGMP in the outer segment slowly approaches a steady level for two reasons: (1) the 8′Br-cGMP is delivered in the inner segment, and has to diffuse to the outer segment; (2) PDE can still hydrolyze 8′Br-cGMP at a slow rate. Together, these issues cause a slow drift in holding current and artifactual increases in noise below 10Hz, making changes in noise in that frequency range uninterpretable. Thus, we focus on changes in noise between 10 and 600Hz (Fig. 3c,e).

With activity of the transduction cascade suppressed, activation of the cGMP-gated channels produced fluctuations in current extending from low frequencies to at least 600 Hz. The increase in noise scaled with the concentration of 8′Br-cGMP (Fig. 3f). High frequency noise was similar under control conditions (without 8′Br-cGMP) and with a concentration of 8′Br-cGMP that matched the initial dark current (Fig. 3b,c). These results indicate that the component of cone noise that extends from low to high temporal frequencies originates from gating transitions in the cGMP-gated channels.

Noise due to fluctuations in cGMP

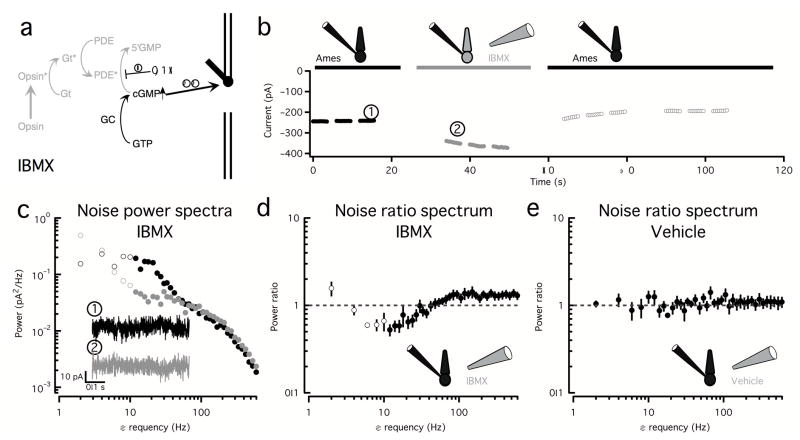
The experiments described above indicate that channel fluctuations produce noise extending from low to high temporal frequencies. To test for other sources of low- to mid-frequency noise, we puffed the membrane-permeable PDE inhibitor IBMX onto the outer segments of voltage-clamped cones. IBMX has two effects: (1) it decreases baseline hydrolysis of cGMP, leading to an increase in [cGMP] and opening of cGMP-gated channels; and, (2) it decreases the fluctuations in [cGMP] produced by dark activation of any of the transduction components upstream of (and including) PDE (Fig. 4a). We performed recordings in darkness to avoid extrinsic noise and again focused on frequencies above 10 Hz to avoid artifacts induced by current drift.

Figure 4. An additional noise source with power in the low to mid frequency range causes fluctuations in cGMP.

a. The membrane-permeable and fast acting PDE inhibitor IBMX increases the cGMP concentration and therefore the number of open channels and inhibits any noise source upstream of (and including) PDE.

b. Changes in holding current in the absence (black) and presence (gray) of IBMX. The filled black and gray circles represent 500 ms stretches of noise used to calculate the spectra in (c). Recordings were performed in complete darkness to avoid extrinsic noise.

c. Corresponding power spectra in the absence (black circles) and presence (gray circles) of IBMX. Insets show example noise traces in each condition corresponding to (1) and (2) in (b). Changes in noise below 10Hz (open circles) are unreliable due to slow drift in the measured current.

d. Average (± SEM) ratio of power spectra in the presence and in the absence of IBMX (n = 10) showing a decrease in noise in the 10 to 50 Hz range and an increase in noise at high frequencies (100 to 600Hz)

e. Average (± SEM) ratio of power spectra before and after puffing a vehicle solution lacking IBMX (n=4). The increase in noise at the high frequencies (100–600Hz) and the decrease at low frequencies (10–30 Hz) seen with IBMX were significantly different than the changes with vehicle.

Inhibition of PDE, as expected, reversibly increased the holding current (Fig. 4b) and slowed the light response (not shown). This was accompanied by an increase in high frequency noise, consistent with an increase in channel noise; additionally, noise in the low- to mid- frequency range (10–50Hz) decreased (Fig. 4c,d). These changes in noise were significantly different from those elicited by puffing a vehicle solution lacking IBMX (Fig. 4e) in the two relevant frequency ranges.

This experiment serves several purposes. First, it corroborates the 8′Br-cGMP experiments, showing that the opening of extra cGMP-gated channels leads to an increase in high frequency channel noise. Second, it unveils a noise source that is suppressed when PDE is inhibited and that, therefore, normally causes fluctuations in the cGMP concentration. Notably, this noise source has significant power in the 10–50Hz range, where opsin noise makes little or no contribution (see Fig. 1c–e). This noise component resembles continuous noise in rods³ and fish cones¹⁷ (see Discussion).

Impact of adaptation on photoreceptor signal and noise

The impact of adaptation on detection of light stimuli depends on how it alters both signal and noise. For example, over a substantial range of backgrounds rod signal and noise are equally affected by adaptation, such that the signal-to-noise ratio is independent of adaptation⁷. As a consequence, the detection threshold for such backgrounds is limited by the Poisson statistics of photon absorption. This provides a simple explanation for the Rose-DeVries regime of behavioral threshold-versus-intensity curves, since the standard deviation of a Poisson process scales as the square-root of the mean⁸. Since much of cone noise originates late in the transduction cascade, it may be less affected by adaptation than cone signals. Thus, the relationship between photoreceptor adaptation and behavioral threshold-versus-intensity curves may be fundamentally different for rods and cones. The experiments described in the next two sections show that this is indeed the case.

Rods

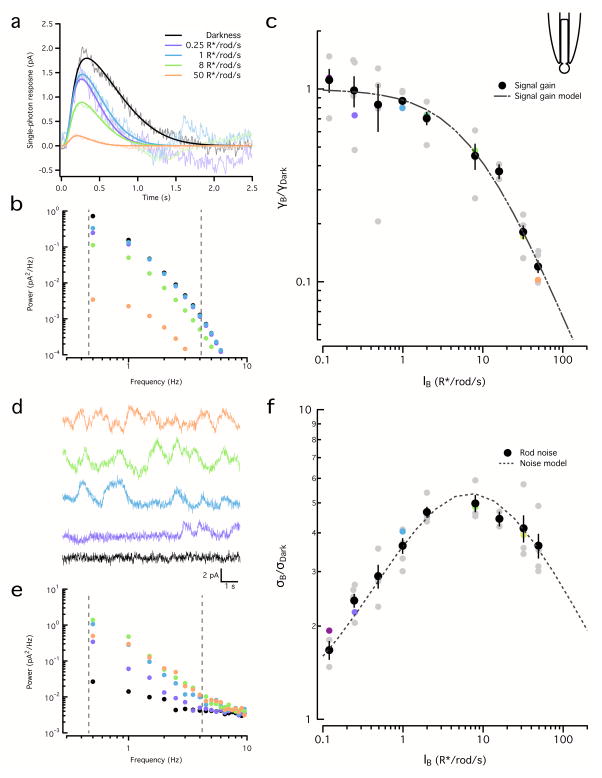
We begin by characterizing the dependence of rod signal and noise on background. While our overall conclusions are consistent with previous studies⁷, we felt that inclusion of the rod data was important to provide a direct comparison with the cone results described below.

We measured rod flash responses and noise across a range of backgrounds using suction electrodes¹⁸. Background light abbreviated and decreased the amplitude of the estimated single photon response (Fig. 5a); adaptation was pronounced for backgrounds exceeding 8 R*/s. To facilitate direct comparison, we quantified both signal and noise adaptation using spectral analysis. We integrated the power spectra of fits to the single photon response at each background (Fig. 5a) between 0.5 and 4Hz (Fig. 5b) and quantified changes in gain as the square root of this integral, normalized by the value in darkness (Fig. 5c). Gain changes were well described by a Weber-Fechner function:

$$\frac{{\gamma }_B}{{\gamma }_D}=\frac{1}{\left(1+\frac{I_B}{I_0}\right)}$$ (1)

where γ_B corresponds to gain at a given background (in pA/R*), γ_D to gain in darkness (in pA/R*), I_B to intensity of the background illumination (in R*/s) and I₀ to the background illumination that halves gain. The best fit for I₀ was 7.1 R*/s (95% confidence interval (CI) 6.0–8.2 R*/s).

Figure 5. Adaptation similarly affects rod signal and noise.

a. Linear estimates of the rod single photon responses for a range of backgrounds. Increasing backgrounds resulted in faster and smaller responses. Fits were obtained using Equation 6. Correspondence between light levels and color scale is maintained throughout the figure.

b. Power spectra of the fitted single photon responses in (a). Dashed lines show integration limits.

c. Square root of the integrated signal power (0.5 Hz–4 Hz) normalized by that in darkness for the example rod in (a) and (b) (colored circles) and for a population of rods (gray circles). The population data (black circles, mean ± SEM, n=5) was fit with Equation 1 with I₀ = 7.1 R*/s.

d. Examples of noise traces for the same rod and backgrounds as in (a).

e. Power spectra of the noise traces in (d). Dashed lines show integration limits.

f. Square root of the power spectrum integral (0.5 Hz–4 Hz) of the noise normalized by darkness for the example rod in (a) and (d) (colored circles) and for a population of rods (gray circles). The population (black circles, mean ± SEM, n=5) was fit with Equation 2 with I_D = 0.062 R*/s.

We estimated rod noise at the same backgrounds. Noise in darkness was low and composed of continuous noise and rare discrete events (not present in the example trace) (Fig. 5d). Noise increased in dim backgrounds due to current fluctuations produced by random photon absorptions (Fig. 5d,e), peaking at ~8 R*/s with an almost 5-fold increase relative to darkness; higher backgrounds produced a subsequent decrease in noise (Fig. 5f).

These changes in noise can be predicted based on two assumptions: (1) intrinsic phototransduction noise and extrinsic noise are independent and additive; and, (2) both extrinsic and intrinsic noise are subject to the same light adaptation mechanism that affects the rod signals. These assumptions are summarized in the following equation, in which the first term represents the decrease in noise produced by adaptation and the second term corresponds to the increase in noise produced by quantal fluctuations in photon arrival:

$$\frac{{\sigma }_B}{{\sigma }_D}=\frac{1}{\left(1+\frac{I_B}{I_0}\right)}\times \sqrt{\left(1+\frac{I_B}{I_D}\right)}$$ (2)

Here σ_B corresponds to the standard deviation of the noise at a given background (in pA), σ_D to the standard deviation of the noise in darkness (also in pA), I_B is the intensity of the background (in R*/s), I_D represents the intrinsic noise expressed as an equivalent “dark light” (in R*/s; see ⁵), and the half-desensitizing background, I₀=7.1 R*/s, was fixed from fits to the background-dependence of signal gain (Fig. 5c and Equation 1). The best fit was found for a dark light I_D of 0.062 R*/s (95% CI: 0.055 – 0.070 R*/s), which is within 30% of previously published values⁷. The success of this simple model indicates that, in agreement with previous work⁷, rod signals and noise are subject to the same adaptational mechanisms. This in turn is simply explained if rods are dominated by extrinsic noise across a wide range of backgrounds.

Cones

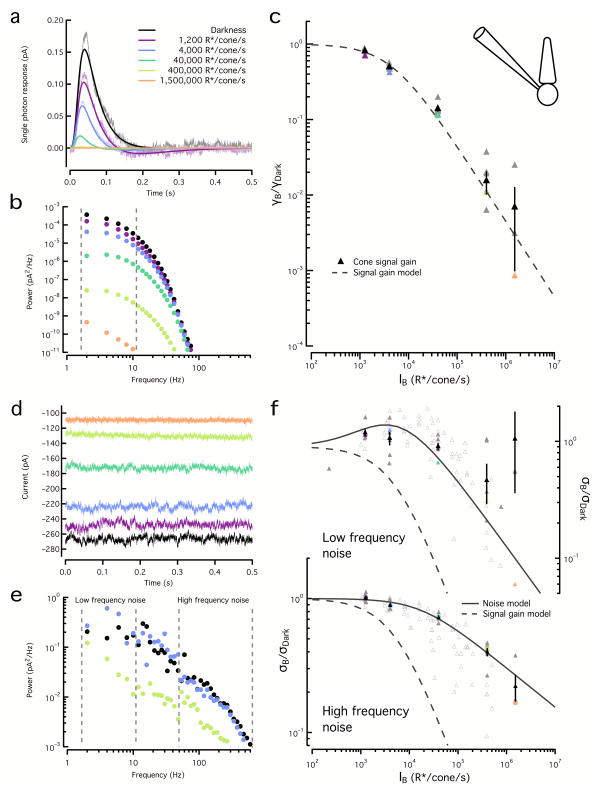
Adaptation affected cones quite differently, as a substantial component of cone noise evaded adaptation. To quantify signal adaptation in cones we estimated and fit single-photon responses (Fig. 6a) and calculated their power spectra (Fig. 6b); gain was estimated as the square root of the integrated power between 1 and 10Hz across a range of backgrounds (Fig. 6c). Changes in gain were also well described by a Weber-Fechner function (Equation 1); the best fit was found for a half desensitizing background of I₀=4500 R*/s (95% CI: 3900 – 5200 R*/s), consistent with previous work¹⁹.

Figure 6. Adaptation affects cone signal and noise differently.

a. Estimated cone single photon responses for a range of backgrounds, fit with Equation 6. Color scale is maintained throughout the figure.

b. Power spectra of the fitted single photon responses in (a). Dashed lines show integration limits.

c. Square root of the integrated signal power (2–10 Hz) normalized by that in darkness for the example cone in (a) and (b) (colored triangles) and for a population of cones (gray triangles). Population data (black triangles, mean ± SEM, n=6) was fit with Equation 1 with I₀ = 4500 R*/s.

d. Example noise traces for the same cone and backgrounds as (a).

e. Example noise power spectra for the same cone as (a).

f. Top, Square root of the integrated noise power at low frequencies (2–10 Hz) normalized by that in darkness for the example cone in (a) (colored triangles) and for a population of cones (gray triangles). Dashed line shows signal gain curve from (c). Noise below 10Hz at the highest backgrounds (black open triangles) was unreliable and was excluded from fitting. Population (black triangles, mean ± SEM, n=6) was fit with Equation 3 with I_D = 620 R*/s. Bottom, Square root of the integrated noise power at high frequencies (50 Hz to 600 Hz) as in top panel. The population data was fit with Equation 7 with I_o=17500 R*/s and η=0.29. Open grey triangles show noise from cones in which signal adaptation was not assessed (n=6); fit to low frequency noise used I_D=1200 R*/s and I₀=9950*/s and fit to high frequency noise used I_o=13 360 R*/s and η=0.34.

We estimated cone noise at the same backgrounds by integrating power spectra across a low (1–10Hz) and a high (100–600 Hz) frequency range (Fig. 6d,e) and calculated the square root of these integrals across backgrounds (Fig. 6f). The background dependence of low- and high-frequency noise differed. Like rod noise, low-frequency cone noise initially increased and then began to fall with further increases in background (Fig. 6f). This initial increase was modest (compare to the rod noise in Fig. 5f) and apparent only for backgrounds exceeding 1000 R*/s. The dependence of low-frequency noise on background could be fit with Equation 2, using the half-desensitizing background for the signal gain (I₀) derived above (4500 R*/s) and a best-fit value for an equivalent dark light of I_D=620 R*/s (95% CI: 480 – 835 R*/s). Thus, low-frequency cone noise can also be described as the sum of intrinsic and extrinsic noise, both subject to the same adaptational mechanism as the cone signals. High-frequency cone noise, however, was little affected by dim backgrounds and began to decline only at much higher backgrounds (Fig. 6f). Furthermore, this decline in high frequency noise was shallow and not proportional to the inverse of the background. Changes in noise at intermediate frequencies (20–100 Hz) showed a mixed behavior.

The background dependence of rod and cone signals and noise differed in two important ways. First, rod dark noise is ~100 times smaller than the backgrounds required for substantial adaptation, while in cones this difference is less than a factor of 10. Second, the majority of noise in rods is affected by adaptation, while a large component of noise in cones evades adaptation. Taken together, these factors mean that extrinsic noise contributes significantly to total cone noise only over a narrow range of backgrounds (~1000–5000 R*/sec). At lower backgrounds, cone noise is dominated by intrinsic noise from both cGMP fluctuations and cGMP channels, while at higher backgrounds the relative contribution of noise from cGMP channels increases.

Threshold vs. background behavior of rod and cone responses

The differences in the effect of adaptation on signal and noise in rods and cones predicts differences in the background-dependence of detection threshold. This in turn relates to how adaptation in the photoreceptors could contribute to behavioral threshold-versus-intensity curves.

We calculated detection thresholds, defined as the flash strength (in R*) required to match the noise in a 200 ms integration time at a given background, from the power spectra exemplified in Figures 5–6. First, we calculated the signal-to-noise ratio (SNR) as a function of frequency by dividing the signal power spectrum by the noise power spectrum; this SNR spectrum has very little power at high frequencies, and such frequencies contribute negligibly to detection. We integrated the SNR spectrum between 0.4 and 8Hz for rods and 3 and 600Hz for cones; the inverse of the square root of this integral corresponds to the detection threshold.

Rod and cone detection thresholds have a different dependence on the intensity of the background illumination (Fig. 7), as the shape of these curves is determined by how both signal and noise adapt. Given that rod noise and signal adapt identically, the rod thresholds follow (derived from Equations 1 and 2):

$${\mathit{Threshold}}_B=\left(\sqrt{1+\frac{I_B}{I_D}}\right)\times {\mathit{Threshold}}_D$$ (3)

with I_D=0.062 R*/s (derived from the noise adaptation in Fig. 5f). This curve closely follows the Poisson statistics of the background illumination for backgrounds exceeding the dark noise.

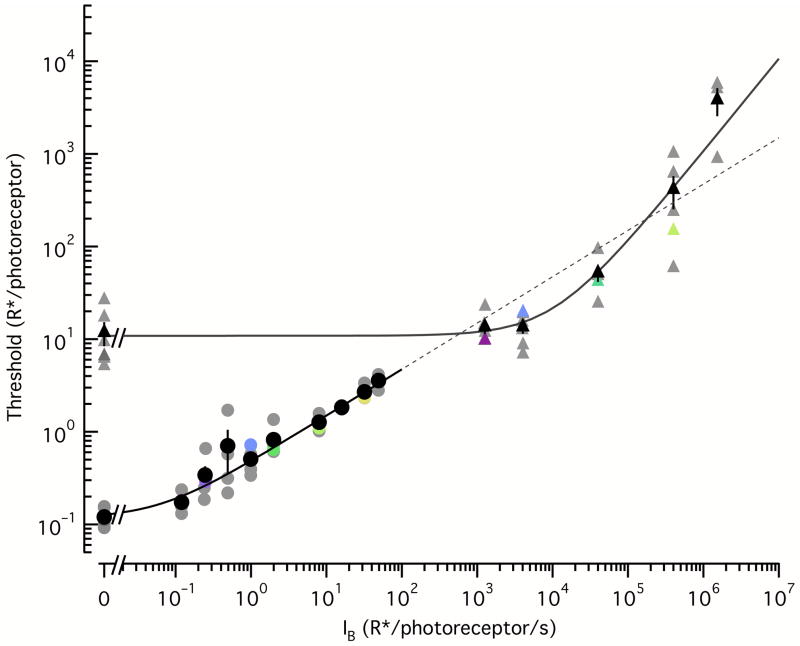
Figure 7. Background dependence of rod and cone detection thresholds.

Detection thresholds were derived for both photoreceptor types from the data shown in Figures 5 and 6 (see Methods). Colored symbols correspond to thresholds for the example rods and cones from Figures 5 and 6, while gray symbols correspond to population data (5 rods, 6 cones). The rod thresholds (black circles show mean ± SEM) were well described by Equation 3, with a dark threshold < 1R*/rod. The cone thresholds (black triangles show mean ± SEM) were well described by a Weber-like function (Equation 4) with a dark threshold of 10.9 R*/cone, and a threshold-doubling background, I_o = 11700 R*/s. The fit to the rod thresholds was extended to higher backgrounds to directly compare the slopes; in this log-log plot, the slope for rods is 0.5 corresponding to a “square root” behavior while the slope for cones is 1, corresponding to a Weber behavior.

Cone threshold increased more steeply with background. The lack of dependence of threshold on backgrounds < 1000 R*/s reflects the relatively high cone dark noise, which obscures extrinsic noise. Once signal gain is reduced by adaptation (I_B>4500 R*/sec), cone channel noise, which is relatively unaffected by adaptation, becomes dominant and hence the increase in threshold directly reflects the decreased signal gain. Thus, the curve is well fit with a Weber-like function:

$${\mathit{Threshold}}_B=\left(1+\frac{I_B}{I_0}\right)\times {\mathit{Threshold}}_D$$ (4)

with a best fit for the threshold-doubling background of I₀=11700 R*/s (95% CI: 7700 – 24400 R*/s). The dark threshold was Threshold_D=10.9 R*/cone (95% CI: 6.8 – 14.9 R*/cone).

Rod and cone threshold vs. intensity curves differed in at least three ways. First, as expected, the absolute threshold was higher in cones due to noise sources that preclude detecting absorption of single photons. Second, higher backgrounds were required to produce changes in cone threshold compared to rod threshold. Third, cone thresholds scaled linearly with background (i.e. Weber behavior), while rod thresholds scaled with the square root of the background (i.e. Rose-DeVries behavior).

DISCUSSION

Our aim was to improve understanding of the origin and functional impact of noise in the responses of primate cone photoreceptors. Our experiments support three main conclusions: (1) most cone noise originates downstream of the photopigment, with a sizable component from gating transitions in cGMP-gated channels; (2) cone noise and detection threshold are consistent with those inferred from behavior; and, (3) much of cone noise evades adaptation, helping provide a simple explanation for how the classic Weber region of behavioral threshold-versus-intensity curves could originate. We discuss these points below.

Origin of cone noise

We identified two primary sources of noise in the responses of primate cones: gating transitions in the cGMP-gated channels produce noise that extends from low to high temporal frequencies (up to 600Hz), and fluctuations in the concentration of cGMP produce noise restricted to low to mid temporal frequencies (below 50 Hz).

Several observations indicate that most of the noise from cGMP fluctuations is not generated by dark activation of the cone opsin: (1) the dim flash response, which reflects the activity directly caused by opsin activation, lacks significant power at frequencies above 10 Hz (Fig. 1c–e), while noise due to cGMP fluctuations extends well beyond 10 Hz (Fig. 4c); (2) the spontaneous isomerization rate of the L-cone opsin, estimated by its expression in mouse rods¹⁰, is ~10 R*/s, a factor of ~60 less than the rate needed to match the cone dark noise measured here; and, (3) preliminary recordings in S cones (where opsin noise should be almost negligible since short-wavelength sensitive opsins are very stable in comparison to middle- and long-wavelength sensitive opsins^9,14) show very similar dark noise to that reported here for L and M cones. Thus, fluctuations in the cGMP concentration originate from another source - e.g. activity of the non-isomerized photopigment due to chromophore dissociation²⁰, spontaneous transducin activation, or spontaneous PDE activation. Spontaneous PDE activation accounts for substantial noise in the responses of rods³, salamander S cones²¹, and fish cones¹⁷ and thus is a likely culprit here.

Impact of cone noise on retinal signals

Comparison of the sensitivity of cone-mediated signals at several locations in guinea pig retina indicates that most noise originates early in the retinal circuitry²². Specifically, a substantial loss of sensitivity was observed between photon capture in the cones and the responses of horizontal cells, consistent with noise intrinsic to the cones or their output synapse. Smaller, but still substantial, losses in sensitivity were observed between horizontal and ganglion cells, consistent with a source of additional noise within the retinal circuitry. Recordings from primate midget and parasol ganglion cells indicate that most noise in their synaptic inputs at cone light levels originates from the cones and has more rapid kinetics than the cone light response²³. These past studies highlight the importance of noise intrinsic to cones or their output synapses. Our results, particularly the high level and rapid kinetics of the cone noise, suggest that much of the noise limiting the sensitivity of the cone-mediated output signals from primate retina originates in the cone transduction cascade itself.

Bridging physiological and behavioral estimates of cone noise and sensitivity

How close does cone vision come to limits imposed by cone noise? The answer to this question is an important constraint on the retinal and cortical circuits that read out the cone signals. However, noise estimates derived from behavioral sensitivity are substantially lower than past measures of noise in primate cones⁵; this discrepancy has hindered our understanding of the relationship between retinal mechanisms and the sensitivity of cone-mediated behavior.

Recent behavioral work provides the lowest estimates of threshold and dark noise for cone vision²⁴, indicating that humans can detect ~200 photons delivered at the cornea or equivalently ~2–5 R*/cone in a region containing ~10 cones. Assuming that cone signals are pooled linearly, sensitivity should improve as the square root of the number of cones conveying the signal; thus the inferred single cone dark threshold estimate would be 6–15 R*, agreeing well with our single cone dark thresholds (7–15 R*) (Fig. 7).

Dark noise estimates require additional assumptions about spatial pooling and integration time of the visual system. Assuming spatial pooling across the entire area of the flash and an integration time equal to the flash duration (34 ms), behavioral sensitivity indicates a dark noise of 180–550 R*/s²⁴. Uncertainties in foveal cone density could further extend this range. This is again consistent with our estimate of ~600 R*/s. Thus, our measures of cone sensitivity and dark noise are consistent with behavior, providing a potential resolution to a long-standing discrepancy. Assuming the most sensitive cones we recorded from (Fig. 6–7) are similar to those in vivo, our results leave little room for noise or inefficiencies introduced by the circuits reading out the cone signals.

Impact of adaptation on threshold vs. intensity curves

The impact of adaptation on the sensitivity of sensory signals depends on how it affects both signal and noise. This is a key issue for how adaptational mechanisms relate to the rich history of measurements of the dependence of behavioral threshold on background light level^5–8.

Consistent with past work⁷, we found that adaptation equally affected rod signal and noise. This observation, along with the low level of intrinsic noise in rods, caused the detection threshold to be limited by extrinsic noise from quantal fluctuations in photon arrival across a wide range of backgrounds. Since quantal fluctuations follow Poisson statistics, the noise they contribute increases as the square root of the background intensity, consistent with the psychophysical Rose-deVries region of rod vision²⁵. It has been difficult to explain why cone vision does not similarly exhibit a clear Rose-deVries region; our results here suggest that the lack of a prominent Rose-deVries region occurs because extrinsic noise makes a relatively small contribution to cone noise except for a narrow range of backgrounds.

Classic work shows that cone-mediated behavioral thresholds across a wide range of backgrounds increase linearly with increases in background intensity (Weber-law behavior)¹². The mechanistic basis of this behavior, however, is unclear. The gain of cone signals decreases proportionally with backgrounds^11,26–28. This decrease in gain, together with a post-adaptation, background-independent source of noise, could explain Weber-law behavior²⁹. Here, we find that channel noise in cones accounts for a substantial fraction of cone dark noise; furthermore, channel noise is little affected by adaptation and thus becomes the dominant source of cone noise across a broad range of backgrounds. The weak dependence of channel noise on background and the decrease in gain of cone signals proportional to the background gives rise to an extended region over which the cone detection threshold follows Weber behavior. If noise downstream of the cones is small relative to cone noise, adaptational mechanisms in the retinal circuitry^8,30 would equally affect signal and noise. In this case, human threshold-vs.-intensity curves could be dominated by the signal and noise adaptation properties of individual photoreceptors. A complete explanation of human threshold versus intensity curves will require understanding where gain controls operate relative to key sources of noise in the circuit.

METHODS

Tissue, cells and solutions

We made electrophysiological recordings from primate retinas (Macaca fascicularis, nemestrina and mulatta of either sex, ages 3–19 yrs) in accordance with the Institutional Animal Care and Use Committee at the University of Washington. We obtained retina through the Tissue Distribution Program of the Regional Primate Research Center. We performed most enucleations under pentobarbital anesthesia. After enucleation, we rapidly separated the retina-pigment epithelium-sclera complex (< 5 min) from the anterior segment, drained the vitreous humour, and dark-adapted the retina for 1h in warm (32 °C) Ames medium bubbled with a mixture of 95% CO₂ - 5% O₂. We performed all subsequent procedures under infrared (> 900 nm) light. For recording, we separated a small piece of retina (~4mm²) from the pigment epithelium and mounted it photoreceptor side up on a poly-lysine coated coverslip (BD Biosciences) forming the floor of a recording chamber. We continually superfused retinas with warm (~31° – 33° C) oxygenated Ames medium. Treatment with DNase I (Sigma-Aldrich) (30 units in ~250 μL of Ames for 4 min) facilitated access to the photoreceptor outer segments. For rod suction recordings, we shredded small pieces of retina with bent needles and transferred them to a recording chamber¹⁸.

Recordings

We measured cone signals using whole-cell voltage-clamp recordings (holding potential −70 mV) with an internal solution containing (in mM): 133 potassium aspartate, 10 KCl, 10 HEPES, 1 MgCl₂, 4 ATP, 0.5 GTP; pH was adjusted to 7.2 with NMG-OH and osmolarity was ~280 mOSM. The internal solution did not contain any calcium buffer (or calcium), as even low concentrations of calcium buffer caused the light response to become increasingly biphasic during the course of a recording (not shown). We recorded rod photocurrents using suction electrodes as described previously¹⁸. Holding potentials have been corrected for a −10 mV liquid junction potential.

In experiments with 8′Br-cGMP we used modified internal solutions lacking ATP and GTP and supplemented with various concentrations of 8′Br-cGMP (from 0 μM to 200 μM). We added IBMX (final concentration of 1 mM) dissolved in DMSO (final DMSO concentration was less than 0.1%) to HEPES-buffered Ames and included it in a puffer pipette. For control experiments we used the same solution without IBMX.

We acquired data using Axoclamp 200B or Multiclamp 700B amplifiers. We low-pass filtered recorded currents at 3 kHz and digitized the data at 20 kHz. We analyzed recorded data through custom routines in Matlab (The Mathworks); we calculated power spectra using built-in fast Fourier transformations and represented them as two-sided power spectral densities (in pA²/Hz). We excluded from analysis cones that showed unusually rapid run-down of light responses, low sensitivity or short-lived recordings. Sensitive cones had holding currents of at least 150 pA (up to 400 pA), and peak responses to bright flashes of similar magnitude.

Light Stimulation

We delivered light stimuli from blue, green and red LEDs (peak wavelengths 470, 510 and 640 nm), which permitted quick identification of cone types. The stimuli illuminated a ~150 μm diameter area centered and focused on the recorded cone. We converted photon densities (photons/μm²) to R*/photoreceptor using a collecting area of 0.6 μm², previously measured cone spectral sensitivities² and the LED spectra.

Two-electrode technique

We performed two electrode recordings by sealing simultaneously onto a single cone cell body with both a recording electrode and a drug delivery electrode. After breaking into the cell with the first electrode, we obtained a baseline recording to assess noise and light response in less than 30 s (in voltage-clamp mode). Then we obtained access with the drug delivery electrode (in current clamp with no holding current) while maintaining the original recording.

Fitting and statistical analysis

Fitting of cone noise

The fits to the noise power spectra presented in Figure 1 correspond to empirical fits (and are not unique) constructed as the sum of the power spectrum of the estimated single-photon response and two separate lorentzian functions. In Fourier-space, a single lorentzian function had the following form:

$$L(\omega )=\frac{\alpha }{1+{\left(\frac{\omega }{{\omega }_c}\right)}^2}$$ (5)

where ω_c corresponds to the corner frequency (frequency at which the power has dropped by half) and α is a scaling constant. We obtained fits on a logarithmic scale through built-in Matlab routines (nlinfit and lsqfit) and we assessed the fits through the coefficient of determination (R²). The fit to the average noise from L and M cones at a background illumination of 5000 R*/s (n=6) did not depart from the measured data by more than 1 SEM, and the R² value for the fit was 0.90, with 5 fitting parameters (Fig. 1D). The same observation holds for the average noise from L and M foveal cones recorded in darkness (n=7) with an R² value for the fit of 0.99 (Fig. 1E).

Pharmacology

We determined significance in pharmacological experiments through two-tailed, Student’s t-tests with α ≤ 0.05, by integrating the average power ratios across the specified frequency ranges. We did not perform a sample size calculation prior to experiments. We chose sample sizes to either establish statistical significance of the effects measured (Fig. 3–4) or to provide relative tight confidence intervals on key parameters. Also, we did not have a sufficient number of samples to test whether the data used in t-tests were indeed normally distributed.

For the experiments involving 8′Br-cGMP (Fig. 3) we compared each concentration to the experiments lacking 8′Br-cGMP (Fig. 2F–J) across the 10–600 Hz frequency range and found significant differences for all concentrations (18 μM: n = 10, p = 0.0009, df = 14; 27 μM: n = 4, p = 0.022, df = 8; 100 μM: n = 3, p = 0.00002, df = 7; 200 μM: n = 2, p = 0.001, df = 6; retinas were derived from 12 different animals).

For the experiments involving IBMX (n=10) (Fig. 4) we compared the changes in noise to those produced by a vehicle solution lacking IBMX (n=4) and found significant differences for both the 10–50 Hz (p = 0.0004, df = 12) and the 100–600Hz frequency range (p = 0.0068, df = 12; retinas were derived from 2 different animals).

Signal and noise adaptation

We restricted analysis of signal and noise adaptation to cones that passed several criteria: stability of the holding current, good and stable access resistance, minimal run-down of the light response and high sensitivity to flashes in darkness. We assume that the most sensitive cones we record from are most representative of cone responses in vivo. We estimated single photon responses by delivering non-saturating flashes at a given background, then averaging the resulting responses and scaling by the nominal flash intensity; this procedure provides a linear estimation of the gain of the light response. We then fitted these estimated single-photon responses with the following equation (modified from Ref. 2):

$$f(t)=\alpha \times \left[\frac{{\left(\frac{t}{{\tau }_{\mathit{rise}}}\right)}^4}{1+{\left(\frac{t}{{\tau }_{\mathit{rise}}}\right)}^4}\right]\times \left[e^{-\left(\frac{t}{{\tau }_{\mathit{decay}}}\right)}\right]\times \left[cos\left(\frac{2\pi t}{{\tau }_{\mathit{osc}}}+\phi \right)\right]$$ (6)

We obtained the best-fit values through automatic fitting routines in Matlab (nlinfit and lsqfit). The changes in signal gain were virtually the same whether fits or directly estimated single-photon responses were used, but the fits eliminated uncertainty due to limited data, especially on mid- to high- frequencies (50–600Hz). The changes in signal gain were also near identical when using the response integral or peak amplitude rather than relying on power spectra.

The fits for the changes in signal gain and noise had only a few parameters, which made them suitable for maximum likelihood estimation; the fit values reported are then the most likely values, bounded by values for which the likelihood of the fit dropped to 2.5% of the maximum, i.e. the 95% confidence intervals (95% CI). The fitting of the changes in cone noise (Fig. 5C,D) did not include the highest background, where isolation of the remaining noise from noise in saturating light was difficult and unreliable.

The changes in high frequency cone noise were described by a modified Weber-Fechner function, with an additional free exponent that would accommodate a different slope:

$$\frac{{\sigma }_B}{{\sigma }_D}=\frac{1}{{\left(1+\frac{I_B}{I_0}\right)}^{\eta }}$$ (7)

The best fits for the data in Fig. 5G were I_o=17500 R*/s (95% CI: 15600 – 19400 R*/s) and η=0.29 (95% CI: 0.28 – 0.31).

Threshold versus Intensity Curves

We obtained threshold versus intensity curves shown in Figure 7 by first calculating the spectrum of the signal to noise ratio (SNR) for each background, using the corresponding power spectra of signal and noise and assuming a 200 ms integration time. We then integrated the square root of this SNR spectrum between 0.4 and 8 Hz for rods and between 3 and 600 Hz for cones. The inverse of this integral corresponds to the flash response that matches the noise at a given background, expressed in R*, or in other words, the just-detectable flash or detection threshold.