Locally Linear Embedding (LLE) for MRI based Alzheimer’s Disease Classification

Abstract

Modern machine learning algorithms are increasingly being used in neuroimaging studies, such as the prediction of Alzheimer’s disease (AD) from structural MRI. However, finding a good representation for multivariate brain MRI features in which their essential structure is revealed and easily extractable has been difficult. We report a successful application of a machine learning framework that significantly improved the use of brain MRI for predictions. Specifically, we used the unsupervised learning algorithm of locally linear embedding (LLE) to transform multivariate MRI data of regional brain volume and cortical thickness to a locally linear space with fewer dimensions, while also utilizing the global nonlinear data structure. The embedded brain features were then used to train a classifier for predicting future conversion to AD based on a baseline MRI. We tested the approach on 413 individuals from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) who had baseline MRI scans and complete clinical follow-ups over 3 years with following diagnoses: Cognitive normal (CN; n= 137), stable mild cognitive impairment (s-MCI; n=93), MCI converters to AD (c-MCI, n=97), and AD (n=86). We found classifications using embedded MRI features generally outperformed (p < 0.05) classifications using the original features directly. Moreover, the improvement from LLE was not limited to a particular classifier but worked equally well for regularized logistic regressions, support vector machines, and linear discriminant analysis. Most strikingly, using LLE significantly improved (p = 0.007) predictions of MCI subjects who converted to AD and those who remained stable (accuracy/sensitivity/specificity: = 0.68/0.80/0.56). In contrast, predictions using the original features performed not better than by chance (accuracy/sensitivity/specificity: = 0.56/0.65/0.46). In conclusion, LLE is a very effective tool for classification studies of AD using multivariate MRI data. The improvement in predicting conversion to AD in MCI could have important implications for health management and for powering therapeutic trials by targeting non-demented subjects who later convert to AD.

1. Introduction

Machine learning methods have attracted considerable interest in recent years for analyzing neuroimaging data. The multivariate nature of machine learning algorithms overcomes limitations of traditional methods by using available information simultaneously to understand how variables jointly characterize data structures. One area of neuroimaging research where the use of machine learning has been growing rapidly is the prediction and early detection of Alzheimer’s disease (AD), the most frequent cause of age-related dementias (Brookmeyer et al., 2007). Machine learning has been explored for its potential to uncover subtle patterns of distributed brain tissue loss in AD that traditional methods may fail to detect (Stonnington et al., 2010; Vemuri et al., 2008; Fan et al., 2008; Filipovych and Davatzikos, 2011; Casanova et al., 2011; Davatzikos, 2004). In a typical example of machine learning applied to brain MRI, an algorithm is trained on a set of MRI features, such as regional volumes and cortical thickness, to create a classifier which predicts the correct diagnostic outcome for new observations. To reduce the high dimensionality of the MRI features and to stabilize predictions, shrinkage methods, such as principal components analysis or partial least squares have sometimes been added prior to the training step (Franke et al., 2010; Pelaez-Coca et al., 2011; Teipel et al., 2007; Phan et al., 2010). MRI data pose an especially challenging problem for predictions because of the difficulty in finding a good representation of brain features that makes them easily extractable and reveals their essential structure. The problem is perhaps most evident when it comes to choosing the optimal kernel function, or avoiding kernels all together, when transforming the data for feature extraction. Unless the transformation for a good representation of the brain MRI features is known a-priori, any arbitrary choice of remapping could potentially result in a loss of information and in inferior results.

We propose embedding the data into a system of linear coordinates of fewer dimensions prior to training a classifier to alleviate the problem of finding a good data representation for MRI based predictions. To relax assumptions of conventional approaches for reducing dimensionality, such as global linearity in principal components analysis (PCA) or particular kernel shapes in supervised learning algorithms (Westman et al., 2011; Koikkalainen et al., 2011; Eskildsen et al., 2013), we tested the use of local linear embedding (LLE) (Roweis and Saul, 2000). LLE neither relies on linear transformations nor requires supervised learning. The algorithm can transform the brain MRI data into a linear space of fewer dimensions by capturing local linear symmetries in the data while learning from the global nonlinear data structure. We also predict that accuracy will become less dependent on the particular choice of classifiers once the data are linearly embedded. Since LLE was introduced in 2000, the algorithm has been used successfully in a wide range of applications, including image classification (Ridder and Duin, 2002; Zheng and Jie, 2005), feature fusion (Sun et al., 2010), remote sensing (Ma et al., 2010), and face recognition (Sun et al., 2010; Chang and Yeung, 2006; Chen et al., 2007; Geng et al., 2005). More recently, LLE has also been used in MRI, e.g. for shape analysis of the hippocampus in AD (Yang et al., 2011), breast lesion segmentation (Akhbardeh and Jacobs, 2012), functional MRI (Chaillou et al., 2008; Mannfolk et al., 2010) and diffusion tensor imaging (Goh and Vidal, 2008). The overall goal of our study was to explore whether LLE benefits the classification of individuals with various levels of cognitive deficits, including AD, based on multivariate brain MRI data. Specifically, using baseline brain MRI data we aimed to determine the extent to which LLE improves the differentiation between subjects with mild cognitive impairments (MCI) who later decline to AD (within 3 years of baseline MRI) and subjects who remain stable in comparison to traditional methods that do not use LLE.

The rest of this paper is organized as follows. In Section 2, we describe the experimental data and also explain the theoretical basis of LLE in greater detail. In Section 3, we compare classifications using embedded MRI features of either regional brain volume, cortical thickness, or volume and thickness together, with classifications using the features directly. We also compare the classification performance from an LLE for different standard classifiers, i.e. elastic nets (EN) regularized regressions, support vector machine (SVM), and linear discriminant analysis (LDA). In Section 4, we interpret the findings and discuss limitations of the study.

2. Methods

2.1. Subjects and MRI

Subjects

Data used in the preparation of this article were obtained from the Alzheimers Disease Neuroimaging Initiative (ADNI) database (adni.loni.ucla.edu).¹

For the purpose of this study, we included all subjects recruited between 2005 and 2008 from the ADNI database who had 1.5T MRI scans, had successful evaluations of their MRIs using FreeSurfer (version 4.4) (Reuter et al., 2012), and also had a diagnosis over 3 years consistent with either stable cognitive normal (CN), stable mild cognitive impairment (s-MCI), MCI converters to AD (c-MCI), or AD. Subjects were excluded if their diagnosis reverted, e.g. MCI reversion to CN or AD reversion to MCI, or their MRI data was of insufficient quality for FreeSurfer processing. The final sample included 413 subjects total of which 137 were CN, 93 s-MCI, 97 c-MCI and 86 AD. The study codes of the subjects and other relevant information are provided as supplementary material to give readers the opportunity for direct comparisons with other methods. The subjects also had a battery of clinical and cognitive assessments each time they had their MRI scans. Each subject’s cognitive evaluation included: 1) The minimental state examination (MMSE) (Folstein et al., 1975), which provides a global measure of mental status and 2) the Alzheimer’s disease assessment scale-cognitive subscale (ADAS-Cog) with 11 test items, which provides a summary measure of disease severity by evaluating the most characteristic AD symptoms, such as disturbances in memory, language, attention and judgment (Mohs et al., 1997). We also used the clinical dementia rating sum of boxes (CDR-SOB) scale as a measure of cognitive and functional impairment (Morris, 1993). The CDR-SOB is a well validated instrument that assesses three domains of cognition (memory, orientation, judgement) and three domains of function (community affairs, home/hobbies, personal care) using structured interviews. More details about the tests can be found on the ADNI website www.loni.ucla.edu/ADNI. The average time of MCI conversion to AD was 19±8 months from baseline visit. A summary of the demographic and neurocognitive data of each group is provided in Table 1.

Table 1.

Group demographics and clinical summary

	CN	s-MCI	c-MCI	AD	p-value a	p-value b
No. of subjects	138	93	97	86
Male (%)	59.7	69.1	61.8	53.5	0.01c	0.01c
APOE e4 carrier (%)	28.3	48.4	68.0	68.6	< 0.001 c	0.14c
Baseline
Age (years)	76±5	75±7	75±7	75±8	0.6	0.78
MMSEd	29.2±1	27.4±2	26.7±2	23.1±2	< 0.001	0.02
ADAS-Cog11e	6±3	10±4	13±4	19±6	< 0.001	< 0.001
LIMMTOTAL f	14±3	8±3	7± 3	3±3	< 0.001	0.02
LDELTOTAL g	13±3	4±3	3±3	1±2	< 0.001	< 0.001
CDR-SOB h	0±0	1±1	2±1	4±1	< 0.001	0.001
Annual rate of change
MMSE(×10−3)	−0.1±1	−1±3	−5±4	−5±7	< 0.001	< 0.001
ADAS-Cog11	0±3	1±6	5±8	7±9	< 0.001	< 0.001
LIMMTOTAL	1±2	0±2	−1±1	0±1	< 0.001	< 0.001
LDELTOTAL	1±2	1±2	−1±1	0±1	< 0.001	< 0.001
CDR-SOB(×10−3)	0±1	1±1	2±2	3±4	< 0.001	< 0.001

^ap-values indicate effects across the groups.

^bp-value indicate differences between s-MCI and c-MCI. The p-values for all pair-wise comparisons are provided in Supplementary Material.

^cUsing Fisher exact test; all other tests using analysis of variance (ANOVA) (Fisher, 1925);

^dMMSE: Mini-mental state examination score (Folstein et al., 1975); total score range 0–30 with lower scores indicate greater cognitive impairment.

^eADAS-Cog11: Alzheimer’s Disease Assessment Scale-cognitive subscale with 11 items (Mohs et al., 1997); total score range 0–70 with larger scores indicate greater impairment.

^fLIMMTOTAL: Memory score of immediate recall, maximal range 0–24, lower score indicate greater impairment (Wechsler, 2008).

^gLDELTOTAL: Memory score of delay recall, maximal range 0–25, lower score indicate greater impairment.

^hCDR-SOB: Clinical dementia rating sum of boxes, maximal range 0–18, higher score indicate greater impairment (Morris, 1993).

MRI acquisition and brain morphometry

The subjects underwent at each site the standardized 1.5 T MRI protocol of ADNI as described in http://www.loni.ucla.edu/ADNI/Research/Cores/index.shtml. Briefly, the protocol includes T1-weighted MRI based on a sagittal volumetric magnetization prepared rapid gradient echo (MP-RAGE) sequence (echo time/repetition time TE/TR= 4/9ms, 8° flip angle, 0.94×0.94×1.2 mm nominal resolution). Image quality and pre-processing was performed at a designated MRI center, as described in (Jack et al., 2008). The images were intensity-normalized, aligned to a brain atlas, skull-stripped, and segmented into regional volume using freely available FreeSurfer software, version 4.4 (http://surfer.nmr.mgh.harvard.edu/). For a more complete description of the FreeSurfer processing steps, see (Fischl et al., 2002; Fischl, 2004; Reuter et al., 2012). The outcome measures of the FreeSurfer work flow were 94 automatically labeled anatomical regions including cortical gyri and subcortical structures, yielding the volume of 94 brain regions and average cortical thickness of 68 regions for each subject. Accuracy of anatomical labeling was visually rated by experienced staff. If quality criteria were not met, the data were excluded from the analysis.

2.2. Locally Linear Embedding

Consider the region volume and cortical thickness across brain regions and subjects are arranged in matrix format X̂ ∈ R^n×D, where n is the number of subjects and D is the number of brain features. Because high-dimensional features often bear many redundancies and correlations that hide important relationships, we seek a more compact representation of X̂ prior to the classification of the subjects. In more detail, we use LLE to map the high-dimensional manifold X̂ ∈ R^n×D to one of lower dimensions Y = {y₁, y₂,…,y_n} ∈ R^n×d, where d < D. The dimension reduction is accomplished in LLE based on the the principle idea that each point in a manifold and its nearest neighbors lie on or close to a patch whose local geometry is approximately linear even if the manifold is globally nonlinear. By recovering each point from its neighbors, LLE yields low-dimensional, neighborhood-preserving embeddings of the high-dimensional inputs, while learning from global relationships.

The LLE algorithm consists of three main steps:

1. Assign K neighbors to each data point x̂_i = x̂_i1, x̂_i2,…,x̂_iD. In the context of our study, each point represents a particular subject who is characterized by her/his individual features of brain regional volume and/or cortical thickness. Most commonly, nearest neighbors are defined using Euclidean distance or normalized dot products. We use the nearest neighbors in Euclidean space in our study.

2. Compute the weights W_i that best recover linearly the subject’s data x̂_i from the nearest neighbors by minimizing the error function:

   $${\tilde{W}}_i=\text{arg min}{\parallel {\widehat{\mathbf{x}}}_i-\sum _{k\in N(i)}{w}_{ik}{\widehat{\mathbf{x}}}_k\parallel }^2.$$ (1)

   In order to linearly reconstruct data point x̂_i from its nearest neighbors, there are several constraints on the weights: Σ_k w_ik = 1, and w_ik = 0 if k ∉ N(i).N represents nearest neighbors.
3. Compute the low-dimensional embeddings y_i that best estimate the local data ỹ_i given the weights W_i:

   $${\tilde{\mathbf{y}}}_i=\text{arg min}{\parallel {\mathbf{y}}_{\mathbf{i}}-\sum _{\mathbf{k}}{\mathbf{w}}_{\mathbf{i}\mathbf{k}}{\mathbf{y}}_{\mathbf{k}}\parallel }^{\mathbf{2}}$$ (2)

   with respect to y_i ∈ R^d. The cost function can be rewritten as:

   $$\tilde{Y}=\text{arg min}{Y}^{T}MY,$$ (3)

   where M = (I – W)^T(I – W) and with the following two constraints on Y. First, Y^TY = I, so that the solution is of rank d. Second, Σ_i Y_i = 0, to ensure that the embedding is centered on the local origin of the original feature space coordinates. The third step can be reduced to an optimization problem according to:

   $$\tilde{Y}=\text{arg min}(Y^{T}MY),s.t.\frac{1}{n}Y{Y}^T=I.$$ (4)

This is an eigenvalue problem, and also the step of LLE learning the global structure of the data. All the eigenvectors of M are solutions of Y, but the eigenvectors corresponding to the smallest eigenvalues minimize the cost function in Eq. 2. After discarding the smallest eigenvalue, which will always be zero, the next n – 1 smallest eigenvalues are used as dimensions of the transformed data (the smallest given the first dimension for each point in the data, the next smallest the 2nd dimension and so on).

After LLE, three different classifiers were compared for performing pair-wise classifications. We trained regularized logistic regressions with elastic nets (EN)(Hastie et al., 2009), support vector machines (SVM) (Cortes and Vapnik, 1995) as well as a linear discriminant analysis (LDA) to predict future diagnosis (within 3 years) from baseline MRI scans. Since LLE provides embedded features globally in linear coordinates, we limited the tests to linear classifiers, including SVM with a linear kernel only. We implemented the EN classifier using the MATLAB toolbox Glmnet (Friedman et al., 2010) and SVM and LDA using the respective MATLAB build-in functions. The optimal thresholding algorithm by Otsu (Otsu, 1979) was used to obtain binary classification results. Although automated methods for the optimal numbers of neighbors K and corresponding dimensionality D have been proposed (Kayo, 2006), in this study we choose to tune K and D by cross-validation in combination with cross-validations of the parameters of the linear classifiers. We used leave-one-out (LOO) cross validation and evaluated classification performance in terms of a receiver operator characteristic (ROC) analysis for parameter optimization. Measures of sensitivity and specificity, followed by computation of overall classification accuracy were obtained. Note, LLE can remain outside the LOO loop, since the algorithm performs dimension reduction unsupervised, i.e. without the requirement of labeling a training set. LOO was performed exactly once for each subject and per comparison hence no bias was introduced at the subject level. For each classification problem, the cross-validated results were then used to build a ROC curve using the pROC package in R and augmented by a stratified bootstrap with 2000 repetitions to obtain a distribution.

3. Experimental Results

The demographic and clinical characteristics of the study groups are shown in Table 1. Differences between the groups were tested using t-tests or Chi-squared tests, as appropriate. Age and gender variations across the groups were well matched. As expected, the groups differed significantly in their respective levels of cognitive deficits at baseline as well as in the annual rates of cognitive decline, based on MMSE and ADAS-Cog11 scores.

Visualization

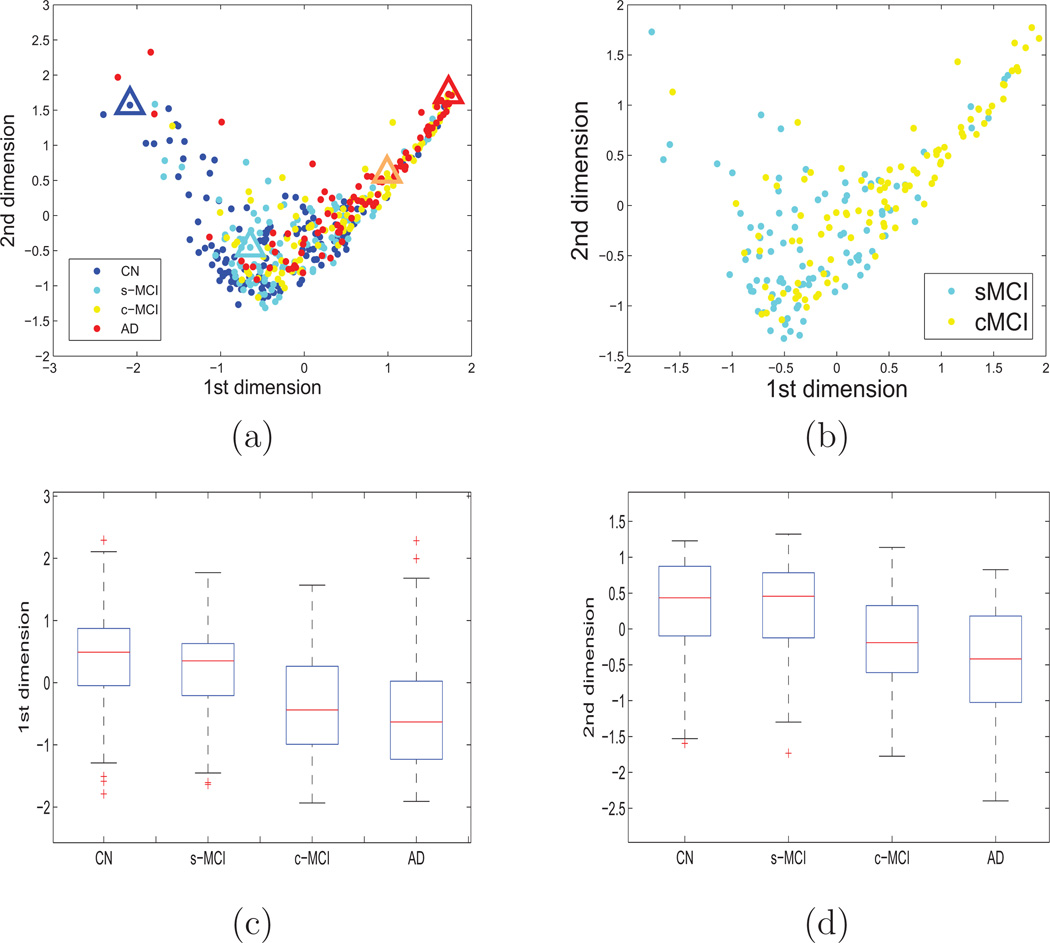
Figure 1(a) shows the locations of all 413 subjects in an embedded feature space of 162 brain features, which include 94 regional brain volume and 68 cortical thickness values, reduced to two dimensions. The figure demonstrates a distinct clustering of the healthy subjects shown in blue and the AD patients shown in red. Furthermore, the c-MCI subjects (yellow) appear on average localized near the AD patients, whereas s-MCI subjects (cyan) appear closer to the CN subjects. The separation between s-MCI and c-MCI subjects in LLE space is depicted in more detail in Figure 1(b). In addition, the distributions of the subject locations along the first and second LLE dimension are depicted in Figure 1(c) and (d), respectively and separately by group.

Figure 1.

Visualization of all 413 subjects in LLE space based on brain volume and cortical thickness. Only the first two dimensions of the LLE space are shown for visualization purpose. Color indicates diagnosis (blue = normal control, cyan = s-MCI, yellow = c-MCI, and red = AD). Part (a) shows all four goups’ subjects in the embedded space, (b) depicts the separation between s-MCI and c-MCI in greater detail; (c) and (d) show the distribution of subject locations by group along the first and second LLE dimension, respectively.

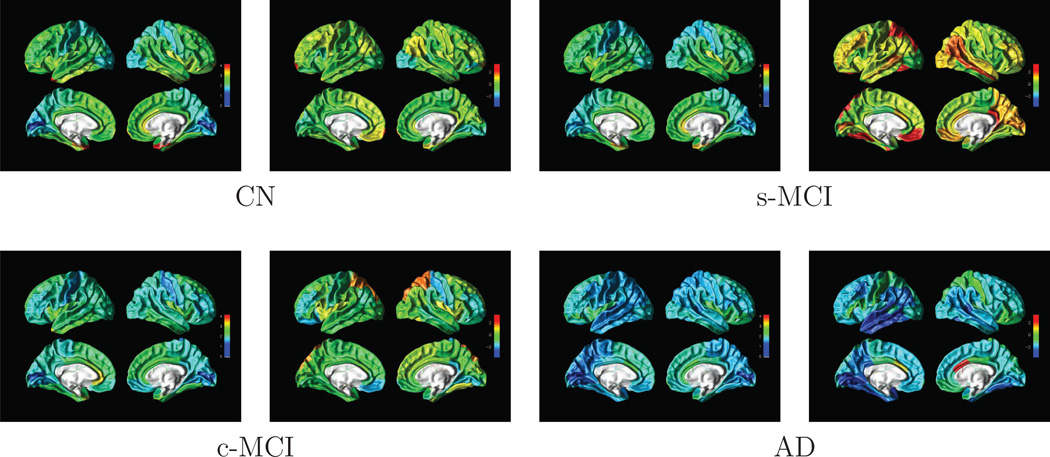
To demonstrate benefit of LLE for data visualization, we selected an example subject from each group based on the subject’s LLE coordinates and then compared the patterns of regional brain volume and cortical thickness. The example subjects were selected based on their extreme location in the embedded space within each population cluster to visualize the variability in MRI features for the classification problem. The triangles in Figure 1 indicate the locations of these example subjects in LLE space. The patterns of cortical thickness and regional brain volume of each of these subjects are depicted on surface rendered brain plots in Figure 2. Note, however, that from the locations in LLE space alone it remains uncertain whether the differences are related to the subjects’ diagnosis or individual variability in atrophy. Cooler colors indicate a thinner than average cortical thickness or smaller than average volume whereas warmer colors indiate a thicker than average cortical thickness or larger than average volume. Together, Figures 1–2 indicate that the locations of the subjects in LLE space reflect generally their differences in cortical thickness and regional brain volumes. Specifically, comparing the surface rendered plots of the control subject and AD patient shown in Figure 2(a), we can see a substantial thinning in parietal lobe, temporal lobe and temporal lobe in the AD patient compared to the control subject. Similarly, comparing the plot of the c-MCI subject in Figure 2, whose location in LLE space is closer to that of the AD patient than to the CN subject as well as to s-MCI subject, has in general a thinner cortex than the CN and s-MCI subjects but still a thicker cortex than the AD patient. In particular, this c-MCI subject has a thicker temporal cortex than the AD patient, while differences in other regions between the two are more subtle. Also of note in these plots from 4 individual subjects is the level of individual variability in atrophy.

Figure 2.

Surface rendered illustrations of cortical thickness and z-score normalized regional volumes from four example subjects, one from each group. The location of each subject in LLE space is indicated by a color coded triangle in Figure 1. For each subject, the left panel illustrates cortical thickness and the right panel illustrates normalized regional volumes. Cooler colors indicate a thinner cortex and a smaller regional volume than average; whereas warmer colors indicate a thicker cortex and a larger regional volume than average.

Classifications

Tables 2– 4 summarize group classifications with and without LLE embedding, separately for the three different classifiers. Classifications differentiating s-MCI from c-MCI patients based on baseline MRI are highlighted. Overall, classifications using LLE features performed significantly better (p<0.05) or at least as good as classifications that used the features directly. Most importantly, almost all predictions of the MCI subjects who later converted to AD and those who remained stable became reliable with the use of LLE (exception SVM+LLE using thickness, see Table 3 in comparison to the same classifications without LLE that performed not better than by chance. The improvement in classification was driven by the LLE transformations of brain volume features and to a lesser extent by cortical thickness. Although it may seem a surprise that the classification between AD and CN based on linear SVM and brain volumes was not better than by chance (see Table 3), one needs to note that we deliberately chose a linear kernel and accepted irrelevant features in the SVM for a fair comparison with LLE. Together, these steps may have sacrificed SVM performance.

Table 2.

Accuracy of classifications based on elastic net regression with and without LLE feature embeddings

		CN vs. s-MCI			CN vs. c-MCI			CN vs. AD			s-MCI vs. c-MCI			s-MCI vs. AD			c-MCI vs. AD
		ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE
Volumes	EN	0.56a	0.59	0.54	0.78	0.79	0.77	0.82	0.85	0.80	0.46a	0.48	0.44	0.59a	0.70	0.48	0.50a	0.45	0.54
	EN+LLE	0.64	0.53	0.72	0.81	0.80	0.82	0.87	0.80	0.91	0.69	0.66	0.72	0.77	0.85	0.69	0.51a	0.52	0.51
	p-valueb	0.09			0.02			0.01			<0.001			<0.001			0.62
Cortical thickness	EN	0.55a	0.53	0.57	0.75	0.69	0.80	0.83	0.78	0.86	0.56a	0.53	0.59	0.67	0.79	0.56	0.59a	0.69	0.51
	EN+LLE	0.62	0.57	0.66	0.78	0.79	0.78	0.85	0.79	0.89	0.61	0.48	0.74	0.71	0.78	0.65	0.58a	0.70	0.48
	p-valueb	0.09			0.03			0.09			0.54			0.37			0.39
Thickness +volumes	EN	0.55a	0.53	0.57	0.75	0.67	0.80	0.80	0.73	0.84	0.56a	0.65	0.46	0.60	0.59	0.61	0.48a	0.67	0.30
	EN+LLE	0.64	0.65	0.63	0.82	0.81	0.82	0.90	0.86	0.93	0.68	0.80	0.56	0.75	0.77	0.73	0.56a	0.51	0.61
	p-valueb	0.01			<0.001			<0.001			0.007			<0.001			0.02

^aindicates classification is not better than by chance (p>0.05), whereas no superscripts indicate a significant classification;

^bp-value of improvement with LLE compared to non-LLE.

Table 4.

Accuracy of classifications based on linear discriminant analysis with and without LLE feature embeddings

		CN vs. s-MCI			CN vs. c-MCI			CN vs. AD			s-MCI vs. c-MCI			s-MCI vs. AD			c-MCI vs. AD
		ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE
Volumes	LDA	0.56a	0.60	0.54	0.77	0.75	0.78	0.83	0.85	0.82	0.46a	0.48	0.44	0.58a	0.66	0.51	0.49a	0.45	0.53
	LDA+LLE	0.59	0.56	0.61	0.81	0.79	0.83	0.84	0.77	0.89	0.61	0.70	0.62	0.67	0.72	0.62	0.45a	0.47	0.43
	p-valueb	0.59			0.01			0.14			0.08			0.05			0.88
Cortical thickness	LDA	0.55a	0.54	0.57	0.73	0.66	0.78	0.84	0.81	0.86	0.57a	0.54	0.60	0.66	0.80	0.53	0.56a	0.58	0.55
	LDA+LLE	0.69	0.67	0.71	0.78	0.79	0.77	0.85	0.79	0.77	0.65	0.52	0.56	0.66	0.71	0.61	0.58a	0.70	0.48
	p-valueb	0.002			0.07			0.61			0.04			0.79			0.66
Thickness +volume	LDA	0.55a	0.56	0.54	0.67	0.69	0.65	0.69	0.62	0.73	0.51a	0.57	0.45	0.58a	0.63	0.54	0.45a	0.43	0.46
	LDA+LLE	0.51a	0.48	0.49	0.75	0.69	0.80	0.89	0.86	0.91	0.68	0.82	0.53	0.65	0.70	0.60	0.57a	0.51	0.63
	p-valueb	0.89			<0.001			<0.001			0.01			0.03			0.15

^aindicates classification is not better than by chance (p>0.05), whereas no superscripts indicate a significant classification;

^bp-value of improvement with LLE compared to non-LLE.

Table 3.

Accuracy of classifications based on support vector machine with and without LLE feature embeddings

		CN vs. s-MCI			CN vs. c-MCI			CN vs. AD			s-MCI vs. c-MCI			s-MCI vs. AD			c-MCI vs. AD
		ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE	ACR	SEN	SPE
Volume	SVM	0.55a	0.60	0.52	0.52a	0.40	0.60	0.53a	0.49	0.55	0.51a	0.54	0.48	0.50a	0.56	0.45	0.49a	0.38	0.58
	SVM+LLE	0.64	0.52	0.72	0.81	0.80	0.82	0.85	0.86	0.85	0.67	0.74	0.59	0.76	0.86	0.67	0.54a	0.86	0.67
	p-valueb	0.08			0.01			0.03			0.001			<0.001			0.67
Cortical thickness	SVM	0.57a	0.46	0.64	0.72	0.66	0.77	0.86	0.79	0.91	0.56a	0.52	0.61	0.72	0.78	0.66	0.60	0.62	0.58
	SVM+LLE	0.62	0.53	0.68	0.78	0.82	0.74	0.84	0.78	0.88	0.56a	0.45	0.58	0.69	0.71	0.67	0.56a	0.72	0.41
	p-valueb	0.1			0.03			0.85			0.85			0.5			0.34
Thickness +volume	SVM	0.45a	0.65	0.32	0.52a	0.41	0.60	0.50a	0.48	0.51	0.53a	0.66	0.49	0.57a	0.48	0.51	0.57a	0.48	0.66
	SVM+LLE	0.64	0.58	0.67	0.80	0.72	0.86	0.90	0.87	0.92	0.66	0.75	0.56	0.73	0.73	0.72	0.57a	0.48	0.65
	p-valueb	0.01			<0.001			<0.001			0.008			<0.001			0.90

^aindicates classification is not better than by chance (p>0.05), whereas no superscripts indicate a significant classification

^bp-value of improvement with LLE compared to non-LLE.

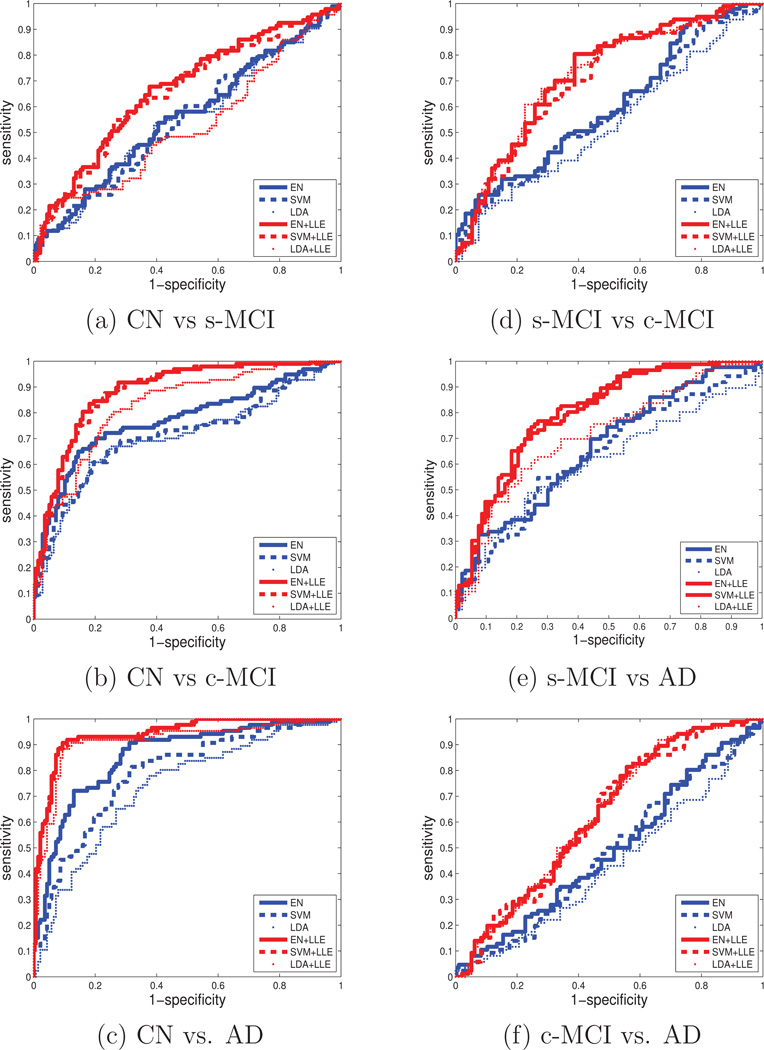
A summary illustration of the improvements with LLE is shown in Figure 3, separately for each pairwise classification. ROC curves are shown from cross-validated classifications, separately for each classifier (EN, SVM, or LDA) when both regional volume and cortical thickness features were used together with and without LLE. The figures indicate classifications using LLE improved across the board. The figure also indicates that the improvements were achieved regardless of the type of classifier.

Figure 3.

ROC curves of pairwise classifications with and without feature embeddings by LLE and separately using as classifier either elastic net (EN) regularized linear regression, a support vector machine (SVM) with a linear kernel, or linear discriminant analysis (LDA). The features are brain regional volume and cortical thickness used together. Accuracy of the classifications generally improves significantly with LLE features, regardless which classifier EN, SVM or LDA is used. FPR stands for false positive rate, and TPR stands for true positive rate.

Since manifold learning can be sensitive to sample size, we also tested the robustness of LLE with fewer samples. Specifically, we repeated the predictions of MCI conversion with 20% and 50% fewer samples by removing subjects at random while still maintaining the group balance. We performed the tests using the EN classifier with or without LLE. Accuracy (and similarly AUC) decreased progressively from 0.68 at 100% of the sample to as low as 0.60 at 50% (AUC decrease: 0.72 at 100% to 0.63 at 50%), as expected. However, the decline was not worse and still remained better in comparison to predictions without LLE with fewer samples (accuracy change: 0.51 at 100% and 0.57 at 50%; AUC change: 0.53 at 100% and 0.61 at 50%).These results indicate that LLE does not exacerbate the sensitivity of manifold learning to sample size.

Lastly, we compared the benefit of LLE for predicting MCI conversion with traditional MRI and clinical methods in terms of accuracy and AUC values. The MRI methods included feature reduction by PCA, a nonlinear SVM using a Gaussian kernel, and selection of region-of-interest (ROI), e.g. the hippocampus or entorhinal cortex. The clinical measures included MMSE and ADAS-Cog11 scores. The results are summarized in Table 5 and ranked from best to worst accuracy. The outcome shows that LLE performance ranked at the top.

Table 5.

Comparison of MRI and clinical measures for prediction of MCI conversion to AD

Method	Measures	Classifier	ACR	AUC	p-value
MRI: whole brain	volume+thickness	LLE+LDA	0.68	0.72	–
MRI: ROI	hippocampus		0.66	0.69	0.19
	hippocampus +entorhinal corex	LDA	0.65	0.69	0.26
	entorhinal cortex		0.61	0.62	0.08
MRI: whole brain	volume+thickness	SVM (Gaussian)	0.61	0.62	< 0.001
neuropsychological scores	ADAS-Cog11+LDEL+CDR+MMSE		0.62	0.69	0.27
	ADAS-Cog11		0.59	0.67	0.14
	LDEL	LDA	0.60	0.61	0.01
	CDR		0.56	0.52	< 0.001
	MMSE		0.57	0.54	< 0.001
MRI: whole brain	volume+thickness	SVM (linear)	0.53	0.58	0.002
		PCA+LDA	0.51	0.53	< 0.001

The results are ranked by accuracy values from high to low.

p-values indicate prediction performance compared with LLE.

All predications used a LDA classifier. ROI = region of interest; PCA = principal component analysis; all other abbreviations are explained in the text.

4. Discussion

In this study, we presented a new approach for classification which transformed MRI features to a linear space of fewer dimensions using LLE, prior to training a classifier. We applied this approach to high-dimensional classifications, especially for the differentation between MCI subjects who remain stable and those who decline to AD based on brain volume and cortical thickness measurements at baseline. The three main findings were: First, LLE generally improved classifications, implying that conventional classification methods that exploited original features without embedding, were not optimal. Second, the improvements in classifications with LLE worked equally well for three types of frequently used linear classifiers: EN, SVM and LDA. This result implied that the benefit of LLE was generally valid and not confined to a particular classifier class. Third, and perhaps most important clinically, was that LLE significantly improved the differentiation between MCI subjects who converted to AD within 3 years from baseline MRI and those who remained stable. In contrast, the same differentiation performed without LLE achieved outcomes that were not better than by chance. Taken together, the results suggested that machine learning methods of AD classification using brain MRI should incorporate LLE.

The finding of a general improvement in high-dimensional classifications of MCI and AD when embeddings of the features are used implies that alterations of regional brain volume and cortical thickness as seen on MRI can involve inherently nonlinear feature structures. Training linear classifiers directly on MRI features may therefore under-utilize the classification power, since these classifiers cannot capture nonlinearity. One might argue that even nonlinear classifiers may sacrifice classification power, if the nonlinear feature structure is not adequately modeled. LLE, on the other hand, generally benefits classifications not only by reducing the dimensionality of features but also by embedding them into linear coordinates while learning their potential nonlinear characteristics. In the context of brain imaging, linear embedding is consistent with the reasonable assumption that subjects who are clinically similar will also have similar distributions of brain features even if the features across all subjects is globally nonlinear. LLE is therefore crucial for maximizing classifications based on structural MRI data. This point is further supported by our finding that LLE outperformed popular traditional MRI methods, including PCA and nonlinear SVM.

However, LLE is not the only algorithm for linear embedding. Various other techniques have been proposed over the years, including high-dimensional scaling (Lespinats et al., 2007), maximum variance unfolding (Weinberger and Saul, 2004), Isomap (Tenenbaum et al., 2000), Laplacian eigenmaps (Belkin and Niyogi, 2001), and nonlinear PCA (Scholz et al., 2005). These algorithms can differ in performance, depending on the data dimensionality, noise, and sampling uniformity among other factors. The extent to which LLE performs better or worse than other embedding algorithms will be a subject of future research. In this study, we choose LLE for two reasons. First, there is only one parameter which needs to be tuned in LLE: the number of nearest neighbors. Although algorithms for automatic optimal tuning this parameter are available (Kayo, 2006), we performed optimization by cross-validation to demonstrate the robustness of LLE. Second, LLE, being rooted in the concept of unsupervised statistical learning, has a non-iterative solution, thus avoiding the convergence to local minima that often plaque iterative techniques (Roweis and Saul, 2000). In addition, we verified that LLE does not exacerbate the sensitivity of manifold learning to sample size.

Compared to other structural MRI studies predicting conversion to AD, LLE performance was among the best (Chupin et al., 2009; Querbes et al., 2009; Davatzikos et al., 2011; Westman et al., 2011; Wolz et al., 2011; Cho et al., 2012; Eskildsen et al., 2013; Suplber et al., 2010). Findings of conversion to AD over a period of at least 30 months are summarized in Table 6. It shows that our LLE approach was only surpassed by studies which had either a much smaller sample size (Ferrarini et al., 2009; Plant et al., 2010) or a much smaller ratio of non-converters to converters (Misra et al., 2009; Koikkalainen et al., 2011). Although comparisons between studies are limited since the number of subjects and processing methods vary, we like to point out that in our study in contrast to most others - the ratio of converters to non-converters was much more balanced. A greater balance is expected to yield better measures of accuracy, since an unbalance can induce bias toward the minority group (Imam et al., 2006). Let alone, we used a much larger sample size (93+97=190), compared with the other three studies. The accuracy with LLE was also surpassed by two MRI studies that used hippocampal shape as predictor for conversion to AD. Although one of the studies (Ferrarini et al., 2009) had a much smaller sample size compared to our study and the other (Costafreda et al., 2011) had only 12 months follow-up, their findings suggest that shape is potentially an addition feature to volume and thickness for LLE. The only other MRI reports (not listed in Table 6) which outperformed LLE were studies that used MRI together with either other imaging modalities (Zhang and Shen, 2012), or cognitive scores, or CSF biomarkers (Hinrichs et al., 2011; Zhang et al., 2011; Vemuri et al., 2008).

Table 6.

Other MRI studies predicting MCI conversion beyond 30 months.

Study	Data open source	Data type	Region	sMCI/cMCI	Follow-up (months)	ACR	SEN	SPE
Misra et al. (2009)	ADNI	VBM (GM and WM)	Whole Brain	76/27	0–36	82%	-	-
Ferrarini et al. (2009)	N/A	Shape	Hippocampus	15/15	0–33	80%	90%	80%
Plant et al. (2010)	N/A	VBM	Whole Brain	15/9	0–30	75%	56%	87%
Koikkalainen et al. (2011)	ADNI	TBM	Whole Brain	215/154	0–36	72%	77%	71%
Our Study	ADNI	VBM	Whole Brain	93/97	0–36	69%	66%	72%
Wolz et al. (2011)	ADNI	TBM+CTH+VBM+CSF	Whole Brain	238/167	0–48	68%	67%	69%
Suplber et al. (2010)	AddNeuroMed+ADNI	CTH+VBM	Whole Brain	261/173	0–36	68%	70%	67%
Eskildsen et al. (2013)	ADNI	CTH	Whole Brain	227/161	0–36	67%	66%	68%

AddNeuroMed is an Integrated Project funded by the European Union Sixth Framework program.

VBM represents voxel based morphometry, GM: gray matter, WM: white matter, TBM: tensor based morphometry, CTH: cortical thickness, CSF: cerebrospinal fluid.

The comparison of LLE performance with ROI methods is also interesting and worth a discussion. Some MRI studies have questioned the benefit of machine learning methods over ROI methods for predicting AD (Cuingnet et al., 2011; Chu et al., 2012). Our results are generally in agreement with these studies in that using the volume of the hippocampus (or the entorhinal cortex) alone for AD prediction remained competitive to using LLE. On the other hand, the classification accuracy for AD patients decreased substantially in our data using the hippocampus alone compared to classifications using LLE. The result suggests that ROI methods may not work always well across various disease stages. For intermediate disease stages, the use of multiple ROIs has been proposed as alternative to using the hippocampus alone (Cuingnet et al., 2011). Here, however, LLE has a conceptual advantage over multiple ROI methods, since the algorithm learns unsupervised global MRI features and can therefore detect changes in the brain without specific input how the disease spreads.

Aside from the advantage of LLE for MRI based predictions, LLE also outperformed predictions based on the clinical MMSE and ADAS-Cog11 scores. The result further supports the benefit of LLE for predicting conversion and also justifies the use of this sophisticated methodology as substitute for simpler clinical tests. Whether or not the use of LLE helps to improve such predictions over longer periods than 36 months, when disease progression is slower and MRI effects are presumably more subtle, needs to be determined.

Another observation requiring further investigation is that LLE improved classification accuracy unequally for volume and cortical thickness with volume often outperforming cortical thickness in classifications. The reason for this outcome is not clear but there are several explanations. One explanation is that there is much less global structure in the thickness data than in volumes to regulate the learning step in LLE according to Equation 4. This can result in the diminished separation of subjects who otherwise differ in cortical volume.

A potentially practical benefit of LLE is that it can help readers to perceive similarities in high-dimensional data from visualization. In the context of this study and as illustrated in Fig. 1, individuals can be localized relative to others in an embedded feature space of few dimensions. As seen in Fig. 1 the c-MCI subjects appear on average at locations close to AD patients, whereas s-MCI subjects appear at locations closer to controls. The visualization of the features in a low-dimensional embedded space can also help to design more efficient classification schemes by keeping only the most important dimensions, e.g. the ones that hold the most information to identify subjects.

One limitation of the study is lack of confirmed diagnosis of AD. Another limitation is that Freesurfer was used for MRI pre-processing, which involved excluding data of substandard quality. The extent to which LLE performs better or worse in combination with other pre-processing software that has less stringent quality requirements than Freesurfer warrants further tests. In addition, LLE sacrifices simple means to track which brain features contributed to the classifications. Recovering this critical information is in principle feasible by exploring the distribution of the weights in Eq. 1, but this requires further investigations and it is beyond the scope of the present work. In addition, the dimensionality of features was restricted to the number of anatomical brain regions that FreeSurfer provides. Potentially, all MRI voxels or vertices could be used for a more comprehensive classification analysis. The performance of LLE as dimensionality increases is also a subject for future investigations. Although the LLE approach is promising, more studies are warranted to understand in greater detail the susceptibility of LLE to outliers, skewed distributions, and noise in MRI data. Improved LLE versions that are more robust to noise and outliers have been proposed (Yin et al., 2007; Wang et al., 2006, 2011), but their benefit for MRI needs to be determined in future studies. It should be noted that the stable MCIs and MCI converters differed already at baseline in major clinical measures and not in MRI alone, as indicated in Table 1. Further studies on a population with less advanced symptoms are warranted to test the full benefit of LLE for predictions.

In summary, we introduced LLE to improve classifications based on high-dimensional MRI data of regional brain atrophy. In combination with linear classifiers such as regularized logistic regression, support vector machine, and linear discriminant analysis, LLE significantly improved classification accuracy, especially for predictions of which MCI subjects would convert to AD and which one would remain stable based on baseline MRI scan. We conclude, LLE is a very effective tool for classification studies of AD using multivariate MRI data. The improvement in predicting conversion to AD in MCI could have important implications for health management and for powering therapeutic trials by targeting non-demented subjects who later convert to AD.

Highlights.

• Locally linear embedding (LLE) is an unsupervised learning algorithm.

• It was used to extract characteristic MR features of brain alternations.

• It was used to classify normal aging subjects, MCI and AD patients from ADNI data.

• The performance of predicting AD in MCIs was significantly improved by using LLE.

• LLE benefitted various classifiers, such as SVM, LDA and regularized regressions.