Faithful Representation of Stimuli with a Population of Integrate-and-Fire Neurons

Abstract

We consider a formal model of stimulus encoding with a circuit consisting of a bank of filters and an ensemble of integrate-and-fire neurons. Such models arise in olfactory systems, vision, and hearing. We demonstrate that bandlimited stimuli can be faithfully represented with spike trains generated by the ensemble of neurons. We provide a stimulus reconstruction scheme based on the spike times of the ensemble of neurons and derive conditions for perfect recovery. The key result calls for the spike density of the neural population to be above the Nyquist rate. We also show that recovery is perfect if the number of neurons in the population is larger than a threshold value. Increasing the number of neurons to achieve a faithful representation of the sensory world is consistent with basic neurobiological thought. Finally we demonstrate that in general, the problem of faithful recovery of stimuli from the spike train of single neurons is ill posed. The stimulus can be recovered, however, from the information contained in the spike train of a population of neurons.

1 Introduction

In this letter, we investigate a formal model of stimulus encoding with a circuit consisting of a filter bank that feeds a population of integrate-and-fire (IAF) neurons. Such models arise in olfactory systems, vision, and hearing (Fain, 2003). We investigate whether the information contained in the stimulus can be recovered from the spike trains at the output of the ensemble of integrate-and-fire neurons. In order to do so, we provide a stimulus recovery scheme based on the spike times of the neural ensemble and derive conditions for the perfect recovery of the stimulus. The key condition calls for the spike density of the neural ensemble to be above the Nyquist rate. Our results are based on the theory of frames (Christensen, 2003) and on previous work on time encoding (Lazar & Tóth, 2004; Lazar, 2005, 2006a, 2007).

Recovery theorems in signal processing are usually couched in the language of spike density. In neuroscience, however, the natural abstraction is the neuron. We shall also formulate recovery results with conditions on the size of the neural population as opposed to spike density. These results are very intuitive for experimental neuroscience. We demonstrate that the information contained in the sensory input can be recovered from the output of integrate-and-fire neuron spike trains provided that the number of neurons is beyond a threshold value. The value of the threshold depends on the parameters of the integrate-and-fire neurons. Therefore, while information about the stimulus cannot be perfectly represented with a small number of neurons, this limitation can be overcome provided that the number of neurons is beyond a critical threshold value. Increasing the number of neurons to achieve a faithful representation of the sensory world is consistent with basic neurobiological thought.

We also demonstrate that the faithful recovery of stimuli is not, in general, possible from spike trains generated by individual neurons; rather a population of neurons is needed to faithfully recover the stimulus of single neurons. This finding has important applications to systems neuroscience since it suggests that the recovery of the stimulus that is applied to single neurons cannot in general be recovered from the spike train of single neurons. Rather, the spike train of a population of neurons is needed to get faithful stimulus recovery.

Our theoretical results provide what we believe to be the first rigorous model demonstrating that the sensory world can be faithfully represented by using a critical-size ensemble of sensory neurons. The investigations presented here further support the need to shift focus from information representation using single neurons to a population of neurons. As such, our results have some important ramifications to experimental neuroscience.

This letter is organized as follows. In section 2, the neural population encoding model is introduced. The encoding model is formally described, and the problem of faithful stimulus recovery is posed. A perfect stimulus recovery algorithm is derived in section 3. In the same section, we also work out our main result for neural population encoders using filter banks based on wavelets. Two examples are given in section 4. The first details the stimulus recovery for filters with arbitrary delays arising in dendritic computation models. The second presents the recovery of stimuli for a gammatone filter bank widely used in hearing research. For both examples, we show that the quality of stimulus reconstruction gracefully degrades when additive white noise is present at the input. Finally section 5 discusses the important ramifications that formal neural population models can have in systems neuroscience.

2 A Neural Population Encoding Model

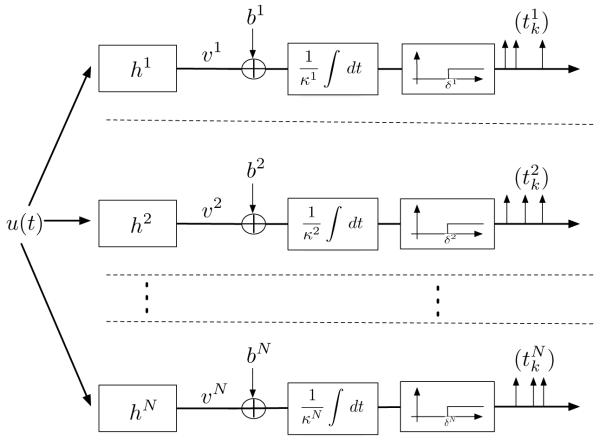
In this section we introduce a formal model of stimulus representation consisting of a bank of N filters and an ensemble of N integrate-and-fire neurons (see Figure 1). Each filter of the filter bank is connected to a single neuron in the ensemble. The stimulus is modeled as a band-limited function—a function whose spectral support is bounded.

Figure 1.

Single-input multi-output time encoding machine.

2.1 Stimulus Encoding with Filter Banks and Integrate-and-Fire Neurons

Let Ξ be the set of band-limited functions with spectral support in [−Ω, Ω]. A function u = u(t), t ∊ ℝ, in Ξ models the stimulus and Ω is its bandwidth. Ξ is a Hilbert space endowed with the L²-norm. A brief overview of Hilbert spaces can be found in appendix A. Let h : ℝ ↦ ℝ ^N be a (vector) filtering kernel defined as

$$\mathbf{h}\left(t\right)={[h^1\left(t\right),h^2\left(t\right),\dots ,h^N\left(t\right)]}^T,$$ (2.1)

where h^j : ℝ → ℝ for all j, j = 1, 2, … , N, and T denotes the transpose. Throughout this letter, we shall assume that supp(ĥ^j) ⊇ [−Ω, Ω] (supp denotes the spectral support). Filtering the signal u with h leads to an N-dimensional vector-valued signal v = v(t), t ∊ ℝ, defined by

$$\mathbf{v}\left(t\right)=(\mathbf{h}\ast u)\left(t\right)={[(h^1\ast u)\left(t\right),(h^2\ast u)\left(t\right),\dots ,(h^N\ast u)\left(t\right)]}^T,$$ (2.2)

where * denotes the convolution operator.

A bias b^j is added to the component ʋ^j of this signal, and the sum is presented at the input of the jth integrate-and-fire neuron with integration constant Κ^j and threshold δ^j, for all j, j = 1, 2, …, N (see Figure 1). $\left(t_k^j\right)$, k ∊, ℤ, is the output sequence of trigger (or spike) times generated by neuron j, j = 1, 2, …, N.

The neural population encoding model in Figure 1 therefore maps the input band-limited stimulus u into the vector time sequence $\left(t_k^j\right)$, k ∊ ℤ, j = 1, 2, … , N. It is an instance of a time encoding machine (TEM) (Lazar & Tóth, 2004; Lazar, 2006a).

2.2 The t-Transform

The t-transform (Lazar & Tóth, 2004) formally characterizes the input-output relationship of the TEM, that is, the mapping of the input stimulus u(t), t ∊ ℝ, into the output spike sequence ${\left(t_k^j\right)}_{k\in \mathbb{\mathbb{Z}}}$ of the jth neuron, j = 1, 2, … , N. The t-transform for the jth neuron be can written as

$${\int }_{t_k^j}^{t_{k+1}^j}((h^j\ast u)+b^j)\left(s\right)\mathit{ds}={\kappa }^j{\delta }^j,$$

or

$${\int }_{t_k^j}^{t_{k+1}^j}(h^j\ast u)\left(s\right)\mathit{ds}=q_k^j,$$ (2.3)

where $q_k^j={\kappa }^j{\delta }^j-b^j(t_{k+1}^j-t_k^j)$, for all k, k ∊ ℤ, and all j, j = 1,2, …, N.

2.3 Recovery of the Encoded Stimulus

Definition 1. A neuronal population encoding circuit faithfully represents its input stimulus u = u(t), t ∊ ℝ, if there is an algorithm that perfectly recovers the input u from the output spike train $\left(t_k^j\right)$, k ∊ ℤ, j = 1,2, … , N.

We have seen that the t-transform of the population encoding circuit in Figure 1 maps the input u into the time sequence $\left(t_k^j\right)$, k ∊ ℤ, j = 1, 2, …, N. The faithful recovery problem seeks the inverse of the t-transform, that is, finding an algorithm that recovers the input u based on the output vector time sequence $\left(t_k^j\right)$, k ∊ ℤ, j = 1, 2, …, N.

Let the function g(t) = sin(Ωt)/πt, t ∊ ℝ, be the impulse response of a low-pass filter (LPF) with cutoff frequency at Ω. Clearly, g ∊ Ξ. Since u is a band-limited function in Ξ, the t-transform defined by equation 2.3 can be rewritten in an inner-product form as

$$\langle h^j\ast u,g\ast 1_{[t_k^j,t_{k+1}^j]}\rangle =q_k^j$$

or

$$\langle u,{\tilde{h}}^j\ast g\ast 1_{[t_k^j,t_{k+1}^j]}\rangle =q_k^j,$$ (2.4)

where h̃^j is the involution of h^j, that is, h̃^j =h^j (—t), for all t, t ∊ ℝ, and for all k, k ∊ ℤ, and j, j = 1, … , N. After firing, without any loss of generality, all neurons are reset to the zero state. A description of the firing mechanism with arbitrary reset can be found in Lazar (2005).

Equation 2.4 has a simple interpretation. The stimulus u is measured by projecting it onto the sequence $({\tilde{h}}^j\ast g\ast 1_{[t_k^j,t_{k+1}^i]})$, k ∊ ℤ and j = 1,2, … , N. The values of these measurements form the sequence $q_k^j$, j = 1, 2, …, N which is available for recovery. Thus, the TEM acts as a sampler on the stimulus u. Furthermore, since the spike times depend on the stimulus, the TEM acts as a stimulus-dependent sampler. How to recover the stimulus from these measurements is detailed in the next section.

3 Recovery of Stimuli Encoded with the Neural Population Model

As discussed in the previous section, we assume N integrate-and-fire neurons each with bias b^j, integration constant Κ^j, and threshold δ^j for all j, j = 1, 2, …, N. Before the stimulus u is fed to neuron j, the stimulus is passed through a linear filter with impulse response h^j = h^j(t), t ∊ ℝ. With $\left(t_k^j\right)$, k ∊ ℤ, the spike times of neuron j, the t-transform, equation 2.4, can be written as

$$\langle u,{ɸ}_k^j\rangle =q_k^j,$$ (3.1)

where ${ɸ}_k^j={\tilde{h}}^j\ast g\ast 1_{[t_k^j,t_{k+1}^j]}$. If the sequence $ɸ=\left({ɸ}_k^j\right)$, k ∊ ℤ, j = 1, 2, …, N, is a frame for Ξ, the signal u can be perfectly recovered. Thus, our goal in this letter is to investigate the condition for the sequence ɸ to be a frame (called analysis frame in the literature; Teolis, 1998; Eldar & Werther, 2005) and provide a recovery algorithm.

Before we proceed with the recovery algorithm we also need the following definition of the filters that model the processing taking place in the dendritic trees:

Definition 2 The filters h^j = h^j(t), t ∊ ℝ, are said to be bounded-input bounded-output (BIBO) stable if

$${\parallel h^j\parallel }_1\triangleq {\int }_{\mathbb{ℝ}}\mid h^j\left(s\right)\mid \mathit{ds}<\infty .$$

In the next section, we investigate the faithful representation of the stimulus u given the spike sequence $\left(t_k^j\right)$, k ∊ ℤ, j = 1, 2, … , N (see theorem 1) and provide sufficient conditions for perfect recovery. An algorithm for stimulus recovery is explicitly given (see corollary 1). We show that the sensory world modeled through the stimulus u can be perfectly recovered provided that the number of neurons is above a threshold value (see theorem 2).

3.1 Faithful Stimulus Recovery

The t-transform in equation 3.1 quantifies the projection of the stimulus u onto the sequence of functions $\left({ɸ}_k^j\right)$, k ∊ ℤ, j = 1, 2, … , N. As such, it provides a set of constraints for stimulus recovery. These constraints might be related if the corresponding functions are related. For example, for two integrate-and-fire neurons with the same parameters and the same preprocessing filters, ${ɸ}_k^1={ɸ}_k^2$, for all k, k ∊ ℤ. Thus, the two neurons impose identical constraints on recovery. For two neurons whose preprocessing filters and biases are the same and the threshold of one of the neurons is an integer multiple of the threshold of the other neuron, say, δ² = Lδ¹, ${\sum }_{l=0}^{L-1}{ɸ}_{m+l}^1={ɸ}_n^2$ for infinitely many pairs of integers (m, n).

In the simple examples above, the constraints that a neuron imposes on stimulus recovery can be linearly inferred from the constraints imposed by another neuron. This redundancy in the number of constraints is undesirable, and in proposition 1 we seek sufficient conditions to avoid it.

Definition 3. The filters (h^j), j = 1, … , N, are called linearly independent if there do not exist real numbers a_j, j = 1 … , N, not all equal to zero, and real numbers α^j, j = 1, … , N, such that

$$\sum _{j=1}^N{a}_j(h^j\ast g)(t-{\alpha }^j)=0$$

for all t, t ∊ ℝ (except on a set of Lebesgue-measure zero).

Proposition 1. If the filters (h^j), j = 1, … , N, are linearly independent, then the functions $\left({ɸ}_k^j\right)$, k ∊ ℤ, j = 1, 2, … , N, are also linearly independent.

Proof. The functions $\left({ɸ}_k^j\right)$, k ∊ ℤ, j = 1, 2, … , N, are linearly dependent if there exist real numbers a_j, j = 1, … , N, not all equal to zero, integers k_j , j = 1, … , N, and positive integers L_j, j = 1, … , N, such that

$$\sum _{j=1}^N{a}_j\left(\sum _{l=0}^{L_j-1}{ɸ}_{k_j+l}^j\left(t\right)\right)=0,$$ (3.2)

for all t, t ∊ ℝ. By substituting the functional form of ${ɸ}_k^j$ in the equation above, we obtain

$$\sum _{j=1}^N{a}_j\left({\tilde{h}}^j\ast g\ast 1_{[t_{k_j}^j,t_{k_j+L_j}^j]}\right)\left(t\right)=0.$$ (3.3)

For equation 3.3 to hold, $t_{k_j+L_j}^j-t_{k_j}^j=\Delta$ for all j, j = 1, … , N, with a_j ≠ 0, where Δ is a constant. By taking the Fourier transform of equation 3.3, we have

$$\sum _{j=1}^N{a}_j\widehat{\left({\tilde{h}}^j\right)}\hat{g}\left(e^{-i\omega t_{k_j}^j}\frac{1-e^{-i\omega \Delta }}{i\omega }\right)=0,$$ (3.4)

where ĝ is the Fourier transform of g and $i=\sqrt{-1}$. After canceling the summation independent terms and taking the inverse Fourier transform, we obtain

$$\sum _{j=1}^N{a}_j({\tilde{h}}^j\ast g)(t-t_{k_j}^j)=0.$$ (3.5)

The latter equality can hold only if the filters are not linearly independent.

Remark 1. In order to satisfy equation 3.3, the spikes generated by the N neurons do not have to coincide. For two neurons, for example, the spikes might be generated at times $t_k^1=t_k^2+\alpha$, while the preprocessing filters satisfy the relationship h¹(t) = h²(t+α. Here ${ɸ}_k^1={ɸ}_k^2$, that is, the constraints are linearly dependent. The allowance of time shifts that also appears in the definition of linear independent filters is therefore essential.

Remark 2. Two neurons might generate spikes at the same time infinitely often. A simple example is provided by the case when the first neuron is described, after generating L spikes, by the t-transform

$${\int }_{t_k^1}^{t_{k+L}^1}(h^1\ast u)\left(s\right)\mathit{ds}=L\cdot {\kappa }^1{\delta }^1-b^1(t_{k+L}^1-t_k^1),$$

and the second neuron is described between two consecutive spikes by

$${\int }_{t_k^2}^{t_{k+1}^2}(h^2\ast u)\left(s\right)\mathit{ds}={\kappa }^2{\delta }^2-b^2(t_{k+1}^2-t_k^2).$$

It is easy to see that if the initial spikes coincide in time, that is, $t_k^1=t_k^2$, the filters h¹ and h² and the other parameters of the two integrate-and-fire neurons can be chosen in such a way as to have $t_{k+L}^1=t_{k+1}^2$. Thus, the spikes generated by the two neurons are identical infinitely often. However, the spike coincidence just described will be of no concern to us provided that the filters are linearly independent. This consideration arises when constructing the synthesis frames throughout this letter.

We are now in a position to state our main theorem. It pertains to the neural circuit model depicted in Figure 1.

Theorem 1. Assume that the filters h^j = h^j(t), t ∊ ℝ, are linearly independent, BIBO stable, and have spectral support that is a superset of [−Ω, Ω] for all j, j = 1, 2, … , N. The stimulus u can be represented as

$$u\left(t\right)=\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{c}_k^j{\psi }_k^j\left(t\right),$$ (3.6)

where ${\psi }_k^j\left(t\right)={\tilde{h}}^j\ast g(t-s_k^j)$ and $c_k^j$, Κ ∊ ℤ, j = 1, … , N are suitable coefficients, provided that

$$\sum _{j=1}^N\frac{1}{{\kappa }^j{\delta }^j}\left(b^j-c{\int }_{\mathbb{ℝ}}\mid h^j\left(s\right)\mid \mathit{ds}\right)>\frac{\Omega }{\pi },$$ (3.7)

|u(t)| ≤ c.

Proof. Clearly the theorem holds if we can show that the sequence of functions $\left({\psi }_k^j\left(t\right)\right)$, k ∊ ℤ, j = 1, … , N, is, respectively, a frame for Ξ (called the synthesis frame in the literature; Teolis, 1998; Eldar & Werther, 2005).

Given the structure of the t-transform in equation 3.1 and noting that the N filters are independent, the definition of the lower spike density D (given in appendix B) reduces to (see also the evaluation of D below)

$$D=\underset{t\to \infty }{\lim \inf }\underset{t_0\in \mathbb{ℝ}}{\inf }\frac{N(t_0,t_0+t)}{t},$$ (3.8)

where N(a, b) is the number of spikes in the interval (a, b). Since

$$\mid v^j\left(t\right)\mid =\mid {\int }_{\mathbb{ℝ}}{h}^j(t-s)u\left(s\right)\mathit{ds}\mid \le {\int }_{\mathbb{ℝ}}\mid h^j(t-s)\mid \mid u\left(s\right)\mid \mathit{ds}\le c{\int }_{\mathbb{ℝ}}\mid h^j\left(s\right)\mid \mathit{ds},$$

the condition for the spike density D becomes

$$\begin{array}{cc}\hfill D=& \underset{t\to \infty }{\lim \inf }\underset{t_0\in \mathbb{ℝ}}{\inf }\sum _{j=1}^N\frac{1}{t}\lceil \frac{{\int }_{t_0}^{t+t_0}(b^j+v^j\left(s\right))\mathit{ds}}{{\kappa }^j{\delta }^j}\rceil \hfill \\ \hfill =& \underset{t\to \infty }{\lim \inf }\underset{t_0\in \mathbb{ℝ}}{\inf }\sum _{j=1}^N\frac{1}{t}\left(\frac{{\int }_{t_0}^{t+t_0}(b^j+v^j\left(s\right))\mathit{ds}}{{\kappa }^j{\delta }^j}\right)\hfill \\ \hfill \ge & \sum _{j=1}^N\frac{1}{{\kappa }^j{\delta }^j}\left(b^j-c{\int }_{\mathbb{ℝ}}\mid h^j\left(s\right)\mid \mathit{ds}\right),\hfill \end{array}$$ (3.9)

where ⌈x⌉ denotes the greatest integer less than or equal to x.

We note that the computation of the lower density above possibly includes identical spikes. However, the linear independence condition on the filters h^j, j = 1, 2, …, N, guarantees that the sequence $\left({ɸ}_k^j\right)$, k ∊ ℤ, j = 1, 2, …, N, is a frame. The theorem holds since condition 3.7 guarantees that the lower spike density is above the Nyquist rate, and thus by lemma 2, given in appendix C, the sequence of functions $\left({\psi }_k^j\left(t\right)\right)$, k ∊ ℤ, j = 1, … , N, is a frame for Ξ.

Remark 3. Theorem 1 has a very simple interpretation. The stimulus u can be faithfully represented provided that the number of spikes exceeds the lower bound in equation 3.7. This lower bound is the Nyquist rate and arises in the Shannon sampling theorem (Lazar & Tóth, 2004). Thus, inequality 3.7 is a Nyquist-type rate condition.

According to theorem 1 (see equation 3.6), under a Nyquist-type rate condition, the stimulus u can be written as

$$u\left(t\right)=\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{c}_k^j({\tilde{h}}^j\ast g)(t-s_k^j).$$ (3.10)

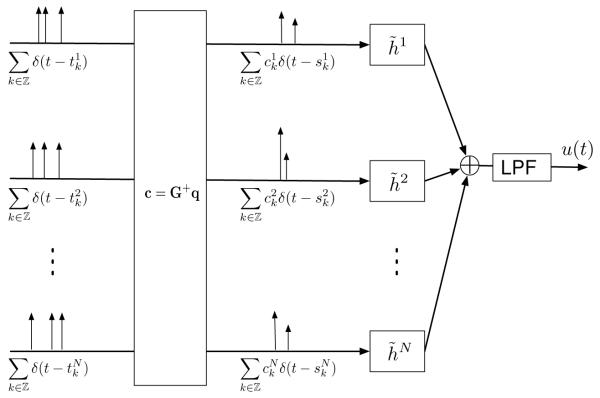
The recovery algorithm of u in block diagram form is shown in Figure 2. It is an instantiation of a time decoding machine (Lazar & Tóth, 2004; Lazar, 2007).

Figure 2.

Single-input multi-output time decoding machine.

This suggests the following recovery scheme in matrix notation:

Corollary 1. Let c = [c¹, … , c^N]^T, with ${\left[{\mathit{c}}^j\right]}_k=c_k^j$. Then

$$\mathit{c}={\mathit{G}}^{+}\mathit{q},$$ (3.11)

where T denotes the transpose, G⁺ denotes the pseudoinverse of G, and

$$\mathit{q}={[{\mathit{q}}^1,\dots ,{\mathit{q}}^N]}^T,{\left[{\mathit{q}}^j\right]}_k={\kappa }^j{\delta }^j-b^j(t_{k+1}^j-t_k^j),$$

$$\mathit{G}=\left[\begin{array}{cccc}\hfill {\mathit{G}}^{11}\hfill & \hfill {\mathit{G}}^{12}\hfill & \hfill \dots \hfill & \hfill {\mathit{G}}^{1N}\hfill \\ \hfill {\mathit{G}}^{21}\hfill & \hfill {\mathit{G}}^{22}\hfill & \hfill \dots \hfill & \hfill {\mathit{G}}^{2N}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathit{G}}^{N1}\hfill & \hfill {\mathit{G}}^{N2}\hfill & \hfill \dots \hfill & \hfill {\mathit{G}}^{\mathit{NN}}\hfill \end{array}\right]{\left[{\mathit{G}}^{\mathit{ij}}\right]}_{\mathit{kl}}={\int }_{t_k^i}^{t_{k+1}^i}(h^i\ast {\tilde{h}}^j\ast g)(s-s_l^j)\mathit{ds}.$$ (3.12)

Proof. The equation c = G⁺q can be obtained by substituting the representation of u in equation 3.6 into the t-transform equation 3.1,

$$\langle u,{ɸ}_l^j\rangle =\sum _{i=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{c}_k^i\langle {\psi }_k^i,{ɸ}_l^j\rangle ,$$

and therefore

$${\mathit{q}}_l^j=\sum _{i=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{c}_k^i{\left[{\mathbf{G}}^{\mathit{ij}}\right]}_{\mathit{kl}}$$

for all i, i = 1, 2, …, N and all l, ∊ ℤ. Since the sequences Φ and ψ are frames for Ξ, the result follows (Eldar & Werther, 2005).

Remark 4. For the particular case of a TEM without filters, that is, h^j(t) = δ(t), where δ(t) is the Dirac-delta function for all j, j = 1, 2, … N, we have

$${\psi }_k^j\left(t\right)=(\delta \ast g)(t-s_k^j)=g(t-s_k^j),$$

for all k, k ∊ ℤ, and t, t ∊ ℝ. Consequently, we obtain the representation and recovery result of Lazar (2007).

Remark 5. Assume that the band-limited stimulus u is filtered with an arbitrary time-invariant filter with impulse response h. A bias b is added to the output of the filter, and the resulting signal is passed through an integrate-and-fire neuron with threshold δ. Thus, the t-transform of the signal can be written as

$${\int }_{t_k}^{t_{k+1}}(h\ast u)\left(s\right)\mathit{ds}=\kappa \delta -b(t_{k+1}-t_k),$$ (3.13)

for all k, k ∊ ℤ. According to theorem 1, under appropriate conditions, the stimulus can be writen as

$$u\left(t\right)=\sum _{k\in \mathbb{\mathbb{Z}}}{c}_k(\tilde{h}\ast g)(t-s_k),$$ (3.14)

for all t, t ∊ ℝ. In matrix notation, c = G⁺q, where [c]_k = c_k, [q]_k = kδ − b(t_k+1 − t^k), k ∊ ℤ, and ${\left[\mathbf{G}\right]}_{\mathit{kl}}={\int }_{t_k}^{t_{k+1}}(h\ast \tilde{h}\ast g)(s-s_k)\mathit{ds}$. Alternatively, in order to recover the stimulus u, we can first obtain h * u using the classical recovery algorithm (Lazar & Tóth, 2004) and then pass h* u through the inverse filter h⁻¹.

Theorem 1 provides a technical condition for faithful representation in terms of the minimum density of spikes as in equation 3.7. Instead of this technical condition, we give a much simpler condition in terms of the number of neurons. Such a condition is more natural in the context of encoding stimuli with a population of neurons. The latter also provides a simple evolutionary interpretation (see remark 6 below).

Theorem 2. Assume that the filters h^j = h^j (t), t ∊ ℝ, are linearly independent, BIBO stable, and have spectral support that is a superset of [−Ω, Ω] for all j, j = 1,2, … , N. If the input to each neuron is positive, that is, b^j + ʋ^j ≥ ε^j > 0, and ${\sum }_{j=1}^N{\epsilon }^j∕{\kappa }^j{\delta }^j$ diverges in N, then there exits a number 𝒩 such that if N ≥ 𝒩, the stimulus u, |u(t)| ≤ c, can be recovered as

$$u\left(t\right)=\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{c}_k^j{\psi }_k^j\left(t\right),$$ (3.15)

where the constants $c_k^j$, k ∊ ℤ, j = 1, … , N, are given in matrix form by c = G⁺q.

Proof. Since b^j + v^j ≥ ε^j for all j, j = 1, 2, … , N, the lower spike density amounts to

$$D=\underset{t\to \infty }{\lim \inf }\underset{t_0\in \mathbb{ℝ}}{\inf }\sum _{j=1}^N\frac{1}{t}\left(\frac{{\int }_{t_0}^{t+t_0}(b^j+v^j\left(s\right))\mathit{ds})}{{\kappa }^j{\delta }^j}\right)\ge \sum _{j=1}^N\frac{{\epsilon }^j}{{\kappa }^j{\delta }^j},$$ (3.16)

and the lower bound diverges in N. Therefore, there exists an 𝒩 such that for N > 𝒩,

$$D>\frac{\Omega }{\pi },$$

and the theorem follows.

Remark 6. The result of theorem 2 has a simple and intuitive evolutionary interpretation. Under the condition that every neuron responds to the stimulus with a positive frequency, the stimulus can be faithfully represented with a finite number of neurons.

3.2 Stimulus Representation and Recovery Using Overcomplete Filter Banks

Receptive fields in a number of sensory systems, including the retina (Masland, 2001) and the cochlea (Hudspeth & Konishi, 2000), have been modeled as filter banks. These include wavelets and Gabor frames.

We briefly demonstrate how to apply the results obtained in the previous section when using the overcomplete wavelet transform (OCWT) (Teolis, 1998). A similar formulation is also possible with other classes of frames (e.g., Gabor frames). Let u be a band-limited stimulus, h the analyzing wavelet, and s_n, n = 1, … , N, the scaling factors used in the filter bank representation (for more information, see, e.g., Teolis, 1998). Then the filters h^j are defined by h^j = D_sj h, j= 1, 2, … , N, where D_s is the dilation operator (D_su)(t) =|s|^1/2u(st).

From theorem 1 and the simple relation (D_sh)^~ = D_s h̃, the stimulus can be represented as

$$u\left(t\right)=\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{c}_k^j(g\ast D_{s_j}\tilde{h})(t-s_k^j),$$ (3.17)

where c = G⁺q with [q] = [q¹, q², …, q^N]^T and ${\left[{\mathbf{q}}^j\right]}_k={\kappa }^j{\delta }^j-b_j(t_{k+1}^j-t_k^j)$. The matrix G is given by

$${\left[{\mathbf{G}}^{\mathit{ij}}\right]}_{\mathit{kl}}={\int }_{t_k^i}^{t_{k+1}^i}(D_{s_i}h\ast D_{s_j}\tilde{h}\ast g)(s-s_l^j)\mathit{ds}.$$ (3.18)

Note that representation 3.17 uses the same filters (D_sj h̃), j = 1, 2, …, N, for recovery as the ones that are employed in the classical signal representation with filter banks (Teolis, 1998). The density condition for equation 3.17 calls for the sum of the whole neuron population activity to exceed the Nyquist rate. As before, by adding more neurons and filters to the filter bank results, in general, in an improved representation. The TEM and time decoding machine realizations are shown in Figure 3.

Figure 3.

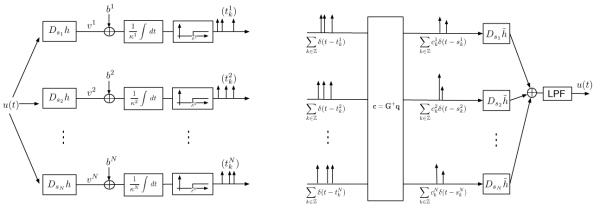
Time encoding machine (left) using an overcomplete wavelet filter bank for stimulus representation. Recovery is achieved with a time decoding machine (right).

Remark 7. Our analysis above provides an algorithm for recovering the stimulus even in the case where the actual input is undersampled by each of the neurons. Thus, our findings in this section extend the results of Lazar (2005).

4 Examples

In this section, we present two numerical examples of the theory presented above that have direct applications to stimulus representation in sensory systems.

4.1 Neural Population Encoding Using Filters with Arbitrary Delays

We present an example realization of the recovery algorithm for a filter bank consisting of filters that introduce arbitrary but known delays on the stimulus. Such filters model dendritic tree latencies in the sensory neurons (motor, olfactory) (Fain, 2003). They are analytically tractable as their involutive instantiations can be easily derived. Indeed, a filter that shifts the stimulus in time by a quantity α has an impulse response h(t) = δ(t−α). Consequently, h̃(t)= δ(t)+α). Note that although the filter h̃ is, in this case, noncausal, it can easily be implemented by delaying the recovery.

It is assumed that each filter h^j shifts the stimulus in time by an amount α^j, where α^j is an arbitrary positive number for all j, j =1, 2, … , N. The quantities of interest become, according to equations 3.6 and 3.12,

$${\psi }_k^j\left(t\right)=g(t-s_k^j+{\alpha }^j)$$

$${\left[{\mathbf{G}}^{\mathit{ij}}\right]}_{\mathit{kl}}={\int }_{t_k^i}^{t_{k+1}^i}g(s-s_l^j-{\alpha }^i+{\alpha }^j)\mathit{ds}.$$ (4.1)

The stimulus u(t) is given in the standard Shannon form,

$$u\left(t\right)=\sum _{k=1}^{35}u\left(kT\right)\frac{\sin \left(\Omega (t-kT)\right)}{\pi (t-kT)},$$ (4.2)

with Ω = 2π · 80 Hz, T = π/Ω. Out of the 35 samples, the first and last five were set to zero. Thus shifts of the stimulus in the time window do not lead to any loss of important information. The rest of the 25 active samples were chosen randomly from the interval [−1, 1]. Sixteen neurons were used for recovery. Filter delays were randomly drawn from an exponential distribution with mean T/3, biases b^j , j = 1, … , 16, were randomly drawn from a uniform distribution in [0·8, 1·8]and the thresholds δ^j, j = 1, … , 16, were drawn randomly from a uniform distribution in [1·4, 2·4]. Finally, all neurons had the same integration constant Κ = 0·01. The stimulus and three of its translates, each delayed by the filters, as well as the spikes generated by the 16 neurons in the time window of interest [6T, 30T], are shown in Figure 4.

Figure 4.

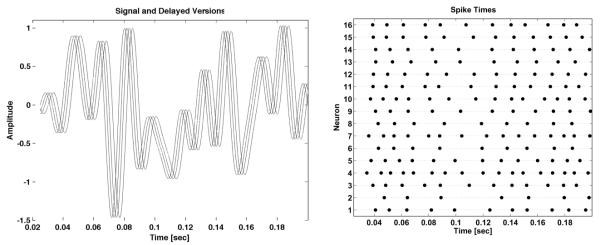
Band-limited stimulus u(t) and three of its translates (left) and the spike train generated by each of the 16 neurons (right).

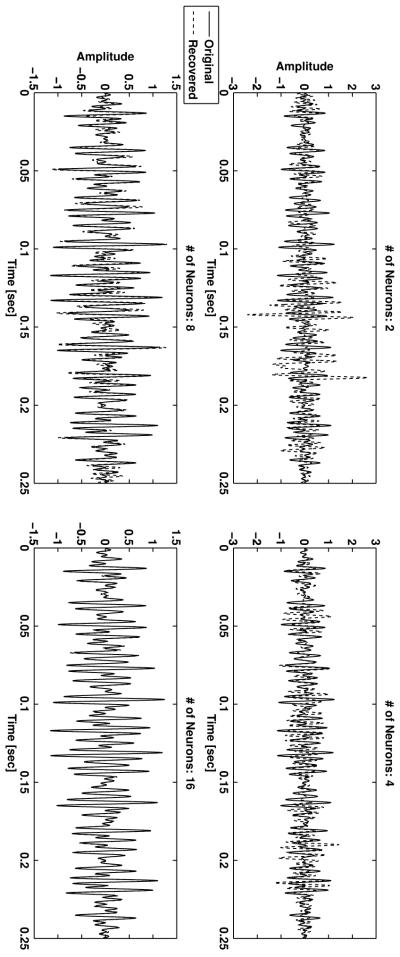
The recovered stimulus based on the spikes from 1, 2, 3, 4, 8, and all 16 neurons, respectively, is depicted from top to bottom in Figure 5. Note the different amplitude scale at the top and at the bottom row of Figure 5. The recovered signal converges to the original one with the number of neurons used. The recovery becomes acceptable when the spikes of at least the first four neurons are used. Since the density of the sinc functions is invariant under a time shift, the density criterion of theorem 1 above can be applied. Here we have 27 samples, and the individual neurons elicit between 7 and 17 spikes, respectively. The threshold is exceeded when the first four or more neurons are used. The recovery results in Figure 5 are consistent with this observation.

Figure 5.

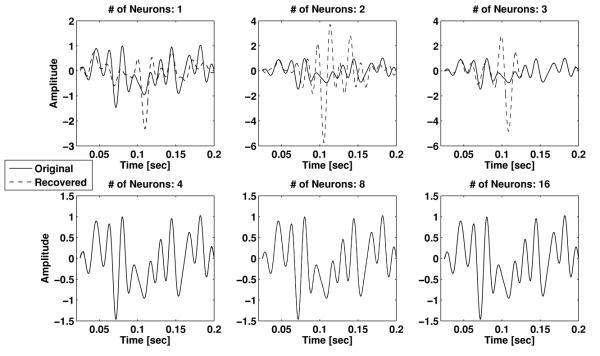
Stimulus recovery as a function of the number of neurons.

To quantify accuracy of the recovered signal, we provide the mean square error (MSE) for the various recovery scenarios. The MSE is defined as

$$\mathrm{MSE}=10{\log }_{10}\left(\frac{1}{T_{\max }-T_{\min }}{\int }_{T_{\min }}^{T_{\max }}{[u\left(s\right)-{\stackrel{-}{u}}^j\left(s\right)]}^2\mathit{ds}\right),$$ (4.3)

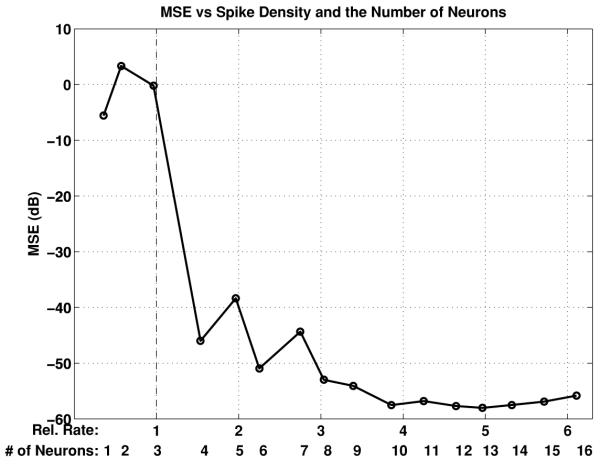
where [T_min, T_max] is the interval of interest ([6T, 30T] in our case) and û^j (s) denotes the result of stimulus recovery with a total of j, j = 1, 2, … , 16, neurons. In Figure 6 we show the dependence of the MSE on the relative interspike rate. The relative interspike rate is defined as the number of interspike intervals per second divided by the Nyquist rate. Figure 6 demonstrates that when the relative rate is below 1, meaning the average spike rate is less than the Nyquist rate, the MSE is big and the recovery inaccurate. However, when the spike rate exceeds the Nyquist rate, the MSE decreases dramatically, and the recovery improves substantially. Moreover, the MSE decreases overall as more neurons are added to stimulus representation and, recovery.

Figure 6.

Dependence of the mean square error on the relative interspike rate and the number of neurons.

Remark 8. The MSE in Figure 6 is shown as a function of both the relative spike rate and the number of neurons. In neuroscience, the natural abstraction, however, is the number of neurons. Consequently, in what follows, we shall provide only the MSE as a function of the number of neurons.

Remark 9. It is easy to see that the filters h^j(t) = δ(t − α^j), j 1, 2, … , 16, above do not satisfy the independence condition of definition 3. Nevertheless, as the example illustrates, the input can be perfectly recovered. Similarly, if no preprocessing filters are used, the stimulus can be perfectly recovered from the representation provided by a population of integrate-and-fire neurons (Lazar, 2007). Thus, having linear independent filters is a sufficient but not a necessary condition for recovery.

It is important to note that the input to each neuron cannot in general be faithfully recovered from the spike train generated by single neurons. To see that, we applied the classical time decoding algorithm (Lazar & Tóth, 2004) for signal recovery solely using the spike train of each individual neuron. The results for four of the neurons are illustrated in Figure 7. The other 12 neurons exhibited similar results. As shown, the recovered dendritic currents are significantly different from the stimulus.

Figure 7.

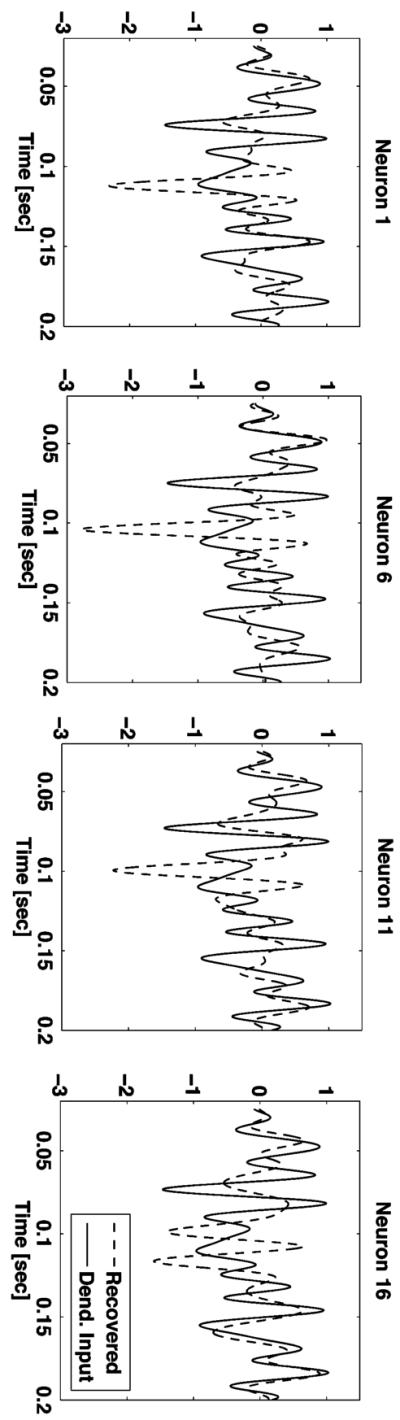
Recovery of the dendritic currents for four of the neurons, using the classical time decoding algorithm.

The recovery is not perfect because each individual neuron generates only sparse neural spike trains (fewer than 28 spikes). However, this sparsity did not affect perfect recovery of the original stimulus because the total number of neurons fired a significant number of spikes. These results have some important ramifications to experimental neuroscience because they demonstrate that in general, stimuli of individual neurons cannot be faithfully recovered from the spike train they generate. Rather, the spike trains from a larger population of neurons that encode the same stimulus need to be used.

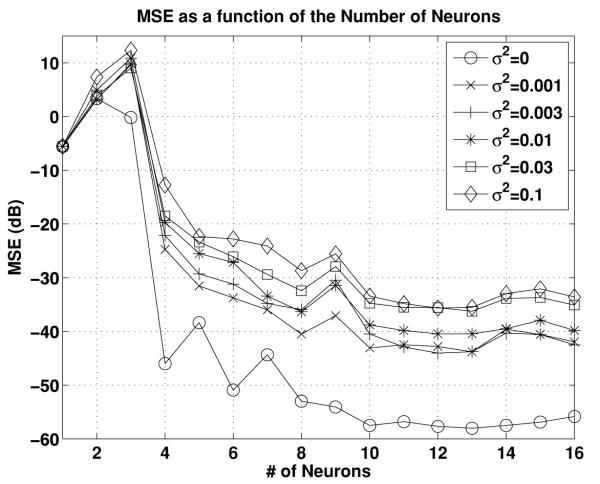
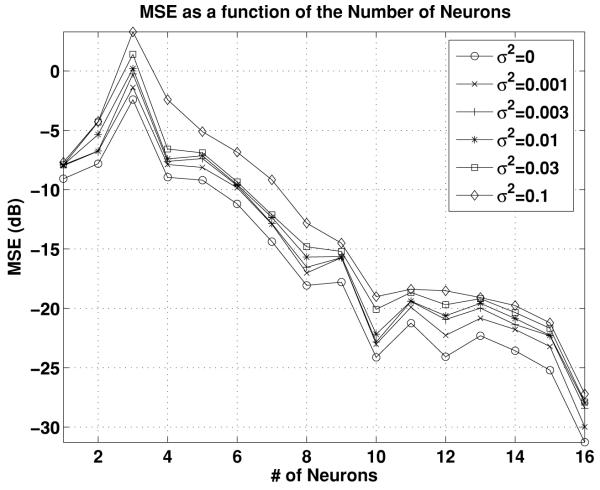
Finally, we briefly show the effect of noise on the performance of the recovery algorithm. The setting is as before, except that we also applied additive independent white gaussian noise at the input of each filter. Since all filters in this example are performing delay operations, delayed white noise reaches the integrators. The average MSE (in dB) is shown in Figure 8 for the noiseless case and for five variance values σ² = 0.001, 0.003, 0.01, 0.03, 0.1. For each value of the variance, 100 repetitions of the simulation were performed. The 95% confidence interval, measured here as twice the standard deviation of the MSE, was in each case between 3 and 5 dB (not shown). Even though we added an infinite bandwidth white noise component to a narrow band stimulus, we see a predictable degradation of the MSE as a function of the noise variance.

Figure 8.

Effect of noise on the accuracy of recovery.

4.2 Neural Population Encoding with a Gammatone Filter Bank

In this section we present a simple example of stimulus representation and recovery using gammatone filter banks. The stimulus of interest is bandpass with frequency support essentially limited to [150, 450] Hz and a duration of 250 ms. The filter bank consists of 16 gammatone filters that span the range of frequencies [100, 500] Hz. The gammatone filters, developed by Patterson et al. (1992), are widely used in cochlear modeling. The general form of the (causal) gammatone filter is

$$h\left(t\right)=\alpha t^{n-1}\exp (-2\pi \beta \cdot \mathrm{ERB}\left(f_c\right)t)\cos \left(2\pi f_{c}t\right),t\ge 0,$$ (4.4)

where the equivalent rectangular bandwidth (ERB) is a psychoacoustic measure of the bandwidth of the auditory filter at each point along the cochlea. The filters employed were generated using Slaney's auditory tool-box (Slaney, 1998). This toolbox generates the auditory filterbank model proposed by Patterson et al. (1992). The bandwidth of each filter with a center frequency at f_c is given by ERB(f_c) = 0.108 f_c + 24.7. Parameter n corresponds to the filter order and is picked to be equal to 4 (n = 4). For this filter order, Patterson et al. proposed β = 1.019. Finally, the scalar α is picked in such a way that each filter has unit gain at its center frequency. Gamma-tone filter banks are approximately equivalent to wavelet filter banks since all the impulse responses are obtained from dilated versions of the kernel function 4.4 (mother wavelet) at its center frequency. Moreover, the center frequencies are spaced logarithmically along the frequency axis, giving rise to an overcomplete filter bank.

The frequency responses of the 16 filters and the entire filter bank support are shown in Figure 9. The filter bank support is defined as

$$\sum _{j=1}^N{\mid -{\hat{h}}^j\left(\omega \right)\mid }^2,$$ (4.5)

where ĥ^j(ω) = ∫_ℝh_j(s)e^−iωs ds is the Fourier transform of the jth filter impluse response.

Figure 9.

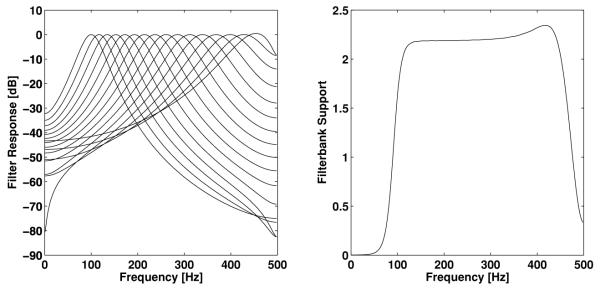
Characterization of the gammatone filter bank: Frequency responses of the filter bank elements (left) and filter bank support (right).

The biases and the thresholds of the neurons were picked randomly from the interval [1, 2]. Each neuron produced approximately 25 spikes, for a total of approximately 400 spikes. In Figure 10, we show the recovery of the stimulus when 2, 4, 8, or all 16 filters were used, respectively. Note the amplitude scale at the top and at the bottom row of Figure 10.

Figure 10.

Stimulus recovery using a gammatone filter bank as a function of the size of the population of neurons.

To quantify the recovery results and also the effect of noise, the MSE is depicted as a function of the number of neurons in Figure 11 for the noiseless case and for white noise with five different variances. The noise variances were again σ² = 0.001, 0.003, 0.01, 0.03, 0.1, and the noise was applied again at the input of the filters. However since each filter in the gammatone filter bank has only a limited frequency support, most of the noise gets filtered out. Thus, the effect of the white noise on the accuracy of the recovery is much smaller here when compared to its effect in the delay filter bank example (see also Figure 8). Again, as an overall trend, the MSE decreases as the size of neuron population increases and the noise power decreases.

Figure 11.

MSE of recovery.

5 Discussion

The problem of stimulus recovery based on the spike trains generated by a population of neurons is central to the field of neural representation and encoding. In order to achieve a faithful stimulus representation, our method assigns a kernel function to each neuron. With these kernels, a frame can be constructed by spike-dependent shifts. Frame theory provides the machinery needed for faithful stimulus recovery.

In the reverse correlation method of Rieke, Warland, de Ruyter van Steveninck, and Bialek (1997), the recovered stimulus is obtained by convolving the output spike train with a suitable kernel. The choice of the kernel is actively investigated (Tripp & Eliasmith, 2007). Kernel methods have also been investigated for sparse representations of auditory and visual stimuli in Smith and Lewicki (2005) and Olshausen (2002), respectively. The models used lack, however, explicit neural encoding schemes. In addition, the faithful representation of stimuli has not been addressed.

Related work in information coding with a population of neurons is based on stochastic neuron models. These neuron models (known as linear-nonlinear-Poisson models) produce spikes with underlying Poisson statistics. The activity of the neurons is measured in spikes per seconds rather than actual spike times, and it is given as a (nonlinear) function of the projection of the stimulus on a suitable vector modeling the receptive field. For a population of neurons, different receptive field models can be used; the latter can be chosen so as to span the space of interest. Computational models, based mostly on maximum likelihood techniques, for the suitable choice of receptive fields or neurons, and of actual encoding and decoding mechanisms based on such setups, have been extensively studied in the literature. (See, e.g., Deneve, Latham, & Pouget, 1999, or Sanger, 2003, for a review, and Huys, Zemel, Natarajan, & Dayan, 2007, for a more recent treatment.)

Our neural population model is, in contrast, deterministic. This assumption allowed us to formally focus on the question of faithful representation of stimuli. The key result shows that faithful representation can be achieved provided that the total number of spikes of the neural ensemble is above the Nyquist rate. We have demonstrated that this condition can be replaced with a more intuitive one that stipulates that the size of the population of neurons is beyond a threshold value. We have also shown that, in general, the stimulus of a neuron cannot be faithfully recovered from the neural spike train that it generates. Rather, a population of neurons is needed to achieve faithful recovery.

The basic population encoding circuit investigated in this letter significantly extends previous work on population time encoding (Lazar, 2005, 2007). From a modeling standpoint, it introduces a set of constraints on the number of spikes that can be generated by an individual neuron. In addition, it incorporates arbitrary filters that can model the dendritic tree of the neurons or their receptive fields. Note that this work formalizes the results of Lazar (2007) by using frame arguments and introducing the notion of linear-independent preprocessing filters that guarantees that each neuron can provide additional information about the stimulus being encoded.

Our theoretical results provide what we believe to be the first rigorous model demonstrating that the sensory world can be faithfully represented by using a critical size ensemble of sensory neurons. The investigations presented here further support the need to shift focus from information representation using single neurons to populations of neurons. As such, our results have some important ramifications to experimental neuroscience.

Although the model investigated in this letter employs only ideal IAF neurons, it is highly versatile for modeling purposes. It provides theoretical support for modeling arbitrary linear operations associated with dendritic trees. For example, arbitrary stable filters can be used to characterize synaptic conductances. Moreover, the input-output equivalence of IAF neurons with other more complex neuron models (Hodgkin-Huxley, and conductance based models in general) (Lazar, 2006b) elevates the proposed circuit to a very general framework for faithful stimulus representation with neural assemblies.

Appendix A: Basic Concepts of Hilbert Spaces

Definition 4. A nonnegative real-valued function ∥·∥ defined on a vector space E is called a norm if for all x, y ∊ E, and α ∊ ℝ:

$$\begin{array}{cc}\hfill \parallel x\parallel & =0\iff x=0\hfill \\ \hfill \parallel x+y\parallel & \le \parallel x\parallel +\parallel y\parallel \hfill \\ \hfill \parallel \alpha x\parallel & =\mid \alpha \mid \parallel x\parallel .\hfill \end{array}$$ (A.1)

Definition 5. A normed linear space is called complete if every Cauchy sequence in the space converges, that is, for each Cauchy sequence (x_n), n ∈ ℕ, there is an element x in the space such that x_n → x.

Definition 6. An inner product on a vector space Ε over ℂ or ℝ is a complex-valued function <·,·>: E × E ↦ ℂ such that

$$\begin{array}{cc}\hfill \langle x+y,z\rangle & =\langle x,z\rangle +\langle y,z\rangle \hfill \\ \hfill \langle \alpha x,y\rangle & =\alpha \langle x,y\rangle \hfill \\ \hfill \langle x,y\rangle & ={\langle y,x\rangle }^{\ast }\hfill \\ \hfill \langle x,x\rangle & \ge 0,\langle x,x\rangle =0,\mathit{if}x=0.\hfill \end{array}$$ (A.2)

Definition 7. A complete vector space whose norm is induced by an inner product is called a Hilbert space.

Example 1. Let L² be the space of functions of finite energy, that is,

$$L^2\left(\mathbb{ℝ}\right)=\left\{f:{\int }_{\mathbb{ℝ}}{\mid f\left(s\right)\mid }^2\mathit{ds}<\infty \right\},$$ (A.3)

with norm ǁfǁ = (∫_ℝ f(s)²ds)^½. L²(ℝ) endowed with the inner product 〈x,y〉 = ∫_ℝx(s)y(s)ds is a Hilbert Space.

Definition 8. For a given Ω > 0,

$$\Xi =\{f\in L^2\left(\mathbb{ℝ}\right):\mathit{supp}\stackrel{-}{f}\subseteq [-\Omega ,\Omega ]\},$$ (A.4)

endowed with the L² inner product is called the space of band-limited functions.

Appendix B: Basic Theorems on Frames

A formal intoduction to the theory of frames can be found in Christensen (2003). For a signal processing approach, see Teolis (1998). Here we present all the necessary definitions and propositions that were used throughout the letter. In what follows, ℐ denotes a countable index set (e.g., ℕ, ℤ, [1, 2, … , M]).

Definition 9. A (countable) sequence (ɸ_k)_k∊ℐ in ℋ is a frame for the Hilbert space ℋ if there exist frame bounds A, B > 0 such that for any f ∊ ℋ,

$$A{\parallel f\parallel }^2\le \sum _{k\in \mathcal{I}}{\mid \langle f,{ɸ}_k\rangle \mid }^2\le B{\parallel f\parallel }^2.$$ (B.1)

Proposition 2. If A sequence (ɸ_k)_k∊ℐ in ℋ is a frame for ℋ, then $\stackrel{‒}{\mathit{span}}\left\{{\left({ɸ}_k\right)}_{k\in \mathcal{ℐ}}\right\}$.

Proof. See Christensen (2003, pp. 3–4) for a proof for finite dimensional spaces. The proof for infinite dimensional spaces is essentially the same.

Proposition 3. Let (ɸ_k)_k∊ℐ be a frame for ℋ with bounds A, B,and let U : ℋ → ℋ be a bounded surjective operator. Then (Uɸ_k)_k∊ℐ is a frame sequence with frame bounds A||U⁺||⁻², B||U||², where U⁺ denotes the pseudoinverse operator of U.

Proof. See Christensen (2003, p. 94).

Definition 10. The frame operator of the frame (ɸ_k)_k∊ℐ is the mapping S : ℋ → ℋ defined by

$$\mathit{Sf}=\sum _{k\in \mathcal{I}}\langle f,{ɸ}_k\rangle {ɸ}_k.$$ (B.2)

Proposition 4. Let (ɸ_k)_k∊ℐ be a frame for ℋ with frame operator S. Then

1. S is bounded, invertible, self-adjoint, and positive.

2. For all f ∊ ℋ we have

   $$f=\sum _{k\in \mathcal{I}}\langle f,S^{-1}{ɸ}_k\rangle {ɸ}_k,$$ (B.3)

   where S ⁻¹ is the inverse of the frame operator.

Proof. See Christensen (2003, pp. 90–91).

Finally we state some basic results about frames of exponentials and their relationship to frame sequences in the space of band-limited functions.

Definition 11. A sequence (λ_k)_k∊ℐ is called relatively separated if there exists an ε ₀ such that for any n, m ∊ ℐ, we have |λ_m − λ_n| ≥ ε.

The following result is due to Jaffard (1991).

Lemma 1. (Jaffard's lemma). Let Λ = (λ_k)_k∊ℐ be sequence of real numbers that is relatively separated. Let N(a, b), be the number of elements of Λ that are contained in the interval (a, b). Then the sequence (exp(−i λ_k ω))_k∊ℐ generates a frame for the space L² (−Ω, Ω) if

$$D=\underset{t\to \infty }{\lim \inf }\underset{t_0\in \mathbb{ℝ}}{\mathit{inf}}\frac{N(t_0,t_0+t)}{t}>\frac{\Omega }{\pi }.$$ (B.4)

Proof. See Jaffard (1991).

This result is connected to results about frames in the space of band-limited functions by the following proposition:

Proposition 5. If the sequence (exp(−i λ_k ω))_k∊ℐ is a frame for the space L²(−Ω, Ω), then the sequence (g(t − λ_k))_k∊ℐ is a frame for the space of bandlimited function Ξ.

Proof. Let ℱ denote the Fourier transform. Then we clearly have ℱg(t − λ_k) = e^{−i λk ω}. By definition, the sequence (g(t − λ_k))_k∊I is a frame for Ξ if there exist positive constants A, B > 0 such that

$$A{\parallel u\parallel }^2\le \sum _{k\in \mathcal{I}}{\mid \langle u\left(t\right),g(t-{\lambda }_k)\rangle \mid }^2\le B{\parallel u\parallel }^2,$$ (B.5)

for all u ∊ Ξ. From Parsevals identity, we have that ∥u∥ = ∥ℱu∥ and 〈u(t), g(t − λ_k)〉 = 〈(⌒u)(ω), e^−iλ_kω〉 . Therefore equation B.5 can be rewritten as

$$A{\parallel \mathcal{ℱ}u\parallel }^2\le \sum _{k\in \mathcal{I}}{\mid \langle \left(\mathcal{ℱ}u\right)\left(\omega \right),e^{-i{\lambda }_k\omega }\rangle \mid }^2\le B{\parallel \mathcal{F}u\parallel }^2.$$ (B.6)

But this holds since ℱu ∈ L²(−Ω, Ω), and the sequence (exp(−i λ_k ω))_k∊I is a frame for the space L²(−Ω, Ω)

Appendix C: Three Frames

Lemma 2. Assume that the lower density of spikes satisfies the Nyquist rate, that is, $D\frac{\Omega }{\pi }$. The following holds:

1. $\left(g(t-s_k^j)\right)$, k ∊ ℤ, j = 1, …, N, with $s_k^j=(t_{k+1}^j+t_k^j)∕2$, is a frame for Ξ

2. $\left({\psi }_k^j\left(t\right)\right)=({\tilde{h}}^j\ast g)(t-s_k^j)$, k ∊ ℤ, j = 1, …, N, is a frame for Ξ

3. $\left({ɸ}_k^j\left(t\right)\right)=({\tilde{h}}^j\ast g\ast 1_{[t_k^j,t_{k+1}^j]})\left(t\right)$, k ∊ ℤ, j = 1, …, N, is a frame for Ξ,

provided that the filters h^j, j = 1,…, N, are BIBO stable and thire spectral support is a superset of [−Ω, Ω].

Proof. (i) The derivation is based on Jaffard's lemma (Jaffard, 1991) (lemma 1, appendix B) and is given in proposition 5 in the same appendix. See also Jaffard's lemma for a definition of D, the lower density of the spikes.

(ii) Let S be the frame operator of the frame $\left(g(t-s_k^j)\right)$, k ∊ ℤ, j=1, … ,N (the definition of the frame operator is given in appendix B). Then each function u ∊ Ξ has a unique expansion of the form

$$u=\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^{j}g(t-s_k^j),$$ (C.1)

with $a_k^j=\langle u,S^{-1}g(\cdot -s_k^j)\rangle$. Note that any operator defined on the functions of the frame is well defined for the whole space of band-limited functions Ξ. Let us now define the nonlinear operator 𝒰 : Ξ ↦ Ξas

$$\mathcal{U}u\equiv \mathcal{U}\left(\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^{j}g(t-s_k^j)\right)\triangleq \sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^j{\psi }_k^j\left(t\right).$$ (C.2)

.

In order to prove that the sequence of functions $\left({\psi }_k^j\left(t\right)\right)$, k ∊ ℤ, j=1,…N, is a frame for Ξ, we a key proposition from Christensen (2003, p. 94), also included as proposition 3 in appendix B. According to propostion 3, the family $\left({\psi }_k^j\right)$, k ∊ ℤ, j=1,…N is a frame for Ξ, if the operator 𝒰 is bounded and has closed range. To show these two properties, we observe that 𝒰 can be written as the synthesis of N operator 𝒰¹ , … 𝒰^N with 𝒰ⁿ :Ξ ↦ Ξ,n = 1, 2, … ,N defined as

$${\mathcal{U}}^{n}u\equiv {\mathcal{U}}^n\left(\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^{j}g(t-s_k^j)\right)\triangleq \sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^n({\tilde{h}}^n\ast g)(t-s_k^n)+\sum _{j=1j\ne n}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^{j}g(t-s_k^j).$$ (C.3)

Then 𝒰 = 𝒰¹𝒰²,…𝒰^N, and 𝒰 is bounded and has closed range whenever all operators 𝒰ⁱ, i = 1, 2,… N, are But 𝒰ⁱ is bounded if and only if the filter with impulse response ĥⁱ (t), and therefore also the one with hⁱ (t), is BIBO stable.

Moreover, 𝒰ⁱ has closed range if for any sequence u_n ∈ Ξ n ∊ ∊ ℕ that converges to u ∊ Ξ the sequence 𝒰ⁱu_n also converges to an element in Ξ. Since the sequence $\left(g(t-s_k^j)\right)$, k ∊ ℤ, j = 1, …N is frame for Ξ, u_n ∊ Ξ can be represented as

$$u_n\left(t\right)=\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_{k,n}^{j}g(t-s_k^j),$$

with $a_{k,n}^j=\langle u_n,S^{-1}g(\cdot -s_k^j)\rangle$ and

$$u\left(t\right)=\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^{j}g(t-s_k^j),$$

with $a_k^j=\langle u,S^{-1}g(\cdot -s_k^j)\rangle$. From the continuity of the inner product, it follows that ${\lim }_{n\to \infty }{a}_{k,n}^j=a_k^n$, and therefore we have that lim_n→∞Uⁱu_n= Uⁱuε Ξ. Therefore the operator U has closed range and $\left({\psi }_k^j\right)$, k ∊ ℝ, j = 1, … , N is a frame. To ensure that the operator U spans the whole space Ξ, it suffices that the frequency support of each filter is a superset of [−Ω,Ω].

(iii) Since $\left(g(\cdot -s_k^j)\right)$, k ∊ ℤ, j = 1, … , N, is a frame for the space of band-limited functions with finite energy, any function u ∊ Ξ can be uniquely represented as

$$u\left(t\right)=\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^{j}g(t-s_k^j)$$ (C.4)

for all t, t ∊ ℝ, with $a_k^j=\langle u,S^{-1}g(\cdot -s_k^j)\rangle$, where S frame operator. Consider the operator 𝒰 : Ξ ↦ Ξ defined as

$$\mathcal{U}u\left(t\right)\triangleq \mathcal{U}\left(\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^{j}g(t-s_k^j)\right)=\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^j(g\ast 1_{[t_k^j,t_{k+1}^j]})\left(t\right).$$ (C.5)

The right-hand side of equation can be rewritten as

$$\begin{array}{cc}\hfill \mathcal{U}u\left(t\right)& =\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^j{\int }_{t_k^j}^{t_{k+1}^j}g(t-s)\mathit{ds}\hfill \\ \hfill & =\sum _{j=1}^N\sum _{k\in \mathbb{\mathbb{Z}}}{a}_k^j\left({\int }_t^{+\infty }g(s-t_{k+1}^j)\mathit{ds}-{\int }_t^{+\infty }g(s-t_k^j)\mathit{ds}\right).\hfill \end{array}$$ (C.6)

The integral operator is bounded, and the sequence $\left(g(\cdot -t_k^j)\right)$, k ∊ ℤ j =1, 2, … ,N, is a frame because of the Nyqist density condition in Jaffard's lemma. Therefore, the operator 𝒰 is bounded. Moreover by following a similar reasoning as before, 𝒰 has closed range. Proposition 3 implies that $\left((g\ast 1_{[t_k^j,t_{k+1}^j]})(\cdot )\right)$, k ∊ ℤ ,j = 1, … ,N, is a frame for Ξ. Finally by working as in (ii), we conclude that $\left({ɸ}_k^j\right)$, k ∊ ℤ, j = 1, … , N is also a frame for Ξ