Structural insights for designed alanine-rich helices: Comparing NMR helicity measures and conformational ensembles from molecular dynamics simulation

Abstract

The temperature dependence of helical propensities for the peptides Ac-ZGG-(KAAAA)₃X-NH₂ (Z = Y or G, X = A, K, and d-Arg) were studied both experimentally and by molecular dynamics simulations. Good agreement is observed in both the absolute helical propensities as well as relative helical content along the sequence; the global minimum on the calculated free energy landscape corresponds to a single α-helical conformation running from K4 – A18 with some terminal fraying, particularly at the C-terminus. Energy component analysis shows that the single helix state has favorable intramolecular electrostatic energy due to hydrogen bonds, and that less-favorable two-helix globular states have favorable solvation energy. The central lysine residues do not appear to increase helicity; however, both experimental and simulation studies show increasing helicity in the series X = Ala → Lys → d-Arg. This C-capping preference was also experimentally confirmed in Ac-(KAAAA)₃X-GY-NH₂ and (KAAAA)₃X-GY-NH₂ sequences. The roles of the C-capping groups, and of lysines throughout the sequence, in the MD-derived ensembles are analyzed in detail.

INTRODUCTION

Helix-coil theory is one of the most fundamental and intensively studied aspects of biomolecular structure formation¹. There are several reasons: first, the α-helix is a key secondary structure element in globular protein structure². Second, there are several experimental methods available which can detect the α-helical content. Third, the formation of α-helices is fast (sub-microsecond scale) relative to folding of proteins with multiple secondary structure units. This fast rate permits the all-atom simulations of α-helix formation and also makes helix formation a likely pre-transition state equilibrium event in the folding of proteins with multiple secondary structure units.

Helix formation has long been known to show significant cooperativity, with coupling of hydrogen bonding and ϕ/ψ propensities between neighboring residues indicated by early theoretical^3–5, and experimental^{6, 7} studies. The recent investigations of amyloid fibrils have also found that sequences that adopt α-helices in globular proteins can form β–strands in amyloid aggregates^{8, 9}. The quest to understand these secondary structure transitions has, once again, brought helix studies into the spotlight.

Designed alanines-rich helices in which solubility is enhanced through inclusion of polar residues (most commonly Lys and Arg), are the most common short sequences used to study helix formation both experimental^{7, 10–15} and in MD simulations^15–18. Other roles, including solvation changes that increase helicity,^7,18 have been suggested for the Arg and Lys residues in designed helices.^7,17–19 MD simulations of Ala-rich helices of this type have been carried out using both continuum and explicit solvent models. Helix bundles, sequences with two helical segments in close association in a more globular state, have been predicted to be the low energy state for (AAARA)-repeat peptides in continuum solvent models¹⁷, particularly at somewhat warmer temperatures¹⁶. More typically, ensembles are dominated by single helix structures. Incorrect parameterization of H-bonds has been proposed as the reason for the differences.¹⁷ Sequence differences could also play a role, but the same sequence has yielded both types of structures depending on the solvent model and temperature. With residue-specific measures of helicity these states should be distinguishable.

We now report NMR and molecular dynamics simulation studies on a series of peptides of the general form N-cap-(KAAAA)₃-C-cap. One series is very closely related to the parent system (Ac-YGG-(KAAAA)₃-K-NH₂) of the series used by the Baldwin group and others to determine the propagation values of X in Ac-YGG-(KAXAA)₃-KNH₂ and other helical peptides.^12–14 Contrary to the prior theoretical predictions that peptides of such a short length would not adopt measurable helix content in aqueous solution, Marqusee et al.¹⁰ demonstrated that peptides containing lysine and alanine can be as much as 70% helical in water and this is usually attributed to a uniquely large helix propensity of alanine. Other experimental studies have shown that the α-helix conformation is not favorable for short polyalanine peptides in water at room temperature^7,20,21, and several roles have been suggested for the stabilizing effects of polar side chains, particularly Lys and Arg.^7,17,18 Other simulations, particularly in continuum solvent models, suggest that polar sidechains do not increase helicity,¹⁷ and recent experimental studies have provided propagation values for alanines (1.6) and a non-terminal lysine (0.82) that are in accord with those from the Baldwin group and not indicative of helix stabilization by the lysine side chain when it is not in the C-terminal turn of the helix.²² Positive charges at the C-terminus of a helix are expected to favor helix formation due to a favorable interaction with the helix macrodipole. d-Arg has been reported to be a particularly favorable C-cap.²³ Explicit solvent simulation has suggested that charged side chains throughout the sequence can favor helix formation by shielding the intramolecular backbone hydrogen bonds from exposure to solvent¹⁸. As a result, this study also focuses on the contributions of the charged residues to the stabilization of the helix conformation. In this report, the results from all-atom simulations are compared to those obtained primarily from NMR experiments. There is excellent agreement regarding both the distribution of helicity along the sequence and the net helicity that provides: a validation of our simulation protocols and force field parameters, a determination of relative C-capping capabilities, and an atomic-detail model for the structure ensembles that give rise to the experimental observables.

MATERIALS AND METHODS

Peptide synthesis and purification

Peptides were synthesized on an Applied Biosystem 433A synthesizer employing standard Fmoc solid-state peptide synthesis methods and were acetylated while still on-resin. Rink resin provided an amidated C-terminus upon cleavage using 95% trifluoroacetic acid, with 2.5% triisopropylsilane and 2.5% water present. The cleavage products were purified using reverse-phase HPLC on a Varian C¹⁸ preparatory-scale column with gradients of water and acetonitrile spiked with 0.1% and 0.085% trifluoroacetic acid, respectively. Collected fractions were lyophilized and their identity and molecular weight confirmed on a Bruker Esquire ion trap mass spectrometer. The following peptides (r = d-Arg, A = ¹³C=O-labeled alanine) were synthesized specifically for this study: (Ac-) indicates that these series of peptides were examined in both the acetylated and non-acetylated form.

(Ac-)KAAAAKGY-NH2	(Ac-)KAAAArGY-NH2	Ac-KGGKAAAAK-NH2
(Ac-)(KAAAA)3KAAAAKGY-NH2		Ac-GGG(KAAAA)3K-NH2
(Ac-)(KAAAA)3XGY-NH2 X = A, K		YGG(KAAAA)3A-NH2
(Ac-)(KAAAA)2KAAAAXGY-NH2 & (Ac-)YGG-KAAAA(KAAAA)2X-NH2 (X = A, r, R)

The single repeat systems were prepared to serve as random coil controls together with the prior data²⁴ for Ac-GKAAAKG-NH₂. The same report provided extensive chemical shift deviation (CSD) data for Ac-YGG-KAAAA(KAAAA)₂K-NH₂. With the exception of the single repeat systems, several alternate isotopomers were made of each peptide in order to establish secure assignments of the shifts of the different ¹³C=O labeled sites. The four repeat system, Ac-(KAAAA)₃KAAAAKGY-NH₂, was used to determine whether larger structuring shifts could be obtained with a longer, more stable helix. The largest structuring shift observed for a four-repeat peptide to date is +3.41 ppm for GASEDEAAAAK(AAAAK)₂GY-NH₂ [James Stewart, unpublished data²⁵].

Experimental Measures of Helicity

CD spectroscopy

Circular dichroism stock solutions were prepared by dissolving weighed amounts of peptide in 20 mM aqueous pH 7.0 phosphate buffer to make solutions with a circa 700 µM peptide concentration. The concentration of stock solutions of peptides containing a tyrosine residue was determined by UV based on the absorptivity coefficient, ε = 1420 M⁻¹ cm⁻¹ at 276 nm due to tyrosine. CD samples were diluted appropriately with buffer to obtain 35 µM peptide solutions. Spectra were recorded on a Jasco J720 spectropolarimeter using 0.10 cm pathlength cells. The calibration of the wavelength and degree ellipticity scales has been described previously^26,27. Typical spectral accumulation parameters were a scan rate of 100 nm/min and a 0.2 nm step resolution over the range of 190–270 nm with 16 scans averaged for each spectrum. The accumulated average spectra were trimmed at a dynode voltage of 600 V prior to blank subtraction and smoothing, the latter of which used the reverse Fourier transform procedure in the Jasco spectra analysis software. For melting experiments, the temperature was increased from ca. 275K to 340K in 5° to 10° increments, depending on the degree of resolution required to elucidate the response. Each step was equilibrated at the target temperature for at least five minutes before data was acquired; larger temperature changes were provided additional time. CD data is reported in residue-molar ellipticity units (deg cm²·residue·dmol⁻¹).

NMR spectroscopy

¹³C-NMR experiments were routinely performed on Bruker DRX-500 or AV500 spectrometers, with occasional use of a DMX750 to improve resolution when the ¹³C’ signals were badly overlapped. The samples consisted of ca. 2 mM peptide in 20mM phosphate buffer at pH 7.0 with 10% D₂O. All samples also contained 0.005mM ¹³C-labeled urea as a chemical shift reference. Sodium 2,2-dimethyl-2-silapentane-5-sulfonate (DSS) was used as the direct or indirect (below) internal chemical shift reference and set to 0 ppm for all conditions independent of temperature, pH, and co-solvent concentration. The method has been described in greater detail in an account of prior studies of Ac-YGG-(KAXAA)₃-K-NH₂) with X = A, V.²⁴ The chemical shift of ¹³C-urea is given by (165.609 ∓ 0.0056 T ppm, T = °C). Unlike other experimental methods, this method can determine the fractional helicity at individual residue sites.

Determining chemical shift deviations (CSDs) and fractional helicities

The reference chemical shifts for the unstructured state of ¹³C’-Ala probes was, with two exception, in the range 177.59 – 177.70 ppm at 280K; both the AAAK- and -KAAAA-(d-Arg)- values were downfield, in the 177.91 – 178.05 range depending on the C-terminal sequence. All these resonances shift upfield on warming, 0.007 – 0.012 ppm/°C, a feature that must be taken into account in calculating melting curves. When a full sequence identity was not available in a control peptide, the effects of replacing Lys and/or Gly by Ala was assumed to correspond to the differences in the sequence-dependent corrections reported by Schwarzinger et al.²⁸ The specific sequence-dependent random coil values employed are available upon request. CSDs are converted to fractional helicities assuming that a 0 – 100% helicity structuring shift at all but the extreme termini corresponds to +3.50 ppm. The following corrections were applied at the termini for Ncap-N1(=K)-N2-N3 - - - C3-C2-C1-Ccap(=K or d-Arg) sequences – +0.25 (N2), +0.10 (N3), −1.15 (C2), −1.3ppm (C1). The N-terminal adjustments reflect helix macrodipole effects; the larger corrections at the C-termini reflect these and the absence of a helical H-bonding interaction. When the C-cap residue does not have a positively charged sidechain to offset helix macrodipole, the Cterminal corrections are larger: −1.25 (C2) and −1.45ppm (C1). The large C-terminal corrections (as much as a 41% reduction in the 0 – 100% helicity structuring shift), are based on both theoretical and experimental measures of this effect. As previously noted²⁴, a priori calculations of the H-bond effect²⁹ suggest a 1.4 ppm contribution. Park et al.³⁰ deconvoluted experimental ¹³C’ melts and arrived at the following %-contributions: 32% backbone geometry, 35% hydrogen bonding by the NH in the amide unit, and 33% by hydrogen bonding to the ¹³C=O. A recent study of a miniprotein helix suggest that the central residue 100% shift may be as large as 3.7 ppm, with H-bonding responsible for 54% of the shift.³¹ The resulting uncertainty in the adjustments introduces additional error into derived fractional helicity measures for the two C-terminal sites in a helix.

Computational Studies

Replica exchange molecular dynamics simulations

Standard molecular dynamics simulations can become trapped in local minima during computationally affordable simulations. Therefore, replica exchange molecular dynamics (REMD)^32,33 (also known as parallel tempering MD³⁴) was used as an enhanced sampling method for this study. We used REMD as implemented in AMBER version 8³⁵ following procedures we reported previously³⁶. REMD employs multiple non-interacting replicas of the system that are simulated independently and simultaneously at several different temperatures. At intervals of 1 ps, exchanges were attempted between conformations at neighboring temperatures based on a Metropolis-type criterion that considers the probability of sampling each conformation at the alternate temperature. The advantage of this method is that the simulations can escape from kinetic traps by “jumping” into alternate local minima being sampled more efficiently at higher temperatures. We employed 12 replicas at 253, 276, 300, 326, 355, 386, 420, 457, 497, 541, 588, and 640 K.

A modified force field based on AMBER parm94³⁷ was used to represent the peptide. Many AMBER parameter sets have been reported to over stabilize α-helical structure^38,39. In the parameters that we used, the torsional angle terms were adjusted to reduce this tendency⁴⁰. The generalized Born implicit solvent model^41,42, with intrinsic Born radii taken from Tsui and Case⁴³ as implemented in AMBER, was used to represent the effects of solvent. All non-bonded interactions were evaluated at every step. The SHAKE algorithm⁴⁴ was used to constrain the bonds involving hydrogen atoms. A 0.002 ps time step was used. Each replica was coupled to a constant-temperature bath using a weak-coupling algorithm⁴⁵. The REMD simulations were carried out for 56 nanoseconds (a total of 672 ns simulation), and 56,000 snapshots were saved for each temperature. The REMD simulations were performed for three sequences: AcGGG-(KAAAA)₃-X-NH₂ with X = Lys, d-Arg and Ala.

Analysis of secondary structure content

To compare our results with previous studies, Lifson-Roig helix-coil theory^5,14,46 has been used. In Lifson-Roig theory, there are three states for residues: the “c” state is the residue in random coil conformation, “w” is the residue in helical conformation, and its previous and next neighbor residues are in helical conformation as well, and “v” is a helical residue neighboring with one or two non-helical residues. Overall helical content corresponds to the number of w state residues, with a maximum helix length of N−2 for N residues. Following the work of Garcia and Sanbonmatsu¹⁸ and Sorin and Pande⁴⁷, a residue is considered in a helical conformation if ϕ = −60(±30)° and ψ = −47(±30)°. The melting curve is generated based on the temperature dependence of the average helical fraction (f_H), calculated using equation 1, where Nw is the number of w-state residues assigned by Lifson-Roig theory and N is the total number of residues. In order to correspond to experimental melting measurements, only the K4 to X19 sequence is considered, setting N to 16 and the maximum helix length to 14.

$$f_H=Nw/(N-2)$$ Equation 1

To complement this approach, we also used DSSP⁴⁸ (as implemented in the ptraj module of AMBER) to analyze secondary structure content.

Free energy landscapes

We reconstructed free energy landscapes using principle component analysis (PCA), as implemented in ptraj, to define the reaction coordinates and 2-D histogram analysis to obtain relative free energy for each bin. Due to their high flexibility, Gly residues were not included in this analysis. The alpha carbon coordinates of all other residues were used to generate the covariance matrix. The two largest eigenvalues from the PCA analysis were used to represent order parameters. These two eigenvectors represent only 42% of the total fluctuations in the system, suggesting that more than 2 coordinates are required for a comprehensive view of the free energy landscape even for this short peptide. The relative free energy of each bin was calculated via equation 2, where x is a histogram bin corresponding to a set of PCA eigenvector values, G(x) is the free energy relative to the most populated bin, R is the gas constant, T is the temperature, P(x) is the population in bin x and P(x0) represents the population of the most populated bin.

$$\mathrm{G}(\mathrm{x})=-\mathrm{R}\mathrm{T}\text{log}(\mathrm{P}(\mathrm{x})/\mathrm{P}(\mathrm{x}0))$$ Equation 2

Structure analysis

Cluster analysis was used to separate the ensembles into conformational families and representative structures. Moil-view⁴⁹ was used to perform the cluster analysis using backbone RMSD for non-Gly residues as a similarity criterion, with average linkage. Clusters were formed with a bottom-up approach using a similarity cutoff of 2.5 Ǻ. The radius of gyration (R_gyr) was also used to characterize structural properties of the overall ensemble and individual clusters. The carnal module of AMBER was used for Rgyr calculation. All alpha carbon atoms of non-Gly residues were included in this analysis.

Energy decomposition analysis

To analyze the relative importance of various energy components in different structure families, energy decomposition analysis was carried out using post-processing in the sander module of AMBER. Average total energies were separated into electrostatic, van der Waals and GB solvation terms.

Estimation of simulated data uncertainties

Lower bounds to data uncertainties were estimated as the absolute value of the difference between properties obtained using the entire ensemble sampled and that using only the second half of the data set.

RESULTS AND DISCUSSION

All NMR and CD studies were performed in low ionic strength media (20 mM phosphate, no added salt) in order to retain unscreened Coulombic effects that might be present due to Lys and Arg sidechains as well as, when present, the uncapped N-terminus. CD has been the classic method for accessing net helicity with the [θ]₂₂₂ value as the standard measure. Baldwin & Luo provided the most commonly used equation for converting CD data to a measure of the net per cent helicity. The [θ]₂₂₂ value for 100% helicity is given by θ₂₂₂ = (1 – 1/Nr) (−44000 + 250 T).⁵⁰ For the three repeat systems in the present study, Nr = 16. The thermal gradient of θ₂₂₂ for 100% helicity in this equation is, however, nearly twice as large as the experimental value observed for stable helical proteins and coiled coils well below their melting transitions; this has prompted us to employ a circa 0.38%/°C, rather than 0.57%/°C, loss of ellipticity for the 100%-folded baseline in our calculations of CD melts.^{51, 52} The temperature dependence of the random coil state for (KAAAA)-repeat peptides bearing a single tyrosine residue separated from the helix N-terminus is θ₂₂₂ = +2120 – 64T.⁵¹ In the present study, CD is used only in a qualitative manner, with data appearing in Table I and full CD melts for several species in the Supporting Materials (Figure S1).

TABLE I.

NMR Structuring Shifts and CD Measures of Helicity for Peptides with Different N- and C-Capping Motifs

Peptide Sequence	13C=O structuring shifts at 280K			CD, 278K
	A4	A8	A9	− [θ]222
Ac-GGG(KAAAA)3K-NH2	2.37	2.41	n. d.	n.d.
YGG(KAAAA)3A-NH2	1.98	2.07	1.82	18,700
Ac-YGG(KAAAA)3A-NH2	2.29	2.28	2.01	16,700
Ac-YGG(KAAAA)3K-NH2	2.22	2.33	1.98	21,400a
Ac-YGG(KAAAA)3R-NH2	n. d.	2.51	n. d.	19,300
Ac-YGG(KAAAA)3r-NH2	n. d.	2.45	2.05	18,700b
(KAAAA)3rGY-NH2	0.87	1.01	0.90	2,900
Ac-(KAAAA)3AGY-NH2	2.30	2.34	2.01	11,900
Ac-(KAAAA)3KGY-NH2	2.54	2.51	2.18	12,200
Ac-(KAAAA)3rGY-NH2	2.47	2.43	2.16	14,300
Ac-(KAAAA)3KAAAAKGY-NH2	2.94	3.13	2.85	18,700
(KAAAA)3KAAAAKGY-NH2	1.54	2.18	2.08	n.d.

^aPrior value from a graph reported by Andersen et al.⁵¹

^bHuang et al.¹¹ reported [θ]₂₂₂․ = −18,300°.

Experimental Helicities from NMR Data

Helix formation results in a downfield shift at ¹³C=O sites^53,54 and the resulting structuring shifts melt out. Representative CSD data, and a comparison with CD measures, appear in Table I. CD comparisons between the different series of peptides in this study suggested that the CD value for a comparable degree of helicity at central sites (A8 and A9 in these peptides) were not directly comparable. One rationale for this observation, is that the contribution due to the Tyr sidechain⁵⁵ is different when the residue is placed near the C- rather than N-terminus of the helix; the -(KAAAA)₃GY-NH₂ series peptides always display lower CD values than YGG-(KAAAA)₃ species with comparable NMR measures of helicity. The Tyr sidechain contribution also appears to be different for Ac-YGG- versus YGG-. Over the systems examined in the present study, the CD data suggested helix termination with d-Arg rather than Lys or Ala, did not uniformly increase the value of [θ]₂₂₂. The largest increase (21%) was observed in the Ac-(KAAAA)₃XGY-NH₂ comparison (X = r versus A) and was not accompanied by a comparable increase in the CSDs at the labeled central alanine sites. As a result, we employ only the NMR data in the present comparisons of experimental measures of helicity and those observed in MD simulations.

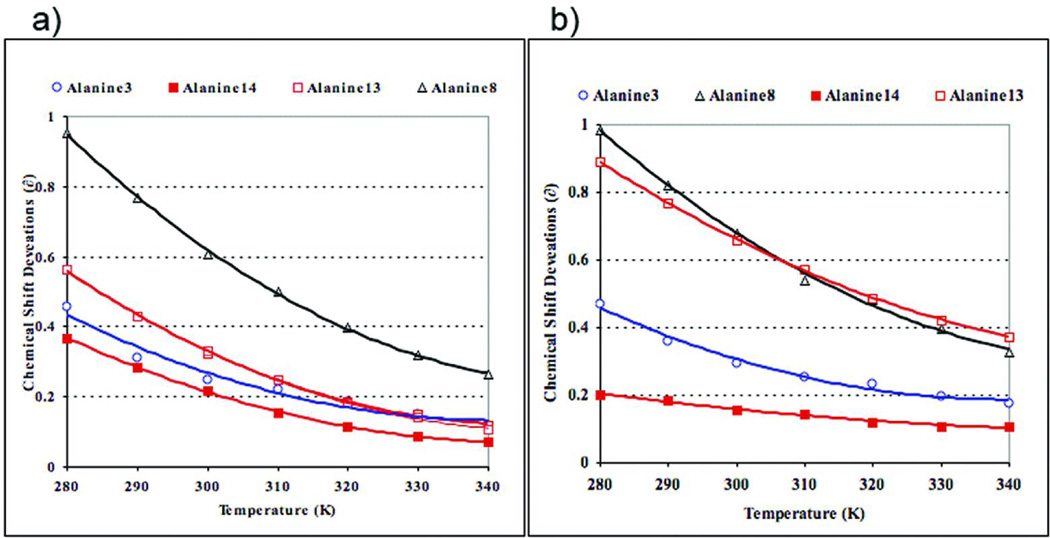
Turning to our analysis of the ¹³C=O chemical shift data, initially we employed the reference shifts previously derived from Ac-GKAAAKG-NH₂²⁴ as coil controls for estimate structuring shifts. When this method was used over complete melting curves, chemical shift deviation (CSD) versus T, anomalies were observed. For the Cterminal ¹³C’-Ala sites of a number of peptides, particularly the less helical ones lacking a positively charged residue at the C-terminus or a capping unit at the N-terminus, the melting data provided “negative” CSDs as helicity melted out at the higher temperatures. The melting data, as CSD vs T(°C) for four sites (A3, A8, A13, and A14) of (KAAAA)₃XGY-NH₂ (X = K, r ) appear in Figure 1. The exaggerated downfield shift (0.89 ppm) at A13 for X = r, (vs 0.56 ppm for X = K), with little change at the central sites, was initially taken as possible evidence for a d-Arg16 sidechain-NH → O=C-A13 H-bond which would be present in a specific C-capping interaction by d-Arg. However, the melting data A13 in the X = r peptide suggests that the high temperature unfolded limit corresponds to a non-zero (positive) CSD: the CSD at this site, calculated using the prior random coil values, did not melt out as much as central sites in the same peptide and the corresponding site in the Lys-terminated helix. The X = r versus K CSD difference at A13 is also retained (1.61 vs 1.39 ppm) in the more helical Ac-(KAAAA)₃XGY-NH₂ species. These observations prompted us to prepare a new series of more closely matched reference peptides: Ac-KGGKAAAAK-NH₂ and -KAAAAXGY-NH₂ (X = K, r) with and without an N-acetyl cap. In KAAAAKGY-NH₂, the two labeled sites were essentially shift coincident (δ²⁹⁰ = 177.43 ± 0.02 ppm); acetylation induced downfield shifts (and a small extent of factional helicity) and increased the Δδ for the two probes to 0.045 ppm. In the corresponding d-Arg-GY-NH₂ terminated series, the Δδ for the two labels was 0.38 ± 0.02 ppm independent of whether acetylated or not. A similar Δδ is observed at the melting limit in panel b of Figure 1; thus, the downfield shift of A13 cannot be attributed to a helix-capping interaction. Rather it appears to be a random coil shift effect of d-Arg. A new set of position and N-terminus capping specific reference values for 0% helicity was derived based on the expanded set of reference peptides available. The ¹³C=O shifts in KAAAAXGY-NH₂ (X = K, r) display a temperature gradient of − 0.008 ± 0.0005 ppm/°C. In the N-capped reference peptides, the ¹³C=O shift gradient was − 0.011 ± 0.0014 ppm/°C. These values were used to correct the reference shifts in melting studies.

FIGURE 1.

Structuring shift melts for the non-acetylated (KAAAA)₃X peptides with X = Lys (a) and d-Arg (b). Random coil shifts were derived from AcGKAAAKG-NH₂ and thus assume no differences in sequence effect for Lys and D-Arg. The more remote probes, A3 and A8, are, presumably, not influenced by the C-terminal substitution; these indicate that the D-Arg species is slightly more helical and resistant to melting.

All comparisons with computed ensembles, require a measure of the structuring shift expected for 100% helicity so that the fractional helicity (f_H) can be calculated. In prior studies²⁴, ¹³C’ CSDs were converted to fractional helicities using equation 3. This equation resulted from cross-calibration ¹³C’-CSD melts with IR and CD melts. Both of these, however, required making some assumptions about the “100%-folded parameters” for other spectroscopic assays.

$${\mathrm{f}}_{\mathrm{H}}(\mathrm{T})=({\mathrm{\delta }}_{\text{obs}}-{\mathrm{\delta }}_{\text{ref peptide}})/(3.040+0.00715\mathrm{T}(°\mathrm{C}))$$ Equation 3

The NMR study of Ac-(KAAAA)₃KAAAAKGY-NH₂ (given, in part in Table 1) yielded structuring shifts greater than the maximal value from equation 3. Helices with a 21-residue span with more effective caps have CSD values as large as 3.41 ppm; since 100% helicity cannot be achieved, as a result, we use equation 4 to convert CSDs to fractional helicities in the present account.

$${\mathrm{f}}_{\mathrm{H}}(\mathrm{T})=({\mathrm{\delta }}_{\text{obs}}-{\mathrm{\delta }}_{\text{ref peptide}})/(3.50+0.006\mathrm{T}(°\mathrm{C}))$$ Equation 4

Given the small remaining error in CSDs, this equation should provide residue-specific fractional helicities that are accurate to 0.03. This degree of accuracy, however, applies only to central portions of helices, and still assumes that there are no position specific structuring shift differences in the fully helical state. Errors are greater, particularly at the C-terminus, due to uncertainty about the contribution of H-bonding to the helical CSD (see Methods). In addition, the current corrections at C-terminal sites may be more problematic for the helices with a DArg C-cap.

For now, however, the data is presented as CSDs rather than fractional helicities. The first question we address is the relative helix stabilizing effects of N-caps. All of the helix ensemble simulations employ Ac-GGG as the N-cap. We wanted to be able to use the more extensive labeling available from the prior studies of Ac-YGG-KAAAAKAAAAKAAAAK-NH₂ and the newly synthesized Ac-(KAAAA)₃-XGY-NH₂ peptides in comparisons of sequence position dependence of helicity with simulated conformational ensembles. The calculated CSDs for a variety of N-capped (and uncapped) species bearing Lys, Ala, and d-Arg (r) at the C-terminus appeared in Table I.

Experimental measures of N- and C-capping

With the exception of the long, (KAAAA)₄K, helix, N-capping is essential for obtaining systems displaying fractional helicities greater 0.40 (CSD ≥ 1.4) at any position. This is the case even with the d-Arg C-cap species: the maximal central repeat CSD value corresponds to f_H = 0.29 for (KAAAA)₃ rGY-NH₂ and indicates that the best reported²³ C-cap does not lead to greatly enhanced helicity at the center of the helix in these systems. From the NMR data in Table I, it is apparent that the N-capping effects of Ac-GGG, YGG and Ac-YGG are very similar and likely result from the effect of two glycines before a helical segment; further, these capping effects are nearly as large as those observed for N-acetylation. A quantitative treatment of N-capping effects will appear in a subsequent publication; for now our attention is focused on the effects of the C-capping residues.

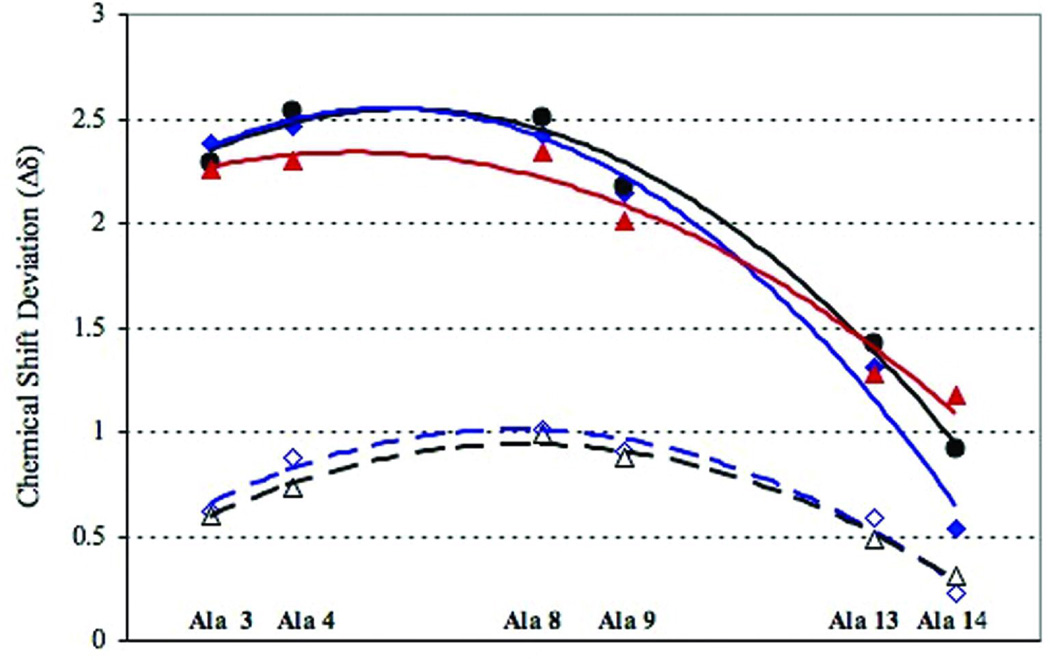
Figure 2 collects the CSD data for a series of peptides that probe C-capping effects, Ac-(KAAAA)₃XGY-NH₂. The Lys- and d-Arg-terminated sequences are distinctly more helical than the Ala-terminated sequence, but still display a loss in structuring shifts near the C-terminus with little loss at the N-capped terminus. Enhanced f_H values at central helical positions for the d-Arg vs Lys C-capped sequences is only evident in the non-acetylated species. While field effects due to the helix macrodipole, positive near the N-terminus and negative at the C-terminus, are expected to change the CSD corresponding to 100% helicity at the termini (see Methods section), the near absence of N-terminal fraying is still evident. N-capping effects are very substantial; the comparisons in Table I provided a number of examples of the N-capping effect on structuring shifts as does the acetylated versus non-acetylated examples in Figure 2. In the absence of an N-capping unit, fraying reappears at the N-terminus.

FIGURE 2.

The CSDs observed for Ac-(KAAAA)₃XGY-NH₂ (X = A, K, d-Arg) at the probed helix positions (initial K = #1) at 280K are shown as filled symbols. The corresponding points for KAAAA(KAAAA)₂-X-GYNH₂ (X = K, d-Arg) are shown as open symbols. The lines are trendlines drawn through the data to guide the eye and have no theoretical significance. Throughout C-caps are color-coded: X = d-Arg points and lines are in blue, Lys in black, and Ala in red. The same color-coding is used in Figure 3.

As previously noted²⁴, the ¹³C’ CSDs towards the C-terminus provide much smaller f_H estimates than those expected based on the AGADIR algorithm⁵⁶ and an extended Lifson-Roig statistical mechanical helix/coil model¹⁴. H-bonding contributions to the ¹³C’ CSD are expected and could be a significant contributor to the net structuring shift. Chemical shift calculations based on density functional theory have previously estimated the contribution of hydrogen bond formation to the ¹³C’ CSD observed for a central helical residue to be as much as 1.4 ppm²⁹; others studies^{30, 31} suggest that as much as 60% the experimental CSD for central residues may be due to H-bonding. In the absence of corrections for H-bond contributions, CSD-derived f_H value calculated for C-terminal ¹³C’ positions would therefore underestimate the degree of folding as the residues are not capable of forming intramolecular, i /i+4 or i/i+3 hydrogen bonds. Corrections applied in comparisons with simulated ensemble statistics are given in the Methods section; for example, the CSD required for 100% helicity at the penultimate site in a (KAAAA)₃A helical sequence is only 59% of the value required at a central residue. Even with these substantial corrections, the experimental data for N-capped species still required more C-terminal fraying than that calculated by current helicity prediction methods. This was one of driving forces for computational studies in the present account.

Direct Comparison of Experimental Data and Helical Ensembles from Computational Simulation

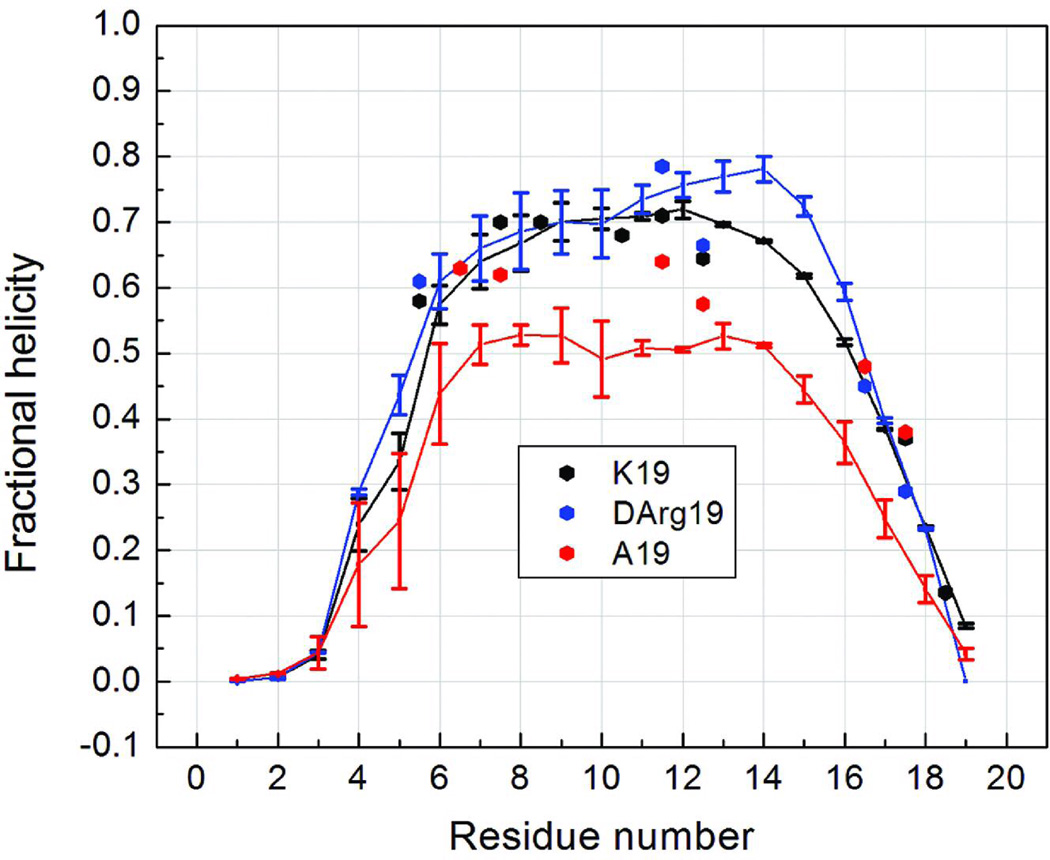
Molecular dynamics simulations were performed for AcGGG-(KAAAA)₃-X-NH₂ with X = Lys, d-Arg and Ala. Henceforth these are designated as peptides K19, dR19 and A19. For all three peptides, the residues which are near the C-terminus have greatly reduced average helical content corresponding to the substantial helix fraying evident in the ¹³C-NMR studies. The GGG units were non-helical (f_H < 0.04) with a rapid helicity increase beginning at K4 consistent with a significant N-capping effect by the GGG unit. The helical domain is viewed as K4 – A18/X19 (X19 can be either a helix C-cap or the frayed end of a helix). [Residue locations are given by the residue number, thus the A8/A9 central probes in Table I and Figures 1 and 2, are, henceforth, designated as A11/A12.] The dynamics simulations indicated a greater overall helicity for peptides K19 and dR19, bearing a positively charged side chain at the C-terminus.

The fractional helicities at each residue generated from NMR data and from the simulation ensembles at 275K are compared in Figure 3. Both methods show that the structure ensembles have sequence-dependent helicity measures, and the computational and experimental results are in good agreement, suggesting that further detailed analysis of the simulated structure ensemble is warranted. The relatively high helical content and flat profile across the central portion of these sequences (Figure 3) suggest that the most populated conformation for the peptides is a single helix, rather than isolated smaller helical fragments. Although this is a reasonable expectation and has been observed in an explicit solvent REMD simulation of a (AAARA)-repeat peptide^15,17, some simulations using GB solvation indicated that a single helix structure was not favored^16,17. This is in disagreement with the present results using GB, but the differences may arise from differences in protein force field model employed in the two studies or possibly sensitivity of the GB model to the identity of the charged residue (d-Arg vs. Lys). Helix-turn-helix conformations have also been reported, as folding intermediates and transition states, in GB AMBER folding trajectory simulations for a (AAAKA)-repeat peptide, but the equilibrated folded state was a single helix with varying degrees of end-fraying.⁵⁷

FIGURE 3.

Fractional helicities at each residue of peptides A19, K19 and dR19. The continuous lines connect perresidue values obtained from REMD ensembles at 275 K. The experimental values (points) are from ¹³C-NMR for the corresponding Ac-YGG-capped peptides; the A19 data was for the peptide lacking the N-terminal acetyl. Since the NMR data reports on the amide linkage between residue i and i+1, we place the experimental point based on the ¹³C=O CSD of residue i halfway between i and i+1 on this plot.

Although the three peptides show similar helical content profiles in Figure 3, the absolute values are different. The largest differences in the simulated ensembles are in the residues in the middle of the sequence: the peptides with charged residues (K19 and dR19) have noticeably higher fractional helicities than the peptide without a positive side chain at the C-terminus (A19). This can be attributed to a favorable sidechain interaction with the helix macrodipole. The helical content profiles of K19 and dR19 are similar. (Other simulations, data not shown, reveal that further decreases in the central helicity of in conformational ensembles of K19 analogs are very modest when the remaining Lys residues are mutated to Ala.) In the simulations shown in Fig. 3, the largest differences are between residues 14–16 in two peptides, with 10% greater helicity for the d-Arg species; this region is not well probed in the experimental study. The experimental probes at A11/A12 do, however, reflect the same trend seen in the simulations. The effects of the C-terminal residue are somewhat greater in the simulations than in the experimental data. The increasing helicity for the C-capping series, Ala → Lys → d-Arg was also experimentally verified for the (KAAAA)₃-XGY-NH₂ peptides (see Figure 2). In both the Ac-(KAAAA)₃-XGY-NH₂ and Ac-YGG-(KAAAA)₃-X-NH₂ series, central repeat Ala ¹³C=O CSDs were comparably increased for X= d-Arg and L-Arg. In both cases, the NMR data indicates that the N-terminal KAAAA repeat is nearly as folded as the central one, with fraying most notable at the C-terminus; the simulations show nearly the same pattern.

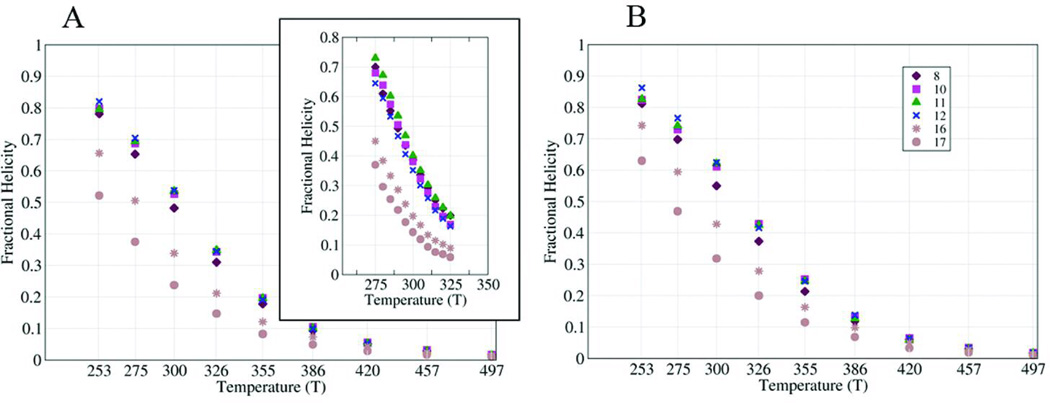
Since the helical profiles from simulation and experiment are in reasonable agreement at low temperature, we examined the stability as a function of increasing temperature (Figure 4). The melting curves for seven Ala residues in an XGG-(KAAAA)₃K-span were obtained through both NMR experiments and simulations. These residues were chosen to probe the termini and the central portion of the sequence (which would be affected by equilibrium between single helix and helix-turn-helix conformations). Melting curves for the simulated ensembles were calculated in two ways: from local phi/psi values (panel A) and from the DSSP algorithm (panel B). The fractional helicities calculated from the chemical shift melts (inset in Figure 4A) are in closer agreement with those from Lifson-Roig theory based on the phi/psi angle in the MD simulated ensembles. The melting curves for the central and N-terminal repeat sites were very similar, with enhanced melting observed in the less structured C-terminal repeat, particularly in the experimental data. In general, melting curves generated by the simulations are flatter than the ones from the NMR experiments, likely due to the lack of temperature dependence in the continuum solvent model that we employed.

FIGURE 4.

Average α-helical propensities of representative residues at different temperatures. Different symbols are used for each residue examined. Helical propensity was calculated using local backbone conformation of the residue (left) and DSSP (right). The inset in A shows the NMR shift melts.

Features of the Computed Helical Ensembles

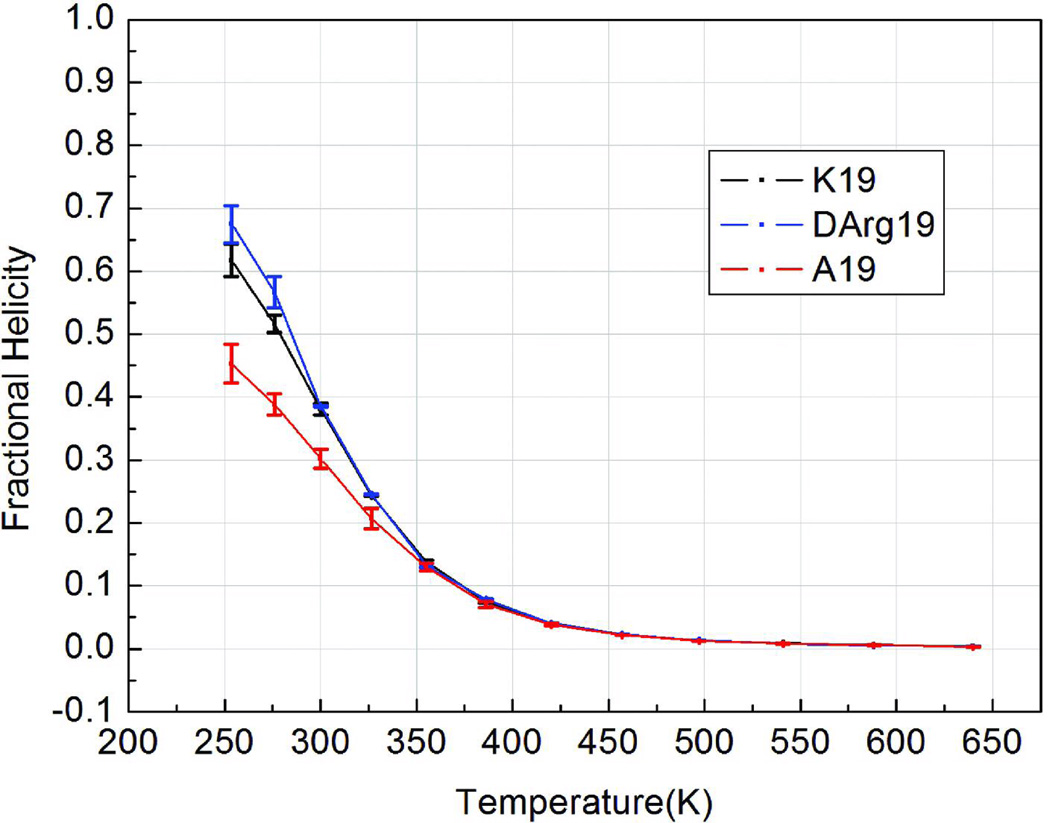
Figure 5 shows the melting profile for average overall helical content in the peptide as assigned by Lifson-Roig theory. Two interesting observations can be drawn. One is that the d-Arg C-capped sequence displays enhanced stability in the lower temperature simulations. One possible rationale is that only a particular d-Arg conformation can stabilize the helix structure; as d-Arg becomes more disordered, the Lys and d-Arg capped sequences have similar helicities at temperatures higher than 300 K.

FIGURE 5.

Lifson-Roig based melting curves for the helical segment (K4 through X19, normalized for this region of the three peptides.

The predicted Tm for K19 is 282K with f_H = 0.58 at 273K. There are a number of experimental determinations for comparison, all reported for Ac-YGG- (rather than Ac-GGG-) capped system. Baldwin’s estimate, based on CD, was f_H = 0.676 at 273K¹². Given the adjustment in the 100% helicity value (3.50 versus 3.04 ppm, in CSD terms) this is excellent agreement. FT-IR monitored T-jump experiments indicate that k_F = k_U at 285K⁵⁸.

Number and length of helical segments

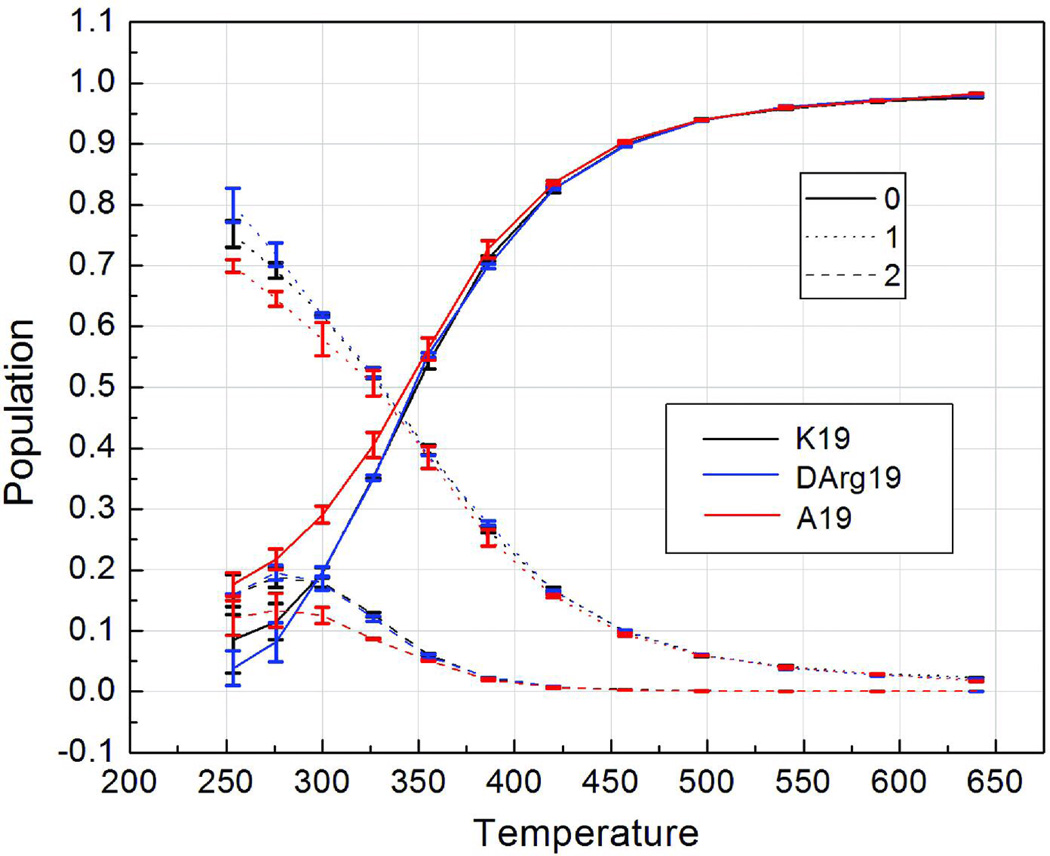
As previously noted, the high α-helical content at 275 K and flat profile across the central portion of the sequence (Figure 3) implies the predominant population of a conformation consisting of a single α-helix. To verify this feature of the simulations, we calculated the population of structures in the ensemble containing different number of continuous α-helix segments using the Lifson-Roig model, in which a helical segment is defined as 3 or more continuous residues adopting helical backbone conformation. We note that the resulting helix conformation populations (Figure 6) only take into account the number of helices, not their length (discussed below). At 275 K, more than half of structures (64(±0.5)% for A19, 69(±1)% for K19, and 71(±1.5)% for dR19) contain only a single continuous helix; this is also consistent with the general practice of applying the single sequence approximation in helix/coil treatments of short peptides. The population of conformations with a single helix decreases with increasing temperature slightly faster than the two helix conformation populations (helix-turn-helix bundle motifs).

FIGURE 6.

Temperature-dependent populations of structures containing different number of continuous helical segments (shown using different line styles) sampled in the REMD simulation ensembles. The numbers in the legend refer to the number of continuous helical segments. Different peptide sequences are indicated using different colors.

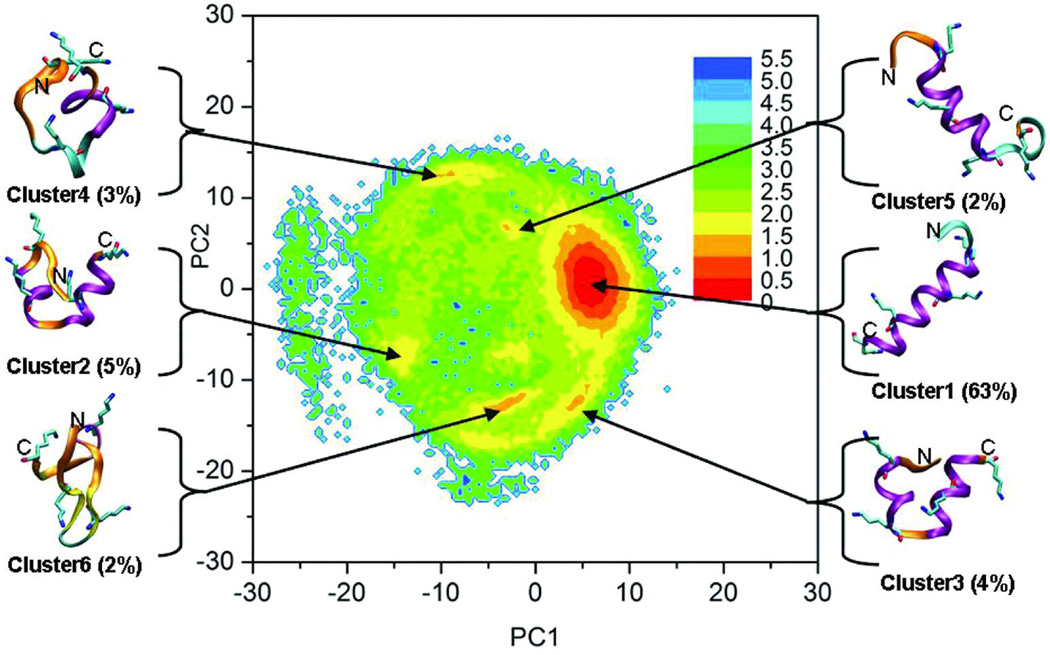
Free energy landscape and structure families

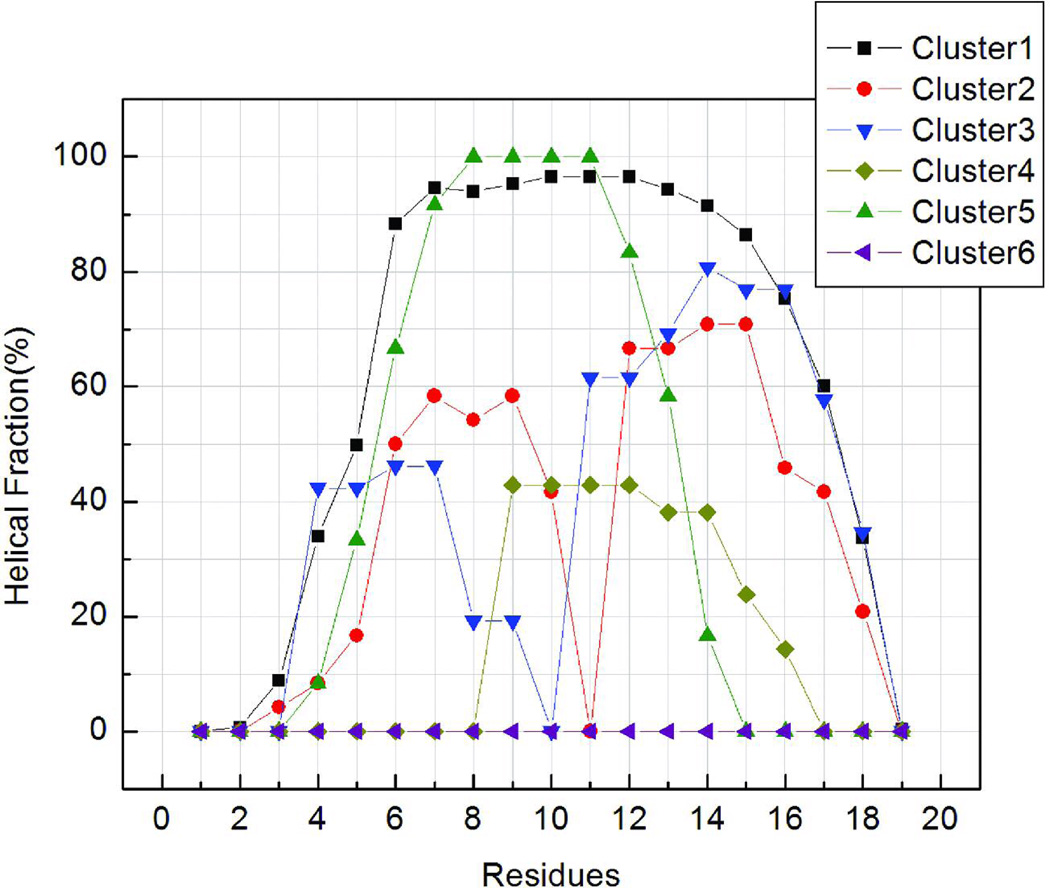
To illustrate the structural ensembles sampled in our simulation, we constructed the free energy landscape using principle component analysis (PCA) of the ensemble sampled at 275K. Previous analyses showed that the three peptides have similar overall structural ensembles, therefore the peptide K19 was chosen as a representative for the PCA landscape analysis. As described in Methods, the largest eigenvectors from PCA were used to define reaction coordinates for the landscapes, and relative free energies along these coordinates were calculated from histogram populations. We complemented these landscapes with cluster analysis of the ensemble of structures. Following cluster analysis, eigenvalues were calculated for samples of structures in each of the six most populated clusters (which together represent 78% of the ensemble), and these were projected onto the landscape in order to clarify the structural properties of the different basins. The results are shown in Figure 7, along with representative conformations which illustrate the general features adopted by structures in each basin. The arrows indicate their positions on the free energy landscape. In order to more fully characterize the extent of secondary structure formation in structural families, we calculated average helical content for each residue, similar to Figure 3, except that each cluster was considered separately. The results are shown in Figure 8, which provides insight into basis for the end-fraying seen in Figure 3. The diminished net helicity in the early portion of the N-terminal repeat represents the contribution of two single helix conformers that begin later in the sequence and the lesser helicity in the N-terminal vs C-terminal helices of the two helix bundle conformations. All clusters within the ensemble display a similar progression of helix fraying at the C-terminus.

FIGURE 7.

The free energy landscape for peptide K19 at 275 K, along with representative structures obtained from cluster analysis of the ensemble. X and Y axes represent the first 2 principle components. Relative free energy values (in kcal/mol) are represented by color as indicated by the legend. Representative structures for each basin are shown. The colors of the structures reflect secondary structure type: alpha helix – purple, extended beta – yellow, turn – cyan, coil – orange. Only lysine side chains are shown. The populations of the clusters are shown in parentheses.

FIGURE 8.

The normalized average helical propensity as a function of sequence for each cluster shown in Figure 7. Similar to the overall ensemble shown in Figure 3, helical content is reduced at the termini of most clusters. Most clusters also have nearly flat profiles along the middle of the sequence, with the exception of clusters 2 and 3 which correspond to helix-turn-helix motifs. Cluster 6 shows no helical content.

The calculated free energy landscape demonstrates that this peptide has a well-defined and deep global free energy minimum at 275K, approximately 1.5–2.0 kcal/mol lower than alternate local minima. Consistent with the Lifson-Roig analysis, the global free energy minimum corresponds to a family of conformations with a single long helix (Figure 7) with large fractional helicities for residues 5–17 (Figure 8). The population of this cluster is ~63%; the next two most populated clusters (clusters 3 and 2, with 4–5% population) are α-helix bundle structures, with each corresponding to a different local minimum on the free energy landscape. Both have turns near the middle of the sequence, as shown in Figure 8, but the turns occur at different points. This diversity in the location of the turn or coil in structures with 2 helical segments is also reflected in the observation that structures with 2 helical segments comprise ~20% of the low-temperature ensemble (Figure 6), yet none of the individual conformation clusters have a population of more than 5%.

In order to investigate the specific interactions that determine the relative stabilities of these conformation types, we performed energy and hydrogen bond analysis on the structures in the six largest clusters. Average values for number of intramolecular hydrogen bonds and energy components are shown in Table 2. The single long helix cluster (cluster 1) has an average of 2–3 more intramolecular hydrogen bonds than the other conformations, and as a result, a more favorable electrostatic energy. This is partially offset by a less favorable solvation energy (EGB) (>10 kcal/mol higher than other clusters). Several of the less populated clusters, including the two-helix bundle states, display a more favorable intramolecular van der Waals energy.

Table 2.

The average number of hydrogen bonds and average values of nonbonded energy components (in kcal/mol) for the six structural clusters shown in Figure 7. Electrostatic is the intramolecular electrostatic energy. VDW is the intramolecular van der Waals energy. EGB is the electrostatic component of solvation energy as calculated by the generalized Born model. The free energy relative to cluster #1 is calculated based on the population of the clusters. The total energy is lowest for cluster 1, which has the highest population, and similar for all of the other clusters except #6, which has no helical content.

	# Intramolecular H-bonds	Electrostatic	VDW	EGB	Sum	Free energy
Cluster1	11.3	142.8	−29.4	−488.3	−374.8	0
Cluster2	8.3	168.3	−33.4	−504.9	−369.9	1.43
Cluster3	9.1	160.7	−30.9	−498.8	−369.1	1.45
Cluster4	8.8	167.2	−31.2	−504.7	−368.8	1.70
Cluster5	8.3	162.5	−26.4	−503.7	−367.6	1.78
Cluster6	6.4	170.6	−32.3	−503.6	−365.3	1.83

The radius of gyration at different temperatures

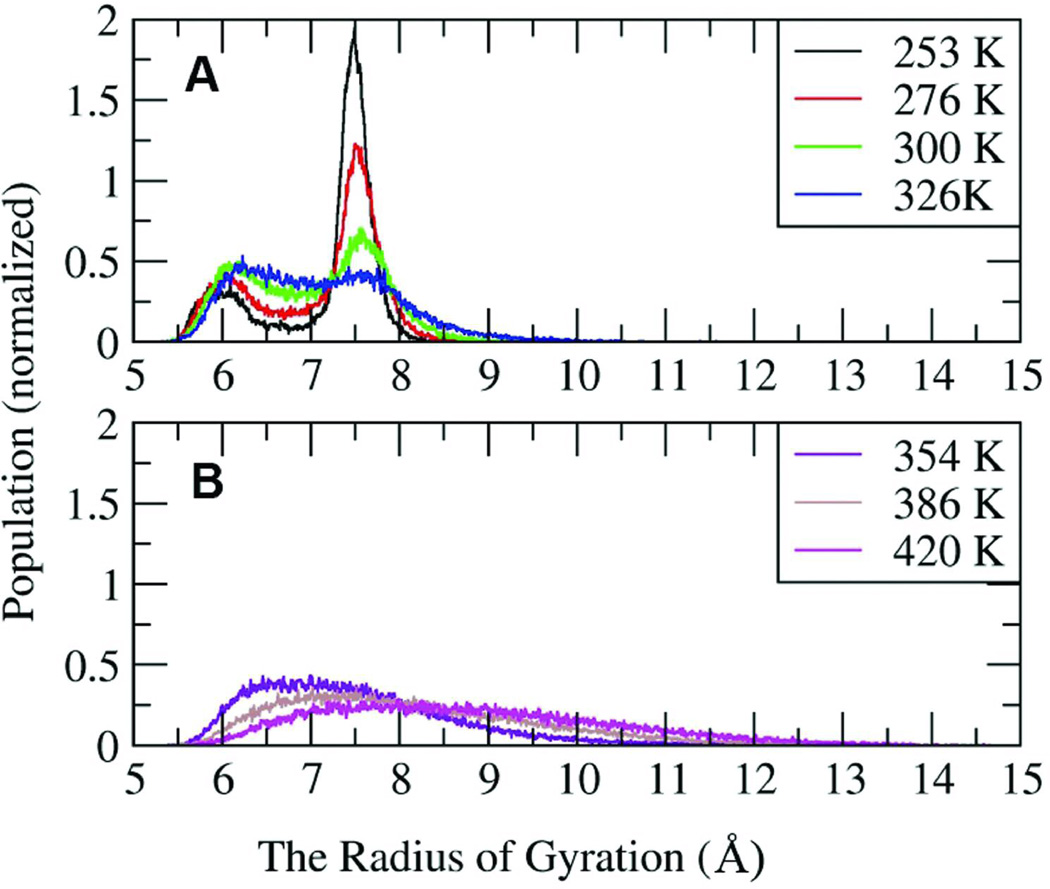
The radius of gyration is used to characterize the effective size and shape of the molecule. Figure 9 shows the radius of gyration (R_gyr) distributions at seven temperatures. To clarify the representation, the data are divided into groups according to temperature. Four temperatures, 253 K, 276 K, 300 K and 326 K are shown in Figure 9A. At these four temperatures, there are two peaks in the R_gyr distribution. One is located at 7.5 Ǻ, which represents the single helix structures (cluster 1 in Figure 7). The other peak is near 6 Ǻ, which represents more compact structures such as partial helices, helical bundles, and collapsed coils. The 7.5Å peak is most populated at temperatures ≤ 300 K. With increasing temperatures, the height of the single helix peak is reduced, and the height and the width of the globular state peak are increased slightly. At 354 K (Figure 9B), the peak for the single helix structure has disappeared; only the globular collapsed coil conformations remain. With increasing temperature, the peak shifts to higher values. At temperatures above 450K, the ensemble is composed of random coil structures, with a broad Gaussian distribution of R_gyr centered about 9.5 Å.

FIGURE 9.

The distributions of the radius of gyration for peptide K19 at different temperatures.

The Role of the Lysine Sidechains in Helices

MD simulations of, and theoretical conformation searches for, (AAAXA)-repeat peptides (X = R or K)^18,59 and some experimental studies^{7, 60, 61} have shown that amino acids with charged sidechains can significantly enhance α–helix formation. Other experimental data indicate that central lysines in helices have a net destabilization effect (versus alanine at the same position).^{12, 22, 31, 62, 63} The stabilization of helical content by the charged side chains, when observed in computational studies, arises from shielding of the α-helical intramolecular backbone hydrogen bonds from the solvation due to sequestration with the solvent localized at the sidechain terminus.^{7, 18, 59} However, some previous GB simulations indicated that helical conformations were actually destabilized by the presence of ionizable sidechains, due to competition between α-helical i-i+4 backbone hydrogen bonds and those involving the arginine guanidinium groups and backbone carbonyl oxygen atoms¹⁷. These backbone-sidechain interactions were not observed in similar simulations using explicit water molecules. The current argument concerning the effects of central polar residues in Ala-rich helices appears to focused on whether or not sidechain-induced backbone desolvation increases net helicity. Evidence has been presented that branched non-polar sidechains owe a portion of their helix destabilization to an enthalpic effect (backbone desolvation)⁶⁴ rather than only the classical unfolding entropy expectation. The present experimental studies only confirm a helix-favoring effect of C-terminal Lys/Arg residues, which likely reflects a Coulombic interaction with the helix macrodipole⁶⁵ rather than backbone desolvation or an H-bonding interaction.

These continuing issues prompted us to examine the role of lysine sidechains in our simulations. To determine the extent of Lys sidechain interaction with the backbone, we calculated hydrogen bond populations in the 275K simulated ensembles of peptide K19. The Lys9 site was selected as a representative because its location in the central region of the sequence would allow interaction with backbone residues on either the N-terminal or C-terminal side. The data shows that no significant sidechain hydrogen bonding is present in the ensemble, with all possible Lys9 Nζ - backbone carbonyl hydrogen bonds having less than 1.5% population (Figure S2). A similar situation applies to Lys14, but hydrogen bonding involving the sidechain amino group of Lys19 reaches populations approaching 5%. It is, however, unclear whether this is a statistically significant difference.

Since the controversy concerning lysine’s potential α-helix stabilizing effects centers on Lys residues in the central helical repeat, we calculated the correlation between helix formation and Lys9’s sidechain position. To quantify the position of the sidechain, two distances were measured: one is the distance between Ala5 Cα and Lys9 Nζ, the other is the distance between Ala13 Cα and Lys9 Nζ. The preference of Lys to interact with the N- and C-terminal end of the chain is indicated by the difference in the two distances (Figure S3). At low radius of gyration values corresponding to compact coil and helical bundle conformations, a broad, flat distribution of Lys distances is observed with no apparent preference for N-terminal or C-terminal direction: the slight bias toward the N-terminus may reflect the partial formation of helices in that region. For the larger radius of gyration values that correspond to extended helical conformations, the amino group is 5 Å closer to the Ala5 than to Ala13; in a significant conformational peak. For further insights, structures belonging to the single helix cluster were reclustered based on the Lys9 side chain conformation (Figure S4). In one cluster the methylene groups of the Lys9 sidechain shields the carbonyl oxygen of the upstream i-4 residue (A5) from solvent. In the other, the two distances are same: the sidechain is perpendicular to the axis of the helix. Interestingly, two highly similar conformations were reported in a previously explicit solvent simulations of a (AAARA)-repeat peptide¹⁸. Our implicit water simulations exhibit a similar preference for a configuration with protection of backbone hydrogen bonds by the nonpolar region of the ionizable sidechain, with the charged amino group interacting with solvent. This type of conformation for Lys sidechains in a helix is also supported by NMR experiments done by Groebke et al⁶⁰: medium intensity NOEs were observed between the (i-3) Ala α-H and the β-, γ-, δ-H protons of the Lys, with a weak interaction with the ε-H. These NOEs were absent in the random coil model. Our simulation data (Figure S5) are consistent with these observations.

Conclusion

We have studied the temperature dependence of helical propensities for the peptides Ac-GGG-(KAAAA)₃X-NH₂ (X = A, K, and d-Arg) using replica exchange molecular dynamics simulations and the generalized Born continuum solvent model. In contrast to prior simulations of (AAARA)-repeat peptides with continuum solvent models, which showed that the structures that were most populated were two helix bundles^16,17, we found a large population (62%) of single-helix structures at 275 K, more than 10 times the size of any other conformation family. For X = Lys, the calculated Tm was 282 K, fully consistent with T-jump rate studies⁵⁸ of the corresponding Ac-YGG capped species. We did find some helix bundle structures (clusters 2 and 3, in Figure 7), and their contribution to the helical states increases somewhat at higher temperatures (reflected in the increasing peak at R_gyr = 6 Å in Figure 9). Compact structures that are helix bundles never account (Figure 6) for more than 20% of the total conformations (and ≤ 20% of the helical states) at ≤ 326 K. Above 326 K, the bundle conformations melt out more rapidly than the single helix state. Our continuum solvent simulations are, thus, in better agreement with explicit water simulations of (AAARA)-repeat peptides and support the common use of the single sequence approximation for helix-coil equilibrium calculations. The apparent discrepancy between our and prior GB helix simulations could be the result of differences in backbone parameters employed in the studies, although the high population of single helix conformation observed by the same group using explicit solvent¹⁷ suggests that this is not the cause if the explicit solvent data is well converged. Of course, sequence differences in the two peptides are another possible reason for the discrepancy: peptide K19 has solubilizing Lys residues rather than the Arg residues. We have shown that this GB model performs less well for Arg than Lys, leading to insufficient desolvation penalty for the Arg guanidinium group upon formation of intramolecular hydrogen bonds⁶⁶. Peptide K19 is, among the helical peptides that have been studied in MD folding simulations, most closely analogous to AK16, Ac-YGAA(KAAAA)₂KA-NH₂, which was found to be 64% helical at equilibrium with only minor contributions due to two-helix bundle conformations.⁵⁷ In the AK16 folding trajectories, helix-turn-helix conformations were viewed as folding transition states. The equilibrium folded state, with enhanced helicity starting abruptly after the Gly linker, appears late in the AK16 trajectory with the breaking of non-native hydrophobic interactions with the tyrosine viewed as the slow step in extended single helix formation. Similar observations in the initial stages of the present study prompted us to use Ac-GGG(KAAAA)₃X-NH₂ rather than Ac-YGG(KAAAA)₃X-NH₂ (X = A, K, and d-Arg) for the MD simulations herein.

Our simulation results are compared with data obtained from NMR chemical shifts of -ZGG(KAAAA)₃X-NH₂ and Ac-(KAAAA)₃XGY-NH₂ sequences (X = A, K, and d-Arg) and good agreement is found with both the absolute helical propensities as well as relative helical content along the sequence. Since the melting temperatures are also in reasonable agreement with the experimental results, detailed structural analysis of the simulation ensembles was performed. Cluster analysis showed that the global minimum on the calculated free energy landscape corresponds to a nearly full-length α-helical conformation. Helical bundle conformations were populated, but these local minima were 1.5–2.0 kcal/mol higher in free energy. Energy component analysis shows that the single helix state has favorable intramolecular electrostatic energy due to hydrogen bonds, while the globular states have favorable solvation energy due to the exposure of the polar atoms. The agreement in helicity profiles for the sequences examined in experimental and molecular dynamics ensembles indicates that MD will continue to be a useful method for examining the details of polypeptide secondary structuring.

The analysis of lysine sidechain conformations suggests that polar residues could favor helix formation by protecting the backbone hydrogen bonds; but the effect does not appear to offset the presumed entropic advantage of unfolding; Lys effects a net increase in helicity (versus Ala) only at the C-terminal position. This is in agreement with the view of Baldwin⁶⁴ rather than Scheraga^7,59 and Kemp⁶⁰ regarding the relative helix propensities of Lys and Ala and the consequences of backbone desolvation for Ala-rich helices. Here it worth noting that a more recent report⁶⁷ from the Kemp laboratory places the propagation value for alanine in an (Ala)¹⁵ segment at 1.5, essentially the value we used to reproduce the experimental fractional helicities observed in the present study. A structural analysis of C-terminal ending group d-Arg in the simulated helical ensembles shows that it can from H-bonds with Ala16, which may provide some additional stability to helical structures. Both experimental and simulation studies show increasing helicity in the series X = Ala → Lys → d-Arg; however, none of the data sets show a specific DArg effect as large as that quoted in the initial reports (1.2 kcal/mol helix stabilization)²³ on this C-capping function: the largest net helical stabilization observed in the present NMR studies for a C-terminal Ala → d-Arg equates to less than a 0.4 kcal/mol helicity increment. A similar increase in helicity was observed in the MD studies. A modest increase in helicity due to placing Lys, Arg or d-Arg at the C-terminal position can be rationalized as an interaction with the helix macrodipole.⁶⁵ A resolution of the questions concerning the specific Ccapping effects of positively charged sidechains, particularly of the d-Arg function, will require studies of additional peptides with both L- and d-configured terminal groups and other polar functions. Here also, the comparison of experimental data and computational simulations should be particularly useful.