Cell mediated contraction in 3D cell-matrix constructs leads to spatially regulated osteogenic differentiation

Abstract

During embryonic development, morphogenetic processes give rise to a variety of shapes and patterns that lead to functional tissues and organs. While the impact of chemical signals in these processes is widely studied, the role of physical cues is less understood. The aim of this study was to test the hypothesis that the interplay of cell mediated contraction and mechanical boundary conditions alone can result in spatially regulated differentiation in simple 3D constructs. An experimental model consisting of a 3D cell-gel construct and a finite element (FE) model were used to study the effect of cellular traction exerted by mesenchymal stem cells (MSCs) on an initially homogeneous matrix under inhomogeneous boundary conditions. A robust shape change is observed due to contraction under time-varying mechanical boundary conditions, which is explained by the finite element model. Furthermore, distinct local differences of osteogenic differentiation are observed, with a spatial pattern independent of osteogenic factors in the culture medium. Regions that are predicted to have experienced relatively high shear stress at any time during contraction, correlate with the regions of distinct osteogenesis. Taken together, these results support the underlying hypothesis that cellular contractility and mechanical boundary conditions alone can result in spatially regulated differentiation. These results will have important implications for tissue engineering and regeneration.

Introduction

Morphogenesis is a complex process that gives rise to a wide variety of tissue shapes and patterns. Understanding the robust spatial and temporal control of cell behavior leading to functional tissue formation would have important implications for the field of regenerative medicine. However, the intricate interplay of factors involved remains poorly understood. Most reports in literature suggest that morphogenesis is genetically determined^1,2, but more recent evidence also indicates a pivotal role for mechanical factors^3-10. For example, a significant role was proposed for cellular contractility and the mechanical interaction with the deformable tissue in sculpting the developing embryo^11-13. It was first shown that fibroblasts are able to homogeneously contract a collagen matrix to form a tissue-like structure, with a potential clinical application in wound healing¹⁴. Later studies identified mechanically controlled pattern formation on 2D substrates¹⁵, and tissue specific patterns created in 3D hydrogels by tractions exerted by embedded embryonic explants^12,16. Theoretical models have substantiated the potential role of cell-mediated contraction in morphogenesis^17-19, but robust experimental models are still missing.

From the mechanical point of view, morphogenesis involves three main factors: cellular traction forces acting on a deformable tissue, the mechanical properties of that tissue, and a set of mechanical boundary conditions. While traction forces can directly sculpt the tissue into different shapes and patterns, they have the additional ability to change the local properties of that tissue, thereby potentially affecting the differentiation of the embedded cells. It has been shown that various mechanical cues, like substrate stiffness, cell shape, and cytoskeletal tension, have a direct effect on stem cell differentiation^20-24. Also, in skeletal tissue development, local stress distributions are suggested to determine tissue differentiation^25-28. In addition, the mechanical boundary conditions of a developing tissue, such as geometrical constraints or the rigidity of a neighboring tissue, could influence the effect of cell mediated contraction. Given the highly dynamic character of embryonic development, one has to take into account that critical mechanical cues may change strongly in space and time. It is unknown how cell mediated contraction is involved in creating and changing these cues and how cells respond to such dynamic microenvironments.

Mesenchymal stem cells (MSCs) are known for their potential to differentiate towards multiple lineages, including osteogenic, chondrogenic, and myogenic²⁹. The process of osteogenic differentiation involves multiple stages. Alkaline phosphatase (ALP) expression serves as an early marker, specific osteogenic genes (e.g. collagen I, osteocalcin) are subsequently upregulated, and mineralization of the matrix is considered the final and definitive state of osteogenic differentiation³⁰. In this study, we used mesenchymal stem cells from a clonally derived cell line for their robustness and homogeneity²². Because of negligible baseline levels of ALP and low spontaneous differentiation, this cell line serves as an appropriate model for the conceptual study presented.

In this study, we asked whether cell mediated contraction in combination with inhomogeneous mechanical boundary conditions can lead to patterned differentiation. To address this question, we employed a simple, widely used model system consisting of a three-dimensional cell-matrix construct which contracts under inhomogeneous boundary conditions. A simplified finite element (FE) model was used to explain the specific shape changes due to contraction, as well as calculate relative stress distributions within the construct. The calculations are used to identify qualitative differences in stress levels in time and space. Together, these result in a model that allowed us to demonstrate that cell mediated contraction leads to spatially regulated osteogenic differentiation correlating with relative stress levels in the construct.

Results

Experimental model of cell-mediated contraction

In order to investigate whether cell mediated contraction and mechanical boundary conditions alone are sufficient to induce considerable shape change in an initially homogeneous construct, we designed a simple experimental model. Mesenchymal stem cells were embedded in a typical model extracellular matrix (ECM): gels formed by the self-assembly of collagen fibrils. The embedded MSCs contracted the matrix, a phenomenon well described in the literature^14,16,31. First, cell-gel constructs were cultured in non-adherent well plates. In this condition, the gels are free floating, thus without restricting boundary conditions. The constructs demonstrated a homogeneous contraction (Fig 1A). Within 24 hours, the diameter of the construct has decreased to about 40% of its original value. Secondly, constructs were cultured in wells that allow initial adhesion of the collagen to the bottom and sides of the well. Initially, the gel stayed attached to the wells, but after approximately 3 days, the construct started to detach from the side-walls, with a subsequent appearance of a clear ring shape (Fig. 1B). Examination of the gel cross section at multiple time points provides more insight into this process. At the start of the culture, at day 0, the top surface of the construct displays a meniscus shape due to the hydrophilic character of the dish material, and the cells are evenly distributed throughout the gel (Fig. 1C). At this point in time, the cells have just started to spread, and extensions in all directions indicate that there is no preferred direction of elongation (Fig. 1C′). After 2 days in culture, the free top surface has contracted downwards, resulting in a decreased overall thickness (Fig. 1D). The cell density has increased, however the even distribution of cells at this time point indicates a spatially homogeneous rate of proliferation. After 3 days, the top surface has contracted further down, and the attachment of the gel to the wall has started to fail (Fig. 1E). At both day 2 and day 3, no apparent local differences in cell morphology are observed (Fig. 1D′-E′). After 5 days, the adhesion of the construct to the sides of the well has failed completely. A considerable volumetric contraction is observed, and the outside edges of the gel have contracted towards the center of the well (Fig. 1F). The construct then retained this shape for the rest of the culture period (Fig. 1G). Gel cross sections stained for F-actin at day 5 and day 7 provide insight into the shape and cytoskeletal tension of the cells in different regions of the construct. After the gel has contracted off the wall and the ring shape has formed, stretched cells with elongated actin fibers were found along the bottom boundary, while cells in the concavity of the ring show more rounded morphologies and more diffuse actin staining (Fig. 1F′-G′).

Fig. 1. Cell mediated contraction in experimental cell-gel constructs.

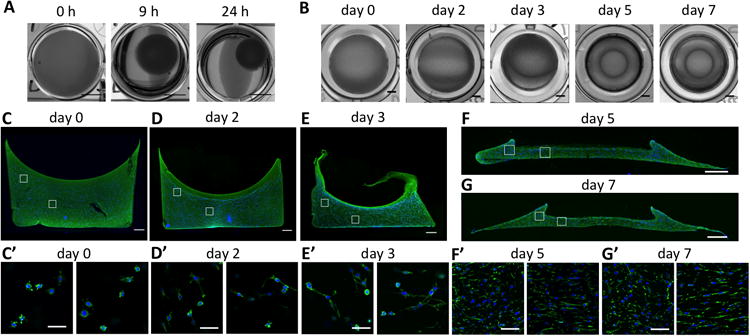
(A) Top view photographs of a freely contracting construct cultured in a non-adhesive 24-well plate (Scale: 5 mm). (B) Top view photographs showing the appearance of a ring pattern in constructs cultured in tissue culture treated 96-well plates (Scale: 1 mm). (C-G) Immunofluorescent micrographs of cross sections of the contracting construct after 0, 2, 3, 5, and 7 days in culture in control medium, showing the overall shape and cell distribution. Collagen type I is stained green, cell nuclei are stained blue. The images at day 0 (C), day 2 (D), and day 3 (E) are acquired from 200 μm vibratome sections, while images at day 5 (F) and day 7 (G) are from 10 μm frozen sections. (Scale: 500 μm). (C′-G′) Fluorescent micrographs showing the local actin fiber arrangement of embedded cells at day 0 (C′), day 2 (D′), day 3 (E′), day 5 (F′), and day 7 (G′). The images are taken at locations indicated by the white boxes in corresponding figure C-F, where left boxes correspond to the left images, and right boxes correspond to right images. F-actin is stained green and cell nuclei are stained blue (Scale: 50 μm).

Finite element model of cell mediated matrix contraction

In parallel with the experimental model, a simplified finite element model was designed to investigate whether the observed specific shape change of the construct could be explained based on the cell mediated contraction and the given mechanical boundary condition, and to calculate the shear stresses generated inside the construct. The initial shape of the experimental construct and the observed volume decrease of the gel over time (Fig. 1) were used as input for the FE model. During the first few days, while the gel is stably attached to the walls of the well, the gel is only able to contract to a certain extent in the vertical direction, but is constrained otherwise. As a result, shear and normal stresses build up over time, specifically so along the side walls (Fig. 2). At day 2, apart from the sites where the gel is attached to the walls, von Mises stress also increases in the center of the construct along the top surface, due to large expected deformation in that specific area. At day 3, the adhesion between the side surface of the gel and the wall cannot withstand the stresses due to the cell mediated contraction. Therefore, the gel detaches from the side walls with a corresponding relief in stresses in those areas, and the sides of the construct fold in towards the center. This corresponds to what is observed in the experimental model (Fig. 1C-G). Now stresses build up along the bottom boundary. The stress distribution in the construct thus changes with time and is spatially inhomogeneous at each point in time, until stresses reach a maximum after the gel has reached its final shape at day 5. Although stresses are expected to be high throughout the construct after 5 days, the observed differences in actin cytoskeletal morphology at day 5 and 7 (Fig. 1F′-G′) correspond to the stress distribution after the gel is released from the side wall, with elongated cells matching high stresses along the bottom of the plate, and rounded cells matching low stresses in the concavities of the ring.

Fig. 2. Relative Von Mises stresses in contracting 3D constructs simulated by a finite element model.

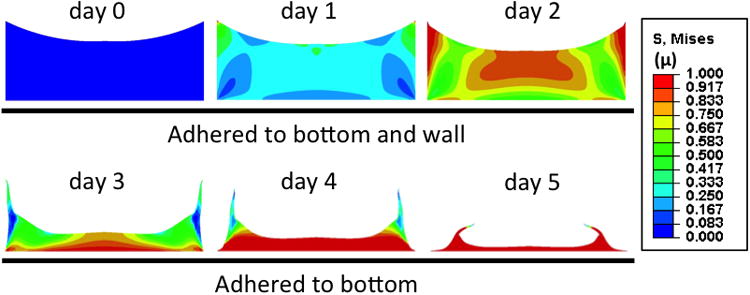
Cross sectional view of constructs at increasing time points during contraction. The color scale indicates relative von Mises stresses.

Validation of the experimental model

In order to validate the experimental model, a variety of experiments was performed in which the cellular contractility and physical boundary conditions were varied. First, the initial cell density in the cell-gel constructs was varied to alter the net contractile force acting on the gel. As expected, the specific shape change as indicated by the appearance of the ring shape, occurred faster with higher initial cell densities (Fig. 3A). The role of cell-mediated contraction was further confirmed by treating the embedded cells with the non-muscle myosin-II inhibitor Blebbistatin, as this inhibits cell contractility in a dose dependent manner. Treatment with 5 μM Blebbistatin inhibited gel contraction as well as formation of the ring shape (Fig. 3B). It was also confirmed that in both the untreated and 5 μM Blebbistatin treated cultures the vast majority of embedded cells were viable (Fig. 3C). Finally, the effect of the system boundary conditions on the specific shape of the contracted construct was studied by varying the size and geometry of the original gel construct. When constructs were cultured in rectangular wells, the pattern resulting from contraction was shaped accordingly (Fig. 3D). Furthermore, when the gels were cultured in wells of increasing radius, ranging from 3.2 mm to 17.5 mm, keeping the thickness of the construct constant, the absolute distance between the ring and the wall was constant in the larger wells (Fig. 3E). In the smaller wells, the higher curvature of the constructs' perimeter and restricted space might prevent the ring from appearing further towards the center. When the initial thickness of the constructs was increased from 2.3 mm to 6.3 mm, while keeping the diameter constant, the absolute distance between the ring and the wall increased linearly with the thickness of the construct (Fig. 3F). Differently sized constructs are expected to show comparable stress patterns since the inhomogeneous stress distributions calculated by the FE model (Fig. 2) are mainly caused by the inhomogeneous character of the boundary conditions, as opposed to the dimensions of the construct.

Fig. 3. Validation of the experimental model.

(A) Plot of the timing of the appearance of a ring shape in the constructs as a function of the initial cell density (n=6). (B) Top view photographs of cell-gel constructs cultured in either control medium (left), or control medium supplemented with 5μM Blebbistatin (right). (Scale: 1mm) (C) Plot of cell viability in constructs cultured in either control medium, or supplemented with 5 μM Blebbistatin as a function of time (n=6). (D) Top view photographs of construct cultured in a rectangular well, before (left) and after (right) contraction (Scale: 1mm). (E) Top: top view photographs of contracted constructs cultured in wells of increasing diameter. Photographs are resized to show the relative position of the ring in the well (Scale: 5mm in all images). Bottom: Plot of the distance between the wall and the ring as a function of the well radius (n=7). (F) Top: top view photographs of constructs with increasing initial thickness cultured in 48-well plates. (Scale: 2mm) Bottom: Plot of the distance between the wall and the ring as a function of the initial gel thickness (n=6).

Spatially regulated differentiation

Within the contracted constructs, we then studied the behavior and fate of the mesenchymal stem cells. The experiments were performed in control medium as well as osteogenic medium to probe the importance of biophysical cues as compared to soluble cues. Firstly, alkaline phosphatase activity was assessed in whole cell populations retrieved from the gel constructs as an early marker for osteogenic differentiation. While ALP levels were negligible initially (day 0), they increased significantly over the first 7 days when cultured in control medium (Fig. 4A). A similar trend in ALP levels is seen for constructs cultured in osteogenic medium. Based on the significant increase of ALP activity in the first 7 days in culture, the 7-day time point was chosen to look into the spatial distribution of ALP expression within the construct. ALP expression was found to be inhomogeneous throughout the construct. While expression was high in most regions, little ALP expression was consistently observed in the concavities of the ring (Fig. 4B). The spatial pattern was similar for constructs cultured in control medium and osteogenic medium (compare Fig. 4B and 4C-top). Moreover, the pattern was maintained, even more pronounced, at day 14 and day 21 (Fig. 4C-middle and bottom). When the gel constructs were treated with increasing concentrations of Blebbistatin, which progressively inhibits cell contractility, the construct does not contract and after 7 days in culture overall levels of ALP in the construct are shown to be decreasing with increasing drug concentration (Fig. 4D).

Fig. 4. Spatially regulated differentiation in contracted constructs.

(A) Time course of alkaline phosphatase activity per 10⁶ cells retrieved from constructs cultured in either control medium or osteogenic medium. Error bars represent SD, n=3. (B,C) Color micrographs of 30μm cross sections of constructs stained for ALP (blue) after (B) 7 days in control medium, or (C) 7 days (top), 14 days (middle), and 21 days (bottom) in osteogenic medium (Scale: 200μm). (D) Color micrograph of representative areas of 200 μm cross sectionsof non-contracted constructs stained for ALP (blue) after 7 days of culture in osteogenic medium supplemented with either 10 μM (left) or 25 μM (right) Blebbistatin (Scale: 200 μm). (E) Top view photographs of whole gel constructs cultured in osteogenic medium for 7 days (left), 14 days (middle), and 21 days (right) stained for mineralized matrix with Alizarin Red (top row) or von Kossa (bottom row). The gray/brown appearance of the construct at day 7 stained with Alizarin Red is caused by non-specific background staining (Scale: 1mm).(F) Color micrographs of 30μm cross sections of constructs cultured in osteogenic medium for 7 days (top), 14 days (middle), or 21 days (bottom), stained for mineralized matrix with Alizarin Red (Scale: 200μm). (G) Higher magnification images of indicated areas in F. Alizarin Red staining of constructs cultured for 7, 14, and 21 days (Scale: 25 μm, applies to all images). (H) Color micrographs of 30 μm cross sections of constructs cultured in osteogenic medium for 7, 14, and 21 days, stained for mineralized matrix by von Kossa. The images represent areas corresponding to the indicated areas in F (Scale: 25 μm, applies to all images).

While ALP is widely used to assess osteogenesis, it is not a definitive marker for osteogenic differentiation. Therefore, the deposition of mineralized matrix within the constructs, as an indicator of definitive differentiation, was also analyzed to determine its relation to pattern formation. Both Alizarin Red and Von Kossa staining were performed to definitively demonstrate the deposition of calcium phosphate salts. Constructs cultured for 7 days did not show any mineralization (Fig. 4E-H). However, in agreement with the pattern of ALP expression, after 14 days the constructs had formed mineralized matrix at the outer edges, outside the ring (Fig. 4E-H). After 21 days, mineralization had spread throughout most of the construct, though mineralization was least in the concavities of the ring (Fig. 4E-H).

To gain insight into local differences in the construct that might be involved in the observed spatial patterns of differentiation, specific regions of high versus low ALP expression were identified (Fig. 5A-A′), and relative cell densities were compared for those regions (Fig. 5B-B′). Local cell densities were found to be significantly higher in regions of low ALP expression as compared to regions of high ALP expression (Fig. 5C). Also, the cells in the concavity of the ring, where low ALP expression is observed, had a more rounded shape, while the cells near the lower boundary were elongated (Fig. 1F′-G′).

Fig. 5. Local cell densities are higher in regions with low ALP expression.

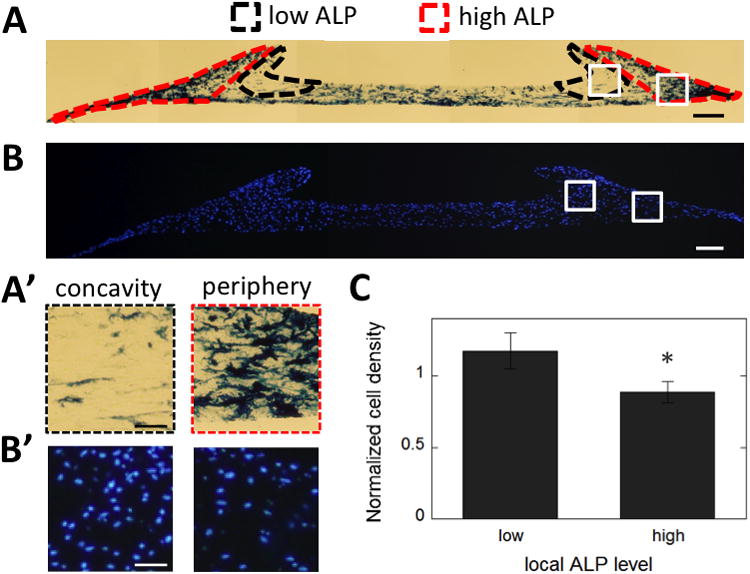
(A) Regions of high (red contour) and low (black contour) ALP expression are highlighted on a representative cross section of a construct cultured for 14 days in osteogenic medium, stained for ALP (blue) (Scale: 200 μm). (A′) Magnifications of the highlighted areas in A (Scale: 50 μm)(B) Representative fluorescence micrograph of a 10μm cross section stained for cell nuclei (blue) as used for quantifying local cell densities (Scale: 200 μm). (B′) Magnifications of the highlighted areas in B (Scale: 50 μm).(C) Normalized local cell densities are compared between regions of low and high ALP expression. Data are averages of n=12 constructs from 3 independent experiments, including constructs cultured in control and osteogenic medium, for either 7 or 14 days. Error bars represent SD. *, P<0.0001.

Discussion

The interplay of mechanical factors in morphogenetic processes is poorly understood, partly due to a lack of simplified model systems. The aim of this study was to investigate the combined role of cell-mediated contraction and mechanical boundary conditions on spatially patterned differentiation in simple 3D constructs. It was shown that contraction of an initially homogeneous construct by embedded MSCs under time-varying boundary conditions leads to a considerable shape change of the construct. These conditions lead to temporally and spatially inhomogeneous stress distributions within the construct as calculated using a FE model. Spatially regulated differentiation of the embedded MSCs was subsequently observed, where regions of high shear stress correlated directly with the regions of osteogenic differentiation (Fig. 6).

Fig. 6. Regions of low shear stress correlate with low ALP expression.

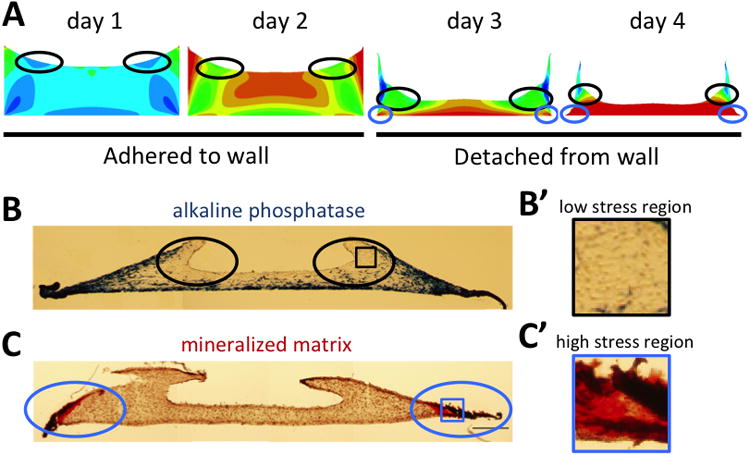
(A) Black circles indicate regions of relatively low shear stress as calculated by the FE model at different time points before and after the construct is released from the side wall. Blue circles indicate regions of high stress once the gel has contracted off the wall.(B) Regions of low ALP expression are indicated by black circles in a cross section after 14 days in culture. (B′) Magnification of the indicated area in B. (C) Blue circles indicate the formation of mineralized matrix (red) at the outer edges of the construct after 14 days in culture. (C′) Magnification of the indicated area in C.

The direct effect of mechanical boundary conditions, in concert with cell mediated contraction, is evident from the considerable change in shape that takes place under inhomogeneous boundary conditions in the presented experimental setup. The observed shape change is stable, reproducible, and can be explained using a finite element model. In general, collagen hydrogels are widely used as a 3D cell culture system³¹, and more specifically, traction forces exerted on collagen matrices by embedded cells have been previously proposed as a mechanism for connective tissue morphogenesis^12-14,16. Over the last decades, substantial progress has been made towards characterizing the forces that cells exert on their substrate, both on 2D surfaces and within 3D substrates, as single cells, groups, and sheets^32-35. It is reported that single cells are able to exert forces in the order of 1-100nN per focal adhesion^32,36,37, which adds up to a force in the order of μNs per cell³⁸. On the multicellular scale, the cumulative force of the cell-exerted tractions and the subsequent deformation of the tissue is determined by a complex set of parameters such as the orientation and spreading area of the cells, the compliance of the matrix, and the density of force-generating cells. In our model, the direct effect of the cellular contractility and boundary conditions was validated by varying the input parameters to control timing, shape, and geometry of the final contracted construct (Fig. 3). The high proliferation rate of the used mesenchymal stem cell line compared to primary MSCs could affect the timing of the contraction process, however this would not affect the interpretation of the presented results. The actin cytoskeletal morphology in the different regions of the construct after the final pattern has formed, corresponds with the relative stress distribution after the gel detaches from the side walls, as calculated by the FE model. Although the stress distribution homogenizes after day 5 according to the FE model, the differences in actin cytoskeletal morphology persist, likely due to remodeling of the collagen matrix.

Interestingly, osteogenic markers were expressed in a non-homogeneous manner throughout the construct. The concavity of the ring, a region that was originally located at the periphery of the top surface of the construct, shows specifically low ALP expression compared to the other regionsover a 21-day culture period. Remarkably, comparing these patterns with the stress distributions as calculated by the FE model, the regions of low ALP correlate strongly with the regions that are relatively low in shear stress, both before and after the construct is released from the side walls (compare Fig. 6A and B). Regions of predicted high stress at either early time points (along the side edges) and later time points (along the bottom boundary), show considerable ALP expression. Additionally, when cell contractility is progressively inhibited by treatment with increasing concentrations of Blebbistatin, overall levels of stress in the gel are expected to decrease, which correlates with decreasing overall levels of ALP in the constructs (Fig. 4D). One has to take caution when interpreting these results however, since drugs such as Blebbistatin can have multiple effects. Definitive osteogenic differentiation, indicated by the formation of mineralized matrix, starts at the regions of highest stress (Fig. 6C), and then propagates further into the construct following regions of high ALP expression. After 21 days, while the concavity of the ring is still low in ALP, mineralization has started to spread into these regions as well (Fig.4F-bottom), although to a lesser extent. The mineralization in these areas can possibly be explained by the presence of extracellular ALP produced by cells in the surrounding regions, or the physical propagation of the mineralization front, due to the absence of inhibiting signals.

Previous studies have also associated stress gradients with patterned differentiation, and in particular high stress with osteogenic differentiation^23,39-41. In contrast to the static stress gradients used in past reports, the patterns of differentiation shown in the current study occur in a construct in which the stress distribution is changing with time. High stresses are first expected in the outer edges where the construct is still adhered to the wall, while after the construct is released from the wall, the stresses are highest along the bottom constraint. Both those regions show high ALP expression. The only region that is experiencing low shear stress both before and after the attachment fails, the concavity of the ring, shows low ALP expression (Fig.6A-B). This suggests that a few days in a high stress environment might be sufficient for the cells to commit to the osteogenic lineage, even if they return to a low stress environment during the process of differentiation. After 5 days, the construct has reached its final shape and no further contraction takes place. The stresses then become homogeneous throughout the construct. Since commitment of the MSCs likely takes place during the first 5 days of culture, we focus on the changing stress distribution during that time. Previous studies support the notion that several days in a certain mechanical environment can be sufficient for MSC commitment to take place⁴². Given the highly dynamic nature of morphogenetic processes in vivo, the implied role of stress history is important to consider. Further studies should be conducted to elucidate the exact relationship between shear stress levels and osteogenic commitment.

In this study, definitive osteogenic differentiation is shown by the formation of mineralized matrix. Since the presence of phosphates as a supplement in the osteogenic medium is essential for mineralization to occur, mineralization cannot take place in constructs cultured in control medium. However, alkaline phosphatase can be studied as an early marker of osteogenic differentiation independent of the media supplements, as its activity can be induced by both soluble and non-soluble cues^21-24,43. In our model system, when comparing between constructs cultured in control medium versus osteogenic medium, overall ALP activity increased similarly over the first 7 days (Fig. 4A), and the spatial patterns of ALP expression were comparable (Fig 4B and 4C-top). Independent of the media supplements, specific regions of the construct show marked expression of ALP, while in other regions no ALP expression is observed. Since virtually all cells are ALP negative at the start of the experiments (Fig. 4A and ²²), this suggests that the cues responsible for early osteogenic induction and its specific pattern are non-soluble and localized.

Local cell densities are significantly higher in regions of low ALP expression compared to regions of high ALP (Fig.5). Also, in the regions of low ALP, the cells have adopted a more rounded morphology (Fig. 1F′-G′). In embryonic development, densifications of mesenchymal stem cells, so called condensations, are generally identified as the first stage in cartilaginous differentiation during skeletal development^44,45. A rounded cell morphology is a result of the physical condensation and is suggested to provide an inductive signal for differentiation⁴⁶. This led us to hypothesize that the regions of low ALP expression may be undergoing chondrogenic differentiation. However, we were not able to detect specific chondrogenic markers (data not shown). While the characteristics of these regions might be favorable, they were not sufficient to induce chondrogenesis. This could possibly be explained by the lack of specific soluble factors required for chondrogenic differentiation. Furthermore, a collagen type I matrix might not be optimal for chondrogenic induction, or to mimic specific developmental events. We show that cells in specific locations differentiate towards the osteogenic lineage, while cells in other locations do not. Whether these cells maintain their stem cell capacity, or have differentiated towards a different lineage remains to be investigated.

In the presented model system, a correlation is shown between the stress distribution in a 3Dcell-matrix construct and the osteogenic differentiation of the embedded MSCs. The collagen matrix that the cells reside in is a natural substrate for the cells, and apart from the apparent compaction of the construct, the cells have the ability to actively remodel this matrix. Especially over a culture period of several weeks, digestion and alignment of the collagen fibers potentially takes place, as well as synthesis of new matrix. These processes have the potential to change the local properties of the matrix, such as the local substrate stiffness. Possible changes in local mechanical properties are not taken into account in the simplified finite element model, which is qualitative only. Remodeling of the collagen matrix could play a role in the observed patterned differentiation, but further experimentation is needed to elucidate the exact mechanism.

Taken together, these results suggest a critical interplay of cell mediated contraction and time-varying boundary conditions, leading to patterned differentiation. Spatially and temporally inhomogeneous stress distributions are implicated as a key element therein. Although the model used in this study is highly artificial and does not attempt to mimic the morphogenesis of a specific tissue in vivo, its simplicity supports the notion that patterned differentiation directly relates to cellular contractility and in homogeneous boundary conditions. In future studies, more complex boundary conditions could be introduced to yield more complex or relevant patterns aimed to resemble a specific tissue. In addition, the signaling pathways responsible for patterning could be elucidated with further experimentation. This line of investigations will likely provide a better understanding of tissue patterning and morphogenesis, and has implications for the development of functional tissue engineering constructs.

Materials and Methods

Cell culture

Clonally derived mouse bone marrow stromal mesenchymal stem cells (D1 mMSCs), originally obtained from Balb/c mice⁴⁷, were purchased from ATCC (D1 ORL UVA, cat# CRL12424) and used between passages 20-25. The mMSCs were cultured in standard Dulbecco's Modified Eagles Medium (DMEM, Invitrogen) supplemented with 10% Fetal Bovine Serum (Invitrogen) and 1% penicillin/streptomycin (Invitrogen). This will be referred to as control medium. Cells were maintained at sub-confluency in the incubator at 37°C and 5% CO₂. The culture medium was refreshed every three days. For osteogenic medium, the control medium was supplemented with 50 μg/mL L-ascorbic acid (Sigma) and 10 mM β-glycerophosphate (Sigma). To inhibit cell contractility in the constructs, 5 μM, 10 μM or 25 μM Blebbistatin (Sigma) was added to the culture medium. The Blebbistatin containing medium on the gels was refreshed every two days.

Collagen hydrogels

Rat tail Type I collagen was purchased from BD Biosciences. A collagen working solution was made by mixing one part 10× DMEM with 10 parts of collagen stock solution, and adjusting the pH to 7.4 by adding 1 M NaOH. Gel-cell solutions were then made by mixing the collagen working solution with the cell suspension and regular DMEM to yield a final collagen concentration of 1.2 mg/mL and a final cell density of 10⁶ cells/mL, unless stated otherwise. All steps were carried out on ice. Unless stated otherwise, 100 μL gel-cell solution was added to tissue culture treated 96-well plates (BD Falcon) coated with Poly-L-Lysine (Sigma) to improve attachment of the collagen to the well. This results in a gel geometry allowing for sufficient oxygen and nutrient diffusion into the construct. The gels were left in the incubator at 37°C and 5% CO₂ for 60 minutes to allow gelation, after which 200 μL of medium was added to each gel. The medium was refreshed every two days. For rectangular gels, 219 μL of gel-cell solution was added to 8-well Lab-Tek chamber slides (BD Falcon). When gels were made in larger wells, the volume was increased in parallel with the increase of the surface area, to keep the final thickness of the gel constant. Thicker gels were made in 48-well plates, by increasing the volume of gel-cell solution used. Free floating gels were prepared in ultra low attachment 24-well plates (Costar 3473).

Finite element model

An axisymmetric model was constructed using finite-element software package ABAQUS 10.1 to simulate the contractions and stress of the gel constructs. The mesh accuracy of the model was ascertained through a mesh refinement study. For simplicity, the gel was set to follow an elasto-plastic neo-hookean law with a shear modulus μ⁴⁸. The yield stress of the gel is set to be the same as its shear modulus under von Mises yield criterion. To model the cell mediated contraction, the gel was further set to shrink its volume over time matching the experimentally observed volume decrease. Since even cell distributions in the gels were observed in the experimental model during the time of active contraction, we assume the contraction is uniform throughout the model. Observed differences in local cell density at later time points (Fig. 5) will not influence the contraction process since the construct has already reached its final shape. The bottom and side surfaces of the gel model were set to be initially fixed to the tissue culture plate, following experimental observation. When the contraction of the gel reaches a critical point, in this case the observed decrease to 40% of the initial volume at day 3, the side surface of the gel model was detached from the wall and the gel was allowed to shrink further until day 5. The spatial distribution of von Mises stress in the gel was calculated throughout the process of contraction. Since the model is qualitative, the absolute value of the stress that induces detachment of the construct from the side surface was not calculated.

Viability assay

Cells were retrieved from the constructs by digestion of the collagen gel with 5 mg/mL Collagenase P (Roche) in serum free medium for 1 hour at 37°C and 5% CO₂. Viable cell counts were performed on the retrieved cells using a Countess automated cell counter (Invitrogen) based on Trypan Blue exclusion.

Cryotome and vibratome sectioning

Cell-gel constructs were fixed for 30 minutes in 4% paraformaldehyde, and washed in PBS overnight. For cryosectioning, constructs were soaked in 30% sucrose in PBS overnight at 4°C, subsequently embedded in OCT Compound (Optimal Cutting Temperature, Tissue-Tek Sakura) and flash frozen in 2-methylbutane cooled in liquid nitrogen. Sections were cut on a Leica cryotome. ‘day 0’, ‘day 2’, ‘day 3’ and Blebbistatin treated constructs were sectioned using a vibratome. After fixation, the gels were embedded in 2.5% low gelling temperature agarose (Lonza), and a Leica vibratome was used to cut 200 μm sections.

Immunohistochemistry

10 μm frozen sections and 200 μm vibratome sections were probed for collagen type I with a rabbit-anti-mouse collagen I polyclonal antibody (Millipore) and stained with an Alexa Fluor 488 conjugated Goat-anti-Rabbit IgG (Invitrogen). To visualize F-actin, samples were stained with Alexa Fluor 488 conjugated Phalloidin (Invitrogen). After staining, the samples were mounted with Prolong Gold with DAPI (Invitrogen).

Histological staining

30 μm frozen sections were stained for alkaline phosphatase (ALP) by Fast Blue staining. After equilibrating for 15 min in alkaline buffer (100 mM Tris-HCl, 100 mM NaCl, 0.1% Tween-20, 50 mM MgCl2, pH 8.2), the sections were stained in a working solution of 500 μg/mL naphthol AS-MX phosphate (Sigma) and 500 μg/mL Fast Blue BB Salt Hemi (ZnCl) salt (Sigma) in alkaline buffer. The sections were then washed in alkaline buffer, neutralized in PBS, and mounted with Prolong Gold with DAPI (Invitrogen). Whole gel constructs and 30 μm frozen sections were probed for mineralized matrix by Alizarin Red and Von Kossa staining. For Alizarin Red staining, samples were equilibrated in distilled water and stained in 2% Alizarin Red S (Sigma) in dH₂O for 2-5 minutes. Samples were then washed and kept in dH₂O. For Von Kossa staining, samples were equilibrated in distilled water and incubated in a 3% silver nitrate solution under UV light for 20 min. The samples were then washed in distilled water and incubated in a 5% sodium thiosulphate solution for 2 minutes, followed by washes in distilled water.

ALP activity assay

Cells were retrieved by digestion of the collagen gel with 5 mg/mL Collagenase P (Roche) in serum free medium for 1 hour at 37°C and 5% CO₂. The retrieved cells were counted and then lysed for 30 min in lysis buffer (50 mM Tris-HCl, 0.1% Triton X-100) on an orbital shaker at room temperature. 10 μL of each lysate was added to 100 μL 4-Methylbelliferyl phosphate (4-MUP) substrate (Sigma) and incubated for 25 minutes at 37°C. Bovine ALP (Sigma) was used to make a standard curve. After incubation, fluorescence of each well was read by a fluorescent plate reader (Biotek). ALP activity was normalized to cell counts.

Image acquisition

Digital photographs of whole gels were taken with a Nikon Coolpix P90 digital camera. Color micrographs of the Fast Blue, Alizarin Red and von Kossa staining were acquired using a Nikon E800 upright microscope and an Olympus DP-70 color camera. An Upright Zeiss LSM 710 confocal microscope was used for acquisition of fluorescent micrographs. Local cell densities were calculated by image processing in ImageJ using fluorescent images of DAPI staining of 10 μm cross sections of the constructs.

Statistical analysis

All data are expressed as means ± standard deviation (SD). Statistical comparisons were performed with a one-tailed paired Student's t-test.