Abstract
Theoretical treatment of ozone forming reaction is developed within the framework of mixed quantum/classical dynamics. Formation and stabilization steps of the energy transfer mechanism are both studied, which allows simultaneous capture of the delta zero-point energy effect and η-effect and identification of the molecular level origin of mass-independent isotope fractionation. The central role belongs to scattering resonances; dependence of their lifetimes on rotational excitation, asymmetry; and connection of their vibrational wave functions to two different reaction channels. Calculations, performed within the dimensionally reduced model of ozone, are in semiquantitative agreement with experiment.
Keywords: collisional energy transfer, isotope effect, recombination rate constant, width of resonant states, quantum resonance
The recombination reaction that forms ozone,
is one of the most important processes in Earth’s atmosphere, and is one of the most difficult puzzles atmospheric chemists have to solve. At the fundamental physics level, almost every aspect of this seemingly simple reaction appears to be quite complicated. Of paramount importance for the geosciences community is the mass-independent fractionation (MIF) effect that leads to enrichment of stratospheric ozone in the heavy isotopes of oxygen. The anomalous enrichments in stratosphere (1) and the MIF in laboratory experiments (2) were discovered more than 30 y ago. These phenomena attracted the attention of some of the best geoscientists and physical chemists in experimental (3–8) and theoretical (9–20) communities but, despite the significant recent progress made (21–24), remained a gray area for those who used MIF as an analytical tool, and a longstanding problem for those who tried to explain it (25–27).
It has been recognized that quantum mechanics plays a crucial role in dynamics of ozone formation. The overall reaction 1 proceeds in two steps: through formation of quantum scattering resonances––metastable O3* states excited rotationally and vibrationally above the dissociation threshold:
The quantum delta zero-point energy (ΔZPE) effect (8), observed in experiments on formation of asymmetric isotopomers of ozone such as 16O16O18O, has been attributed to lifetimes and energies of  states (14–16) and by now has been reproduced by statistical (9–11), quantum-mechanical (15, 16, 21, 23), and even classical trajectory (17, 18) models of the process 2. It has also been recognized that to explain why the symmetric ozone isotopomers such as 16O18O16O are produced at a lower rate (compared with the trend of asymmetric isotopomers), one needs another kind of isotope effect in addition to the ΔZPE effect. It was hypothesized that quantum symmetry plays role during the process 3––stabilization of
states (14–16) and by now has been reproduced by statistical (9–11), quantum-mechanical (15, 16, 21, 23), and even classical trajectory (17, 18) models of the process 2. It has also been recognized that to explain why the symmetric ozone isotopomers such as 16O18O16O are produced at a lower rate (compared with the trend of asymmetric isotopomers), one needs another kind of isotope effect in addition to the ΔZPE effect. It was hypothesized that quantum symmetry plays role during the process 3––stabilization of 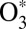 by collisions with bath gas M. Indeed, in symmetric molecules some state-to-state transitions are forbidden by symmetry (28), which could lead to reduced stabilization cross-section and lowered recombination rate (29). Marcus called this the “η-effect” (9–11) and, among other possible causes of it, discussed the dynamic density of states, chaotic behavior of resonances, spin–orbit coupling, and, more recently (22), the Coriolis coupling effect, different in symmetric and asymmetric isotopomers. By 2010, three attempts were made to treat the dynamics of process 3 quantum-mechanically (12, 19, 24) but all of them encountered significant computational difficulties and were forced to follow crude approximations (besides neglecting rotation and looking at J = 0 only). Notably, no isotope effects due to symmetry were found (24). The origin of the mysterious η-effect (9–11) remained unidentified.
by collisions with bath gas M. Indeed, in symmetric molecules some state-to-state transitions are forbidden by symmetry (28), which could lead to reduced stabilization cross-section and lowered recombination rate (29). Marcus called this the “η-effect” (9–11) and, among other possible causes of it, discussed the dynamic density of states, chaotic behavior of resonances, spin–orbit coupling, and, more recently (22), the Coriolis coupling effect, different in symmetric and asymmetric isotopomers. By 2010, three attempts were made to treat the dynamics of process 3 quantum-mechanically (12, 19, 24) but all of them encountered significant computational difficulties and were forced to follow crude approximations (besides neglecting rotation and looking at J = 0 only). Notably, no isotope effects due to symmetry were found (24). The origin of the mysterious η-effect (9–11) remained unidentified.
In this paper we present results of sophisticated mixed quantum/classical theory for collisional energy transfer and rovibrational energy flow (30–32). Our theory involves no adjustable parameters or empirical dependencies. All our results are obtained from first principles, giving insight into the molecular level origin of mass-independent isotope fractionation effect. The focus is on the following three reactions:
in the bath of 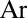 . These three reactions are representative because the processes 4 and 5 form an asymmetric isotopomer from two different channels and allow the ΔZPE effect to be seen, whereas the process 6 forms a symmetric isotopomer and allows the η-effect to be seen. Indeed, experimental rates for all studied symmetric isotopomers (five, including
. These three reactions are representative because the processes 4 and 5 form an asymmetric isotopomer from two different channels and allow the ΔZPE effect to be seen, whereas the process 6 forms a symmetric isotopomer and allows the η-effect to be seen. Indeed, experimental rates for all studied symmetric isotopomers (five, including 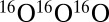 ; see table 1 in ref. 8) are very close to the rate of process 6, whereas the channel-specific rates for all asymmetric isotopomers (eight, including four with isotope
; see table 1 in ref. 8) are very close to the rate of process 6, whereas the channel-specific rates for all asymmetric isotopomers (eight, including four with isotope 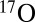 ) follow the linear trend set up by processes 4 and 5. So, three processes studied here represent the minimal but most important subset of relevant reactions. Conclusions obtained in this work should help to understand other isotopic combinations.
) follow the linear trend set up by processes 4 and 5. So, three processes studied here represent the minimal but most important subset of relevant reactions. Conclusions obtained in this work should help to understand other isotopic combinations.
Recombination Kinetics
The kinetics of reactions 2 and 3 is treated within the microcanonical framework, where different metastable states of 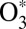 (different scattering resonances) are treated as different chemical species (13, 16, 29, 32). For each metastable state
(different scattering resonances) are treated as different chemical species (13, 16, 29, 32). For each metastable state 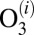 at energy
at energy 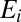 the processes affecting its population
the processes affecting its population 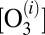 are considered and the corresponding rate constants are introduced. Those are
are considered and the corresponding rate constants are introduced. Those are
- i) formation of
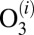 characterized by the second-order rate coefficient
characterized by the second-order rate coefficient 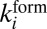 :
:
- ii) spontaneous unimolecular decay of
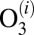 characterized by the first-order rate coefficient
characterized by the first-order rate coefficient 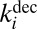 :
:
- iii) stabilization of
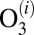 by collision with bath gas particle M characterized by the second-order rate coefficient
by collision with bath gas particle M characterized by the second-order rate coefficient 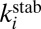 :
: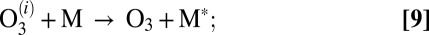
- iv) collision-induced dissociation
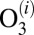 characterized by the second-order rate coefficient
characterized by the second-order rate coefficient 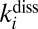 :
: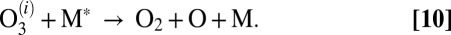
The coefficients 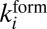 and
and 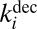 for each metastable state are related through the microcanonical equilibrium constant (16, 32):
for each metastable state are related through the microcanonical equilibrium constant (16, 32): 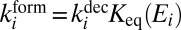 , computed statistically. All other moieties are obtained from quantum mechanics. Namely, the width
, computed statistically. All other moieties are obtained from quantum mechanics. Namely, the width 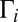 of quantum scattering resonance
of quantum scattering resonance 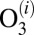 gives us directly the value of
gives us directly the value of 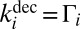 . The values of
. The values of 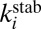 and
and 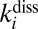 are computed from corresponding cross-sections in the
are computed from corresponding cross-sections in the 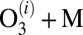 collision dynamics simulations. We do not use the low-pressure assumption here, but assume steady-state conditions for concentration of each state
collision dynamics simulations. We do not use the low-pressure assumption here, but assume steady-state conditions for concentration of each state 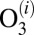 , which allows derivation of the analytic expression for the third-order recombination rate coefficient of the overall reaction (16, 23, 32):
, which allows derivation of the analytic expression for the third-order recombination rate coefficient of the overall reaction (16, 23, 32):
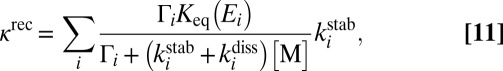 |
where the sum is over all metastable states 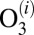 . Several processes less important than 7–10 are neglected in this treatment of kinetics. Namely, we do not include the possibility of back excitations
. Several processes less important than 7–10 are neglected in this treatment of kinetics. Namely, we do not include the possibility of back excitations 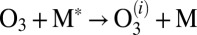 , assuming that concentration of formed ozone
, assuming that concentration of formed ozone 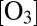 is small. We also neglect the collision-induced transitions between different metastable states
is small. We also neglect the collision-induced transitions between different metastable states 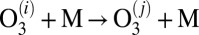 , assuming that their populations are entirely determined by equilibrium with reagents and products. These assumptions are reasonable at low and moderate pressures of the bath gas [M].
, assuming that their populations are entirely determined by equilibrium with reagents and products. These assumptions are reasonable at low and moderate pressures of the bath gas [M].
It is instructive to rewrite Eq. 11 in the following transparent form:
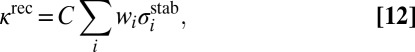 |
to emphasize that the recombination rate coefficient is computed as a weighted sum of stabilization cross-sections 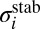 for all metastable states. The temperature- and pressure-dependent unitless weight
for all metastable states. The temperature- and pressure-dependent unitless weight 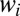 for each state is given by
for each state is given by
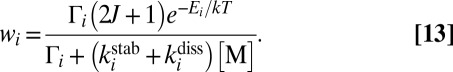 |
Factor C, common for all of the metastable states and introduced for convenience, is
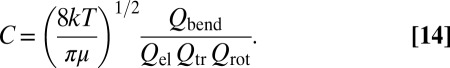 |
In Eq. 14 the equilibrium constant 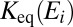 was replaced by a ratio of relevant partition functions, whereas the rate coefficient
was replaced by a ratio of relevant partition functions, whereas the rate coefficient 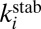 was expressed through cross-section
was expressed through cross-section 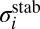 (32).
(32).
Isotope Effects
Eqs. 12 and 13 demonstrate that some metastable states may be more important for the recombination process than others due to higher weights 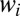 . Energies and widths of scattering resonances, entering the numerator of Eq. 13, are the most important factors to consider. According to Eq. 13, very narrow resonances (long-lived metastable states) contribute little to recombination. This property may seem somewhat counterintuitive, but it makes sense if one realizes that such
. Energies and widths of scattering resonances, entering the numerator of Eq. 13, are the most important factors to consider. According to Eq. 13, very narrow resonances (long-lived metastable states) contribute little to recombination. This property may seem somewhat counterintuitive, but it makes sense if one realizes that such 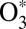 states not only decay slowly, but also receive their population from
states not only decay slowly, but also receive their population from 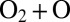 slowly. So, they remain weakly populated and contribute little to recombination. An example is a scattering resonance with low vibrational energy trapped deep and behind the centrifugal barrier of the molecule highly excited rotationally. Such a resonance would be very narrow and long-lived but, in terms of dynamics, it would be hard to populate in a typical
slowly. So, they remain weakly populated and contribute little to recombination. An example is a scattering resonance with low vibrational energy trapped deep and behind the centrifugal barrier of the molecule highly excited rotationally. Such a resonance would be very narrow and long-lived but, in terms of dynamics, it would be hard to populate in a typical 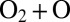 collision because this would require depositing most of the system’s energy into rotation and little into vibration (32). Mathematically, this dynamical information is contained in the small value of quantum width
collision because this would require depositing most of the system’s energy into rotation and little into vibration (32). Mathematically, this dynamical information is contained in the small value of quantum width 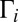 for such a resonance. In contrast, a broader resonance at energy near the top of the centrifugal barrier or slightly above it would be easy to populate in a typical
for such a resonance. In contrast, a broader resonance at energy near the top of the centrifugal barrier or slightly above it would be easy to populate in a typical 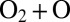 collision. Such resonances are characterized by larger values of
collision. Such resonances are characterized by larger values of 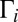 and contribute more to recombination, according to Eq. 13. The maximum value of weight
and contribute more to recombination, according to Eq. 13. The maximum value of weight 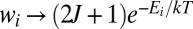 is achieved for broad resonances when
is achieved for broad resonances when 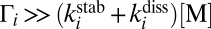 , or in the low-pressure regime (32).
, or in the low-pressure regime (32).
To see the η-effect in calculations, it is sufficient to compute and compare the third-order rate coefficients  for formation of symmetric 16O18O16O and asymmetric 16O16O18O isotopomers. This involves two formation/decay channels (say A and B) in each case:
for formation of symmetric 16O18O16O and asymmetric 16O16O18O isotopomers. This involves two formation/decay channels (say A and B) in each case:
and requires introducing the channel-specific reaction rates  and
and 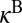 . In the symmetric case
. In the symmetric case 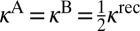 because two channels in Eq. 15 are identical. In the asymmetric case of Eq. 16, two channels are different and the total recombination rate should be computed as a sum
because two channels in Eq. 15 are identical. In the asymmetric case of Eq. 16, two channels are different and the total recombination rate should be computed as a sum 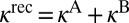 , where
, where 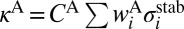 and
and 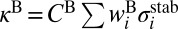 . The channel-specific weights
. The channel-specific weights 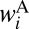 and
and 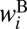 are (16, 23)
are (16, 23)
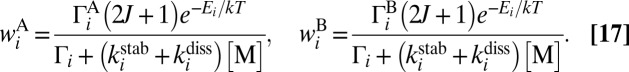 |
Here, 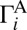 and
and 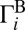 are rates of decay into channels A and B, respectively. The total decay rate is
are rates of decay into channels A and B, respectively. The total decay rate is 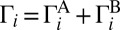 . The values of
. The values of 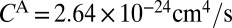 and
and 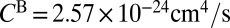 are only slightly different (within ∼3%), so the difference between
are only slightly different (within ∼3%), so the difference between 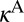 and
and 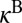 is mostly due to uneven splitting of
is mostly due to uneven splitting of 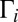 onto
onto 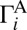 and
and 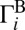 , which gives rise to the ΔZPE isotope effect (8, 10, 16, 23).
, which gives rise to the ΔZPE isotope effect (8, 10, 16, 23).
Collision Dynamics
To make theoretical treatment of the ozone forming reaction computationally affordable and physically sound, we developed a mixed quantum/classical theory for the collisional energy transfer and rovibrational energy flow (30–32). In our method, the vibrational motion of 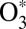 is treated quantum-mechanically using the time-dependent Schrödinger equation and the wave-packet technique. This allows incorporation of all quantum effects associated with molecular vibration (such as ZPE, quantization of states, tunneling, resonances, and symmetry) and captures most of the important physics in the process. At the same time, the collisional
is treated quantum-mechanically using the time-dependent Schrödinger equation and the wave-packet technique. This allows incorporation of all quantum effects associated with molecular vibration (such as ZPE, quantization of states, tunneling, resonances, and symmetry) and captures most of the important physics in the process. At the same time, the collisional 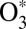 + M motion responsible for scattering is described by quasi-classical trajectories. The rotation of
+ M motion responsible for scattering is described by quasi-classical trajectories. The rotation of 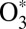 is also treated classically within the fluid rotor model (30). These classical approximations are well justified in the atmospherically relevant temperature range for a heavy molecule, such as ozone.
is also treated classically within the fluid rotor model (30). These classical approximations are well justified in the atmospherically relevant temperature range for a heavy molecule, such as ozone.
In such mixed quantum/classical approach the evolution of classically treated degrees of freedom (scattering and rotation) affects the dynamics of the quantum part of the system (vibrational modes), and vice versa. The energy is exchanged between translational, rotational, and vibrational degrees of freedom, but the total energy is conserved. The sudden collision approximation (12, 19, 24) is avoided, whereas rotation of 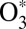 (including rotational deexcitation by collisions with M) is treated explicitly in a broad range of J values up to J ∼ 90.
(including rotational deexcitation by collisions with M) is treated explicitly in a broad range of J values up to J ∼ 90.
The present calculations were carried out within the dimensionally reduced model of 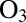 , in which only two most relevant vibrational degrees of freedom (the O–O bond distances) were treated explicitly, whereas the bending motion of O–O–O was treated adiabatically (30). To compensate for the reduced density of states, we introduced the bending partition function
, in which only two most relevant vibrational degrees of freedom (the O–O bond distances) were treated explicitly, whereas the bending motion of O–O–O was treated adiabatically (30). To compensate for the reduced density of states, we introduced the bending partition function  into the expression for the equilibrium constant, Eq. 14. This model allows the study of state-to-state transitions between quantized vibrational states of symmetric and asymmetric stretch normal-mode progressions (Fig. 1 A and B) but also involves the local-mode progression of states, found closer to dissociation threshold (Fig. 2 A and B). Within the dimensionally reduced model the calculations for
into the expression for the equilibrium constant, Eq. 14. This model allows the study of state-to-state transitions between quantized vibrational states of symmetric and asymmetric stretch normal-mode progressions (Fig. 1 A and B) but also involves the local-mode progression of states, found closer to dissociation threshold (Fig. 2 A and B). Within the dimensionally reduced model the calculations for 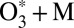 dynamics are computationally affordable and offer a unique mechanistic time-dependent insight into the energy-transfer process (30).
dynamics are computationally affordable and offer a unique mechanistic time-dependent insight into the energy-transfer process (30).
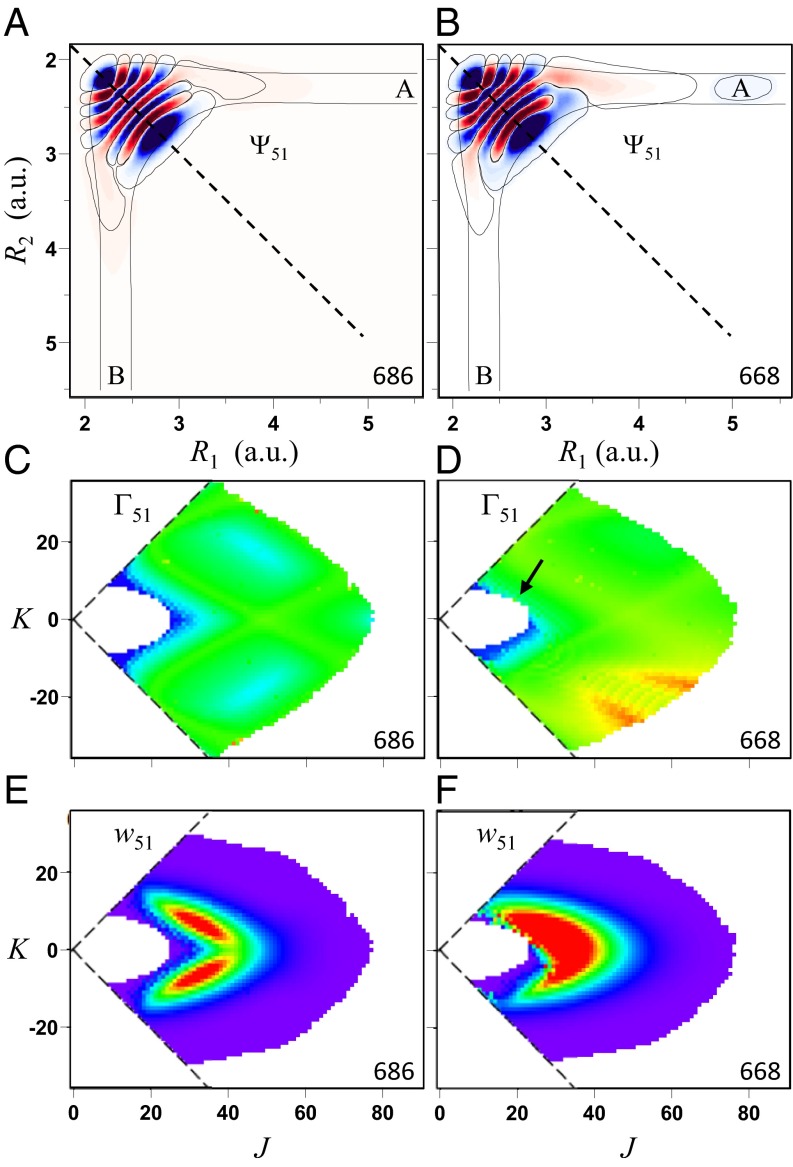
Fig. 1.
(A and B) Wave functions, (C and D) resonance widths, and (E and F) weights for the normal-mode vibrational state 51 of symmetric (Left) and asymmetric (Right) isotopomers of ozone in the dimensionally reduced model. One low-amplitude contour of wave function illustrates weaker (A) and stronger (B) connection to channel A. Black arrow indicates region where resonance widths in 16O16O18O are larger than in 16O18O16O. Wave functions are shown for typical values J = 15, K = 9.
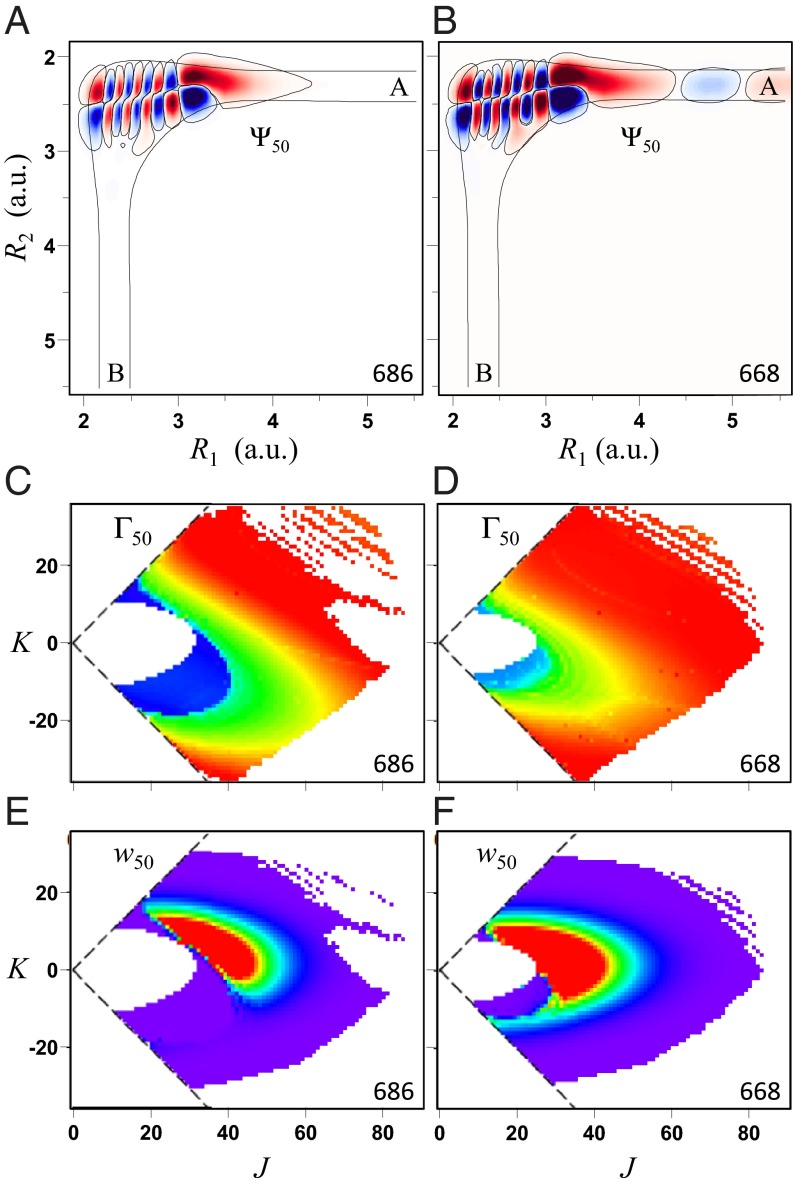
Fig. 2.
Same as Fig. 1, but for the local-mode vibrational state 50. Wave functions are shown for typical J = 20, K = 11.
Energies and Widths
The spectra of vibrational states were computed for one symmetric and one asymmetric ozone isotopomer, 16O18O16O and 16O16O18O, within the dimensionally reduced model discussed above. The values of energies for J = 0 are given in Table 1, together with state assignments in terms of the normal or local vibration mode quantum numbers. Each isotopomer has 51 vibrational states, but only 14 upper states most relevant to the recombination process are included in Table 1. In symmetric 16O18O16O the local-mode states are exactly degenerate at J = 0. This degeneracy is lifted at J > 0 as molecule rotates with K ≠ 0 and |K| ≠ J. In the asymmetric 16O16O18O the local-mode states are split by more than 100 cm−1 even at J = 0 (e.g., states 48 vs. 50 of 16O16O18O in Table 1).
Table 1.
Energies, assignments, properties, and contributions to recombination rates for upper vibrational states of symmetric and asymmetric ozone isotopomers in the dimensionally reduced model
| Symmetric 16O18O16O |
Asymmetric 16O16O18O |
|||||||||||||||
| State | 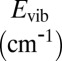 |
Modes, quanta | 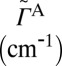 |
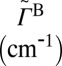 |
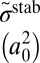 |
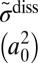 |
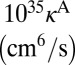 |
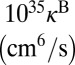 |
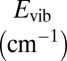 |
Modes, quanta | 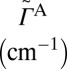 |
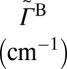 |
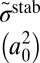 |
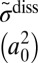 |
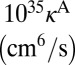 |
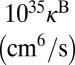 |
| 51 | −241.5 | N(8,0) | 2.39E-03 | 2.39E-03 | 18.6 | 4.4 | 0.306 | 0.306 | −194.0 | N(8,0) | 4.74E-03 | 2.69E-03 | 32.3 | 8.6 | 1.300 | 0.185 |
| 50 | −355.1 | L(8,1) | 3.16E-01 | 2.90E-02 | 55.2 | 43.7 | 2.087 | 0.119 | −207.0 | L(8,1) | 3.19E-01 | 3.88E-03 | 51.7 | 62.3 | 3.559 | 0.026 |
| 49 | −355.1 | L(1,8) | 2.90E-02 | 3.16E-01 | 55.2 | 43.7 | 0.119 | 2.087 | −315.0 | L(10,0) | 3.83E-01 | 1.42E-03 | 60.3 | 73.6 | 3.695 | 0.016 |
| 48 | −409.6 | N(7,1) | 7.81E-03 | 7.81E-03 | 18.4 | 4.6 | 0.181 | 0.181 | −318.9 | L(1,8) | 1.49E-02 | 1.73E-01 | 44.8 | 26.1 | 0.067 | 1.680 |
| 47 | −456.1 | L(10,0) | 2.18E-01 | 3.64E-02 | 55.0 | 38.3 | 1.902 | 0.039 | −331.0 | N(7,1) | 6.81E-02 | 5.77E-03 | 26.5 | 8.6 | 0.105 | 0.496 |
| 46 | −456.1 | L(0,10) | 3.64E-02 | 2.18E-01 | 55.0 | 38.3 | 0.039 | 1.902 | −435.0 | L(0,10) | 5.91E-02 | 2.00E-01 | 51.9 | 36.9 | 0.074 | 1.708 |
| 45 | −573.9 | N(6,2) | 1.97E-02 | 1.97E-02 | 45.9 | 9.2 | 0.707 | 0.707 | −466.1 | N(6,2) | 6.84E-02 | 2.31E-02 | 38.0 | 8.1 | 0.853 | 0.097 |
| 44 | −734.3 | N(5,3) | 1.37E-01 | 1.37E-01 | 29.1 | 13.5 | 0.139 | 0.139 | −601.9 | L(6,2) | 1.02E-01 | 4.95E-03 | 31.7 | 8.0 | 0.191 | 0.265 |
| 43 | −785.0 | N(4,4) | 2.70E-01 | 2.70E-01 | 26.4 | 17.1 | 0.078 | 0.078 | −671.4 | L(2,6) | 1.50E-01 | 1.86E-01 | 27.9 | 11.2 | 0.124 | 0.170 |
| 42 | −959.3 | L(9,0) | 3.46E-02 | 2.41E-02 | 19.8 | 8.9 | 0.055 | 0.003 | −814.8 | L(9,0) | 4.13E-02 | 3.10E-03 | 26.5 | 9.1 | 0.158 | 0.005 |
| 41 | −959.3 | L(0,9) | 2.41E-02 | 3.46E-02 | 19.8 | 8.9 | 0.003 | 0.055 | −922.1 | L(7,1) | 8.10E-02 | 5.77E-04 | 26.3 | 12.1 | 0.149 | 0.000 |
| 40 | −1080.2 | L(7,1) | 8.10E-02 | 2.12E-03 | 22.5 | 13.4 | 0.050 | 0.000 | −952.4 | L(0,9) | 8.03E-06 | 1.71E-02 | 18.0 | 8.0 | 0.000 | 0.030 |
| 39 | −1080.2 | L(1,7) | 2.12E-03 | 8.10E-02 | 22.5 | 13.4 | 0.000 | 0.050 | −1028.5 | L(1,7) | 8.12E-03 | 5.86E-02 | 16.5 | 8.1 | 0.001 | 0.046 |
| 38 | −1240.8 | N(7,0) | 5.61E-04 | 5.61E-04 | 11.1 | 1.5 | 0.006 | 0.006 | −1196.9 | N(7,0) | 5.99E-02 | 7.82E-04 | 9.7 | 2.3 | 0.005 | 0.003 |
| Total | 5.668 | 5.668 | 10.279 | 4.727 | ||||||||||||
As values of J and K increase, energies of state increase smoothly but the order of states can change. To keep track of vibrational identity of the rovibrational states through the entire interval of relevant rotational excitations (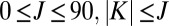 ), we developed an ad hoc diabatization procedure, based on vibrational energies and shapes of wave functions of the rovibrational states. Energies and widths of resonances were determined by introducing a complex absorbing potential into the asymptotic part of the potential energy surface and computing complex eigenvalues
), we developed an ad hoc diabatization procedure, based on vibrational energies and shapes of wave functions of the rovibrational states. Energies and widths of resonances were determined by introducing a complex absorbing potential into the asymptotic part of the potential energy surface and computing complex eigenvalues 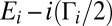 using an iterative Arnoldi procedure of the ARnoldi program PACKage (ARPACK) library. Obtained values of
using an iterative Arnoldi procedure of the ARnoldi program PACKage (ARPACK) library. Obtained values of 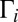 change smoothly as J and K increase. Several representative
change smoothly as J and K increase. Several representative 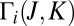 dependencies are shown in Figs. 1 C and D and 2 C and D). Green corresponds roughly to the interval
dependencies are shown in Figs. 1 C and D and 2 C and D). Green corresponds roughly to the interval 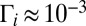 to
to 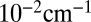 . We see that for the normal-mode state 51 the width of resonance does not increase beyond this value, even at very high levels of rotational excitation (Fig. 1 C and D). This is explained by the vibrational character of this state, which is a pure symmetric stretch. Indeed, exciting vibrations of two O–O bonds simultaneously and in-phase does not promote dissociation onto
. We see that for the normal-mode state 51 the width of resonance does not increase beyond this value, even at very high levels of rotational excitation (Fig. 1 C and D). This is explained by the vibrational character of this state, which is a pure symmetric stretch. Indeed, exciting vibrations of two O–O bonds simultaneously and in-phase does not promote dissociation onto 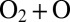 , which leads to increased lifetimes and relatively narrow resonance widths. Alternatively, for the local-mode state 50, resonances exhibit much broader widths, up to
, which leads to increased lifetimes and relatively narrow resonance widths. Alternatively, for the local-mode state 50, resonances exhibit much broader widths, up to 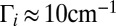 (red in Fig. 2 C and D) because the vibrational character of this state correlates well with asymptotic
(red in Fig. 2 C and D) because the vibrational character of this state correlates well with asymptotic 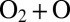 motion. Note that the picture of
motion. Note that the picture of 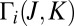 for the normal-mode state of symmetric isotopomer is perfectly symmetric (Fig. 1 C), whereas it is highly asymmetric for the local-mode states of both isotopomers (Fig. 2 C and D). Importantly, in the asymmetric isotopomer 16O16O18O some appreciable asymmetry of
for the normal-mode state of symmetric isotopomer is perfectly symmetric (Fig. 1 C), whereas it is highly asymmetric for the local-mode states of both isotopomers (Fig. 2 C and D). Importantly, in the asymmetric isotopomer 16O16O18O some appreciable asymmetry of 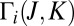 is apparent even in the case of the normal-mode state (Fig. 1D).
is apparent even in the case of the normal-mode state (Fig. 1D).
The weights 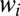 of resonances are presented in Figs. 1 E and F and 2 E and F. These pictures show very clearly which values of J and K are important for the recombination process and which are not. We see that at high
of resonances are presented in Figs. 1 E and F and 2 E and F. These pictures show very clearly which values of J and K are important for the recombination process and which are not. We see that at high 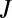 the weights
the weights 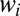 are small due to the Boltzmann factor vanishing at high energies, according to Eq. 13. At low
are small due to the Boltzmann factor vanishing at high energies, according to Eq. 13. At low 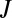 the weights
the weights 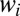 can also be small, due to very small values of
can also be small, due to very small values of 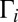 in the numerator of Eq. 13. For example, at P = 0.1 bar the weights
in the numerator of Eq. 13. For example, at P = 0.1 bar the weights 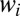 are negligible when
are negligible when 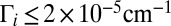 (dark blue in Figs. 1 C and D and 2 C and D). Larger weights are obtained for broader resonances,
(dark blue in Figs. 1 C and D and 2 C and D). Larger weights are obtained for broader resonances, 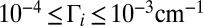 (cyan to green), at moderate energies near
(cyan to green), at moderate energies near 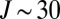 . Resonances with
. Resonances with 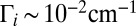 (lemon yellow) exhibit weights close to maximum possible
(lemon yellow) exhibit weights close to maximum possible 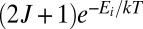 . Further increase of
. Further increase of 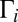 values does not lead to larger weights.
values does not lead to larger weights.
Using the weights 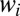 we calculated lifetimes averaged over the rotational states for different vibrational states:
we calculated lifetimes averaged over the rotational states for different vibrational states: 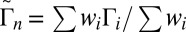 . Here the vibrational states are labeled by n, whereas the rotational states are labeled by i; summation is over rotational states within a given vibrational state. The average values of
. Here the vibrational states are labeled by n, whereas the rotational states are labeled by i; summation is over rotational states within a given vibrational state. The average values of 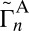 and
and 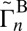 reported in Table 1 are not used in the calculations of rates, but are instructive to discuss. They show that for both symmetric and asymmetric molecules the widths of resonances for the normal-mode states are consistently smaller, by 1–2 orders of magnitude, compared with those of the local-mode states (e.g., 51 vs. 50 in Table 1). Also, we see that each state of the local-mode pair strongly favors only one decay channel (e.g.,
reported in Table 1 are not used in the calculations of rates, but are instructive to discuss. They show that for both symmetric and asymmetric molecules the widths of resonances for the normal-mode states are consistently smaller, by 1–2 orders of magnitude, compared with those of the local-mode states (e.g., 51 vs. 50 in Table 1). Also, we see that each state of the local-mode pair strongly favors only one decay channel (e.g., 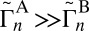 for state 50, but
for state 50, but 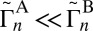 for state 48 in Table 1). Finally, if we compare 16O16O18O vs. 16O18O16O, we find that the majority of states in asymmetric molecules exhibit larger values of
for state 48 in Table 1). Finally, if we compare 16O16O18O vs. 16O18O16O, we find that the majority of states in asymmetric molecules exhibit larger values of 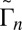 than those in symmetric molecules.
than those in symmetric molecules.
The weights 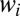 are also used to sample most efficiently the initial rotational states during the mixed quantum/classical calculations of
are also used to sample most efficiently the initial rotational states during the mixed quantum/classical calculations of 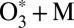 collision dynamics (30). In our sampling algorithm the number of trajectories propagated for each initial value of
collision dynamics (30). In our sampling algorithm the number of trajectories propagated for each initial value of 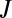 and
and 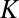 is proportional to its weight
is proportional to its weight 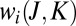 in Eq. 12.
in Eq. 12.
Results and Discussion
Major results of the 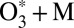 collision dynamics simulations are summarized in Table 1, where we present stabilization cross-sections for different vibrational states averaged over the rotational states:
collision dynamics simulations are summarized in Table 1, where we present stabilization cross-sections for different vibrational states averaged over the rotational states: 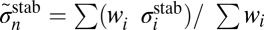 , and contributions of different vibrational states to the recombination rate coefficient:
, and contributions of different vibrational states to the recombination rate coefficient: 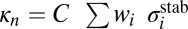 , summed over the rotational states. The overall rate is summed over vibrational states,
, summed over the rotational states. The overall rate is summed over vibrational states, 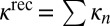 . The data in Table 1 demonstrate that upper vibrational states make more significant contributions to the recombination rate. States 38–40 and all states below them are of minor importance (at least for the value of pressure considered here, P = 0.1 bar). The local-mode states usually contribute more than the normal-mode states at similar energies.
. The data in Table 1 demonstrate that upper vibrational states make more significant contributions to the recombination rate. States 38–40 and all states below them are of minor importance (at least for the value of pressure considered here, P = 0.1 bar). The local-mode states usually contribute more than the normal-mode states at similar energies.
As discussed in the introduction, the main purpose of this study was to reproduce, from first principles, the η-effect observed in experiments of the Mauersberger group (8, 33). For this, we should compare the values of 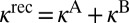 for 16O18O16O and 16O16O18O. Indeed, our results indicate that the rate of formation of symmetric 16O18O16O is 16% lower than the rate of formation of asymmetric 16O16O18O. This is very similar to experiment, where the corresponding difference is 15%. (Note that for the comparison above we added, to the computed rates of the energy transfer mechanism from Table 1, the contribution of chaperon mechanism which is assumed to be isotopomer-independent and account for ∼40% of the total rate at room temperature, ref. 34).
for 16O18O16O and 16O16O18O. Indeed, our results indicate that the rate of formation of symmetric 16O18O16O is 16% lower than the rate of formation of asymmetric 16O16O18O. This is very similar to experiment, where the corresponding difference is 15%. (Note that for the comparison above we added, to the computed rates of the energy transfer mechanism from Table 1, the contribution of chaperon mechanism which is assumed to be isotopomer-independent and account for ∼40% of the total rate at room temperature, ref. 34).
The most important question: What causes this effect? Detailed analysis showed that the decay rates (widths) of resonances are strongly affected by asymmetry of wave functions with respect to two dissociation channels. First consider the normal-mode resonance in symmetric 16O18O16O. Its wave function is connected weakly and equally to two dissociation channels (Fig. 1A) and exhibits low and equal decay rates 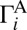 and
and 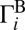 . Fig. 1E indicates that the weight
. Fig. 1E indicates that the weight 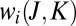 for this state remains low when the molecule rotates with
for this state remains low when the molecule rotates with 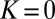 or
or 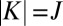 , just because it remains symmetric. The largest weight for this state is observed at
, just because it remains symmetric. The largest weight for this state is observed at 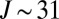 and
and 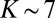 , when the nonsymmetric rotation distorts the vibrational wave function. One can say that asymmetric rotation introduces some local-mode character into the normal-mode states, which promotes decay into one of the channels, increasing the overall decay rate
, when the nonsymmetric rotation distorts the vibrational wave function. One can say that asymmetric rotation introduces some local-mode character into the normal-mode states, which promotes decay into one of the channels, increasing the overall decay rate 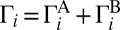 . Now consider the same state of asymmetric 16O16O18O. Due to deformation of the vibration modes, its wave function is turned slightly more toward one of the channels and slightly less toward the other, as shown in Fig. 1B. This intrinsic asymmetry of vibrations, even without any rotation, favors dissociation into one of the channels and leads to larger values of
. Now consider the same state of asymmetric 16O16O18O. Due to deformation of the vibration modes, its wave function is turned slightly more toward one of the channels and slightly less toward the other, as shown in Fig. 1B. This intrinsic asymmetry of vibrations, even without any rotation, favors dissociation into one of the channels and leads to larger values of 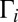 , most notably in the region of
, most notably in the region of 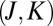 distribution indicated by the arrow in Fig. 1D. This translates into systematically higher weights
distribution indicated by the arrow in Fig. 1D. This translates into systematically higher weights 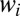 than those in symmetric molecule (compare frames E vs. F in Fig. 1).
than those in symmetric molecule (compare frames E vs. F in Fig. 1).
If we look at the local-mode states that occur in pairs, we will see that each state of the pair is connected to one of the channels (e.g., channel A for state 50, as shown in Fig. 2 A and B). The channel-specific decay rates 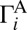 and
and 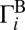 favor one of the channels almost exclusively. Thus, for a given pair of the local-mode states, we can introduce two dominant decay rates
favor one of the channels almost exclusively. Thus, for a given pair of the local-mode states, we can introduce two dominant decay rates 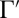 and
and 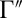 . For symmetric 16O18O16O the two rates are equal:
. For symmetric 16O18O16O the two rates are equal: 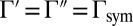 , whereas for asymmetric 16O16O18O they are different:
, whereas for asymmetric 16O16O18O they are different: 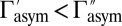 . Most importantly, we found that
. Most importantly, we found that
This property, valid for all of the local-mode states, comes from analysis of distributions of 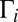 values in a very broad range (6 orders of magnitude). Again, larger values of
values in a very broad range (6 orders of magnitude). Again, larger values of 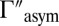 translate to systematically higher weights
translate to systematically higher weights 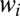 for asymmetric isotopomers) compare frames E vs. F in Fig. 2). On the mechanistic side we found that rates of decay of the local-mode states into dominant channel are consistent with a simple 1D model of tunneling through the parabolic barrier. The tunneling rates correlate well with depth and width of the barrier, and also depend on masses of atoms as expected, but the reason for Eq. 18 is, again, in the intrinsic asymmetry of vibrations in the asymmetric isotopomer.
for asymmetric isotopomers) compare frames E vs. F in Fig. 2). On the mechanistic side we found that rates of decay of the local-mode states into dominant channel are consistent with a simple 1D model of tunneling through the parabolic barrier. The tunneling rates correlate well with depth and width of the barrier, and also depend on masses of atoms as expected, but the reason for Eq. 18 is, again, in the intrinsic asymmetry of vibrations in the asymmetric isotopomer.
We can summarize that in the asymmetric isotopomer, due to slight asymmetry of the vibration modes, the vibrational 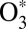 states are better connected to entrance channels compared with symmetric isotopomers. These states receive population from
states are better connected to entrance channels compared with symmetric isotopomers. These states receive population from 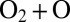 collisions more efficiently, which leads to increased rates of formation of asymmetric isotopomers––the η-effect. This effect should not be called the symmetry effect, even if the words “symmetric” and “asymmetric” are inherent to this problem. Rather, this is manifestation of the tunneling effect, because resonances tunnel in and out through the centrifugal barrier; this process appears to be more efficient for slightly distorted vibrational wave functions of asymmetric ozone molecules.
collisions more efficiently, which leads to increased rates of formation of asymmetric isotopomers––the η-effect. This effect should not be called the symmetry effect, even if the words “symmetric” and “asymmetric” are inherent to this problem. Rather, this is manifestation of the tunneling effect, because resonances tunnel in and out through the centrifugal barrier; this process appears to be more efficient for slightly distorted vibrational wave functions of asymmetric ozone molecules.
Next to discuss is the ΔZPE effect, which manifests as difference of rates for two formation channels of asymmetric isotopomer 16O16O18O. In the experiment the ratio of 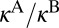 is 1.58, whereas in our calculations it is close to 1.62 (obtained from Table 1, but also taking into account contribution of the chaperon mechanism). In both the model and the experiment channel A is favored, which is
is 1.58, whereas in our calculations it is close to 1.62 (obtained from Table 1, but also taking into account contribution of the chaperon mechanism). In both the model and the experiment channel A is favored, which is 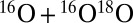 . This channel is characterized by heavier diatomic and smaller quantum ZPE, which means that this channel is effectively deeper (8, 10, 16, 23). Resonances decay faster into the deeper channel (16, 23), which leads to
. This channel is characterized by heavier diatomic and smaller quantum ZPE, which means that this channel is effectively deeper (8, 10, 16, 23). Resonances decay faster into the deeper channel (16, 23), which leads to 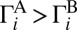 , translates to
, translates to 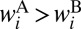 , and finally to
, and finally to 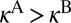 . All of the data for average values of
. All of the data for average values of 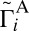 and
and 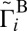 presented in Table 1 are consistent with this idea.
presented in Table 1 are consistent with this idea.
The next thing to discuss is absolute values of the reaction rate coefficients. According to recent analysis of temperature dependence of the ozone forming reaction (34), the experimental recombination rate coefficients for energy transfer mechanism at room temperature are expected to be 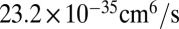 for 16O18O16O and
for 16O18O16O and 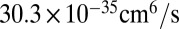 for 16O16O18O (6, 33). Theoretical values of
for 16O16O18O (6, 33). Theoretical values of  from Table 1 are
from Table 1 are 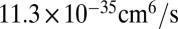 and
and 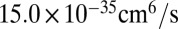 , respectively, which is 50% smaller. Lower formation rates in the dimensionally reduced model are expected, due to lowered density of states and less efficient vibrational state-to-state transitions. Absence of the excited bending states leads to larger energy gaps between quantized states and smaller values of vibrational state-to-state transitions and stabilization cross-sections
, respectively, which is 50% smaller. Lower formation rates in the dimensionally reduced model are expected, due to lowered density of states and less efficient vibrational state-to-state transitions. Absence of the excited bending states leads to larger energy gaps between quantized states and smaller values of vibrational state-to-state transitions and stabilization cross-sections 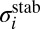 , which reduces recombination rates. Overall, the agreement between our theory and the experiment is semiquantitative.
, which reduces recombination rates. Overall, the agreement between our theory and the experiment is semiquantitative.
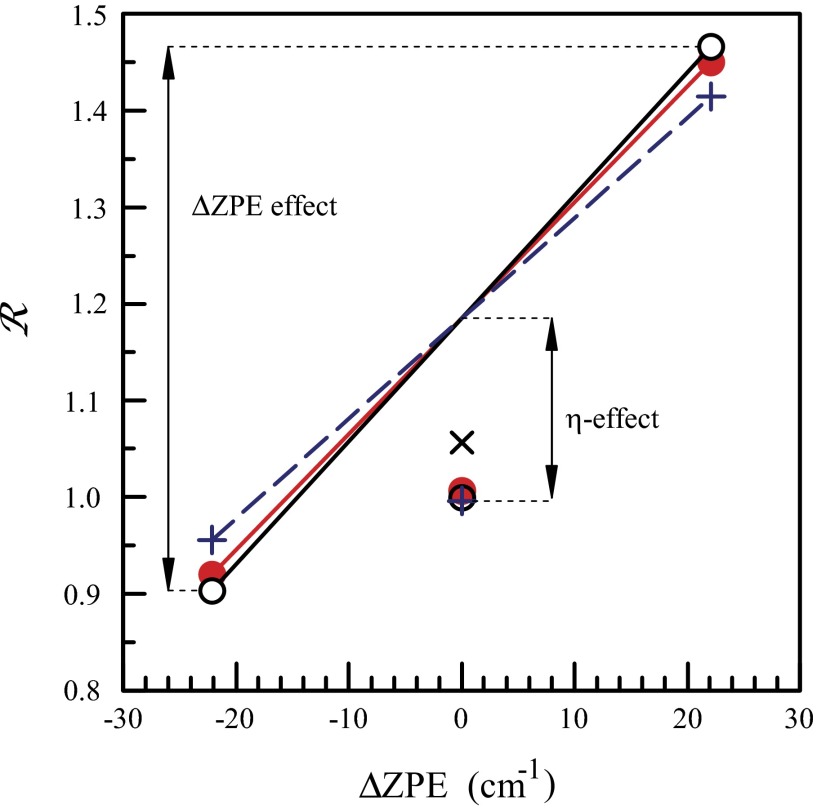
Finally, Fig. 3 represents both the η-effect and the ΔZPE effect in the way proposed by Janssen et al. (8). For experimental data the reference is the rate of 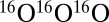 formation. For theoretical data, to make the comparison illustrative, reference was chosen such that the ratio computed for
formation. For theoretical data, to make the comparison illustrative, reference was chosen such that the ratio computed for 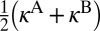 is made equal to the experimental ratio. Both isotope effects are seen in Fig. 3 very clearly (empty black vs. filled red circles). The relative magnitudes of both the ΔZPE effect and the η-effect are reproduced quite well.
is made equal to the experimental ratio. Both isotope effects are seen in Fig. 3 very clearly (empty black vs. filled red circles). The relative magnitudes of both the ΔZPE effect and the η-effect are reproduced quite well.
Fig. 3.
Comparison of experimental relative formation rates for symmetric and asymmetric ozone isotopomers (red filled circles) with predictions of the model (black open circles). Two isotope effects are clearly seen.
To demonstrate that the decay lifetimes are more important than the stabilization cross-sections, we recomputed recombination rates assigning the same 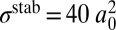 and
and 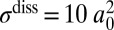 to every rovibrational state of both isotopomers, but keeping accurate isotope-specific values of
to every rovibrational state of both isotopomers, but keeping accurate isotope-specific values of 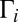 . Results of this test (shown by “+” in Fig. 3) indicate small change in the ΔZPE effect and almost no change in the η-effect. Also, to estimate influence of the dimensionally reduced approximation, we recomputed the rates without correcting for density of absent bending states by setting
. Results of this test (shown by “+” in Fig. 3) indicate small change in the ΔZPE effect and almost no change in the η-effect. Also, to estimate influence of the dimensionally reduced approximation, we recomputed the rates without correcting for density of absent bending states by setting 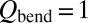 in Eq. 14 (instead of
in Eq. 14 (instead of 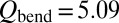 for
for 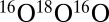 and
and 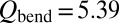 for
for 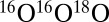 ). This modification did not change the ΔZPE effect at all, but reduced the η-effect (shown by “×” in Fig. 3). This last example underlines the importance of correct density of states for reproducing the η-effect.
). This modification did not change the ΔZPE effect at all, but reduced the η-effect (shown by “×” in Fig. 3). This last example underlines the importance of correct density of states for reproducing the η-effect.
Conclusions
We developed the mixed quantum/classical theory for collisional energy transfer and rovibrational energy flow and applied it to treat the recombination reaction that forms symmetric and asymmetric isotopomers of ozone. As expected, our calculations showed a large isotope effect for formation of an asymmetric isotopomer of ozone through two different channels, due to difference of associated vibrational zero-point energies––the ΔZPE effect. We also reproduced the experimental observation that the symmetric isotopomer of ozone is formed at a rate lower, compared with the asymmetric isotopomer––the so-called η-effect. Here, the η-effect was obtained by the first-principle calculations, without being postulated and adjusted to fit experiment. Most importantly, we identified the molecular level origin of the η-effect. Interestingly, it is not caused by the absence of some state-to-state transitions due to quantum symmetry selection rules, and does not occur during the stabilization step of the ozone forming process. The largest source of η-effect is in lifetimes of the metastable O3* states, more precisely, in differences of tunneling rates in/out of the reaction channels for symmetric and asymmetric isotopomers due to distortion of vibrational wave functions by isotopic substitutions. This important finding places our understanding of oxygen MIF on solid ground.
Existence of 3 stable isotopes of oxygen (16O, 17O and 18O) leads to as many as 36 isotopically different recombination reactions that form ozone (see table 1 in ref. 8). It is practically impossible to treat all of these processes computationally with quantum mechanics but, fortunately, not all of them are equally important. Analysis of experimental data shows that rates of these reactions follow two major trends–the ΔZPE effect and the η-effect. These two phenomena can be explored within a subset of a few reactions. In this paper we focused on Eqs. 4–6 that form singly substituted 16O16O18O and 16O18O16O. The case of 16O16O16O is not so interesting because its experimental formation rate is very close to that of all other symmetric isotopomers (e.g., 16O18O16O and 18O16O18O). Isotopomers containing 17O are not special either because experimental data for them follow the same two trends (8). So, the next step is to model formation of doubly substituted asymmetric 16O18O18O and symmetric 18O16O18O, three reactions similar to (Eqs. 4–6) that also exhibit the ΔZPE effect and η-effect in the experiment. These calculations are ongoing and will be reported elsewhere.
Acknowledgments
This research was supported by the National Science Foundation Atmospheric Chemistry Program, Division of Atmospheric Sciences, Grant 0842530. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the US Department of Energy under Contract DE-AC02-05CH11231.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1. Mauersberger K (1981) Measurement of heavy ozone in the stratosphere. Geophys Res Lett 8:935.
- 2. Thiemens MH, Heidenreich JE III (1983) The mass-independent fractionation of oxygen: A novel isotope effect and its possible cosmochemical implications. Science 219(4588):1073–1075. [DOI] [PubMed]
- 3. Heidenreich JE III, Thiemens MH (1986) A non-mass-dependent oxygen isotope effect in the production of ozone from molecular oxygen: The role of molecular symmetry in isotope chemistry. J Chem Phys 84:2129.
- 4.Krankowsky D, Mauersberger K. Heavy ozone–A difficult puzzle to solve. Science. 1996;274:1324. [Google Scholar]
- 5.Anderson SM, Hulsebusch D, Mauersberger K. Surprising rate coefficients for four isotopic variants of O + O2 + M. J Chem Phys. 1997;107:5385. [Google Scholar]
- 6.Janssen C, Günther J, Krankowsky D, Mauersberger K. Relative formation rates of 50O3 and 52O3 in 16O/18O mixtures. J Chem Phys. 1999;111:7179. [Google Scholar]
- 7.Mauersberger K, Erbacher B, Krankowsky D, Günther J, Nickel R. Ozone isotope enrichment: Isotopomer-specific rate coefficients. Science. 1999;283(5400):370–372. doi: 10.1126/science.283.5400.370. [DOI] [PubMed] [Google Scholar]
- 8.Janssen C, Günther J, Mauersberger K, Krankowsky D. Kinetic origin of the ozone isotope effect: A critical analysis of enrichments and rate coefficients. Phys Chem Chem Phys. 2001;3:4718. [Google Scholar]
- 9.Gao YQ, Marcus RA. Strange and unconventional isotope effects in ozone formation. Science. 2001;293(5528):259–263. doi: 10.1126/science.1058528. [DOI] [PubMed] [Google Scholar]
- 10.Gao YQ, Marcus RA. On the theory of the strange and unconventional isotopic effects in ozone formation. J Chem Phys. 2002;116:137. [Google Scholar]
- 11.Gao YQ, Chen W-C, Marcus RA. A theoretical study of ozone isotopic effects using a modified ab initio potential energy surface. J Chem Phys. 2002;117:1536. [Google Scholar]
- 12.Charlo D, Clary DC. Quantum-mechanical calculations on thermolecular association reactions XY+Z+M→XYZ+M: Application to ozone formation. J Chem Phys. 2002;117:1660. doi: 10.1063/1.1635361. [DOI] [PubMed] [Google Scholar]
- 13.Charlo D, Clary DC. Quantum-mechanical calculations on pressure and temperature dependence of three-body recombination reactions: Application to ozone formation rates. J Chem Phys. 2004;120(6):2700–2707. doi: 10.1063/1.1635361. [DOI] [PubMed] [Google Scholar]
- 14.Babikov D, et al. Metastable states of ozone calculated on an accurate potential energy surface. J Chem Phys. 2003;118:6298. [Google Scholar]
- 15.Babikov D, Kendrick B, Walker RB, Schinke R, Pack RT. Quantum origin of an anomalous isotope effect in ozone formation. Chem Phys Lett. 2003;372:686. [Google Scholar]
- 16.Babikov D, Kendrick B, Walker RB, Pack RT. Formation of ozone: Metastable states and anomalous isotope effect. J Chem Phys. 2003;119:2577. [Google Scholar]
- 17.Schinke R, Fleurat-Lessard P, Grebenshchikov SYu. Isotope dependence of the lifetime of ozone complexes formed in O+O2 collisions. Phys Chem Chem Phys. 2003;5:1966. [Google Scholar]
- 18.Schinke R, Fleurat-Lessard P. The effect of zero-point energy differences on the isotope dependence of the formation of ozone: A classical trajectory study. J Chem Phys. 2005;122(9):094317. doi: 10.1063/1.1860011. [DOI] [PubMed] [Google Scholar]
- 19.Xie T, Bowman JM. Quantum inelastic scattering study of isotope effects in ozone stabilization dynamics. Chem Phys Lett. 2005;412:131. [Google Scholar]
- 20.Schinke R, Grebenshchikov SY, Ivanov MV, Fleurat-Lessard P. Dynamical studies of the ozone isotope effect: A status report. Annu Rev Phys Chem. 2006;57:625–661. doi: 10.1146/annurev.physchem.57.032905.104542. [DOI] [PubMed] [Google Scholar]
- 21.Vetoshkin E, Babikov D. Semiclassical wave packet treatment of scattering resonances: Application to the delta zero-point energy effect in recombination reactions. Phys Rev Lett. 2007;99(13):138301. doi: 10.1103/PhysRevLett.99.138301. [DOI] [PubMed] [Google Scholar]
- 22.Kryvohuz M, Marcus RA. Coriolis coupling as a source of non-RRKM effects in ozone molecule: Lifetime statistics of vibrationally excited ozone molecules. J Chem Phys. 2010;132(22):224305. doi: 10.1063/1.3430514. [DOI] [PubMed] [Google Scholar]
- 23.Grebenshchikov SY, Schinke R. Towards quantum mechanical description of the unconventional mass-dependent isotope effect in ozone: Resonance recombination in the strong collision approximation. J Chem Phys. 2009;131(18):181103. doi: 10.1063/1.3253994. [DOI] [PubMed] [Google Scholar]
- 24.Ivanov MV, Schinke R. Vibrational energy transfer in Ar–O3 collisions: comparison of rotational sudden, breathing sphere, and classical calculations. Mol Phys. 2010;108:259. [Google Scholar]
- 25.Thiemens M. Treatise on Geochemistry. Amsterdam: Elsevier; 2007. Nonmass-dependent isotopic fractionation processes: Mechanisms and recent observations in terrestrial and extraterrestrial environments; pp. 1–24. [Google Scholar]
- 26.Thiemens MH. History and applications of mass-independent isotope effects. Annu Rev Earth Planet Sci. 2006;34:217. [Google Scholar]
- 27.Thiemens MH, Chakraborty S, Dominguez G. The physical chemistry of mass-independent isotope effects and their observation in nature. Annu Rev Phys Chem. 2012;63:155–177. doi: 10.1146/annurev-physchem-032511-143657. [DOI] [PubMed] [Google Scholar]
- 28.Babikov D, Walker RB, Pack RT. A quantum symmetry preserving semiclassical method. J Chem Phys. 2002;117:8613–8622. [Google Scholar]
- 29.Pack RT, Walker RB. Some symmetry-induced isotope effects in the kinetics of recombination reactions. J Chem Phys. 2004;121(2):800–812. doi: 10.1063/1.1758697. [DOI] [PubMed] [Google Scholar]
- 30.Ivanov MV, Babikov D. Mixed quantum-classical theory for the collisional energy transfer and the rovibrational energy flow: Application to ozone stabilization. J Chem Phys. 2011;134(14):144107. doi: 10.1063/1.3576103. [DOI] [PubMed] [Google Scholar]
- 31.Ivanov MV, Babikov D. Collisional stabilization of van der Waals states of ozone. J Chem Phys. 2011;134(17):174308. doi: 10.1063/1.3585690. [DOI] [PubMed] [Google Scholar]
- 32.Ivanov MV, Babikov D. Efficient quantum-classical method for computing thermal rate constant of recombination: Application to ozone formation. J Chem Phys. 2012;136(18):184304. doi: 10.1063/1.4711760. [DOI] [PubMed] [Google Scholar]
- 33.Tuzson B. 2005. Symmetry specific study of ozone isotopomer formation. PhD Thesis. (Univ of Heidelberg, Heidelberg)
- 34.Luther K, Oum K, Troe J. The role of the radical-complex mechanism in the ozone recombination/dissociation reaction. Phys Chem Chem Phys. 2005;7(14):2764–2770. doi: 10.1039/b504178c. [DOI] [PubMed] [Google Scholar]