Multiplatform single-sample estimates of transcriptional activation

Significance

We present our Universal exPression Code (UPC) approach for deriving “barcodes,” which estimate the active/inactive state of genes in a sample. UPCs normalize for technological variance and standardize data so they can be combined across microarray and RNA-sequencing experiments with high concordance. Because our method is applied to one sample at a time and thus bypasses the need to standardize samples together, it is distinctively suitable for situations in which samples arrive serially rather than in batches. We demonstrate our method’s utility in various biomedical research applications and compare against technology-specific approaches.

Abstract

Over the past two decades, many biotechnology platforms have been developed for high-throughput gene expression profiling. However, because each platform is subject to technology-specific biases and produces distinct raw-data distributions, researchers have experienced difficulty in integrating data across platforms. Data integration is crucial to data-generating consortiums, researchers transitioning to newer profiling technologies, and individuals seeking to aggregate data across experiments. We address this need with our Universal exPression Code (UPC) approach, which corrects for platform-specific background noise using models that account for the genomic base composition and length of target regions; this approach also uses a mixture model to estimate whether a gene is active in a particular profiling sample. The latter produces standardized UPC values on a zero-to-one scale, so that they can be interpreted consistently, irrespective of profiling technology, thus enabling downstream analysis pipelines to be developed in a platform-agnostic manner. The UPC method can be applied to one- and two-channel expression microarrays and to next-generation sequencing data (RNA sequencing). Furthermore, UPCs are derived using information from within a given sample only—no ancillary samples are required at processing time. Thus, UPCs are suitable for personalized-medicine workflows where samples must be processed individually rather than in batches. In a variety of analyses and comparisons, UPCs perform comparably to other methods designed specifically for microarrays or RNA sequencing in most settings. Software for calculating UPCs is freely available at www.bioconductor.org/packages/release/bioc/html/SCAN.UPC.html.

In high-throughput expression profiling, researchers often characterize transcription in relative terms—for example, transcript A is overexpressed in one condition compared with another. Such relative measurements counterbalance systematic biases in genomic data that can obfuscate determination of transcriptional activity. However, for many research questions, absolute expression measures—representations indicating whether a transcript is “active” or “inactive”—are essential because they enable researchers to characterize a gene’s transcriptional activity in individual samples and in studies for which a variety of conditions and/or tissues are being evaluated. Such measures also allow researchers to characterize biological activity independent of comparative analyses. Furthermore, these methods enable researchers to aggregate evidence across multiple experiments, which are often performed using disparate profiling technologies and protocols. This data integration capability is essential to help researchers leverage the vast amounts of publicly available genomic data.

One method for estimating absolute expression is the “barcode” methodology (1–3), which is applied to oligonucleotide expression microarrays. Absolute measures of transcriptional activation are calculated through probe-level comparisons against a large reference database of microarray samples. When applied to a diverse set of publicly available data comprising many batches, experiments, and tissues, insights about tissue-independent, disease-specific pathophysiology have been derived using these absolute estimates of expression (4). However, a limitation of previous barcode approaches is that they require a diverse collection of previously hybridized samples, yet acquiring such a collection is infeasible for many platforms.

To overcome this limitation, we present a barcoding technique that requires no ancillary samples at processing time and can be applied to short-oligonucleotide microarrays, long-oligonucleotide microarrays, and RNA-sequencing (RNA-Seq) read counts (5). Our Universal exPression Code (UPC) algorithm consists of two main steps: (i) for each platform, linear statistical models correct for background noise by modeling the genomic base composition and length of target regions; and (ii) estimates of transcriptional activation are calculated using a two-component mixture model, which assumes that background expression levels should be similar for genes having similar molecular characteristics. The background model parameters are estimated using the data in each sample individually, adapting the background distribution estimates to account for sample-specific biases. A gene’s UPC value is determined by how much its actual expression deviates from model-estimated background levels within the sample (Materials and Methods and Fig. S1). Therefore, by design, UPC values represent standardized “evidence codes” (on a zero-to-one scale) that have a consistent interpretation across gene expression platforms: lower values indicate that a given gene’s expression more likely belongs to the background distribution and higher values indicate transcriptional activation. Previous methods have applied background/signal mixture models to microarray preprocessing (2, 6, 7) and to differential expression analysis for RNA-Seq (8, 9), but the UPC approach derives standardized estimates of absolute expression that are applicable to both microarray and RNA-Seq technologies.

In this study, we illustrate UPC’s utility through various evaluations and comparisons against existing methods. Initially, we show that UPCs enable data integration. For tissue samples profiled using both microarrays and RNA-Seq, UPC values can be highly concordant (98.7%) across the technologies for a large subset of genes. Second, we show that UPC values are robust to variations in RNA-Seq sample processing. Furthermore, our data indicate that UPC-based biomarkers can be used to classify tissue types for an independent dataset that was profiled using a different instrument type, library preparation protocol, and read depth. Using quantitative PCR (qPCR) expression data as a reference standard, we also show that UPCs perform as well as or better than other RNA-Seq normalization methods in estimating activation status. Finally, using spike-in transcript levels and RNA-Seq read counts as reference standards, we compare the performance of UPCs against the prior barcode method for microarrays (1, 2).

Our single-sample approach also provides logistical advantages. Unlike most standard approaches that require a group of samples to be renormalized when additional samples arrive, UPC values remain static even when additional patient samples have been added to a study. Therefore, genomics-based clinical trials—in which patients are recruited at different times—are one target application of our method. Single-sample approaches also have computational advantages: because each sample is processed separately, large datasets can be processed with a minimal memory footprint and can be executed in parallel to decrease processing time.

Results

General Approach to Estimating Transcriptional Activation.

To derive UPC values for an individual sample, we assume that gene expression measurements come from two distinct populations, namely, genes that are inactive (measurement = background variation) and genes that are active (measurement = background variation + biological signal). Our modeling of background variation relies on data-driven statistical models that estimate the effects in each sample of the structure, base composition, length, or genomic copy number of a gene, exon, or other expression feature of interest. The intuition behind the UPC approach is that the background distribution for a gene should be similar to the background distribution for other genes in the sample that have similar molecular characteristics. Under this assumption, we use a two-component mixture model to simultaneously classify genes as active/inactive while estimating the gene-specific background and background-plus-signal distributions. The intuition behind this approach is that UPC values approximate the probability of gene expression that would be obtained from a well-defined Bayesian model with priors that are uniform over their appropriate parameter space. For one-color microarrays, we use a mixture of normal distributions. For two-color microarray and RNA-Seq data, any of three distributions can be used: normal, log-normal, or negative-binomial. The normal and log-normal distributions model continuous data (nonskewed or skewed, respectively); the negative-binomial distribution models discrete data. Although RNA-Seq read counts are inherently discrete, our data indicate (see below) that treating logged RNA-Seq data as a continuous variable performs quite well. Regardless of the modeling distribution used, a UPC value represents an estimate of whether a given gene is transcriptionally active in a given sample.

Data Integration Across Expression Platforms.

A key purpose of the UPC method is to enable researchers to integrate data across the many technologies available for gene expression profiling. This capability is relevant for researchers (i) acquiring expression data on multiple platforms, (ii) transitioning to newer technologies, and (iii) combining samples across laboratories and experiments. Expression measurements that are tied to any particular platform will be unable to support inevitable advances in profiling technologies. Contrarily, platform-agnostic measurements enable development of downstream applications—such as diagnostic, prognostic, or treatment biomarkers—that have broader applicability and greater longevity. Recent research has demonstrated that even simple data integration approaches based on relative expression are valuable for combining data in personalized-medicine applications (10). UPCs address this need more rigorously and uniformly by correcting for platform-specific biases and representing transcriptional activation consistently for all platforms. Thus, these expression codes can be interpreted consistently, irrespective of the underlying technology used for profiling.

To evaluate UPC’s ability to integrate data across platforms, we obtained microarray and RNA-Seq data from a study of liver and kidney tissue (11). The study contains three replicates for each tissue, profiled on Affymetrix U133 Plus 2.0 arrays and RNA-Seq (Illumina Genome Analyzer platform). Fig. S2 contains heat maps of these data for the UPC method and for alternative normalization approaches. When UPC values were used, the samples clustered correctly by tissue type rather than by expression-profiling technology. Samples processed using the alternative normalization approaches also clustered properly—after an additional z-score standardization step. However, even after z-score standardization, the value ranges and distributions resulting from the alternative normalization approaches differed substantially between microarrays and RNA-Seq due to differences in the underlying data distributions. Contrarily, UPC values always fall within the same scale, an essential characteristic of standardization approaches used for integrating data across technologies.

In practice, we have found that RNA-Seq profiling is more sensitive than microarrays at detecting relatively low levels of expression and thus results in more active UPC calls than for microarrays. Although advantageous when working with RNA-Seq data alone, this increased sensitivity impacts the ability to integrate data across these two technologies. However, we have found that an effective way to integrate data across these technologies is to focus on the large subset of genes called active by microarrays or inactive by RNA-Seq. For example, for the first kidney replicate, we transformed UPC values to active (>0.5) or inactive (≤0.5) calls for each gene. Of the 12,359 (74.2%) genes designated as active by microarray or inactive by RNA-Seq, 12,201 (98.7%) were concordantly barcoded across both platforms (Table 1). Most genes called as active for microarrays were also active for RNA-Seq, and most genes called as inactive for RNA-Seq were also inactive for microarrays. The number of inconsistencies between the two platforms for genes that met these criteria were 27 times fewer in number than for the remaining genes. Thus, the large subset of genes called as active for microarrays or inactive for RNA-Seq will be the most useful for integrating data in downstream applications.

Table 1.

Agreement between microarray and RNA-Seq active/inactive calls

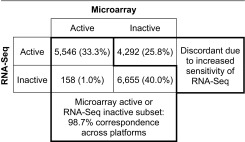To ensure that the above observations were not specific to TopHat-aligned data, we also performed the above analyses using the Genomic Next-generation Universal MAPper (GNUMAP) read aligner (12). The UPC (normal-normal) values were strongly correlated (Spearman’s ρ = 0.875) with the TopHat-aligned data, exhibited similar clustering patterns (Fig. S3), and attained similar levels of concordance.

Comparisons Between RNA-Seq Normalized Values and qPCR Values.

To further evaluate our method on RNA-Seq data, we used TaqMan qPCR expression levels for brain tissue from the Microarray Quality Control (MAQC) project (13) as a reference standard. In the absence of a competing method that produces absolute expression measures for RNA-Seq data on a single-sample basis, we compared the UPC method against two RNA-Seq normalization methods that also correct for technological biases: reads per million kilobases mapped (RPKM) (5) and conditional quantile normalization (CQN) (14). RPKM values are designed to correct for transcript-length and sequencing-depth biases. CQN also corrects for GC composition.

Initially, we compared continuous expression values between qPCR and each RNA-Seq method using Spearman’s rank correlation coefficient (Fig. S4). UPC (normal-normal, log-normal) and CQN values correlated better with qPCR values than RPKM or UPC (negative-binomial) (Table 2). Next, we used receiver operating characteristic (ROC) curves to compare continuous RNA-Seq values against present (P)/absent (A) calls from qPCR. To quantify whether present qPCR calls tended to have higher RNA-Seq values than absent calls, the area under the ROC curve (AUC) was used. By this metric, each UPC method performed consistently better than RPKM, which is a single-sample approach. UPCs did not perform as well as CQN at distinguishing “low” expression levels from “very low” levels. However, its overall performance was relatively similar (achieving an AUC of 0.864 versus 0.874 for CQN), even though CQN benefits from being a multisample method. We also note that the target applications for UPC and CQN will in many cases be different. CQN may be better suited for differential expression analyses where it is essential to identify subtle expression differences between conditions in a given experiment, whereas the UPC method is designed more for settings where data are being integrated across experiments and platforms and thus where more granular comparisons are being made. These observations were consistent across read aligners (Table S1 and Fig. S5).

Table 2.

Summary of comparisons performed across RNA-Seq normalization methods

Dataset	Comparison	UPC (nn)	UPC (ln)	UPC (nb)	RPKM	CQN
Marioni et al. (11)	Correlation between microarray and RNA-Seq*	0.801	0.786	0.625	0.698	0.798
	Genes designated as active in microarray or inactive in RNA-Seq	74.2%	61.9%	64.9%	N/A	N/A
	Concordance for microarray active/RNA-Seq inactive genes	98.7%	99.4%	97.4%	N/A	N/A
MAQC	Correlation between RNA-Seq and qPCR*	0.871	0.869	0.673	0.762	0.866
	AUC for present/absent calls	0.864	0.869	0.870	0.834	0.874
Body Map 2.0	Accuracy in predicting Wang et al. (15) tissue types (10 genes)†	0.739	0.733	0.455	0.783	0.794
	Accuracy in predicting Wang et al. tissue types (50 genes)†	1.000	0.889	0.722	0.944	0.900
	Accuracy in predicting Wang et al. tissue types (100 genes)†	1.000	1.000	0.722	1.000	1.000
	Accuracy in predicting Wang et al. tissue types (500 genes)†	1.000	1.000	0.833	1.000	1.000
	Correlation between single-end and paired-end data*	0.979	0.967	0.966	0.957	0.927
	Correlation between data aligned using either TopHat or BWA*	0.889	0.847	0.381	0.890	0.847
	Correlation between 100- and 32-bp data (pooled tissue)*	0.973	0.963	0.929	0.926	0.974

ln, log-normal; nb, negative-binomial; nn, normal-normal.

^*Correlation coefficients were calculated using Spearman's rank-based method.

^†Prediction accuracy is represented by the area under the ROC curve.

UPC-Based, Multigene Profiles Generalize Across RNA-Seq Experiments.

To assess how well UPCs can produce values that are robust to technical and experimental variations, we analyzed two RNA-Seq datasets that had been processed on different instrument types, using different protocols, and at substantially different read depths. The first dataset was from the Illumina BodyMap 2.0 Transcript project; it profiles the transcriptomes of various human tissue types using two distinct library-preparation protocols that produced either (i) single-end, 75-bp reads or (ii) paired-end, 50-bp reads. The second tissue-profiling dataset was generated by Wang et al. (15) and contains 32-bp, single-end RNA-Seq reads.

To evaluate the consistency of gene expression profiles across the datasets, we derived multigene biomarkers to predict tissue type in a training/testing validation design. We applied the RELIEF-F algorithm (16) to the Body Map data to identify genes that best distinguish the tissue types. We then used the k-nearest neighbor algorithm (17) (k = 1) to derive a biomarker from the BodyMap data and then to predict tissue type for the Wang et al. samples. When the number of genes was at least 50, the UPC (normal-normal) biomarker predicted tissue type correctly for all samples (Table 2). Biomarkers based on RPKM and CQN attained similar levels of accuracy.

We used the BodyMap data to evaluate the consistency of UPC values when either single-end or paired-end libraries were used for a given tissue type or when different read aligners were used. UPC (normal-normal) values were more highly correlated on average between the single-end and paired-end libraries (Spearman’s ρ = 0.979) than CQN (ρ = 0.927) or RPKM (ρ = 0.957) values. The UPC (normal-normal) values derived from TopHat-aligned reads were more consistent with values derived from reads aligned using Burrows-Wheeler Aligner (18) than CQN values (Table 2).

We observed that UPC values are robust to differences in read length. We evaluated a separate set of Body Map samples consisting of pooled-tissue replicates that were sequenced using stranded, 100-bp libraries; we compared measurements derived using the full read length against measurements derived from the same samples but where the reads had been trimmed to 32-bp. UPC (normal-normal) values were highly correlated (ρ = 0.973) between the two datasets, outperforming RPKM (ρ = 0.926) and performing comparably to CQN (ρ = 0.974).

These examples demonstrate that the UPC approach is robust to variations that occur commonly in RNA-Seq experiments. Such variations can include equipment type, library preparation protocols, personnel, read depth, and read length. In addition, the biomarker example illustrates that our approach can be applied in settings where it is important to differentiate among a large number of experimental conditions/categories. The UPC normal-normal model consistently performed as well as or better than the other approaches. Performance of the log-normal model was slightly lower than the normal-normal model but consistently higher than the negative-binomial model. RNA-Seq count data typically exhibit a high level of skewness; however, when the data have been transformed to a log scale, a pattern of bimodality becomes apparent. The normal-normal and log-normal mixture models appear to more stably and consistently identify a convergence point between the two modes than the negative-binomial approach. Although negative-binomial approaches have been invaluable for identifying genewise differential expression across multiple samples (8, 19), they may not be as well suited to deriving absolute measures of expression within single samples.

Comparisons Against Prior Microarray Barcode Approach.

Next, we compared the effectiveness of the UPC method against the McCall et al. barcode method, which is designed specifically for oligonucleotide microarrays (1, 2). We assessed the ability of each method to estimate transcriptional activation for 14 spike-in concentrations ranging between 0 and 512 pM in the Affymetrix Human Genome U133 Latin Square data. Using the frma package in R/Bioconductor (7, 20), we obtained barcode P values that indicate whether each transcript belongs to the “unexpressed” distribution and then subtracted these values from 1 (so they would be analogous to our UPC values).

Fig. S6 A and B display value ranges produced by the two methods for each spike-in concentration. As the spike-in concentration increases, the expression values also tend to increase for both methods. We tested whether expression values for nonzero spike-in concentrations tended to be higher than expression values for the zero concentration. We tested this separately for each spike-in concentration; in each case, we only considered nonzero concentrations greater than the given concentration threshold. Fig. S6 C and D show that both methods were highly sensitive at concentrations greater than 1 pM; however, for the lowest concentrations, barcode values resulted in an average AUC of 0.952, and the average AUC for UPCs was 0.911.

In an additional comparison, we used RNA-Seq read counts from the liver and kidney data (11) as a reference standard and assessed whether genes with higher RNA-Seq read counts tended to be called as active by the two microarray approaches (and vice versa). First, we rounded barcode and UPC values to zero/1 activation calls; then we compared those calls against RNA-Seq read counts using ROC curves. Irrespective of the threshold used, the UPC method attained higher AUC values (Fig. S7).

Finally, we emphasize that the UPC method offers a key logistical advantage compared with the prior barcode method. Because the background distribution is derived from a given sample, there is no need to derive a background distribution from a large number of external samples. In addition, the UPC approach provides standardized absolute expression measures for integration across multiple platforms, whereas the previous barcoding method is only available for Affymetrix arrays.

Discussion

A key goal of researchers in the genomics era is to identify gene expression profiles—multigene transcriptional biomarkers—that reliably characterize specific biomedical phenomena. Such profiles may be useful in clinical settings, for example, to refine diagnoses and treatment plans (21–23), to estimate disease prognoses (24), and to delineate biological activity occurring within tissue types. To achieve this goal, gene expression profiles must robustly generalize across experiments that have been performed in different laboratories, with different equipment, and by different personnel. If not accounted for, even minor differences in such factors can introduce technical artifacts into raw data, which can drastically confound biomedical interpretations (25). Also importantly, the divergent raw-data distributions produced by different platforms can impede researchers from developing generalizable models. For example, extreme RNA-Seq read counts in a few genes can dominate expression profiles and thus obscure biologically meaningful patterns in other genes. The UPC method addresses such challenges by (i) processing each sample independently to avoid perpetuating biases from one sample into another, (ii) correcting for technological variations through statistical modeling, and (iii) producing a consistently interpretable representation for each sample regardless of the underlying technology.

UPC is a completely intrinsic, single-sample processing approach that can be applied to microarray (one-color and two-color) and RNA-Seq data. Additionally, unlike previous barcode methods, which require hundreds of samples to inform model derivation, we used a relatively small sample set to inform derivation of the UPC models. Thus, when a new gene expression technology emerges, the approach can be tailored to that technology relatively early in the technology’s life cycle because it is not necessary for a large body of samples to have accumulated. Having derived a UPC model for a given technology, data from ancillary samples need not be considered when the model is applied to new samples. However, we have observed that increased probe-level sensitivity can be obtained by estimating the gene or probe-specific background based on a large set of curated samples from the same profiling platform.

Many normalization approaches are designed for experiments where a single platform is used and where comparisons only need to be made among samples in a given experiment (e.g., differential expression analyses). Although we have shown that UPCs can perform comparably to existing methods on various such applications, we recognize that a possible disadvantage of the UPC approach is that it may not be best suited to identifying subtle differences in expression between conditions—for example, moderately active and highly active genes would both be labeled as active by the UPC method. However, we have shown that UPC values are useful in diverse applications, such as integrating samples across experiments and platforms, constructing generalizable biomarkers, and classifying tissue samples. The ability to integrate data across multiple platforms will enable researchers to continue taking advantage of the vast pool of microarray samples that have accumulated over the past decade and to integrate them with the emergent pool of samples now being profiled with next-generation technologies.

The UPC approach standardizes data from distinct platforms into consistent representations of expression—whether a given gene is expressed above the model-estimated background level in a sample. However, different technologies may have different background levels and sensitivities in detecting gene activity. For example, in the results described above, we showed that RNA-Seq designated more genes as active than Affymetrix microarrays on the same biological samples. This is likely due to decreased background noise and thus higher sensitivity of RNA-Seq platforms. This did create a discrepancy between the active genes called by both methods. However, by focusing on genes called active by the less sensitive technology (arrays) and those called inactive by the more sensitive platform (RNA-Seq), we were able to identify a large subset (74.2%) of genes that were 98.7% concordant across the platforms. This provides a simple and direct approach for combining data across technologies that have different sensitivities; this approach can also be applied to other expression-profiling technologies.

In sum, the UPC method facilitates cross-platform expression analyses, the ability to aggregate data across independent experiments, and robustness in the face of inevitable variations in experimental protocols and conditions. Our general approach can be tailored to any high-throughput expression-profiling platform. It also can be applied not only to expression values representing gene activity but also to exon-level, transcript-level, and noncoding expression values.

Materials and Methods

We have developed a general approach for estimating transcriptional activation, which we term UPC. This section describes the method’s general approach and how it has been customized for each type of gene expression platform.

Formal Derivation of UPC Approach.

For a given expression profiling sample, we let 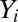denote the unnormalized expression measurement for gene i. We assume that

where 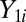is a random variable from the “background” distribution for the gene, 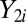originates from the “background-plus-signal” distribution, and 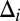is an unobserved indicator variable that is equal to 1 if gene i is active and 0 if the gene is inactive in the sample. Formulating the model in Eq. 1 based on a “missing data” approach (where the 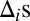are the missing data), we arrive at a complete data likelihood of

where 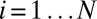indexes the probes, π is the proportion of active genes in the sample, 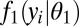is the density function of the background, and 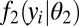is the density function of the background-plus-signal distribution. Parameter estimation is conducted using the expectation–maximization (EM) algorithm (26). Application of the EM algorithm is straightforward in this case as it entails a probabilistic assignment of each data point to each mixture component (expectation step) and then an estimate of each component’s parameters using the imputed probabilities from the previous step as weights (maximization step). These two steps are then iterated to convergence, taking note that convergence is to a global, not local, maximum. Once the algorithm has converged, the UPC value for gene i, denoted 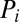, is given by the expected value of 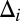given that the parameters π, 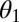, and 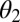are set to their maximum-likelihood estimates:

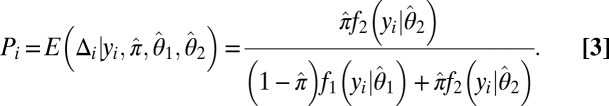Deriving UPCs for Affymetrix Microarrays.

Our approach for Affymetrix expression arrays builds upon our single-channel array normalization (SCAN) approach (6), which is a modification of model-based analysis of tiling arrays (MAT) (27). The MAT/SCAN background model has been shown to account for as much as 63% of the variation due to array, probe-composition, and cross-hybridization effects in tiling-array samples and was previously applied successfully to Affymetrix exon arrays by another group (28), thus showing the broad applicability and robustness of this modeling approach. 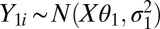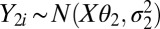For our approach, using the logged probe intensity, we assume and , where 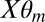is the mth mixture component MAT/SCAN model for probe i represented in the equation below for a given m:

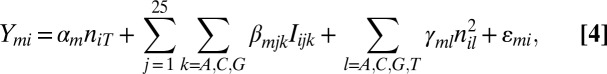where 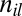is the number of nucleotides l in probe i, 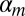is a baseline value derived from the number of Ts on the probe, 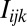is a function that indicates 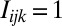if the nucleotide at position j is k for probe i, 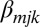represents the effect of each base k (except T, which is already modeled via 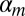) at each position j, 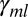is the squared effect of the nucleotide count, and 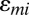is an error term specific to each probe and is assumed to follow a Gaussian distribution. The background model parameter estimates and UPC values are then obtained for each sample individually using the EM algorithm as described above.

Deriving UPCs for Two-Color Microarrays.

In addition to bias introduced by probe composition effects, two-color arrays suffer from bias stemming from the different dyes used as well as from correlation between the two channels. For these arrays, we use a two-step approach: the first step is a standardization that removes the probe and dye effects as well as the correlation between channels. The probes are grouped into “bins” based on the total number of G and C nucleotides (G + C count), and the probes are then standardized within the G + C bin. This approach accounts for array and probe composition effects and for differences in the channel correlation across G + C bins as illustrated by our previous work (29). Our approach assumes that the probe intensities from probe i in G + C bin k, denoted 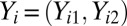follow a bivariate normal distribution on the log scale, namely,

where 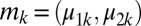is the vector of means for the logged probe intensities and 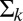is the variance–covariance matrix for G + C bin k. We standardize the data as follows:

where 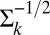is the inverse “square root” of the variance–covariance matrix. This square root is obtained by first obtaining the eigenvalue decomposition of the matrix, namely 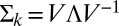, where V is a matrix of eigenvectors and 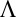is a diagonal matrix containing the eigenvalues. The inverse square root is obtained by inverting and square rooting the diagonal matrix of eigenvalues and then reconstructing the matrix, 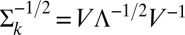. It can be shown that the transformation in Eq. 6 will zero-center and variance-standardize the data while removing the correlation between channels. Once the data are standardized, we can barcode the samples one channel at a time by assuming a simple mixture model, namely for channel c: 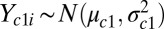and 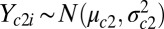and applying the general approach described above. The background model parameter estimates and UPC values are obtained for each sample individually using the EM algorithm as described previously.

Deriving UPCs for RNA-Seq Experiments.

There is also a need for background and normalization models for RNA-Seq data, although the bias comes from different sources than in microarrays. Potential sources of bias are sequencing errors, read-mapping errors, nucleotide composition effects, and gene length biases (longer genes are likely to be sequenced more often than shorter genes). In addition, we have observed that, in RNA-Seq experiments, at least a few reads are typically mapped to a large proportion of genes. We do not believe this high number is caused by mapping errors or that all of the genes in these tissues are active. Instead, we attribute this high number to a phenomenon we term “leaky transcription,” meaning that, in any given gene in a tissue, there are at least a handful of cells expressing the gene (30). When we log the read counts, this effect manifests itself in a strong bimodal distribution that clearly justifies the need for a mixture-modeling approach.

In one approach, we approximate the background and background-plus-signal distributions of the log-read counts using a mixture of normal distributions, namely 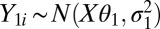and 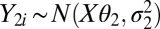, where 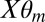is the mth mixture component of the bias model for a given m:

where 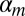is the intercept, 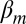is the effect of the gene’s G + C 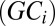content, and 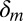is the effect of the log of the gene length .

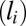Alternatively, because of the discrete nature of RNA-Seq (count) data and therefore a possibly skewed background distribution, we have also approximated the background and background-plus-signal distributions using mixtures of log-normal or negative-binomial distributions. The log-normal approach is identical to the normal approach, except that we replace the normal density with a log-normal distribution, namely 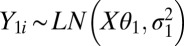and 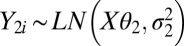. For the negative-binomial regression, we used 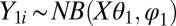and 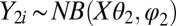, where 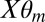represents the mean and 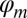represents the dispersion factor as described previously (8, 31). Implementations of all three approaches (normal, log-normal, negative-binomial) are provided in our software package. However, in general, we have observed that the mixture of Gaussian distributions is more stable and performs better based on comparisons across platforms and technical replicates (described above).

Due to the large number of zero values commonly observed in RNA-Seq data, we excluded these values before UPC calculations and output a default value of zero for these genes.

Data Processing Performed for Comparative Analyses.

Microarray and qPCR data were downloaded from the Gene Expression Omnibus (GSE11045, GSE12946, GSE5350) and from www.affymetrix.com/support/technical/sample_data/datasets.affx. Raw RNA-Seq data were downloaded from the Short Read Archive (SRA000299, ERP000546, SRP000727). RNA-Seq reads from SRA000299 were trimmed to 32 bp in accordance with a recommendation from the original authors.

Microarray probe values were mapped either to Affymetrix probe set identifiers or to genes [using BrainArray mappings (32)] and then summarized using a 10% trimmed mean.

RNA-Seq reads were mapped to the human reference genome using TopHat (33), GNUMAP (12), and/or Burrows–Wheeler Aligner (18). Default GNUMAP settings were used, other than an alignment-score threshold of 80%. The HTSeq (www-huber.embl.de/users/anders/HTSeq/) and mpileup (34) tools were used to generate read counts for genes and/or genomic regions covered by the microarrays. RPKM values (5) were calculated using a custom script. CQN values were calculated using the cqn package (14). UPC values were calculated using convergence thresholds of 0.01 (microarray), 0.001 (RNA-Seq normal-normal, log-normal), or 0.01 (RNA-Seq negative-binomial).

The Weka (35) and ML-Flex software packages (36) were used for the biomarker analysis. The k-nearest neighbor implementation in Weka uses the Mahalanobis distance (37), which is invariant to scale. The ROCR package (38) was used to generate ROC plots. The gplots package (39) was used to generate heat maps. All scripts used to execute the analyses described in this paper are available upon request. Software for deriving UPCs is freely available from www.bioconductor.org/packages/release/bioc/html/SCAN.UPC.html.