Passive energy recapture in jellyfish contributes to propulsive advantage over other metazoans

Significance

Jellyfish have the ability to bloom and take over perturbed ecosystems, but this is counterintuitive because jellyfish are described as inefficient swimmers and rely on direct contact with prey to feed. To understand how jellyfish can outcompete effective visual hunters, such as fish, we investigate the energetics of propulsion. We find that jellyfish exhibit a unique mechanism of passive energy recapture, which can reduce metabolic energy demand by swimming muscles. Contrary to prevailing views, this contributes to jellyfish being one of the most energetically efficient propulsors on the planet. These results demonstrate a physical basis for the ecological success of medusan swimmers despite their simple body plan and have implications for bioinspired design, where low-energy propulsion is required.

Abstract

Gelatinous zooplankton populations are well known for their ability to take over perturbed ecosystems. The ability of these animals to outcompete and functionally replace fish that exhibit an effective visual predatory mode is counterintuitive because jellyfish are described as inefficient swimmers that must rely on direct contact with prey to feed. We show that jellyfish exhibit a unique mechanism of passive energy recapture, which is exploited to allow them to travel 30% further each swimming cycle, thereby reducing metabolic energy demand by swimming muscles. By accounting for large interspecific differences in net metabolic rates, we demonstrate, contrary to prevailing views, that the jellyfish (Aurelia aurita) is one of the most energetically efficient propulsors on the planet, exhibiting a cost of transport (joules per kilogram per meter) lower than other metazoans. We estimate that reduced metabolic demand by passive energy recapture improves the cost of transport by 48%, allowing jellyfish to achieve the large sizes required for sufficient prey encounters. Pressure calculations, using both computational fluid dynamics and a newly developed method from empirical velocity field measurements, demonstrate that this extra thrust results from positive pressure created by a vortex ring underneath the bell during the refilling phase of swimming. These results demonstrate a physical basis for the ecological success of medusan swimmers despite their simple body plan. Results from this study also have implications for bioinspired design, where low-energy propulsion is required.

During jellyfish swimming, acceleration is achieved in the contraction phase, whereas peak drag and deceleration occur in the relaxation phase. Thus, studies investigating the propulsion of jellyfish have primarily focused on the contraction phase (1–4). Potential advantages in swimming efficiency of gelatinous zooplankton locomotion have been previously overlooked because efficiency of swimming is commonly estimated using the Froude number (E_f) (5–7), a metric originally designed to quantify the propulsive performance of ships. The E_f is defined as the ratio of useful power produced during locomotion to the useful power plus the power lost to the fluid (8). It has been used to compare biological species of different sizes and morphology. Previous work describes jellyfish as inefficient swimmers with E_f values of 0.09–0.53 (5), compared with ≈0.8 in fish (9, 10). However, this method, does not account for large interspecific differences in the net metabolic energy demand of swimming, and there is no protocol for including the relaxation phase of pulsating swimmers in such a calculation (11).

A more comprehensive and ecologically relevant method of estimating energetic costs of locomotion is the net cost of transport (COT) analysis (Fig. 1 A and D). COT is defined as 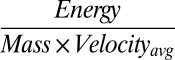, and it is a suitable metric for interspecific comparisons of swimming efficiency because the energetic expenditures for generating kinematic and fluid motion are not constant among species (Fig. 1 B and C). By this measure, the moon jellyfish, Aurelia aurita, expends significantly less energy per unit of wet mass per unit distance traveled than other animals. The ability to exhibit a low COT has also been reported in another jellyfish species (Stomolophus meleagris) (12).

Fig. 1.

Energetic swimming comparisons of propulsive modes. (A) Net COT based on wet mass. Data for fliers and runners are replotted from the study by Schmidt-Nielsen (30). Crustaceans and squid are replotted from the study by Larson (12). Fish data were combined from both of these studies (12, 30). Data for A. aurita were calculated with swimming speed vs. body size from the current study and supplemented with data from the studies by Martin (27) and McHenry and Jed (28) and by metabolic data from the study by Uye and Shimauchi (29). (B) Net respiration rates of locomotion for the salmon (O. nerka) and a rhizostome jellyfish (S. meleagris). (C) Net respiration rates of locomotion for S. meleagris and A. aurita. (D) Net COT for all three species. Data used for respiration and COT in salmon were obtained from the study by Brett and Glass (31), and Stomolophus data were replotted from the study by Larson (32). WW, wet weight.

How can jellyfish swim with such a low COT, and how do jellyfish species (Aurelia and Stomolophus) compare with each other and with fish? Using the salmon (Oncorhynchus nerka), another efficient swimmer, as a reference, we show that net COT is ≥3.5-fold greater for salmon and twofold or more greater for Stomolophus relative to Aurelia (Fig. 1D). The lower COT for Aurelia is primarily a function of its low net metabolic rate for swimming, which is 15-fold lower than that of Stomolophus (Fig. 1C).

Medusae can exhibit such low respiration rates due to the large proportion of metabolically inactive tissue during swimming. Jellyfish have low body carbon relative to other swimmers (13), which results in ≤1% of the body mass represented by muscle (12, 14). Fish, in comparison, have a body mass that is ≥50% muscle (15). Expending such little energy to generate propulsive thrust is an adaptive advantage for gelatinous zooplankton. However, consider the tradeoff. Low body carbon and muscle mass limit propulsive options for jellyfish (16). Swimming proficiency is forfeited because low muscle mass in gelatinous zooplankton restricts them to low velocities, and burst swimming velocities are only 30% greater than that of routine swimming (12). Low velocities typically increase COT; however, in jellyfish, this is more than compensated for by low metabolic demand.

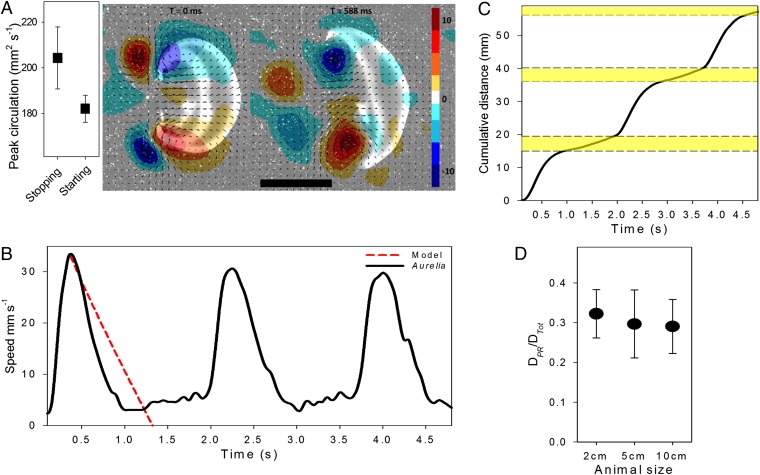
Although low muscle mass limits the thrust jellyfish can produce during contraction (16, 17), we show that jellyfish use a form of passive energy recapture to enhance their swimming and reduce their COT further. Contraction of the bell generates a starting vortex at the bell margin and a stopping vortex with opposite-sign vorticity forms upstream of the starting vortex (11). After shedding of the starting vortex, the relaxation or refilling phase begins and enhances stopping vortex circulation and vorticity while drawing the fluid under the bell (Fig. 2A and Movie S1). Although medusae exhibit greater accelerations and peak velocities during contraction (Fig. 2B and Fig. S1), peak circulation of the stopping vortex (which is proportional to the thrust generated) can be significantly greater (ANOVA, P = 0.01; n = 10) than the starting vortex (Fig. 2A), illustrating the potential importance of stopping vortices during swimming. A study using computational fluid dynamics (CFD) has previously demonstrated that power can be generated during the refilling (relaxation) phase (18), but relative contributions to efficiency and distance are unknown.

Fig. 2.

Swimming performance of A. aurita. (A) Maximum circulation and vorticity starting and stopping vortices during normal swimming (cruising). (Scale bar, 1 cm.) (B) Representative swimming sequence of a 3-cm A. aurita, showing an increase in speed during periods of no kinematic body motion (postrecovery). The model (red) shows a conservative estimate of the change in speed with time from inertia alone. (C) Cumulative distance of the jellyfish shown in B. Yellow represents the distance gained from passive energy recapture. (D) Effect of passive energy recapture with size (bell diameter). No difference (P = 0.550) is observed between body size and the relationship between distance traveled from passive energy recapture (D_PR) relative to the total distance traveled per swimming stroke (D_Tot).

The mesogleal tissue of jellyfish has both viscoelastic (19) and elastic properties (20). However, the refilling phase, responsible for the secondary thrust, is found to be powered exclusively from the elastic properties of mesoglea (20) (Fig. S2). The stress–strain relationship within this elastic tissue exhibits a nonlinear, J-shaped relationship (21, 22). This allows the tissue to strain easily at the beginning of the contraction when the potential for hydrodynamic output is high and to store most strain energy near the end of the contraction. This can aid in optimizing energetic efficiency because nearly all energy is devoted to thrust generation during periods of acceleration, whereas elastic strain storage occurs mostly at the end of the contraction cycle. Therefore, the large stopping vortex is produced and positioned under the bell using only stored strain energy and no additional energy from antagonistic muscle groups. An examination of multiple jellyfish species demonstrates that this translates to only a small proportion of each swimming cycle in jellyfish (∼20%) requiring muscle contraction (Fig. 3 A–C). The energy required to decelerate the contracting bell is translated to refilling the bell, similar to the mechanism demonstrated in flying insects, which greatly reduces energetic costs for thrust production (23).

Fig. 3.

Swimming performance for three species of jellyfish showing species variation in the durations of contraction (I), relaxation/refilling (II), and the interpulse duration during which thrust from passive energy recapture occurs (III). All three species exhibit enhanced thrust during this third phase. (A) Oblate scyphomedusae, A. aurita. (B) Hydromedusae, Eutonina indicans. (C) Rhizostome, Phyllorhiza punctata. (D) Cumulative swimming distance for all three species.

Our results show that 32% (SD = 0.6%) of the total distance traveled per pulse can occur during the postrelaxation period (interpulse phase), where the animal produces no kinematic motion (i.e., coasting) and after inertial motion would have ceased (Fig. 2 B and C). Anesthetized A. aurita were artificially propelled forward at natural swimming velocities to allow observation of the stopping vortex influence beyond the duration at which the subsequent contraction normally begins. We show that passive bell refilling can produce thrust for an extended period after bell motion ceases (Fig. S2). The force produced can carry a 4-cm Aurelia an additional 10.1 mm (SD = 0.8, n = 4) each pulse, which is 80% of the measured 12.7 mm (SD = 3.5, n = 5) achieved during the kinematically active portion of normal swimming.

To elucidate how thrust is generated after refilling of the bell, we measured pressure around the body of the jellyfish using a combination of CFD and a newly developed empirical technique for pressure estimation from velocity field measurements. Oblate medusae are known to produce more complex pressure fields at the subumbrellar surface relative to jetting medusae (24). We find that during bell relaxation, the pressure is typically low as refilling occurs but that subsequent induced flow from the stopping vortex builds against the subumbrellar surface and creates a large region of positive pressure between the low-pressure cores of the vortex ring (Fig. 4 and Movie S2). The resulting high pressure creates enough force to cause an additional acceleration of the body after initial contraction and before the next cycle (Fig. 4 B and C).

Fig. 4.

CFD of a 3-cm swimming A. aurita. (A) Pressure around the body during a swimming cycle. Note the secondary increase in pressure at the subumbrellar surface (VI–VIII) and the resulting axial force and boost in velocity. (B) Axial force shows the corresponding locations from A. A secondary peak is shown corresponding to positive pressure of the induced flow created by the stopping vortex accumulating against the subumbrellar surface. (C) Velocity-time plot shows the corresponding locations from A. (D) Results from an empirically based technique for pressure estimation from velocity field measurements around a 3.5-cm A. aurita. (E) Velocity-time plot shows the corresponding locations from D.

A simple, conservative estimate can be made to understand how passive energy recapture contributes to COT in Aurelia. Eliminating the interpulse duration (and thus any influence of passive energy recapture) will result in doubling of the pulse frequency as = 0.50 (SD = 0.05, n = 20), where T_ip is the time of the interpulse duration and T_tot is the total time of each pulse. Although the relationship between pulse frequency and respiration is unknown for jellyfish, it is exponential for fish (25). Conservatively, we assume a linear relationship between respiration rate and pulse frequency. By applying the measured velocity during the active phase (V_A) of the swimming cycle over the total velocity (V_T) for animals 2–10 cm in diameter (V_A/V_T = 1.35, n = 12), we find that COT will increase at least by 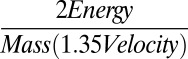= 1.48-fold, or 48% in Aurelia if passive energy recapture is not used.

Although cnidarian swimming muscle structure and force production resemble those of other animal groups (16), the cnidarian muscle fibers are housed solely within epitheliomuscular cells. This single cell layer limits the thickness of swimming muscles within cnidarians, and thus force production during medusan swimming. Therefore, beyond a certain size, and unlike other animals, jellyfish do not continue to increase swimming velocity with size. As a result, the additional force required to continue increasing swimming speed with body size is limited to a specific range in jellyfish. This has consequences with respect to COT because jellyfish appear to have the greatest advantage over other metazoans when they are small. However, extrapolating the results from Fig. 1 indicates that fish only begin to exhibit a lower COT than Aurelia beyond a body mass of ∼100 kg.

The ability of jellyfish to use passive energy recapture reduces metabolic demand while increasing fluid (and thus prey) encountered by feeding structures and translates to more energy available for growth and reproduction. Such energetic advantages would enable jellyfish populations to exploit environments with excess prey and contribute to the demonstrated ability of some jellyfish species to bloom rapidly over short periods and outcompete other species, such as fish (26). Our results show that because COT can vary by more than twofold in jellyfish alone, the species-specific influence of passive energy recapture should be taken into account when trying to understand bloom dynamics and trophic competition. In addition, the passive energy recapture demonstrated in Aurelia may be an important consideration in biomimetic design, where low-energy demands are required for efficient vehicle design. The fact that passive energy recapture appears to scale well with animal size also suggests there are important design implications to be explored over a wide range of size scales.

Materials and Methods

Swimming Kinematics.

Free-swimming jellyfish (1.5–6 cm) were recorded in a glass filming vessel (30 × 10 × 25 cm) by a high-speed digital video camera (Fastcam 1024 PCI; Photron) at 1,000 frames per second. Only recordings of animals swimming upward were used in the analysis to eliminate the possibility of gravitational force aiding forward motion of the animal between pulses. Detailed swimming kinematics (2D) were obtained using Image J v1.46 software (National Institutes of Health) to track the x and y coordinates of the apex of the jellyfish bell and the tips of the bell margin over time. Swimming speed was calculated from the change in the position of the apex over time as:

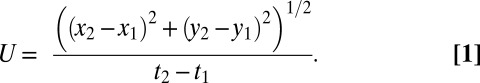Jellyfish were illuminated with a laser sheet (680 nm, 2W continuous wave; LaVision) oriented perpendicular to the camera’s optical axis to provide a distinctive body outline for image analysis and to ensure the animal remained in-plane, which ensures accuracy of 2D estimates of position and velocity. Swimming kinematics of large (>6 cm) A. aurita were obtained using a high-definition Sony HDV Handycam (model HDR-FX1) at a dedicated off-exhibit tank at the New England Aquarium. Here, a 500-mW laser (432 nm, Hercules series; Laserglow) was formed into a thin sheet to illuminate (from above) the outline of the animal for kinematic analysis.

COT.

The metabolic COT per unit mass and distance (joules per kilogram per meter) for the moon jellyfish (A. aurita) was estimated from mass-specific swimming speeds and respiration rates. Mass-specific swimming speeds were obtained from kinematic data (current study) and supplemented with data from studies by Martin (27) and McHenry and Jed (28). Mass-specific active respiration data for A. aurita were obtained from Uye and Shimauchi (29). Conversion of metabolic respiration to energy expended (joules) is accomplished by using the conversion factor of 19 J⋅mL⁻¹ of O₂ (12). To obtain net COT, which accounts only for energy expended toward locomotion, basal energy consumption must be subtracted from the active rates. Because basal rates are found to be half of the active rates in medusae (12), we calculate the proportion of energy dedicated to location in Aurelia as 0.5-fold the active rate. It should be noted that this makes our net COT_Aurelia estimates conservative, because pulsation rates in Aurelia are lower than in species that were studied (12). This is because Aurelia spends proportionally less time actively contracting compared with many other species (Fig. S1), and because this is the only time energy is expended for swimming, due to passive relaxation (19), the proportion of the active-to-total metabolic rate in Aurelia (and COT) will likely be lower. The mass-specific respiration and swimming data for salmon (30) were used for comparative purposes.

Net COT was calculated using the equation:

Net COTs for runners, fliers, and other swimmers were obtained and replotted from studies by Larson (12), Uye and Shimauchi (29), and Schmidt-Nielsen (30), using graph digitizing software (GetData v2.25).

Fluid Properties Around Swimming Jellyfish.

Fluid motion created by the jellyfish while swimming was quantified using 2D digital particle image velocimetry. Using the setup described above, the filtered seawater was seeded with 10-μm hollow glass beads. The velocities of particles illuminated in the laser sheet were determined from sequential images analyzed using a cross-correlation algorithm (LaVision software). Image pairs were analyzed with shifting overlapping interrogation windows of a decreasing size of 64 × 64 pixels to 32 × 32 pixels or 32 × 32 pixels to 16 × 16 pixels. Details on circulation and pressure estimates are provided in SI Materials and Methods.

Kinematic data were log-transformed and checked for normality using a Shapiro–Wilks test. Data were subsequently tested using one-way ANOVA to determine if a significant difference existed between means.

CFD Model of a Swimming Jellyfish.

We developed a jellyfish model using the bell kinematics of an individual 3-cm diameter, free-swimming moon jellyfish (A. aurita). Digitized points along this half of the body were spatially interpolated using eighth-order polynomials, temporally smoothed using a Butterworth filter, and temporally interpolated using cubic-spline polynomials (Fig. S3).

The Fluent 13.0 commercial package (ANSYS) was used to solve the unsteady, incompressible, axisymmetrical Navier–Stokes equations. Swimming was modeled by coupling the forward motion of the jellyfish to the hydrodynamic forces exerted on the bell. Pressure and shear forces acting in the axial direction were integrated across the jellyfish surface at the end of each time step, and the resulting body acceleration was calculated. The discrete form of this force balance is given by the equation:

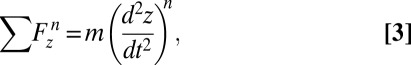where 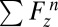is the sum of all pressure and shear forces in the axial direction at time step , is the mass of the jellyfish (fluid density assumed to be the same as the surrounding water: = 998.2 kg⋅m⁻³), and is the axial acceleration at the center of mass of the jellyfish. Using Taylor series expansions, the acceleration can be approximated by a second-order accurate, backward finite difference equation:

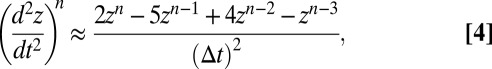where is the axial displacement and 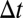is the time step. Combining Eqs. 7 and 8, the displacement at time step can be approximated:

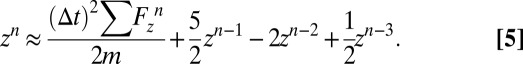Finally, to ensure stable coupling between the solver and the jellyfish displacement, we used an exponentially weighted moving average to smoothen the raw displacement , :

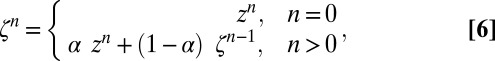where 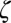is the smoothed displacement prescribed to the jellyfish and 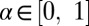is the smoothing factor. We found was required for a robust simulation.

Verification and validation studies were performed to ensure the numerical and physical accuracy of our simulation. We first checked the sensitivity of our results to mesh and time step refinement (Fig. S4). A base mesh of 60,895 cells (64 and 58 cell faces on the top and bottom bell contours, respectively) was refined to 135,765 cells (86 and 82 cell faces on the top and bottom bell contours, respectively) and showed that the sum of forces acting on the jellyfish, and consequently its swimming performance, was insensitive to spatial refinement. Similarly, simulations run using a time step refined from 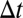= 1/90 s to = 1/180 s resulted in no appreciable change in the hydrodynamic forces acting on the jellyfish. Next, the instantaneous displacement of the numerical jellyfish was compared with that of the natural jellyfish used for the swimming kinematics (Fig. S5). Both show similar trends and indicate similar velocities throughout the swimming period, resulting in a nearly identical total displacement.