Catalytically powered dynamic assembly of rod-shaped nanomotors and passive tracer particles

Significance

Microscale catalyst particles suspended in fluids can convert the energy of chemical reactions that occur on their surfaces to movement. Collections of particles undergoing powered motion exhibit behavior that mimics living microparticles such as bacteria: swarming, predator–prey interactions, and chemotaxis. These behaviors originate from pairwise interactions of particles that so far have not been measured or understood. In this article, short-range attractive interactions of catalytic nanorod motors were shown to arise from electrical forces. These forces drive the transient formation of dimers and trimers, and are also responsible for the collection of passive tracer particles at the ends of the nanorods. The quantitative description of these interactions lays the theoretical groundwork for understanding and manipulating the collective behavior of nanomotors.

Abstract

Nano- and microscale motors powered by catalytic reactions exhibit collective behavior such as swarming, predator–prey interactions, and chemotaxis that resemble those of biological microorganisms. A quantitative understanding of the catalytically generated forces between particles that lead to these behaviors has so far been lacking. Observations and numerical simulations of pairwise interactions between gold-platinum nanorods in hydrogen peroxide solutions show that attractive and repulsive interactions arise from the catalytically generated electric field. Electrokinetic effects drive the assembly of staggered doublets and triplets of nanorods that are moving in the same direction. None of these behaviors are observed with nanorods composed of a single metal. The motors also collect tracer microparticles at their head or tail, depending on the charge of the particles, actively assembling them into close-packed rafts and aggregates of rafts. These motor–tracer particle interactions can also be understood in terms of the catalytically generated electric field around the ends of the nanorod motors.

The dynamic interactions between moving objects, in particular their response to external stimuli and their communication with each other, govern their collective behavior on many length scales. Schooling of fish and flocking of birds are good examples of emergent phenomena that are orchestrated by communication between individuals in a large group. In these systems, macroscale organization is typically driven by nearest neighbor interactions that follow simple rules. To reach the level of organization seen in such living assemblies, fast and precise (in terms of distances, angles, and velocities) communication and control are required from the members. It is now straightforward to create computational models from which such dynamic structures emerge, but artificial systems that mimic behaviors as complicated as fish schooling have very rarely been realized experimentally in macroscopic engineered systems (1). On the other hand, self-assembly at the nano- and molecular levels already demonstrates a certain level of complexity and has furthered our understanding of dynamic interactions at small scales (2, 3).

There are already many examples of particle assembly driven by local forces or externally applied fields. Externally applied light, magnetic, electric, and acoustic fields can drive symmetric particles into ordered arrays (4–7). Colloidal Janus particles self-assemble into complex structures by various mechanisms (8–12). However, in these examples the particle aggregates hardly approach the complexity of assemblies of living organisms; the interactions are passive responses to local forces and external fields with very limited interparticle communication or active response to the behavior of nearest neighbors.

Interactions between active particles, on the other hand, can more closely mimic those of living organisms (13–17). Powered particles generate signals, typically in the forms of chemical gradients, pressure, or electric potential, which can induce responses from nearby particles. When the particle density is high, collective behaviors can emerge. For example, rotating millimeter scale objects assemble into organized patterns (1, 18). Patterns also emerge in collections of dipolar disks that are mechanically propelled along their polar axis (19). Autonomously moving nano- and micromotors (20) exhibit rich collective behavior including swarming and schooling (21–27), predator–prey interactions (25), attraction and repulsion between rotors (28, 29), spatiotemporal oscillations (21, 25), and dynamic self-assembly (29, 30). Hydrophobicity and hydrodynamic interactions can also drive the assembly of nanomotors (31, 32). Although theoretical models and numerical simulations have furthered our understanding of these systems (33–37), there is still a lack of information on the pairwise interactions of particles that result in emergent behavior. Quantifying these interactions at the level of individual microparticles should lead to better understanding of active matter (whether it is composed of synthetic and biological micromotors) and may ultimately enable the prediction, design, and application of collective behavior.

Here we report dynamic intermotor interactions and particle self-assembly in systems of self-electrophoretically driven platinum–gold nanorods. These catalytic nanomotors move autonomously at ∼20 μm/s when placed in 1–2 M H₂O₂ solution (38–40). In addition to their axial movement, which is well known from previous reports, we have observed that powered nanorods dynamically associate to form staggered doublets and triplets. When the nanomotors are mixed with charged tracer particles (the sizes of the motor and tracer particles are shown in Figs. S1–S4), they collect the passive particle “cargo” at the front or back end of the rods, depending on the charge on the passive particles, and drive their assembly into close-packed 2D rafts. None of these behaviors are observed with nanorods composed of a single metal. Analysis of tracking data and numerical simulations show that all of these behaviors originate from electrokinetic and electrostatic effects in systems of powered nanorods.

Results and Discussion

Interactions Between Active Nanomotors.

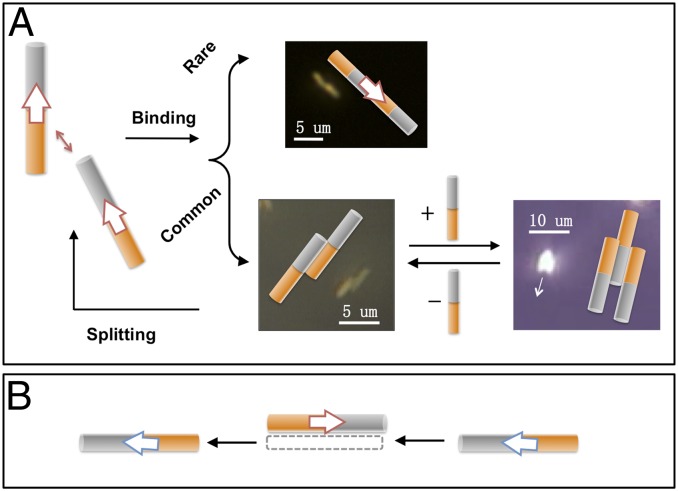
When suspended in 5 wt% H₂O₂ solution, bimetallic Au–Pt nanorods (Fig. S1) move autonomously at axial speeds in the range of 10 body lengths per second. The rods can associate to form staggered doublets when moving close to one other. Once formed, these doublets travel in arcs as illustrated in Fig. 1A and Movie S1. In almost all cases, the doublets are formed by two nanomotors moving in the same direction. Motors moving in opposite directions quickly move past each other without significantly interacting (Fig. 1B). The assembly of doublets is reversible in that they can separate and resume their individual axial motion, or recombine after separation. Although it is not frequently observed, a doublet can attract a third nanomotor to form a triplet (Fig. 1A). These triplets are symmetric about their central rod and move in a relatively linear trajectory. The assembly of doublets and triplets was observed only in systems of active nanomotors. In contrast, passive nanorods (i.e., rods with only one metal component) were subject only to Brownian motion and did not associate into dimers. Although most experiments were done with Au–Pt nanorods, Au–Ru nanorods had similar interactions in 5% (wt/wt) H₂O₂ solutions.

Fig. 1.

Interactions between self-electrophoretic nanomotors moving in the same and opposite directions. (A) Two nanomotors moving in the same direction can form a staggered doublet that moves in a clockwise or counterclockwise arc. Such doublets can attract a third nanomotor to form triplets. In rare cases two nanomotors can associate with each other head-to-tail. (B) The interaction between two nanomotors moving in the opposite direction is typically much more short-lived and weaker.

Mechanism of Nanomotor Interaction and Assembly.

As discussed in earlier reports, the movement of bimetallic nanorods in hydrogen peroxide solution is primarily driven by an electrophoretic mechanism involving a self-generated electric field (39, 41–43). H₂O₂ molecules are oxidized and both H₂O₂ and O₂ are reduced preferentially on the anode (Pt) and cathode (Au) segments of the rods, respectively, as shown in Eqs. 1–4.

and

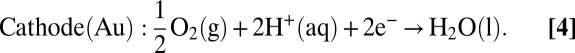This leads to a concentration gradient of protons and counteranions along the motor surface, and therefore results in a local electrical field pointing from Pt to Au. The self-generated electric field then drives the electrophoretic motion of the negatively charged nanorod itself. These proton gradients and electric fields also play important roles in the dynamic interactions between these motors, which are also subject to van der Waals attraction and electrostatic forces. The van der Waals force is short-ranged and may contribute to the attraction between two metallic nanorods when they come close to each other. However, it does not explain the staggered shape of the doublets, nor can it be solely responsible for their assembly, because bimetallic nanorod suspensions are stable with minimal aggregation in the absence of H₂O₂. Further, homogeneous Au rods do not assemble in H₂O₂ solutions. Therefore, additional forces must exist when the nanorods are bimetallic and are exposed to H₂O₂.

We propose that this additional attractive force arises from the electric field generated by the active motors. This force, which is also manifested in the interactions of the motors with charged tracer particles (see Interactions Between Nanomotors and Passive Tracer Particles), begins to affect the trajectory of motors when they pass within about 1 µm of each other. Because each end of the nanorod is surrounded by a layer of solution that is either positively (Pt) or negatively charged (Au), the segments surrounded by oppositely charged solutions attract each other. The specific interaction pattern depends on the trajectories of the two nanomotors, as illustrated in Fig. 2. Typically, the result of a collision of rods moving in the same direction is a staggered doublet, although head-to-tail dimers are sometimes observed. A numerical simulation of the space charge distribution around a Au–Pt nanomotor (Fig. 2) shows that the electrostatic energy is minimized when opposite ends of two nanomotors meet (Fig. 2, Left). Simulations for pairs of rods in contact show similar electric field distributions (Fig. S5). Although the simulations suggest that two motors moving in opposite directions can also minimize their electrical energy by overlapping in parallel (Fig. 2, Right), such a doublet should have only a transient existence because the shear stress between nanomotors at a relative speed of ∼40 μm/s would quickly separate them. We have not observed the formation of dimers from motors moving in opposite directions.

Fig. 2.

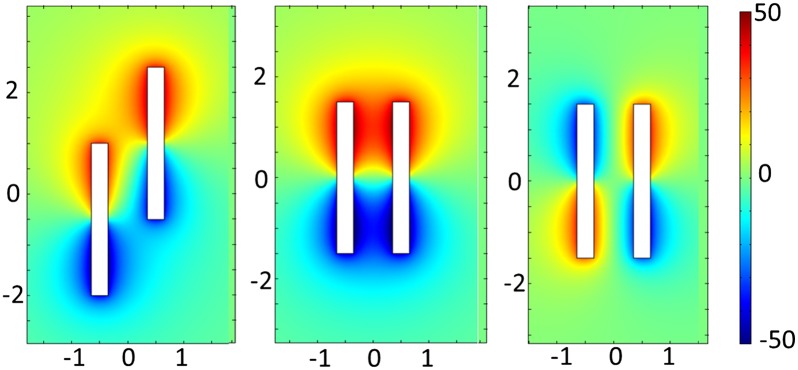
Numerical simulation of the electrostatic interactions between two nanomotors at different relative positions. Distances on both x and y axes in the images are shown in μm. These images are slices of the xz planes of 3D simulation results. Colors in the images represent the space charge density (C/m³), with red being positive and blue negative. Cartoons of Au–Pt nanomotors are superimposed over the simulation results for illustrative purposes, with coloring of the two segments of the rods.

Rotation and Splitting of Doublets.

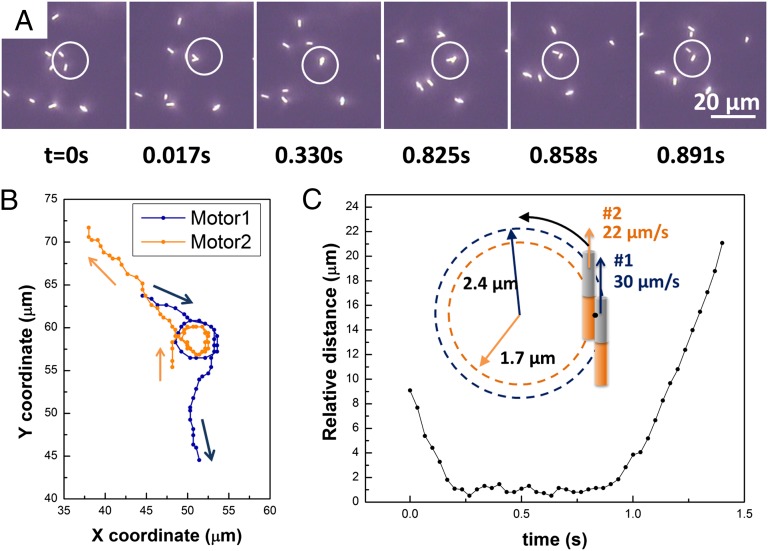
Nanomotor doublets, after they form, typically move in circular trajectories and eventually split. In most cases, the doublets rotate to the side of the motor that had the lower speed before assembly. Typical tracking data for such a doublet from Movie S1 are as shown in Fig. 3. The two motors attract each other and form a staggered doublet that immediately begins to rotate. The doublet then splits and the two nanomotors resume their respective trajectories. All of the doublets were observed to split on a time scale from 0.1 s to several seconds. The speeds of the two nanomotors in Fig. 3 were initially 34 ± 3 μm/s and 30 ± 9 μm/s and dropped to 30 ± 10 μm/s and 22 ± 7 μm/s, respectively, once the doublet formed. The doublet rotates in the direction of the slower motor. The ratio of the motor speeds in the doublet (1.4) agrees well with the ratio of the radii in which they rotate (1.4 from tracking data). This indicates that the two motors, which are constrained to move at the same angular velocity, retain their ratio of axial speeds. Furthermore, the distance between the centers of the two nanomotors stabilized at 1.0 ± 0.3 μm in the doublet, and a clear departure from that value was observed when the nanomotors were moving separately before the doublet formed or after it dissociated (Fig. 3C).

Fig. 3.

Tracking results and analysis of the interactions between two Au–Pt nanomotors. (A) Snapshot sequence of two nanomotors (white circle) binding together and splitting apart within 1 s. Attachment begins at 0.017 s, and the splitting begins at 0.825 s and finishes at 0.858 s. (B) Tracking results showing the trajectory of the two nanomotors. (C) The relative distance between the centers of the two nanomotors during the period of interaction. (C, Inset) The circular trajectory of the centers of the two nanomotors.

In principle the doublet can maintain a linear trajectory if the speeds of the two component motors are the same. However, bimetallic nanomotors typically exhibit a range of speeds, probably due to the nonuniformity induced in their growth (see SI Text for details). Experimentally, all of the doublets we observed rotated toward the slower motor, whether it was the leading or trailing rod in the doublet. The circular movement of the doublets can be understood by considering the individual propulsion forces of the two motors, as shown in Fig. S6A. At low Reynolds number, the propulsion force (F_prop) of a nanomotor is balanced by the viscous drag force (F_drag) the solution exerts on it, as shown in Eq. 5 (44):

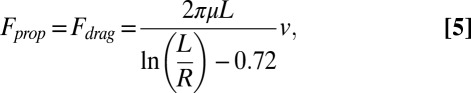where μ is the dynamic viscosity of water, L is the length of the cylindrical rod, R is its radius, and v is the motor speed. For two nanomotors of similar size, the propulsion forces are proportional to the individual velocities. Unequal propulsion forces generate a nonzero net torque, which causes the doublet to rotate to the side of the slower motor.

The splitting of nanomotor doublets and triplets appears to be driven by random Brownian motion, and this mechanism enables us to estimate the binding energy of the doublets. The splitting rate can be expressed in terms of the Arrhenius equation:

where k is the first-order rate constant for the process, A is the attempt frequency, E is the binding energy of the doublet, and kT is the thermal energy (4.1 × 10⁻²¹ J at 298 K). The value of k from our observations is on the order of 1 s⁻¹. The attempt frequency can be estimated as A = f/2m, where f = F_drag/v is the drag coefficient and m is the mass of the rod (45). This calculation gives A on the order of 6 × 10⁵ s⁻¹ and a binding energy E of 5 × 10⁻²⁰ J. If we assume that the attractive force acts over a distance of ∼300 nm (one rod diameter), then the force can be estimated as F = E/dx, or 0.2 pN. This is on the same order as F_prop (and F_drag) acting on an individual motor. Once Brownian motion separates the leading ends, catalytic propulsion of the individual motors quickly leads to splitting of the doublet.

Interactions Between Nanomotors and Passive Tracer Particles.

In addition to driving the formation of nanomotor dimers and trimers, the catalytic decomposition of H₂O₂ also causes passive tracer particles to assemble at the ends of the rods. Au–Pt bimetallic rods were mixed with passive particles [gold nanorods of similar dimensions to the bimetallic nanorods (Fig. S2), 1.7 µm diameter polystyrene (PS) spheres and gold spheres of roughly 1 μm diameter]. in 5% H₂O₂ solution. All three kinds of tracer particles had negative zeta potentials (ζ_{Au rod} = –47 ± 4 mV, ζ_PS = –64 ± 2 mV, ζ_{Au sphere} = –64 ± 7 mV). In all three cases the bimetallic nanomotors moved autonomously as they did in the absence of tracer particles. The charged tracer particles, when not interacting with the nanomotors, exhibited typical Brownian motion

Attraction between active nanomotors and charged tracer particles was observed in all cases, yet the attraction between nanomotors and gold nanorods was the weakest and shortest lived (Movie S2). This is in contrast to the interaction between pairs of bimetallic nanorods, which results in a rotating doublet. The distortion of the trajectory of both the nanomotor and the gold nanorod is subtle; the nanomotor quickly cruises past the gold nanorod, and they resume their original individual paths. Very rarely do they form doublets, and when they do the doublets split quickly. These observations strongly suggest that the interaction between two nanomotors is not purely due to van der Waals or electrostatic forces. Otherwise gold rods would show similar interactions with themselves as well as with active nanomotors. Gold microspheres, however, exhibit much stronger interactions with active nanomotors (Movie S3). In this case the spheres attach to the nanomotor surface at the Pt end. Subsequently, more gold microspheres attach until a close-packed raft forms at the Pt end of the nanomotor. The details of these interactions will be discussed later. The more persistent attachment of gold microspheres relative to gold rods can be attributed to the different drag forces experienced by rods and spheres. The drag force on a sphere at low Reynolds number is given by Eq. 7:

where μ is the dynamic viscosity of water, r is the sphere radius, and v is the motor speed. Compared with 1 µm diameter gold spheres moving at the same speed, gold rods (3 μm long and 300 nm in diameter) should experience 30% higher drag force when they are moving along their long axis (Eq. 6). Therefore, nanomotors carrying a gold rod would be subject to larger shear forces than those carrying gold spheres. Furthermore, the gold spheres carry a more negative charge (ζ_{Au sphere} = –64 ± 7 mV) than the gold rods (ζ_{Au rod} = –47 ± 4 mV), and this translates to a stronger electrokinetic force experienced by the gold spheres than by the rods.

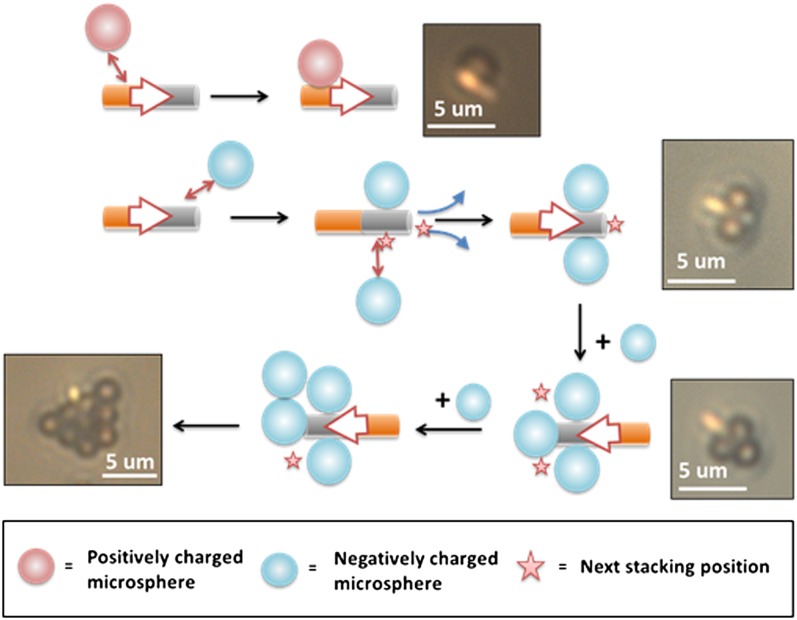
PS microspheres also exhibited strong interactions (Movie S4), very similar to those of gold spheres, when mixed with active Au–Pt nanomotors in H₂O₂. Fig. 4 summarizes the interactions and common types of assembly that were observed. When moving nanorods approach charged tracer particles (gold or PS microspheres), the particles move toward the rods and eventually attach to their surface. Typically, the tracer particles attach to only one end of the nanomotor. Negatively charged microparticles (gold or PS spheres) attach to the Pt end, and positively charged microparticles (1.5 μm amidine-functionalized PS microspheres, ζ = 24 ± 5 mV) attach to the Au end (Movie S5). This behavior can be understood in terms of the catalytically generated electric field. Protons are generated at the Pt end and consumed at the Au end, so negatively charged particles migrate up the electric field toward the Pt end.

Fig. 4.

Assembly of charged tracer microspheres on nanomotors. Charged microspheres are attracted to and eventually attach to the surface of the motors (Pt is silver in color and Au is golden in color). Depending on the charge type of the microparticles, they can attach to the Pt end (negatively charged particles) or Au end (positively charged particles). This stacking process can continue until a close-packed particle assembly is formed around the moving nanorod. (Insets) Optical microscopic images of the assemblies formed by Au–Pt nanomotors. The top image is the interaction between an Au–Pt nanomotor and a amidine functionalized PS sphere, and the other images show the assembly of negatively charged PS spheres on Au–Pt nanomotors.

The tracer particle assembly process is also reversible, as manifested by the detachment of tracer particles from the motor surface through collisions with other particles. However, a doublet formed between a nanorod and sphere is much more stable than a doublet of two active motors in the sense that motor–sphere aggregates do not spontaneously disintegrate over the time span of our observations (up to a few minutes). Therefore, it is possible for the assembly to continue attracting and “capturing” additional tracers one by one, or to interact with another motor.

In general, tracer particles follow the electric field gradient and attach to nanorods in a way that most efficiently covers the nanorod surface. This preferential attachment leads to a close-packed assembly of spheres around the nanorod. However, the spheres populate only one end of the nanomotor because the electric field at the other end repels the tracer particles. In addition, only 2D assembly is observed; no particles are observed above or below the close-packed plane, presumably because there is no force in the z direction. This was confirmed by adjusting the microscope focus. It is important to note that the attractive electrophoretic force that moves the tracer particles to the surface of the nanomotors dominates over the repulsive force between particles of like charge. This is evidenced by the fact that assembly occurs and is consistent with the observations that active nanorods can form dimers and trimers despite that fact that the particles are all negatively charged.

Because of their uniform size distribution, negatively charged 1.7 µm diameter PS spheres were chosen for a more in-depth study of the interactions between active motors and charged tracer particles. Fig. S7 presents an example of how the charged tracer particles assemble with free-moving Au–Pt nanomotors, as is shown in Movie S4. In this movie, the nanomotor interacts with and attaches the microspheres one by one, eventually forming a raft in which one nanomotor carries four spheres in a close-packed arrangement.

The nanomotor trajectory is altered upon attachment of tracer particles, especially when the assembled structure is asymmetric. On a time scale of 1–2 s, an Au–Pt nanomotor by itself has a relatively linear trajectory, which is randomized on a longer time scale by Brownian motion. When the first sphere attaches to the nanorod surface, the trajectory of the doublet typically changes to circular due to the asymmetry of the doublet. The second sphere attaches to the other side of the nanorod in most cases, and the trajectory becomes roughly linear. Further addition of spheres causes relatively little distortion of the trajectory because the aggregate is relatively symmetric.

The speed of the motor–sphere aggregate decreases as more spheres are attached to the nanomotor, as illustrated in Fig. S8. This trend qualitatively agrees with a previous report by Solovev et al., who observed that the speed of motor–cargo aggregates decreases with increasing number of cargo particles (46).

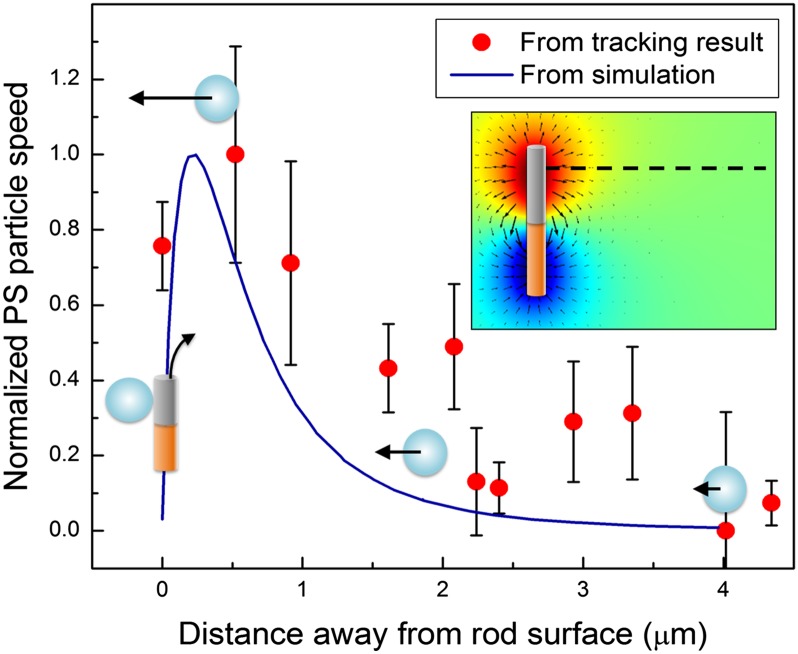
Finally, by tracking the speed of the tracer particles during their migration toward the motor, we were able to obtain strong evidence that the attraction originates from the electric field generated by the motors—that is, through localized electrophoresis. The electric field distribution around the motors was simulated by using the COMSOL multiphysics package (see ref. 47 for modeling details). Then, an electrophoretic velocity profile as a function of the distance between the tracer particle and the motor was calculated based on the electric field distribution (Fig. 5). This velocity profile agreed qualitatively with the tracking data of the first PS particle to attach in Fig. S7. Both simulation and tracking results show that the tracer particle is relatively idle at distances more than a few micrometers away from the motor, and that it accelerates as it moves closer to the nanomotor. Its speed reaches a peak when the PS particle is about 0.5 μm away from the motor, and then drops significantly as it moves closer to the nanomotor. Although the simulation and experiment show similar trends at distances greater than 0.5 µm, the behavior of the PS particle very close to the motor surface should be different in the experiments and the simulation. In the simulation, which does not include short-range van der Waals forces, the electric field magnitude tends to zero at the nanomotor surface due to a vanishing potential gradient, resulting in a speed of zero for the PS particle. However, in the experiment, when the PS particle is close to the motor surface, the short-range van der Waals attractive force draws it toward the nanomotor, resulting in a nonzero velocity. Experimentally the PS bead reached a peak velocity of ∼20 µm/s when it was 500 nm away from the motor, yielding an attractive force of roughly 0.3 pN. The close correspondence between the magnitude of this force and the attractive force that is responsible for binding two motors into a doublet (estimated to be 0.2 pN above) suggests a similar origin for the two phenomena.

Fig. 5.

Electrophoretic speed of a tracer PS particle as it approaches the nanomotor. (Inset) Numerical simulation of the electric potential distribution around an Au–Pt nanomotor. Red and blue shading represents the electric potential, with red and blue being positive and negative, respectively. The arrows indicate the electric field vector. The electrophoretic speed of a PS particle with a zeta potential of –64 mV along the black dashed line is simulated and plotted as the blue curve (normalized to the peak speed). Red data points are from the tracking results of the first PS particle in Fig. S7 (and are normalized to the peak speed). The effect of Brownian motion was subtracted from the velocity profile of the tracking results.

In catalytic motor systems, non-charge–specific forces can also contribute to motion through pumping. These effects include electroosmotic pumping along the surface of the charged substrate (glass) and dielectrophoresis in response to the distribution of the electric field around the nanorods. However, these effects are clearly weak in the migration of charged microspheres toward Au–Pt nanorods. Positively and negatively charged spheres move toward the Au and Pt ends of the rods, respectively. Electroosmosis and dielectrophoresis would simply move all particles in the same direction regardless of their surface charge.

Comparison with Interacting Motor Systems Based on Self-Diffusiophoresis.

Interactions between active motors are receiving a wealth of attention as they imply communication and cooperation between “intelligent” microparticles. In most systems that have been studied, the motors are spherical and their interactions are based on a diffusiophoretic mechanism. In such systems, active motors produce electrolytes at their surfaces as a result of chemical reactions, and the electrolyte concentration gradients power particle movement through a combination of electrophoretic and chemophoretic effects. The motors interact with other particles that respond to the chemical gradients and flows surrounding them, and such systems consequently exhibit collective emergent patterns (24–26, 48). The current system complements these in that the interaction between active self-electrophoretic motors has several unique features. First, the interaction is short range (roughly one rod body length) as the motors interact with each other only when they share a path. In contrast, diffusiophoretic motors can interact over distances of 10 µm or more. The difference arises from the fact that the electric fields generated by self-electrophoretic motors are highly localized and do not extend over the diffusion length scale (∼30 µm) as do the chemical signals in diffusiophoretic systems. Second, because bimetallic nanorod motors are anisotropic, their assembly is strongly influenced by the relative position and orientation of the motors. This is significantly different from the case of self-diffusiophoretic motors, which emit and receive chemical signals in a relatively isotropic fashion. Finally, electrostatic interactions enforce the staggered structures of nanorod dimers and trimers, as well as the shapes of rod-tracer particle assemblies, which determine their trajectories. Such controlled asymmetry is difficult to build into diffusiophoretic systems.

Potential Application as a Microassembler and Microtransporter.

The bimetallic nanomotors become microengines once tracer particle assemblies form, carrying a large number of particles (cargo) in solution at speeds of a few μm per second (Movie S6). Over time, more particles are driven into close-packed rafts and merge together. Depending on the configuration of the merged assemblies, the cargo particles can be asymmetrically distributed along the periphery and impart torque to the aggregate, causing them to rotate. Because the power provided by one nanomotor is very limited, roughly on the order of 10⁻¹⁸ W/rod (47), a rotation rate of only a few rpm was observed for large aggregates.

A considerable amount of effort has been dedicated to designing nano- and micromotors capable of loading, transporting, and delivering microscale cargo (49, 50). Different techniques haven been developed to achieve cargo pickup, such as electrostatic attraction (51), specific or nonspecific binding (51–56), magnetic interactions (57, 58), hydrodynamic interactions (59), hydrophobic affinity (31), molecular imprinting (60), and even purely mechanical force (46, 61). Most of these cargo transport systems require the cargo and/or the cargo carrier to be functionalized in some way (31, 51, 53–56, 60). Those that do not have such a requirement typically involve the use of magnetic fields to find and manipulate cargo (29, 30, 33, 34). Some catalytic microtransporter systems drive particle assembly at the air–water interface (46) or at a hydrophobic motor surface (31, 61). The system presented here is so far unique in the sense that the forces driving the assembly are generated by catalysis and offer a level of control in mixtures of active and passive particles. An assembler that can be used with generic particles of either surface charge (positive or negative, as neutral colloidal particles are rare in water) is therefore a potentially useful addition. Moreover, the ability to assemble multiple generic cargo particles in an organized way is particularly desirable for creating complex assemblies, and is hard to achieve with previously reported systems (46). The microassembler system we demonstrate here is based on a well-studied bimetallic self-electrophoretic nanomotor and addresses these challenges positively.

Conclusions

The dynamic interactions between active bimetallic nanomotors in H₂O₂ solution drive the formation of staggered doublets and triplets, as well as the 2D assembly of charged tracer particles at one end of the nanomotor. Motor tracking data are consistent with numerical simulations of the assembly process, and together these data support the conclusion that the assembly interactions are driven by local, catalytically generated electric fields. Because the assembly of the rod-shaped particles is strongly orientation-dependent and results in changes in the direction of motion, there is some potential to use these effects in chemical sensing, and also in applications involving the assembly, transport, and separation of particles. These ideas will be explored in future experiments.

Materials and Methods

Synthesis of Metallic Nanowires.

The nanowires were prepared by electrodeposition of metals at constant current in porous alumina membranes (purchased from Whatman Inc., 200 nm pore size) (39). The length of the nanowires was controlled by monitoring the charges passed. Metal plating solutions were purchased from Technic Inc. Details of the synthesis can be found in SI Text.

Tracking of Autonomous Nanomotors and Microparticles.

Bimetallic nanorods (and tracer particles if necessary) were suspended in 5% H₂O₂ solution for observation. An Olympus BX60M optical microscope (reflective mode) and a commercial video capturing bundle (Dazzle Video Creator Plus) were used for observing the particles and recording movies. Movies were then analyzed with PhysMo 2 (http://physmo.sf.net), and the coordinates of the centers of the particles (nanomotors and/or tracer particles) were recorded as a function of time. The speed of microparticles was calculated by dividing the displacement of the particle center between frames by the corresponding time intervals, and then averaging the speed over the selected tracking period.

Finite Element Modeling.

The ion distribution and electrical charges around the Au–Pt nanomotors operating by self-electrophoresis were simulated by using a finite element model. The simulation was carried out with the COMSOL multiphysics package (47). Details of this simulation model can be found in SI Text.