Abstract
Signatures of mass-independent isotope fractionation (MIF) are found in the oxygen (16O,17O,18O) and sulfur (32S, 33S, 34S, 36S) isotope systems and serve as important tracers of past and present atmospheric processes. These unique isotope signatures signify the breakdown of the traditional theory of isotope fractionation, but the physical chemistry of these isotope effects remains poorly understood. We report the production of large sulfur isotope MIF, with Δ33S up to 78‰ and Δ36S up to 110‰, from the broadband excitation of SO2 in the 250–350-nm absorption region. Acetylene is used to selectively trap the triplet-state SO2 ( 3B1), which results from intersystem crossing from the excited singlet (
3B1), which results from intersystem crossing from the excited singlet (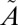 1A2/
1A2/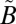 1B1) states. The observed MIF signature differs considerably from that predicted by isotopologue-specific absorption cross-sections of SO2 and is insensitive to the wavelength region of excitation (above or below 300 nm), suggesting that the MIF originates not from the initial excitation of SO2 to the singlet states but from an isotope selective spin–orbit interaction between the singlet (
1B1) states. The observed MIF signature differs considerably from that predicted by isotopologue-specific absorption cross-sections of SO2 and is insensitive to the wavelength region of excitation (above or below 300 nm), suggesting that the MIF originates not from the initial excitation of SO2 to the singlet states but from an isotope selective spin–orbit interaction between the singlet (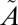 1A2/
1A2/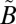 1B1) and triplet (
1B1) and triplet (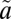 3B1) manifolds. Calculations based on high-level potential energy surfaces of the multiple excited states show a considerable lifetime anomaly for 33SO2 and 36SO2 for the low vibrational levels of the
3B1) manifolds. Calculations based on high-level potential energy surfaces of the multiple excited states show a considerable lifetime anomaly for 33SO2 and 36SO2 for the low vibrational levels of the 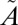 1A2 state. These results demonstrate that the isotope selectivity of accidental near-resonance interactions between states is of critical importance in understanding the origin of MIF in photochemical systems.
1A2 state. These results demonstrate that the isotope selectivity of accidental near-resonance interactions between states is of critical importance in understanding the origin of MIF in photochemical systems.
Keywords: photochemistry, sulfur dioxide, excited electronic states, absorption spectrum
Stable isotope fractionation theory predicts that the magnitude of stable isotope fractionation scales with the differences in isotopic mass (1, 2). Almost all physical, chemical, and biological processes in nature follow this mass-dependent scaling law, resulting in nearly all terrestrial materials with oxygen having δ17O = 0.52 × δ18O, whereas those with sulfur have δ33S = 0.515 × δ34S and δ36S = 1.90 × δ34S.† Significant deviations from these mass-dependent scaling laws are referred to as mass-independent fractionation (MIF), and serve as important tracers in the earth and planetary sciences (see refs. 3–5).
Early studies suggested that MIF could result only from nucleosynthetic processes (6), and the earliest measurements of oxygen MIF in calcium–aluminum inclusions of meteorites originally were interpreted to be nucleosynthetic in origin (7). It eventually was suggested (8) that chemical processes, such as tunneling or processes associated with predissociation, also might produce MIF. The first experimental evidence for a chemical origin of MIF came from ozone generated by an electric discharge or UV radiation (9, 10). The discovery of oxygen MIF in stratospheric ozone (11) soon triggered intense research into the physiochemical origin of MIF in the ozone system (see refs. 12–14). The possible chemical origins of MIF signatures still are poorly understood.
For the sulfur isotope system (32S, 33S, 34S, and 36S), Farquhar et al. (15) made the remarkable discovery that mass-independent sulfur isotope fractionation (S-MIF) is prevalent in sedimentary rocks older than ca. 2.4 Ga but absent in rocks from subsequent periods. The disappearance of S-MIF at about 2.4 Ga (16, 17) signifies a fundamental change in the earth’s surface sulfur cycles, and generally is linked to the suppression of both SO2 photolysis and the formation of elemental sulfur aerosols by the rise of atmospheric oxygen levels (15, 18, 19). The Archean S-MIF is considered the most compelling evidence for an anoxic early atmosphere and constrains Archean oxygen levels to be less than 10−5 of present levels (19). This model of oxygen evolution, however, depends critically on the assumption that UV photolysis of SO2 by ∼200 nm radiation is the ultimate source of the anomalous sulfur isotope signature (18). Constraining the source of the S-MIF requires a thorough understanding of the physiochemical origins of S-MIF during the photochemistry of SO2.
SO2 exhibits two strong absorption band systems in the UV region: one between 185 nm and 235 nm (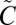 1B2←
1B2←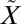 1A1) and the other from 240 to 350 nm (
1A1) and the other from 240 to 350 nm (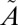 1A2,
1A2,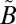 1B1 ←
1B1 ←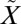 1A1) (ref. 20 and references therein); we will refer to them as the photolysis and photoexcitation bands, respectively. Excitation into the photolysis band leads to the predissociation of SO2 into SO and O below 220 nm. Laboratory experiments by Farquhar et al. (18) showed production of large (Δ33S up to 70‰) S-MIF by SO2 photolysis using an ArF (193-nm) excimer laser source. This was used to link the high-energy photolysis band system to Archean S-MIF, and fueled subsequent detailed investigations (e.g., refs. 21–26) into the S-MIF production from photochemistry in this region. However, recent experiments (24–26) using broadband (as opposed to laser) light sources show S-MIF patterns different from the 193-nm experiments by Farquhar et al. (18). Large-magnitude (Δ33S > 2.5‰) MIF is produced only by experiments with high SO2 column densities, suggesting a strong contribution from spectroscopic self- and mutual-shielding, although additional mechanisms also may play a role (26). The elemental sulfur products produced by these experiments are characterized by large δ34S fractionations and Δ36S/Δ33S ratios that differ from those observed in the Archean rock record (24–26). Discrepancies between experimental results and the geological record require a reanalysis of the origin of Archean S-MIF signatures.
1A1) (ref. 20 and references therein); we will refer to them as the photolysis and photoexcitation bands, respectively. Excitation into the photolysis band leads to the predissociation of SO2 into SO and O below 220 nm. Laboratory experiments by Farquhar et al. (18) showed production of large (Δ33S up to 70‰) S-MIF by SO2 photolysis using an ArF (193-nm) excimer laser source. This was used to link the high-energy photolysis band system to Archean S-MIF, and fueled subsequent detailed investigations (e.g., refs. 21–26) into the S-MIF production from photochemistry in this region. However, recent experiments (24–26) using broadband (as opposed to laser) light sources show S-MIF patterns different from the 193-nm experiments by Farquhar et al. (18). Large-magnitude (Δ33S > 2.5‰) MIF is produced only by experiments with high SO2 column densities, suggesting a strong contribution from spectroscopic self- and mutual-shielding, although additional mechanisms also may play a role (26). The elemental sulfur products produced by these experiments are characterized by large δ34S fractionations and Δ36S/Δ33S ratios that differ from those observed in the Archean rock record (24–26). Discrepancies between experimental results and the geological record require a reanalysis of the origin of Archean S-MIF signatures.
SO2 photochemistry in the photoexcitation (240–350-nm) band also has been shown to produce S-MIF (18, 25, 27, 28) and has been implicated as the source of S-MIF in stratospheric sulfate aerosols trapped in polar ice (28–31). It also has been suggested that SO2 photochemistry in the photoexcitation band might have made secondary contributions to the S-MIF signatures during some periods of the Archean (25, 32). This band system is associated with the excitation of SO2 into a mixed 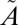 1A2/
1A2/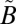 1B1 state, which also interacts with lower-lying triplet states (
1B1 state, which also interacts with lower-lying triplet states (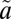 3B1, possibly also
3B1, possibly also 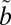 3A2) (Fig. 1) (20). Recently published absorption cross-sections of isotopically enriched SO2 (27) in this region allow the accurate prediction of the MIF produced during the initial excitation step (28). In this study, we focus on the production of S-MIF by SO2 excited into the photoexcitation band, and compare the results with the measured isotopologue specific cross-sections, to test the importance of chemistry after photoexcitation. Our results show a strong dependence of the S-MIF on the SO2 and bath gas pressures but not on the detailed spectrum regions of excitation, suggesting that isotopologue selective vibronic coupling produces significant S-MIF independent of absorption cross-section differences. A theoretical model also is presented to test this hypothesis.
3A2) (Fig. 1) (20). Recently published absorption cross-sections of isotopically enriched SO2 (27) in this region allow the accurate prediction of the MIF produced during the initial excitation step (28). In this study, we focus on the production of S-MIF by SO2 excited into the photoexcitation band, and compare the results with the measured isotopologue specific cross-sections, to test the importance of chemistry after photoexcitation. Our results show a strong dependence of the S-MIF on the SO2 and bath gas pressures but not on the detailed spectrum regions of excitation, suggesting that isotopologue selective vibronic coupling produces significant S-MIF independent of absorption cross-section differences. A theoretical model also is presented to test this hypothesis.
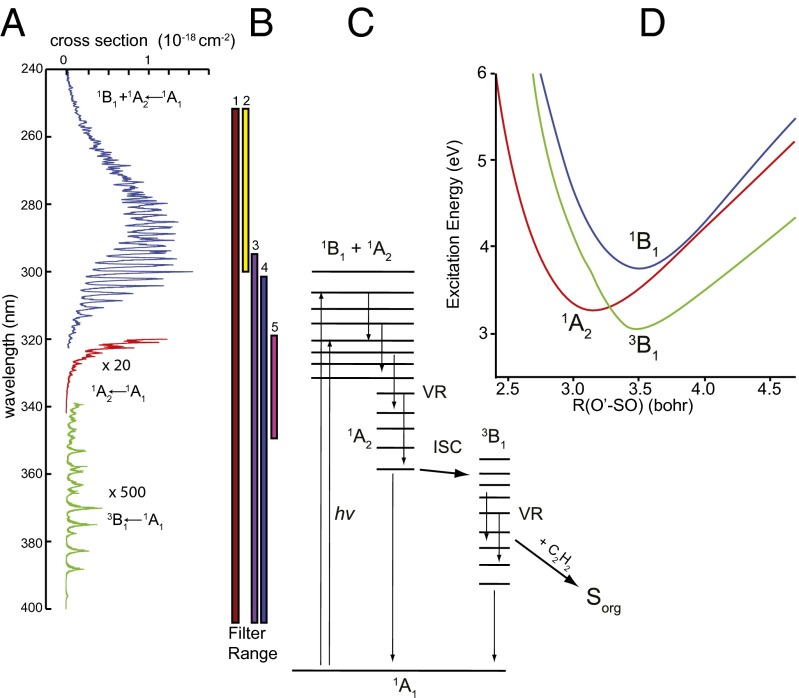
Fig. 1.
Photochemistry of SO2 in the 240–400-nm region. (A) UV absorption cross-section for SO2 between 240 and 400 nm (from refs. 33 and 34). (B) Vertical lines showing the spectral ranges for the different optical filters tested. (C) Schematic of the photochemistry of the experiments. SO2 initially is excited into the coupled 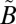 1B1/
1B1/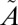 1A2 states. It vibrationally relaxes (VR) via collisions with the bath gas. At low vibrational levels of the
1A2 states. It vibrationally relaxes (VR) via collisions with the bath gas. At low vibrational levels of the 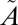 1A2 state, intersystem crossing may lead to irreversible crossing to the
1A2 state, intersystem crossing may lead to irreversible crossing to the 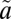 3B1 state as the result of vibrational relaxation of the
3B1 state as the result of vibrational relaxation of the 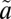 3B1 state below the origin of the
3B1 state below the origin of the 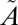 1A2 band. Isotope effects due to near-resonant spin–orbit coupling between the singlet and triplet states in this region may lead to mass-independent isotope anomalies in the resulting triplet-state SO2. The triplet-state SO2 finally reacts with acetylene (C2H2) to form the organosulfur products analyzed in this study. (D) Potential energy surfaces for the singlet and triplet states of SO2 as a function of the O'-SO Jacobi distance with the S-O distance and the Jacobi angle optimized.
1A2 band. Isotope effects due to near-resonant spin–orbit coupling between the singlet and triplet states in this region may lead to mass-independent isotope anomalies in the resulting triplet-state SO2. The triplet-state SO2 finally reacts with acetylene (C2H2) to form the organosulfur products analyzed in this study. (D) Potential energy surfaces for the singlet and triplet states of SO2 as a function of the O'-SO Jacobi distance with the S-O distance and the Jacobi angle optimized.
Methods
A series of SO2 photochemical experiments were carried out using a flow-through photochemical system to investigate S-MIF signatures as a function of SO2 [0.1–10 millibars (mbar)] and nitrogen bath gas (260–1,010 mbar) pressures (SI Text, Table S1). A broadband radiation source (150-W Xe arc lamp) was used to excite SO2 to the mixed 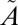 1A2/
1A2/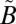 1B1 manifold. A 250-nm longpass filter was used to avoid photochemistry from the higher-energy photolysis band (
1B1 manifold. A 250-nm longpass filter was used to avoid photochemistry from the higher-energy photolysis band (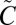 1B2←
1B2← 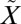 1A1) of SO2. Photochemistry of SO2 in the photoexcitation band was studied previously and showed rapid quenching of singlet SO2 by bath gas (e.g., N2, CO2) and reaction of the resulting triplet SO2 with CO, SO2, and organic molecules (see ref. 20) (Fig. 1). Experiments were carried out in the presence of acetylene (10 mbar), which efficiently reacts with triplet-state SO2 (35) and produces organosulfur aerosols, previously characterized as (C3H4S2O3)3 (36). These were captured and analyzed for quadruple sulfur isotope ratios using techniques described in Oduro et al. (37) and Ono et al. (26).
1A1) of SO2. Photochemistry of SO2 in the photoexcitation band was studied previously and showed rapid quenching of singlet SO2 by bath gas (e.g., N2, CO2) and reaction of the resulting triplet SO2 with CO, SO2, and organic molecules (see ref. 20) (Fig. 1). Experiments were carried out in the presence of acetylene (10 mbar), which efficiently reacts with triplet-state SO2 (35) and produces organosulfur aerosols, previously characterized as (C3H4S2O3)3 (36). These were captured and analyzed for quadruple sulfur isotope ratios using techniques described in Oduro et al. (37) and Ono et al. (26).
Results of Photochemical Experiments
All experiments produced organosulfur compounds that had minor fractionations in 34S (−7.0‰ < δ34S < 20.8‰), but were highly enriched in both 33S and 36S (9.1‰ < δ33S < 87.3‰ and 13.8‰ < δ36S < 135.7‰) (Table S1 and Fig. 2). This resulted in positive Δ33S (11.9–77.8‰) and Δ36S (24.3–109.8‰) values, and positive Δ36S/Δ33S ratios of 1.12–2.25. With the exception of our lowest pSO2 experiment (0.1 mbar), experiments at lower SO2 pressures produced higher Δ33S and Δ36S values than experiments at higher SO2 pressures under the range of conditions studied, suggesting isotopologue self-shielding is not the dominant source of observed S-MIF anomaly. The sensitivity to pSO2 might reflect energy transfer between mass-independently fractionated singlet or triplet-state SO2 and mass-dependently fractionated ground-state SO2. Such energy transfer might dilute the MIF signal by exciting non-MIF SO2 into the reactive triplet state. In addition to pSO2 dependence, Δ33S values increased as total pressure decreased for experiments run at the same SO2 pressure. Δ36S/Δ33S ratios were sensitive to the total pressure of the system, with higher values (1.98–2.25) at the highest pressure tested (1,013 mbar) and lower values (1.12–1.27) at the lowest pressure (253 mbar) (Fig. 2A). These results, particularly the positive Δ36S and Δ33S values and small δ34S values, are consistent with the previous experiments (25) performed with pure SO2 without N2 or C2H2, suggesting that the observed isotope signature is characteristic of this absorption band system and not a result of the N2 or C2H2 used in the experiment.
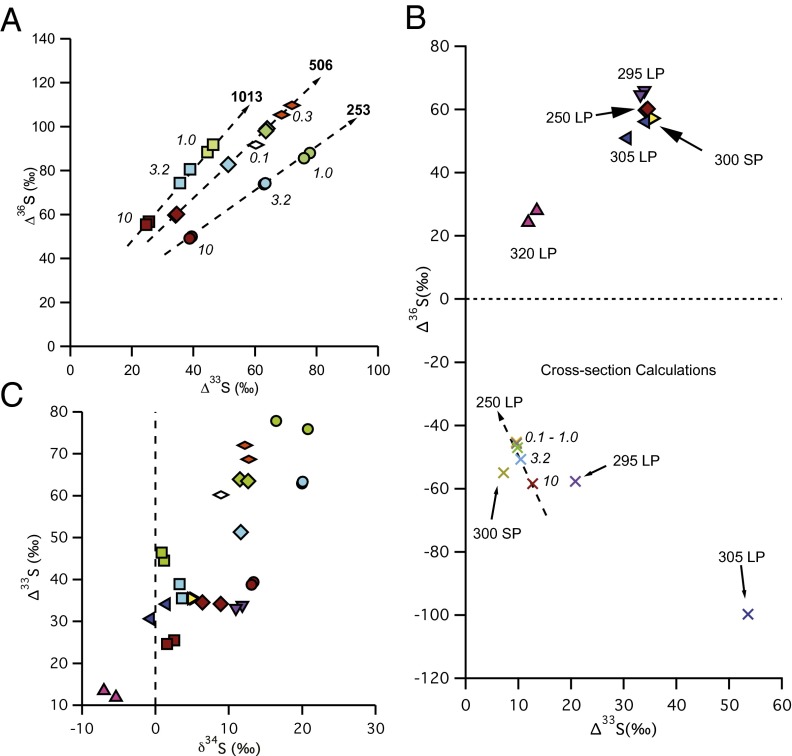
Fig. 2.
Isotopic results from experiments and calculations. (A) Results (Δ36S vs. Δ33S) from experiments using the 250-nm longpass filter for a variety of SO2 pressures (italics, in millibars) and total pressures (bold, in millibars). (B) Results (Δ36S vs. Δ33S) from experiments using various combinations of shortpass (SP) and longpass (LP) filters. The 320 LP experiments also used a 350 SP filter, and the 300 SP experiments also used a 250 LP filter. Also in the figure (× symbols) are the results from calculations based on the Danielache et al. (27) cross-sections for the conditions tested here. (C) Results (Δ33S vs. δ34S) from all experiments, showing the large Δ33S values associated with small δ34S values. Symbols are the same as in A and B.
To test the sensitivity of the isotope effects to the detailed spectral regions of the excitation, experiments were performed with a series of longpass (250-, 295-, and 305-nm) and shortpass (300- and 350-nm) filters (Fig. S1). The use of optical filters allows testing for S-MIF signals from the high- or low-energy side of the band system (Fig. 1). Experiments performed at the same SO2 pressure (10 mbar) and total pressure (507 mbar) conditions but with different filters to isolate the 250–300-nm, >295-nm, or >305-nm regions produced remarkably similar isotopic results, with Δ33S between 30‰ and 36‰ and Δ36S between 49‰ and 66‰ (Fig. 2B). This result suggests that the anomalous enrichment in 33S and 36S is not a strong function of excitation wavelength within this absorption band, at least within a broadband regime. Several experiments were performed with 320-nm longpass and 350-nm shortpass filters. This wavelength region corresponds to excitation into the 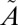 1A2 state only; it is below the origin of the
1A2 state only; it is below the origin of the 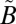 1B1 state (38) and above the spin-forbidden
1B1 state (38) and above the spin-forbidden 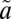 3B1←
3B1←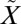 1A1 transition of SO2, which lies between 350 and 390 nm (see references in ref. 20). The experiments were carried out at higher SO2 (50.7 mbar) and acetylene (101 mbar) pressures, but the same total pressure (507 mbar). These produced lower Δ33S (11.9–13.5‰) and Δ36S (24.3–28.0‰) values, consistent with the higher SO2 pressure, but with Δ36S/Δ33S values (2.05–2.08) similar to the rest of the filter experiments (1.61–1.95) (Fig. 2). The presence of S-MIF signatures from excitation exclusively into the
1A1 transition of SO2, which lies between 350 and 390 nm (see references in ref. 20). The experiments were carried out at higher SO2 (50.7 mbar) and acetylene (101 mbar) pressures, but the same total pressure (507 mbar). These produced lower Δ33S (11.9–13.5‰) and Δ36S (24.3–28.0‰) values, consistent with the higher SO2 pressure, but with Δ36S/Δ33S values (2.05–2.08) similar to the rest of the filter experiments (1.61–1.95) (Fig. 2). The presence of S-MIF signatures from excitation exclusively into the 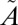 1A2 state suggests that vibronic interactions between the two singlet states (
1A2 state suggests that vibronic interactions between the two singlet states (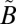 1B1 and
1B1 and 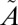 1A2) make a negligible contribution to the observed S-MIF signatures.
1A2) make a negligible contribution to the observed S-MIF signatures.
Source of MIF Signatures
Danielache et al. (27) reported UV cross-sections for isotopically enriched SO2 (i.e., 32SO2, 33SO2, 34SO2, and 36SO2) in the 250–320-nm region. These cross-sections are measured at 8-cm−1 resolution, at room temperature, and ∼1–7 mbar SO2, and characterize the magnitude of the isotopic shifts in band positions and intensities. The measured cross-sections (27) were used to predict S-MIF signatures under the experimental conditions (spectral irradiance and SO2 column densities) tested here and are compared with experimental results in Fig. 2B. The results show that differences in the absorption cross-sections can account for only a small fraction (<25‰) of the large (up to 78‰) Δ33S values observed in the 250-nm longpass experiments and cannot account for the large positive Δ36S values (up to 110‰) observed. In particular, the cross-sections predict large negative Δ36S values for a variety of broadband light sources (Fig. 2B and figure 7 in ref. 27), in contrast to the large positive values observed. Even accounting for the systematic errors (2.5%) and SEM (5–10%) for the measured cross-sections (see results and discussion in ref. 27), the cross-sections still cannot explain the Δ36S values observed (Fig. 2B).
The above cross-section model also includes the effect of self- and mutual-shielding of absorption lines under experimental conditions. Self-shielding occurs when the major isotopologue line (i.e., 32SO2) saturates under optically thick conditions. In this study, large S-MIF signatures are observed even under optically thin conditions. The experiments with the lowest pSO2 (column density of 4 × 1016 molecules per cm−2) had over 95% optical transmission, where self-shielding is not expected to play a major role. The magnitude of S-MIF increases with decreasing SO2 pressure, which is opposite from what is expected from self-shielding. We therefore exclude absorption-based effects, such as self-shielding or absorption cross-section differences as the main source of the observed S-MIF signatures.
Other proposed mechanisms of MIF production include nuclear field shift isotope effects, magnetic isotope effects, and symmetry-based isotope effects. The magnitude of nuclear field shift isotope effects has been estimated to be insignificant for the sulfur isotope system because of the small nuclear size difference among isotopologues (39). Magnetic isotope effects would produce anomalies only in 33S and cannot explain the large Δ36S values observed in the experiments. A symmetry-based isotope effect also is unlikely because of the lack of any intermediates or transition states with symmetrically equivalent sulfur atoms. In addition, a symmetry-based isotope effect would predict positive Δ33S values and negative Δ36S values (40), whereas positive Δ33S and positive Δ36S values are observed in the present experiments.
Intersystem Crossing as a Potential Origin of S-MIF
Although isotope substitution shifts the vibrational and rotational energy level spacing in a mass-dependent manner, the magnitudes of the shifts will be different for different excited electronic states. In systems in which the vibration–rotation levels of multiple low-lying electronic states overlap, the interactions between states may exhibit strong and level-specific isotope selectivity. In particular, pairs of levels capable of interacting with each other and that are near-degenerate for one isotopologue may be nondegenerate for other isotopologues. These effects were cited previously as a source of S-MIF during the photopolymerization of CS2 (41, 42) and oxygen MIF during the photodissociation of CO2 (43) and CO (44). In these three cases, the anomalous isotope effects have been attributed to differences in intersystem crossing (ISC) rates from an initially excited singlet state to a reactive (or dissociative) triplet state. Similar spin–orbit effects have been shown to cause anomalous LIF intensities in 37ClO2 vs. 35ClO2 for particular vibrational bands (45). A recent study by Muskatel et al. (46) demonstrates a theoretical basis for similar isotope effects during the photolysis of N2. In particular, they note that the accidental overlap between different electronic states of N2 may cause large isotope effects in certain regions of the spectrum. The importance of accidental degeneracies between interacting states in producing environmentally relevant MIF signatures remains controversial, as it has been suggested that self-shielding might have contributed to the isotope signatures observed during the CS2 (47) and CO (48–50) (see also ref. 51) experiments. In addition, isotope effects from local interactions are likely to be isolated to narrow spectral regions where the interactions occur.
Several previous spectroscopic studies of SO2 showed isotopologue-specific perturbations in the 250–350-nm absorption region. Analysis of several absorption bands of S18O2 corresponding to the Clements “B” and “E” bands (310.9 and 304.4 nm, respectively) revealed that these bands of S18O2 were significantly less perturbed than the corresponding bands of S16O2 (52), suggesting different coupling strengths for the different isotopologues. Baskin et al. (53) reported a strong 32SO2 vibrational peak at 30,995 cm−1 (322.6 nm) that had no corresponding 34SO2 peak at the expected location. This was attributed to perturbations caused by accidentally near-degenerate vibronic interactions in one isotopic species but not the other.
If the anomalous isotope effects were purely the result of isolated interactions at particular vibrational levels, a strong wavelength selectivity to the anomalous isotope effects would be expected, with certain regions (i.e., around the localized near-degeneracies) producing considerably larger MIF than other regions. One of the features of the present experiments is that the MIF signature shows remarkable similarity in both the higher- (250–300-nm) and lower- (295–350-nm and 305–350-nm) energy regions of the absorption band (Figs. 1 and 2B). Experiments isolating only the 320–350-nm absorption region, which lies below the origin of the 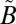 1B1 state and corresponds to excitation into only the
1B1 state and corresponds to excitation into only the 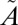 1A2 state, also produce S-MIF consistent with the other experiments, although with a smaller magnitude, because of the different experimental conditions (i.e., higher SO2 pressure).
1A2 state, also produce S-MIF consistent with the other experiments, although with a smaller magnitude, because of the different experimental conditions (i.e., higher SO2 pressure).
All our experiments were performed at relatively high total pressures (253–1,013 mbar) in the presence of a bath gas (N2). Under these conditions, the collision lifetime (on the order of nanoseconds) is considerably shorter than the fluorescence lifetime (on the order of microseconds), allowing rapid collision-induced rotational and vibrational relaxation of the excited state (20, 54). Time-resolved fluorescence experiments performed at 1.33 mbar pure SO2 showed strong resonance fluorescence from the excited level accompanied by significant fluorescence from vibrationally relaxed molecules (55). At higher SO2 pressures of 26.6 mbar, fluorescence from highly excited states (266 nm) contained no resonance fluorescence, with the dominant fluorescence occurring around 325.5 nm and 370 nm, near the origin of the 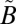 1B1 and
1B1 and 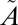 1A2 states, respectively, suggesting rapid and nearly complete collisional vibrational thermalization (56). Although the collision-induced ISC might occur from any state, the rate of collision-induced vibrational relaxation is faster than the rate of collision-induced ISC (55), at least for some states. Thus, at high bath gas pressures, the ISC reaction more likely will occur from lower vibrational levels of the singlet state. This also increases the likelihood of vibrational relaxation of the
1A2 states, respectively, suggesting rapid and nearly complete collisional vibrational thermalization (56). Although the collision-induced ISC might occur from any state, the rate of collision-induced vibrational relaxation is faster than the rate of collision-induced ISC (55), at least for some states. Thus, at high bath gas pressures, the ISC reaction more likely will occur from lower vibrational levels of the singlet state. This also increases the likelihood of vibrational relaxation of the 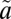 3B1 state below the origin of the
3B1 state below the origin of the 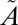 1A2 state, preventing crossing back to the singlet manifold. As a result, localized near-degenerate interactions at low vibrational levels of the singlet state will be selectively expressed regardless of the state and vibrational levels initially excited into. This allows a mechanism for the expression of S-MIF from localized near-degenerate spin–orbit interactions, and also may explain the pressure dependence on the relationship between Δ36S and Δ33S values.
1A2 state, preventing crossing back to the singlet manifold. As a result, localized near-degenerate interactions at low vibrational levels of the singlet state will be selectively expressed regardless of the state and vibrational levels initially excited into. This allows a mechanism for the expression of S-MIF from localized near-degenerate spin–orbit interactions, and also may explain the pressure dependence on the relationship between Δ36S and Δ33S values.
Theoretical Basis for Proposed Mechanism
To better understand the isotope effects during the ISC reaction of SO2, high-level ab initio calculations of the global potential energy surfaces (PESs) for the low-lying singlet and triplet states of SO2 were carried out (SI Text). In the Clements bands (57), about 3.5 eV above the ground electronic (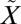 1A1) state, there are two nonadiabatically coupled singlet (
1A1) state, there are two nonadiabatically coupled singlet (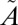 1A2 and
1A2 and 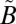 1B1) and three triplet (
1B1) and three triplet (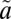 3B1,
3B1, 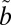 3A2, and
3A2, and 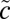 3B2) electronic states (58–60) (Fig. 2D). The
3B2) electronic states (58–60) (Fig. 2D). The 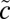 3B2 state was not included in the present analysis, as it has no interaction with other states because of its symmetry. For each of the remaining states, ∼19,000 symmetric unique points were determined at the internally contracted multireference configuration interaction (MRCI) level (61) with the augmented correlation-consistent polarized valence triple-zeta (aug-cc-pVTZ) basis set (62) for both the sulfur and oxygen atoms. The Davidson correction (Q) (63) was applied to account for the effect of higher excitations and to reduce size-consistency errors. Nonadiabatic couplings between the two singlet states have been determined in a quasi-diabatic representation (64). In addition, the spin–orbit (SO) interactions between the singlet and triplet states has been computed using the unperturbed MRCI wave functions and Breit–Pauli Hamiltonian. As shown in SI Text (Fig. S2), the calculated absorption cross-section for the Clements bands is in good agreement with experiment. Importantly, the potential energy minimum of the
3B2 state was not included in the present analysis, as it has no interaction with other states because of its symmetry. For each of the remaining states, ∼19,000 symmetric unique points were determined at the internally contracted multireference configuration interaction (MRCI) level (61) with the augmented correlation-consistent polarized valence triple-zeta (aug-cc-pVTZ) basis set (62) for both the sulfur and oxygen atoms. The Davidson correction (Q) (63) was applied to account for the effect of higher excitations and to reduce size-consistency errors. Nonadiabatic couplings between the two singlet states have been determined in a quasi-diabatic representation (64). In addition, the spin–orbit (SO) interactions between the singlet and triplet states has been computed using the unperturbed MRCI wave functions and Breit–Pauli Hamiltonian. As shown in SI Text (Fig. S2), the calculated absorption cross-section for the Clements bands is in good agreement with experiment. Importantly, the potential energy minimum of the 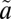 3B1 state is about 0.2 eV lower than that of the lowest singlet state, facilitating ISC.
3B1 state is about 0.2 eV lower than that of the lowest singlet state, facilitating ISC.
Franck–Condon transitions with a 250–350-nm photon bring SO2 from the ground 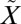 1A1 state to the excited
1A1 state to the excited 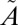 1A2/
1A2/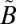 1B1 manifold. As discussed above, we assume that the excited SO2 is relaxed quickly to low vibrational levels (Table S2) of the lowest singlet
1B1 manifold. As discussed above, we assume that the excited SO2 is relaxed quickly to low vibrational levels (Table S2) of the lowest singlet 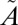 1A2 state because of fast nonadiabatic mixing between the two singlet states and efficient collisions with the bath gas. The ISC to the lowest triplet
1A2 state because of fast nonadiabatic mixing between the two singlet states and efficient collisions with the bath gas. The ISC to the lowest triplet 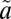 3B1 state follows (Table S2), which was modeled using a wave packet method. In particular, the time-dependent Schrödinger equation was solved numerically (65) with the nonadiabatically coupled full-dimensional Hamiltonian for the
3B1 state follows (Table S2), which was modeled using a wave packet method. In particular, the time-dependent Schrödinger equation was solved numerically (65) with the nonadiabatically coupled full-dimensional Hamiltonian for the 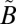 1B1/
1B1/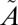 1A2/
1A2/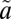 3B1 manifold (J = 0), as described in SI Text. Four (000, 100, 010, and 001) vibrational eigenfunctions on the
3B1 manifold (J = 0), as described in SI Text. Four (000, 100, 010, and 001) vibrational eigenfunctions on the 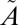 1A2 state were used as the initial wave packet, and the
1A2 state were used as the initial wave packet, and the 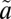 3B1 triplet-state population is artificially absorbed to account for the irreversibility of the ISC as a result of collisional relaxation. The parameters used in our calculations are listed in Table S3.
3B1 triplet-state population is artificially absorbed to account for the irreversibility of the ISC as a result of collisional relaxation. The parameters used in our calculations are listed in Table S3.
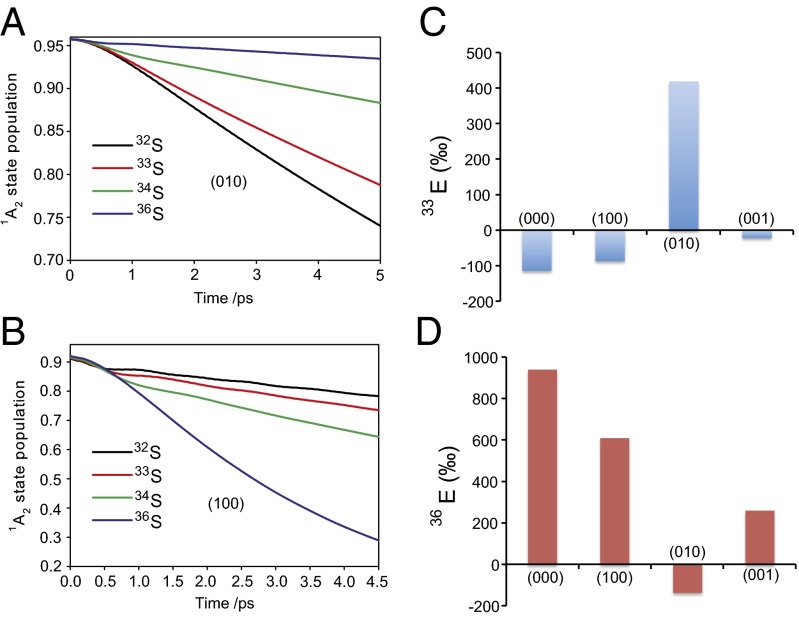
The lifetime of the 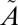 1A2 state is extracted from the population decay curve (Table S4) and used to estimate the isotope effects for ISC from each vibrational level. As shown in Fig. 3 and Fig. S3, the results clearly show the decay rates are different among the sulfur isotopologues and are not mass dependent. In particular, the (000), (100), and (001) vibrational levels show large anomalies in the decay rate of 36SO2, suggesting a strong mass-independent effect in 36S. Similarly, decay from the (010) level shows large MIF in 33S. Therefore, combined contributions from MIF at the (100) and (010) levels would explain the experimental results of positive Δ33S and Δ36S values. It is clear that this simple model cannot fully account for the experimental results; a significant number of approximations were involved. For example, the relative energies of various electronic states might not be determined accurately by the ab initio method. In addition, it is likely that the singlet excited-state SO2 decays from a range of vibrational and rotational levels. Nevertheless, these results clearly demonstrate that there is a very strong, isotope-specific dependence on the excited-state lifetimes from individual vibrational levels.
1A2 state is extracted from the population decay curve (Table S4) and used to estimate the isotope effects for ISC from each vibrational level. As shown in Fig. 3 and Fig. S3, the results clearly show the decay rates are different among the sulfur isotopologues and are not mass dependent. In particular, the (000), (100), and (001) vibrational levels show large anomalies in the decay rate of 36SO2, suggesting a strong mass-independent effect in 36S. Similarly, decay from the (010) level shows large MIF in 33S. Therefore, combined contributions from MIF at the (100) and (010) levels would explain the experimental results of positive Δ33S and Δ36S values. It is clear that this simple model cannot fully account for the experimental results; a significant number of approximations were involved. For example, the relative energies of various electronic states might not be determined accurately by the ab initio method. In addition, it is likely that the singlet excited-state SO2 decays from a range of vibrational and rotational levels. Nevertheless, these results clearly demonstrate that there is a very strong, isotope-specific dependence on the excited-state lifetimes from individual vibrational levels.
Fig. 3.
Results for lifetime calculations for 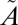 1A2 states. (A and B) Decay of singlet populations for several sulfur isotopologues from the (010) and (100) vibrational states, which have rates faster than those of the (000) and (001) states (Table S4). (C and D) Isotope fractionation factor estimated from the lifetime of
1A2 states. (A and B) Decay of singlet populations for several sulfur isotopologues from the (010) and (100) vibrational states, which have rates faster than those of the (000) and (001) states (Table S4). (C and D) Isotope fractionation factor estimated from the lifetime of 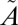 1A2 state calculated for the four low-lying vibrational levels:
1A2 state calculated for the four low-lying vibrational levels: 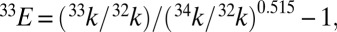 and
and 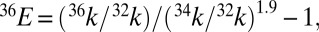 where xk are rate constants for xSO2.
where xk are rate constants for xSO2.
Implications to S-MIF Signatures Observed in Nature
The photolysis of SO2 in the 185–220-nm absorption region currently is considered the most likely source reaction for Archean S-MIF (18, 19, 22–24). However, there are several issues with SO2 photolysis as a source of the Archean S-MIF signatures. Broadband photolysis of SO2 under a range of experimental conditions (e.g., SO2 pressures, bath gas pressures, light sources) produces large δ34S values (up to 212‰) associated with relatively small Δ33S enrichments (maximum 25‰), resulting in low δ33S/δ34S ratios of 0.55–0.66 (24–26). In contrast, the Archean record contains large Δ33S values (from −4 to +12 ‰) associated with high δ33S/δ34S ratios of up to 1.4 (e.g., refs. 66 and 67). In addition, S-MIF signatures produced during SO2 photolysis become very small (Δ33S < 2.5‰) at low SO2 column densities (26), indicating that the production of large (Δ33S > 2.5‰) S-MIF anomalies would require the maintenance of high SO2 column densities in the atmosphere. Sediment digenesis and biological processes in the oceans likely mix sulfides with different Δ33S values and dilute the S-MIF signal (68) such that the source reaction likely would have produced Δ33S values much larger than 12‰. Significant questions remain as to whether 185–220-nm photolysis of SO2 was the source of Archean S-MIF.
The S-MIF signatures produced in this study contain large (Δ33S up to 78‰) MIF associated with small (<25‰) δ34S values. In contrast to the photolysis band, the S-MIF signatures from the excitation band do not require a high SO2 column density to produce large S-MIF. The major issues with the excitation band as a source of the Archean S-MIF signature are the difficulty in preserving the isotope signatures from excited-state SO2 (relative to SO produced from SO2 photolysis) and the positive Δ36S/Δ33S ratios (Archean rocks have Δ36S/Δ33S ∼−1.5 to –0.9; see refs. 15, 32, and 67). Several authors (25, 32) have suggested that SO2 photochemistry from the photoexcitation region might have contributed to the Archean S-MIF signatures, and studies have shown that the UV irradiation of SO2 in the presence of methane produces organosulfur aerosols (presumably derived from 3SO2) that might have contributed to preservation of the Archean S-MIF signature (69). The discrepancy in Δ36S/Δ33S values requires additional study, but our calculations suggest that MIFs in 33S and 36S are produced from ISC at different vibrational levels, and our experiments demonstrated that the Δ36S/Δ33S ratio is a function of pN2 and could potentially produce the Archean ratio under certain conditions. It should be noted that the Δ36S/Δ33S values produced from experimental photolysis of SO2 using broadband radiation sources is too low (−1.6 under pure SO2 but as low as −6.0 with N2) to explain the Δ36S/Δ33S ratios observed for the Archean record. As suggested in Whitehill and Ono (25), contributions from both absorption regions might explain the Archean S-MIF signal.
Several authors (e.g., refs. 28–31) have suggested that excited-state photochemistry in the photoexcitation band might be responsible for the S-MIF signatures observed in modern stratospheric sulfate aerosols. Reaction of excited-state SO2, particularly triplet 3SO2, with either ground-state SO2 [i.e., *SO2+SO2→SO+SO3 (29)] or O2 [i.e., *SO2+O2→SO3+O (28)] theoretically could preserve mass-independently fractionated SO3, and SO3 might be hydrolyzed to form stable sulfuric acid aerosols. Whitehill and Ono (25), however, presented isotopic evidence that the *SO2+SO2 reaction primarily occurs via O-atom transfer from the excited-state species to the ground-state species, thus producing MIF signatures in SO, but mass-dependently fractionated SO3. Hattori et al. (28) modeled the modern stratosphere following a large volcanic eruption and suggested that the *SO2 formed from the photoexcitation band might react with O2 to form mass-independently fractionated SO3 (29–31). Their isotopic agreement, however, critically depends on the assumption that the cross-sections of Danielache et al. (27) accurately predict the isotope ratios of the reactive (i.e., triplet) SO2 species. As we demonstrate here, significant differences between the isotope signatures predicted by the cross-sections and those observed experimentally are the result of vibronic effects after the initial excitation step, which are not taken into account in ref. 28. Ono et al. (26) showed that the isotopic signatures from SO2 photolysis in a self-shielding regime match those from stratospheric sulfate aerosols, although a mechanism for the preservation of SO in the modern atmosphere requires additional research.
Conclusions
We report the production of very large S-MIF signatures, with Δ33S up to 78‰ and Δ36S up to 110‰, from SO2 photochemistry in the 250–350-nm region. The origin of the S-MIF is attributed to ISC at excitation wavelengths below 320 nm. Isotope effects due primarily to absorption, as predicted by isotopologue-specific cross-sections, do not contribute significantly to the large S-MIF observed, particularly in 36S. Rapid vibrational relaxation allows expression of S-MIF signatures from localized accidental degeneracies regardless of the initially excited vibronic level. The same mechanism, however, may not be applied to the 180- and 220-nm band systems of SO2 because the quantum efficiency of photolysis is near unity below 205 nm (59), and the lifetime is sufficiently short that little vibrational relaxation occurs. Although the S-MIF signatures observed in this study, particularly the Δ36S/Δ33S ratios, do not match those from the Archean, the photochemistry in the photoexcitation band can produce large mass-independent signatures (i.e., Δ33S values) with relatively small mass-dependent fractionations (i.e., δ34S values), which is necessary to explain the preservation of large Archean S-MIF signatures. Photochemistry from the 250–350-nm absorption region should be explored further as a possible source for the geological S-MIF signatures.
Supplementary Material
Acknowledgments
The authors thank William J. Olszewski for assistance in sulfur isotope analysis, and Harry Oduro and Eliza Harris for discussion. The authors also thank Robert Field for his input and suggestions. This work was supported by the National Aeronautics and Space Administration Exobiology Program, Grant NNX10AR85G (to S.O.); the National Natural Science Foundation of China (21133006, 91221301, and 91021010); the Ministry of Science and Technology (2013CB834601 to D.X.); and the Department of Energy, Grant DF-FG02-05ER15694 (to H.G.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
 |
 |
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1306979110/-/DCSupplemental.
References
- 1.Urey HC. The thermodynamic properties of isotopic substances. J Chem Soc. 1947;69:562–581. doi: 10.1039/jr9470000562. [DOI] [PubMed] [Google Scholar]
- 2.Bigeleisen J, Mayer M. Calculation of equilibrium constants for isotopic exchange reactions. J Chem Phys. 1947;15(5):261–267. [Google Scholar]
- 3.Thiemens MH. Mass-independent isotope effects in planetary atmospheres and the early solar system. Science. 1999;283(5400):341–345. doi: 10.1126/science.283.5400.341. [DOI] [PubMed] [Google Scholar]
- 4.Thiemens M. History and applications of mass-independent isotope effects. Annu Rev Earth Planet Sci. 2006;34:217–262. [Google Scholar]
- 5.Thiemens MH, Chakraborty S, Dominguez G. The physical chemistry of mass-independent isotope effects and their observation in nature. Annu Rev Phys Chem. 2012;63:155–177. doi: 10.1146/annurev-physchem-032511-143657. [DOI] [PubMed] [Google Scholar]
- 6.Hulston J, Thode H. Variations in the S33, S34, and S36 contents of meteorites and their relation to chemical and nuclear effects. J Geophys Res. 1965;70(14):3475–3484. [Google Scholar]
- 7.Clayton RN, Grossman L, Mayeda TK. A component of primitive nuclear composition in carbonaceous meteorites. Science. 1973;182(4111):485–488. doi: 10.1126/science.182.4111.485. [DOI] [PubMed] [Google Scholar]
- 8.Arrhenius G, McCrumb J, Friedman N. Primordial condensation of meteorite components—experimental evidence of the state of the medium. Astrophys Space Sci. 1979;65:297–307. [Google Scholar]
- 9.Thiemens MH, Heidenreich JE., 3rd The mass-independent fractionation of oxygen: A novel isotope effect and its possible cosmochemical implications. Science. 1983;219(4588):1073–1075. doi: 10.1126/science.219.4588.1073. [DOI] [PubMed] [Google Scholar]
- 10.Thiemens M, Jackson T. Produciton of isotopically heavy ozone by ultraviolet light photolysis of O2. Geophys Res Lett. 1987;14(6):624–627. [Google Scholar]
- 11.Mauersberger K. Ozone isotope measurements in the stratosphere. Geophys Res Lett. 1987;14(1):80–83. [Google Scholar]
- 12.Mauersberger K, Krankowsky D, Janssen C, Schinke R. Assessment of the ozone isotope effect. In: Bederson B, Walther H, editors. Advances in Atomic, Molecular, and Optical Physics. Vol 50. Amsterdam: Elsevier; 2005. pp. 1–54. [Google Scholar]
- 13.Schinke R, Grebenshchikov SY, Ivanov MV, Fleurat-Lessard P. Dynamical studies of the ozone isotope effect: A status report. Annu Rev Phys Chem. 2006;57:625–661. doi: 10.1146/annurev.physchem.57.032905.104542. [DOI] [PubMed] [Google Scholar]
- 14.Ivanov MV, Babikov D. On molecular origin of mass-independent fractionation of oxygen isotopes in the ozone forming recombination reaction. Proc Natl Acad Sci USA. 2013;110:17708–17713. doi: 10.1073/pnas.1215464110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Farquhar J, Bao H, Thiemens M. Atmospheric influence of Earth’s earliest sulfur cycle. Science. 2000;289(5480):756–759. doi: 10.1126/science.289.5480.756. [DOI] [PubMed] [Google Scholar]
- 16.Bekker A, et al. Dating the rise of atmospheric oxygen. Nature. 2004;427(6970):117–120. doi: 10.1038/nature02260. [DOI] [PubMed] [Google Scholar]
- 17.Guo Q, et al. Reconstructing Earth’s surface oxidation across the Archean-Proterozoic transition. Geology. 2009;37(5):399–402. [Google Scholar]
- 18.Farquhar J, Savarino J, Airieau S, Thiemens M. Observation of wavelength-sensitive mass-independent sulfur isotope effects during SO2 photolysis: Implications for the early atmosphere. J Geophys Res. 2001;106(E12):32829–32839. [Google Scholar]
- 19.Pavlov AA, Kasting JF. Mass-independent fractionation of sulfur isotopes in Archean sediments: Strong evidence for an anoxic Archean atmosphere. Astrobiology. 2002;2(1):27–41. doi: 10.1089/153110702753621321. [DOI] [PubMed] [Google Scholar]
- 20.Heicklen J, Kelly N, Partymiller K. The photophysics and photochemistry of SO2. Res Chem Intermed. 1980;3:315–404. [Google Scholar]
-
21.Ran H, Xie D, Guo H. Theoretical studies of
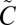 1B2 absorption spectra of SO2 isotopomers. Chem Phys Lett. 2007;439:280–283. [Google Scholar]
1B2 absorption spectra of SO2 isotopomers. Chem Phys Lett. 2007;439:280–283. [Google Scholar] - 22.Lyons J. Mass-independent fractionation of sulfur isotopes by isotope-selective photodissociation of SO2. Geophys Res Lett. 2007;34:L22811. [Google Scholar]
- 23.Danielache S, Eskebjerg C, Johnson M, Ueno Y, Yoshida N. High-precision spectroscopy of 32S, 33S, and 34S sulfur dioxide: Ultraviolet absorption cross sections and isotope effects. J Geophys Res. 2008;113:D17314. [Google Scholar]
- 24.Masterson A, Farquhar J, Wing B. Mass-independent fractionation patterns in the broadband UV photolysis of sulfur dioxide: Pressure and third body effects. Earth Planet Sci Lett. 2011;306:253–260. [Google Scholar]
- 25.Whitehill A, Ono S. Excitation band dependence of sulfur isotope mass-independent fractionation during photochemistry of sulfur dioxide using broadband light sources. Geochim Cosmochim Acta. 2012;94:238–253. [Google Scholar]
- 26.Ono S, Whitehill A, Lyons J. Contribution of isotopologue self-shielding to sulfur mass-independent fractionation during sulfur dioxide photolysis. J Geophys Res Atmos. 2013;118(5):2444–2454. [Google Scholar]
- 27.Danielache S, et al. Photoabsorption cross-section measurements of 32S,33S, 34S, and 36S sulfur dioxide for the B1B1–X1A1 absorption band. J Geophys Res Atmos. 2012;117(D24):D24301. [Google Scholar]
- 28.Hattori S, et al. SO2 photoexcitation mechanism links mass-independent sulfur isotopic fractionation in cryospheric sulfate to climate impacting volcanism. Proc Natl Acad Sci USA. 2013;110:17656–17661. doi: 10.1073/pnas.1213153110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Savarino J, Romero A, Cole-Dai J, Bekki S, Thiemens M. UV induced mass-independent sulfur isotope fractionation in stratospheric volcanic sulfate. Geophys Res Lett. 2003;30(21):2131. [Google Scholar]
- 30.Baroni M, Thiemens MH, Delmas RJ, Savarino J. Mass-independent sulfur isotopic compositions in stratospheric volcanic eruptions. Science. 2007;315(5808):84–87. doi: 10.1126/science.1131754. [DOI] [PubMed] [Google Scholar]
- 31.Baroni M, Savarino J, Cole-Dai J, Rai V, Thiemens M. Anomalous sulfur isotope compositions of volcanic sulfate over the last millennium in Antarctic ice cores. J Geophys Res. 2008;113:D20112. [Google Scholar]
- 32.Zerkle A, Claire M, Domagal-Goldman S, Farquhar J, Poulton S. A bistable organic-rich atmosphere on the Neoarchaean Earth. Nat Geosci. 2012;5:359–363. [Google Scholar]
- 33.Vandaele A, Hermans C, Fally S. Fourier transform measurements of SO2 absorption cross sections: II.: Temperature dependence in the 29000–44000 cm−1 (227–345 nm) region. J Quant Spectrosc Radiat Transf. 2009;110(18):2115–2126. [Google Scholar]
- 34.Hermans C, Vandaele A, Fally S. Fourier transform measurements of SO2 absorption cross sections: I. Temperature dependence in the 24000 – 29000 cm-1 (345 – 420 nm) region. J Quant Spectrosc Radiat Transf. 2009;110:756–766. [Google Scholar]
- 35.Kelly M, Meagher J, Heicklen J. Photolysis of sulfur dioxide in the presence of foreign gases: VII. Acetylene. J Photochem. 1976;5:355–376. [Google Scholar]
- 36.Luria M, de Pena R, Olszyna K, Heicklen J. Kinetics of particle growth. III. Particle formation in the photolysis of sulfur dioxide–acetylene mixtures. J Phys Chem. 1974;78(4):325–335. [Google Scholar]
- 37.Oduro H, Kamyshny A, Guo W, Farquhar J. Multiple sulfur isotope analysis of volatile organic sulfur compounds and their sulfonium precursors in coastal marine environments. Mar Chem. 2011;124:78–89. [Google Scholar]
- 38.Shaw R, Kent J, O’Dwyer M. Single vibronic level fluorescence spectra of sulfur dioxide. J Mol Spectrosc. 1980;82(1):1–26. [Google Scholar]
- 39.Schauble E. Role of nuclear volume in driving equilibrium stable isotope fractionation of mercury, thallium, and other very heavy elements. Geochim Cosmochim Acta. 2007;71:2170–2189. [Google Scholar]
- 40.Ono S, Beukes N, Rumble D. Origin of two distinct multiple-sulfur isotope compositions of pyrite in the 2.5 Ga Klein Naute Formation, Griqualand West Basin, South Africa. Precambrian Res. 2009;169(1-4):48–57. [Google Scholar]
- 41.Colman JJ, Xu X, Thiemens MH, Trogler WC. Photopolymerization and mass-independent sulfur isotope fractionations in carbon disulfide. Science. 1996;273(5276):774–776. doi: 10.1126/science.273.5276.774. [DOI] [PubMed] [Google Scholar]
- 42.Zmolek P, Xu X, Jackson T, Thiemens M, Trogler W. Large mass independent sulfur isotope fractionations during the photopolymerization of 12CS2 and 13CS2. J Phys Chem A. 1999;103(15):2477–2480. [Google Scholar]
- 43.Bhattacharya S, Savarino J, Thiemens M. A new class of oxygen isotopic fractionation in photodissociation of carbon dioxide: Potential implications for atmospheres of Mars and Earth. Geophys Res Lett. 2000;27(10):1459–1462. [Google Scholar]
- 44.Chakraborty S, Ahmed M, Jackson TL, Thiemens MH. Experimental test of self-shielding in vacuum ultraviolet photodissociation of CO. Science. 2008;321(5894):1328–1331. doi: 10.1126/science.1159178. [DOI] [PubMed] [Google Scholar]
- 45.Lim G, Lim S, Kim S, Choi Y. Unexpectedly large O37ClO/O35ClO intensity ratios of the fluorescence from the low-energy vibrational levels of OClO (Ã2A2) J Chem Phys. 1999;111:456–459. [Google Scholar]
- 46.Muskatel BH, Remacle F, Thiemens MH, Levine RD. On the strong and selective isotope effect in the UV excitation of N2 with implications toward the nebula and Martian atmosphere. Proc Natl Acad Sci USA. 2011;108(15):6020–6025. doi: 10.1073/pnas.1102767108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lyons J. Atmospherically-derived mass-independent sulfur isotope signatures, and incorporation into sediments. Chem Geol. 2009;267:164–174. [Google Scholar]
- 48.Lyons J, Lewis R, Clayton R. Comment on “Experimental test of self-shielding in vacuum ultraviolet photodissociation of CO.”. Science. 2009;324(5934):1516. doi: 10.1126/science.1167717. [DOI] [PubMed] [Google Scholar]
- 49.Federman S, Young E. Comment on “Experimental test of self-shielding in vacuum ultraviolet photodissociation of CO.”. Science. 2009;324(5934):1516. doi: 10.1126/science.1169923. [DOI] [PubMed] [Google Scholar]
- 50. Yin QZ, Shi X, Chang C, Ng CY (2009) Comment on “Experimental test of self-shielding in vacuum ultraviolet photodissociation of CO.” Science 324(5934):1516, author reply 1516. [DOI] [PubMed]
- 51.Chakraborty S, Ahmed M, Jackson T, Thiemens M. Response to comments on “Experimental test of self-shielding in vacuum ultraviolet photodissociation of CO.”. Science. 2009;324(5934):1516. doi: 10.1126/science.1170488. [DOI] [PubMed] [Google Scholar]
- 52.Hamada Y, Merer A. Rotational structure in the absorption spectrum of SO2 between 3000 Å and 3300 Å. Can J Phys. 1975;53:2555–2576. [Google Scholar]
- 53.Baskin J, Al-Adel F, Hamden A. Unexpectedly rich vibronic structure in supersonic jet spectra of sulfur dioxide between 360 and 308 nm. Chem Phys. 1995;200:181–199. [Google Scholar]
- 54.Su F, et al. Kinetics of fluorescence decay of SO2 excited in the 2662–3273 Å region. Int J Chem Kinet. 1978;10:125–154. [Google Scholar]
- 55.Bae S, Yoo H, Ku J. Intersystem crossing rate constants from the (0,4,1) and (1,2,1) levels of the à 1A2 to ã 1B1 state of SO2. J Chem Phys. 1998;109(4):1251–1258. [Google Scholar]
- 56.Zhang G, Zhang L, Jin Y. Emission spectrum and relaxation kinetics of SO2 induced by 266 nm laser. Spectrochim Acta A Mol Biomol Spectrosc. 2010;77(1):141–145. doi: 10.1016/j.saa.2010.04.041. [DOI] [PubMed] [Google Scholar]
- 57.Clements J. On the absorption spectrum of sulphur dioxide. Phys Rev. 1935;47:224–232. [Google Scholar]
- 58.Müller H, Köppel H. Adiabatic wave-packet motion on conically intersecting potential energy surfaces. The case of SO2 (1B1 – 1A2) Chem Phys. 1994;183:107–116. [Google Scholar]
- 59.Katagiri H, et al. Experimental and theoretical exploration of photodissociation of SO2 via the C1B2 state: Identification of the dissociation pathway. J Molec Struct. 1997;413:589–614. [Google Scholar]
- 60.Lévêque C, Komainda A, Taïeb R, Köppel H. Ab initio quantum study of the photodynamics and absorption spectrum for the coupled 1(1)A2 and 1(1)B1 states of SO2. J Chem Phys. 2013;138(4):044320. doi: 10.1063/1.4776758. [DOI] [PubMed] [Google Scholar]
- 61.Werner H, Knowles P. An efficient internally contracted multiconfiguration-reference configuration interaction method. J Chem Phys. 1988;89:5803–5814. [Google Scholar]
- 62.Dunning T. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J Chem Phys. 1989;90:1007–1023. [Google Scholar]
- 63.Langhoff S, Davidson E. Configuration interaction calculations on the nitrogen molecule. Int J Quantum Chem. 1974;8(1):61–72. [Google Scholar]
- 64.Simah D, Hartke B, Werner H. Photodissociation dynamics of H2S on new coupled ab initio potential energy surfaces. J Chem Phys. 1999;111(10):4523–4534. [Google Scholar]
- 65.Kosloff R. Time-dependent quantum-mechanical methods for molecular dynamics. J Phys Chem. 1988;92(8):2087–2100. [Google Scholar]
- 66.Ono S, et al. New insights into Archean sulfur cycle from mass-independent sulfur isotope records from the Hamersley Basin, Western Australia. Earth Planet Sci Lett. 2003;213:15–30. [Google Scholar]
- 67.Kaufman AJ, et al. Late Archean biospheric oxygenation and atmospheric evolution. Science. 2007;317(5846):1900–1903. doi: 10.1126/science.1138700. [DOI] [PubMed] [Google Scholar]
- 68.Halevy I, Johnston DT, Schrag DP. Explaining the structure of the Archean mass-independent sulfur isotope record. Science. 2010;329(5988):204–207. doi: 10.1126/science.1190298. [DOI] [PubMed] [Google Scholar]
- 69.DeWitt HL, et al. The formation of sulfate and elemental sulfur aerosols under varying laboratory conditions: implications for early earth. Astrobiology. 2010;10(8):773–781. doi: 10.1089/ast.2009.9455. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.