Micro-compartment specific ${\mathrm{T}}_2^{\ast }$ relaxation in the brain

Abstract

MRI at high field can be sensitized to the magnetic properties of tissues, which introduces a signal dependence on the orientation of white matter (WM) fiber bundles relative to the magnetic field. In addition, study of the NMR relaxation properties of this signal has indicated contributions from compartmentalized water environments inside and outside the myelin sheath that may be separable. Here we further investigated the effects of water compartmentalization on the MRI signal with the goal of extracting compartment-specific information. By comparing MRI measurements of human and marmoset brain at 7 T with magnetic field modeling, we show that: (1) water between the myelin lipid bilayers, in the axonal, and in the interstitial space each experience characteristic magnetic field effects that depend on fiber orientation (2) these field effects result in characteristic relaxation properties and frequency shifts for these compartments; and (3) compartmental contributions may be separated by multi-component fitting of the MRI signal relaxation (i.e. decay) curve. We further show the potential application of these findings to the direct mapping of myelin content and assessment of WM fiber integrity with high field MRI.

Introduction

At high magnetic field strength (7 T and above), in vivo MRI can visualize human brain structure in exquisite detail (Duyn et al., 2007). High field provides improved sensitivity by increasing nuclear polarization, allowing substantially better spatial definition than the about 1 mm resolution achieved with clinical “high resolution MRI”. An equally important aspect of high field MRI is increased magnetic susceptibility contrast, which is based on subtle differences in the extent to which brain tissues become magnetized by application of an external magnetic field. This type of contrast demonstrates aspects of neuroanatomical structure not otherwise visible by imaging (Abduljalil et al., 2003; Duyn et al., 2007) and has catalyzed the development of methods to map magnetic susceptibility distributions in vivo (Reichenbach, 2012). This approach has also yielded novel insights into brain diseases (Ge et al., 2008; Hammond et al., 2008; Kwan et al., 2012; Kwon et al., 2012).

The MRI signal, originating predominantly from water protons, is sensitive to spatial variations in tissue magnetic susceptibility, as these alter the local magnetic field. Such field disturbances shift the resonance frequency (indicated by Δf). Spatial variations in Δf within the MRI resolution may increase the apparent rate of MRI signal decay (also called “relaxation”), which is approximately exponential and indicated by time constant ${\mathrm{T}}_2^{\ast }$ (in contrast to T₂, which indicates relaxation in absence of susceptibility effects). Variations in Δf have been observed across the brain, and this contrast has allowed visualization of laminar structure in cortical gray matter and improved visualization of subcortical structures, such as the basal ganglia and thalamus (Duyn et al., 2007). Contrast in these brain regions has been attributed to local variations in the concentration of iron, which is paramagnetic. In brain regions were iron is the dominant contributor to image contrast, local frequency and decay rate may allow quantification of tissue iron content (Haacke et al., 2005; Ogg et al., 1999; Schweser et al., 2011b; Yao et al., 2009).

Two intriguing observations have emerged recently from susceptibility-based MRI at high field: (i) complex, non single-exponential signal decay in WM (Hwang et al., 2010; van Gelderen et al., 2012); and (ii) dependence of this decay on fiber orientation relative to the magnetic field (Bender and Klose, 2010; Denk et al., 2011; Lee et al., 2011; van Gelderen et al., 2012; Wiggins et al., 2008). These findings in WM are surprising, as many of the major fiber bundles of the brain have low iron content (Drayer et al., 1986; Fukunaga et al., 2011; Lodygensky et al., 2012). What, then, is the source of this contrast?

Several recent studies suggest that susceptibility contrast in WM originates predominantly from the myelin sheath that surrounds axons (Duyn et al., 2007; Lee et al., 2012; Liu et al., 2011; Lodygensky et al., 2012). Because of its characteristic multilayer distribution around axons, myelin is thought to slow the exchange of water across the three main tissue compartments within WM: interstitial water (between axons), intra-axonal water, and water between the myelin layers. As these compartments may be differentially sensitive to susceptibility effects originating from myelin, they may have distinct relaxation characteristics (i.e. different Δf and ${\mathrm{T}}_2^{\ast }$). Furthermore, the highly anisotropic structural organization of myelin at the cellular level may be responsible for the observed orientation dependence (He and Yablonskiy, 2009; Lee et al., 2010; Li et al., 2012). Finally, susceptibility itself may be orientation dependent, a phenomenon that is prominent in crystals with highly ordered molecular structure, and recently has also been observed in WM (Lee et al., 2010; Li et al., 2012). Thus, the study of ${\mathrm{T}}_2^{\ast }$ relaxation in WM may provide novel structural information at the micron scale, well below the nominal MRI resolution.

Despite this intriguing possibility, little is known about the magnetic properties of myelin and the extent to which its cellular and molecular level organization may contribute to compartment-specific relaxation and orientation dependence. Such knowledge is critical for extracting cellular-level information, and for interpretation of susceptibility-based imaging studies in health and disease. We therefore measured relaxation characteristics in the brains of humans and marmoset monkeys and compared with predictions based on magnetic field simulations of white matter.

We first investigated ${\mathrm{T}}_2^{\ast }$ relaxation and its orientation dependence in marmosets, who are amenable to head rotation in the bore of an MRI system (Sati et al., 2012), and whose brain has a relatively straightforward WM fiber geometry. Signal amplitude and phase evolution were measured with multi gradient echo (MGRE) MRI, and the results were analyzed by multi-component fitting of the complex (amplitude and phase) data. To investigate whether the fitted components originate from distinct water compartments within and around the axonal myelin sheath, the ${\mathrm{T}}_2^{\ast }$ relaxation curve was also simulated based on magnetic field modeling assuming an anisotropic susceptibility of the myelin sheath. Susceptibility values that resulted in the best fit were then verified with a macroscopic model of white matter fiber bundle geometry derived from diffusion tensor imaging (DTI). The putative assignment of the most rapidly relaxing component to water within the myelin sheath (so-called myelin water) was confirmed with a pulsed magnetization transfer (MT) experiment on marmoset. Lastly, the possibility of assigning relaxation components to cellular-scale water compartments was evaluated in vivo in human brain.

Materials and methods

In vivo MRI measurement of WM ${\mathrm{T}}_2^{\ast }$ relaxation in marmoset brain

Two separate MRI experiments were performed on marmosets. The first aimed at investigating dependence of white matter relaxation properties on fiber orientation relative to the magnetic field B₀, and the second at verifying the origin of the most rapidly relaxing signal component.

The NINDS/NIDCD Animal Care and Use Committee approved all animal experiments. Experiments were carried out on five common marmosets (Callithrix jacchus) aged 6.6 ± 3.2 years (mean ± standard deviation) and weighing 429 ± 37 g. The animals were sedated and anesthetized as described previously (Sati et al., 2012). MRI experiments were performed on a 7 T/30 cm USR/AVIII animal MRI scanner (Bruker-Biospin Corp., Ettlingen, Germany). In the experiment on orientation dependence, one monkey was first imaged with the body in prone position and the head looking out to the service end of magnet (sphinx position). The monkey was then repositioned with the body in supine position and imaged again with the head looking up perpendicularly to the main field (supine position). For the MGRE sequence, twenty coronal slices were acquired with an in-plane resolution of 200 × 200 μm² and slice thickness of 600 μm (field-of-view (FOV) = 38.4 mm × 38.4 mm × 24 mm and matrix = 192 × 192 × 20). Eighteen echoes (first echo time (TE₁) = 2.92 ms and echo spacing = 2.92 ms) were collected using fast flyback between GRE readout gradients. Other parameters were: repetition time (TR) = 2500 ms, flip angle (FA) = 90°, slice gap = 600 μm, number of signal averages = 8. Total scan time for the MGRE acquisition was around one hour per position.

The second MRI experiment investigated the origin of the rapidly relaxing component using a pulsed magnetization transfer (MT) experiment similar to what has been done previously to demonstrate that the high R₂ component originates from myelin water (Vavasour et al., 2000). In this MT experiment, the magnetization of protons bound to large molecules, abundant in myelin, is selectively saturated, and over time this saturation transfers to water protons due to exchange. The saturation is established with an MT pulse applied at a variable delay before the image acquisition. At short delays, the saturation primarily affects myelin water, whereas at longer delays, the saturation effect is seen to transfer from the myelin water compartment to the axonal and interstitial water.

Four monkeys were scanned in the supine position. The protocol included a T₂-weighted spin-echo three-plane localizer, a 3D B₀ field mapping sequence followed by first and second-order localized shimming, and a modified 2D MGRE sequence. For the modified MGRE sequence, a preparation MT segment (one 50 ms Gaussian pulse at 4 kHz positive offset from the water resonance with maximum B₁ of 22.5 μT) was added. The experiment was repeated with five different delay times (1 ms, 50 ms, 100 ms, 200 ms and 500 ms) between MT pulse and MGRE readout. Again, eighteen gradient echoes were acquired (TE₁ = 2.5 ms, echo spacing = 2.5 ms, TR = 2500 ms, FA = 90°). A single coronal slice was acquired (FOV = 38.4 mm × 38.4 mm, matrix = 128 × 128, slice thickness = 600 μm) with 4 signal averages to keep the total scan time under two hours.

Mapping fiber geometry in marmoset brain with DTI

To map WM fiber geometry, which was used for the magnetic field modeling, diffusion tensor imaging (DTI) MRI was performed on formalin-fixed brain from a sacrificed healthy female marmoset (age = 4 years, weight = 350 g) using procedures described previously (Sati et al., 2012). The use of ex vivo tissue was motivated by the need for long scan times to achieve high spatial resolution (150 × 150 × 150 μm) for resolving the WM fiber architecture with sufficient signal-to-noise ratio (SNR) for precise measurement of the individual fiber directions. Fractional anisotropy (FA) maps and color-encoded FA maps were generated. For the color-encoded FA maps, principal colors (red, green, and blue) were assigned to each axis of reference on the magnet, with red indicating the right–left axis; green, the antero-posterior axis; and blue, the rostro-caudal axis. In addition, the DTI data were used to generate angle maps indicating the predominant local fiber orientation (see macroscopic field simulation section below).

In vivo MRI measurement of WM ${\mathrm{T}}_2^{\ast }$ relaxation in human brain

To investigate multi-component relaxation in human brain, four healthy volunteers (three women, one man, ages 24–44 years, average age 34.7 years) and one relapsing–remitting multiple sclerosis subject (man, age 43 years) were studied under an Internal Review Board approved human protocol. MRI experiments were performed on a 7 T actively shielded human MRI scanner (Siemens, Erlangen, Germany) equipped with gradients of 70 mT/m strength and 200 T/m/s slew rate, with a birdcage-type RF transmit coil and a 32-channel receive coil. The MRI protocol included a gradient-echo three-plane localizer, a 3D B₀ field mapping sequence followed by first and second-order shimming, and MGRE acquisition for mapping the ${\mathrm{T}}_2^{\ast }$ decay. Twenty-five echoes were acquired with TE₁ = 2.84 ms, echo spacing = 2.2 ms, TR = 1 s, FA = 70 deg. Fifteen slices with 1.5 mm slice thickness and 1.5 mm gap were measured per scan, with a nominal in-plane resolution of 1 mm × 1 mm and a FOV of 240 mm × 180 mm. The slices were acquired in axial orientation and captured a section of the corpus callosum. Between 9 and 12 signal averages were acquired, with total scan time varying between 25 and 40 min.

Image reconstruction and multi-component fitting of decay curves

The MGRE datasets were analyzed using IDL (Excelis Visual Information Solutions) and Matlab (MathWorks, Inc.). For both marmoset and human data, the images from individual receiver channels were combined in a phase-sensitive manner with coil weighting factors based on the first echo of the first repetition. The phase of the images was high-pass filtered to reduce the effects of macroscopic susceptibility differences (for example at the air-tissue interfaces at the frontal sinuses) and any remaining system phase (Schweser et al., 2011a). This was done by subtracting a constant phase offset and a linear phase increment with TE, both derived from a linear fit to the low-pass filtered phase data. Low-pass filtering was achieved through convolution with a Gaussian kernel with σ = 16 voxels (or 16 mm).

Using magnitude ( ${\mathrm{T}}_2^{\ast }$-weighted) images, regions of interest (ROIs) were drawn manually in the optic radiations (human and marmoset), the splenium of the corpus callosum (human), and in the surrounding cortical gray matter (human and marmoset). After region selection and data averaging across the selected voxels, the frequency of the white matter ROI signal was referenced to that of surrounding gray matter ROIs. The resulting complex signals were fitted to a three-component model using the following equation:

$$S(t)=\sum _{i=1}^3{A}_i{e}^{-{tR}_{2,i}^{\ast }-jt2\pi \mathrm{\Delta }{f}_i}$$ (1)

where S(t) is the complex signal as function of time, j is the imaginary unit, A_i is the amplitude, Δf_i the frequency shift with respect to the local mean resonance frequency as determined by subtracting the low-pass filtered phase (see above), and ${\mathrm{R}}_{2,\mathrm{i}}^{\ast }$ the relaxation rate of the component i. To improve robustness of this 9-parameter estimation problem, a fitting procedure was followed in which in successive iterations every component in the model was optimized in turn by minimizing the sum of squares of the residue of the fit for a given range of its parameters. The search was limited to positive values for the amplitude and relaxation rates. The initial search range was ±30% of the initial guess for each parameter. After each iteration, this range was reduced by 50% to refine the search if an optimum was found within the given range; otherwise the range was increased by a factor two. The optimization was halted when no significant further residue reduction resulted. To verify that the three-component model provided the best fit, ROI-fitting was also performed using a one- and two-component model. A goodness of fit estimate was then derived, expressed as the variance of the residue compared to the variance of the data, scaled by the number of degrees of freedom (or adjusted coefficient of determination R²). Assignment of the components to water pools in the myelin, axonal and interstitial compartments was done based on the consistency of the fitted parameters (A_i, ${\mathrm{R}}_{2,\mathrm{i}}^{\ast }$, and Δf_i) with those used in the microscopic model (see below).

Three-component fitting was also performed on single pixel data, and this was more challenging than the ROI fits due to inferior SNR. To improve robustness of the pixel-by-pixel fit, a nested model was used involving successively a one-component fit, then a two-component fit, and finally a three-component fit. First, results obtained fitting a single exponential model (with A, ${\mathrm{R}}_2^{\ast }$, Δf) were used to derive the initial conditions for fitting a two-exponential model (with A₁, ${\mathrm{R}}_{2,1}^{\ast }$, Δf₁, A₂, ${\mathrm{R}}_{2,2}^{\ast }$, Δf₂). These initial conditions were defi_{ned as:} A₁ = A₂ = 0.5*A, ${\mathrm{R}}_{2,1}^{\ast }={\mathrm{R}}_{2,2}^{\ast }={0.8}^{\ast }{\mathrm{R}}_2^{\ast }$, and Δf₁ = − Δf₂ = Δf. The results of the two-exponential model were then used as initial conditions for the two long components (components 2 and 3) of the three-exponential model. For this purpose, their amplitudes were reduced by 5%, leaving 10% signal fraction as starting amplitude for component 1 (the shortest component). The ${\mathrm{R}}_2^{\ast }$ and Δf values of component 1 were set to 150 Hz and 0 Hz, respectively. In an attempt to assign the components to myelin water, axonal water, and interstitial water, they were sorted based on the fitted parameter values. First, myelin water was identified as the component with the highest ${\mathrm{R}}_2^{\ast }$. Of the remaining two components, the component with the lowest Δf was interpreted as axonal water. Note that for fibers close to parallel with the magnetic field, this classification may not be correct, as theoretical frequency differences for such fibers approach zero (see microscopic field simulations). All the pixels used in this fitting procedure were selected from brain masks drawn manually, where skull and cerebrospinal fluid inside the ventricles were excluded. Some pixels were also excluded from the edges of the brain due to poor B₀ shimming, which strongly affected signal decay.

For the marmoset data acquired with the MT experiment, the phase-corrected averaged complex signal of the ROI for the optic radiations acquired without the MT pulse was first fitted with the three-component model. ${\mathrm{R}}_2^{\ast }$ and Δf where then fixed for analysis of the MT data, for which only the amplitudes of the three components were determined from linear regression. The magnetization transfer ratios (MTRs) of the individual components i were finally computed according to:

$${\mathit{MTR}}_i=\left(1-\frac{A_{s,i}}{A_{0,i}}\right)\times 100$$ (2)

where A_s,i and A_0,i are the amplitudes of component i acquired with and without the MT pulse, respectively.

Simulation of magnetic field effects of myelin

The distinct magnetic susceptibility of myelin leads to macroscopic and microscopic field variations that affect the MRI image contrast as well as the signal decay curve at each image location. Both effects can be simulated when assuming each image element in white matter contains myelinated, cylindrical, parallel fibers at a certain orientation with respect to the magnetic field. The approach followed here was to first optimize model parameters with the microscopic simulation of signal decay and then check their validity with a macroscopic simulation of whole brain MRI phase images.

To calculate the field shift ΔB (in the direction of the applied field) originating from myelin (relative to the field in water), we used the Fourier transform (FT) of the Maxwell equations (Salomir et al., 2003) in tensor form to accommodate anisotropic magnetic susceptibility χ (Liu, 2010):

$$\mathrm{\Delta }B={FT}^{-1}\left\{\frac{1}{3}FT(\chi )H-k\frac{k^{T}FT(\chi )H}{k^2}\right\}$$ (3)

where H is the applied magnetic field (H = {0,0,H_z}), k is the wave vector (k = {k_x,k_y,k_z}), and χ is relative to water and represents a rank 2 susceptibility tensor:

$$\chi =\left(\begin{array}{ccc}{\chi }_{\perp }& 0& 0\\ 0& {\chi }_{\perp }& 0\\ 0& 0& {\chi }_{\Vert }\end{array}\right)$$ (4)

In the microscopic simulation, χ_⊥ and χ_|| represent the magnetic susceptibility perpendicular and parallel to the myelin layer normal, respectively, whereas in the macroscopic simulation, they represent voxel-averaged white matter susceptibility when fibers run perpendicular and parallel to the main magnetic field, respectively. To calculate ΔB, the laboratory frame (along H) was first transformed to the frame of the myelin fiber. The myelin magnetization χH was then calculated and back transformed to the laboratory frame:

$$\chi H=\left(\begin{array}{c}({\chi }_{\Vert }-{\chi }_{\perp })\mathit{sin}\theta \mathit{cos}\theta \mathit{cos}\varphi \\ ({\chi }_{\Vert }-{\chi }_{\perp })\mathit{sin}\theta \mathit{cos}\theta \mathit{sin}\varphi \\ {\chi }_{\perp }{\mathit{sin}}^2\theta +{\chi }_{\Vert }{\mathit{cos}}^2\theta \end{array}\right)H$$ (5)

with θ the angle of the field with the myelin layer normal and fiber direction for microscopic and macroscopic simulations respectively, and ϕ the azimuthal angle. The Fourier transform was then performed over χH, which is equivalent to FT(χ)H.

Microscopic field simulations

Microscopic field simulations at the scale of white matter fiber structure were performed to estimate signal decay characteristics, i.e. the evolution of signal amplitude and frequency evolution as a function of TE. Simulated characteristics were compared with measurements in the optic radiations of marmosets at orientations parallel and perpendicular to the magnetic field. Simulation parameters were optimized by minimizing root-mean-square differences with the measurement data.

Randomly placed, infinitely long, parallel, hollow cylinders of varying size were used. Radii varied from 1 to 3 micron (Aboitiz et al., 1992), and the g-ratio (inside myelin radius/outside radius) was 0.75 (Chatzopoulou et al., 2008). To simulate the effects of anisotropic susceptibility, interstitial water (water between the axons) susceptibility was set to zero. Although initially axons were allowed to have nonzero susceptibility, this turned out to not improve the match with the measurement data. Several iterations of axon placements were used to achieve realistic compartmental volume fractions. The final placement led to a 37% axonal compartment, a 34% extracellular compartment, and a 29% volume fraction of the myelin–water complex. As a 60% water content of the myelin sheath was assumed, these numbers are equivalent to 41%, 37%, and 20% fractional contributions to the total water signal, which is in the range of previous estimates based on combined analysis of T₁ and T₂ data (Lancaster et al., 2003). Note that the 60% water content of the myelin sheath is relative to that of the water content of axonal and interstitial space (which may be around 85%) and thus in absolute sense may be closer to estimates of around 40% derived from x-ray diffraction (Vandenheuvel, 1965). Although more precise values might affect the susceptibility estimate of myelin, they will not modify the interpretation of the three-compartment model.

Based on these compartment sizes, the corresponding T₂ values were estimated from the decay of the signal amplitude for fibers parallel to B₀. For this orientation, myelin-induced field shifts are contained within the myelin itself and therefore do not substantially affect ${\mathrm{T}}_2^{\ast }$ relaxation. Indeed, the experimentally determined frequency shifts were found to be small and to vary minimally over TE. T₂ values of 34 ms, 37 ms, and 9.5 ms were found for axonal, interstitial, and myelin water respectively. These T₂ values may have included ${\mathrm{T}}_2^{\ast }$ effects from the intra-compartment susceptibility structure, which was ignored in the simulations. The resolution of the field simulation was 20 nm, and the field of view perpendicular to fiber axes was 15 × 15 micron. Based on the observation that FT (χ) in the direction of the fiber axes (l) leads to a single nonzero value for k_l = 0, a 2D model (in planes perpendicular to l) sufficed to simulate signal decay characteristics from the 3D susceptibility distribution. Myelin water was assumed to occupy spherical compartments.

Simulation of field averaging effects from diffusion was included for fibers angled with the field, in a plane perpendicular to the fiber axis, to which susceptibility induced field variations are constrained. This was done by a random walk model in the axonal and interstitial compartments assuming an isotropic (in plane) diffusion constant D between 1.0 and 2.0 μm²/ms. As variation in this range of D did not substantially affect the simulation results, optimization of the other model parameters was first done at D = 1.5 μm²/ms, after which D was fine-adjusted to 1.3 μm²/ms, in the range of values reported in literature (Clark and Le Bihan, 2000; Yoshiura et al., 2001). The same D value was used for both compartments.

The simulations involved independently adjusting 3 susceptibility parameters to optimally match the evolution of signal amplitude and frequency. This was first done in coarse steps (of 0.05 ppm) using the measurement for fibers perpendicular to B₀. Adjustments in smaller steps (0.01 ppm) were subsequently performed around the optimum found with coarse steps. This was done again using the perpendicular fiber measurements, but now also including the frequency evolution for the parallel fiber measurement. The error range of susceptibility values was estimated by searching values resulting in a root-sum-of-squares (RMS) difference between model and data equal the mean standard deviation over the region of interest of the measurement data. Frequency shifts relative to gray matter were calculated by assuming spherical gray matter water compartments and varying the gray matter susceptibility. The latter did not affect the shape of the signal evolution over TE; rather, it resulted in a TE-independent frequency offset. It was found that a small (paramagnetic) gray matter susceptibility of 0.008 ppm led to optimal match between measurement and simulations. Similarly, an axonal susceptibility of 0 ppm was found to be optimal. Both values were used in the macroscopic simulations to confirm their validity.

Macroscopic field simulations

3D macroscopic field simulations at the scale of brain structures (millimeter) were also performed to determine whether the parameter values found with the microscopic simulations were consistent with the macroscopic features of the experimental data obtained from marmoset brain. For this purpose, a macroscopic model for the brain’s susceptibility distribution was generated from high-resolution 3D DTI data obtained from post mortem marmoset brain. This involved the following steps.

After alignment to the in vivo MRI data, DTI data were first used to identify gray matter, white matter, and non-brain regions. In white matter of the DTI data, for each of the two specific B₀ orientations used in the orientation experiment, main fiber orientation and the angles θ and ϕ were calculated. These were then used to calculate the local susceptibility based on susceptibility values found in the microscopic field simulations. Using the Fourier method described above, the macroscopic frequency for every voxel was derived from this susceptibility distribution. Fiber susceptibilities of ${\chi }_{\perp }^{\prime }$ and ${\chi }_{\Vert }^{\prime }$ perpendicular and parallel to the fiber axis were used for this purpose, with ${\chi }_{\perp }^{\prime }=\frac{1}{2}({\chi }_{\perp }+{\chi }_{\Vert }),{\chi }_{\Vert }^{\prime }={\chi }_{\perp }$. This calculation used the same volume fractions and the same assumption for the compartment shapes (infinite cylinders for axonal and interstitial water, spherical for myelin water and water in gray matter). Frequency shifts originating from the microstructure (i.e. compartment shapes at the cellular scale) were incorporating based on a recently published analytical equation for an axon in isolation (Wharton and Bowtell, 2012b). These shifts were added to the macroscopically determined frequencies.

Results

Orientation dependent, multi-component relaxation

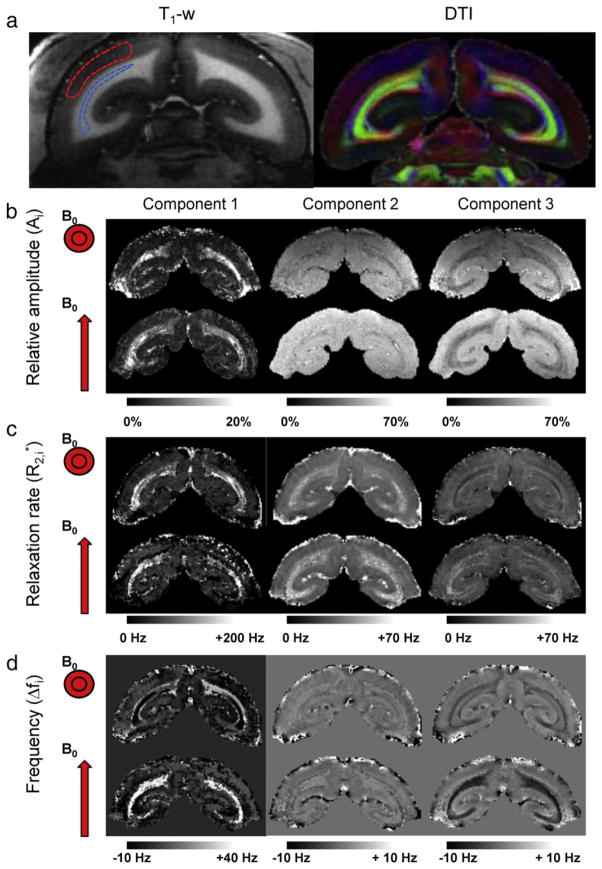
Consistent with observations in human (Hwang et al., 2010; van Gelderen et al., 2012) relaxation in WM fibers in marmoset was found to be complex. Results of curve-fitting to the average signal in the optic radiations, one of the major fiber bundles in marmoset brain, suggest the presence of three major signal components with different values of Δf and ${\mathrm{R}}_2^{\ast }$ (Table 1). Indeed, this three-component model provided a better fit when compared to one- or two-component model as judged by goodness of fit estimates (see Inline Supplementary Table S1). In addition, several of the values, most notably the frequency shifts of components 1 and 3, strongly depended on fiber orientation relative to the magnetic field. These observations were further confirmed by curve-fitting to single pixel data (Fig. 1). However, because of insufficient SNR and the presence of macroscopic field effects in some brain regions, the single pixel fits were not as robust as those on the region-averaged signal. In addition, axonal and interstitial water assignments appeared sometimes switched for fibers parallel to B₀ (Fig. 1), which is attributed to the small frequency difference between these components and the fact that fiber orientation is not a-priori known in these data. Nevertheless, the relative amplitudes of the components were similar for both fiber orientations studied (Table 1, Fig. 1), suggesting that they may represent physically meaningful quantities.

Table 1.

ROI-based 3-component fitting for white matter fibers in marmoset and human brains. Mean and standard deviation (between parentheses) across n experiments are reported for the relative amplitude A_i, relaxation rate ${\mathrm{R}}_{2,\mathrm{i}}^{\ast }$, and frequency shift Δf_i for each of the three components (i). In marmoset, orientation dependence was studied in the optic radiations (OR) showing increases in ${\mathrm{R}}_2^{\ast }$ and Δf for component 1, increases in ${\mathrm{R}}_2^{\ast }$ for component 2, and more negative Δf for component 3 when fibers are perpendicular to B₀. The component values for this orientation are confirmed by separate measurements in OR of marmoset (used for the MT experiment), and OR and splenium of the corpus callosum (SCC) in human.

	n	WM fiber	B0	A1 (%)	${\mathrm{R}}_{2,1}^{\ast }$ (Hz)	Δf1 (Hz)	A2 (%)	${\mathrm{R}}_{2,2}^{\ast }$ (Hz)	Δf2 (Hz)	A3 (%)	${\mathrm{R}}_{2,3}^{\ast }$ (Hz)	Δf3 (Hz)
Marmoset	1	OR	⊥	18.4	188.6	35.7	32.8	37.8	1.9	48.8	33.2	−6.9
	1	OR	||	21.3	134.8	−5.4	30.9	16.1	−2.5	47.9	34.7	1.1
	4	OR	⊥	20.2 (1.5)	186.4 (25.7)	25.7 (3.1)	32.7 (3.0)	32.1 (2.9)	2.5 (0.3)	47.1 (2.2)	30.6 (4.5)	−6.3 (0.5)
Human	4	OR	⊥	19.0 (1.5)	165.1 (10.7)	25.1 (1.8)	42.3 (1.6)	28.3 (2.9)	1.5 (0.3)	38.7 (1.0)	27 (2.0)	−6.0 (0.6)
	4	SCC	⊥	12.6 (1.1)	164.2 (20.1)	31.8 (2.3)	50.1 (2.4)	39.5 (1.5)	2.0 (0.2)	37.3 (2.2)	24.1 (2.9)	−4.1 (0.7)

Fig. 1.

Multi-component orientation-dependent ${\mathrm{T}}_2^{\ast }$ relaxation in marmoset brain. (a) T₁-weighted MRI (left) and DTI (right) indicate WM geometry. Red, blue, and green in DTI indicate fiber bundles along the right–left, up–down, and through-plane directions. (b–d) Results of curve fitting of the ${\mathrm{T}}_2^{\ast }$ relaxation curve for sphinx (top rows) and supine head orientation (bottom rows). Distinctly different parameter maps are obtained for each of the three components (left, middle, and right). Strong dependence on fiber orientation is observed for Δf₁ and Δf₃ (d). Reduced or negligible orientation dependence is observed for ${\mathrm{R}}_2^{\ast }$ (c) and amplitude A (b) respectively. Dashed lines in T₁-weighted MRI shown in (a) indicate typical areas in the optic radiations (blue) and GM used for ROI-based fitting (Table 1) and phase reference (red) respectively.

Inline Supplementary Table S1 can be found online at http://dx.doi.org/10.1016/j.neuroimage.2013.03.005.

Relaxation curve reproduced by magnetic field simulations

The temporal evolution of signal amplitude and Δf contrast for both parallel and perpendicular fiber orientations in marmoset could be fully explained by modeling an anisotropic susceptibility of the myelin sheath (Fig. 2a,b). The best match between measurements and simulations was found when assuming diamagnetic myelin susceptibilities of −0.06 ± 0.03 ppm (B₀ tangential to the myelin sheath) and −0.28 ± 0.10 ppm (B₀ radial to the myelin sheath). Without diffusion, a poor match between experiment and simulation was found (Fig. 2c,d). This was particularly apparent at longer TEs (TE > 20 ms) where simulations poorly matched both amplitude and frequency of the signal. Similarly, poor matching resulted when myelin susceptibility was assumed to be isotropic (Fig. A.1).

Fig. 2.

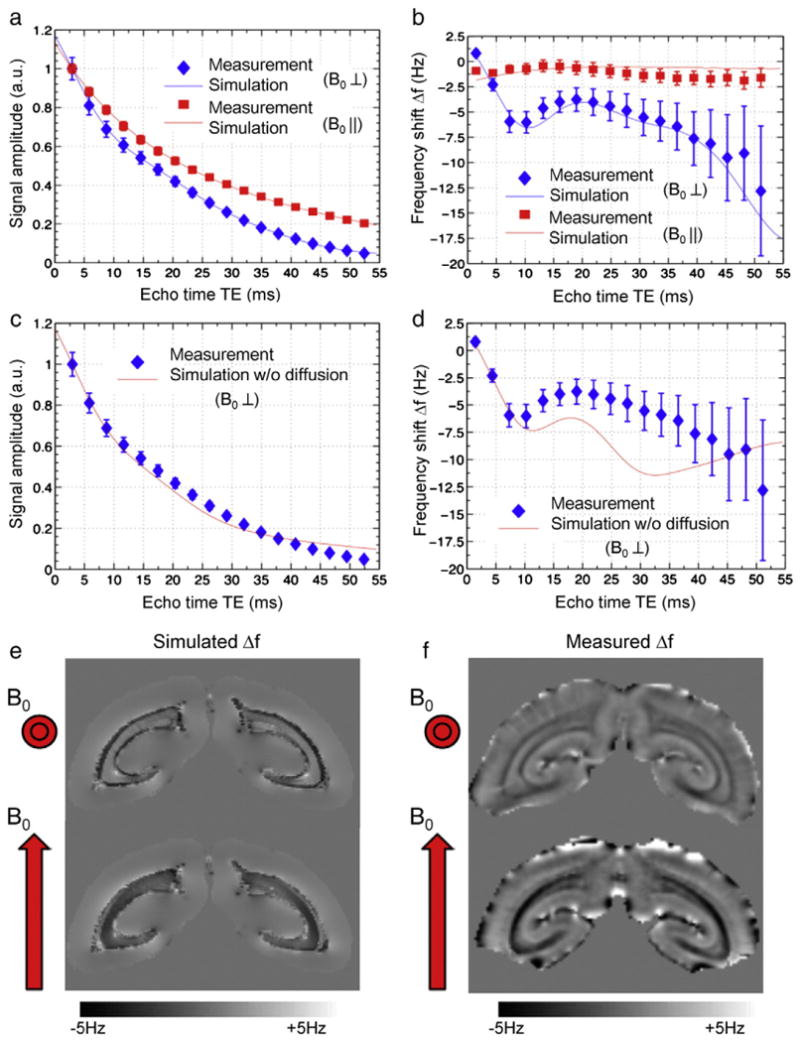
Fiber orientation-dependent signal decay and frequency shift in marmoset brain. Effect of fiber orientation on signal amplitude (a) and frequency shift Δf (b) measured in the optic radiations of marmoset at 7T. The measurement data (symbols) are well matched by the model (lines) for both orientations. This is not the case when ignoring the effects of diffusion (c,d). The simulated (e) and measured (f) macroscopic frequency shift at TE = 35 ms agree well for both head orientations, confirming that susceptibility contrast in fiber bundles can be fully explained by anisotropic susceptibility of the myelin sheath.

The validity of this model was further supported by simulations at the macroscopic (whole brain) scale, which incorporated information about fiber orientation derived from diffusion tensor imaging. Using the susceptibility values determined from the microscopic simulations, the macroscopic model (Fig. 2e) reproduced the frequency shift patterns observed in the measurements (Fig. 2f).

Compartmental assignment of components

Can the three components extracted by fitting of the decay curve be assigned to myelin water, axonal water and interstitial water? The simulations at the microscopic level indeed showed that, when fibers are angled relative to the B₀ field, relaxation properties of axonal and interstitial water are distinctly different (Fig. 3). When B₀ is perpendicular to the fiber axis (Fig. 3a,c,e), the axonal water experiences a negative frequency shift of −8 Hz, whereas interstitial water has an average frequency shift close to 0 Hz (Fig. 3e). On the other hand, when B₀ is parallel to the fiber axis (Fig. 3b,d,f), both axonal and interstitial water have a similar average frequency shift close to 0 Hz (Fig. 3f). At the same time, myelin water experiences a negative shift (−6 Hz) when B₀ is parallel to the fiber axis and a stronger positive shift (+22 Hz) when B₀ field is perpendicular. These compartmental frequency shifts and their orientation dependence are consistent with the measurement values reported in Table 1. Note that these shifts for axonal and interstitial water are not reproduced using isotropic myelin susceptibility (Fig. A.2). In addition, a broadening of the frequency distribution of interstitial water is seen for the perpendicular orientation consistent with the behavior of ${\mathrm{R}}_2^{\ast }$ for component 2 (Table 1). Based on this, we tentatively assign component 1 to myelin water, whereas components 2 and 3 can be interpreted as interstitial and axonal water, respectively.

Fig. 3.

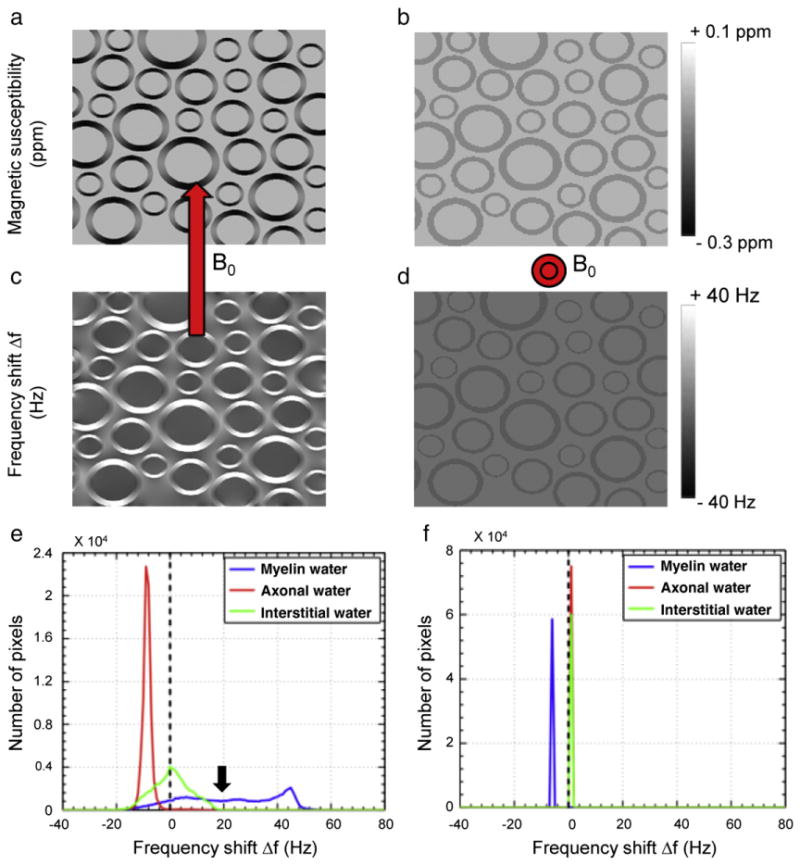
Microscopic simulations of magnetic field effects associated with anisotropic susceptibility of the myelin sheath. The microscopic distribution of susceptibility (a,b) and the resulting frequency shifts (c–f) are different for perpendicular (a,c,e) and parallel (b,d,f) fiber orientations. In addition, compartment specific frequency shifts are seen for axonal, myelin, and interstitial water for fibers perpendicular to B₀ (e). For the parallel orientation (f) frequency differences between compartments reduce or vanish.

A further confirmation of the compartment-specificity of the relaxation effects in WM is provided by the results of the MT experiment (Fig. 4). The component assigned to myelin water (component 1) indeed sees the strongest saturation effect at short MT delays, whereas components 2 and 3 experience their maximum effect at longer delays.

Fig. 4.

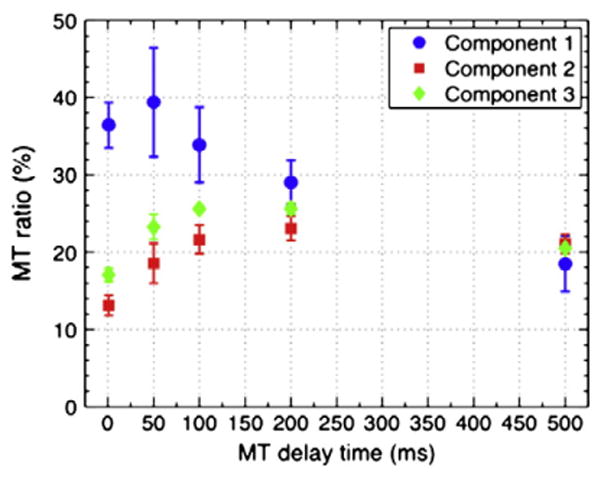
Component specific magnetization transfer (MT). At delay times below 100 ms, MT preferentially affects component 1, attributed to myelin water. At longer delay times, this preference decreases until similar MT effects are seen for all three components. This behavior is attributed to mixing between the different water pools due to diffusion and exchange. Mean values and standard deviations were calculated from ROIs located in the optic radiations across the four marmosets studied.

Multi-component relaxation in human brain

The ability to distinguish microscopic tissue compartments, and specifically that of myelin, may find application in the study of demyelinating diseases such as multiple sclerosis (MS). Demyelination is expected to most strongly affect the rapidly relaxing component, and therefore quantification of this component may help assess the impact of the disease. Previous attempts to distinguish myelin water solely based on ${\mathrm{R}}_2^{\ast }$ have had limited success, in part because they did not consider frequency shifts between the compartments (Du et al., 2007; Hwang et al., 2010). Consistent with the findings in marmoset, our fitting results of data from a healthy human (Fig. 5, Table 1, Fig. A.3) confirm the presence of three relaxation components with distinct frequencies. In addition, in an initial application to MS, there is clear evidence of abnormal signal for the three separate components (Fig. 5). This is particularly the case for the component attributed to myelin water.

Fig. 5.

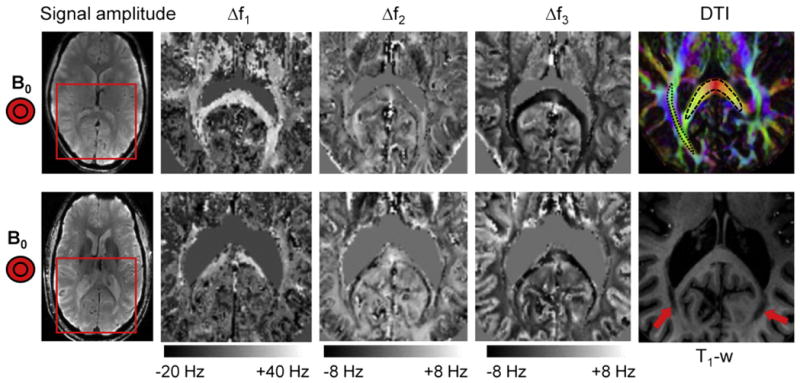
Multi-component relaxation in human brain. Multi-component fitting was performed on normal (top row) and MS brain (bottom row) in regions indicated by the red rectangle on the leftmost images (Signal amplitude at TE = 20 ms). As in marmoset brain, distinct frequency distributions are observed for the three components. The most notable differences seen in the MS brain are a strong reduction in Δf₁ (assigned to myelin water) in the major fiber bundles and in areas of major lesions (indicated with arrows on the T₁-weighted image). The complete set of fitted parameters for both subjects is provided in Fig. A.3. DTI (top right) shows fiber orientations and areas in the splenium of corpus callosum (black dashed line) and optic radiations (black dotted line) used for ROI-based fitting (Table 1).

Discussion

Compartment-specific magnetic susceptibility contrast

The results presented here confirm earlier suggestions that WM exhibits multi-component relaxation (Hwang et al., 2010; MacKay et al., 1994; van Gelderen et al., 2012) in both human and marmoset brain. The ${\mathrm{R}}_2^{\ast }$ signal decay is well described by a three-component model with distinct relaxation rates and frequencies for each component, all of which are dependent on fiber orientation relative to the magnetic field. This three-component model is also further supported by the fact that a three-component model provided a better fit (including consideration of the loss in degrees of freedom) when compared to one- or two-component model (see Inline Supplementary Table S1). Experimental data and magnetic field simulations suggest that the three components originate from distinct microscopic water pools between the myelin lamellae, in the axonal lumen, and in the interstitial (inter-axonal) space.

In analogy with previous work on R₂ and ${\mathrm{R}}_2^{\ast }$ decay in WM, the most rapidly decaying component is attributed to myelin water. Because of its slow exchange with other water molecules in the axonal and interstitial spaces, it displays characteristic MT effects. It also experiences the largest frequency shift, which is strongly positive when fibers are perpendicular to the magnetic field. Previous low field (1.5 T) MRI studies based on R₂ signal decay in WM (which is insensitive to the effects of magnetic susceptibility) found two major components with a high (~50 s⁻¹) and low (~10 s⁻¹) R₂ (MacKay et al., 1994; Whittall et al., 1997). These components have been respectively attributed to water trapped between the myelin lamellae on the one hand, and axonal and interstitial water on the other (MacKay et al., 1994; Menon and Allen, 1991). This compartment-specific relaxation in part arises from differences in water mobility in the different pools, which appear distinct due to limited myelin membrane permeability on the T₂ (= 1/R₂) time scale (Harkins et al., 2012; Kalantari et al., 2011; Stanisz et al., 1999). However, the R₂ contribution to the ${\mathrm{R}}_2^{\ast }$ effects explains only part of the difference seen between the compartments, as our measured ${\mathrm{R}}_2^{\ast }$ values are substantially (up to three-fold) larger than previously reported R₂ values.

The finding of multiple frequencies in WM signal is consistent with previous reports (Miller et al., 2010; van Gelderen et al., 2012; Wharton and Bowtell, 2012a). The current work establishes the compartmental origin of these frequencies and ties them to susceptibility effects of the myelin sheath. The relative sizes of the two longer ${\mathrm{T}}_2^{\ast }$ components appear consistent with their assignment to axonal and interstitial water, in contrast to the study by van Gelderen et al., where a very small third (longest ${\mathrm{T}}_2^{\ast }$) was found. This difference is attributed to the fact that analysis of the complex signal performed in the current study (rather than magnitude signal in the previous study) allows better distinction based on frequency differences. Inspection of the frequency evolution of the signal decay curves in both human and marmoset data (Fig. 2, Fig. A.4) furthermore supports the presence of a frequency difference between interstitial and axonal water. This can be inferred from the change in frequency with TE, in particular at TE > 30 ms, when the contribution of myelin water is small. This change cannot be explained without a frequency difference between the remaining components. Multi-component curve fitting allows assessment of relative pool sizes, something that has been elusive with previous attempts based on R₂ and R₁ contrast. Separation based on R₂ is complicated because of the small difference between the pools, whereas separation based on R₁ may not be possible because of considerable exchange between the two pools on the T₁ = 1/R₁ (i.e., seconds) time scale. The improved separation possible with ${\mathrm{R}}_2^{\ast }$ contrast is attributed to the distinctly different relaxation properties in the three compartments, in particular the difference in mean frequencies. It should be pointed out however that the single pixel fits were not as robust as the ROI-based fits. This is attributed to the fact that the multi-parametric fitting performed has significant challenges, and requires SNR well in excess of 100:1. An additional issue is the fact that frequency differences between interstitial and axonal water component is rather small for fibers parallel with B₀. Incorporation of information about the fiber orientation (from DTI data or possibly the MGRE data itself) may help this issue.

Our simulations of the magnetic field in WM based on anisotropic susceptibility of myelin predict the observed frequency and relaxation rate differences between the three pools. This finding of frequency differences from microscopic simulations is consistent with very recently published modeling work (Wharton and Bowtell, 2012a, 2012b). In extension of this previous work, the frequency behavior at long TE (>30 ms) suggests the contribution of not two but three distinct tissue compartments. Moreover, our simulations suggested that incorporation of water diffusion is necessary to accurately describe the experimental behavior (Fig. 2). For fibers perpendicular to B₀, the strongest intra-compartmental field inhomogeneities are generated for myelin and interstitial water, whereas the axonal water experiences a relatively uniform field distribution. As the effect of field inhomogeneities is only partially averaged out by diffusion (Yablonskiy and Haacke, 1994), they increase ${\mathrm{R}}_2^{\ast }$ predominantly in interstitial and myelin compartments. Thus, with increasing TE, the relative contribution of axonal water to the overall signal increases. On the other hand, the mean frequency shift within each compartment is largest for myelin water and axonal water (positive and negative respectively). As a result, the most negative frequency shifts are generally experienced at long echo times, when the signals of myelin water and interstitial water have decayed the most (Figs. 2, A.4).

Origin and strength of anisotropic magnetic susceptibility

The field modeling data suggested a strong anisotropic behavior of myelin susceptibility. Without anisotropy, frequency shifts of myelin water are largest when the magnetic field is parallel with the fiber, and no shift between axonal and interstitial water is expected (Fig. A.2), inconsistent with the observations (Table 1). We attribute the anisotropic behavior of myelin magnetic susceptibility to the highly ordered structure of the membranes making up the myelin sheath, as has been suggested previously (Lee et al., 2011; Li et al., 2012). In fact, membranes in lipoprotein particles have been found to have a susceptibility which is about 0.2 ppm more diamagnetic when oriented perpendicular to the field compared to the parallel orientation (Lounila et al., 1994). For myelin, much of the observed anisotropy may come from the linear hydrocarbon chains of the phospholipid molecules of the myelin sheath. In fact, magnetic birefringence measurements of stearic acid crystals containing 17-carbon alkyl chains have indicated an anisotropy amounting to about 10% of their volume susceptibility (Lonsdale, 1939). Assuming the latter to be around the 9.04 ppm susceptibility of water, the alkyl chains, which occupy a volume fraction of about 15–25% of the bilayer-water system of brain myelin in vivo, could contribute in the range of 0.14–0.23 ppm to its anisotropy. An additional contribution may come from the phospholipid head groups (Sakurai et al., 1980). Thus, much of the 0.22 ppm susceptibility difference between the two bi-layer orientations (estimated from the model simulations) may originate from the alkyl chains. It should be noted however that this 0.22 ppm estimate is somewhat dependent on model parameters such as compartmental volume fractions and myelin g-ratio. When translating the anisotropy of the bilayer estimated from the simulations to a value for WM (consisting of cylindrical myelin tubules, assuming a 20% volume fraction of hydrated myelin in WM, and taking into account the orientational averaging of the radially oriented carbohydrate chains when fibers are perpendicular to the field (Lounila et al., 1994)), we find a value of 0.027 ppm. This WM value is in the range of estimates based on susceptibility maps calculated from MRI phase data (Lee et al., 2011; Li et al., 2012), which range from 0.01 to 0.028 ppm. However, one needs to consider that these calculations did not take into account the selective sampling of the magnetic field because of the compartmental distribution of water, and therefore have limited accuracy.

The reported susceptibility values of −0.06 ppm and −0.28 ppm for fields tangential and radial to the myelin sheath respectively can be directly compared with those found in recently published modeling work (Wharton and Bowtell, 2012a). Converted to notations used in that work, our susceptibility values correspond to χ_I = −0.13 ppm and χ_A = −0.15 ppm, which compares to χ_I = −0.06 ppm and χ_A = −0.12 ppm in Wharton et al. The somewhat larger values found in the current work could be due to methodological differences between the studies. Notably, the current work included longer TEs, diffusion, and multiple axons in model, but on the other hand omitted effects of exchange. Nevertheless, both studies point to the importance of anisotropic myelin susceptibility to explain the ${\mathrm{T}}_2^{\ast }$ decay curve.

Contributions to WM susceptibility by compounds other than myelin

Although the finding of myelin-dominated susceptibility of WM is consistent with the virtual absence of susceptibility contrast in brains with reduced concentration of myelin (Liu et al., 2011; Lodygensky et al., 2012; Zhong et al., 2011), there may be other contributors to susceptibility contrast in the major fiber bundles. Aside from iron, which is paramagnetic but present at relatively low concentration in the main fiber bundles (Drayer et al., 1986; Fukunaga et al., 2011; Lodygensky et al., 2012) (Fig. A.5), WM constituents have a magnetic susceptibility not known to differ strongly from that of water. Some information may be gleaned from examining ${\mathrm{R}}_2^{\ast }$ and frequency values for fibers parallel to the field, when intra-compartmental field differences caused by myelin are mostly absent (He and Yablonskiy, 2009). In marmoset, ${\mathrm{R}}_2^{\ast }$ relaxivities of water in myelin, axonal, and interstitial spaces were 135 s⁻¹, 33 s⁻¹, and 16 s⁻¹, respectively (Table 1). This is substantially higher than reported values of 20–100 s⁻¹ for R₂ of myelin water (Dortch et al., 2010; MacKay et al., 1994) and 13 s⁻¹ for R₂ of overall water signal (Bartha et al., 2002; Grohn et al., 2005). Thus, it appears that sources other than myelin affect ${\mathrm{R}}_2^{\ast }$ relaxivity. Possibilities include iron and proteins whose effects on ${\mathrm{R}}_2^{\ast }$ were not modeled. Such sources should affect ${\mathrm{R}}_2^{\ast }$ more than R₂, as they likely introduce field variations whose effects on resonance frequency are not fully averaged out by diffusion. In addition, differences in concentration of iron and proteins between axonal and interstitial compartments may cause a frequency difference between compartments. However, as was verified with the simulations, such differences invariably lead to the largest frequency difference for the parallel orientation, inconsistent with the observations.

Nanostructure versus microstructure

The findings presented here also confirm the notion that MRI susceptibility effects in WM are not only affected by chemical composition, but also have strong contributions from tissue nanostructure and microstructure. First, on the sub-nanometer (angstrom) scale, molecular ordering results in orientation-dependent (or anisotropic) magnetic susceptibility. Second, on the micron-size scale of axons, the anisotropic shape of the myelin sheath results in orientation-dependent field distributions in the different water compartments, affecting their average relaxation rates and frequencies differently. The simulations suggested that both effects contribute. Specifically, the use of elongated, cylindrical shapes for the interstitial and axonal water compartments in the simulation resulted in an excellent match of signal amplitudes and frequencies along the decay curves. In contrast, the simulations suggested that the myelin water compartment needed to be close to spherical to explain the sign and the size of its frequency shift. How is this possible considering that the myelin lamellae have cylindrical shapes? The answer may be found when considering the water-accessible spaces around the myelin bilayers. At the nanometer scale, the myelin sheath is far from a cylindrical boundary, but rather has substantial irregularity. For example, there are water-accessible pits of about 0.4 nm surrounding the hydrophilic phospholipid head groups of the myelin bilayers, comparable to the ~0.2 nm dimension of the water molecule and the ~4 nm gap between adjacent layers (Vandenheuvel, 1965; Zaccai et al., 1975). Thus, a substantial portion of myelin water (possibly 10% to 20%) may sample fields within an approximately spherical boundary, affecting the pool-averaged frequency. Nevertheless, this effect appears to be too small to fully explain the observed frequency shift of myelin water.

Another possibility is a contribution of magnetization exchange to the frequency of myelin water (Shmueli et al., 2010; Zhong et al., 2008). In fact, an exchange-attributed shift for myelin water, of between 0.05 and 0.13 ppm, has been observed in previous studies (Chen et al., 1996; Doherty and Hong, 2009). However, such a contribution does not explain the observed dependence of myelin water frequency on the fiber direction relative to the magnetic field. Thus, neither MT effects nor micro-compartmental shape appear to explain the size and orientation dependence of the myelin water frequency. This remains an area for future investigation.

Brain myelin content derived from signal decay curve

Despite the small (micronscale) size of cellular water compartments in WM, which is 2–3 orders of magnitude smaller than MRI resolution, their signals can be distinguished by analyzing ${\mathrm{R}}_2^{\ast }$ signal decay. At high field, the use of ${\mathrm{R}}_2^{\ast }$, rather than the R₂ decay used in previous studies (MacKay et al., 1994; Whittall et al., 1997), substantially increases the contrast-to-noise ratio of the images (Duyn, 2012). In addition, the frequency information available with ${\mathrm{R}}_2^{\ast }$ contrast, and not with R₂ contrast, improves the discrimination between compartments because of their different frequency shifts. The results obtained in humans (Fig. 5, Table 1) suggest that identification of myelin water, and possibly a distinction between axonal and interstitial water, may have a clinical impact for demyelinating diseases such as MS.

General implications for use of susceptibility contrast

In addition to implications for the detection of myelin, our findings also have more general implications for the use of susceptibility contrast in MRI of the human brain, specifically the recently introduced methods for susceptibility mapping (Liu, 2010; Shmueli et al., 2009; Wharton and Bowtell, 2010). These methods, which are finding increasing application, use signal frequency to reconstruct magnetic susceptibility and therefore may be affected by some of the phenomena described above. Specifically, the non-spherical shape of microscopic tissue compartments introduces an orientation dependence (He and Yablonskiy, 2009), whereas the compartmentalization introduces both orientation and echo-time dependencies. Measurements at multiple echo times and a correction for fiber orientation will therefore be required to correctly estimate tissue susceptibility, especially in WM. Another confound that may affect the measured frequency shift is the fact that the relative contributions of the different compartments may vary because they may be differentially weighted by proton density, MT, and T₁ effects. Conversely, this may also offer an opportunity to improve detection of certain compartments by selectively suppressing or enhancing them with experimental manipulation of the MT and T₁ weighting.

Conclusions

Comparison of ${\mathrm{T}}_2^{\ast }$ relaxation in white matter fiber bundles with magnetic field modeling shows that water inside the myelin sheath, water in the axonal, and water in the interstitial space each experience characteristic magnetic field effects that depend on fiber orientation, and that these field effects result in characteristic relaxation properties and frequency shifts for these compartments. These compartmental contributions may be separated by multi-component fitting of the MGRE signal relaxation curve.

Appendix A. Supplementary data

Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.neuroimage.2013.03.005.