Progress in developing Poisson-Boltzmann equation solvers

Abstract

This review outlines the recent progress made in developing more accurate and efficient solutions to model electrostatics in systems comprised of bio-macromolecules and nano-objects, the last one referring to objects that do not have biological function themselves but nowadays are frequently used in biophysical and medical approaches in conjunction with bio-macromolecules. The problem of modeling macromolecular electrostatics is reviewed from two different angles: as a mathematical task provided the specific definition of the system to be modeled and as a physical problem aiming to better capture the phenomena occurring in the real experiments. In addition, specific attention is paid to methods to extend the capabilities of the existing solvers to model large systems toward applications of calculations of the electrostatic potential and energies in molecular motors, mitochondria complex, photosynthetic machinery and systems involving large nano-objects.

Introduction

The macromolecular stability, dynamics and interactions are governed by a precise balance of various forces among which the electrostatics plays a prominent role. The reason for that is the fact that practically all atoms carry partial charge and the distance between atoms are of the order of several angstroms. At such conditions, the magnitude of the electrostatic force is comparable to and even exceeds some of the other components. In addition, the main difference between electrostatics and other effects and energies is that pH- and salt-dependent effects are primarily electrostatics in origin. Taking all these facts together, indeed modeling of electrostatics is must for understanding the effects in molecular biophysics^{[14, 15, 87, 97, 164, 173, 184]}. A collection of relevant papers can be found in the special issues of the journal Communications in Computational Physics^{[118, 121, 127, 148, 156, 183]}, where various methods for modeling electrostatics and their applications in molecular biology are presented.

However, while the modeling of electrostatic potential and the corresponding energies is an important task, accomplishing the task is not trivial. In explicit-solvent models the difficulty comes from the large number of atoms (macromolecular and water atoms) which have to be simulated while computing their mutual interactions at each step of the simulation. Having in mind the long-range effect of electrostatic interactions, many existing modeling packages apply a cut-off for electrostatic interactions to speed up the calculations or utilize Particle-Mesh-Ewald (PME)^{[1, 39, 140]} and fast multipole methods (FMM)^[12] to account for it. Combining this with the potential problems of reaching convergence as the size of the system gets large, modeling large systems with explicit methods is still a challenge^[99], although significant progress has been made in developing fast molecular dynamics packages such as NAMD^{[91, 132, 170]}, GROMACS^{[137, 161]} and the development made by D.E. Shaw's group^{[62, 133, 138]}, just to mention some. On the other side of the spectrum are methods utilizing continuum electrostatics, which generally consider the water as continuum medium with a high dielectric constant, while the macromolecule(s) is treaded as a cavity with a low dielectric constant^{[15, 22, 87]}. These approaches have the advantages of modeling the system at equilibrium, so convergence is not an issue, and are much faster than the explicit methods. However, it comes with the price of losing most of the atomic details, which in cases involving specific macromolecular-water molecules interactions may lead to significant error. Hybrid methods do exist as well, but the main problem arises in modeling the interface and interactions between the explicit and implicit phases^[65].

In this review we will focus on a particular subset of continuum electrostatic approaches, namely the approaches utilizing the Poisson-Boltzmann equation (PBE) to deliver the electrostatic potential and energies (see the recent excellent review^[118]). The popularity of PBE in macromolecular electrostatics is due to the fact that it is a solution of a well-defined physical problem and that there are many computational techniques to obtain the solution of the PBE for irregularly shaped objects. Combined with the ever increasing capabilities of modern computers and computer clusters, the methods based on the PBE enjoy a huge user base and are used in many biophysical applications. Such a demand prompted many groups to develop software and web-based resources to utilize PBE method^{[144, 153, 160]}.

In our opinion, the methods utilizing PBE and the efforts in developing new or improving existing solutions can be roughly grouped into two main categories: (a) mathematical and computational developments to improve the PBE solution provided a well-defined system made of two or more dielectric regions and (b) physics-based approaches to better capture the affects originating from atomistic nature of the macromolecule(s) and water phase. Although these groups of methods share the common ultimate goal to better model macromolecular electrostatics, they differ in their emphases and approaches and will be outlined in separate sections of the review.

This review will also outline the progress made in developing faster PBE solvers capable to handling large systems^{[17, 106]} (larger than thousands of Angstroms). Such a development was inspired by the availability of atomic structures of large macromolecular assemblages typically obtained via combined efforts of X-ray crystallography and electron microscopy. Thus, recently large assemblages of mitochondria complex^[8], photosynthetic machinery^{[2, 66]}, ribosome complex^{[67, 73, 155]} and many others [41, 53] were obtained. Frequently such complexes are involved in electron or proton transfer via long and complex pathways, the revealing of which requires precise calculations of the global electrostatic map and energy components.

Mathematical and computational developments

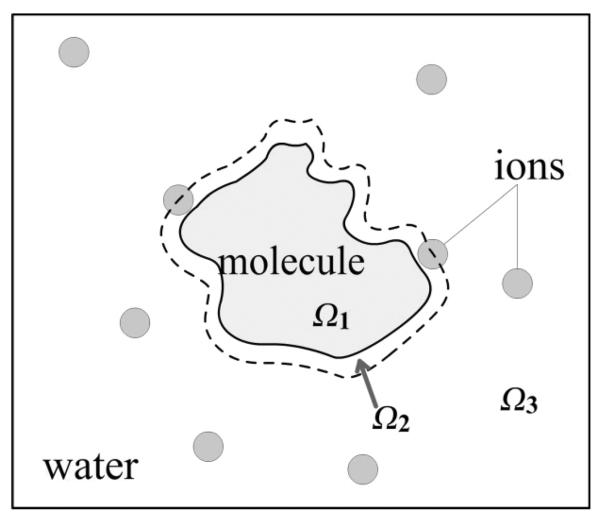
In order to proceed with this section, we need first to define the framework of the problem. Typically it is defined as the two dielectric media problem (Figure 1)^[118], where the macromolecule is consider to be a low dielectric cavity and the water phase to be a homogeneous high dielectric medium. The goal is to develop methods and computer code to deliver more accurate solution in shorter execution time. By more accurate solution one means that the numerical solution is very close to the analytical one in cases of simple geometry, when analytical solution can be obtained^[109]. It is assumed that if this is achieved, the corresponding method will be accurate even for cases for which analytical solution does not exist. Another way of defining the accuracy is as the mathematical approach that suffers the fewest assumptions. Alternatively, one can argue that if the results at various levels of resolution converge quickly to a particular value, the corresponding method is accurate^{[42, 187]}. The execution time strongly depends on the size of the system to be modeling and required resolution to achieve accurate results. For relatively small biological macromolecules of size smaller than one hundred Angstroms and resolution of about 0.5Å or 0.25Å, most existing software for solving PBE are capable of delivering the results in minute-time scale. One can argue that such a speed is sufficient even in the case of computing a large number of cases, because the jobs can be submitted in parallel over multiple processors within a computer cluster, a computational resource which nowadays is abundant. However, in cases of large systems (larger than 500Å) and the same resolution as above, the computational time can be prohibitively large which combined with the memory requirements prompts developing new computational approaches for solving the PBE.

Figure 1.

A two dielectric media problem. The space is divided into 3 regions by the molecular surface(solid curve) and the ion-exclusion layer (broken curve): Ω₁(molecule), Ω₂(stern layer) and Ω₃(water environment). Mobile ions, carrying either positive or negative charges, are only present in the water phase.

We will begin this section by outlining the most popular methods for solving the PBE for irregularly shaped dielectric cavities (macromolecules) immersed in a water phase. By doing so, we will omit the details of mathematical derivation of the corresponding equations and formulae, and will skip the discussion about the boundary conditions at the interface macromolecule-water while focusing on the basis principles of each of the methods, recent developments, and describing their capabilities. Readers interested in more detailed discussion about the boundary conditions and formulation of the corresponding equations should be directed to a recent excellent review^[118].

1. The Poisson-Boltzmann equation

The PBE is a nonlinear elliptic partial differential equation taking the form of^{[58, 85, 87]}

$$\nabla \cdot \left(\epsilon \right(\chi )\nabla \varphi (x\left)\right)-k{\left(\chi \right)}^2\sin \text{h}\left(\varphi \right(x\left)\right)=-4\pi \rho \left(\chi \right),$$ (1)

where ϕ is the electrostatic potential, ε is the spatial dielectric function, k is a modified Debye-Huckel parameter, and ρ is the charge distribution function. Eqn. (1) is simplified and linearized by approximatingsinh(ϕ) ≈ ϕ when the atoms are not highly charged. Eqn. (1) takes different forms in different space domains indicated in Figure 1.

The ultimate goal is to obtain the ϕ throughout the space and then to deliver the corresponding electrostatic energy. The electrostatic energy then can be further broken into components such as Coulomb and solvation energies and the energy of interactions between ions and permanent charges^[141]. Below we describe the basic concepts of several popular numerical approaches of solving the PBE.

2. Finite difference

Finite difference (FD) methods for solving PBE are more intuitive when comparing to others (finite element, boundary element methods, etc.). They are based on superimposition of regular rectangular Cartesian mesh over the system where the PBE will be solved. Following the standard Finite volume approach, one can deliver a formula to calculate the potential of eqn. (1) at each grid point^[36]

$$\begin{array}{cc}\hfill & {\epsilon }_{i-1∕2,j,k}[{\varphi }_{i,j,k}-{\varphi }_{i-1,j,k}]+{\epsilon }_{i+1∕2,j,k}[{\varphi }_{i,j,k}-{\varphi }_{i+1,j,k}]+\hfill \\ \hfill & {\epsilon }_{i,j-1∕2,k}[{\varphi }_{i,j,k}-{\varphi }_{i,j-1,k}]+{\epsilon }_{i,j+1∕2,k}[{\varphi }_{i,j,k}-{\varphi }_{i-1,j,k}]+\hfill \\ \hfill & {\epsilon }_{i,j,k-1∕2}[{\varphi }_{i,j,k}-{\varphi }_{i,j,k-1}]+{\epsilon }_{i,j,k+1∕2}[{\varphi }_{i,j,k}-{\varphi }_{i,j,k+1}]+\hfill \\ \hfill & {\left(\kappa h\right)}^2\sin \text{h}\left({\varphi }_{i,j,k}\right)=4\pi q_{i,j,k}∕h,\hfill \end{array}$$ (2)

where ε's are the dielectric constants at neighboring mid points, h is the uniform grid spacing in x-, y-and z- direction and q_{i, j,k}, is the total charge within the cubic volume centered at grid (i, j, k). One should iterate eqn. (2) over all grid points until desired criterion is achieved. We should mention that there are many alternative formulations of eqn. (2), depending on the approximations made. For more details interested readers are advised to see Ref^[36].

The obvious advantage of Cartesian grid method is that there is practically no computational cost for the grid generation. However, the major disadvantage is the charge distribution singularities and the artificial component of the grid energy originating from interactions between grid points carrying partial charges from the same atomic charge. However, these problems can be avoided by utilizing energy decomposition method^[141], instead of dealing with the grid energy itself.

There are various solvers that utilize FD schemes for solving the PBE, among them PBSA^{[36, 168]},MEAD^[21], MIBPB^[42], PBEQ^[92], UHBD^[122], ZAP^[134], DELPHI^[109], and many others (Table 1). Below we will briefly outline several particular implementations, which are currently among the most popular software used in the computational community.

Table 1.

Existing numerical methods and corresponding solvers for solving PBE

Program name	charge	Program available for download	URL	description
Finite Difference
PBSA (AMBER)	Part of Amber package	yes	http://ambermd.org	FD scheme offering numerous algorithms to deliver the solution; polarizable force field
DELPHI	No charge for academia	yes	http://compbio.clemson.edu/DelPhi.php	FD scheme with the Gauss-Seidel iteration technique
MEAD	No charge	yes	http://hospital.stjude.org/mead_filerequest/request.html	FD algorithm; includes modeling of a membrane as a low dielectric slab, possibly with a water-filled channel through a protein in the membrane
MIBPB	No charge	yes	http://www.math.msu.edu/~wei/MIBPB	High order discretization scheme close to the molecule-solvent interface; Dirichletto Neumann mapping method
PBEQ	Part of Charmm package	yes	http://www.charmmgui.org/?doc=input/pbeqsolver	Calculates electrostatic potential and solvation energy, in both aqueous solvent and membrane environments.
UHBD	No charge	yes	http://proiects.hits.org/mcm/projects/afwb2002/uhbd.html	Capable of solving the linear and nonlinear Poisson-Boltzmann equation using a finite-difference method; performing Brownian dynamics simulations of the association of two molecules and of the internal dynamics of a protein.
ZAP	commercial	yes	http://www.eyesopen.com/zaptk	Very fast algorithm with Gaussian representation of the dielectric constant
Finite element
APBS	No charge	yes	www.poissonboltzmann.org/apbs	An adaptive finite element Poisson–Boltzmann solver
NA	NA	no	NA	Numerical solution of the Poisson–Boltzmann equation using tetrahedral finite-element meshes
NA	NA	no	NA	FEM using Newton-Krylov iterations
NA	NA	no	NA	A mortar FEM Poisson–Boltzmann solver
NA	NA	no	NA	A first-order system least-squares FEM for the PBE
Boundary element
AFMPB	NA	yes	http://cpc.cs.qub.ac.uk/summaries/AEGB v1 0.html	An adaptive fast multipole Poisson–Boltzmann solver
FTWARE	NA	yes	http://cvcweb.ices.utexas.edu/software	Derivative boundary formulation of the problem; A smooth approximation of the molecular surface.
FFTSVD	NA	no	NA	multiscale algorithm and FFT method
FPB	commercial	no	http://continuum-dynamics.com/lib-pro-fpb.html	A hybrid approach for solving the nonlinear Poisson–Boltzmann equation

Most of the recent developments in the area of Finite Difference Poisson-Boltzmann (FDPB) method were done by Luo and co-workers (readers interested in earlier developments are advised to check the works due to Honig, Nicholls, Sharp and Gilson^{[70, 128, 146]} and McCammon group^{[56, 57, 120]}). It is outside the scope of this review to describe all contributions made by Luo's lab, since it will require writing a separate paper. Currently, the PBSA is one of the most popular PBE solvers and is incorporated into the Amber package^{[36, 168]}. Both linear and non-linear forms of PBE are supported. Among linear PBE solvers users can choose between conjugate gradient, modified incomplete Cholesky conjugate gradient (ICCG), geometric multigrid, and successive over-relaxation methods (SOR)^[167]; to solve a non-linear equation one can select either the Inexact Newton (NT) method in conjunction with modified ICCG or geometric multigrid, conjugate gradient, SOR, adaptive SOR and damped SOR^[36]. In addition to the traditional methods^[166], which were shown to yield a very high degree of consistency with DELPHI^[142], a new discretization method, the Immersed Interface method (IIM), was developed and implemented in the PBSA^[165]. In IIM the standard FD scheme is used for regular grid points, which are far from the interface. The linear equations on the irregular grid point (close to the interface) involve 27 grid points and are constructed by minimization of the local truncation error magnitude^[165]. Many other features are currently available in the PBSA as separate treatments of attractive and repulsive components to determine non-polar solvation energy^[157] and polarizable force field^[158].

The ZAP software developed by Nicholls and co-workers is part of the OpenEye library^[72]. Perhaps the most distinctive feature that makes ZAP unique among all FDPB methods is the presentation of the atoms within the macromolecule. In ZAP, the density of atom is treated as Gaussian density function, instead of more commonly used van der Waals spheres:

$${\rho }_A^G\left(r\right)=p_A\exp \left(\frac{-k{r}_A^2}{{\sigma }_A^2}\right),$$ (3)

where p_A, k and σ_A are parameters of Gaussian function and r_A is the radial distance from atom A.

The delivered density is then used for dielectric mapping and molecular surface assignment. It is emphasized that such an approach results in a smooth change of dielectric constant between solute and solvent areas. Later, in 2004, the ZAP algorithm was incorporated in the CHARMM^[34] package, providing a fast and stable smooth permittivity model for implicit salvation energy calculations in molecular dynamics simulations^[135]. Furthermore, in order to increase the speed of calculations, a modified ZAP (CHARMM-ZAPI model) was introduced as a hybrid implicit solvent model^[134]. In this model, the solute-solvent area is described by the mean of two-zone model, where the non-polar effect of the water molecules is treated implicitly with the accessible area model; electrostatic is calculated with previously described smooth permittivity based FD model for solving PBE when close to the solute and by Coulombic model when far from the solute; ions in solution and the macromolecule itself are treated explicitly with a Langevin dynamics. In comparison with totally explicit-solvent model, the two zone one, presented in ZAP, shows significant reduction in computational time, while retaining an accurate treatment of the electrostatics near the solute. At the same time, ZAP-based algorithm for predicting pKa's was used in pKa-cooperative^{[5, 129]} and it was demonstrated that it delivers accurate predictions^[174].

Matched interface and boundary method (MIB), developed by Wei and co-authors, is another novel method for delivering solution of the PBE in conjunction with the FD scheme^{[69, 180, 188, 189]}. The MIB, in addition to the standard scheme, allows for special treatment of the solute-solvent interface jump condition, which makes the original PBE well-posed at for sharp solvent-solute interfaces^{[42, 69]}. The basic idea of the MIB scheme is to define sets of regular and irregular grid points near the interface, according to the desired convergence order. Irregular grid points near the interface are calculated by applying a smooth extended potential function according to the need of a high order discretization scheme by the iterative use of lowest order jump conditions. A subgrid information given by interface and mesh intersecting position, fictitious values determined by interface, and values of function in regular grid points are implemented in finite-difference central scheme. Fictitious values of the potential function guarantee the smooth change of parameters on the solute-solvent interface, and eliminate dielectric constant discontinuity and molecular surface shape singularity. The charge source term singularity (delta function) is removed by decomposition of PBE into regular and singular part (Dirichlet to Neumann mapping method)^[180]. The MIB performance was shown to be impressive resulting in short computational time and high accuracy at a given mesh size^{[42, 69, 180]}. The MIB is the first and still the only known second-order convergent FD PB solver tested on singular protein surfaces generated by the MSMS software package^[187], although other methods such as curved boundary method^[20] and fast multipole boundary element^[11] were reported to achieve similar or even better convergence on the spherical geometry (Kirkwood model), for which the MIB method achieves six order convergence^[181].

DelPhi, originally developed in Honig lab and currently maintained in Alexov's lab, provides a numerical solution for PBE based on the finite-difference scheme coupled with unique implementations of Gauss-Seidel and SOR iterations^[109]. Among the unique DelPhi features are the abilities to assign different dielectric constants to multiple regions, to treat mixed ions with various valence^[141] and to generate the molecular surface by utilizing marching cube algorithm^[142]. Perhaps the most unique feature of DelPhi is the capability to handle geometrical objects^[142]. Recently it was extended to an atomic-style presentation of the geometrical figures along with visualizing and manipulating the sizes and shapes of the geometrical objects^[152]. As output files, the DelPhi allows for calculating not only electrostatic potential map, but also dielectric constant and ion concentration maps. Recently a parallelized DelPhi was reported which allows calculating the electrostatics of large supramolecular structures^{[106, 107]}.

It should be mentioned that DelPhi was implemented into DelPhi web server (http://compbio.clemson.edu/sapp/delphi_webserver/). It calculates electrostatic energies, electrostatic potential, ions, and dielectric maps for given macromolecule^[172]. The extra features implemented in the web server allow for fixing structural defects of the molecule and placing the missing hydrogen atoms with selected force field parameters before DelPhi calculations. The DelPhi web server utilizes Jmol viewer^[77] to visualize the corresponding structural file and, if requested, electrostatic potential can be mapped onto a molecular surface^[144]. Furthermore, the server was upgraded to generate atomic-style geometrical figures such as Parallelepiped, Sphere, Cylinder, Cone, as well as more complicated geometric objects^[153]. The position and size of the object can be manipulated by the user in real time.

3. Finite element

The Finite Element Method (FEM) is another popular mathematical technique for finding numerical approximation to the solutions of differential/integral equations by discretizing the bounded problem domain into a number of subdomains, called the finite elements, over which the solutions are approximated by local basis functions, usually low-order polynomials. This method is enjoying increasing attention from many research areas due to its capabilities of solving nonlinear equations, adaptively refining local meshes, providing rigorous convergence analysis and delivering highly accurate approximations to the exact solutions of the original equations. Following the Galerkin approach, the FEM approximates the exact solution ϕ of eqn. (1) by ${\stackrel{‒}{\varphi }}_h$, a linear combination of the basis functions u_h of a subspace V_h of the Sobolev space $H_0^1\left(\Omega \right)$, such that

$$<F\left({\stackrel{‒}{\varphi }}_h\right),{\upsilon }_h>≔{\int }_{\Omega }(\epsilon \nabla {\stackrel{‒}{\varphi }}_h)\cdot \nabla {\upsilon }_h+k^2\sin \text{h}\left({\stackrel{‒}{\varphi }}_h\right){\upsilon }_h-f{\upsilon }_{h}dx=0,\forall {\upsilon }_h\in V_h,$$ (4)

provided ${\tilde{\varphi }}_h$ is an approximation to the boundary condition $\tilde{\varphi }$, ${\stackrel{‒}{\varphi }}_h\in {\tilde{\varphi }}_h+V_h$ and f is a sum of square integrable functions approximating the right-hand side of eqn. (1).

One FEM approach to solve the PBE can be traced back to Bowen and Sharif's work^[33] and further improved by Holst and co-workers^{[13, 79, 80]}. In their work, piecewise linear finite elements over a simplex tessellation of a truncated solvent-filled sphere around the biomolecule, as well as a posteriori error estimation for adaptive mesh refinement, was used^[80]. The FEM, coupled with the inexact-Newton-multilevel methods^{[82, 84, 86]}, was implemented in the software Manifold Code (MC) aiming at solving a general class of nonlinear elliptic equations, including PBE, in 2- and 3-dimensional spaces^[78]. It wasn't until recently that the first rigorous a priori error estimate for a Galerkin-based FEM applied to solve the PBE and corresponding approximation theory were established in^{[3, 44, 81]} and briefed in^[83]. These developments are expected lead to another major improvement of FEM PBE solvers.

Motivated by the success of the MC package, the numerical routines for solving the PBE in MC libraries, as well as other algorithms developed by Baker and co-workers, were implemented in the Adaptive Poisson-Boltzmann Solver (APBS)^[17] and reported in^[13] (Table 1). The APBS now has become one of the most popular FEM solvers for PBE. Other recent developments of APBS include a) parallel computing of the PBE on massively parallel computers^{[16, 17]} by the parallel refinement techniques introduced in^[18], b) a Java-based graphical user interface (GUI) for electrostatic calculations at the membrane with APBS as a back-end for solving the PBE^[38], c) web servers and services for electrostatic calculations using APBS and PBD2PQR^[160], and d) a modular programmatic interface to the APBS library of electrostatic calculation routines^[96].

A newly developed weighted adaptive Least-Squares FEM, also known as the first-order system least-squares (FOSLS) FEM, proposed by Olson and co-workers^{[23, 40]} for solving linear Regularized PBE (RPBE) can be viewed as an alternative to traditional Galerkin and mixed Galerkin FEMs and are worth being mentioned here. In this method, the linear RPBE is reformulated into a system of first-order equations. A quadratic functional based on the residual of the system of equations is constructed. Minimizing the functional provides a posteriori error estimation for adaptive mesh refinement. This approach, when comparing to other FEMs, delivers optimal convergence for both the potential and its gradient field, yielding accurate calculations of solvation free energy and other physical quantities^[40].

Other variations of the FEM and acceleration techniques are available^[118]. Such methods include the FEM developed by Friesner and co-worker^[51], the FEM using Newton-Krylov iterations developed by Noy and co-workers^[147], and a mortar FEM developed by Zhou and co-workers^[175]. These methods could lead to new numerical approaches for interested readers and thereby are listed here for the completeness of this section.

4. Boundary element

Since a biological molecule in water can be considered as a low dielectric media immersed in a high dielectric media, the boundary of these two different mediums is the surface of the molecule, termed S (solid curve in Figure 1). Thus the entire space is divided into two different regions (note the difference with respect to the three regions shown in Figure 1: 1)Ω₁, the region inside the molecule with dielectric constant ε₁; and 2)Ω₂ and Ω₃, the regions outside the molecule with dielectric constant ε₂. In water phase, ε₁ < ε₂, and one can define the dielectric ratio, $\epsilon =\frac{{\epsilon }_2}{{\epsilon }_1}$.

Using Green's theorem, Boundary Element Method (BEM) converts the volume integral of the entire space into a surface integral on the boundary S. The electrostatic potential at position $\overrightarrow{R}$ can be obtained via the following equations (for more detail and the corresponding derivation see Refs.^{[31, 68, 93, 111, 112, 116, 143, 182]}:

(5)

(6)

where $q_{\kappa }=\frac{Q_{\kappa }}{{\epsilon }_1}$ is the normalized charge, n is the normal directed from Ω₁ to Ω₂, ${\kappa }^2=\frac{8\pi e^{2}I}{{\epsilon }_2{k}_{B}T}$ denotes the Debye-Huckel screening parameter, and $G_{\kappa }(\overrightarrow{R},\overrightarrow{\rho })=\frac{\exp [-\kappa \mid \overrightarrow{R}-\overrightarrow{\rho }\mid ]}{4\pi \mid \overrightarrow{R}-\overrightarrow{\rho }\mid }$ is the fundamental solution of the linear PBE such that $G_0(\overrightarrow{R},\overrightarrow{\rho })$ (where κ = 0) represents the fundamental solution of the Poisson equation.

By converting the volume integral into a surface integral, the number of points concerned is reduced. However, the accuracy of the surface representation is extremely important for this method. Although lots of works used different definitions of the surfaces, such as van der Waals^[131], solvent-accessible^[102], or solvent-excluded surfaces^[50], there is no clear conclusion indicating which definition is the best.

In order to make BEM suitable for electrostatic calculations for biological macromolecules, many groups have made improvements^{[20, 93, 111, 136, 163, 185]} into the original BEM work^[182] and developed different solvers (Table 1). To accelerate the Boundary Element Method, different techniques have been implemented, such as fast multipole method^{[10, 24, 31, 74, 113]}, fast Fourier transform (FFT) method^{[35, 98]}, and other methods^{[75, 114, 159]}. The largest BEM calculation for biomolecules on a serial platform was performed on a ribosome complex, which contains about 500K atoms^[45]; while the largest BEM calculation on parallel (GPU) platform was performed on multi-million atom systems^[179].

McCammon and co-workers developed a BEM solver called AFMPB^[114], which implements various techniques to accelerate calculations. At the surface generating stage, the traditional BEM discretizes the surface into triangular elements and the number of unknowns is equal to the number of triangular elements. In AFMPB, a “node-patch” approach is developed to reduce the number of unknowns on the surface, thus the calculation time is reduced as well. The idea of “node-patch” is to construct a “working” patch around each node, using the centroids of adjacent elements and midpoints of surrounding edges, and assume the unknowns are constants on each new “node-patch”. Therefore, the charge on the patch is approximated by the product of the unknown at the node and the total area of the node-patch for far-field integration, while normal quadrature method is used as in the constant or linear element method for near-field integration. After discretizing the surface in a “node-patch” way, adaptive fast multipole method and Krylov subspace method are used to speed up the iterations.

The FFTSVD is another fast BE solver^[9], developed by White and co-workers, which is aimed at modeling electrostatics problems in bio-microelectromechanical systems (bio-MEMS). The main feature of FFTSVD is that the calculation of total actions is done via a fast multiscale algorithm. This algorithm calculates the actions at different length scales separately, and then combines them together at the end. In order to calculate the long-range interactions, a FFT method is implemented to project the sources onto grids and then interpolate the results back from the grids.

The BEM section will not be completed without mentioning the contributions made by Fenley and Boschitsch. Their fast multipole linear PBE is described in series of papers^[31]. Further, they developed a nonlinear PBE solver that combines boundary element and finite difference to solve the nonlinear PBE[28, 31]. Special attention was paid on the boundary formulation^{[29, 30]}. These methods were applied to solve various problems in molecular biology^{[76, 95, 176, 177]}.

It should be mentioned as well that polarizable continuum models (PCMs) are another group of widely used implicit solvent models based on reaction-field theory and boundary-element discretization of the solute/continuum interface[100]. Typically in these methods one forces the integral equation to be satisfied exactly at a set of discrete points on the boundary, utilizing various techniques^[19]. In addition, the PCM was used to develop various models as SMD, a continuum solvation model based on the quantum mechanical charge density of a solute molecule interacting with a continuum description of the solvent^[124]; a Debye-Hückel-like screening model (DESMO)^[101]; and to calculate hydration free energies of small molecules^[126].

Other methods

Besides the three primary classes of methods mentioned above, there is another category of methods, termed the indirect approaches^[118], to achieve the numerical solution of the PBE by approximating the solutions of other equations or systems of equations in the equilibrium state, which solve the PBE as well.

One such indirect approach was introduced by Ortoleva and co-workers^[145]. A vibrational functional £ is defined as

$$\pounds \left[\varphi \right]={\int }_{\Omega }\left(\frac{1}{2}\epsilon \right(r)\mid \nabla \varphi (r){\mid }^2-4\pi {\int }_0^{\varphi \left(r\right)}d{\varphi }^{\prime }\rho (r,{\varphi }^{\prime }\left)\right)d^{3}r$$ (7)

and the PBE can be obtained by minimizing the functional (7) with respect to ϕ, provided that ϕ and its derivatives vanishes on the boundaries of the domain Ω.

Using a Largevin steepest descent approach with friction coefficient ε⁻¹

$$\epsilon \left(\overrightarrow{r}\right)\frac{\partial \varphi }{\partial t}=-\frac{\delta \pounds }{\delta \varphi }$$ (8)

to minimize the function £ yields an advection-diffusion equation

$$\frac{\partial \varphi }{\partial t}={\nabla }^2\varphi +\frac{\nabla \epsilon \cdot \nabla \varphi }{\epsilon }+\frac{4\pi F}{\epsilon }{\Sigma }_{i=1}^{N_{\text{ions}}}{Z}_i{C}_i^{\infty }\exp \left(\frac{-z_{i}F\varphi }{RT}\right)+\frac{4\pi }{\epsilon }{\Sigma }_{i=1}^{N_{\text{charges}}}{q}_i\delta (\overrightarrow{r}-{\overrightarrow{r}}_i),$$ (9)

where t is a pseudo time variable.

The Parabolic eqn (9) is solved by an operator splitting scheme, the 3D Douglas alternating direction method (ADI)^[61], such that the advection and nonlinear terms are calculated explicitly, while the diffusion term is computed implicitly with modifications described in^[55] for fast convergence and unconditional stability. The steady-state solution to eqn. (9) agrees with the solution to the PBE due to the existence and uniqueness of the solution to the PBE.

The pseudo-time indirect method described above provides a new insight and points out a new direction of numerical methods development to solve the PBE. However, the intermediate potentials obtained while the pseudo-time t evolves do not possess clear physical meaning. It is the reason that, in this method, the time increment Δt is preferred to be chosen to be as large as possible without considering the accuracy of the computed intermediate values as long as the steady state can be reached. It has been shown that extremely large Δt could be used for particular runs^[147].

Another real-time indirect method introduced by recent work of Lu, Zhou and co-workers relates the PBE to the system of Poisson-Nernst-Planck equations (PNP)^[119]

$$\frac{\partial p^i(r,t)}{\partial t}=\nabla \cdot \left(D^i\left(r\right)(\nabla p^i(r,t)+\beta \nabla (q^i\varphi (r,t)\left)p^i\right(r,t\left)\right)\right),r\in {\Omega }_s,i=1,\cdots ,k$$ (10)

$$\nabla \cdot \epsilon \left(r\right)\nabla \varphi (r,t)=-{\rho }^f\left(r\right)-{\Sigma }_i{q}^i{p}^i(r,t),r\in \Omega ,i=1,\cdots ,k$$ (11)

where pⁱ(r, t) is the density distribution function of the diffusing particles of the ith species with diffusion coefficient Dⁱ(r), ρⁱ is the fixed source charge distribution, k is the number of species, β = 1/k_BT is the inverse Boltzmann energy, and Ω_S is the solvent region consisting of one or multiple diffusive species, such as mobile ions and small diffusing molecules. It is easy to see that eqn. (11) is reduced to the PBE when assuming 1:1 ionic solution and no other diffusing species except mobile ions. Solving the PNP equation is out of the scope of this work. Interested readers are directed to^{[105, 115, 117, 119]} for more details.

The solution of the PBE can also be achieved by solving the coupled system of PNP equations at the equilibrium state

$$\nabla \cdot \left(D^i\left(r\right)(\nabla p^i(r,t)+ϐ\nabla (q^i\varphi (r,t)\left)p^i\right(r,t\left)\right)\right)=0,r\in {\Omega }_s,i=1,\cdots ,k$$ (12)

$$-\nabla \cdot \epsilon \left(r\right)\nabla \varphi (r,t)-{\rho }^f\left(r\right)-{\Sigma }_i{q}^i{p}^i(r,t)=0,r\in \Omega ,i=1,\cdots ,k$$ (13)

Eqn (12–13) extends the PBE to include more physical effects that could affect diffusion and electrostatics, and can be solved by previously described numerical methods, such as the Gauss-Seidel iteration method^{[118, 119]}.

A stochastic approach utilizing Monte Carlo methods for solving the PBE was developed by Mascagni, Fenley and co-workers and was shown that the stochastic based linear 3D PBE solvers have very low memory demands^{[64, 121, 125, 150]}. It was demonstrated that by applying series of numerical optimizations one can make the computational time of these Monte Carlo LPBE solvers competitive with deterministic methods.

Physics based approaches

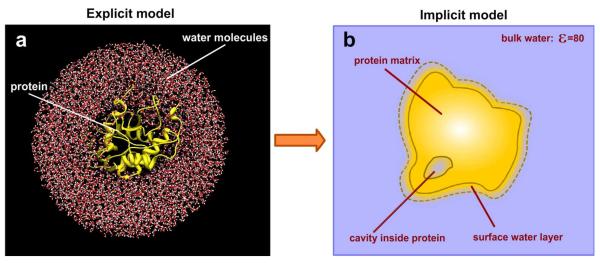
At atomistic level of detail, a system made up of macromolecules immersed in water can be considered as a multitude of atoms: atoms of water molecules and amino acids (nucleic acids). The goal of physics based continuum electrostatics is to capture (or mimic) as many atomic details as possible into the continuum model. In doing so, several considerations should be made as described below (see Figure 2). Thus, water molecules in the bulk are relatively free to move and reorient, although there is a tendency of forming dynamic water clusters. However, near to the macromolecular surface, water molecules may be involved in specific interactions with protein moiety either via hydrogen bonds or van der Walls interaction. If such interactions cannot be formed, the water molecules are considered to lose their flexibility (cannot flip among alternative hydrogen bonds). Because of that the biophysical properties of the bulk water and the shell of water molecules surrounding the macromolecule are different, especially in terms of their ability to reorient in response to the local electrostatic field, which in turn reflects their rotational polarizability. The polarizability of bulk water results in a dielectric constant of about 80, while the dielectric constant of the water shell should be lower, due to the restricted orientational and translational motions (Figure 2). Frequently small or large cavities and channels can be seen inside the macromolecule. Some of them can be filled with “crystallographic” water, i.e. water molecules with large residential time and low flexibility that can be seen in the X-ray experiment. Other cavities may appear empty either because they are filled with transient water or they may be really empty. How to treat such cavities and channels in the continuum electrostatics is the second important question that physics based approaches must address. Obviously several water molecules, either with restricted flexibility or being transient, will not have the bulk water dielectric properties, but rather should be modeled with a low dielectric constant (Figure 2). Finally, the amino acids (or nuclei acids) making up the macromolecule interior, have different polarity and different flexibility. The amino acids in the hydrophobic core are well packed and their atoms do not carry much partial charge. Thus their ability to reduce the local electrostatic field is very limited which in terms of continuum electrostatic is described as low dielectric constant. In contrast, at the macromolecular surface or around co-factors binding sites, the amino acids may not be tightly packed and may be quite polar. Because of that they are capable of responding to the local electrostatic field and such a response results in a high dielectric constant (Figure 2). These thoughts indicate that in order to mimic the effects occurring in atomistic models into the continuum models, the two dielectric-constant approaches are not sufficient and more sophisticated models are needed. In addition, the presence of mobile ions in the water phase deserves special attention and will be discussed further below.

Figure 2.

The continuum electrostatic model for macromolecule immersed in water phase. The water phase is colored in blue and the molecule is colored in orange. A. the immediate shell of water molecule surrounding the macromolecule. B. A cavity inside the macromolecule filled with water. C. The macromolecule interior with inhomogeneous dielectric distribution indicated with grey color.

1. Treating the water shell around macromolecule

Significant efforts were invested to reveal the importance of water molecules in the first level of water shell in various reactions^{[49, 52, 171, 178]}. It was demonstrated that the water molecules which are most tightly bound to the biomolecules have significantly different features as compared to the bulk water, indicating that the surface-bound water molecules need to be treated differently from the bulk phase. This prompted development of hybrid methods which combine the implicit solvent model with explicit solvent model to improve the PB calculations^{[54, 103]}. In this approach, the surface-bound water molecules are explicitly treated into the PB equation in the same manner as the macromolecule, while the rest of the water phase is considered to be continuum high dielectric medium. As alternative, from the angle of continuum electrostatics, the specific dielectric properties of the water shell surrounding the macromolecule can be modeled (a) with dielectric constant (or function) different from the bulk one or (b) the effect can be mimicked with specific definition of molecular surface.

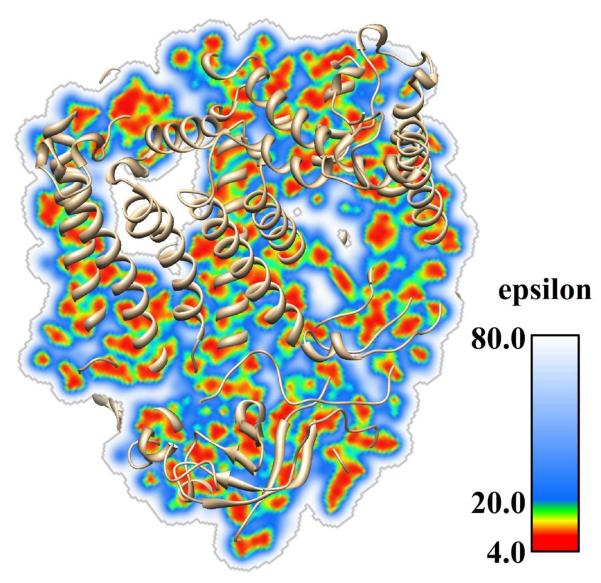
In terms of a continuum description of the surface-bound waters, there are currently only a few existing solutions. Beginning with macromolecule interior and moving toward the macromolecular surface and further into the water phase, the ability of the corresponding medium to respond to local electrostatic field constantly increases^[151]. This suggests that an appropriate continuum dielectric function would be able to provide a “correct” description of the dielectric property of the system. Such an approach was recently taken and implemented in DelPhi^[108]. This development is based on the original work of Nicholls and co-worker^[72], but uses different formalism to convert atomic densities into local dielectric constant and does not flatten out the dielectric distribution inside the macromolecule. As a result, the dielectric constant smoothly increases from the protein interior to the water phase, and the surface-bound water shell is described with a dielectric constant larger than the protein and lower than the bulk water (Fig. 3). An alternative approach was developed by Wei and co-workers^{[43, 186]} where the dielectric jump at the interface solute-solvent is replaced by interpolation function in MIBPB. With this regard, Luo and co-workers introduced a computation of dielectric boundary force based on the definition of the Maxwell stress tensor. This is followed by a new formulation of the dielectric boundary force suitable for the finite-difference Poisson-Boltzmann methods^[37].

Figure 3.

Dielectric constant distribution map for the reaction center protein calculated with Gaussian approach implemented in DelPhi. The reaction center protein is in a cartoon presentation; A plane of dielectric distribution is also shown in this figure.

As mentioned above, the molecular surface definition is another important step in any PB algorithm, either from a geometrical perspective or for mimicking the effects of surface-bound water molecules. The most commonly used definitions of boundary macromolecule-water are the solvent accessible surface (ASA) definition^[102] and the solvent excluded surface^[50] definition, which is also well known as molecular surface (MS surface). Other definitions were also used including van der Waals surface^[131], Gaussian surface^[71], spline surface^[90], geometric flow surface^[46], blobby and skin surfaces^[59]. Depending on the task and the problem studied, different surface definitions are preferred. For example, in the last round of pKa-cooperative, the best results of ZAP were reported for MS definition at epsilon of protein equal to 8.0.

2. Treating cavities and channels inside macromolecule

Another important consideration is the treatment of cavities and channels inside biomolecules. Almost all existing PBE solvers treat the macromolecular interior as a homogeneous medium and small water cavities are deleted. One plausible solution was suggested by Zhou and co-workers to use a zero probe radius in calculating epsilon map^[131]. It results in many mid grid points being assigned the high dielectric constant of water^{[4, 60]}. However, small cavities filled with a few water molecules do not have a dielectric constant of bulk water. The water molecules flexibility is much restricted and such cavities should be assigned dielectric constant higher than that of the macromolecule but lower than that of the bulk water. Based on these considerations, it seems to us, the smooth Gaussian-based dielectric constant approach is the best suited to the task. Indeed, it is currently implemented in DelPhi and provides physically adequate dielectric description of the internal macromolecular cavities (Fig. 3)^[108].

3. Treating macromolecule inhomogeneous dielectric response

Biomolecules are inhomogeneous objects, which are quite polar but not very polarizable. The polarizability and the dielectric response are not uniform and vary within the structure of the molecule^{[6, 7]}. To address this, DelPhi allows the users to assign multiple dielectric constants throughout the molecule^[141]. This feature was shown be successful for solvation energy calculation^{[141, 169]}. In principle, ZAP Gaussian function is used to assign different dielectric constant for molecules, however, in the original description of the method, the dielectric function was flattened inside the macromolecule resulting in an almost homogeneous dielectric distribution^[72]. The current Gaussian-based smooth dielectric constant function implemented in DelPhi assigns different dielectric constant at each mid grid point as can be seen in Figure 3 showing the dielectric constant distribution for a protein and water phase^[108]. Besides the two popular PB solvers mentioned above, there are other methods developed for modeling the inhomogeneous dielectric property of biomolecules^{[130, 154, 162]}.

4. Treating mobile ions in the water phase

The PBE is a continuum mean-field approach assuming point-charge ions in thermodynamic equilibrium and neglecting ion-ion correlations and fluctuations. Because of that, PBE is capable of describing only non-specific interactions between solvent and solute and may not be applicable for cases where more detailed interactions are important (highly charged macromolecule, strong coordination between solvent molecules, and specific solute-solvent interactions). For example, in the case of a highly charged surface area of a macromolecule which attracts counterions from the solvent, the calculated ionic concentration close to the surface could be non-physically large, resulting in ion packing which is physically impossible due to the finite size of ions.

Two main directions of PBE modification were undertaken: (a) explicitly include empirically calculated sizes of ions in PBE; and (b) incorporate non-electrostatic interactions in interaction potential by applying liquid-state theory^[63], which automatically accounts for ion size and includes ion correlations and electrostatic fluctuations. The main advantage of the first type approach is its simplicity, but the appropriate size of ions should be known a priori. The second approach describes the system in more detail but is more complicated and computationally expensive.

More physically reasonable ion treatment in PBE is developed throughout size modified PB theory (SMPBE) which accounts for the entropic penalty cost due to the volume exclusion and is described as “lattice-gas model”^{[26, 27]}. In this model each ion occupies a certain volume and its interactions are dictated only by non-bonded potential energy functions. The non-electrostatic (Lennard-Jones potential) interactions among the ions are modeled with a hard-wall potential energy function so that the ions cannot overlap each other. It was shown^[27] that at high ion densities located close to the surface, the short range ion–ion interactions become comparable to the Coulomb interactions and can no longer be neglected. In particular, the ion density is bounded by the maximum value which is obtained when the ions are closely packed. The standard way of including the finite size of the ions in the Poisson–Boltzmann approach is to define a narrow layer close to the surface as impenetrable to the ions. This layer is usually referred to as the Stern layer and its width is equal to the ion radius. Outside this layer the regular Poisson–Boltzmann equation is implemented. Inside the layer, the modified PBE is used instead:

$$\nabla \cdot \left(\epsilon \right(\overrightarrow{r})\nabla \varphi (\overrightarrow{r}\left)\right)+\frac{4\pi }{a^3}\frac{\sum _{i=1}^N{q}_i\exp (ϐ{\mu }_i-ϐq_i\varphi (\overrightarrow{r}\left)\right)}{1+\sum _{i=1}^N\exp (ϐ{\mu }_i-ϐq_i\varphi \overrightarrow{r}))}=-4\pi \rho \left(\overrightarrow{r}\right),$$ (14)

where a is the size of the ions (for simplicity it was assumed that positively and negatively charged ions are of the same size), μ_i is the chemical potential of ith ion, and β is 1/kT. Notice that the only difference between eqn. (14) and eqn. (1) is the 2^nd term on the left-hand side.

In recent work^[149], the finite ion size effect upon the electrostatic free energy the ion SMPBE was tested on the model of a low-dielectric spherical cavity containing a central charge in an aqueous salt solution. The results were compared with ones obtained by solving nonlinear PBE. SMPBE showed a very different electrostatic free energy than the nonlinear PBE due to the additional entropic cost of placing ions in solution. Authors pointed out that although the energy predictions of the SMPBE can be reproduced by fitting an appropriately sized Stern layer, or ion-exclusion layer to the nonlinear PBE calculations, the size of the Stern layer is difficult to estimate a priori.

In 1992 Coalson and Duncan introduced lattice-field theory (LFT)^[47], which generalizes the statistical mechanics of a classical Coulomb gas by treating gas particles of finite size. Authors suggested that short-range repulsions between pairs of simple ions can be taken into account by adding an appropriate Yukawa pair potential (V_Yukawa(r)) to the long-range Coulomb interactions between particles separated on a distance r in the simple ion gas. That is,

$$V_{Yukawa}\left(r\right)=-g^2\frac{\exp (-mr)}{r},$$ (15)

where g is a magnitude scaling constant, m is the mass of the affected particle and r is the distance to the particle. The theory was then generalized to treat gas particles of finite size^[48]. It was shown that the LFT provides a stable, flexible and efficient real-space lattice algorithm for solving the PB equation.

Other investigations focused on the importance of nonelectrostatic interactions between molecules via the excluded-volume interactions, which can be described by the Boublik-Mansoori-Carnahan-Starling-Leland (BMCSL) equation of state^{[32, 123]}. This approach accounts not only for the excluded-volume effect but also for the differences between the anion and the cation diameters. By using different equations of state, it is possible to include different types of nonelectrostatic interactions between the ions such as dispersion interactions, quadrupolar interactions, and binding interactions.

Improving the speed of the methods for solving PBE via parallelization techniques

All existing serial solvers, despite the numerical algorithms implemented, are limited to solve the PBE for relatively small biomolecules and systems due to high computational demand (time and memory) when calculating the electrostatics of large systems such as viruses^{[104, 139]}, molecular motors^[94], and systems made of nano-objects and biomolecules^[25]. For such large systems, even the fastest solvers, like the DelPhi program, typically take more than half a day to carry out the calculations at the minimum requirement of grid resolution in order to deliver accurate results. Obviously significant speedup is needed to make these serial algorithms applicable to study large macromolecular assemblages.

Acceleration of calculations can be achieved either by introducing new techniques to improve the performance of existing numerical algorithms, which is under development in cooperation with mathematicians in many labs, or by utilizing cutting-edge parallel computing techniques to make use of the computing power of multiple computing units (CPU/GPU) to fulfill the computational task in parallel by breaking the task into pieces so that each of them is carried out on one unit. In this section, we will focus on the second approach which seems more promising and easier to achieve and thereby attracts more attention due to current fast development of high performance scientific computing techniques.

As far as we know, several popular PBE solvers have been parallelized via different techniques to allow users perform intensive calculations on parallel computers/clusters, such as APBS, PBSA and DelPhi, and parallelization is taken into consideration and is under construction in other solvers, such as MIBPB. Here we will describe the parallelization techniques implemented in PBSA, APBS and DelPhi, as well as another technique developed recently^[89] in order to effectively parallelize specific numerical methods for solving the PBE.

APBS inherits the parallel refinement technique in MC adaptive multilevel finite element package, developed by Band and Holst^[18], to achieve parallel computing. We summarize the Bank-Holst parallel refinement technique here. Given P processors, a global (in the entire problem domain) approximation of the solution to the equation is calculated using an initially coarse mesh on all processors. Then, the problem domain is partitioned into P subdomains, each of which is assigned to one processor for local updating, with possible surrounding overlaps, according to the achieved approximate solution in conjunction with an a posteriori error estimator. Finally, each processor solves the same equation over the entire problem domain with the confinement that the adaptive mesh refinement only occurs within the local subdomain.

APBS extends the usage of the Bank-Holst parallel refinement technique to finite difference solvers and introduces a new “parallel focusing” algorithm by combining it with the commonly used electrostatic “focusing” technique. In the “parallel focusing” algorithm, the subset of the global mesh surrounding the area of interest is partitioned into P subdomains with overlap region spanning about 5–10% of the neighboring subdomains. Each subdomain is given to one processor for fine-scale finite difference calculation but only the results obtained on the non-overlap regions are used for assembling the fine-scale global solution, as well as calculating forces and energies^[17].

Similarly, Luo and co-workers implemented and evaluated a coarse-grained distributive method for FDPB calculations of large biomolecular systems. The method is based on the electrostatic focusing principle of decomposing a large fine-grid FDPB calculation into multiple independent FDPB calculations, each of which focuses on only a small and a specific portion (block) of the large fine grid. It was shown that given the proper settings, the distributive method was able to achieve respectable parallel efficiency with tested biomolecular systems on a loosely connected computer cluster^[88].

Parallelization of the DelPhi program, on the other hand, is achieved by noticing that the procedure for calculating electrostatics can be classified into 3 major tasks: determination of the molecular surface, calculation of the potential, and obtaining the corresponding electrostatic energies. Specific techniques were applied to parallelize each of the three major solution steps, which reflect the physical nature of the quantities being modeled. Thus, the construction of the molecular surface, being a geometrical problem, is parallelized via geometrical clustering and extended boundaries; the iterations of the electrostatic potential, being long-range, are parallelized via a combination of numerical techniques and specific software design, but without any assumptions^[106], and finally the calculations of the corresponding electrostatic energies, being independent of the geometry, are parallelized via multi-threading^[107]. It should be emphasized that the reported parallelization techniques are equally applicable for solving the linearized and nonlinear PBEs. Moreover, these techniques are not restricted to the DelPhi program. They can be easily modified and recruited by other software to parallelize the surface construction, iteration algorithms, and energy calculations. Performance of this method implemented in parallelized DelPhi is reported in refs^{[106, 107]}.

Recently, Hwang et. al^[89] introduced a new fully parallel Newton-Krylov-Schwarz (NKS) algorithm for finite element discretization of the PBE. The NKS algorithm uses an inexact Newton method with backtracking (INB) as the nonlinear solver. In each Newton step, a Krylov subspace method serves as the linear solver for the corresponding Jacobian system, in conjunction with a parallelized overlapping Schwarz method via domain decomposition serving as a preconditioner to accelerate the convergence of the linear solver^[89]. This algorithm was tested and benchmarked on examples arising from simulations of colloidal particle interactions. It was observed that this algorithm, coupled with local mesh refinement near charged particles, systematically increased the solution accuracy, as well as the accuracy of other sensitive quantities like the electrostatic force, and obtained 71% or better efficiency on up to a hundred processors for a 3D problem with 5 million unknowns^[89]. The parallel PBE solver that uses parallel adaptive mesh refinement techniques described in^[110] is under development and is expected to be a powerful and efficient simulation tool for studying three-dimensional colloidal and interfacial problems in the future.

Conclusion

In this review, current developments in the area of PBE were outlined from two different perspectives: one was mathematical and the other was physical. It was indicated that significant efforts are being invested in developing novel mathematical approaches to provide more efficient methods for solving the PBE via FDM, FEM, BEM and other numerical algorithms. Hybrid approaches were reported as well. At the same time, relatively fewer efforts were invested in better description of the physical effects originating in systems made of macromolecules immersed in water phase. Perhaps, simultaneous development reflecting the modern techniques in computer science and mathematics along with better physical models will be best approach of improving the applicability, accuracy and scalability of PBE based methods for modeling electrostatics in molecular biology.